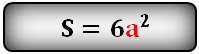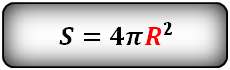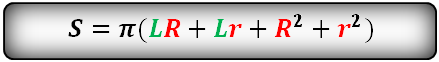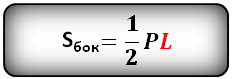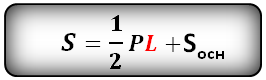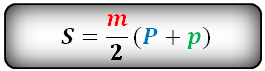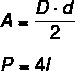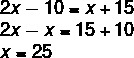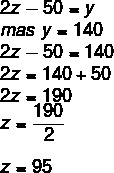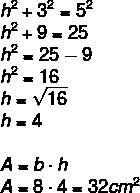Как найти sбок параллелограмма

Как найти sбок параллелограмма

Все формулы для площадей полной и боковой поверхности тел

1. Площадь полной поверхности куба

Площадь поверхности куба

a – сторона куба

Формула площади поверхности куба,(S):

Формула площади полной поверхности куба

2. Найти площадь поверхности прямоугольного параллелепипеда

Найти площадь поверхности прямоугольного параллелепипеда

a, b, c – стороны параллелепипеда

Формула площади поверхности параллелепипеда, (S):

Формула площади поверхности параллелепипеда

3. Найти площадь поверхности шара, сферы

Найти площадь поверхности шара

R – радиус сферы

π ≈ 3.14

Формула площади поверхности шара (S):

Формула площади поверхности сферы

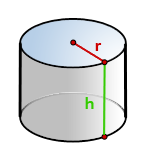
4. Найти площадь боковой и полной поверхности цилиндра

расчет площади поверхности цилиндра

r – радиус основания

h – высота цилиндра

π ≈ 3.14

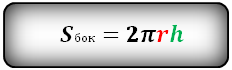
Формула площади боковой поверхности цилиндра, (Sбок):

Площадь боковой поверхности цилиндра

Формула площади всей поверхности цилиндра, (S):

Площадь всей поверхности цилиндра

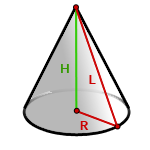
5. Площадь поверхности прямого, кругового конуса

Площадь поверхности конуса

R – радиус основания конуса

H – высота

L – образующая конуса

π ≈ 3.14

Формула площади боковой поверхности конуса, через радиус (R) и образующую (L), (Sбок):

Формула площади боковой поверхности конуса

Формула площади боковой поверхности конуса, через радиус (R) и высоту (H), (Sбок):

Формула площади боковой поверхности конуса

Формула площади полной поверхности конуса, через радиус (R) и образующую (L), (S):

Формула площади полной поверхности конуса

Формула площади полной поверхности конуса, через радиус (R) и высоту (H), (S):

Формула площади полной поверхности конуса

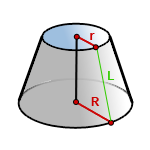
6. Формулы площади поверхности усеченного конуса

площадь поверхности усеченного конуса

R – радиус нижнего основания

r – радиус верхнего основания

L – образующая усеченного конуса

π ≈ 3.14

Формула площади боковой поверхности усеченного конуса, (Sбок):

Формула площади боковой поверхности усеченного конуса

Формула площади полной поверхности усеченного конуса, (S):

Формула площади полной поверхности усеченного конуса

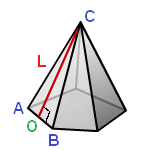
7. Площадь поверхности правильной пирамиды через апофему

Площадь поверхности правильной пирамиды

L – апофема (опущенный перпендикуляр OC из вершины С, на ребро основания АВ)

P – периметр основания

Sосн – площадь основания

Формула площади боковой поверхности правильной пирамиды (Sбок):

Формула площади боковой поверхности правильной пирамиды

Формула площади полной поверхности правильной пирамиды (S):

Формула площади полной поверхности правильной пирамиды

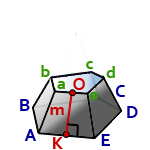
8. Площадь боковой поверхности правильной усеченной пирамиды

Площадь боковой поверхности правильной усеченной пирамиды

m – апофема пирамиды, отрезок OK

P – периметр нижнего основания, ABCDE

p – периметр верхнего основания, abcde

Формула площади боковой поверхности правильной усеченной пирамиды, (S):

Формула площади боковой поверхности правильной усеченной пирамиды

9. Площадь поверхности шарового сегмента

Площадь поверхности шарового сегмента

R – радиус самого шара

h – высота сегмента

π ≈ 3.14

Формула площади поверхности шарового сегмента, (S):

Формула площади поверхности шарового сегмента

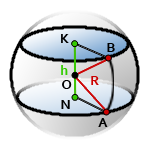
10. Площадь поверхности шарового слоя

Площадь поверхности шарового слоя

h – высота шарового слоя, отрезок KN

R – радиус самого шара

O – центр шара

π ≈ 3.14

Формула площади боковой поверхности шарового слоя, (S):

Формула площади боковой поверхности шарового слоя

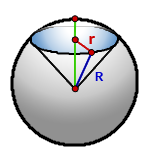
11. Площадь поверхности шарового сектора

Площадь поверхности шарового сектора

R – радиус шара

r – радиус основания конуса = радиус сегмента

π ≈ 3.14

Формула площади поверхности шарового сектора, (S):

Формула площади поверхности шарового сектора

Источник

Параллелогра́мм (др.-греч. παραλληλόγραμμον ← παράλληλος «параллельный» + γραμμή «линия») — четырёхугольник, у которого противолежащие стороны попарно параллельны, то есть лежат на параллельных прямых. (См. другие определения Перейти к разделу «Признаки параллелограмма»)

Частными случаями параллелограмма являются прямоугольник, квадрат и ромб.

Свойства[править | править код]

Противоположные стороны параллелограмма равны, а диагонали в точке пересечения делятся пополам.

Сумма углов у основания параллелограмма равна 180°

  • Противолежащие стороны параллелограмма равны.
  • Противолежащие углы параллелограмма равны.
  • Сумма углов, прилежащих к одной (любой) стороне, равна 180° (по свойству параллельных прямых).
  • Диагонали параллелограмма пересекаются, и точка пересечения делит их пополам:
    left|AOright|=left|OCright|,left|BOright|=left|ODright|.
  • Точка пересечения диагоналей является центром симметрии параллелограмма.
  • Параллелограмм диагональю делится на два равных треугольника.
  • Средние линии параллелограмма пересекаются в точке пересечения его диагоналей. В этой точке две его диагонали и две его средние линии делятся пополам.
  • Тождество параллелограмма: сумма квадратов диагоналей параллелограмма равна удвоенной сумме квадратов его двух смежных сторон: пусть
a — длина стороны AB,
b — длина стороны BC,
d_{1} и d_{2} — длины диагоналей; тогда

d_{1}^{2}+d_{2}^{2}=2(a^{2}+b^{2}).
Тождество параллелограмма есть простое следствие формулы Эйлера для произвольного четырехугольника: учетверённый квадрат расстояния между серединами диагоналей равен сумме квадратов сторон четырёхугольника минус сумма квадратов его диагоналей. У параллелограмма противоположные стороны равны, а расстояние между серединами диагоналей равно нулю.
  • Аффинное преобразование всегда переводит параллелограмм в параллелограмм. Для любого параллелограмма существует аффинное преобразование, которое отображает его в квадрат.

Признаки параллелограмма[править | править код]

Четырёхугольник ABCD является параллелограммом, если выполняется одно из следующих условий (в этом случае выполняются и все остальные):

  1. У четырёхугольника без самопересечений две противоположные стороны одновременно равны и параллельны: AB=CD,ABparallel CD.
  2. Все противоположные углы попарно равны: angle A=angle C,angle B=angle D.
  3. У четырёхугольника без самопересечений все противоположные стороны попарно равны: AB = CD, BC=DA.
  4. Все противоположные стороны попарно параллельны: AB parallel CD, BC parallel DA.
  5. Диагонали делятся в точке их пересечения пополам: {displaystyle AO=OC,BO=OD}.
  6. Сумма расстояний между серединами противоположных сторон выпуклого четырёхугольника равна его полупериметру.
  7. Сумма квадратов диагоналей равна сумме квадратов сторон выпуклого четырёхугольника: {displaystyle AC^{2}+BD^{2}=AB^{2}+BC^{2}+CD^{2}+DA^{2}}.

Площадь параллелограмма[править | править код]

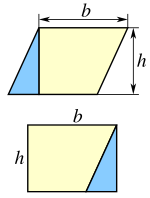
Площадь параллелограмма, выражение через высоту

Здесь приведены формулы, свойственные именно параллелограмму. См. также формулы для площади произвольных четырёхугольников.
  • Площадь параллелограмма равна произведению его основания на высоту:
{displaystyle S=bh} , где b — сторона, h — высота, проведённая к этой стороне.
  • Площадь параллелограмма равна произведению длин его смежных сторон и синуса угла между ними:
{displaystyle S=absin alpha ,}
где a и b — смежные стороны, alpha  — угол между сторонами a и b.
{displaystyle S=2cdot {sqrt {p(p-a)(p-b)(p-d)}}}
где {displaystyle p=(a+b+d)/2.}

См. также[править | править код]

  • Параллелепипед
  • Прямоугольник
  • Ромбоид
  • Параллелограмм Вариньона
  • Теорема Тебо 1

Примечания[править | править код]

Источник

Содержание:

  • Формула площади параллелограмма:
  • Формула периметра параллелограмма:

Параллелограмм

Параллелограмм – это четырёхугольник, у которого противолежащие
стороны попарно параллельны, т.е. лежат на параллельных прямых. Частными случаями параллелограмма являются прямоугольник,
квадрат и ромб.

Формула площади параллелограмма:

Площадь геометрической фигуры – часть поверхности, ограниченная замкнутым контуром данной фигуры.
Величина площади параллелограмма выражается числом заключающихся в него квадратных единиц.

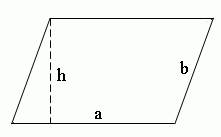
1) Площадь параллелограмма равна произведению длины его основания на длину высоты (a, h).

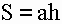
Площадь параллелограмма, формула площади параллелограмма

S – площадь параллелограмма

a – длина основания

h – длина высоты

См. также: Программа для расчета площади параллелограмма.

Формула периметра параллелограмма:

Периметр геометрической фигуры – суммарная длина границ плоской геометрической фигуры.
Периметр имеет ту же размерность величин, что и длина.

1) Периметр параллелограмма равен удвоенной сумме 2-х его смежных сторон (a, b).

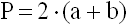
Периметр параллелограмма, формула периметра параллелограмма

P – периметр параллелограмма

a – длина 1-ой стороны параллелограмма

b – длина 2-ой стороны параллелограмма

См. также: Программа для расчета периметра параллелограмма.

236

проверенных автора готовы помочь в написании работы любой сложности

Мы помогли уже 4 396 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!

Источник

Ты параллелограммы многоугольники плоская геометрия широко изучается как обычные геометрические фигуры в нашей повседневной жизни. Мы определяем параллелограмм как многоугольник, имеющий противоположные стороны параллельны, характеристика, которая приводит к исключительным свойствам.

Частными случаями параллелограммов являются квадраты, прямоугольники и ромбы. Для каждого из этих многоугольников есть свои формулы для расчета площади и периметра.

Читайте тоже: Круг и окружность – геометрические фигуры с множеством особенностей

Элементы параллелограмма

Чтобы быть параллелограммом, многоугольник должны иметь параллельные противоположные стороны. В качестве специфических особенностей мы должны:

  • Каждый параллелограмм состоит из четырех сторон, а противоположные стороны равны параллели.

В этом случае стороны параллелограмма - это AB, BC, CD и AD. Также AB // CD (читается: AB параллельно CD), BC // AD.
В этом случае стороны параллелограмма – это AB, BC, CD и AD. Также AB // CD (читается: AB параллельно CD), BC // AD.

  • Каждый параллелограмм имеет четыре внутренних угла, а сумма этих углов всегда равен 360º.

Желтым цветом обозначены четыре внутренних угла параллелограмма.
Желтым цветом обозначены четыре внутренних угла параллелограмма.

  • У каждого параллелограмма две диагонали.

AC и BD - диагонали, обозначенные соответственно d1 и d2.
AC и BD – диагонали, обозначенные соответственно d1 и из2.

Помните, что параллелограммы частные случаи четырехугольники, поэтому есть особенности, унаследованные от этих геометрических фигур, такие как наличие двух диагоналей, четыре стороны и четыре угла, а также сумма внутреннего и внешнего углов всегда равна 360º.

Свойства параллелограмма

  • 1-й объект: Противоположные стороны параллелограмма равны, то есть имеют одинаковую меру.

AB ≡ CD и AD ≡ BC
AB ≡ CD и AD ≡ BC

  • 2-е свойство: Противоположные углы параллелограмма равны, а два последовательных угла всегда являются дополнительными (сумма равна 180 °).

Зная, что AB и CD параллельны, тогда стороны BC и AD поперечны AB и CD; следовательно, углы сформированные (w и x) являются дополнительными, поскольку они являются внутренними боковыми углами. Кроме того, можно показать, что углы x и z совпадают.

  • 3-е свойство: Диагонали параллелограмма разрезаются пополам.

Когда мы рисуем две диагонали параллелограмма, их точка встречи делит каждую на ее середины.

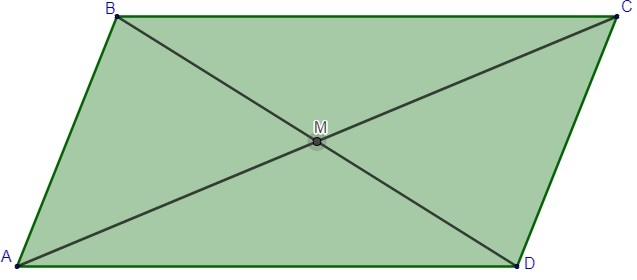
M - середина двух диагоналей.
M – середина двух диагоналей.

AM = см

BM = DM

Смотрите также: Точка, линия, плоскость и пространство: основные понятия геометрии

Площадь параллелограмма

Площадь параллелограмма, в общем, рассчитывается как произведение основания и высоты. Есть частные случаи (прямоугольники, ромбы и квадраты), которые имеют определенные формулы – они будут представлены в этом тексте – но вытекают из общей формы.

А = b.h

b: база

h: высота

Периметр параллелограмма

О периметр дан кем-то сумма со всех сторон. Поскольку параллелограмм обычно имеет две равные стороны, его периметр можно определить следующим образом:

п = 2 (а + б)

Частные случаи параллелограммов

Как мы знаем, по определению, чтобы быть параллелограммом, многоугольник должен иметь параллельные стороны. Есть три четырехугольника, которые рассматриваются как частные случаи параллелограмма: прямоугольник, ромб и квадрат.

  • Квадратный

мы называем квадратный четырехсторонний многоугольник с четырьмя сторонами и четырьмя равными углами – каждый угол равен точно 90 градусам. Поскольку квадрат является параллелограммом, все свойства действительны для квадрата.

Площадь квадрата и его периметр рассчитываются аналогично тому, как это делается с параллелограммом, но поскольку все стороны квадрата равны, мы можем представить площадь и периметр квадрата следующим образом:

A = l²

P = 4,1

  • Прямоугольник

О прямоугольник это параллелограмм, у которого есть все совпадающие углы. Он получил такое название, потому что все твои углы прямые, то есть четыре угла составляют 90º. Область прямоугольника идентична области параллелограмма, но мы можем рассматривать вертикальную сторону как высоту, в конце концов, она перпендикулярна основанию.

А =а.б

P = 2 (а + б)

  • Алмаз

О алмаз это параллелограмм, у которого все стороны равны. Учтите, что ограничений по углам нет, они могут быть разными или нет. В отличие от предыдущих примеров, Расчет площади алмаза производится по его диагоналям. Также существует очень важная взаимосвязь между диагоналями алмаза и его стороной.

D: большая диагональ

d: малая диагональ

l: сторона

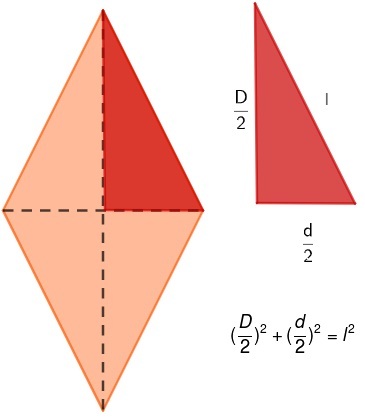
Для любого ромба мы знаем, что диагонали пересекаются в средней точке, образуя четыре прямоугольных треугольника. Анализируя один из этих треугольников, можно увидеть Пифагорейские отношения между стороной и половиной каждой из диагоналей.

Также доступ: длина окружности и площадь круга

Связь параллелограммов

Важно понимать определение параллелограмма, чтобы не было никаких сложностей при классификации. Всегда полезно помнить, что каждый параллелограмм – четырехугольник, но не каждый четырехугольник – параллелограмм.

Мы также можем утверждать, что каждый прямоугольник, каждый квадрат и каждый ромб являются параллелограммами. Более того, сравнивая частные случаи параллелограммов, мы можем увидеть другую взаимосвязь, потому что квадрат он имеет конгруэнтные углы, что является определением прямоугольника, а также конгруэнтные стороны, что является определением алмаз. Как следствие, можно сказать, что каждый квадрат – это прямоугольник, а также ромб.

Большой параллелограмм, образованный другими геометрическими фигурами.
Большой параллелограмм, образованный другими геометрическими фигурами.

решенные упражнения

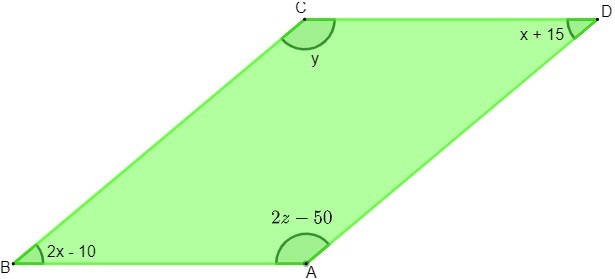
Вопрос 1 – Зная, что рисунок ниже представляет собой параллелограмм, каковы будут значения x, y и z соответственно?

а) 40,140 и 180

б) 30, 100 и 100

в) 25, 140 и 95

г) 30, 90 и 145

д) 45, 55 и 220

разрешение

1 шаг: Используя свойство параллелограмма, мы знаем, что противоположные углы равны. При анализе изображения удобнее использовать это свойство при углах при вершинах B и D, так как они имеют одно и то же неизвестное.

2-й шаг: Зная, что последовательные углы являются дополнительными и что x = 25, можно найти значение y.

3 шаг: Поскольку углы вершин C и A противоположны, они совпадают, поэтому мы можем найти значение z.

Альтернатива C.

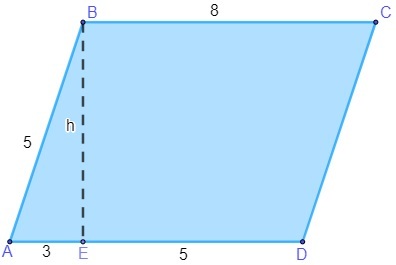
Вопрос 2 – Вычислите площадь параллелограмма (стороны, измеренные в сантиметрах) ниже.

а) 16 см²

б) 32 см²

в) 8 см²

г) 64 см²

д) 40 см²

разрешение

Чтобы найти площадь параллелограмма, сначала необходимо найти значение h. Обратите внимание, что треугольник AEB – это прямоугольник гипотенузы, равный 5, поэтому мы можем применить теорему Пифагора, чтобы найти значение h.

Альтернатива Б.

Рауль Родригес де Оливейра
Учитель математики

Источник: Бразильская школа – https://brasilescola.uol.com.br/matematica/paralelogramos.htm

Источник
  1. Главная
  2. Справочники
  3. Справочник по геометрии 7-9 класс
  4. Площадь
  5. Площадь параллелограмма

Назовем одну из сторон параллелограмма основанием, а перпендикуляр, проведенный из любой точки противоположной стороны к прямой, содержащей основание, – высотой параллелограмма.

Теорема

Площадь параллелограмма равна произведению его основания на высоту

Доказательство

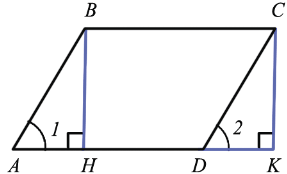
Дано: ABCD – параллелограмм, S – площадь ABCD, ВН и СК – высоты

Доказать: S = AD BH

Доказательство:

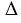
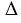
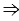
Докажем, что площадь прямоугольника НВСК также равна S. Рассмотрим трапецию АВСК: с одной стороны, она составлена из параллелограмма ABCD и треугольника DCK. Но с другой стороны, она составлена из прямоугольника НВСК и треугольника АВН. Но DCK = АВН (по гипотенузе (АВ = CD, т.к. они противоположные стороны параллелограмма) и острому углу(углы 1 и 2 как соответственные углы при пересечении параллельных прямых АВ и CD секущей AD)), а равные фигуры имеют равные площади, поэтому их площади равны.

площадь параллелограмма ABCD и прямоугольника НВСК также равны, т.е. площадь прямоугольника НВСК равна S. По теореме площадь прямоугольника равна произведению его смежных сторон, т.е. S = BC BH, а так как BC = AD, то S = AD BH. Теорема доказана

Советуем посмотреть:

Понятие площади многоугольника

Площадь квадрата

Площадь прямоугольника

Площадь треугольника

Площадь трапеции

Теорема Пифагора

Теорема, обратная теореме Пифагора

Формула Герона

Площадь


Правило встречается в следующих упражнениях:

7 класс

Задание 459,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник

Задание 460,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник

Задание 464,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник

Задание 502,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник

Задание 503,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник

Задание 510*,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник

Задание 832,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник

Задание 841,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник

Задание 1021,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник

Задание 1241,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник

Источник

Добавить комментарий