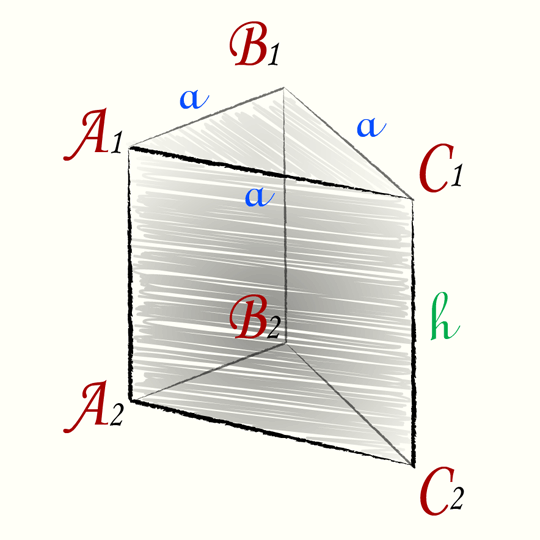
В данной публикации мы рассмотрим, как можно вычислить площадь поверхности правильной призмы разных видов (треугольной, четырехугольной и шестиугольной), а также, разберем примеры решения задач для закрепления материала.
Правильная призма – это прямая призма, основанием которой является правильный многоугольник. А прямой фигура является в том случае, если ее боковые грани перпендикулярны основаниям.
-
Формула площади правильной призмы
- 1. Общая формула
-
2. Площадь правильной треугольной призмы
- 3. Площадь правильной четырехугольной призмы
- 4. Площадь правильной шестиугольной призмы
- Примеры задач
Формула площади правильной призмы
1. Общая формула
Площадь (S) полной поверхности призмы равна сумме площади ее боковой поверхности и двух площадей основания.
Sполн. = Sбок. + 2Sосн.
Площадь боковой поверхности прямой призмы равняется произведению периметра ее основания на высоту.
Sбок. = Pосн. ⋅ h
Формула периметра и площади основания правильной призмы зависит от вида многогранника. Ниже мы рассмотрим самые популярные виды.
2. Площадь правильной треугольной призмы
Основание: равносторонний треугольник.
| Площадь | Формула |
| основание |  |
| боковая поверхность | Sбок. = 3ah |
| полная |  |
microexcel.ru
3. Площадь правильной четырехугольной призмы
Основание: квадрат.
| Площадь | Формула |
| основание | Sосн. = a2 |
| боковая поверхность | Sбок. = 4ah |
| полная | Sполн. = 2a2 + 4ah |
microexcel.ru
Примечание: Если высота правильной четырехугольной призмы равняется длине стороны ее основания, значит мы имеем дело с кубом, площадь одной грани которого равна a2. А так как все шесть граней куба равны, то полная площадь его поверхности равняется 6a2.
4. Площадь правильной шестиугольной призмы
Основание: правильный шестиугольник
| Площадь | Формула |
| основание |  |
| боковая поверхность | Sбок. = 6ah |
| полная |  |
microexcel.ru
Примеры задач
Задание 1:
Сторона правильной треугольной призмы равна 6 см, а ее высота – 8 см. Найдите полную площадь поверхности фигуры.
Решение:
Воспользуемся подходящей формулой, подставив в нее известные нам значения:
Задание 2:
Площадь полной поверхности правильной шестиугольной призмы составляет 400 см2. Найдите ее высоту, если известно, что сторона основания равна 5 см.
Решение:
Выведем выражение для нахождения высоты призмы из формулы ее полной площади:
На чтение 4 мин Просмотров 61.8к. Опубликовано 13 февраля, 2019
Здесь вы найдёте: Объем правильной треугольной призмы понятие, Объем призмы треугольной формула нахождения, Площадь треугольной призмы
Треугольная призма — это трехмерное тело, образованное соединением прямоугольников и треугольников. В этом уроке вы узнаете, как найти размер внутри (объем) и снаружи (площадь поверхности) треугольной призмы.
Содержание
- Призма треугольная — определение
- Элементы треугольной призмы
- Виды треугольных призм
- Прямая треугольная призма
- Наклонная треугольная призма
- Основные формулы для расчета треугольной призмы
- Объем треугольной призмы
- Площадь боковой поверхности призмы
- Площадь полной поверхности призмы
- Правильная призма — прямая призма, основанием которой является правильный многоугольник.
- Пример призмы
- Задачи на расчет треугольной призмы
Призма треугольная — определение
Треугольная призма — это пятигранник, образованный двумя параллельными плоскостями, в которых расположены два треугольника, образующих две грани призмы, и оставшиеся три грани — параллелограммы, образованные со-сторонами треугольников.
Элементы треугольной призмы
Треугольники ABC и A1B1C1 являются основаниями призмы.
Четырехугольники A1B1BA, B1BCC1 и A1C1CA являются боковыми гранями призмы.
Стороны граней являются ребрами призмы (A1B1, A1C1, C1B1, AA1, CC1, BB1, AB, BC, AC), всего у треугольной призмы 9 граней.
Высотой призмы называется отрезок перпендикуляра, который соединяет две грани призмы (на рисунке это h).
Диагональю призмы называется отрезок, который имеет концы в двух вершинах призмы, не принадлежащих одной грани. У треугольной призмы такой диагонали провести нельзя.
Площадь основания — это площадь треугольной грани призмы.
Площадь боковой поверхности призмы — это сумма площадей четырехугольных граней призмы.
Виды треугольных призм
Треугольная призма бывает двух видов: прямая и наклонная.
У прямой призмы боковые грани прямоугольники, а у наклонной боковые грани — параллелограммы (см. рис.)
Прямая треугольная призма
Призма, боковые ребра которой перпендикулярны плоскостям оснований, называется прямой.
Наклонная треугольная призма
Призма, боковые ребра которой являются наклонными к плоскостям оснований, называется наклонной.
Основные формулы для расчета треугольной призмы
Объем треугольной призмы
Чтобы найти объем треугольной призмы, надо площадь ее основания умножить на высоту призмы.
Объем призмы = площадь основания х высота
или
V=Sосн . h
Площадь боковой поверхности призмы
Чтобы найти площадь боковой поверхности треугольной призмы, надо периметр ее основания умножить на высоту.
Площадь боковой поверхности треугольной призмы = периметр основания х высота
или
Sбок=Pосн.h
Площадь полной поверхности призмы
Чтобы найти площадь полной поверхности призмы, надо сложить ее площади оснований и площадь боковой поверхности.
так как Sбок=Pосн.h, то получим:
Sполн.пов.=Pосн.h+2Sосн
Правильная призма — прямая призма, основанием которой является правильный многоугольник.
Свойства призмы:
Верхнее и нижнее основания призмы – это равные многоугольники.
Боковые грани призмы имеют вид параллелограмма.
Боковые ребра призмы параллельные и равны.
Совет: при расчете треугольной призмы вы должны обратить внимание на используемые единицы. Например, если площадь основания указана в см2, то высота должна быть выражена в сантиметрах, а объем — в см3 . Если площадь основания в мм2, то высота должна быть выражена в мм, а объем в мм3 и т. д.
Пример призмы
В этом примере:
— ABC и DEF составляют треугольные основания призмы
— ABED, BCFE и ACFD являются прямоугольными боковыми гранями
— Боковые края DA, EB и FC соответствуют высоте призмы.
— Точки A, B, C, D, E, F являются вершинами призмы.
Задачи на расчет треугольной призмы
Задача 1. Основанием прямой треугольной призмы служит прямоугольный треугольник с катетами 6 и 8, боковое ребро равно 5. Найдите объем призмы.
Решение: Объем прямой призмы равен V = Sh, где S — площадь основания, а h — боковое ребро. Площадь основания в данном случае это площадь прямоугольного треугольника (его площадь равна половине площади прямоугольника со сторонами 6 и 8). Таким образом, объём равен:
V = 1/2 · 6 · 8 · 5 = 120.
Задача 2.
Через среднюю линию основания треугольной призмы проведена плоскость, параллельная боковому ребру. Объем отсеченной треугольной призмы равен 5. Найдите объем исходной призмы.
Решение:
Объём призмы равен произведению площади основания на высоту: V = Sосн ·h.
Треугольник, лежащий в основании исходной призмы подобен треугольнику, лежащему в основании отсечённой призмы. Коэффициент подобия равен 2, так как сечение проведено через среднюю линию (линейные размеры большего треугольника в два раза больше линейных размеров меньшего). Известно, что площади подобных фигур соотносятся как квадрат коэффициента подобия, то есть S2 = S1k2 = S122 = 4S1.
Площадь основания всей призмы больше площади основания отсечённой призмы в 4 раза. Высоты обеих призм одинаковы, поэтому объем всей призмы в 4 раза больше объема отсечённой призмы.
Таким образом, искомый объём равен 20.
Площадь боковой поверхности правильной треугольной призмы
Боковая поверхность правильной треугольной призмы складывается из площади трех ее боковых граней:
Площадь боковой поверхности правильной треугольной призмы
Три боковых стороны представляют из себя прямоугольники со сторонами a и h
Площадь боковой поверхности правильной треугольной призмы есть сумма трех площадей боковых граней.
[ S_{призмы} = 3S_{бок} ]
Подставим сюда формулу площади прямоугольника и получим:
[ S_{бок.призмы} = 3ah ]
Вычислить, найти площадь боковой поверхности правильной треугольной призмы
площадь боковой поверхности правильной треугольной призмы |
стр. 336 |
|---|
1.Теорема
Боковая поверхность прямой призмы равна произведению периметра основания на высоту призмы, т. е. на длину бокового ребра.
Дано: прямая n-угольная призма
Доказать: Sбок=p? h.
Доказательство:
Прямой называется призма, у которой боковые ребра перпендикулярны основаниям, т. е. боковые грани прямой призмы будут являться прямоугольниками. Площадь боковой поверхности призмы равна сумме площадей боковых граней призмы Sбок=S1+ S2+ S3+…+Sn. Площадь боковой грани определяется как площадь прямоугольника и равна произведению длины основания на высоту. Основания этих прямоугольников будут составлять многоугольник, являющийся основанием призмы, а высоты являются боковыми ребрами призмы. Отсюда: Sбок=a1?h+ a2?h + a3?h + .+an?h=( a1+ a2 +a3 +..+aп)? h.
Cумма ( a1+ a2 +a3 +..+aп) равна периметру многоугольника р, являющегося основанием пирамиды, поэтому: Sбок=р? h.
Теорема доказана.
2.В прямой треугольной призме все ребра равны. Боковая поверхность равна 12 см2. Найдите высоту.
Дано: Пряма призма ABCA1B1C1,
AB=BC=AC=AA1,
Sбок=12 м2.
Найти: Высоту АА1
Решение:
Высота будет равна длине любого из ребер призмы (так как по условию задачи призма прямая и все ребра равны между собой) . Площадь боковой грани призмы будет равна длине ребра возведенной в квадрат – Sб. г. =АА12, а площадь всей боковой поверхности призмы – Sбок=3АА12. Но по условию известно, что боковая поверхность призмы равна 12 см2.
Отсюда: 3АА12=12
АА12=4
АА1=2
Ответ: высота призмы равна 2 м.