Как узнать из какого сборника учитель берет контрольную работу?
Кирилл Кирилленко
Ученик
(159),
на голосовании
2 года назад
Как узнать из какого сборника учитель взял контрольную работу по одному заданию?
Например у меня есть задание (Из 140г. оксида кальция получили 182 гидроксида кальция. Вычислите массовую долю выхода гидроксида кальция.) Мне нужно узнать откуда учитель взял это задание (из какого сборника)
Голосование за лучший ответ
Фёдор Кирсанов
Ученик
(156)
2 года назад
Забей в инете эту задачу и у тебя выскочит
Кирилл КирилленкоУченик (159)
2 года назад
Нет, выскакивает решение этой задачи на всяких сайтах типа знания или ответы майл ру
Фёдор Кирсанов
Ученик
(156)
Кирилл Кирилленко, зайди в картинках есть фото страниц с задачами, может там найдёшь, обычно ещё там и название учебника с автором в строке написано
λ
Искусственный Интеллект
(193345)
2 года назад
Кирилл КирилленкоУченик (159)
2 года назад
Да ты не понял. В контрольной работе несколько заданий, и я хочу узнать откуда она взяла контрольную в которой есть это задание
λ
Искусственный Интеллект
(193345)
Кирилл Кирилленко,
Не факт, что они обязательно изданы в каком-то сборнике
или учебнике.
Просто в интернете тонны таких задачек по разным предметам
имеется.
Задания к контрольной она могла и сама подобрать
из самых разных источников.
Математика : Задачи и решения
84 / 536
Записей показано: 84, всего в разделе «Математика»: 536
Содержание рубрики: сборники задач по всем направлениям, сборники задач по отдельным дисциплинам или видам, материалы олимпиад и кружков, методы решения задач и рекомендации по их решению.
Сборники задач по отдельным дисциплинам также дублируются в соответствующих тематических рубриках каталога.
Задачники, являющиеся основными пособиями при прохождении курса математики, см. в разделе «Школьные учебники».
Арнольд В. И. Задачи для детей от 5 до 15 лет. — 2004 
Арнольд В. И. Задачи для детей от 5 до 15 лет. — М. : МЦНМО, 2004. — 16 с.Баранова И. В., Ляпин С. Е. Задачи на доказательство по алгебре. — 1954 
Баранова И. В., Ляпин С. Е. Задачи на доказательство по алгебре : пособие для учителя. — Л. : Учпедгиз, 1954. — 160, [1] с.Бартенев Ф. А. Нестандартные задачи по алгебре. — 1976 
Бартенев Ф. А. Нестандартные задачи по алгебре : пособие для учителей. — М. : Просвещение, 1976. — 96 с. — Библиогр.: с. 93—94 (22 назв.).Башмаков М. И. Математика в кармане «Кенгуру». — 2010 
Башмаков М. И. Математика в кармане «Кенгуру» : международные олимпиады школьников. — М. : Дрофа, 2010. — 302 с. — (Олимпиады школьников).Беккер Б. М., Некрасов В. Б. Применение векторов для решения задач. — 2002 
Беккер Б. М., Некрасов В. Б. Применение векторов для решения задач : [учебное пособие по математике для учащихся 8—11 классов]. — [2-е изд., испр.]. — СПб. : СМИО Пресс, 2002. — 88 с. — Библиогр.: с. 86 (6 назв.).Беляева Э. С., Монахов В. М. Экстремальные задачи. — 1977 
Беляева Э. С., Монахов В. М. Экстремальные задачи : пособие для учащихся VIII—X классов. — М. : Просвещение, 1977. — 64 с.Березанская Е. С., Нагибин Ф. Ф. Сборник вопросов и упражнений по алгебре и тригонометрии. — 1951 
Березанская Е. С., Нагибин Ф. Ф. Сборник вопросов и упражнений по алгебре и тригонометрии для VIII—X классов средней школы : пособие для учителей. — М. : Учпедгиз, 1951. — 160 с.Беррондо М. Занимательные задачи. — 1983 
Беррондо М. Занимательные задачи / пер. с франц. Ю. Н. Сударева ; под ред. И. М. Яглома. — М. : Мир, 1983. — 232 с.Билецкий Ю. А., Филипповский Г. Б. Чертежи на песке: в мире геометрии Архимеда. — 2000 
Билецкий Ю. А., Филипповский Г. Б. Чертежи на песке : в мире геометрии Архимеда. — Киев : Факт, 2000. — 100 с. — Лит.: с. 99 (11 назв.).Буттер И. Занимательные и увеселителные задачи. — 1831 
Буттер И. Занимательные и увеселителные задачи. — М. : в тип. А. Семена, 1831. — 55, [1] с.Бычкова Т. И., Эпштейн Л. А. Задачи математических олимпиад школьников Карелии. — 1992 
Бычкова Т. И., Эпштейн Л. А. Задачи математических олимпиад школьников Карелии : метод. пособие по внеклассной работе / Карел. гос. пед. ин-т. — Петрозаводск, 1992. — 48 с.Василевский А. Б. Обучение решению задач по математике. — 1988 
Василевский А. Б. Обучение решению задач по математике. — Минск : Вышэйшая школа, 1988. — 256 с. — Библиогр.: с. 251—252.Галкин Е. В. Нестандартные задачи по математике. Алгебра. — 2004 
Галкин Е. В. Нестандартные задачи по математике. Алгебра : учебное пособие для учащихся 7—11 классов. — Челябинск : Взгляд, 2004. — 448 с. — Библиогр.: с. 441—444 (61 назв.).Галкин Е. В. Нестандартные задачи по математике. Задачи логического характера. — 1996 
Галкин Е. В. Нестандартные задачи по математике. Задачи логического характера : книга для учащихся 5—11 классов. — М. : Просвещение, 1996. — 160 с. — Библиогр.: с. 155—158 (84 назв.).Галкин Е. В. Нестандартные задачи по математике. Задачи с целыми числами. — 2005 
Галкин Е. В. Нестандартные задачи по математике. Задачи с целыми числами : учебное пособие для учащихся 7—11 классов. — Челябинск : Взгляд, 2005. — 272 с. — Библиогр.: с. 263—268 (101 назв.).Гарднер М. Есть идея! — 1982 
Гарднер М. Есть идея! / пер. с англ. Ю. А. Данилова. — М. : Мир, 1982. — 304 с. — Библиогр.: с. 303—304.Генкин С. А. и др. Ленинградские математические кружки. — 1994 
Генкин С. А. и др. Ленинградские математические кружки / С. А. Генкин, И. В. Итенберг, Д. В. Фомин ; при участии И. С. Рубанова. — Киров : АСА, 1994. — 270 с. — Библиогр.: с. 264—268 (90 назв.).Гольдберг Я. Е. С чего начинается решение стереометрической задачи. — 1990 
Гольдберг Я. Е. С чего начинается решение стереометрической задачи : пособие для учителя. — Киев : Радянська школа, 1990. — 120 с., [16] л. черт.Давыдов У. С. Задачи и упражнения по теоретической арифметике целых чисел. — 1963 
Давыдов У. С. Задачи и упражнения по теоретической арифметике целых чисел : пособие для математических кружков. — Минск : Учпедгиз БССР, 1963. — 79 с. — Библиогр.: с. 77.Депман И. Я. Рассказы о решении задач. — 1957 
Депман И. Я. Рассказы о решении задач. — Л. : Детгиз, 1957. — 128 с. — (В помощь школьнику).
Вычислительная математика. Приближенные вычисления
Богомолов Н.В. Практические занятия по математике №17
Округлите до первого справа верного разряда приближенные значения данных чисел:
0,3281 ± 0,05
Граница абсолютной погрешности ∆а = 0,05 (разряд – сотые) цифры справа налево:1 – сомнительная, 8 – сомнительная,
2 – сомнительная, 3 – верная цифра
Погрешность округления:
|0,3281 – 0,3| = 0,0281
0,05 + 0,0281 = 0,0781
Ответ: 0,3 ± 0,08
2,0637 ± 0,0025
Граница абсолютной погрешности ∆а = 0,0025 (разряд – тысячные) цифры справа налево:7 – сомнительная, 3 – сомнительная,
6 – верная, 0 – верная, 2 – верная цифра
Погрешность округления:
|2,0637 – 2,06| = 0,0037
0,0025 + 0,0037 = 0,0062
Ответ: 2,06 ± 0,006
14,0367 ± 0,8
Граница абсолютной погрешности ∆а = 0,8 (разряд – десятые) цифры справа налево:7 – сомнительная, 6 – сомнительная,
3 – сомнительная, 0 – сомнительная, 4 – верная, 1 – верная цифра
Погрешность округления:
|14,0367 – 14| = 0,0367
0,8 + 0,0367 = 0,8367
Ответ: 14 ± 1
24,734 ± 0,06
Граница абсолютной погрешности ∆а = 0,06 (разряд – сотые) цифры справа налево: 4 – сомнительная, 3 – сомнительная,
7 – верная, 4 – верная, 2 – верная цифра
Погрешность округления:
|24,734 – 24,7| = 0,034
0,06 + 0,034 = 0,094
Ответ: 24,7 ± 0,1
Вычислительная математика. Граница абсолютной погрешности
Абсолютная погрешность приближенного значения числа, граница абсолютной погрешности, верные и значащие цифры числа
Верные и значащие цифры числа. Округление чисел.
Наша система счета или счисления называется десятичной системой счисления, а 10 – основанием этой системы:
разряд единиц, разряд десятков, разряд сотен и т.д. Аналогично, разряды десятичных дробей: десятые, сотые, тысячные и т.д.
|
Дробь |
Целая часть |
Дробная часть |
||||||
|
разряды |
тысячи |
сотни |
десятки |
единицы |
, |
десятые |
сотые |
тысячные |
|
258,034 |
– |
2 |
5 |
8 |
, |
0 |
3 |
4 |
В приближенном числе различают верные и сомнительные цифры. Цифра какого-либо разряда приближенного числа а считается верной в широком смысле, если граница абсолютной погрешности числа а не превосходит единицы того разряда, в котором записана эта цифра.
Если же граница абсолютной погрешности больше единицы какого-либо разряда, то цифра этого разряда и все цифры, расположенные справа от нее считаются сомнительными. Граница абсолютной погрешности ∆а находится непосредственно по записи приближенного значения а числа х.
Например:
24,5 ± 0,3 (| х – а | ≤ ∆а )
Приближенное значение 24,5
Граница абсолютной погрешности 0,3
0,3 < 1, значит верные цифры (в широком смысле) – это 2 и 4, а цифра 5 – сомнительная.
375 ± 20
Приближенное значение 375
Граница абсолютной погрешности 20
20 < 100, значит верная цифра 3, а цифры 7 и 5 сомнительные.
Когда рассматриваем верные цифры в широком смысле, то достаточно посмотреть на границу абсолютной погрешности и взять цифры приближенного числа, которые на разряд больше, чем граница абсолютной погрешности.
Цифра какого-либо разряда приближенного числа а считается верной в строгом смысле, если граница абсолютной погрешности числа а не превосходит половины единицы того разряда, в котором записана эта цифра. Если же граница абсолютной погрешности больше половины единицы какого-либо разряда, то цифра этого разряда и все цифры, расположенные справа от нее считаются сомнительными.
В числах, полученных в результате измерений или вычислений и используемых при расчётах в качестве исходных данных, а также в десятичной записи приближенного значения числа, все цифры должны быть верными.
Значащими цифрами приближенного числа, выраженного десятичной дробью считаются все верные цифры этой дроби, кроме нулей, стоящих перед первой цифрой (слева направо), отличной от нуля.
Например:
Приближенное число 10,408 имеет 5 значащих цифр, так как крайняя слева цифра числа отлична от нуля (она равна 1)
Приближенное число 0,01104 имеет 4 значащие цифры:1, 1, 0, 4. Два нуля, стоящие слева от 1 не считаются значащими цифрами
Приближенное число 0,030 имеет 2 значащие цифры: 3 и 0 справа, по правилу два нуля, стоящие слева от цифры 3, не относятся к значащим.
Значащими цифрами приближенного целого числа считаются все его цифры, кроме нулей, поставленных взамен отброшенных или
неизвестных цифр.
Например: Частное
Число 6000 имеет 3 значащие цифры, так как один последний нуль поставлен вместо отброшенной цифры (единицы).
Округление чисел. При округлении числа а его заменяют числом а1 с меньшим количеством значащих цифр. Абсолютная величина разности
| а – а1 | называется погрешностью округления.
При округлении числа до m значащих цифр отбрасываются все цифры, стоящие правее m-й значащей цифры, или при сохранении разрядов заменят их нулями. При этом, если первая слева от отброшенных цифр больше или равна 5, то последнюю оставшуюся цифру увеличивают на 1.
При применении этого правила погрешность округления не превосходит половины единицы десятичного разряда, определяемого последней оставленной значащей цифрой.
Округление приближенных значений чисел с сохранением в записи только верных цифр производится до разряда, в котором записана первая справа верная цифра.
Например:
Округлите до первого справа верного разряда приближенные значения данных чисел:
0,3281 ± 0,05
Граница абсолютной погрешности 0,05 (разряд – сотые) цифры справа налево:1 – сомнительная, 8 – сомнительная, 2 – сомнительная, 3 – верная цифра 3
Погрешность округления:
|0,3281 – 0,3| = 0,0281
0,05 + 0,0281 = 0,0781
Ответ 0,3 ± 0,08
Вычислительная математика. Умножение приближенных значений чисел
Задача №25 (Сборник задач по математике Н.В. Богомолов)
Вычислительная математика. Абсолютная погрешность
АБСОЛЮТНАЯ ПОГРЕШНОСТЬ И ЕЕ ГРАНИЦА.
ЗАПИСЬ ПРИБЛИЖЕННОГО ЧИСЛА.
ВЕРНЫЕ И ЗНАЧАЩИЕ ЦИФРЫ ЧИСЛА
х – точное число
а – приближенное число
Разность х – а между точным числом х и приближенным числом а называется погрешностью приближения.
Модуль погрешности называется абсолютной погрешностью и обозначается ∆:
| х – а | = ∆
Погрешность и абсолютная погрешность имеют ту же размерность, что и рассматриваемая величина
Граница абсолютной погрешности ∆а – положительное число, которое больше или равно абсолютной погрешности или:
| х – а | ≤ ∆а
Если задана граница абсолютной погрешности ∆а, то число а есть приближенное значение числа х с точностью до ∆а и записывают
х = а ± ∆а, например: 94,5 ± 0,3
В отличие от абсолютной погрешности, граница абсолютной погрешности не определяется однозначно, поэтому на практике выбирается такое значение границы абсолютной погрешности, которое удобно для вычислений и обеспечивает максимальную точность.
Цифра приближенного числа а, записанного в виде десятичной дроби, называется верной (точной), если граница абсолютной погрешности числа не превышает (меньше или равно) единицы того разряда, в котором стоит эта цифра. В противном случае она называется сомнительной, например:
25,63 ± 0,2
Граница погрешности 0,2 , поэтому рассмотрим
цифру 5, разряд единицы, единица разряда 1 и 0,2 < 1 (граница погрешности не превышает единицу разряда), значит цифра 5 – верная, тогда цифра десятков – 2 данного числа тоже верная.
Цифра 6, разряд десятые, единица разряда 0,1 и 0,2 > 0,1 (граница погрешности превышает единицу разряда), значит цифра 6 – сомнительная. Значит и цифра 3 (сотые) будет также сомнительной
2 и 5 – верные цифры, 6 и 3 – сомнительные цифры числа
Запись чисел с сохранением только верных цифр широко используется во всех математических таблицах, в справочниках (физика, астрономия, техника). При этом, по записи приближенного числа можно оценить погрешность приближения, например:
табличные данные: температура кипения золота – 2700 ºС, значит граница абсолютной погрешности 1 ºС, температура кипения йода – 182,8 ºС, значит граница абсолютной погрешности 0,1 ºС.
Записи приближенных чисел 0,3; 0,30; 0,300 – неравносильны, т.к. приближенное число 0,3 имеет погрешность не более 0,1;
приближенное число 0,30 имеет погрешность не более 0,01;
приближенное число 0,300 имеет погрешность не более 0,001.
Если целое число содержит в конце нули, не являющиеся верными цифрами, то их заменяют множителем 10р, где р – число таких нулей.
В записи приближенных чисел принято соблюдать следующие правила:
- Оставлять в записи приближенного числа только верные цифры;
- Если в десятичной дроби последние верные цифры нули, то их надо выписать;
- Если число содержит в конце нули, не являющиеся верными цифрами, то они должны быть заменены на 10р , где р – число нулей, которые надо заменить
Например,
Записать правильно следующие приближенные числа:
- а = 0,075 ± 0,000005 – здесь погрешность меньше, чем 0,00001 (0,000005<0,00001), значит а = 0,07500 (последние верные цифры нули и их надо выписать, см. правило)
- а = 746000000 ± 5000 здесь погрешность меньше, чем 10000 (5000<10000), значит последние четыре нуля не являются верными цифрами и их надо заменить на 10р а = 74600·104
- а = 0,35 ∆а = 0,00005 – здесь погрешность меньше, чем 0,0001 значит
а = 0,3500 (последние верные цифры нули)
- а = 765000 ∆а = 5 – здесь погрешность 5<10 значит а = 76500·10, т.к. последний нуль не является верной цифрой
- а = 0,3700 ∆а = 0,05 – здесь погрешность 0,05<0,1 и цифра 7 не является верной, она отбрасывается, значит а = 0,4
В некоторых заданиях необходимо наоборот определить абсолютную погрешность по записи приближенного числа, например,
Указать абсолютную погрешность приближенных чисел:
- а = 14,5 ·10, значит ∆а = 10
- а = 34,20 т.к. последний нуль является верной цифрой, то ∆а = 0,01
- а = 263·104 , значит ∆а = 10000
Число в стандартном виде записывают так:
а = а0, а1 а2 … аk ·10m , где 1 ≤ а0 ≤ 10,
а0, а1 а2 … аk – все верные цифры числа,
показатель m – называется порядком числа.
Если число, записанное в виде десятичной дроби содержит все верные цифры, то все его цифры, начиная с первой слева отличной от нуля, называют значащими, например:
7,03 – три значащие цифры
4400 – четыре значащие цифры
0,000270 – три значащие цифры (нули, расположенные левее первой, отличной от нуля цифры, не считаются значащими 0,000270).
Округление числа – это замена его числом с меньшим количеством значащих цифр. При округлении числа до m значащих цифр отбрасывают все цифры, стоящие правее m-ой значащей цифры, заменяя их на нули (при сохранении разряда). При этом, если первая из отбрасываемых цифр ≥ 5, то последнюю оставшуюся цифру увеличивают на единицу,
например:
Округлить число с заданной точностью:
- с точностью до 10-3 (10-3 = 0,001)
1,5783
Значащие цифры – 1, 5, 7 и 8, цифра 3 – сомнительная, т.к. 0,001 > 0,0001 (единицы разряда)
1,5783 ≈ 1,578 (последняя из отбрасываемых цифр 3<5, значит предыдущую оставляем без изменений)
23,4997
Значащие цифры – 2, 3, 4, 9 и 9, цифра 7 – сомнительная
7>5, значит предыдущую увеличиваем на 1, получим
23,4997 ≈ 23,500
- с точностью до 10-2 (10-2 = 0,01)
4,761 ≈ 4,76
31,009 ≈ 31,01
- с точностью до 103 (103 = 1000)
159734 ≈ 160000 = 160·103
28,34 ≈ 0 – ни одна из цифр не является значащей 1000 > 10, т.к. задана точность 1000, а заданное число меньше, чем погрешность.
Лисичкин В.Т., Соловейчик И.Л. Сборник задач по математике с решениями для техникумов (учебное пособие)
Вычислительная математика. Погрешности. Решение задач
ОТНОСИТЕЛЬНАЯ ПОГРЕШНОСТЬ И ЕЕ ГРАНИЦА.
РЕШЕНИЕ ЗАДАЧ
х – точное число
а – приближенное число
Разность х – а между точным числом х и приближенным числом а называется погрешностью приближения.
| х – а | = ∆ – абсолютная погрешность
Отношение абсолютной погрешности к модулю приближенного числа, называется относительной погрешностью
– относительная погрешность является показателем качества данного приближения, и ее часто выражают в процентах %
Граница относительной погрешности больше или равна относительной погрешности:
Если дана граница относительной погрешности, то говорят, что приближение дано с относительной точностью до Ꜫ % и записывают:
х = а (± Ꜫ) или х = а (± Ꜫ %)
В ряде задач границу абсолютной погрешности находят по данной относительной погрешности и модулю приближенного значения величины:
∆а = δ ∙ |а|
Задачи:
- Скорость света в вакууме 299792,5 ± 0,4 км/ч
Скорость звука в воздухе 331,63 ± 0,04 м/с
Какое измерение точнее?
– значит скорость света точнее
- Найдите границы значений грузоподъемности автомобиля, если она равна 2,5 ± (15%)
Дана граница относительной погрешности и необходимо найти границу абсолютной погрешности, используем
∆а = δ ∙ |а|
0,15*2,5 = 0,375 ≈ 0,4
Значит границы значений грузоподъемности автомобиля 2,5 ± 0,4 или 2,1 ≤ 2,5 ≤ 2,9
- Какие из равенств точнее:
?
, значит
точнее
Найдите относительную погрешность в % с точностью до десятых
А = 240 ± 1
Решение: границу абсолютной погрешности находим из условия ± 1, значит ∆а=1, далее по формуле
Найдите относительную погрешность в % с точностью до сотых
Радиус Земли (в км): R = 6380 ± 1
Решение: границу абсолютной погрешности находим из условия ± 1, значит ∆а=1, далее по формуле
Найдите относительную погрешность в % с точностью до сотых
Скорость света в вакууме (в км/с):
Решение: границу абсолютной погрешности находим из условия <100, значит ∆а=100, далее по формуле
Диаметр Луны (в км): d = 3476 ± 1
Решение: границу абсолютной погрешности находим из условия ± 1, значит ∆а=1, далее по формуле
Математический анализ
Искомая величина (путь, давление, сила, работа и т.д.) соответствует некоторому промежутку изменения переменной величины, которая является переменной интегрирования. Эту переменную интегрирования обозначают через Х, а промежуток ее изменения через [a; b]
Математический анализ
Задача
Тело, выпущенное вертикально вверх, движется по закону
, где s(t) измеряется в метрах, а время t в секундах.
Найти:
а) Скорость тела в начальный момент;
б) Скорость тела в момент соприкосновения с землей;
в) Наибольшую высоту подъема тела.
Решение:
Тело движется по параболе, это очевидно, т.к. уравнение, которое описывает движение тела – уравнение параболы (уравнение движения).
а) Скорость тела в начальный момент момент равна первой производной от пути, который описывается уравнением
В момент t=0,
б) В момент соприкосновения с землей
т.е. решаем уравнение
получаем: , второй корень нам не подходит по смыслу, т.к. время t не может быть отрицательным в классической физике.
Значит, скорость в момент
м/с
(минус указывает на то, что скорость тела в момент времени
противоположна направлению начальной скорости.
в) Наибольшая высота подъема будет в момент, когда скорость тела равна нулю (в точке максимума функции) и происходит переход от подъема тела к спуску
(переход от возрастания функции к ее убыванию, критическая точка, в которой производная функции равна 0)
, t = 0,8 с.
Подставляем в уравнение движения
Значит, наибольшая высота подъема равна 8,2 м.
Тригонометрия
Решение квадратных тригонометрических уравнений.
Уравнение распадается на два уравнения: и
Решение первого уравнения: ,
Решение второго уравнения:
Объединяем эти решения и получим:
Ответ:
Уравнение распадается на два уравнения: и
Решение первого уравнения: ,
Решение второго уравнения: ,
Объединяем эти решения и получим:
Ответ:
Решить уравнение
Для решения данного уравнения введен новую переменную: sin(x)=t,
Определим область допустимых значений для нашей переменной:
Получим
Решим квадратное уравнение относительно t:
=
=
Проверяем корни нашего уравнения на область допустимых значений t
t =
, следовательно
t =
, следовательно
Решаем полученные уравнения относительно x:
, получаем
,
, получаем
Ответ: ,
.
Для решения данного уравнения введен новую переменную: cos(x)=t,
Определим область допустимых значений для нашей переменной:
Получим
Решим квадратное уравнение относительно t:
=
=
Проверяем корни нашего уравнения на область допустимых значений t
t = 2 >1, следовательно не имеет решений:
В данном случае решать уравнение является грубейшей ошибкой, т.к.
, а arccos 2 вообще не имеет смысла!
t =
, следовательно
, решаем полученное уравнение:
,
Ответ: .
В данном уравнении необходимо применить основное тригонометрическое тождество, для того чтобы прийти к одной функции
Приводим к функции синуса, т.к. проще представить
Получаем уравнение:
Раскрываем скобки:
, приводим подобные слагаемые:
, умножим на (-1) для простоты решения:
Для решения данного уравнения введен новую переменную: sin(x)=t,
Определим область допустимых значений для нашей переменной:
Получим
Решим квадратное уравнение относительно t:
Проверяем корни нашего уравнения на область допустимых значений t
t = < -1, следовательно,
не имеет решений:
t =
, следовательно,
, ответ
Ответ:
Разберемся с областью определения для решений данного уравнения.
|
Область определения тангенса
Область определения котангенса
Объединив эти промежутки получим:
|
|
Для решения данного уравнения используем тригонометрическое тождество , перепишем уравнение:
, получим
, далее
, произведем замену
Получим
Решим квадратное уравнение относительно t:
t=1, следовательно
,
t= -2, следовательно
Ответ: ,
Математический анализ
Геометрическая интерпретация производной, впервые данная в конце XVII века Лейбницем, состоит в следующем:
Значение производной функции y=f(x) в точке x равно угловому коэффициенту касательной, проведенной к графику
функции в той же точке x, т.е. k = f ’(x) = tg φ
Рассмотрим задачу.
Определение: прямая, проходящая через точку касания, перпендикулярно касательной,
называется нормалью к кривой в этой точке.
Если кривая определена уравнением 
, то уравнение касательной к ней в точке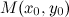 
имеет вид:
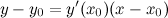
а уравнение нормали:
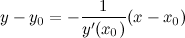
Как Вы заметили нам нужно найти производную, чтобы написать уравнение касательной или нормали.
Существуют общие правила нахождения производной:
(в пояснении – это у(x +∆x) )
Применим эти правила и найдем производную функции y=5x
- y(x +∆x) = 5(x +∆x) = 5x + 5∆x
- ∆y = y(x +∆x) – y(x) = (5x + 5∆x) – 5x = 5∆x
-
=
= 5
Таким образом, мы нашли производную функции, пользуясь непосредственным определением производной.
Но это не очень удобно, хотя и позволяет вычислить производную любой элементарной функции.
Вспомним, элементарные функции — функции, которые можно получить с помощью конечного числа
арифметических действий и композиций из следующих основных элементарных функций: степенная функция
с любым действительным показателем; показательная и логарифмическая функции; тригонометрические и обратные
тригонометрические функции.
Формулы производных основных элементарных функций
Правила вычисления производных
Вычисление производных основано на применении следующих правил, которые мы будем использовать
Правило 1 (производная от произведения числа на функцию).
Справедливо равенство (c f (x))’ = c f ‘ (x) , где c – любое число.
Другими словами, производная от произведения числа на функцию равна произведению этого числа на производную функции.
Правило 2 (производная суммы функций).
Производная суммы функций вычисляется по формуле
(f (x) + g (x))’ = f ‘ (x) + g’ (x),
то есть производная от суммы функций равна сумме производных этих функций.
Правило 3 (производная разности функций).
Производная разности функций вычисляется по формуле
(f (x) – g (x))’ = f ‘ (x) – g’ (x),
то есть производная от разности функций равна разности производных этих функций.
Правило 4 (производная произведения двух функций).
Производная произведения двух функций вычисляется по формуле
(f (x) g (x))’ = f ‘ (x) g (x) + f (x) g’ (x),
Другими словами, производная от произведения двух функций равна производной от первой функции,
умноженной на вторую функцию, плюс первая функция, умноженная на производную от второй функции.
Правило 5 (производная частного двух функций).
Производная от дроби (частного двух функций) вычисляется по формуле
Вычислительная математика. Приближенные вычисления
Действия с приближенными числами.
На практике пользуются более простыми правилами, которые называются
Правила подсчета цифр:
Задача:
Решение:
Задача:
Решение:
Задача:
Найдите произведение двух приближенных чисел: 0,3862 * 0,85
Решение:
Задача:
Решение:
Задача:
Решение:
Задача:
Решение:
(Лисичкин В.Т., Соловейчик И.Л. Сборник задач по математике с решениями для техникумов (учебное пособие))
При решении некоторых задач возникает необходимость указать верные цифры результата,
т.е. найти границу абсолютной погрешности результата вычислений.
На практике сначала находят относительную погрешность результата, а затем, используют формулу:
Формулы для вычисления границ абсолютной и относительной погрешностей некоторых функций приведены в таблице.
Задача:
Решение:
Так как a=0,3862 то ∆a=0,00005 , b = 0,8 значит ∆b=0,05
Находим границу абсолютной погрешности произведения по формуле
(Н.В. Богомолов Практические занятия по математике)
Универсальный способ решения: составить систему уравнений, подставить известные значения и вычислить неизвестные. Раз у нас 2 объекта, то 2 уравнения описывают движение этих объектов, а остальные уравнения берутся из условий задачи.
- s1 = v1 ⋅ t, формула движения, где s1 – длина пути автобуса №1, v1 – скорость автобуса №1, t – время движения каждого объекта.
- s2 = v2 ⋅ t, формула движения, где s2 – длина пути автобуса №2, v2 – скорость автобуса №2, t – время движения каждого объекта.
Отметим, что время движения у них одинаковое, поэтому мы его обозначили одинаково как t.
Базовыми единицами измерения возьмём км для пути, ч для времени и км/ч для скорости.
Итак, у нас в формулах есть 5 величин, из которых 3 известные (s1=100, v1=25, v2=50) и 2 неизвестные (s2, t), которые предстоит найти для получения результата.
Для успешного решения неизвестных должно быть столько же или меньше, чем уравнений. В нашем случае одинаково – 2, то есть скорее всего решение найдётся.
Простые
задачи
Задачи
нахождение суммы двух слагаемых
1. Таня нашла 5
подосиновиков. Потом она нашла ещё 2 лисички. Сколько всего грибов нашла Таня?
2. На стол
поставили 2 вазы и 5 подносов. Сколько всего предметов поставили на стол?
3. На клумбе 2 пчелы
собирали пыльцу. К ним прилетели ещё 3 пчелы. Сколько всего пчёл стало на
клумбе?
4. Во дворе живут
3 собаки и 4 кота. Сколько всего животных живут во дворе?
5. На стоянке было
6 машин. Приехали ещё 4 машины. Сколько всего машин стало на стоянке?
6. В саду растут 2
саженца груши и 5 саженцев вишни. Сколько всего саженцев растёт в саду?
7. На ветке сидели
5 воробьёв и 2 синички. Сколько птиц было на ветке?
8. На лугу паслись
6 коз и 2 лошади. Сколько животных было на лугу?
9. На столе стоят
4 большие тарелки и 5 маленьких. Сколько всего тарелок на столе?
10. Папа купил 3
кг моркови и 5 кг картофеля. Сколько килограммов овощей купил папа?
Задачи на нахождение
остатка
1) В вазе было 10 яблок.
8 яблок съели. Сколько яблок осталось?
2) В пакете лежало 30 конфет.
20 конфет съели. Сколько осталось?
3) Ребята сделали 10
скворечников. 8 скворечников они повесили в школьном саду. Сколько скворечников
им осталось повесить?
4) В автобусе ехали 28
человек. На остановке вышли 5 человек. Сколько человек осталось в автобусе?
5) С начала марта прошло
7 дней. Сколько дней осталось до конца марта? (В марте 31 день).
6) Оля сделала 12
поздравительных открыток. 8 открыток она подарила. Сколько открыток у неё
осталось?
7) В коробке было 24
шоколадных конфеты. 8 конфет съели. Сколько конфет осталось в коробке?
8) Крышка стола имеет 4
угла. Один угол спилили. Сколько углов стало у крышки стола?
9) Ученику надо решить 16
примеров. Он решил 9 примеров. Сколько примеров ему осталось решить?
10) В книге 30 страниц.
Катя прочитала 16 страниц. Сколько страниц осталось прочитать.
11) На дереве сидело 14
ворон и 8 сорок. Улетели все сороки и столько же ворон. Сколько ворон осталось?
12) В классе 13 комнатных
растений. Дежурный полил 7 из них. Сколько растений осталось полить дежурному?
13) На дом было задано
списать 23 слова. Маша списала 15 слов. Сколько слов осталось списать Маше?
14) На клумбе росло 50
цветов, 20 цветов сорвали. Сколько цветов осталось?
15) Купили 30 яблок. 5 из
них съели. Сколько яблок осталось?
Задачи на
нахождение произведения
1) У крольчих
шестеро крольчат. Чтобы их накормить, необходимо каждому дать 2 морковки.
Сколько всего морковок крольчиха должна сорвать для своих крольчат?
2) У четырёх
девочек в этом месяце день рождения. Мальчики решили их поздравить и подарить
каждой по 3 цветка. Сколько цветов надо купить мальчикам?
3) На 3 тарелки
положили по 5 яблок на каждую. Сколько всего яблок положили?
4) На 8 тарелок Чебурашка
положил по 3 апельсина. Сколько всего апельсинов положили на тарелки?
5) Фрекен Бок
подала к чаю 7 тарелок по 4 плюшки в каждой. Сколько всего плюшек подала Фрекен
Бок?
6) В обеих руках
Незнайка держит по 2 воздушных шарика. Сколько воздушных шариков в руках у
Незнайки?
7) Кот Матроскин
всю неделю получал по 3 литра молока от своей коровы Мурки. Сколько литров
молока Матроскин получил за неделю?
8) Буратино так
захотел пройти в кукольный театр на представление, что продал свою азбуку за 5
сольдо, столько стоил 1 билет. А сколько нужно было заплатить за 3 билета?
9) Мачеха
приказала Золушке пришить на 2 платья ее дочерей по 4 пуговицы на каждое
платье. Сколько всего пуговиц пришила Золушка?
10) В одном
стручке 7 горошин. Сколько таких горошин в 3-х стручках?
Задачи
деления на равные части
1. На склад
привезли 3 ящика мандарин, одинаковых повесу, всего 27 килограмма. Сколько
мандарин было в каждом ящике?
2. 20 яблок
разделили поровну между 5 детьми. Сколько яблок досталось каждому ребенку?
3. 18 конфет
раздали детям по 3 штуки. Сколько детей получило конфеты?
4. 24 человека
разбили на 3 группы. По сколько человек оказалось в каждой группе
5. 9 порций
мороженого разделили поровну между 3 детьми. Сколько порций мороженого получил
каждый ребенок?
6. Шесть мальчиков
разделили между собой поровну 18 орехов. По сколько орехов получил каждый из
них?
7. Мама разложила
64 ватрушки на 8 тарелок поровну. По сколько ватрушек лежит на каждой тарелке?
8. 28 яблок
разложили в 4 корзины поровну. Сколько яблок положили в каждую корзину?
9. В 3 дворах 15
лавочек поровну. Сколько лавочек в одном таком дворе?
10. 40 килограмм
картошки разложили поровну в 2 мешка. Сколько картошки положили в каждый мешок?
Задачи на
деление по содержанию.
1. 8 апельсинов разложили
по 4 апельсина на каждую тарелку. Сколько потребовалось тарелок?
2. 10 туристов
разместились в палатки по 5 человек в каждую. Сколько было палаток?
3. 6 кусков сахара
опустили в 3 стакана. Сколько кусков сахара в каждом стакане?
4. Купили 14 попугаев.
Их разместили в клетки по 7 попугаев. Сколько понадобилось клеток?
5. У плотника 24
дощечки. Сколько скворечников можно сделать из этих дощечек, если на один
скворечник идёт 8 дощечек?
6. Для живого
уголка купили 12 рыбок. Их пустили в аквариуме по 6 рыбок в каждый. Сколько
аквариумов понадобилось?
7. На трёх грядках
поровну рассадили 60 луковиц. По сколько луковиц посажено на каждой грядке?
8. На зиму
засолили несколько банок грибов по 2 кг в каждой банке. После того, как съели 6
кг, осталось 8 кг. Сколько банок грибов засолили?
9. Для игры
разделили 8 девочек и 12 мальчиков на 2команды. По сколько человек в каждой
команде?
10. У одной
закройщицы 12 метров ткани, а у другой 16 метров. Из всей этой ткани они
скроили костюмы, расходуя на каждый по 4 метра. Сколько костюмов они скроили?
11. В ателье было
150 м материи. Из этой материи сшили 24 женских халата, расходуя на каждый
халат по 3 м. Из остальной материи сшили детские платья, расходуя на каждое
платье по 2 м. Сколько детских платьев сшили в ателье?
12. участка
собрали 1ц моркови. Первые 2 месяца расходовали по 15 кг. На сколько месяцев
хватит остальной моркови, если расходовать ежемесячно по 14 кг?
13. Длина свечи 25
см. При горении она убывает в минуту на 2 мм. Сколько минут горела свеча, если
от неё остался кусок длиной 16 см?
14. Один каменщик
уложил за 6 дней 102 тысячи кирпичей. Другой на 12 тысяч больше. Сколько
кирпичей уложит второй каменщик за 5 дней?
15. Девочке нужно
прочитать книгу в 132 страницы. После того, как она читала несколько дней по 15
страниц в день, в книге осталось 27 страниц. Сколько дней девочка читала книгу?
Задачи
увеличение на несколько единиц (прямая форма)
1. Надя посадила 3
тюльпана, а Вика на 2 тюльпана больше. Сколько тюльпанов посадила Вика?
2. У школы росло 6
елей, а сосен – на 2 больше. Сколько сосен росло у школы? 3. В коробке лежало 3
простых карандаша, а цветных на 2 больше. Сколько цветных карандашей лежало в
коробке?
4. На тарелке
лежали сливы и персики. Слив было 6, а персиков – на 2 больше. Сколько персиков
было?
5. В первый день
Миша нарисовал 3 рисунка, во второй – на 2 рисунка больше. Сколько рисунков
нарисовал Миша за второй день?
6. В одной коробке
было 10 кг бананов, а во второй — на 5 больше. Сколько килограммов бананов было
во второй коробке?
7. Первый класс
собрал 19 ящиков яблок, а второй — на 4 ящика больше. Сколько ящиков яблок
сорвал второй класс?
8. У Пети есть
марки с автомобилями и самолетами. Марок с автомобилями – 12, а с самолетами –
на 4 больше. Сколько марок с самолетами у Пети?
9. На ветке сидели
4 воробья, а снегирей – на 8 больше. Сколько снегирей сидело на ветке?
10. Бабушка
приготовила 15 банок варенья, а мама – на 3 больше. Сколько банок варенья
приготовила мама?
11. У Володи было
9 зелёных кругов, а синих – на 2 больше. Сколько синих кругов у Володи?
12. В коробке
лежали шарики красного и зеленого цвета. Красных шариков было 9 штук, а зеленых
– на 8 больше. Сколько зеленых шариков лежало в коробке?
13. В пенале у
Вовы 3 ручки, а карандашей – на 4 больше. Сколько карандашей в пенале у Вовы?
14. В букете было
три розы, а гвоздик – на 4 больше. Сколько гвоздик было в букете?
15. У бабушки на
даче росло 7 кустов смородины, а кустов малины на 3 больше. Сколько кустов
малины росло у бабушки на даче?
Задачи
увеличение на несколько единиц (косвенная форма)
1.
Коля
прочитал 3 рассказа, это на 2 рассказа меньше, чел прочитала Люда. Сколько
рассказов прочитала Люда?
2.
У
школы росло 6 елей, это на 2 дерева меньше, чем сосен. Сколько сосен росло у
школы?
3.
У
Васи было 17 открыток, это на 9 открыток меньше, чем у Даши. Сколько открыток у
Даши?
4.
В
первом грузовике 45 ц песка, что на 15 ц меньше, чем во втором. Сколько
центнеров песка во втором грузовике?
5.
Сыну
7 лет, и он на 23 года моложе отца. Сколько лет отцу?
6.
В
парке высадили 11 лип, это на 2 меньше, чем клёнов. Сколько высадили клёнов?
7.
На
берёзе сидело 6 воробьёв, это на 4 меньше, чем на сосне. Сколько воробьёв
сидело на сосне
8.
Одна
наседка вывела 5 цыплят, это на 3 цыпленка меньше, чем вторая. Сколько цыплят
вывела вторая наседка
9.
В
соседнем доме 12 этажей, это на 3 этажа меньше, чем в нашем. Сколько этажей в
нашем доме?
10.
Маше
9 лет, и она на 21 год моложе своей мамы. Сколько лет маме Маши?
Задачи уменьшение
числа на несколько единиц (прямая форма)
1. В первой вазе стояло 5
цветов, а во второй на 2 цветка меньше. Сколько цветов было во второй вазе?
2. У Васи было 17
открыток, а у Даши на 9 открыток меньше. Сколько открыток было у Даши?
3. У Володи было 8
зелёных кругов, а синих в 2 раза меньше. Сколько синих кругов у Володи?
4. Саша принес с огорода
5 редисок, Дима принес столько же, да еще 2. Сколько редисок принес Дима?
5. В живом уголке школы
есть кролик и еж. Кроме них есть еще 6 животных. Сколько всего животных в живом
уголке?
6. Под сосной выросло 7
маслят. Сколько грибов осталось под сосной, если 2 гриба унес ежик?
7. В чайнике 5 стаканов
воды, в кувшине столько же. Сколько стаканов воды входит в кувшин? В самовар
входит на 4 стакана больше. Сколько воды входит в самовар?
8. В пруду плавали 9
гусей, а уток в 3 раза меньше. Сколько уток плавало в пруду?
9. Мальчику нужно было
купить 5 карандашей, а он купил на 1 карандаш больше. Сколько карандашей купил
мальчик?
10. У Лиды было 5
карандашей. Стало на 2 меньше. Сколько карандашей стало у Лиды?
11. Купили 6 красных
мячей, а синих на 3 мяча меньше. Сколько синих мячей купили?
12. У Вани 8 машин, а у
Сережи на 4 меньше. Сколько машинок у Сережи?
13. На тарелке лежали
сливы и персики. Слив было 6, а персиков – на 2 меньше. 14. Сколько персиков
было?
15. У Вити было 9
солдатиков, а у Миши на 2 солдатика меньше. Сколько солдатиков у Миши?
Задачи уменьшение
числа на несколько единиц (косвенная форма)
1. В саду росло 6 кустов
красной смородины. Этот в 2 раза больше, чем чёрной. Сколько кустов чёрной
смородины росло в саду?
2. Высота берёзы 8 м, что
в 4 раза больше, чем высота рябины. Какой высоты рябина?
3. Антон прочитал за
четверть 25 книг, что в 5 раз больше, чем прочитал Олег. Сколько книг прочитал
Оле
4. Мама нашла 36 грибов,
это в 6 раз больше, чем нашла дочка. Сколько грибов нашла дочка?
5. В классе 16 девочек.
Их на 7 больше, чем мальчиков. Сколько мальчиков в классе
6. С первой грядки
собрали 45 огурцов, со второй на 3 больше, чем с 1-ой, а с 3-ей, на 6 меньше,
чем со 2-ой. Сколько огурцов собрали с третьей грядки?
7. На столе восемнадцать
книг, на полке в три раза больше. Сколько книг на полке?
8. Таня купила 12
тетрадей в клетку. Это на 8 тетрадей больше, чем в линейку. Сколько тетрадей в
линейку купила Таня?
9. Ширина прямоугольника
3см, а длина – на 10 см больше. Найди периметр прямоугольника.
Задачи на
разностное сравнение
1. Купили 5
учебников и 9 тетрадей. На сколько меньше купили учебников, чем тетрадей?
2. На столе лежит
7 конфет и 4 яблока. На сколько больше конфет, чем яблок?
3. Вите 7 лет,
Лене 10 лет. На сколько лет Лена старше Вити?
4. Ширина ремешка
3 см, а ширина ремня 8 см. На сколько ремешок уже ремня?
5. Один мальчик
поймал 5 раков, а другой 2. На сколько раков первый мальчик поймал больше
второго?
6. В первой вазе 3
тюльпана, а во второй 9 тюльпанов. На сколько тюльпанов меньше в первой вазе,
чем во второй?
7. Катя нашла 8
грибов, а Аня – 10 грибов. На сколько больше грибов нашла Аня, чем Катя?
8. Длина озера
Сенеж 5 км, ширина 3 км. На сколько километров длина озера больше, чем его
ширина?
9. 22 декабря на
юге нашей страны самая длинная ночь – 17 часов, а день длится всего 7 часов. На
сколько часов день короче ночи?
10. Летом, 22
июня, на юге нашей страны самый длинный день – 18 часов, а ночь продолжается
всего 6 часов. На сколько часов день длиннее ночи?
Задачи на увеличение в
несколько раз (прямая форма)
1.Света купила 5 конфет,
а Петя в 4 раза больше. Сколько конфет купил Петя?
2.Дима вырезал 7 красных
флажков, а синих в 3 раза больше. Сколько синих флажков вырезал Дима?
3.В аквариуме плавало 9
больших рыбок, а маленьких в 3 раза больше. Сколько маленьких рыбок плавало в
аквариуме?
4.Мама купила арбуз весом
6кг, а папа купил арбуз в 3 раза тяжелее. Сколько килограммов весил арбуз,
который купил папа?
5.В корзине 7 кг яблок, а
в мешке в 4 раза больше. Сколько килограммов яблок в мешке?
6.В первом классе учится
8 учеников, а во втором классе в 2 раза больше. Сколько учеников учится во
втором классе?
7.За лето Петя прочитал 6
книг, а Вася в 4 раза больше. Сколько книг прочитал Вася?
8.Миша вырезал 16 снежинок,
а Коля в 2 раза меньше. Сколько снежинок вырезал Коля?
9.В одном пакете лежит 10
кг муки, а в другом пакете в 2 раза меньше. Сколько килограммов муки лежит во
втором пакете?
10.В одной книге 24
страницы, а во второй в 3раза меньше. Сколько страниц во второй книге?
11.На тарелке лежало 15
шоколадных конфет, а карамели было в 5раз меньше. Сколько карамели лежало на
тарелке?
12.Тыква весит 36кг, а
кабачок в 9 раз меньше. Сколько весит кабачок?
13.Лена купила 20
тетрадок, а Света в 4 раза меньше. Сколько тетрадок купила Света?
14.В школу купили 18
стульев, а столов в 3 раза меньше. Сколько столов купили в школу?
15.Вера купила 24кг
картофеля, а моркови в 4раза меньше. Сколько килограммов моркови купила Вера?
Задачи на увеличение в
несколько раз (косвенная форма)
1) У брата было 6 простых
открыток, их было в 2 раза меньше, чем цветных открыток. Сколько цветных
открыток было у брата?
2) Бабушка приготовила 15
банок варенья, это в 3 раза меньше, чем приготовила мама. Сколько банок варенья
приготовила мама?
3) В саду росло 18 яблок.
Это в 3 раза меньше, чем грушевых деревьев. Сколько грушевых деревьев в саду?
4) На озере плавало 6
лебедей, это в 2 раза меньше, чем уток. Сколько уток плавало в озере?
5) В первый день Катя
прочитала 18 страниц, это в 2 раза меньше, чем во второй день. Сколько страниц
Катя прочитала во второй день?
6) Таня прочитала 9
страниц, это в 3 раза меньше, чем прочитал Вова. Сколько страниц прочитал Вова?
7) У Вани 10 орехов, это
в 2 раза меньше, чем у Данила. Сколько орехов у Данила?
8) В банке 5 кг вишнёвого
варенья. Это в 3 раза меньше, чем в бидоне. Сколько кг вишнёвого варенья в
бидоне?
9) В банке 3 л молока.
Это в 4 раза меньше, чем в бидоне. Сколько литров молока в бидоне?
10) Одна наседка вывела 5
цыплят. Это в 3 раза меньше, чем другая. Сколько цыплят вывела вторая наседка?
11) В лыжный поход пошли
24 девочки. Их было в 3 раза меньше, чем мальчиков. Сколько мальчиков пошло в
поход?
12) Ёж, когда ему
угрожает опасность, пробегает в секунду 2 м. Это в 2 раза медленнее, чем
пробегает за секунду заяц. Сколько метров пробегает за секунду заяц?
13) В фильме снималось 8
детей, что в 7 раз меньше, чем взрослых. Сколько взрослых снималось в фильме?
14) В Болгарию поехали 12
школьников. Это в 4 раза меньше, чем в Венгрию. Сколько школьников отправились
в Венгрию?
15) В английской группе
занимаются 22 человека. Это в 2 раза меньше, чем в испанской. Сколько человек
занимается испанским языком?
Задачи на уменьшения
числа в несколько раз (прямая форма)
1) Саше 12 лет, а его
сестре Лене в два раза меньше. Сколько лет Лене?
2) В саду росло 36 груш,
а черешен в 4 раза меньше. Сколько черешен росло в саду?
3) На одной книжной полке
стояло 18 книг, а на второй в 2 раза меньше. Сколько книг стояло на второй
полке?
4) Грузовику нужно
перевезти 42 тонны щебня, но за один раз он может увезти в 6 раз меньше.
Сколько тонн щебня может перевести грузовик за один раз?
5) В кружок умелые руки
записалось 24 ребенка, а на секцию по шахматам в 3 раза меньше. Сколько детей
записались на секцию по шахматам?
6) В парке росло 48
кленов, а берез в 6 раз меньше. Сколько берез росло в парке?
7) Света купила 10
конфет, а Петя в 2 раза меньше. Сколько конфет купил Петя?
8) Мама купила арбуз
весом 9 кг, а папа купил арбуз в 3 раза легче. Сколько килограммов весил арбуз,
который купил папа?
9) В одной книге 24
страницы, а во второй в 3 раза меньше. Сколько страниц во второй книге?
10) На тарелке лежало 15
шоколадных конфет, а карамели было в 5 раз меньше. Сколько карамели лежало на
тарелке?
11) Тыква весит 36 кг, а
кабачок в 9 раз меньше. Сколько весит кабачок?
12) В школу купили 18
стульев, а столов в 3 раза меньше. Сколько столов купили в школу?
13) Вера купила 24 кг
картофеля, а моркови в 4раза меньше. Сколько килограммов моркови купила Вера?
14) В аквариуме плавало
12 больших рыбок, а маленьких в 3 раза меньше. Сколько маленьких рыбок плавало
в аквариуме?
15) Дима вырезал 24
красных флажка, а синих в 6 раз меньше. Сколько синих флажков вырезал Дима?
Задачи на уменьшения
числа в несколько раз (косвенная форма)
1. На одной улице 72
дома. Это в 9 раз больше, чем на другой. Сколько домов на другой улице?
2. Одна верёвка длиной 36
метров, в 9 раз больше, чем другая. Какой длины вторая верёвка?
3. Таня прочитала 54
страницы за 2 дня, это в 6 раз больше, чем прочитал Юра. Сколько страниц
прочитал Юра?
4. Утром Сережа окопал 10
кустов. Это в 2 раза больше, чем вечером. Сколько кустов окопал Сережа вечером?
5. На клумбе 15 гвоздик.
Это в 3 раза больше, чем астр. Сколько астр на клумбе?
6. В палатке 14 ящиков с
яблоками. Это в 7 раз больше, чем ящиков с бананами. Сколько ящиков с бананами
в палатке?
7. В первый день Катя
прочитала 18 страниц, это в 2 раза больше, чем во второй день. Сколько страниц
Катя прочитала во второй день?
8. В лыжный поход пошли
24 мальчика. Их было в 3 раза больше, чем девочек. Сколько девочек пошли в
поход?
9. В тетради 8 чистых
страниц. Это в 2 раза больше, чем исписанных. Сколько исписанных страниц в
тетради?
10. Фотограф сделал 56
черно-белых снимков, это в 7 раз больше, чем цветных. Сколько цветных снимков
сделал фотограф?
Задачи краткое
сравнение
1.В бочке 9 л бензина, в
неё налили ещё 81 л. Во сколько раз бензина стало больше, чем было?
2. В бидоне было 12 л
молока, в него налили ещё 24 л. Во сколько раз больше стало молока в бидоне,
чем было?
3.У Пети 24 марки, а у
Коли 8 марок. Во сколько раз у Пети марок больше, чем у Коли?
4. В саду растут 12
кустов чёрной смородины и 6 кустов красной смородины. Во сколько раз кустов
красной смородины меньше, чем чёрной смородины?
5. Верёвку длиной 16 м
укоротили до 8 м. Во сколько раз верёвка стала короче?
6. Маша вяжет шарф. В
начале недели длина шарфа составляла 2 дм, а к концу недели достигла 8 дм. Во
сколько раз шарф стал длиннее?
7. В одной квартире 9
жильцов, а в другой на 6 жильцов меньше. Во сколько раз во второй квартире
меньше жильцов, чем в первой?
8. В первом классе 6
отличников, а во втором на 3 меньше. Во сколько раз в первом классе отличников
больше, чем во втором?
9. При изготовлении
раствора для укладки кирпича требуется 60 кг песка, а цемента на 40 кг меньше.
Во сколько раз меньше требуется цемента, чем песка?
10. С бахчи собрали 55
арбузов, а дынь на 44 меньше. Во сколько раз больше собрали арбузов, чем дынь?
Задачи на нахождение
неизвестного слагаемого
1) За два дня девочка
прочитала 10 страниц. В первый день она прочитала 2 страницы. Сколько страниц
она прочитала во второй день?
2) Из сада принесли 16
стаканов малины и смородины. Малины принесли 7 стаканов. Сколько принесли
смородины?
3) Витя нашёл в лесу 17
сыроежек и лисичек. Он сказал, что сыроежек у него столько же сколько лисичек.
Не ошибся ли Витя?
4) На полке стояли 15 книг.
Из них 9 книг на английском языке, остальные на французском. Сколько книг на
французском языке стояло на полке?
5) Девочка за два дня
прочитала 22 страницы. В первый день она прочитала 10 страниц. Сколько страниц
прочитала девочка во второй день?
6) На шахматной доске
стояли 15 фигур. Из них 7 чёрных. Сколько белых фигур на шахматной доске?
7) В вазе стояли 17 белых
и красных роз. 5 роз были красными. Сколько белых роз в вазе?
8) В магазин привезли 31
ящик с овощами. Сколько привезли ящиков со свёклой, если с морковью привезли 22
ящика?
9) В двух кусках 30 м
ситца. В первом куске 10 м. Сколько ситца во втором куске?
10) Для изготовления
ёлочных украшений купили 45 листов цветной бумаги. Из них 19 листов зелёной
бумаги, а остальные – жёлтые. Сколько листов жёлтой бумаги купили?
11) Для класса купили 9
мячей. Из них 6 больших, а остальные – маленькие. Сколько маленьких мячей
купили в класс?
12) Ане подарили 8
воздушных шариков. 5 шариков оказались синими, а остальные – красными. Сколько
красных шариков подарили Ане?
13) Для детского сада
сшили 18 игрушек (мишек и зайцев). Сколько сшили зайцев, если было 8 мишек?
14) Во дворе играли 13
ребят. Из них 4 мальчика, а остальные – девочки. Сколько было девочек?
15) На зиму мама
заготовила 34 банки компота. Из них 12 банок вишнёвого компота, а остальные –
клубничного. Сколько банок клубничного компота заготовила на зиму мама?
Задачи на нахождение
неизвестного уменьшаемого
1) На стоянке было
несколько машин. Когда 3 уехало, их осталось 4. Сколько машин было на стоянке?
2) В вазе было несколько
груш. Когда 2 груши съели, их осталось 8. Сколько груш было?
3) В классе учились
ребята. Когда 10 ребят заболели, их осталось 20. Сколько всего ребят училось в
классе?
4) Мама дала Диме на
покупку тетрадей деньги. Когда он истратил 15 рублей, у него осталось 10
рублей. Сколько денег ему дали?
5) Когда из вертолёта
вышли 5 человек, в нём осталось 16 человек. Сколько человек было в вертолёте?
6) Юра подарил товарищу
12 значков и у него осталось ещё 29 значков. Сколько значков было у Юры?
7) Школьники поливали
грядки. После того как они полили 8 грядок, им осталось полить 9 грядок.
Сколько грядок должны были полить школьники?
8) После того как продали
36 кг огурцов, осталось продать ещё 17 кг. Сколько килограммов огурцов было в
ларьке?
9) Для ремонта монтёр
истратил 43 м проволоки. У него осталось ещё 17 м. Сколько метров проволоки
было у монтёра?
10) В туристическом бюро
продали 15 путёвок в Анталию и у них осталось ещё 67 путёвок. Сколько путёвок в
Анталию было в туристическом бюро?
Задачи на нахождение
неизвестного вычитаемого
1) Во дворе гуляли 10
ребят. Когда несколько ушло, во дворе осталось 4 ребят. Сколько ребят ушло?
2) В кувшине было 12
стаканов молока. К обеду из кувшина взяли несколько стаканов. Сколько стаканов
молока взяли к обеду, если в кувшине осталось 7 стаканов молока?
3) У Серёжи было 6 яблок.
Ему дали ещё несколько. После этого у него стало 10 яблок. Сколько яблок дали
Серёже?
4) В вазе было 11 яблок.
Когда несколько яблок съели, то осталось 6 яблок. Сколько яблок съели?
5) У Вани было 2
солдатика. Когда мама купила ему ещё несколько, у него стало 6 солдатиков.
Сколько солдатиков купила мама?
6) На полке стояло 27
книг. Сколько книг взяли с полки, если их осталось 20?
7) У Паши было 7 роботов.
Когда мама купила ему ещё несколько, у него стало 9 роботов. Сколько роботов
купила мама?
8) В классе 25 учеников.
Несколько детей заболело, и в школу пришло 20 учеников. Сколько детей заболело?
9) В автобусе ехали 20
человек. Когда несколько человек вышло, их осталось 15. Сколько человек вышло?
10) На кустике висели 8
ягод земляники. Когда несколько созрело и упало, их осталось 6. Сколько ягод
созрело и упало?
11) На крыше сидело 7
голубей. Когда к ним прилетело еще несколько, их стало 15. Сколько голубей
прилетело?
12) Рыцарь, защищая
прекрасную даму, сразился с 12-главым драконом. После того как дракон трусливо
покинул поле битвы, рыцарю досталось в награду 5 голов дракона. Сколько голов
унёс на своих плечах дракон к себе домой и как его теперь называют?
13) Школьный двор убирали
25 учеников. После того как несколько учеников ушло на урок, во дворе осталось
12 учеников. Сколько учеников ушли на урок?
14) В спортивном зале занимались
16 человек. Когда несколько человек пришло, то стало 32 человека. Сколько
человек пришло в спортивный зал?
15) Жена древнего
охотника заготовила на зиму 12 мешков орехов. Зимой вся семья любила вечерами
сидеть у костра и грызть орехи. К весне осталось всего 3 мешка. Сколько мешков
орехов съела семья древнего охотника зимой?
Задачи на нахождения
неизвестного множителя
1. У Игоря было 14
конфет. Он разложил их в 2 кармана. Сколько конфет в каждом кармане?
2. Бабушка засолила 3
банки с огурцами, по 10 огурцов в каждой. Сколько всего 3. огурцов засолила
бабушка?
4. Ваня поймал 16 окуней
и повесил сушиться их на 3 лески. Сколько окуней на 5. каждой леске?
6. Женя решил 20
примеров. Он записал их в два столбика. Сколько примеров в каждом столбике?
7. Мама купила 8 кустов
роз, она посадила их в два ряда. Сколько кустов роз в 8. каждом ряду?
9. Кира испекла большой
торт. Она разрезала его на 10 кусочков, а потом разложила на 5 тарелок. Сколько
кусочков на каждой тарелке?
10. У Светы было 3
коробки с карандашами по 10 штук в каждой. Сколько всего карандашей было у
Светы?
11. У Киры было 6 кукол,
она рассадила их на 2 коляски поровну. Сколько кукол сидело в каждой коляске?
12. Женя с бабушкой
насобирали яблоки, всего 40 штук. Все яблоки они разложили в 4 ящика. Сколько
яблок в каждом ящике?
13. Вова с братом собрали
2 корзины с грибами, по 10 грибов в каждой. Сколько всего грибов собрали
братья?
14. Первый множитель 2,
второй неизвестен, произведение 8. Найти второй множитель.
Задачи на нахождение
неизвестного делимого
1) В подарочные наборы
разложили 24 ореха, по 8 орехов в каждый. Сколько подарочных наборов было?
2) Когда в парке посадили
несколько ёлок, по 3 елки в каждом ряду, то получилось 7 рядов. Сколько елок
посадили?
3) В одном ящике было 16
кг огурцов, а в другом в 2 раза больше. Сколько огурцов было во втором ящике?
4) В магазин привезли
несколько пакетов муки по 2 кг в каждом пакете. Всего привезли 10 пакетов.
Сколько кг муки привезли в магазин?
5) После того как 27 слив
разложили поровну на тарелки, по несколько штук на каждую, потребовалось 9
тарелок. По сколько слив положили на каждую тарелку?
6) Девочка вымола
несколько глубоких тарелок и 2 мелкие, а всего она вымола 5 тарелок. Сколько
глубоких тарелок она вымола?
7) Мама посадила
несколько астр и 10 роз, а всего она посадила 20цветов? Сколько всего мама
посадила астр?
8) За 2 дня учительнице
надо проверить тетради учеников. Она собирается проверять по 14 тетрадей в
день. Сколько всего тетрадей надо проверить?
9) Переводчик в течение
недели переводил по 6 страниц в день, ему осталось перевести ещё 4 страницы.
Сколько он страниц перевел?
10) Во время экскурсии
учащиеся 3 класса собрали листья клёна и 10 листьев осины, а всего у них было
20 листьев. Сколько листьев клёна собрали учащиеся 3 класса.
Задачи на нахождение
неизвестного делителя
1) Нина разложила 16
елочных шаров в коробки, поровну. В каждой получилось по 8 шаров. Сколько
коробок заняли эти шары?
2) Витя принес 44 конфеты
в класс и поделил их поровну между всеми учениками. Каждый получил по 2
конфеты. Сколько учеников в классе?
3) Всего учительнице
нужно проверить 28 тетрадей. За 1 день она проверила 14 тетрадей. Сколько дней
она проверяла тетради?
4) Масса белого медведя
900 кг, а масса медведицы – 300 кг. Во сколько раз медведь тяжелее медведицы?
5) Купили 3 плитки
шоколада за 150 рублей. Сколько стоит 1 плитка?
6) После представления
клоун раскладывал шары для жонглирования. В каждую коробку он положил по 3
шара. Всего шаров было 18. Сколько коробок понадобилось клоуну?
7) Маша принесла 16
пирожных в группу и угостила всех своих одногруппников. Каждый получил по 2
пирожных. Сколько всего детей в группе?
8) Масса кота 3 кг, а
масса собаки – 15 кг. Во сколько раз кот легче собаки?
9) В класс заказали парты.
Каждый день в течение 10 дней привозили по 2 парты. Сколько всего парт заказали
в класс?
10) В течение 7 дней на
почту поступали письма. В конце недели работники посчитали письма, и получилось
21 письмо. По сколько писем приносили на почту каждый день?
11) В магазин каждый день
привозили по 3 ящика груш. Сколько дней в магазин привозили груши, если всего
привезли 24 ящика?
12) В книжный магазин
один раз в месяц привозили 4 новые книги. Сколько месяцев привозили новые
книги, если всего привезли 28 книг?
13) В школу каждый месяц
приходило по 5 новых учеников. Сколько месяцев они приходили, если всего пришло
10 учеников?
14) В автошколу каждую
неделю поступало 3 ученика. Сколько недель ученики поступали в автошколу, если
всего поступило 36 учеников?
15) Соня прочитала 15
книг. Каждую неделю она читала по 2 книги. Сколько недель читала Соня?
