Как посчитать сдачу?
Ученик
(146),
закрыт
4 года назад
Евгений Шепеленко
Ученик
(201)
6 лет назад
Ну если например сумма покупки 52 рубля тебе дают 100, просишь 2 рубля и отдаешь 50 р. сдачи,
60 значит 10 рублей,
Сколько мелочи не хватает столько и просишь.
Дарья ПоспелковаУченик (108)
3 года назад
Ничего сложного нет! 100-52=48р эти 48 пока насобираешь. или нету 48.а сдачу дать нужно. проси под расчет. проше 50р дать. к 100р просишь 2 р вот и получаеться 102-52=50р даешь сдачу эти 50р элементарно.
Костя Лавриеня
Мудрец
(18623)
6 лет назад
на каких примерах? считать научить?
если я затарился на 420 рублей, дам 500. если есть еще 20 рублей, их следом отправлю, что бы ты сдала мне 100, а не 80 рублей, ибо нафиг мне мелочь?
Алексей Миронов
Гуру
(2589)
6 лет назад
Зачем ты села за кассу если я в этом не бум бум то я и не суюсь. А вообще это арифметика 1 класса мы с тобой её не поняли в младших кассах и теперь будем мучится всю жизнь. А представь себе в магазине под вечер нарду полно и надо быстро все пробить посчитать и дать сдачу сможешь ли? Я бы не смог и турнули меня такого кассира с этого магазина бы очень быстро…
Settlers
Мудрец
(16270)
2 года назад
Я затарился на 616 рупий. Я тебе даю 1000 рублей, сдача = 384 рупий (но у тебя нет мелочи).
Ты сумму на которую я затарился округляешь до 600, и просишь у меня 16 рупий (то что нельзя округлить), я тебе даю 16 рупий.
Ты из 1000 отнимаешь 600, получается 400 – это сдача которую мне должны дать
Олюлюлю
Мастер
(1170)
9 месяцев назад
очень нужный вопрос! спасибо, так как нашла для себя тут ответы. Как тут писали, у многих касса сама пишет сдачу. Но касса ведь не предлагает какой-то аналитический вариант. Тоже с этим проблема, сейчас схему поняла более менее
Решение задачи динамического программирования о сдаче минимальным количеством монет
Содержание:
- Задача ДП о сдаче минимальным количеством монет
- Постановка задачи
- Наивное решение
- Жадный алгоритм (матройды)
- Решение задачи с помощью динамического программирования
Задача ДП о сдаче минимальным количеством монет
Постановка задачи
Теперь поставим задачу о сдаче по-другому:
Задача:
Определить минимальное количество монет (достоинством 1, 3, 5, 10), необходимое для возврата сдачи размером n. Это и есть целевая функция
Пока не нужно отвечать на вопрос: «Какие именно монеты нужно вернуть?»
Нам просто следует ответить на вопрос: «Сколько монет нужно вернуть? (минимум)»
Рассмотрим сколько нужно монет, чтобы вернуть сдачу определенного размера:
| Сдача | F |
|---|---|
0 |
0 |
1 |
1 |
2 |
2 |
3 |
минимум = 1 (3 копейки) |
4 |
минимум = 2 (1+3 копейки) |
5 |
минимум = 1 (5 копеек) |
6 |
минимум = 2 (2 решения: 3+3 копейки,5+1 копейки) |
... |
… |
Итак:
Чтобы вернуть сдачу размера 0, нужно взять: 0 монет по 1 копейки, 0 монет по 3 копейки, 0 монет по 5 копеек, 0 монет по 10 копеек.
…
Чтобы вернуть сдачу размера 3, нужно взять:
1 1 13
Минимум равен 1 — т.е. нужно вернуть монету достоинством 3 копейки
Чтобы вернуть сдачу размера 4, нужно взять:
1 1 1 11 3
…
Как можно было бы решить эту задачу?
Наивное решение
Наивное решение — это полный перебор.
Алгоритм такой:
Рассмотрим всевозможные способы вернуть сдачу размера n и выбрать тот из них, который использует минимальное количество монет (т.е. то, что уже сделано в таблице, тот же алгоритм)
Проблема: Если нам надо вернуть сдачу размером n, то в общем случае количество способов вернуть сдачу n будет пропорционально 2 в степени n/2 (на сколько делить — зависит от монет, но это уже неважно):
для n: 𝜭(2n/2)
Т.е., если надо вернуть 1000 копеек, то общее количество способов — это 2500
𝜭(2500)
Такое решение не реализуемо даже для достаточно малых n.
Таким образом, такое решение не оптимально и не эффективно. Соответственно, оно нам не подходит.
Жадный алгоритм (матройды)
Жадное решение тоже наивное.
Начнем с монеты максимального достоинства, которую можно вернуть — 10.
Зачем брать 10 раз по одной копейке, если можно взять сразу монету наибольшего достоинства — 10.
Алгоритм решения следующий:
Есть сдача размера n. Мы начнем от нее отнимать число 10 столько раз, пока n не станет меньше 10. Как только n стало меньше 10, будем возвращать уже по 5 копеек, и так продолжать до 1 копейки.
Вроде бы решение эффективное, но проблема в том, что оно неверное. Вернее, оно не всегда верное. И еще точнее: Существуют наборы монет, для которых жадное решение будет давать неверное решение, но существуют и наборы монет, для которых жадное решение дает правильное решение.
Так, для набора монет достоинством 1, 10, 100 копеек жадный алгоритм даст верное решение.
Рассмотрим пример набора монет, когда жадный алгоритм не работает:
Пример: Монеты достоинством 10, 9 и 1 копейка. Нужно вернуть сдачу размером 18:
n = 18
Решение:
18 - 10 = 88 - 1 - 1 - 1 - 1 - 1 - 1 - 1 - 1 = 0
Т.е. придется отнимать по 1 копейки 8 раз. Но понятно, что оптимальное решение для этой задачи — это 2 монеты по 9 копеек.
Таким образом, мы пока имеем два варианта решения с наивными алгоритмами: один из них не эффективен, а второй — относительно эффективный, но не всегда работает верно.
Задание: Реализовать жадный алгоритм средствами pascal
Решение задачи с помощью динамического программирования
Еще раз вспомним этапы решения задачи ДП:
- определение целевой функции F(n)
- определение начального условия (или начальных условий)
- определение порядка решения
- вычисление и нахождение общей формулы
1.
Целевая функция F(n) у нас уже определена из предыдущих решений.
Введем обозначения:
Обозначим через F(n) минимальное количество монет достоинством 1, 3, 5, 10, необходимое для возврата сдачи размера n
F(0) = 0
F(1) = 1
F(3) = 1
F(5) = 3
F(6) = 2 (5+1 или 3+3)
F(n) = ?
Решение:
2.
Начнем с самого простого, мы знаем, что
F(0) = 0
Это и будет начальным условием.
В принципе, мы уже знаем и чему равняется F(1), но в общем виде, без частного случая.
3.
Будем получать F(1), исходя из решения F(0), F(2) — исходя из решения F(1) и т.д.
Получаем порядок решения — линейный.
F(0) <- F(1) <- F(2) <- F(3) <- … <- F(n-1) <- F(n)
Таким образом, решив данную последовательность, в результате получим минимальное количество монет, которое можно вернуть в качестве сдачи номиналом n:

Рис. 3.1. Последовательность решения задачи с помощью динамического программирования
4.
Осталось сказать, как осуществляется переход. Как знание F(i) позволяют вычислить F(i+1). Т.е. нам нужно определеить общую формулу (рекурсивную) или правило перехода от решения текущей подзадачи к решению последующей подзадачи.
Посчитаем F(i) для i>=10
Итак, нам нужно вернуть сдачу размера i. F — минимальное количество монет, которое нужно, чтобы вернуть сдачу i.
Если мы для начала вернем сдачу в 1 копейку, то нам останется вернуть F(i-1) копейку.
Т.о., существует 4 способа, чтобы вернуть сдачу i:
- можно взять монету достоинством 1, и нам останется вернуть сдачу наминалом
F(i-1)минимальным количеством монет; - можно вернуть монету достоинством 3, и нам останется вернуть сдачу наминалом
F(i-3)минимальным количеством монет; - можно вернуть монету достоинством 5, и нам останется вернуть сдачу наминалом
F(i-5)минимальным количеством монет; - можно вернуть монету достоинством 10, и нам останется вернуть сдачу наминалом
F(i-10)минимальным количеством монет.
Получаем:
F(i) = 1 + F(i-1); 1 + F(i-3); 1 + F(i-5); 1 + F(i-10)
Нужно решить все 4 способа и выбрать решение с минимальным результатом.

Рис. 3.2. Нахождение общей формулы для задачи о сдаче
Таким образом, получаем общую формулу:
F(i) = min из 1+F[i-j], по всем j ∈ 1, 3, 5, 10, формула верна для всех i>=10
А F[i-j] на каждом конкретном этапе решения у нас уже есть, т.е. если мы на шаге i, то мы к этому моменту уже просчитали F[i-j].
Или рекурсивная формула для Fn:
F(n) = 1 + min [F(n-1), F(n-3), F(n-5), F(n-10)]
Здесь мы ввели индикатор, который указывает для какого n будет работать формула. Например, формула F(n-10) будет работать только при n>=10:

Рис. 3. 3. Формула для целевой функции с индикатором
Как изменится F(i), если i>5 и i<10, то j ∈ 1, 3, 5
если i>3 и i<5, то j ∈ 1, 3
если i<3, то j ∈ 1
Пример: Выполнить задачу о сдаче с минимальном количеством монет для F(15)
Решение:
Подставляем значения в общую формулу:
F(15) = min[1+F(14), 1+F(12), 1+F(10), 1+F(5)]
F(5) у нас уже просчитано (можно сделать это в уме) = 1,
F(10) — тоже в уме = 1
F(12) = ?
F(14) = ?
Рассчитываем F(12) и F(14):
Находим начальное условие (расчитываем в уме количество монет). Получаем, что F(0) = 0; F(1) = 1.
F(2)
F(2) рассчитываем по формуле и получаем:
F(2) = 1 + min[F(1)] = 1 + 1 = 2
F(3)
Посчитаем F(3) по формуле:

Для F(3) по формуле срабатывает индикатор для двух решений — n>=1 и n>=3, значит получаем:
F(3) = 1 + min[F(3-1), F(3-3)] = 1 + min[F(2), F(0)] = 2 или 0, min = 0
F(3) = 1 + 0 = 1
F(4)
Для F(4) по формуле срабатывает индикатор для двух решений — n>=1 и n>=3, значит получаем:
F(4) = 1 + min[F(4-1), F(4-3)] = 1 + min[F(3), F(1)] = 1 или 1, min = 1
F(4) = 1 + 1 = 2
Или просто в уме просчитали, что сдачу в 4 копейки можно получить, как 3 + 1 копейка, соответственно F(3) + F(1) = 2
F(5)
Для F(5) по формуле срабатывает индикатор для n>=5, значит получаем:
F(5) = 1 + min[F(5-1), F(5-3), F(5-5)] = 1 + min[F(4),F(2),F(0)] = 2 или 2 или 0, min = 0
F(5) = 1 + 0 = 1
F(12)
Аналогично рассчитываем все варианты, например, для F(12) получаем:
F(12) = 1 + min[F(11), F(9), F(7), F(2)] = 2 или 3 или 3 или 2, min = 2
F(12) = 3
F(13)
Для F(13) получаем:
F(13) = 1 + min[F(12), F(10), F(8), F(3)] = 3 или 1 или 2 или 1, min = 1
F(13) = 2
F(14)
Для F(14) получаем:
F(14) = 1 + min[F(13), F(11), F(9), F(4)] = 2 или 2 или 3 или 2, min = 2
F(14) = 3
F(15)
Для F(15) получаем:
F(15) = 1 + min[F(14), F(12), F(10), F(5)] = 3 или 3 или 1 или 1, min = 1
F(15) = 2
В итоге получаем таблицу:
| n | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Fn | 0 | 1 | 2 | 1 | 2 | 1 | 2 | 3 | 2 | 3 | 1 | 2 | 3 | 2 | 3 | 2 |
Таким образом, мы получили ответ на нашу задачу: минимальное количество монет, которое потребуется для того, чтобы отдать сдачу размером 15 копеек, равно 2 монетам, для 14 копеек — 3 монетам.
Ответ: F(15) = 2

Рис. 3.4. Пример задачи для F(15)
Долго думал, в чём же подвох в этой задаче…
Ясное дело, что для 4-го класса задачка на вычитание из 100 сначала 32, а потом 33 – не тот уровень. Тут и первоклашка её спокойно решит, тем более задачу с рисунком.
Так где же подвох? Паранойя завела меня в такие дебри:
а) Покупатель подаст сотню и купит, допустим, хлеб за 33 рубля. Сдачу – 67 рублей монетками кинет в кошелёк. Потом вспомнит, что ещё и молока нужно прикупить. Копаться с мелочью ему будет лень и он опять достанет сотню и получит сдачу 68 рублей монетками. Итого он получит сдачи 135 рублей.
б) Молоко тут что-то дешёвое, видимо низкой жирности, вначале он пакет молока возьмёт, а потом вернёт его, купив только хлеб. Сдача 67 рублей.
в) Тоже самое, что и б) только купит вместо молока йогурт.
Сдача 45 рублей, 23 рубля, или 1 рубль в зависимости от того, сколько йогурта он купит.
г) Купит кроме молока и хлеба ещё два бублика, получив сдачу в 1 рубль.
д) Другой вариант – он подаст фальшивую сотню и не получит никакой сдачи с неё. Сдача нуль.
Далее моя фантазия иссякла… Бедные 4-х классники…
Задача о сумме
Время на прочтение
4 мин
Количество просмотров 9.8K
В знаменитой задаче с монетами, которыми необходимо отсчитать сдачу, как известно, есть две беды.
— первая – это количество номиналов монет,
— вторая – это количество разрядов числа, представляющего сдачу.
И обе эти величины оказывают экспоненциальное воздействие на нагрузку машины Тьюринга, которая собственно и занимается подсчётом.
Признавать, что человек имеет сразу две зависимости, не принято даже в обществе алкоголиков. Поэтому я решил подстраховаться и избавиться от одной из этих проблем заранее. Путь это будет количество номиналов монет.
В двух словах суть проблемы описывается так: экспоненциальная зависимость. То есть выпуск нового типа монет несуществующего доселе номинала влечёт за собой увеличение количества комбинаций монет в два раза. Ещё один номинал – ещё в два раза, и так до условной бесконечности. При галопирующей инфляции, когда новые монеты/купюры выпускаются достаточно часто, для решения задачи придётся покупать более мощный компьютер. А где на это взять деньги при галопирующей то инфляции?
Итак, решение, которое на самом деле достаточно просто.
Если представить отрезок от нуля до С (сдача) с нанесёнными на ней точками, соответствующими номиналам монет, то любой интеллектуальный человек увидит примерно следующую картинку:

Ну, возможно в других цветах.
Итак, что мы можем сказать про красные точки? Конечно же то, что число, соответствующее любой этой точке, есть сумма, которую мы можем выдать в виде сдачи. Причём одной монетой. Возможно кто-то увидел что-то другое, но я, как художник, вкладывал именно этот смысл. И, как художник же, дорисую на этой картинке ещё одну точку, соответствующую сумме первой (слева направо) точки с этой же точкой (всё правильно: получится удвоенный номинал). Дорисую этим же цветом, ибо новая точка означает то же самое – эта сумма так же может быть сдачей.
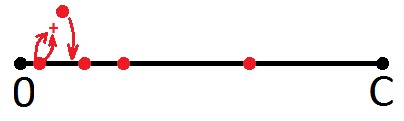
Далее беру первую точку и суммирую со второй, даже если вторая точка это предыдущая сумма (это неважно, ибо все точки здесь равны). Новую точку опять нанесу на отрезок.
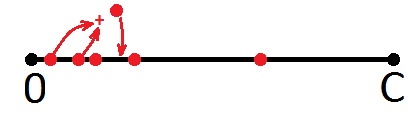
Если новая точка выходит за пределы отрезка, то ничего не рисуем, а возвращаемся к началу отрезка и берём следующую точку, то есть вторую. Далее то же самое (слева направо).
Собственно, когда точка С (напомню, это сдача) станет красной, можно считать, что решение найдено. А можно пройти полный цикл и найти оптимальное решение, что бы количество монет было минимальным.
С точки зрения программирования, здесь два цикла. Первый от 0 до С/2 (нет необходимости брать первую точку большей С/2, т.к. вторая точка всегда больше первой и в сумме они выйдут за границы отрезка). Второй цикл является встроенным в первый, он начинается с той же точки, на которую указывает внешний цикл и до момента, когда сумма покинет границы отрезка.
По сути это перебор: мы не теряем ни одного варианта, и гарантированно найдём оптимальное решение, или придём к выводу, что решения нет.
Давайте подсчитаем количество итерации внутри наших циклов. По внешнему циклу – это С/2, по внутреннему – где-то столько же. Умножим С/2 * С/2 = (С^2) / 4. Округлим до С в квадрате. Это наихудший вариант, когда весь наш отрезок просто состоит из красных точек. Если же между точками будут пробелы, количество итераций значительно уменьшится.
Как видим при определении сложности решения задачи мы не используем количество номиналов монет. Эта величина напрямую совсем никак не влияет на сложность решения. Влияют величины этих номиналов, скажем монета в 1 цент и сделает этот отрезок полностью красным. Поэтому эту монету лучше и не брать в расчёт, а в конце решения взять ближайшую к С красную точку и набросать сверху одноцентовиков. Но это уже момент оптимизации алгоритма, а она за рамками этой статьи.
Вот собственно и всё, что хотелось бы сказать. Рабочую версию программы можно найти здесь: github link
1. В файле init.h задать COINS_NUMBER — количество номиналов монет, и AMOUNT — сумма сдачи.
2. В файле coinc.c указать номиналы монет в массиве coins.
3. Под Linux запустить make_sh.
4. Запустить программу app на выполнение
Note
На экран так же будет выведено время выполнения и количество используемой памяти. Я забыл упомянуть, что придётся использовать дополнительную память. Но её количество не зависит от количества номиналов, так что всё честно.
Приведу какой-нибудь забавный пример. Представим, что в какой-нибудь стране к власти пришли математики и ввели в обращения 32 номинала монет: 2, 3, 5, 7, 11, 13, 17, 19… 131. Для удобства счёта выбрали только простые числа (ну не смешно ли?). И, что бы убедиться, что денежная реформа прошла успешно, послали в магазине гонца разменять купюру 5333 (тоже простое число). Кассир на стареньком одноядернике решил задачу: 39 монет номиналом 131 пифагороцентов, одну монету 127 и одну 97. Расчёт занял 3 секунды и чуть больше мегабайта памяти. Правительству доложили, что народ реформой доволен, считает быстро.
Note
P.S. Кстати иметь номиналы монет в виде простых чисел – на самом деле хорошая идея, ибо любую сумму можно представить двумя или тремя монетами, и нет смысла в больших кошельках.
И пример, который чуточку сложнее проверить. Монеты, сто номиналов в такой вот странной последовательности: 0101, 0202, 0303… 9898, 9999, 100100. Сумма сдачи: 101010. Поиск решения занял 1 секунду и чуть больше мегабайта памяти. А решения, собственно, и нет, то есть нельзя такими монетами набрать такую сумму. С этими же монетами проверка суммы в 1 миллион займёт 26 мегабайт и сотни секунд, что говорит об экспоненциальной зависимости от суммы, но не количества номиналов монет.
PS
Если будет интересно, следующий раз напишу о том, как взять большое число, разбить его на любые две/три/… части, занести эти части в массив, туда же добавить несколько сотен рандомных чисел и, не подсматривая, найти в массиве составляющие исходного большого числа.
Skip to content
В этом руководстве вы познакомитесь с быстрым способом расчета процентов в Excel, найдете базовую формулу процента и еще несколько формул для расчета процентного изменения, процента от общей суммы и т.д.
Расчет процента нужен во многих ситуациях, будь то комиссия продавца, ваш подоходный налог или процентная ставка по кредиту. Допустим, вам посчастливилось получить скидку 25% на новый телевизор. Это хорошая сделка? И сколько в итоге придется заплатить?
Сейчас мы рассмотрим несколько методов, которые помогут вам эффективно вычислять процент в Excel, а также освоим основные формулы процента, которые избавят вас от догадок при расчетах.
- Базовая формула подсчета процента от числа.
- Как посчитать процент между числами по колонкам.
- Как рассчитать процент по строкам.
- Доля в процентах.
- Считаем процент скидки
- Отклонение в процентах для отрицательных чисел
- Вычитание процентов
- Как избежать ошибки деления на ноль
Что такое процент?
Как вы, наверное, помните из школьного урока математики, процент – это доля от 100, которая вычисляется путем деления двух чисел и умножения результата на 100.
Основная процентная формула выглядит следующим образом:
(Часть / Целое) * 100% = Процент
Например, если у вас было 20 яблок и вы подарили 5 своим друзьям, сколько вы дали в процентном отношении? Проведя несложный подсчет =5/20*100% , вы получите ответ — 25%.
Так обычно рассчитывают проценты в школе и в повседневной жизни. Вычислить процентное соотношение в Microsoft Excel еще проще, поскольку он выполняет некоторые операции за вас автоматически.
К сожалению, универсальной формулы расчета процентов в Excel, которая охватывала бы все возможные случаи, не существует. Если вы спросите кого-нибудь: «Какую формулу процентов вы используете, чтобы получить желаемый результат?», Скорее всего, вы получите ответ типа: «Это зависит от того, какой именно результат вы хотите получить».
Итак, позвольте мне показать вам несколько простых формул для расчета процентов в Excel.
Расчет процентов в Excel.
Основная формула для расчета процента от числа в Excel такая же, как и во всех сферах жизни:
Часть / Целое = Процент
Если вы сравните ее с основной математической формулой для процента, которую мы указали чуть выше, то заметите, что в формуле процента в Excel отсутствует часть * 100. При вычислении процента в Excel вам совершенно не обязательно умножать полученную дробь на 100, поскольку программа делает это автоматически, когда процентный формат применяется к ячейке.
И если в Экселе вы будете вводить формулу с процентами, то можно не переводить в уме проценты в десятичные дроби и не делить величину процента на 100. Просто укажите число со знаком %.
То есть, чтобы, к примеру, посчитать 10% в Экселе, то вместо =A1*0,1 или =A1*10/100, просто запишите формулу процентов =A1*10%.
Хотя с точки зрения математики все 3 варианта возможны и все они дадут верный результат.
А теперь давайте посмотрим, как можно использовать формулу процента в Excel для реальных данных. Предположим, в вашей таблице Эксель записана сумма заказанных товаров в столбце F и оставленных товаров в столбце G. Чтобы высчитать процент доставленных товаров, выполните следующие действия:
- Введите формулу =G2/F2 в ячейку H2 и скопируйте ее на столько строк вниз, сколько вам нужно.
- Нажмите кнопку «Процентный стиль» ( меню «Главная» > группа «Число»), чтобы отобразить полученные десятичные дроби в виде процентов.
- Не забудьте при необходимости увеличить количество десятичных знаков в полученном результате.
- Готово! 🙂
Такая же последовательность шагов должна быть выполнена при использовании любой другой формулы процентов в Excel.
На скриншоте ниже вы видите округленный процент доставленных товаров без десятичных знаков.
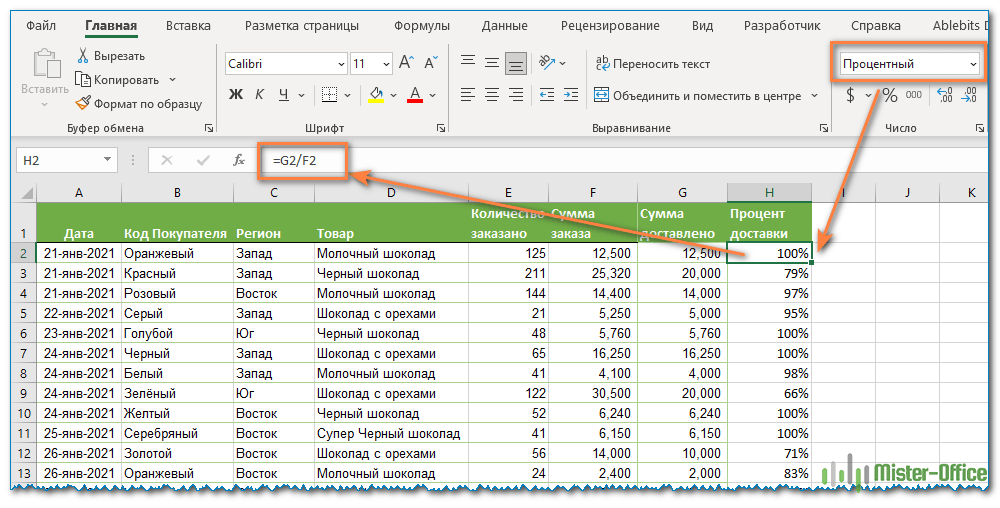
Чтобы определить процент доставки, мы сумму доставленных товаров делим на сумму заказов. И используем в ячейке процентный формат, при необходимости показываем десятичные знаки.
Запишите формулу в самую верхнюю ячейку столбца с расчетами, а затем протащите маркер автозаполнения вниз по столбцу. Таким образом, мы посчитали процент во всём столбце.
Как найти процент между числами из двух колонок?
Предположим, у нас имеются данные о продажах шоколада за 2 месяца. Необходимо определить, какие произошли изменения в реализации. Проще и нагляднее всего отклонения в продажах выразить в процентах.
Чтобы вычислить разницу в процентах между значениями A и B, используйте следующую формулу:
Процентное изменение = (B – A) / A
При применении этой формулы к реальным данным важно правильно определить, какое значение равно A, а какое – B. Например, вчера у вас было 80 яблок, а сейчас — 100. Это означает, что теперь у вас на 20 яблок больше, чем раньше, что произошло увеличение на 25%. Если у вас было 100 яблок, а теперь – 90, то количество яблок у вас уменьшилось на 10, то есть на 10%.
Учитывая вышеизложенное, наша формула Excel для процентного изменения принимает следующую форму:
=(новое_значение – старое_значение)/старое_значение
А теперь давайте посмотрим, как вы можете использовать эту формулу процентного изменения в своих таблицах.
В нашем случае —
=(E2-D2)/D2
Эта формула процентного изменения вычисляет процентное увеличение (либо уменьшение) в феврале (столбец E) по сравнению с январём (столбец В).
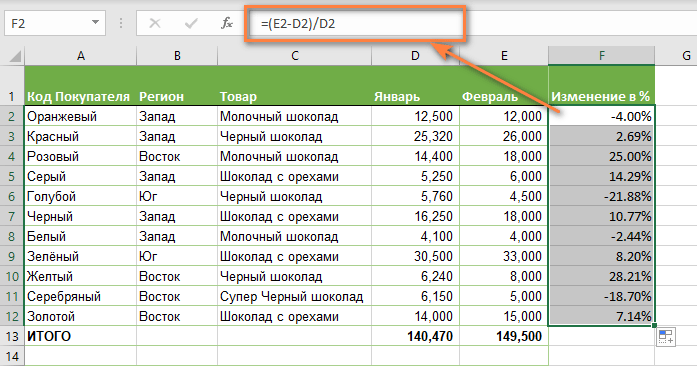
И затем при помощи маркера заполнения копируем ее вниз по столбцу. Не забудьте применить процентный формат.
Отрицательные проценты, естественно, означают снижение продаж, а положительные — их рост.
Аналогичным образом можно подсчитать и процент изменения цен за какой-то период времени.
Как найти процент между числами из двух строк?
Такой расчет применяется? Если у нас есть много данных об изменении какого-то показателя. И мы хотим проследить, как с течением времени изменялась его величина. Поясним на примере.
Предположим, у нас есть данные о продажах шоколада за 12 месяцев. Нужно проследить, как изменялась реализация от месяца к месяцу. Цифры в столбце С показывают, на сколько процентов в большую или меньшую сторону изменялись продажи в текущем месяце по сравнению с предшествующим.

Обратите внимание, что первую ячейку С2 оставляем пустой, поскольку январь просто не с чем сравнивать.
В С3 записываем формулу:
=(B3-B2)/B2
Можно также использовать и другой вариант:
=B3/B2 – 1
Копируем содержимое этой ячейки вниз по столбцу до конца таблицы.
Если нам нужно сравнивать продажи каждого месяца не с предшествующим, а с каким-то базисным периодом (например, с январём текущего года), то немного изменим нашу формулу, использовав абсолютную ссылку на цифру продаж января:
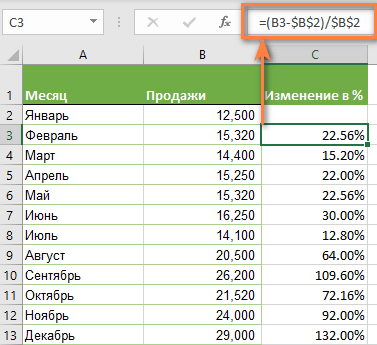
Абсолютная ссылка на $B$2 останется неизменной при копировании формулы в C4 и ниже:
=(B3-$B$2)/$B$2
А ссылка на B3 будет изменяться на B4, B5 и т.д.
Напомню, что по умолчанию результаты отображаются в виде десятичных чисел. Чтобы отобразить проценты , примените к столбцу процентный формат. Для этого нажмите соответствующую кнопку на ленте меню или используйте комбинацию клавиш Ctrl + Shift + %.
Десятичное число автоматически отображается в процентах, поэтому вам не нужно умножать его на 100.
Расчет доли в процентах (удельного веса).
Давайте рассмотрим несколько примеров, которые помогут вам быстро вычислить долю в процентах от общей суммы в Excel для различных наборов данных.
Пример 1. Сумма находится в конце таблицы в определенной ячейке.
Очень распространенный сценарий – это когда у вас есть итог в одной ячейке в конце таблицы. В этом случае формула будет аналогична той, которую мы только что обсудили. С той лишь разницей, что ссылка на ячейку в знаменателе является абсолютной ссылкой (со знаком $). Знак доллара фиксирует ссылку на итоговую ячейку, чтобы она не менялась при копировании формулы по столбцу.
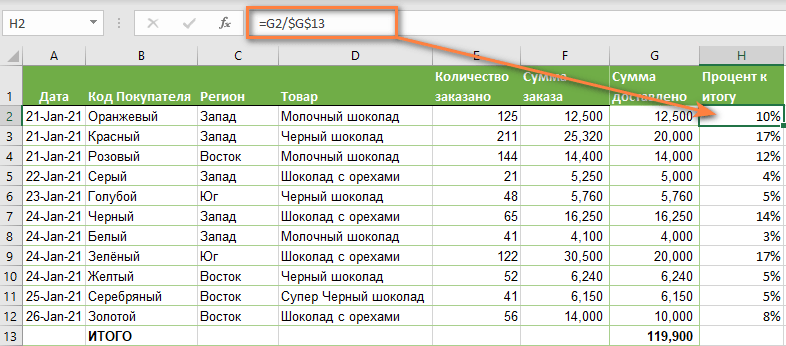
Возьмем данные о продажах шоколада и рассчитаем долю (процент) каждого покупателя в общем итоге продаж. Мы можем использовать следующую формулу для вычисления процентов от общей суммы:
=G2/$G$13
Вы используете относительную ссылку на ячейку для ячейки G2, потому что хотите, чтобы она изменилась при копировании формулы в другие ячейки столбца G. Но вы вводите $G$13 как абсолютную ссылку, потому что вы хотите оставить знаменатель фиксированным на G13, когда будете копировать формулу до строки 12.
Совет. Чтобы сделать знаменатель абсолютной ссылкой, либо введите знак доллара ($) вручную, либо щелкните ссылку на ячейку в строке формул и нажмите F4.
На скриншоте ниже показаны результаты, возвращаемые формулой. Столбец «Процент к итогу» отформатирован с применением процентного формата.
Пример 2. Часть итоговой суммы находится в нескольких строках.
В приведенном выше примере предположим, что у вас в таблице есть несколько записей для одного и того же товара, и вы хотите знать, какая часть общей суммы приходится на все заказы этого конкретного товара.
В этом случае вы можете использовать функцию СУММЕСЛИ, чтобы сначала сложить все числа, относящиеся к данному товару, а затем разделить это число на общую сумму заказов:
=СУММЕСЛИ( диапазон; критерий; диапазон_суммирования ) / Итог
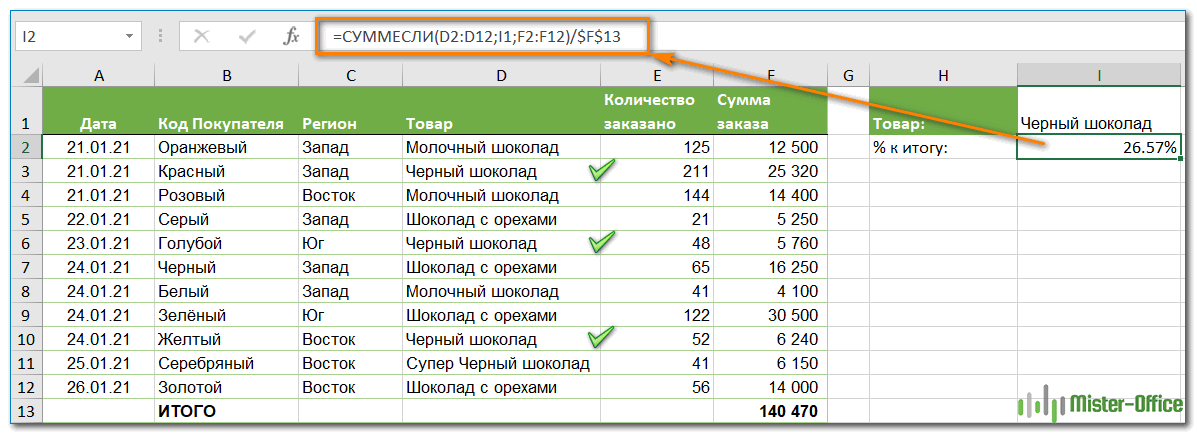
Учитывая, что столбец D содержит все наименования товаров, столбец F перечисляет соответствующие суммы, ячейка I1 содержит наименование, которое нас интересует, а общая сумма находится в ячейке F13, ваш расчет может выглядеть примерно так:
=СУММЕСЛИ(D2:D12;I1;F2:F12)/$F$13
Естественно, вы можете указать название товара прямо в формуле, например:
=СУММЕСЛИ(D2:D12;”Черный шоколад”;F2:F12)/$F$13
Но это не совсем правильно, поскольку эту формулу придется часто корректировать. А это затратно по времени и чревато ошибками.
Если вы хотите узнать, какую часть общей суммы составляют несколько различных товаров, сложите результаты, возвращаемые несколькими функциями СУММЕСЛИ, а затем разделите это число на итоговую сумму. Например, по следующей формуле рассчитывается доля черного и супер черного шоколада:
=(СУММЕСЛИ(D2:D12;”Черный шоколад”;F2:F12)/$F$13 + =СУММЕСЛИ(D2:D12;”Супер черный шоколад”;F2:F12)) / $F$13
Естественно, текстовые наименования товаров лучше заменить ссылками на соответствующие ячейки.
Для получения дополнительной информации о функции суммирования по условию ознакомьтесь со следующими руководствами:
- Как использовать функцию СУММЕСЛИ в Excel
- СУММЕСЛИМН и СУММЕСЛИ в Excel с несколькими критериями
Процент скидки
Формулы процентов пригодятся для расчета уровня скидки. Итак, отправляясь за покупками, помните следующее:
Скидка в % = (цена со скидкой – обычная цена) / обычная цена
Скидка в % = цена со скидкой / обычная цена – 1
В результатах вычисления процент скидки отображается как отрицательное значение, поскольку новая цена со скидкой меньше старой обычной цены. Чтобы вывести результат в виде положительного числа , оберните формулы в функцию ABS. Например:
=ABS((C2-B2)/B2)
или
=ABS((C2/B2 – 1)
Так будет гораздо привычнее.

Как рассчитать отклонение в процентах для отрицательных чисел
Если некоторые из исходных значений представлены отрицательными числами, приведенные выше формулы не будут работать.
Обычный обходной путь – сделать знаменатель в формуле положительным числом. Для этого воспользуйтесь функцией ABS:
( Новое_значение – старое_значение ) / ABS( старое_значение )
Со старым значением в B2 и новым значением в C2 формула выглядит следующим образом:
=(C2-B2)/ABS(B2)
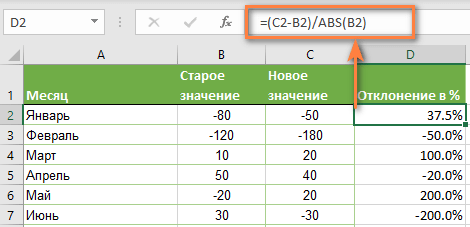
Как видите, достаточно корректно работает с самыми разными комбинациями положительных и отрицательных чисел.
Положительный процент означает рост, отрицательный — снижение величины показателя.
Вычитание процентов.
Часто случается, что вам известен процент скидки на товар. И вам нужно высчитать, какой процент от первоначальной стоимости придётся заплатить. Как мы уже говорили, процент в Экселе — это обычное число. Поэтому и правила вычисления здесь – как с обычными числами.

Формула расчета в Excel будет выглядеть так:
=1 – процент_скидки
Как обычно, не забываем про процентный формат ячеек.
Предотвратить ошибки деления на ноль #ДЕЛ/0
Если вы хотите посчитать процент от числа в таблице, и ваш набор данных содержит несколько нулевых значений, заключите формулы в функцию ЕСЛИОШИБКА, чтобы предотвратить появление ошибок деления на ноль (#ДЕЛ/0! или #DIV/0!).
=IFERROR(=ЕСЛИОШИБКА((C2-B2)/B2;0)
=IFERROR(=ЕСЛИОШИБКА(C2/B2-1;0)

Вот как можно вычислить процент от числа в Excel. И даже если работа с процентами никогда не была вашим любимым видом математики, с помощью этих основных процентных формул вы можете заставить Excel делать работу за вас.
На сегодня все, спасибо, что прочитали!
