Свойства гиперболы
1) Область определения и область значений
По аналитическому заданию функции видно, что х ≠-a, поскольку знаменатель дроби не может ровняться нулю. Таким образом получим:
D(f)=(-∞;-а) U (-a;+∞)
Область значений
Е(f)=(-∞;+∞)
2) Нули функции
Если b=0, то график функции не пересекает ось ОХ;
Если b≠0, то гипербола имеет одну точку пересечения с ОХ:*
x=-(k+ab)/b
3) Промежутки знакопостоянства
Рассмотрим только 2 простых случая, остальные случаи вы можете рассмотреть аналитически самостоятельно по алгоритму из раздела Свойства функций -> Знакопостоянство
Случай 1: a=0, b=0, k>0
f(x)>0, при x ∈ (0; +∞)
f(x)<0, при x ∈ (-∞;0)
Случай 1: a=0, b=0, k<0
f(x)<0, при x ∈ (0; +∞)
f(x)>0, при x ∈ (-∞;0)
4) Промежутки монотонности
Аналогично с промежутками знакопостоянства рассмотрим только 2 случая
Случай 1: a=0, b=0, k>0
Функция убывает при
x ∈ (-∞;0) U (0; +∞)
Функция возрастает при
x ∈ (-∞;0) U (0; +∞)
5) Четность и нечетность
Функция является нечетной при a=0, b=0, то есть если имеет вид y=k/x
Гипербола
Что такое гипербола? Как построить гиперболу? (Для школьников (7-11 классов)).
Функция заданная формулой (y=frac), где к неравно 0. Число k называется коэффициентом обратной пропорциональности.
Определение гиперболы.
График функции (y=frac) называют гиперболой. Где х является независимой переменной, а у — зависимой.
Что нужно знать, чтобы построить гиперболу?
Теперь обсудим свойства гиперболы:
 гипербола, где k y≠0 это вторая асимптота.
гипербола, где k y≠0 это вторая асимптота.
И так, асимптоты x≠0 и y≠0 в данном примере совпадают с осями координат OX и OY.
k=1, значит гипербола будет находится в первой и третьей четверти. k всегда находится в числители.
Построим примерный график гиперболы. 
Пример №2:
$$y=frac<1>-1$$
Находим первую асимптоту.
Знаменатель не может равняться 0, потому что на 0 делить нельзя, поэтому х+2 неравен 0.
х+2≠0
х≠-2 это первая асимптота
Находим вторую асимптоту.
Дробь (color <frac<1>>) отбрасываем
Остается y≠ -1 это вторая асимптота.
Строим примерный график, отмечаем асимптоты (красным проведены прямые х≠-2 и y≠-1): 

Находим первую асимптоту.
Знаменатель не может равняться 0, потому что на 0 делить нельзя, поэтому 1+х неравен 0.
1+х≠0
х≠-1 это первая асимптота.
Находим вторую асимптоту.
Остается y≠1 это вторая асимптота.
Строим примерный график, отмечаем асимптоты (красным проведены прямые х≠-1 и y≠1): 

3. У гиперболы есть центр симметрии относительно начала координат. Рассмотрим на примере:
Возьмем точку А(1;1) с координатами, которая находится на графике у=1/х. На этом же графике лежит точка B(-1;-1). Видно, что точка А симметрична точке В относительна начала координат. 
4. Оси симметрии гиперболы. У гиперболы две оси симметрии. Рассмотрим пример:
Первой осью симметрии является прямая y=x. Посмотрим точки (0,5;2) и (2;0,5) и еще точки (-0,5;-2) и (-2;-0,5). Эти точки расположены по разные стороны данной прямой, но на равных расстояниях от нее, они симметричны относительно этой прямой.
Вторая ось симметрии это прямая y=-x.

5. Гипербола нечетная функция.
6. Область определения гиперболы и область значения гиперболы. Область определения смотрим по оси х. Область значения смотрим по оси у. Рассмотрим на примере:
а) Находим первую асимптоту.
Знаменатель не может равняться 0, потому что на 0 делить нельзя, поэтому x-1 неравен 0.
x-1≠0
х≠1 это первая асимптота.
Находим вторую асимптоту.
Остается y≠ -1 это вторая асимптота.
б) k=-1, значит ветви гиперболы будут находится во второй и четвертой четверти.
в) Возьмем несколько дополнительных точек и отметим их на графике.
х=0 y=0
x=-1 y=-0,5
x=2 y=-2
x=3 y=-1,5
г) Область определения смотрим по оси х. Графика гиперболы не существует по асимптоте х≠1, поэтому область определения будет находится
х ∈ (-∞;1)U(1;+∞).
д) Область значения смотрим по оси y. График гиперболы не существует по асимптоте y≠ -1, поэтому область значения будет находится
y ∈ (-∞;-1)U(-1;+∞).
е) функция возрастает на промежутке x ∈ (-∞;1)U(1;+∞). 

7. Убывание и возрастание функции гиперболы. Если k>0, функция убывающая. Если k Category: 8 класс, База знаний, Уроки Tag: Гипербола Leave a comment
Гипербола: определение, функция, формула, примеры построения
В данной публикации мы рассмотрим, что такое гипербола, приведем формулу, с помощью которой задается ее функция, а также на практических примерах разберем алгоритм построения данного вида графика.
Определение и функция гиперболы
Гипербола – это график функции обратной пропорциональности, которая в общем виде задается следующей формулой:

- x – независимая переменная;
- k ≠ 0;
- при k > 0 гипербола расположена в I и III четвертях координатной плоскости;
- при k 0)
- y = -x (при k Алгоритм построения гиперболы
Пример 1
Дана функция y = 4 /x. Построим ее график.
Решение
Так как k > 0, следовательно, гипербола будет находиться в I и III координатных четвертях.
Чтобы построить график, сначала нужно составить таблицу соответствия значений x и y. То есть мы берем конкретное значение x, подставляем его в формулу функции и получаем y.
” data-lang=”default” data-override=”<“emptyTable”:””,”info”:””,”infoEmpty”:””,”infoFiltered”:””,”lengthMenu”:””,”search”:””,”zeroRecords”:””,”exportLabel”:””,”file”:”default”>” data-merged=”[]” data-responsive-mode=”2″ data-from-history=”0″>
| x | y | Расчет y |
| 0,5 | 8 | 4 / 0,5 = 8 |
| 1 | 4 | 4 / 1 = 4 |
| 2 | 2 | 4 / 2 = 2 |
| 4 | 1 | 4 / 4 = 1 |
| 8 | 0,5 | 4 / 8 = 0,5 |
Теперь отмечаем найденные точки на координатной плоскости и соединяем их плавной линией, которая будет стремиться к осям координат. В итоге получится ветвь гиперболы, расположенная в первой четверти.

Чтобы построить ветвь в третьей четверти, вместо x в формулу подставляем -x. Так мы вычислим значения y.
” data-lang=”default” data-override=”<“emptyTable”:””,”info”:””,”infoEmpty”:””,”infoFiltered”:””,”lengthMenu”:””,”search”:””,”zeroRecords”:””,”exportLabel”:””,”file”:”default”>” data-merged=”[]” data-responsive-mode=”2″ data-from-history=”0″>
| x | y | Расчет y |
| -0,5 | -8 | 4 / -0,5 = -8 |
| -1 | -4 | 4 / -1 = -4 |
| -2 | -2 | 4 / -2 = -4 |
| -4 | -1 | 4 / -4 = -1 |
| -8 | -0,5 | 4 / -8 = -0,5 |
Соединив полученные точки получаем следующий результат. На этом построение гиперболы завершено.

Пример 2
Рассмотренный выше пример был одним из самых простых (без смещения асимптот). Давайте усложним задачу и построим гиперболу, заданную функцией ниже:
Основные сведения о гиперболе в математике
Понятие гиперболы
Гипербола — это множество точек на плоскости, для которых модуль разности расстояний от двух точек (фокусов) — величина постоянная и меньшая, чем расстояние между фокусами.
Каноническое уравнение гиперболы:
где a, b — положительные действительные числа.
Более простое определение:
Гипербола — это график функции обратной пропорциональности, которая задается следующей формулой:
- x — независимая переменная;
- y — функция;
- k — коэффициент пропорциональности. При этом k≠0. При k>0 график расположен в 1 и 3 четвертях координатной плоскости (функция убывает), при k
Форма гиперболы
График гиперболы выглядит следующим образом:
- Зеленые кривые называются ветвями гиперболы. Расположение ветвей гиперболы зависит от знака k.
- Оси абсцисс (OX) и ординат (OY) являются асимптотами графика. Асимптота — прямая, к которой стремится график, но не пересекает ее.
- Ось симметрии (синяя прямая) выражается уравнением: y=x (при k>0) или y=-x (при k y = k / x
Но также для построения необходимо знать, как расположены асимптоты.
В стандартном случае это оси абсцисс и ординат. Но асимптоты могут быть и смещены. Тогда функция будет задаваться уравнением вида:
y = k / ( x – a ) + b , где:
- x=a — вертикальная асимптота графика (при a≠0) вместо оси ординат. Если перед a стоит «минус», то смещение вправо. Если перед a стоит «плюс», то смещение влево;
- y=b — горизонтальная асимптота графика (при b≠0) вместо оси абсцисс. Если перед b стоит «минус», то смещение вниз. Если перед b стоит «плюс», то смещение вверх.
Построение гиперболы
Алгоритм построения гиперболы по точкам:
- Строим систему координат.
- Решить, в каких четвертях будет располагаться график (в зависимости от знака коэффициента k).
- Определяемся со смещением асимптот.
- Составляем таблицу значений. Берем (как минимум) три положительных и три отрицательных значения x, подставляем в уравнение, вычисляем y.
- Наносим точки на координатную плоскость.
- Соединяем точки, получаем график.
Примеры решения задач
Построить гиперболу по заданному уравнению:
y = – 2 / ( x – 3 ) + 4
График будет располагаться во 2 и 4 координатных четвертях, так как k
[spoiler title=”источники:”]
http://wika.tutoronline.ru/geometriya/class/11/osnovnye-svedeniya-o-giperbole-v-matematike
[/spoiler]
Обратная пропорциональность — коротко о главном
Определение:
Функция, описывающая обратную пропорциональность, – это функция вида ( displaystyle y=frac{k}{x-a}+b ), где ( kne 0), ( xne 0) и ( xne а)
По-другому эту функцию называют обратной зависимостью.
Область определения и область значений функции:
( Dleft( y right)=left( -infty ;0 right)cup left( 0;+infty right)) или, что то же самое, ( Dleft( y right)=mathbb{R}backslash left{ 0 right})
( Eleft( y right)=left( -infty ;0 right)cup left( 0;+infty right)) или ( Eleft( y right)=mathbb{R}backslash left{ 0 right}).
График обратной пропорциональности (зависимости) – гипербола.
Коэффициент ( displaystyle k)
( displaystyle k) – отвечает за «пологость» и направление графика. Чем больше этот коэффициент, тем дальше от начала координат располагается гипербола, и, следовательно, она менее круто «поворачивает» (см. рисунок).
Знак коэффициента ( displaystyle k) влияет на то, в каких четвертях расположен график:
если ( displaystyle k>0), то ветви гиперболы расположены в ( displaystyle I) и ( displaystyle III) четвертях;
если ( displaystyle k<0), то во ( displaystyle II) и ( displaystyle IV).
Коэффициент ( displaystyle a)
Если внимательно посмотреть на знаменатель, видим, что ( displaystyle a) – это такое число, которому не может равняться ( displaystyle x).
То есть ( x=a) – это вертикальная асимптота, то есть вертикаль, к которой стремится график функции
Коэффициент ( b)
Число ( b) отвечает за смещение графика функции вверх на величину ( b), если ( b>0), и смещение вниз, если ( b<0).
Следовательно, ( y=b) – это горизонтальная асимптота.
Алгоритм построения графика функции ( displaystyle y=frac{k}{x-a}+b)
- Определяем коэффициенты ( displaystyle k), ( displaystyle a) и ( displaystyle b).
- Строим график функции ( displaystyle y=frac{k}{x}) (сначала по 3-4 точкам правую ветвь, потом симметрично рисуем левую ветвь).
- График должен быть сдвинут вправо на ( displaystyle a). Но проще двигать не график, а оси, так что ось ( displaystyle Oy) сдвигаем влево на ( displaystyle a).
- График должен быть сдвинут вверх на ( displaystyle b). Но проще двигать не график, а оси, так что ось ( displaystyle Ox) сдвигаем вниз на ( displaystyle b).
- Старые оси (прямые, которые служили нам осями в пункте 2) оставляем в виде пунктирных линий. Это теперь просто вертикальная и горизонтальная асимптоты.
Что такое функция
Ты помнишь, что функция – это определенного рода зависимость?
Если ты еще не читал тему «Функции», настоятельно рекомендую бросить все и прочитать, ведь нельзя изучать какую-либо конкретную функцию, не понимая, что это такое – функция.
Также очень полезно перед началом этой темы освоить две более простые функции: линейную и квадратичную.
Там ты закрепишь понятие функции и научишься работать с коэффициентами и графиками.
Ну и на всякий случай немного повторим…
Функция – это правило, по которому каждому элементу одного множества (аргументу) ставится в соответствие некоторый (единственный!) элемент другого множества (множества значений функции).
То есть, если у тебя есть функция ( y=fleft( x right)), это значит что каждому допустимому значению переменной ( x) (которую называют «аргументом») соответствует одно значение переменной ( y) (называемой «функцией»).
Что значит «допустимому значению»?
Если не можешь ответить на этот вопрос, еще раз вернись к теме «Функции»!
Все дело в понятии «область определения»: для некоторых функций не все аргументы можно подставить в зависимость. Например, для функции ( y=sqrt{x}) отрицательные значения аргумента ( x) – недопустимы.
Функция, описывающая обратную зависимость
Это функция вида ( displaystyle y=frac{k}{x}), где ( kne 0).
По-другому ее называют обратной пропорциональностью: увеличение аргумента вызывает пропорциональное уменьшение функции.
Давай определим область определения. Чему может быть равен ( x)? Или, по-другому, чему он не может быть равен?
Единственное число, на которое нельзя делить – это ( 0), поэтому ( xne 0):
( Dleft( y right)=left( -infty ;0 right)cup left( 0;+infty right))
или, что то же самое,
( Dleft( y right)=mathbb{R}backslash left{ 0 right})
Такая запись означает, что ( x) может быть любым числом, кроме ( 0).
- Знак «( mathbb{R})» обозначает множество действительных чисел, то есть всех возможных чисел.
- Знаком «( backslash )» обозначается исключение чего-нибудь из этого множества (аналог знака «минус»).
- Число ( 0) в фигурных скобках означает просто число ( 0).
Получается, что из всех возможных чисел мы исключаем ( 0)).
Множество значений функции, оказывается, точно такое же: ведь если ( kne 0), то на что бы мы его не делили, ( 0) не получится:
( Eleft( y right)=left( -infty ;0 right)cup left( 0;+infty right)) или ( Eleft( y right)=mathbb{R}backslash left{ 0 right}).
Также возможны некоторые вариации формулы ( y=frac{k}{x}). Например, ( y=frac{k}{x+a}) – это тоже функция, описывающая обратную зависимость.
Определи самостоятельно область определения и область значений этой функции. Должно получиться:
- ( Dleft( y right)=left( -infty ;-a right)cup left( -a;+infty right))
- ( Eleft( y right)=left( -infty ;0 right)cup left( 0;+infty right)).
Давай посмотрим на такую функцию: ( displaystyle y=frac{x-5}{{{x}^{2}}-25}).
Является ли она обратной зависимостью?
На первый взгляд сложно сказать: ведь при увеличении ( x) увеличивается и знаменатель дроби, и числитель, так что непонятно, будет ли функция уменьшаться, и если да, то будет ли она уменьшаться пропорционально?
Чтобы понять это, нам необходимо преобразовать выражение таким образом, чтобы в числителе не было переменной:
( displaystyle y=frac{x-5}{{{x}^{2}}-25}=frac{x-5}{left( x-5 right)left( x+5 right)}=frac{1}{x+5},text{ }xne 5).
Действительно, мы получили обратную зависимость, но с оговоркой: ( xne 5).
Почему так? А потому, что выражение ( left( x-5 right)) было в исходном выражении в знаменателе, поэтому если мы возьмём значение ( x=5) и подставим его в исходную функцию (а ведь именно её нам нужно исследовать), то что мы получим?
Ноль, делённый на ноль. Но ведь на ноль нельзя делить ничего, даже другой ноль. Поэтому ( x) никак не может быть равен ( 5).
Но почему тогда мы также не пишем ( xne -5)? Оно ведь тоже в знаменателе!
А всё потому, что оно как было в знаменателе, так там и осталось, следовательно мы и так видим, что такое значение икса невозможно.
А поэтому — зачем лишний раз писать? Да-да, математики — народ ленивый, без надобности напрягаться не станут:)
Решения
Пример 1
( displaystyle y=1-frac{3}{x+2})
Пример 2
Здесь нужно вспомнить, как квадратный трехчлен раскладывается на множители (это подробно описано в теме «Разложение на множители»).
Напомню, что для этого надо найти корни соответствующего квадратного уравнения: ( displaystyle {{x}^{2}}+4{x}-5=0).
Я найду их устно с помощью теоремы Виета: ( displaystyle {{x}_{1}}=-5), ( displaystyle {{x}_{2}}=1). Как это делается? Ты можешь научиться этому, прочитав тему «Квадратные уравнения».
Итак, получаем: ( displaystyle {{x}^{2}}+4{x}-5=left( x+5 right)left( x-1 right)), следовательно:
( displaystyle y=frac{x+5}{left( x+5 right)left( x-1 right)}=frac{1}{x-1},text{ }xne -5)
Пример 3
Ты уже попробовал решить сам? В чем загвоздка?
Наверняка в том, что в числителе у нас ( displaystyle 2x), а в знаменателе – просто ( displaystyle x).
Это не беда. Нам нужно будет сократить на ( displaystyle left( x+2 right)), поэтому в числителе следует вынести ( displaystyle 2) за скобки (чтобы в скобках ( displaystyle x) получился уже без коэффициента):
( displaystyle y=frac{2{x}-3}{x+1}=frac{2left( x-frac{3}{2} right)}{x+1}=2cdot frac{x-1,5}{x+1}=2cdot frac{x+1-1-1,5}{x+1}=…) дальше сам.
Ответ: ( displaystyle y=2-frac{5}{x+1}).
График обратной пропорциональности
Как всегда, начнем с самого простого случая: ( displaystyle y=frac{1}{x}).
Составим таблицу.
Таблица обратной пропорциональности (зависимости)
| ( displaystyle mathbf{x}) | ( displaystyle -3) | ( displaystyle -2) | ( displaystyle -1) | ( displaystyle -0,5) | ( displaystyle 0,5) | ( displaystyle 1) | ( displaystyle 2) | ( displaystyle 3) | ( displaystyle 4) |
| ( displaystyle mathbf{y}) | ( displaystyle -frac{1}{3}) | ( displaystyle -frac{1}{2}) | ( displaystyle -1) | ( displaystyle -2) | ( displaystyle 2) | ( displaystyle ;1) | ( displaystyle frac{1}{2}) | ( displaystyle frac{1}{3}) | ( displaystyle frac{1}{4}) |
Нарисуем точки на координатной плоскости:
Теперь их надо плавно соединить, но как?
Видно, что точки в правой и левой частях образуют будто бы несвязанные друг с другом кривые линии. Так оно и есть.
Это график гиперболы и выглядит он так:
Этот график называется «гипербола» (есть что-то похожее на «параболу» в этом названии, правда?). Как и у параболы, у гиперболы две ветки, только они не связаны друг с другом.
Каждая из них стремится своими концами приблизиться к осям ( displaystyle Ox) и ( displaystyle Oy), но никогда их не достигает. Если посмотреть на эту же гиперболу издалека, получится такая картина:
Оно и понятно: так как ( displaystyle xne 0), график не может пересекать ось ( displaystyle Oy). Но и ( displaystyle yne 0), так что график никогда не коснется и оси ( displaystyle Ox).
Ну что же, теперь посмотрим на что влияют коэффициенты.
На что влияют коэффициенты
Рассмотрим такие функции:
( displaystyle y=frac{1}{x};text{ }y=frac{2}{x};text{ }y=frac{4}{x};text{ }y=-frac{1}{x};text{ }y=-frac{3}{x}):
Ух ты, какая красота!
Все графики построены разными цветами, чтобы легче было их друг от друга отличать.
Итак, на что обратим внимание в первую очередь?
Например, на то, что если у функции перед дробью стоит минус, то график переворачивается, то есть симметрично отображается относительно оси ( displaystyle Ox).
Второе: чем больше число в знаменателе, тем дальше график «убегает» от начала координат.
А что, если функция выглядит сложнее, например, ( displaystyle y=frac{1}{x-1}+2)?
В этом случае гипербола будет точно такой же, как обычная ( displaystyle y=frac{1}{x}), только она немного сместится. Давай думать, куда?
Чему теперь не может быть равен ( x)? Правильно, ( xne 1). Значит, график никогда не достигнет прямой ( x=1).
А чему не может быть равен ( y)? Теперь ( yne 2). Значит, теперь график будет стремиться к прямой ( y=2), но никогда ее не пересечет.
Итак, теперь прямые ( x=1) и ( y=2) выполняют ту же роль, которую выполняют координатные оси для функции ( displaystyle y=frac{1}{x}).
Такие прямые называются асимптотами (линии, к которым график стремится, но не достигает их):
Более подробно о том, как строятся такие графики, мы выучим чуть позже.
А теперь попробуй решить несколько примеров для закрепления.
Обратная пропорциональность в жизни
Где же нам встречается такая функция на практике? Примеров множество. Самый распространенный – это движение: чем больше скорость, с которой мы движемся, тем меньшее время нам потребуется, чтобы преодолеть одно и то же расстояние.
И правда, вспомним формулу скорости: ( displaystyle v=frac{S}{t}), где ( v) – скорость, ( t) – время в пути, ( S) – расстояние (путь).
Отсюда можно выразить время: ( displaystyle t=frac{S}{v})
Пример:
Человек едет на работу со средней скоростью ( 40) км/ч, и доезжает за ( 1) час. Сколько минут он потратит на эту же дорогу, если будет ехать со скоростью ( 60) км/ч?
Решение:
Вообще, такие задачи ты уже решал в 5 и 6 классе. Ты составлял пропорцию:
( displaystyle 60) км/ч – ( 60) мин.
( displaystyle 60) км/ч – ( x) мин.
Далее ты определял, что это обратная пропорциональность, так как чем больше скорость, тем меньше время. Значит, чтобы решить эту пропорцию, нужно поделить числа «крест-накрест»:
( displaystyle frac{40}{x}=frac{60}{60}text{ }Rightarrow text{ }x=40)(мин).
То есть понятие обратной пропорциональности тебе уже точно знакомо. Вот и вспомнили. А теперь то же самое, только по-взрослому: через функцию.
Функция (то есть зависимость) времени в минутах от скорости:
( displaystyle tleft( v right)=frac{S}{v}).
Известно, что ( tleft( 40 right)=60), тогда:
( frac{S}{40}=60text{ }Rightarrow text{ }S=40cdot 60=2400).
Нужно найти ( tleft( 60 right)):
( displaystyle tleft( 60 right)=frac{2400}{60}=40) (мин).
Теперь придумай сам несколько примеров из жизни, в которых присутствует обратная пропорциональность.
Придумал? Молодец, если да. Удачи!
Принципы построения графика обратной пропорциональности (гиперболы)
Теперь давай научимся строить простейшую гиперболу – ( displaystyle y=frac{k}{x}).
Достаточно помнить, как она выглядит, и тогда нам хватит всего трех-четырех точек.
Например, построим гиперболу ( displaystyle y=frac{3}{x}).
Составим таблицу из ( 4) точек, которые принадлежат одной ветке (например, правой):
| ( x) | ( frac{1}{2}) | ( displaystyle 1) | ( displaystyle 3) | ( displaystyle 6) |
| ( y) | ( displaystyle 6) | ( displaystyle 3) | ( displaystyle 1) | ( frac{1}{2}) |
Отмечаем точки на рисунке:
Проводим через них плавную линию, которая краями приближается к осям:
Это одна ветвь гиперболы
Проверить правильность построения этой кривой можно так: она должна быть симметрична относительно биссектрисы угла между осями координат:
Отлично, осталось вспомнить, что собой представляет вторая ветвь?
Это точно такая же кривая, расположенная симметрично относительно начала координат. То есть как будто оси теперь направлены не снизу вверх и слева направо, а наоборот: сверху вниз и справа налево, и мы рисуем ту же самую ветвь гиперболы.
Вот:
Еще один полезный факт.
Посмотри на красные точки на графике. Видно, что их абсцисса совпадает с ординатой. Так вот, эти абсцисса с ординатой равны ( sqrt{k}) для правой ветви гиперболы, и ( -sqrt{k}) для левой.
Для функций, у которых ( k) – точный квадрат (например, ( 1), ( 4) или ( displaystyle frac{1}{4})), эту точку, относительно которой ветвь гиперболы симметрична, будет очень легко поставить.
В этом случае достаточно даже трех точек, чтобы построить график.
Например, построим график функции ( displaystyle y=frac{4}{x})
Как и в прошлый раз, начнем с правой ветви.
Точка симметрии: ( displaystyle x=y=2). Выберем еще одну точку, например, ( displaystyle x=1), ( displaystyle y=4). У третьей точки координаты будут наоборот: ( displaystyle x=4), ( displaystyle y=1).
Рисуем:
И теперь симметрично отображаем эту ветвь в третью координатную четверть:
Теперь выясним, что будет, если ( displaystyle k<0)?
Очень просто: если есть график функции с таким же по величине, но положительным ( displaystyle k), то нужно просто отразить его относительно оси ( displaystyle Ox)
То есть правая ветвь теперь будет ниже оси ( displaystyle Ox) (в ( displaystyle IV) четверти), а левая – выше (в ( displaystyle III) четверти).
Принцип построения же останется прежним:
Ну что же, осталось объединить все то, что мы уже выяснили в один алгоритм:
Гипербола и ее каноническое уравнение
Определение.
Гиперболой называется геометрическое
место точек, разность от каждой из
которых до двух данных точек, называемых
фокусами есть величина постоянная
Возьмем
систему координат, так чтобы фокусы
лежали на оси абсцисс, а начало координат
делило отрезок F1
F2
пополам (рис. 30). Обозначим F1
F2
= 2c.
Тогда F1
(с; 0); F2
(-c;
0)
M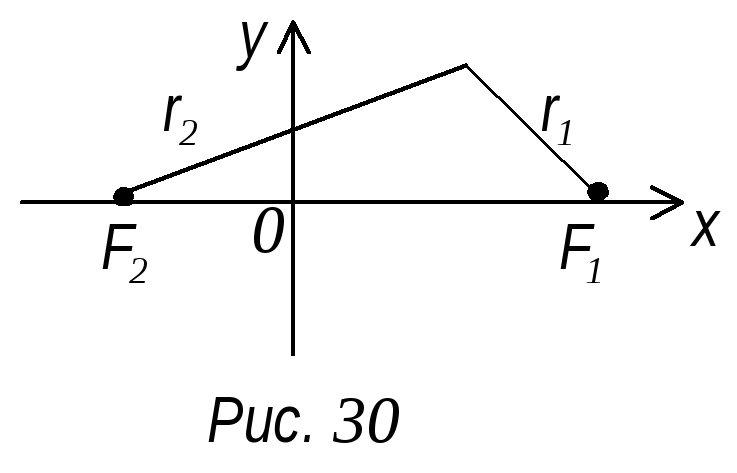 F2
F2
= r2,
MF1
= r1
– фокальные радиусы гиперболы.
Согласно
определения гиперболы r1
– r2
= const.
Обозначим
ее через 2а
Тогда
r2–
r1
= ±2a
итак:
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() =>
=>
каноническое
уравнение гиперболы
Так
как уравнение гиперболы х и у в четных
степенях, то если точка М0
(х0;
у0)
лежит на гиперболе, то на ней лежат также
точки М1
(х0;
-у0)
М2
(-х0;
-у0)
М3
(-х0;
-у0).
Следовательно,
гипербола симметрична относительно
обеих координатных осей.
При
у = 0 х2
= а2
х = ± а. Вершинами гиперболы будут точки
А1
(а; 0); А2
(-а; 0).
![]() .
.
В силу симметрии исследование ведем в
I
четверти
![]()
1)
при
![]()
у имеет мнимое значение, следовательно,
точек гиперболы с абсциссами
![]()
не существует
2)
при х = а; у = 0 А1
(а; 0) принадлежит гиперболе
3)
при x
> a;
y
> 0. Причем при неограниченном возрастании
х ветвь гиперболы уходит в бесконечность.
Отсюда
следует, что гипербола представляет
собой кривую, состоящую из двух бесконечных
ветвей.
П 6. Асимптоты гиперболы
Рассмотрим
вместе с уравнением
![]()
уравнение прямой
![]()
К ривая
ривая
будет лежать ниже прямой (рис. 31).
Рассмотрим точкиN
(x,
Y)
и М (х, у) у которой абсциссы одинаковы,
а У – у = MN.
Рассмотрим
длину отрезка MN
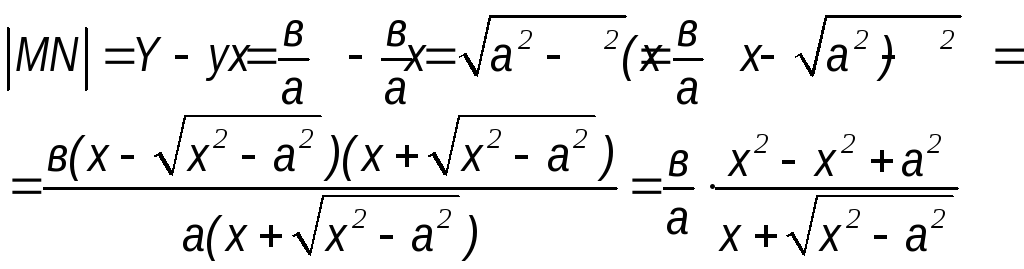
Найдем
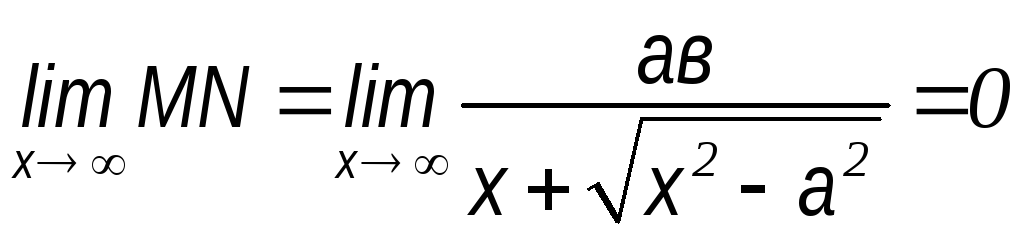
Итак,
если точка М, двигаясь по гиперболе в
первой четверти удаляется в бесконечность,
то ее расстояние от прямой
![]()
уменьшается и стремится к нулю.
В
силу симметрии таким же свойством
обладает прямая
![]() .
.
Определение.
Прямые к которым при
![]()
кривая неограниченно приближается
называются асимптотами.
И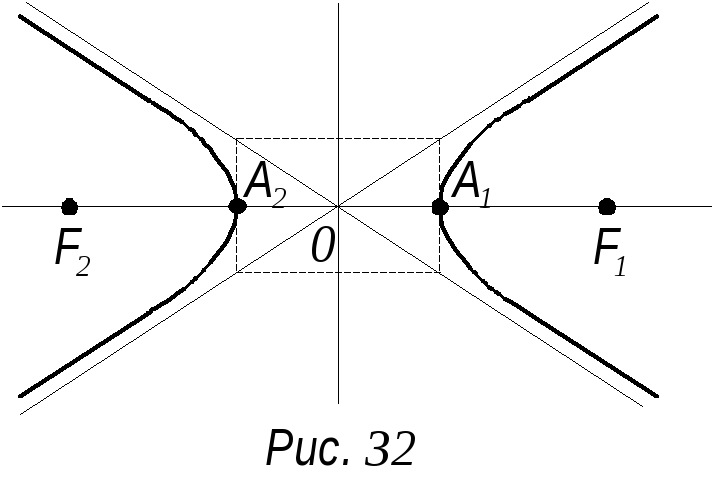 так,
так,
уравнение асимптот гиперболы
![]() .
.
Асимптоты
гиперболы располагаются по диагоналям
прямоугольника, одна сторона которого
параллельна оси ох и равна 2а, а другая
параллельна оси оу и равна 2в, а центр
лежит в начале координат (рис. 32).
П 7. Эксцентриситет и директрисы гиперболы
r2
– r1
= ± 2a
знак + относится к правой ветви
гиперболы
знак
– относится к левой ветви гиперболы
![]()
![]()
![]()
![]()
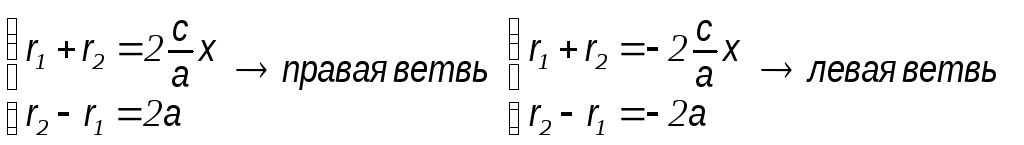
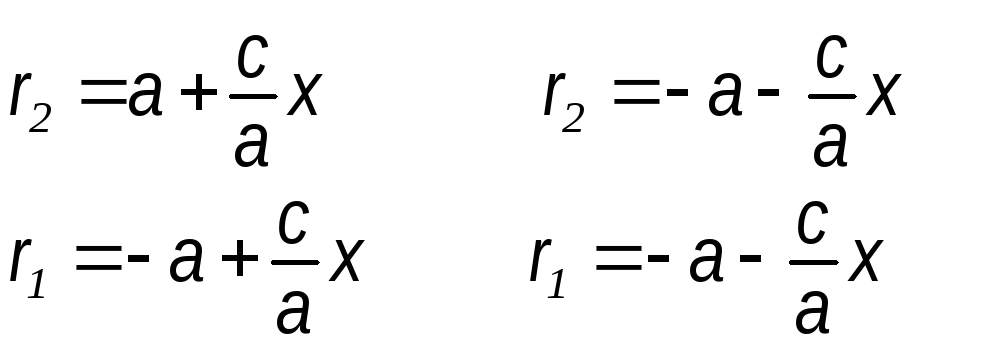
Определение.
Эксцентриситетом
гиперболы называется отношение расстояния
между фокусами этой гиперболы к расстоянию
между ее вершинами.
![]() .
.
Так как c
> a,
ε
> 1
Выразим
фокальные радиусы гиперболы через
эксцентриситет:
![]()
Определение.
Назовем прямые
![]() ,
,
перпендикулярные фокальной оси гиперболы
и расположенными на расстоянии
![]()
от ее центра директрисами гиперболы,
соответствующие правому и левому
фокусам.
Т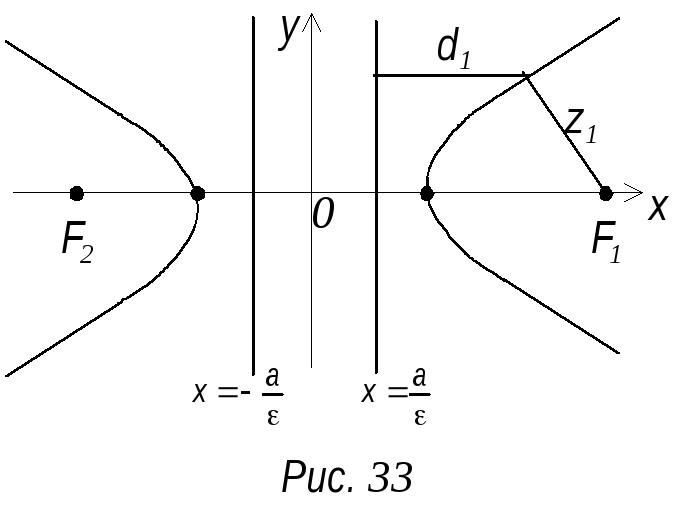 ак
ак
как для гиперболы
![]()
следовательно, директрисы гиперболы,
располагаются между ее вершинами (рис.
33). Покажем, что отношение расстояний
любой точки гиперболы до фокуса и
соответствующей директрисы есть величина
постоянная и равная ε.
![]()
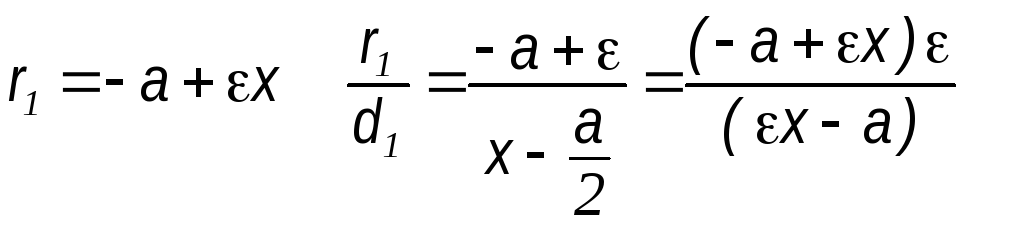
П. 8 Парабола и ее уравнение
О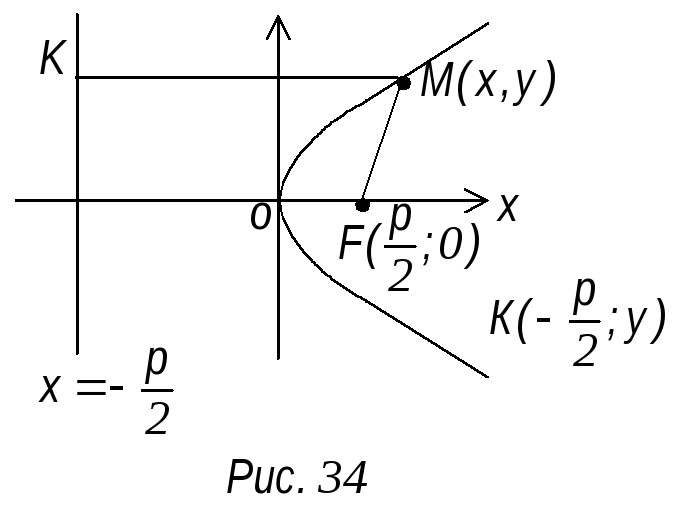 пределение.Парабола
пределение.Парабола
есть геометрическое место точек
равностоящих от данной точки, называемой
фокусом и от данной прямой называемой
директрисой.
Чтобы
составить уравнение параболы примем
за ось х прямую, проходящую через фокус
F1
перпендикулярную к директрисе и будем
считать ось х направленной от директрисы
к фокусу. За начало координат возьмем
середину О отрезка от точки F
до данной прямой, длину которого обозначим
через р (рис. 34). Величину р назовем
параметром параболы. Точка координат
фокуса
![]() .
.
Пусть
М (х, у) – произвольная точка параболы.
Согласно
определению
![]()
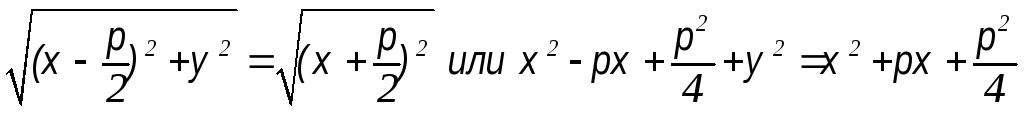 у2
у2
= 2рх – каноническое уравнение параболы
Для
определения вида параболы преобразуем
ее уравнение
![]()
отсюда следует
![]() .
.
Следовательно, вершина параболы находится
в начале координат и осью симметрии
параболы является ох. Уравнение у2
= -2рх при положительном р сводится к
уравнению у2
= 2рх путем замены х на –х и ее график
имеет вид (рис. 35).
У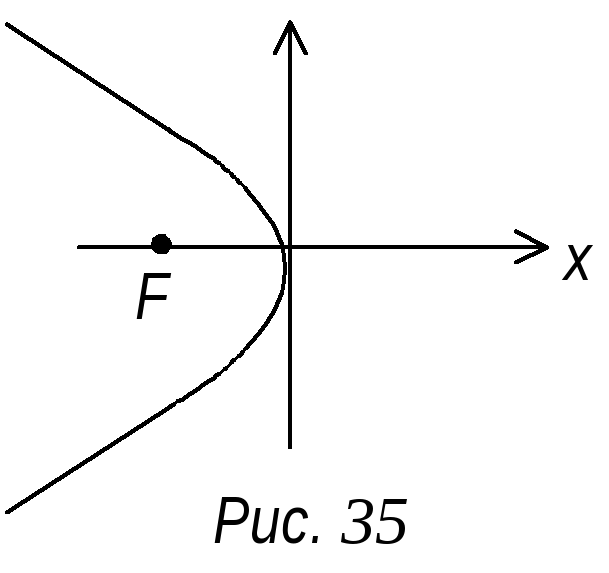 равнение
равнение
х2
= 2ру является уравнением параболы с
вершиной в точке О (0; 0) ветви которой
направлены вверх.
х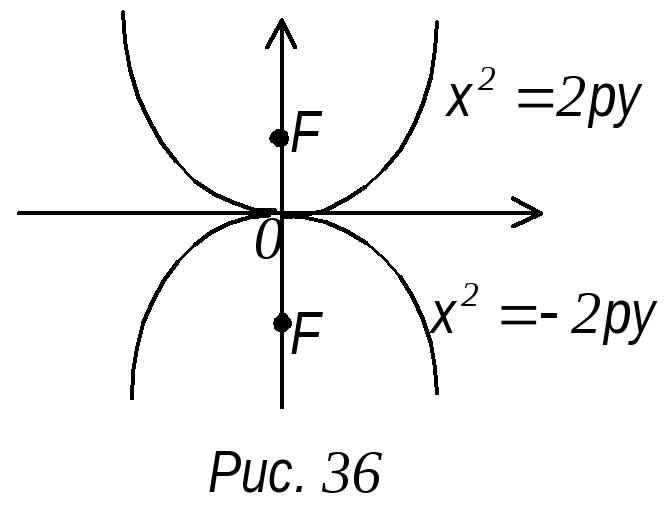 2
2
= -2ру – уравнение параболы с центром в
начале координат симметричная относительно
оси у, ветви которой направлены вниз
(рис. 36).
У
параболы одна ось симметрии.
Если
х в первой степени, а у во второй, то ось
симметрии есть х.
Если
х во второй степени, а у в первой, то ось
симметрии есть ось оу.
Замечание
1.
Уравнение
директрисы параболы имеет вид
![]() .
.
Замечание
2.Так
как для параболы
![]() ,
,
то ε
параболы равен 1. ε
= 1.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Способы построения гиперболы самостоятельно
Содержание:
- Гипербола в математике — что это такое
- Как построить гиперболу самостоятельно
- Построение гиперболы по фокусам
- Как построить гиперболу по точкам
- Как построить график гиперболы по уравнению
Гипербола в математике — что это такое
определение 1
Гипербола представляет собой линию, определяемую в некой декартовой прямоугольной системе координат каноническим уравнением:
(frac{x^{2}}{a^{2}}-frac{y^{2}}{b^{2}}=1.label{ref9})
Согласно записанному правилу, все точки гиперболы (|x| geq a). Таким образом, данные точки расположены за пределами вертикальной полосы ширины (2a), как показано на рисунке. Ось абсцисс канонической системы координат имеет точки пересечения с гиперболой. Координаты этих точек соответствуют: ((a, 0)) и ((-a, 0)). Такие точки называют вершинами гиперболы.
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
Ось ординат не имеет общих точек с гиперболой. В состав гиперболы входят две части, которые не связаны между собой. Они носят название ветвей гиперболы. Числа «a» и «b» являются соответственно вещественной и мнимой полуосями гиперболы.
Определение 2
Ветви гиперболы — это две отдельные кривые, из которых состоит гипербола.
Определение 3
Ближайшие друг к другу точки двух ветвей гиперболы являются вершинами гиперболы.
Определение 4
Большая ось гиперболы — наименьшее расстояние между двумя ее ветвями.
Определение 5
Центр гиперболы — это середина ее большой оси.
Определение 6
Большая полуось гиперболы — расстояние, на которое удалены центр и одна из вершин, обозначается «а».
Определение 7
Фокальное расстояние гиперболы — расстояние, на которое удалены друг от друга центр и один из фокусов, обозначается «с».
Оба фокуса гиперболы расположены на продолжении большой оси и равноудалены от центра гиперболы.
Определение 8
Прямая, включающая в себя большую ось гиперболы, носит название действительной, или поперечной, оси гиперболы.
Определение 9
Прямая в виде перпендикуляра к действительной оси, которая пересекает центр гиперболы — мнимая, или сопряженная ось гиперболы.
Определение 10
Отрезок между фокусом гиперболы и гиперболой, который перпендикулярен к действительной оси, — это фокальный параметр.
Определение 11
Прицельный параметр — расстояние от фокуса до асимптоты гиперболы, обозначается «b».
Определение 12
Перицентрическое расстояние — расстояние, на которое фокус удален от ближайшей вершины гиперболы, обозначается ({displaystyle r_{p}}r_{p}).
Перечисленные характеристики гиперболы взаимосвязаны. Справедливы следующие соотношения:
- ({displaystyle c^{2}=a^{2}+b^{2}}{displaystyle c^{2}=a^{2}+b^{2}})
- ({displaystyle varepsilon =c/a}{displaystyle varepsilon =c/a})
- ({displaystyle b^{2}=a^{2}left(varepsilon ^{2}-1right)}{displaystyle b^{2}=a^{2}left(varepsilon ^{2}-1right)})
- ({displaystyle r_{p}=aleft(varepsilon -1right)}{displaystyle r_{p}=aleft(varepsilon -1right)})
- ({displaystyle a={frac {p}{varepsilon ^{2}-1}}}{displaystyle a={frac {p}{varepsilon ^{2}-1}}})
- ({displaystyle b={frac {p}{sqrt {varepsilon ^{2}-1}}}}{displaystyle b={frac {p}{sqrt {varepsilon ^{2}-1}}}})
- ({displaystyle c={frac {pvarepsilon }{varepsilon ^{2}-1}}}{displaystyle c={frac {pvarepsilon }{varepsilon ^{2}-1}}})
- ({displaystyle p={frac {b^{2}}{a}}}p={frac {b^{2}}{a}})
Определение 13
Оси симметрии гиперболы представляют собой оси канонической системы координат, а начало канонической системы является центром симметрии.
Когда требуется исследовать форму гиперболы, следует начать с поиска ее пересечения с произвольной прямой, пересекающей начало координат. Уравнение прямой можно задать в виде:
(y=kx)
Такой выбор связан с тем, что прямая (x=0 ) не пересекает гиперболу. Абсциссы точек пересечения можно вычислить с помощью уравнения:
(frac{x^{2}}{a^{2}}-frac{k^{2}x^{2}}{b^{2}}=1)
Таким образом, при (b^{2}-a^{2}k^{2} > 0) получим:
(x=pm frac{ab}{sqrt{b^{2}-a^{2}k^{2}}})
Полученное равенство позволит рассчитать координаты точек пересечения:
((ab/v, abk/v))
((-ab/v, -abk/v))
В данном случае:
(v=(b^{2}-a^{2}k^{2})^{1/2})
Руководствуясь свойством симметрии, можно проанализировать смещение первой из точек при изменении k, как показано на рисунке.
Числитель дроби (ab/v) является постоянной величиной, а знаменатель характеризуется максимальным значением, если (k=0). Таким образом, самую маленькую абсциссу имеет вершина ((a, 0)). При увеличении (k ) знаменатель убывает, и x растет, стремясь к бесконечности, когда k приближается к числу (b/a).
Прямая (y=bx/a) с угловым коэффициентом (b/a) не имеет точек пересечения с гиперболой, как и прямые с большими угловыми коэффициентами. Какая-либо прямая, обладающая меньшим положительным угловым коэффициентом, пересекает гиперболу.
При сдвиге прямой от горизонтального положения по часовой стрелке, k будет уменьшаться, (k^{2}) — увеличиваться, и прямая будет иметь удаляющиеся точки пересечения с гиперболой до тех пор, пока не займет положения с угловым коэффициентом (-b/a).
К прямой (y=-bx/a) относится все, что было сказано о (y=bx/a): она не пересекает гиперболу и отделяет прямые, пересекающие ее, от не пересекающих. Из вышесказанного следует вывод, что гипербола имеет вид, изображенный на рисунке.
Определение 14
Асимптоты гиперболы являются прямыми, описываемыми уравнениями (y=bx/a) и (y=-bx/a ) в канонической системе координат.
Предположим, что уравнения асимптот имеют вид:
(bx-ay=0)
(bx+ay=0)
Расстояния от точки (M(x, y)) до асимптот составят
(h_{1}=frac{|bx-ay|}{sqrt{a^{2}+b^{2}}},)( h_{2}=frac{|bx+ay|}{sqrt{a^{2}+b^{2}}})
В том случае, когда точка M расположена на гиперболе:
(b^{2}x^{2}-a^{2}y^{2}=a^{2}b^{2})
(h_{1}h_{2}=frac{|b^{2}x^{2}-a^{2}y^{2}|}{a^{2}+b^{2}}=frac{a^{2}b^{2}}{a^{2}+b^{2}})
Определение 15
Произведение расстояний от точки гиперболы до асимптот является постоянным и соответствует (a^{2}b^{2}/(a^{2}+b^{2})).
Из данного определения можно вывести ключевое свойство, которым обладают асимптоты гиперболы.
Определение 16
В том случае, когда точка совершает движение по гиперболе таким образом, что ее абсцисса по абсолютной величине неограниченно возрастает, расстояние от точки до одной из асимптот стремится к нулю.
В действительности получим, что хотя бы одно из расстояний (h_{1}) или (h_{2}) при этих условиях должно неограниченно увеличиваться. Если предположить, что утверждение не справедливо, то произведение не было бы постоянной величиной.
Введем такое число с, что:
(c^{2}=a^{2}+b^{2})
и (c > 0)
Определение 17
Фокусы гиперболы — точки (F_{1}) и (F_{2}) с координатами ((c, 0)) и ((-c, 0)) в канонической системе координат.
Отношение (varepsilon=c/a), как и для эллипса, называется эксцентриситетом. У гиперболы (varepsilon > 1).
Расстояния от произвольной точки (M(x, y)) на гиперболе до каждого из фокусов определяются абсциссой (x):
(r_{1}=|F_{1}M|=|a-varepsilon x|, r_{2}=|F_{2}M|=|a+varepsilon x|)
Следует отметить, что равенства eqref{ref11} можно представить в более подробной форме:
- для правой ветви гиперболы ((x geq a): r_{1}=varepsilon x-a), ( r_{2}=varepsilon x+a);
- для левой ветви гиперболы ((x leq -a): r_{1}= a-varepsilon x), ( r_{2}=-varepsilon x-a).
Таким образом, для правой ветви (r_{2}-r_{1}=2a), а для левой ветви (r_{1}-r_{2}=2a). В обоих случаях:
(|r_{2}-r_{1}|=2a)
Определение 18
Директрисы гиперболы — прямые, заданные в канонической системе координат уравнениями: (x=frac{a}{varepsilon}), ( x=-frac{a}{varepsilon}).
Директрисы расположены поблизости от центра в отличие от вершин. Из этого можно сделать вывод, что директрисы не имеют точек пересечения с гиперболой. Директриса и фокус, которые расположены по одну сторону от центра, считаются соответствующими друг другу.
Определение 19
Для того чтобы точка (M) была расположена на гиперболе, необходимо и достаточно, чтобы разность ее расстояний до фокусов по абсолютной величине равнялась вещественной оси гиперболы 2a.
С целью доказательства достаточности данного условия его следует записать в виде:
(sqrt{(x-c)^{2}+y^{2}}=pm 2a+sqrt{(x+c)^{2}+y^{2}})
Следующие действия отличаются от доказательства соответствующего утверждения для эллипса только тем, что нужно воспользоваться равенством:
(c^{2}=a^{2}+b^{2}), а не (c^{2}=a^{2}-b^{2})
Определение 20
Для того чтобы точка была расположена на гиперболе, необходимо и достаточно, чтобы отношение ее расстояния до фокуса к расстоянию до соответствующей директрисы равнялось эксцентриситету (varepsilon).
Можно доказать, к примеру, необходимость условия для фокуса (F_{2}(-c, 0).) Предположим, что (M'(x, y)) является точкой гиперболы. Расстояние от (M’) до директрисы с уравнением (x=-a/varepsilon) равно:
(d’=left|x+frac{a}{varepsilon}right|=frac{1}{varepsilon}|varepsilon x+a|)
Таким образом:
(r’/d’=varepsilon).
Уравнение касательной к гиперболе в точке (M_{0}(x_{0}, y_{0})), которая принадлежит данной гиперболе, можно записать так же, как подобное уравнение в случае эллипса. Уравнение касательной к гиперболе:
(frac{xx_{0}}{a^{2}}-frac{yy_{0}}{b^{2}}=1)
Определение 21
Касательная к гиперболе в точке (M_{0}(x_{0}, y_{0})) представляет собой биссектрису угла между отрезками, которые соединяют рассматриваемую точку с фокусами.
Как построить гиперболу самостоятельно
Построение графика гиперболы следует начать с изображения прямоугольной системы координат Декарта. Алгоритм действий:
- На листе бумаги нарисовать горизонтальную прямую. Выполнить действие следует таким образом, чтобы конец прямой с правой стороны был обозначен с помощью стрелки. Данная прямая является осью (X) и носит название абсциссы.
- На середине оси ( Х) необходимо опустить перпендикуляр. Конец полученной прямой в верхней части нужно обозначить стрелкой. В результате получена ось (Y), которую называют ординатой.
- На следующем шаге необходимо пронумеровать шкалу. С правой стороны на оси (Х) расположены положительные значения (Х) в порядке возрастания — от 1 и выше. С левой стороны — отрицательные. В верхней части на оси (Y) расположены положительные значения (Y) в порядке возрастания. В нижней части — отрицательные.
Примечание
Точка, в которой пересекаются абсцисса и ордината является началом координат, то есть числом 0. От данной точки следует откладывать все значения (Х) и (Y).
С помощью прямоугольной системы координат плоскость поделена на четыре части, которые называют четвертями и нумеруют против часовой стрелки. Для того чтобы построить график, требуется определить точки. Каждая точка координатной плоскости определяется парой чисел ((x;y)). Данные числа представляют собой координаты точки, где:
- (х) — абсцисса точки;
- (y) — ордината.
Гипербола представляет собой график функции, которая задана формулой:
(y=k/x)
где (k) — является каким-то коэффициентом, не равным нулю;
(x) — представляет собой независимую переменную.
Гипербола включает в себя две части, расположенные симметрично в разных четвертях. Данные части носят название ветвей гиперболы. При (k>0), ветви расположены в 1 и 3 четвертях. При (k<0), ветви гиперболы размещены во 2 и 4 четвертях.
Принцип построения гиперболы можно рассмотреть на примере, когда функция задана следующей формулой:
(y=3/х)
Так как коэффициент 3 обладает положительным значением, гипербола, соответственно, будет находиться в 1 и 3 четвертях. Можно взять произвольно значения (Х) и найти значения (Y). Таким образом, получатся координаты точек, с помощью которых можно изобразить гиперболу. Важно отметить, что (Х) не должно иметь нулевое значение, так как на 0 делить нельзя.
Поскольку мы знаем, что гипербола располагается в двух четвертях, то берем как положительные значения, так и отрицательные. Предположим, что (Х) равен: -6, -3, -1, 1, 3, 6. Далее можно рассчитать ординаты путем подстановки каждого значение (Х) в начальную формулу:
(y=3/-6)
(у=3/-3)
(у=3/-1)
(у=3/1)
(у=3/3)
(у=3/6)
В результате, значения ( Y) равны: -0.5, -1, -3, 3, 1, 0.5.
Полученные 6 точек с координатами необходимо отложить на системе координат. Далее точки соединяют с помощью кривых линий, как изображено на рисунке. В итоге получилась гипербола.
Построение гиперболы по фокусам
Гиперболу можно построить, зная заданные вершины (А) и (В) и фокусное расстояние (FF1). Алгоритм построения следующий:
- В первую очередь фокусное расстояние следует разделить пополам, чтобы получить точку 0.
- Далее с левой стороны от фокуса (F) можно отметить ряд произвольных точек 1, 2, 3, 4 и так далее, расстояние между которыми постепенно увеличивается.
- Затем нужно начертить вспомогательные окружности с центром в фокусе (F), имеющие радиусы (R1=1B), (R2=2B), (R3=3B), (R4=4B) и так далее.
- На следующем этапе можно изобразить вспомогательные окружности с центром в фокусе (F1) и радиусами (r1=1A), (r2=2A), (r3=3A), (r4=4A) и так далее.
- При пересечении вспомогательных окружностей определяется положение точек гиперболы. (С), (С1 )представляют собой точки, которые образованы в результате пересечения окружностей радиусов (R1) и (r1). Точки (D,D1) являются точками, в которых пересекаются окружности (R2) и (r2).
- Полученные точки остается соединить с помощью плавной кривой линии, чтобы получить правую ветвь гиперболы.
- Аналогичным способом следует выполнить построение левой ветви гиперболы.
Как построить гиперболу по точкам
Исходя из определения гиперболы, разница между расстояниями (r1) и (r2) для всех ее точек является постоянной величиной. Таким образом, переход от одной точки гиперболы к другой осуществляется путем увеличения или уменьшения данных характеристик. Алгоритм действий:
- В первую очередь следует отложить точки (А1) и (А2). Точка ( А2) является точкой касания двух окружностей, центр одной из которых расположен в фокусе ( F1), а радиус составляет F1A2. Другая окружность обладает центром в фокусе (F2) и радиусом (F2A2).
- Следующие точки гиперболы можно определить при пересечении пар окружностей с радиусами, которые равны:
Таким образом, новые значения радиусов превышают предыдущие на одинаковую величину. Чем ближе расположены точки, тем точнее будет построен график гиперболы.
Как построить график гиперболы по уравнению
Каноническое уравнение гиперболы записывают таким образом:
где («a») и («b») являются положительными действительными числами, причем, («а») может быть больше или меньше, чем («b»).
Важно отметить, что гипербола обладает двумя симметричными ветвями и двумя асимптотами.
Построение гиперболы можно рассмотреть на примере. Предположим, что она задана следующим уравнением:
Рассматриваемое уравнение необходимо привести к каноническому виду:
Так как в правой части требуется получить единицу, необходимо обе части начального уравнения поделить на 20:
Далее следует сократить обе дроби:
Затем нужно выделить квадраты в знаменателях:
В результате получено каноническое уравнение:
Существует два подхода к построению гиперболы:
- геометрический;
- алгебраический.
С практической точки зрения, эффективнее воспользоваться расчетами. В первую очередь следует определить асимптоты:
Асимптоты равны:
На втором этапе можно определить вершины гиперболы, которые соответствуют точкам на оси абсцисс с координатами:
При у=0, каноническое уравнение гиперболы примет вид:
Таким образом:
Вершины гиперболы:
Затем необходимо определить дополнительные точки. В каноническом положении гипербола симметрична относительно начала координат и обеих координатных осей, поэтому вычисления достаточно провести для 1-й координатной четверти. Согласно каноническому уравнению, можно выразить:
В результате получим две функции. Первая функция определяет верхние дуги гиперболы:
Вторая функция выражает нижние дуги гиперболы:
Напрашивается нахождение точек с абсциссами:
На последнем этапе следует изобразить асимптоты, вершины, дополнительные точки, симметричные точки в других координатных четвертях:
После того, как все точки соединены, будет изображена гипербола.
