Смещение по горизонтали параболы
Если мы прибаляем к функции (y=x^2) число 3 (y=(x+3)^2), то график смещается по оси (0X) на (-3) еденицы, если вычитаем число (2) (y=(x-2)^2), то график сместится (+2) относительно (0X):
Если мы отнимем от (y=(x+3)^2) 3 , то (y=(x+3)^2-3), то график начнет смещаться уже по вертикали вниз на (3) единицы, а именно по оси (0Y):
Напомним, графиком квадратичной функции (y = ax^2 + bx + c ) является парабола, если забыл что такое парабола, то повтори в этой статье https://myalfaschool.ru/articles/parabola. Вершину параболы можно вычислить по формуле: (x=frac{ – b}{2a}.)
Задача
Здесь нам пригодятся знания нахождения формулы вершины параболы (x=frac{ – b}{2a}), она не такая и тяжелая, так что запомните ее. Если мы видим на графике параболу, то сразу представляем уранение вида (y = ax^2 + bx + c ). По графику выше определяем вершина равна -1:
(frac{-b}{2a}=-1) (–>) (b=2a)
Как видно из рисунка парабола пересекает (OY) в точке 3, поэтому (с=3) и (y = ax^2 + 2ax + 3), так как (b=2a). Находим любую точку проходящую через параболу, возьмем вершину параболы ((-1; 2)) и подставим в уравнение:
(2 = (-1)x^2 + 2(-1)x + 3) (–>) (2=-a+3) (–>) (a=1)
Ответ: 2)1.
Больше уроков и заданий по всем школьным предметам в онлайн-школе “Альфа”. Запишитесь на пробное занятие прямо сейчас!
Запишитесь на бесплатное тестирование знаний!
Предположим, вам попался график функции (y=ax^2+bx+c) и нужно по этому графику определить коэффициенты (a), (b) и (c). В этой статье я расскажу 3 простых способа сделать это.
1 способ – ищем коэффициенты на графике
Данный способ хорош, когда координаты вершины и точка пересечения параболы с осью (y) – целые числа. Если это не так, советую использовать способ 2.
-
Коэффициент (a) можно найти с помощью следующих фактов:
– Если (a>0), то ветви параболы направленных вверх, если (a<0), то ветви параболы направлены вниз.

– Если (a>1), то график вытянут вверх в (a) раз по сравнению с «базовым» графиком (у которого (a=1)). Вершина при этом остается на месте. Это наглядно видно по выделенным точкам.

– Аналогично с (a<-1), только график вытянут вниз.

– Если (a∈(0;1)), то график сжат в (a) раз (по сравнению с «базовым» графиком с (a=1)). Вершина при этом остается на месте.

– Аналогично (a∈(-1;0)), только ветви направлены вниз.

-
Парабола пересекает ось y в точке (c).

-
(b) напрямую по графику не видно, но его можно посчитать с помощью (x_в) – абсциссы (икса) вершины параболы:
(x_в=-frac{b}{2a})
(b=-x_вcdot 2a)

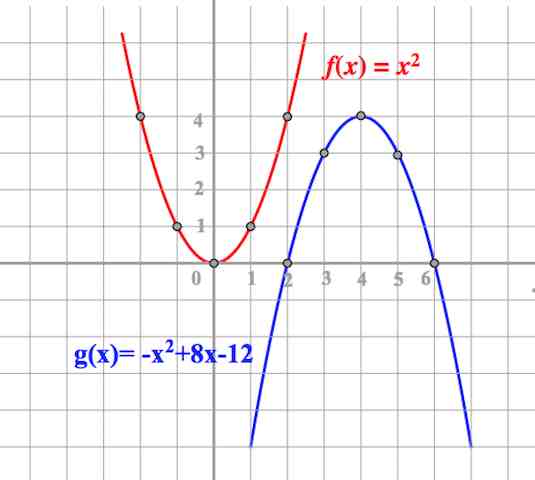
Пример (ЕГЭ):

Решение:
Во-первых, надо разобраться, где тут (f(x)), а где (g(x)). По коэффициенту (c) видно, что (f(x)) это функция, которая лежит ниже – именно она пересекает ось игрек в точке (4).

Значит нужно найти коэффициенты у параболы, которая лежит повыше.
Коэффициент (c) у неё равен (1).
Ветви параболы направлены вниз – значит (a<0). При этом форма этой параболы стандартная, базовая, значит (a=-1).

Найдем (b). (x_в=-2), (a=-1).
(x_в=-frac{b}{2a})
(-2=-frac{b}{-2})
(b=-4)
Получается (g(x)=-x^2-4x+1). Теперь найдем в каких точках функции пересекаются:
(-x^2-4x+1=-2x^2-2x+4)
(-x^2-4x+1+2x^2+2x-4=0)
(x^2-2x-3=0)
(D=4+4cdot 3=16=4^2)
(x_1=frac{2-4}{2}=-1); (x_2=frac{2+4}{2}=3).
Ответ: (3).
2 способ – находим формулу по точкам
Это самый надежный способ, потому что его можно применить практически в любой ситуации, но и самый не интересный, потому что думать тут особо не надо, только уметь решать системы линейных уравнений. Алгоритм прост:
-
Ищем 3 точки с целыми координатами, принадлежащие параболе.
Пример:
-
Выписываем координаты этих точек и подставляем в формулу квадратичной функции: (y=ax^2+bx+c). Получится система с тремя уравнениями.
Пример: (A(-4;5)), (B(-5;5)), (C(-6;3)).
(begin{cases}5=a(-4)^2+b(-4)+c\5=a(-5)^2+b(-5)+c\3=a(-6)^2+b(-6)+c end{cases})
-
Решаем систему.
Пример:(begin{cases}5=16a-4b+c\5=25a-5b+c\3=36a-6b+c end{cases})
Вычтем из второго уравнения первое:
(0=9a-b)
(b=9a)Подставим (9a) вместо (b):
(begin{cases}5=16a-36a+c\5=25a-45a+c\3=36a-54a+c end{cases})
(begin{cases}5=-20a+c\5=-20a+c\3=-18a+c end{cases})Первое и второе уравнения совпали (это нормально для точек, симметричных относительно прямой проходящей через вершину – как точки (A) и (B) в нашем случае), но нас это не остановит – мы вычтем из второго уравнение третье:
(2=-2a)
(a=-1)Найдем (b):
(b=-9)
Подставим в первое уравнение (a):
(5=20+c)
(c=-15).Получается квадратичная функция: (y=-x^2-9x-15).
Пример (ЕГЭ):

Решение:
Сразу заметим, что по графику можно сразу определить, что (c=4). Это сильно облегчит нашу систему – нам хватит 2 точек. Выберем их на параболе: (C(-1;8)), (D(1;2)) (на самом деле, если присмотреться, то можно заметить, что эти точки выделены жирно на изначальной картинке – это вам подсказка от авторов задачи).

Таким образом имеем систему:
(begin{cases}8=a(-1)^2+b(-1)+4\2=a+b+4 end{cases})
(begin{cases}8=a-b+4\2=a+b+4 end{cases})
(begin{cases}4=a-b\-2=a+b end{cases})
Сложим 2 уравнения:
(2=2a)
(a=1)
Подставим во второе уравнение:
(-2=1+b)
(b=-3)
Получается:
(g(x)=x^2-3x+4)
Теперь найдем точки пересечения двух функций:
(-3x+13=x^2-3x+4)
(x^2-9=0)
(x=±3)
Теперь можно найти ординату второй точки пересечения:
(f(-3)=-3cdot (-3)+13)
(f(-3)=9+13)
(f(-3)=22)
Ответ: (22).
3 способ – используем преобразование графиков функций
Этот способ быстрее первого и более универсальный, в частности он может пригодится и в задачах на другие функции.
Главный недостаток этого способа – вершина должна иметь целые координаты.
Сам способ базируется на следующих идеях:
-
График (y=-x^2) симметричен относительно оси (x) графику (y=x^2).

-
– Если (a>1) график (y=ax^2) получается растяжением графика (y=x^2) вдоль оси (y) в (a) раз.
– Если (a∈(0;1)) график (y=ax^2) получается сжатием графика (y=x^2) вдоль оси (y) в (a) раз.
-
– График (y=a(x+d)^2) получается сдвигом графика (y=ax^2) влево на (d) единиц.
– График (y=a(x-d)^2) получается сдвигом графика (y=ax^2) вправо на (d) единиц.
-
График (y=a(x+d)^2+e) получается переносом графика (y=a(x+d)^2) на (e) единиц вверх.
График (y=a(x+d)^2-e) получается переносом графика (y=a(x+d)^2) на (e) единиц вниз.
У вас наверно остался вопрос – как этим пользоваться? Предположим, мы видим такую параболу:

Сначала смотрим на её форму и направленность её ветвей. Видим, что форма стандартная, базовая и ветви направлены вверх, поэтому (a=1). То есть она получена перемещениями графика базовой параболы (y=x^2).

А как надо было перемещать зеленый график чтоб получить оранжевый? Надо сдвинуться вправо на пять единиц и вниз на (4).

То есть наша функция выглядит так: (y=(x-5)^2-4).
После раскрытия скобок и приведения подобных получаем искомую формулу:
(y=x^2-10x+25-4)
(y=x^2-10x+21)
Готово.
Пример (ЕГЭ):

Чтобы найти (f(6)), надо сначала узнать формулу функции (f(x)). Найдем её:
-
Парабола растянута на (2) и ветви направлены вниз, поэтому (a=-2). Иными словами, первоначальной, перемещаемой функцией является функция (y=-2x^2).

-
Парабола смещена на 2 клеточки вправо, поэтому (y=-2(x-2)^2).
-
Парабола поднята на 4 клеточки вверх, поэтому (y=-2(x-2)^2+4).
-
Получается (y=-2(x^2-4x+4)+4=)(-2x^2+8x-8+4=-2x^2+8x-4).
-
(f(6)=-2cdot 6^2+8cdot 6-4=-72+48-4=-28)
Смотрите также:
Как найти k и b по графику линейной функции?
Цели урока:
Образовательная: исследовать смещение
графика квадратичной функции, определить
положение графика в зависимости от значений
коэффициентов b, c.
Воспитательная: умение работать в группе,
организованности.
Развивающая: навыки исследовательской
работы, умение выдвигать гипотезы, анализировать
полученные результаты, систематизировать
полученные данные.
Структура урока
- Организационный момент – 3 минуты.
- Исследовательская работа – 20 минут.
- Закрепление изученного материала – 15 минут.
- Рефлексия – 2 минут.
- Итог урока – 3 минуты.
- Домашнее задание – 2 минуты.
Ход урока
1. Организационный момент.
Цель урока провести исследовательскую работу.
Объектом исследования будут квадратичные
функции разного вида. Вам предстоит определить,
как влияют коэффициенты b, c на график
функций вида y=x2+с, y=(x-b)2, y=(x-b)2+c.
Для выполнения задания необходимо разделиться
на группы (4 группы по 5 человек, одна группа
“эксперты” наиболее подготовленные ученики).
Каждая группа получает план исследования
<Приложение>, лист формата А3 для оформления
результатов.
2. Исследовательская работа.
Две группы (уровень А) исследуют функции вида y= x2+с,
одна группа (уровень В) исследует функцию вида
y=(x-b)2, одна группа (уровень С) исследует
функцию y=(x-b)2+c. Группа “Экспертов”
исследует все функции.
План работы
- Для того чтобы выдвинуть гипотезу сделайте
предположение, как может выглядеть ваша функция. - Постройте график исследуемых функций
(определите вершину параболы (х0, y0),
задайте таблицей 4 точки). - Сравните получившийся график с контрольным
образцом y=x2. - Сделайте вывод (как изменилось положение
графика вашей функции относительно контрольного
образца). - Результаты оформите на листе формата А3 и
представьте “экспертной” группе.
“Экспертная” группа сверяет результаты свои с
результатами остальных групп, систематизирует и
обобщает результаты, выступает с выводами. В
случае неточностей или ошибок учитель вносит
коррекционные замечания.
Сверка полученных результатов со слайдами
№2-5.
Любую квадратичную функцию y=ax2+bx+c, можно
записать в виде y=a(x-x0)2+y0, где x0
и y0 выражаются через коэффициенты a, b, c.
Таким образом, ваши коэффициенты b=x0, c=y0
являются координатами вершины параболы.
3. Закрепление изученного материала.
Фронтальная работа с классом.
1. Найти ошибку в графиках функций (Слайды№6-9).
|
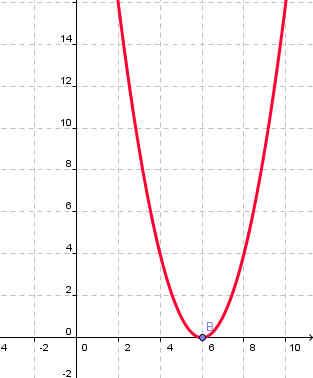
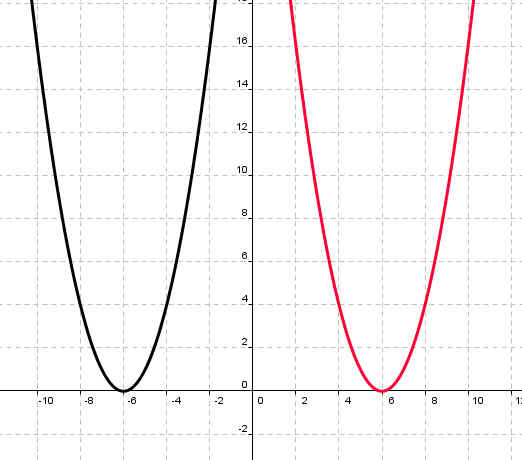
y=(х+6)2 |
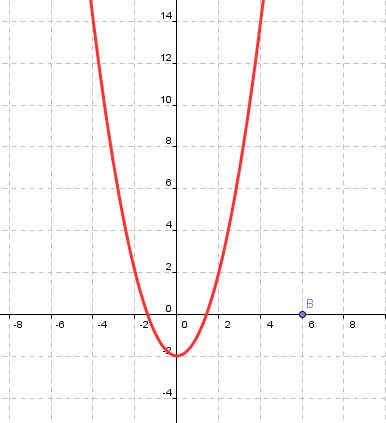
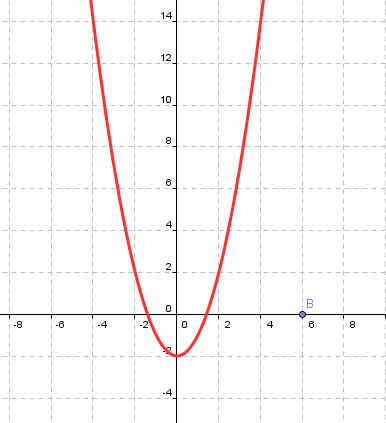
у=х2-2 |
|
Коэффициент b |
Нет ошибки |
|
Рисунок 1 |
Рисунок 2 |
 |
 |
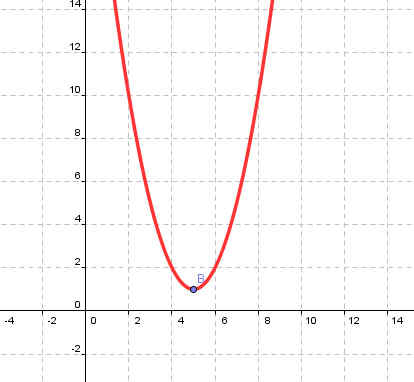
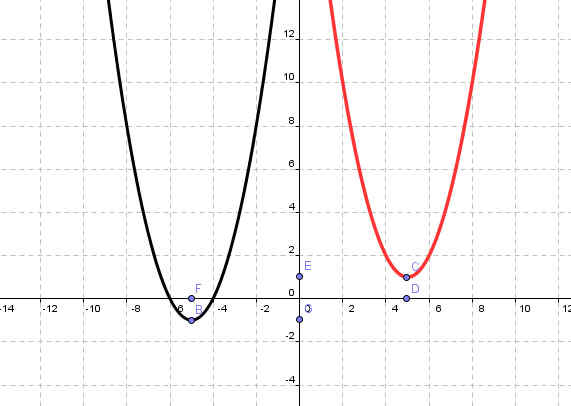
| у=(х+5)2-1 | у=(х-2)2+2 |
| Коэффициент b и с | Коэффициент b |
| Рисунок 3 | Рисунок 4 |
 |
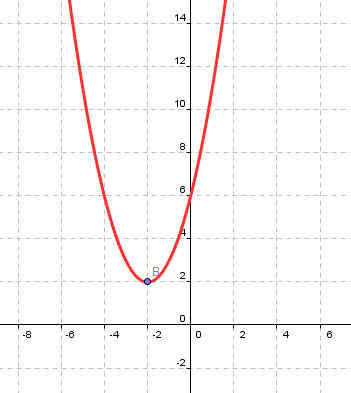 |
Результаты
<Рисунок 7>
<Рисунок 2>
<Рисунок 8>
<Рисунок 9>
Какой коэффициент вам помог найти ошибку?
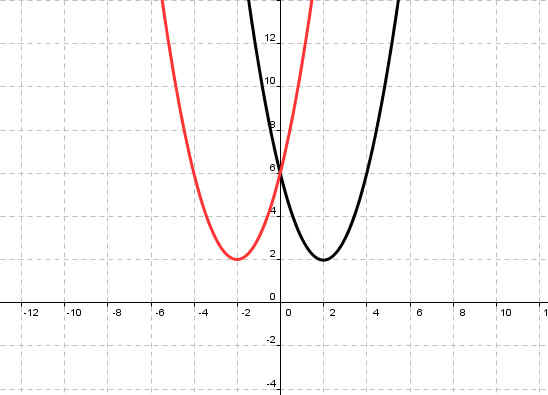
2. Соотнесите графики функций согласно цветам (слайд
№10).
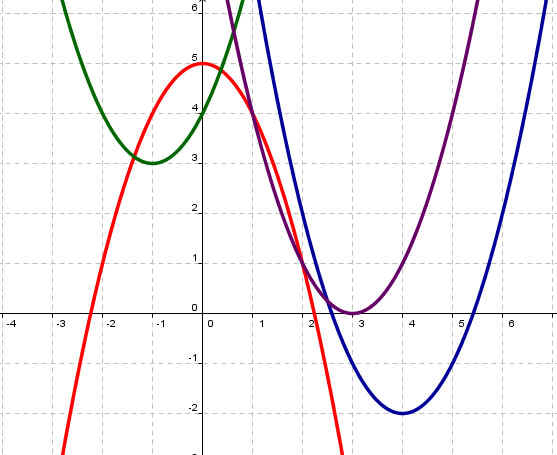
Рисунок 5
| y=(х-4)2-2 | синий |
| y=-x2+5 | красный |
| y=(x+1)2+3 | зеленый |
| y=(x-3)2 | фиолетовый |
4. Рефлексия.
Группа “Экспертов” отвечают на вопросы:
– Какие ошибки допустили группы?
– Достигнута ли цель занятия?
– Соответствуют ли полученные результаты
исследования поставленной гипотезе?
5. Итог урока (слайд №11):
На положение графика функции y=(x-b)2+c
влияют коэффициенты b и c,
“+b” парабола сдвинута вправо по оси абсцисс на
b единичных отрезков,
“–b” парабола сдвинута влево по оси абсцисс на
b единичных отрезков,
“+с” парабола сдвинута вверх по оси ординат на
с единичных отрезков,
“-с” парабола сдвинута вниз по оси ординат на с
единичных отрезков.
6. Домашнее задание
- Построить график квадратичной функции, имеющую
вершину в точке А(1;-2), коэффициент a=1. - Подумайте, в какой области можно использовать
знания по данной теме (практическое применение).
Приложение
Как смещается график параболы?
График квадратичной функции – парабола. Если коэффициент displaystyle a<0, ветви параболы направлены вниз, если displaystyle a>0 – ветви параболы направлены вверх. Чем больше значение displaystyle a (по модулю), тем у́же становится парабола (ветви становятся более крутыми).
Что отвечает за ширину параболы?
Построение квадратичной функции Квадратичная функция задается формулой y = ax2 + bx + c, где x и y — переменные, a, b, c — заданные числа, обязательное условие — a ≠ 0. В уравнении существует следующее распределение: a — старший коэффициент, который отвечает за ширину параболы.
Что такое D в параболе?
Чем больше |a|, тем у́же парабола (больше прижата к оси Y ). Наоборот, чем меньше |a|, тем шире парабола (больше прижата к оси X). где D = b2 − 4ac — дискриминант.
Чему равен коэффициент b в параболе?
1) Коэффициент а влияет на направление ветвей параболы: при а > 0 – ветви направлены вверх, при а < 0 – вниз. 2) Коэффициент b влияет на расположение вершины параболы. При b = 0 вершина лежит на оси оу. 3) Коэффициент с показывает точку пересечения параболы с осью ОУ.
Как найти х вершины?
Воспользуйтесь формулой для вычисления значения координаты x вершины. Вершина также является точкой симметрии параболы. Формула для нахождения координаты x параболы: x = -b/2a.
Как определить А в параболе?
Нахождение коэффициента a :
- По графику параболы определяем координаты вершины (m;n).
- По графику параболы определяем координаты любой точки А (х1;у1).
- Подставляем эти значения в формулу квадратичной функции, заданной в другом виде: у=a(х-m)2 +n.
- Решая полученное уравнение, находим а.
31 янв. 2022 г.
Как найти y0 в параболе?
то абсциссу вершины параболы ( x o ; y o ) можно вычислить по формуле: x o = − b 2 a . Ординату можно вычислить, подставив полученное значение x o в формулу данной функции: y o = a x o 2 + b x o + c .
Какая зависимость называется квадратичной?
Квадратичной функцией называется функция, которую можно задать формулой вида y=ax²+bx+c. Рассмотрим случай, когда a=1,b=0 и c=0. Формула примет вид y=x². Вы, наверно, уже знаете, какая зависимость между площадью квадрата и длиной его стороны.
Что означает D в графике функции?
Область определения функции — это множество всех значений переменной x, которые имеют соответствующие им значения функции. Обозначают: D(f). На графике область определения — это промежутки на оси ОX, над которыми (или под которыми) имеются части графика. Для нашего примера D(f) = [-8; 9,4].
Как в параболе найти B?
нахождение коэффициента b: 1) Сначала находим значение коэффициента a (шаг I, смотри выше). 1) В формулу для абсциссы вершины параболы m= —b/2a подставляем значения m и a. 2) Вычисляем значение коэффициента b.
Что означают коэффициенты k и b?
Понятие линейной функции Геометрический смысл коэффициента b — длина отрезка, который отсекает прямая по оси OY, считая от начала координат. Геометрический смысл коэффициента k — угол наклона прямой к положительному направлению оси OX, считается против часовой стрелки.
Как выглядит парабола?
Парабола — кривая второго порядка. Она имеет ось симметрии, называемой осью параболы. Ось проходит через фокус и вершину перпендикулярно директрисе.
Как найти коэффициенты параболы по графику?
Нахождение коэффициента a :
- По графику параболы определяем координаты вершины (m;n).
- По графику параболы определяем координаты любой точки А (х1;у1).
- Подставляем эти значения в формулу квадратичной функции, заданной в другом виде: у=a(х-m)2 +n.
- Решая полученное уравнение, находим а.
31 янв. 2022 г.
Как определить коэффициент?
Числовой множитель в произведении, где есть хотя бы одна буква, называется коэффициентом. Если чисел несколько, нужно их перемножить, упростить выражение и таким образом будет получен коэффициент.
Как найти x0 и y0?
то абсциссу вершины параболы ( x o ; y o ) можно вычислить по формуле: x o = − b 2 a . Ординату можно вычислить, подставив полученное значение x o в формулу данной функции: y o = a x o 2 + b x o + c .
Какие преобразования графиков вы знаете?
Преобразование графика функции
| Общий вид функции | Преобразования |
|---|---|
| y = f(x + b) | влево, если b > 0; вправо, если b < 0. |
| y = f(x) + m | Параллельный перенос графика вдоль оси ординат на | m | единиц вверх, если m > 0, вниз, если m < 0. |
| Отражение графика | |
| y = f( — x) | Симметричное отражение графика относительно оси ординат. |
Что называется квадратичной функции?
Квадратичной функцией называют функцию, которую можно задать формулой вида у=ах²+bх+c, где а, b и с – некоторые числа, причем а≠0.
Функция вида , где
называется квадратичной функцией.
График квадратичной функции – парабола.
Рассмотрим случаи:
I СЛУЧАЙ, КЛАССИЧЕСКАЯ ПАРАБОЛА
, то есть
,
,
Для построения заполняем таблицу, подставляя значения x в формулу:

Отмечаем точки (0;0); (1;1); (-1;1) и т.д. на координатной плоскости (чем с меньшим шагом мы берем значения х ( в данном случае шаг 1 ), и чем больше берем значений х, тем плавнее будет кривая), получаем параболу:

Нетрудно заметить, что если мы возьмем случай ,
,
, то есть
, то мы получим параболу, симметричную
относительно оси (ох). Убедиться в этом несложно, заполнив аналогичную таблицу:

II СЛУЧАЙ, «a» ОТЛИЧНО ОТ ЕДИНИЦЫ
Что же будет, если мы будем брать ,
,
? Как изменится поведение параболы? При
парабола
изменит форму, она “похудеет” по сравнению с параболой
(не верите – заполните соответствующую таблицу – и убедитесь сами):

На первой картинке (см. выше) хорошо видно, что точки из таблицы для параболы (1;1), (-1;1) трансформировались в точки (1;4), (1;-4), то есть при тех же значениях
ордината
каждой точки умножилась на 4. Это произойдет со всеми ключевыми точками исходной таблицы. Аналогично рассуждаем в случаях картинок 2 и 3.
А при парабола
«станет шире» параболы
:

Давайте подитожим:
III СЛУЧАЙ, ПОЯВЛЯЕТСЯ «С»
Теперь давайте введем в игру (то есть рассматриваем случай, когда
), будем рассматривать параболы вида
. Нетрудно догадаться (вы всегда можете обратиться к таблице), что будет происходить смещение параболы
вдоль оси
вверх или вниз в зависимости от знака
:

IV СЛУЧАЙ, ПОЯВЛЯЕТСЯ «b»
Когда же парабола “оторвется” от оси и будет, наконец, “гулять” по всей координатной плоскости? Когда
перестанет быть равным
.
Здесь для построения параболы нам понадобится формула для вычисления вершины:
,
.
Так вот в этой точке (как в точке (0;0) новой системы координат) мы будем строить параболу , что уже нам по силам. Если имеем дело со случаем
, то от вершины откладываем один единичный отрезок вправо, один вверх, – полученная точка – наша (аналогично шаг влево, шаг вверх – наша точка); если имеем дело с
, например, то от вершины откладываем один единичный отрезок вправо, два – вверх и т.д.
Например, вершина параболы :
,
. Теперь главное уяснить, что в этой вершине мы будем строить параболу по шаблону параболы
, ведь
в нашем случае.

При построении параболы после нахождения координат вершины очень удобно учитывать следующие моменты:
1) парабола обязательно пройдет через точку . Действительно, подставив в формулу
x=0, получим, что
. То есть ордината точки пересечения параболы с осью (оу), это
. В нашем примере (выше), парабола пересекает ось ординат в точке
, так как
.
2) осью симметрии параболы является прямая , поэтому все точки параболы будут симметричны относительно нее. В нашем примере, мы сразу берем точку (0; -2) и строим ей симметричную относительно оси симметрии параболы, получим точку (4; -2), через которую будет проходить парабола.
3) Приравнивая к
, мы узнаем точки пересечения параболы с осью (ох). Для этого решаем уравнение
. В зависимости от дискриминанта, будем получать одну (
,
), две (
,
) или нИсколько (
) точек пересечения с осью (ох). В предыдущем примере у нас корень из дискриминанта – не целое число, при построении нам особо нет смысла находить корни, но мы видим четко, что две точки пересечения с осью (ох) у нас будут (так как
), хотя, в общем, это видно и без дискриминанта.
Итак, давайте выработаем
Алгоритм для построения параболы, если она задана в виде 
1) определяем направление ветвей ( а>0 – вверх, a<0 – вниз)
2) находим координаты вершины параболы по формуле
,
.
3) находим точку пересечения параболы с осью (оу) по свободному члену , строим точку, симметричную данной относительно оси симметрии параболы (надо заметить, бывает, что эту точку невыгодно отмечать, например, потому, что значение
велико… пропускаем этот пункт…)
4) В найденной точке – вершине параболы (как в точке (0;0) новой системы координат) строим параболу . Если
, то парабола
становится у’же по сравнению с
, если
, то парабола расширяется по сравнению с
5) Находим точки пересечения параболы с осью (оу) (если они еще сами “не всплыли”), решая уравнение
Пример 1

Пример 2

Замечание 1. Если же парабола изначально нам задана в виде , где
– некоторые числа (например,
), то построить ее будет еще легче, потому что нам уже заданы координаты вершины
. Почему?
Возьмем квадратный трехчлен и выделим в нем полный квадрат:
Посмотрите, вот мы и получили, что
,
. Мы с вами ранее называли вершину параболы
, то есть теперь
,
.
Например, . Отмечаем на плоскости вершину параболы
, понимаем, что ветви направлены вниз, парабола расширена (относительно
). То есть выполняем пункты 1; 3; 4; 5 из алгоритма построения параболы (см. выше).

Замечание 2. Если парабола задана в виде, подобном этому (то есть
представлен в виде произведения двух линейных множителей), то нам сразу видны точки пересечения параболы с осью (ох). В данном случае – (0;0) и (4;0). В остальном же действуем согласно алгоритму, раскрыв скобки.
