
Сечение конуса — задание в инженерной графике, являющееся одной из часто используемых задач на построение. Я опишу более подробно каждый свой шаг, прикладывая рисунки. Также Вы можете посмотреть видео.
- У вас есть задание на построение сечения конуса с всеми размерами. ( для примера использовал это задание)
 2. Чертим оси и строим 3 вид конуса ( вид слева). Указываем плоскость сечения конуса (зачастую ее располагают под произвольным углом)
2. Чертим оси и строим 3 вид конуса ( вид слева). Указываем плоскость сечения конуса (зачастую ее располагают под произвольным углом) 3. Воспользуемся методом вспомогательных секущих плоскостей (они необходимы для детального построения сечения конуса). Расстояние между секущими плоскостями берем произвольно.
3. Воспользуемся методом вспомогательных секущих плоскостей (они необходимы для детального построения сечения конуса). Расстояние между секущими плоскостями берем произвольно. 4. Находим вид сечения на нижнем рисунке (виде сверху)
4. Находим вид сечения на нижнем рисунке (виде сверху) 5. Затем определим точки на виде слева.
5. Затем определим точки на виде слева. 6. Все точки найдены, приступаем обводить полученную фигуру линиями чертежа.
6. Все точки найдены, приступаем обводить полученную фигуру линиями чертежа. 7. Не забываем пронумеровывать каждую точку полученного сечения.
7. Не забываем пронумеровывать каждую точку полученного сечения.
Просмотрели 1 560
Лекция 16. ПРОЕКЦИИ КОНУСА
Конус – тело вращения.
Прямой круговой конус относится к одному из видов тел вращения.
Коническая поверхность образуется прямой линией, проходящей через некоторую неподвижную точку и последовательно через все точки некото-
рой кривой направляющей линии. Неподвижная точка S называется вершиной. Основанием конуса служит поверхность образованная замкнутой направляющей.
Конус, основанием которого является окружность, а вершина S находится на оси
перпендикулярной основанию, проходящей через его середину, называется прямым кру-
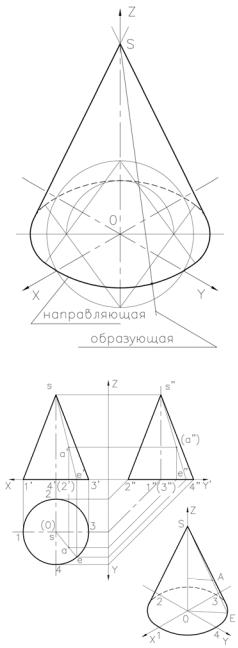
говым конусом. Рис. 1.
Построение ортогональных проекций конуса, приведено на рис. 2.
Горизонтальная проекция конуса представляет собой окружность, равную основанию конуса, а вершина конуса S совпадает с ее центром. На фронтальную и профильную проекции конус проецируется в виде треугольни-
ка, ширина основания которого равна диаметру основания. А высота равна высоте конуса. Наклонные стороны треугольника – проекции крайних (очерковых) образующих конуса.
|
Построение конуса в прямоуголь- |
||
|
ной изометрии приведено на рис. 2. |
||
|
Рис. 1 |
Построение начинаем с расположе- |
|
|
ния аксонометрических осей OX, OY, OZ, |
||
|
проведя их под углом 1200 друг к другу. Ось |
||
|
конуса направим по оси OZ, и отложим на |
||
|
ней высоту конуса, получив точку S. Прини- |
||
|
мая точку O за центр основания конуса, |
||
|
строим овал, представляющий основание |
||
|
конуса. Затем проводим две наклонные ка- |
||
|
сательные из т. S к овалу, которые будут |
||
|
крайними (очерковыми) образующими кону- |
||
|
са. Невидимую часть нижнего основания ко- |
||
|
нуса выполним штриховой линией. |
Построение точек на поверхности конуса в ортогональных и аксонометриче-
ской проекциях показано на рис. 2, 3.
Если на фронтальной проекции конуса Рис. 2 заданы точки А и В, то недостающие проек-
ции этих точек можно построить двумя способами.
Первый способ: с помощью проекций вспомогательной образующей проходящей через заданную точку.
Дано: фронтальная проекция точки А – точка (а’), расположенная в пределах видимой части конуса.
Через вершину конуса и заданную точку (a’) проводим прямую линию до основания конуса и получаем точку (e’) – основание образующей s’e’.
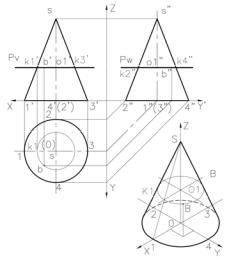
Далее строим горизонтальную проекцию этой образующей на плоскости
H. Найдем горизонтальную проекцию т. e в пределах видимой части окружности основания конуса, проведя проецирующую прямую e’e, и соединим полученную т. е с горизонтальной проекцией вер-
шины конуса s.
Так как искомая т. А принадлежит обра-
зующей s’e’ то она должна лежать на ее горизонтальной проекции. Поэтому с помощью линии связи мы переносим ее на линию se и по-
лучаем горизонтальную проекцию т. a. Профильная проекция a” т. А определя-
ется пересечением той же образующей s”e” на профильной проекции с линиями связи, переносящими т. а с горизонтальной и фронталь-
ной проекций.
Профильная проекция a” т. А в данном
случае невидимая, т. к. находится за проекцией крайней образующей s”4” и обозначается в круглых скобках.
Рис. 3 Второй способ: с помощью построения проекций сечения конической поверхности горизонтальной плоскостью Pv па-
раллельной основанию конуса и проходящей через заданную точку В. Рис. 3. Дано: фронтальная проекция точки В – т. b’, расположенная в пределах
видимой части конуса.
Через т. b’ проводим прямую, Pv параллельную основанию конуса, кото-
рая является фронтальной проекцией секущей плоскости P. Эта линия пересе-
кает ось конуса в т. 01’ и крайние образующие в т. k1’ и k3’. Отрезок прямой k1’k3’ является фронтальной проекцией сечения конуса через т. b’.
Горизонтальной проекцией этого сечения будет окружность, радиус которой определяется на фронтальной проекции как расстояние 01’k1’ от оси ко-
нуса до крайней образующей.
Так как точка b’ лежит в плоскости сечения, то с помощью линии связи переносим ее на горизонтальную проекцию сечения в пределах видимой части конуса.
Профильная проекция т. b” определяется как пересечение профильной
проекции сечения k2”k4” с линией связи, переносящей положение т. b с гори-
зонтальной проекции.
Построение точек на поверхности конуса в аксонометрии.
Строим конус в прямоугольной изометрии. Построение окружности основания конуса в аксонометрии повторяет построение основания цилиндра. (См. раздел 8.2.1.). Отложив на вертикальной оси высоту конуса, проводим две образующие – касательные к овалу основания.
Первый способ. Рис. 2.
Строим образующую SE: на оси X или Y откладываем координаты Х или
Y соответствующие т. Е на горизонтальной проекции и проведем через них линии параллельные оси Y или X соответственно. Пересечение их дает положение точки Е на основании конуса.
Соединим т. Е с вершиной конуса S и с центром основания т. 0. Рассмотрим полученный треугольник S0E: сторона 0S – ось симметрии конуса совпадающая с осью Z. Сторона SE – образующая конуса, на которой находится т. А. Сторона 0E – основание треугольника составляющая с осью Z угол 900.
Рис. 4
Высоту т. А берем на фронтальной проекции по перпендикуляру от ос-
нования конуса до т. a’ и откладываем ее в аксонометрии на оси Z, то есть на стороне 0S.
Через полученную засечку проводим прямую в плоскости треугольника
параллельно основанию треугольника до пересечения с образующей SE. Таким образом, переносим высоту положения т. А на поверхность кону-
са.
Второй способ. Рис. 3.
Строим сечение конуса плоскостью параллельной основанию и проходящей через т. В. Такое сечение конуса есть окружность с радиусом равным
отрезку ОК расположенной на высоте равной высоте т. В. В аксонометрии эта окружность строиться в виде эллипса (или заменяющего его овала).
Затем, на осях X и Y в основании конуса откладываем соответствующие
координаты X и Y т. В взятые с горизонтальной проекции и из точки их пересечения восстанавливаем перпендикуляр до пересечения с эллипсом сечения,
что определит положение т. В.
Сечения конуса.
Взависимости от направления в пространстве секущей плоскости, проходящей через конус, в сечении прямого кругового конуса могут получаться
различные плоские фигуры:
А – прямые (образующие) Б – гипербола
В– окружность
Г – парабола
Д – эллипс Конические сечения – эллипс, парабола и гипербола являются лекаль-
ными кривыми, которые строятся по точкам принадлежащим кривой сечения.
А. Сечение конуса вертикальной плоскостью проходящей через его вершину представляет собой прямые. Рис. 4.
На горизонтальной проекции конуса через точку S проводим линию Ph под произвольным углом к осям X и Y, которая является горизонтальной проекцией секу-
щей вертикальной плоскости. Эта линия
пересекает окружность основания конуса в двух точках a и b, а отрезок aob является горизонтальной проекцией сечения конуса.
Мысленно отбросим левую часть конуса от линии Ph и справа от нее получим горизонтальную проекцию усеченного ко-
нуса.
Отрезки SA и SB – горизонтальные
проекции образующих конуса, по которым и проходит секущая плоскость Ph.
Строим образующие SA и SB на
фронтальной проекции, перенеся на нее точки A и B и соединив полученные точки a’ и b’ с вершиной s’. Треугольник a’s’b’ и будет фронтальной проекцией сечения
конуса, а линия s’3’ – крайней образующей конуса.

Рис. 5
Аналогично строим профильную проекцию сечения конуса, перенеся
точки a и b с горизонтальной проекции на профильную и соединив полученные точки a” и b” с вершиной конуса s”. Треугольник a”s”b” является профильной проекцией сечения конуса, а линия s”2” есть крайняя образующая конуса.
Построение аксонометрии. Рис. 4.
Строим конус в аксонометрии, как описано выше.
Далее с горизонтальной проекции конуса берем координаты по оси X или Y для точек A и B и переносим их на аксонометрические оси X или Y. Через полученные точки проводим вспомогательные линии параллельные осям Y
или X соответственно. Их пересечение с линией основания конуса позволяет получить точки A и B на аксонометрии. Соединив их между собой, и каждую из
них с вершиной конуса S, получим треугольник ABS являющийся сечением конуса вертикальной плоскостью P.
Б. Сечение конуса вертикальной плоскостью, не проходящей через его вершину, представляет собой гиперболу. Рис. 5.
Строим три проекции конуса – горизонтальную, фронтальную и про-
фильную.
Если вертикальная секущая плоскость P не проходит через вершину конуса, то она уже не совпадает с образующими его боковой поверхности, а наоборот – пересекает
их.
На горизонтальной проекции конуса проводим секущую плоскость Ph на произвольном расстоянии от вершины S и парал-
лельную оси Y. В общем случае положение
секущей плоскости относительно осей X и Y может быть любое.
Линия Ph пересекает окружность основания конуса в двух точках a и b. Отрезок ab этой прямой есть горизонтальная проек-
ция сечения конуса. Часть окружности слева от линии Ph делим на произвольное коли-
чество равных частей, в донном случае на 12 и, затем каждую полученную точ-
ку на окружности соединяем с вершиной конуса s. Эти образующие пересека-
ются секущей плоскостью Ph и мы получаем ряд точек, которые принадлежат образующим и проекции сечения конуса ab одновременно.
Строим полученные образующие на фронтальной проекции конуса
.Переносим с горизонтальной проекции все точки на основании конуса (a, 1, …,
5, b) и на фронтальной проекции получаем точки (a’, 1’, …, 5’, a’) и соединяем из с вершиной конуса s’. Проводим на фронтальной проекции через точку b’ секущую плоскость Pv перпендикулярно основанию конуса. Линия Pv пересекает
все образующие, и точки их пересечения принадлежат проекции сечения конуса.
Повторим построение всех образующих на профильной проекции конуса, перенеся на нее точки (a, 1, …, 5, b) с горизонтальной проекции. Полученные точки (a”, 1”, …, 5”, b”) соединим с вершиной s”.
На полученные образующие перенесем с фронтальной проекции точки пересечения соответствующих образующих с секущей плоскостью Pv. Полученные точки соединим кривой линией, которая представляет собой лекальную
кривую – гиперболу.
Построение аксонометрии. Рис. 5.
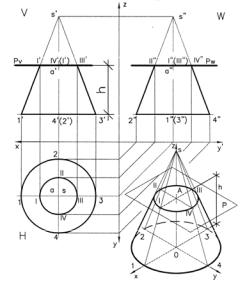
Рис. 6
Строим конус в аксонометрии, как описано выше.
Далее с горизонтальной проекции конуса берем координаты по оси X или Y для всех точек a, 1, …, 5, b и переносим их на аксонометрические оси X или Y находим их положение на основании конуса в аксонометрии. Соединяем
их последовательно с вершиной конуса S и получаем ряд образующих на поверхности конуса соответствующих образующим на ортогональных проекциях.
На каждой образующей найдем точку ее пересечения с секущей плоскостью P аналогично тому, как это было описано выше (см. построение точек на поверхности конуса, первый способ).
Соединив полученные на образующих точки лекальной кривой, а также точки A и B получим аксонометрическую проекцию усеченного конуса.
В Сечение конуса горизонтальной плоскостью. Рис. 6.
Сечение прямого кругового конуса горизонтальной плоскостью параллельной основанию – есть окружность.
Если рассечь конус на произвольной высоте h от основания конуса через точку a’
лежащую на его оси o’s’ плоскостью параллельной его основанию, то на фронтальной проекции мы увидим горизонтальную линию Pv являющуюся фронтальной проекцией секущей плоскости, которая образует сечение
конуса I’, II’, III’, IV’. На профильной проекции
W вид секущей плоскости и сечение конуса аналогичен и соответствует линии Pw.
На горизонтальной проекции сечение
конуса представляет собой круг в натураль-
ную величину, радиус окружности которого проецируется с фронтальной проекции как расстояние от оси конуса в точке a’ до точки I’, лежащей на крайней образующей 1’s’.
Построение аксонометрии. Рис. 6.
Строим конус в аксонометрии, как опи-
сано выше.
Затем на оси Z откладываем высоту h точки А от основания конуса. Через точку А проводим линии параллельные осям X и Y и строим окружность в
аксонометрии радиусом R=a’I’ взятым с фронтальной проекции.
Г Сечение конуса наклонной плоскостью, параллельной образующей. Рис. 7.
Строим три проекции конуса – горизонтальную, фронтальную и профильную. (см. выше).
На фронтальной проекции конуса проводим секущую плоскость Pv параллельно очерковой образующей s’6’на произвольном расстоянии от ее нача-
ла на основании конуса через т. a’(b’). Отрезок a’c’ есть фронтальная проекция сечения конуса.
На горизонтальной проекции строим проекцию основания секущей плоскости Р через точки a, b. Отрезок ab – есть проекция основания сечения конуса.
Далее окружность основания конуса делим на произвольное количество частей и полученные точки соединяем с вершиной конуса s. Получаем ряд образующих конуса, которые последовательно переносим на фронтальную и профильную проекции. (см. пункт Б).
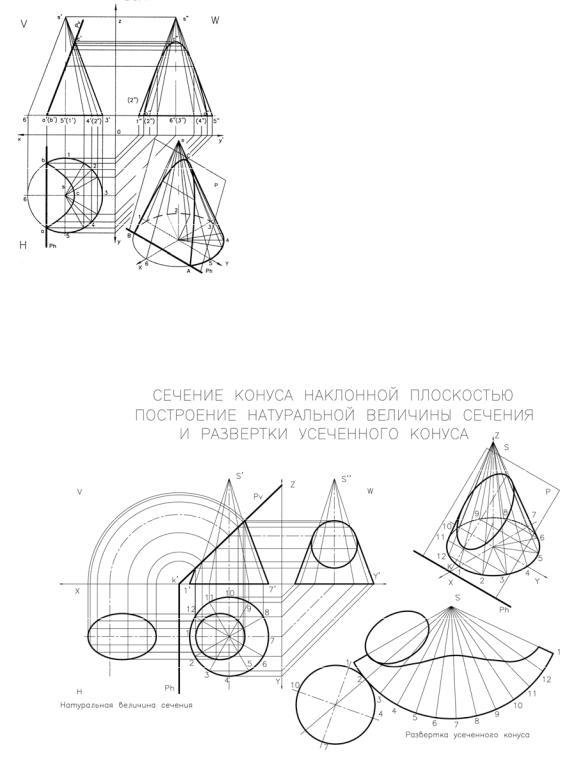
На фронтальной проекции след секущей плоскости Pv пересекает обра-
зующие и в пересечении дает ряд точек, которые принадлежат как секущей плоскости, так и образующим конуса одновременно.
Переносим линиями связи эти точки на проекции образующих на гори-
зонтальную и профильную проекции.
Полученные точки соединим кривой линией, которая представляет собой
лекальную кривую – параболу.
Построение аксонометрии. Рис. 7.
Строим аксонометрическую проекцию конуса, как описано выше.
Далее с горизонтальной проекции конуса берем координаты по оси X или Y для
всех точек (a, b, 1, …, 6) и переносим их на аксонометрические оси X или Y соответственно, определив, таким образом их поло-
жение на основании конуса в аксонометрии. Соединяем их последовательно с вершиной
конуса S и получаем ряд образующих на поверхности конуса, соответствующих образующим на ортогональных проекциях.
На каждой образующей найдем точку ее пересечения с секущей плоскостью P
аналогично тому, как это было описано выше (см. построение точек на поверхности конуса).
|
Соединив полученные на образующих |
||
|
Рис. 7 |
||
|
точки лекальной кривой, а также точки A и B |
||
|
получим сечение конуса в виде параболы. |
||
Д. Сечение конуса наклонной плоскостью, расположенной под произвольным углом к основанию конуса представляет собой эллипс. Рис. 8.
Рис. 8
Строим три проекции конуса – горизонтальную, фронтальную и про-
фильную. (см. выше).
На фронтальной проекции конуса проводим линию секущей плоскости Pv под произвольным углом к основанию конуса.
На горизонтальной проекции, окружность основания конуса делим на произвольное количество равных частей ( в данном случае на 12) и получен-
ные точки соединяем с вершиной конуса S. Получаем ряд образующих, которые с помощью линий связи, последовательно переносим на фронтальную и профильную проекции.
На фронтальной проекции секущая плоскость Pv пересекает все образующие, и полученные точки их пересечения принадлежат одновременно и се-
кущей плоскости и боковой поверхности конуса, являясь фронтальной проекцией искомого сечения.
Переносим эти точки на горизонтальную проекцию конуса.
Затем строим и профильную проекцию сечения конуса (см. выше), соединяя полученные точки лекальной кривой, которая представляет собой эл-
липс.
Построение натуральной величины сечения.
Лекальные кривые (эллипсы) на горизонтальной и профильной проекции представляют собой искаженные изображения сечения конуса.
Истинная (натуральная) величина сечения получается путем совмеще-
ния секущей плоскости P с горизонтальной плоскостью проекций H. Все точки сечения конуса на фронтальной проекции переносим на ось X при помощи циркуля, поворачивая их вокруг точки k’. Далее, на горизонтальной проекции, линиями связи, параллельными оси Y продолжаем их до пересечения их с ли-
ниями связи, взятыми с горизонтальной проекции соответствующих точек. Пе-
ресечение горизонтальных и вертикальных линий связи соответствующих точек позволяет получить точки, принадлежащие натуральной величине сечения. Соединив их лекальной кривой, мы получим эллипс натуральной величины сечения конуса.
Построение аксонометрии усеченного конуса. Рис. 8.
Построение аксонометрии усеченного конуса выполняется путем нахождения точек принадлежащих сечению конуса любым из описанных выше способов (см. выше).
Построение развертки поверхности усеченного конуса. Рис. 8.
Предварительно построим развертку боковой поверхности не усеченного
конуса. Задаемся положением т. S на листе и проводим из нее дугу радиусом равным натуральной величине длины образующей конуса (например, s’1’или s’7’). Задаемся положением т. 1 на этой дуге. Последовательно откладываем от нее столько одинаковых отрезков (хорд) на сколько частей разделена окружность основания конуса. Полученные на дуге точки 1, 2, …, 12, 1 соединяем с т. S. Сектор 1S1 представляет собой развертку боковой поверхности не усе-
ченного конуса. Пристроив к ней в нижней части (например, к т. 2) натуральную величину основания конуса в виде круга взятого с горизонтальной проекции мы
получим полную развертку не усеченного конуса.
Для построения развертки боковой поверхности усеченного конуса необходимо определить натуральную величину всех усеченных образующих. На
фронтальной проекции все точки сечения перенесем на очерковую образующую s’7’ линиями параллельными основанию конуса. Затем каждый отрезок образующей от т. 7’ до соответствующей точки сечения переносим на соответствующую образующую на развертке. Соединив эти точки на развертке, получим кривую линию, соответствующую линии сечения боковой поверхности ко-
нуса.
Затем к линии сечения на развертке (например, к образующей S1) при-
страиваем эллипс натуральной величины сечения полученный на горизонтальной проецирующей плоскости Н.
Развертки поверхности геометрических тел представляют собой чертежи
– выкройки из бумаги и служат для выполнения макета фигуры.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
§ 18. Конус
18.1.Определение конуса и его элементов
Определение. Тело, которое образуется при вращении прямоугольного треугольника вокруг прямой, содержащей его катет, называется прямым круговым конусом (рис. 165, 166).
Отрезок оси вращения, заключённый внутри конуса, называется осью конуса.
Круг, образованный при вращении второго катета, называется основанием конуса. Длина этого катета называется радиусом основания конуса или, короче, радиусом конуса. Вершина острого угла вращающегося треугольника, лежащая на оси вращения, называется вершиной конуса. На рисунках 165, б и 166 вершиной конуса является точка Р.
Высотой конуса называется отрезок, проведённый из вершины конуса перпендикулярно его основанию. Длину этого перпендикуляра также называют высотой конуса. Высота конуса имеет своим основанием центр круга — основания конуса — и совпадает с осью конуса.
Отрезки, соединяющие вершину конуса с точками окружности его основания, называются образующими конуса. Все образующие конуса равны между собой (почему?).
Как и в случае с цилиндром, можно рассматривать конус в более широком, чем у нас, понимании, когда в основании конуса может быть, например, эллипс (эллиптический конус), парабола (параболический конус). Мы будем изучать только определённый выше прямой круговой конус (конус вращения), поэтому слова «прямой круговой» мы будем опускать.

Рис. 165

Рис. 166

Рис. 167
Поверхность, полученная при вращении гипотенузы, называется боковой поверхностью конуса, а её площадь — площадью боковой поверхности конуса и обозначается Sбок. Боковая поверхность конуса является объединением всех его образующих.
Объединение боковой поверхности конуса и его основания называется полной поверхностью конуса, а её площадь называется площадью полной поверхности конуса или, короче, площадью поверхности конуса и обозначается Sкон. Из этого определения следует, что
Sкон = Sбок + Sосн.
Если вокруг данной прямой — оси — вращать пересекающую её прямую, то при этом вращении образуется поверхность, которую называют круговой конической поверхностью или конической поверхностью вращения. Уравнение  +
+  –
–  = 0 задаёт коническую поверхность вращения с осью вращения Oz (рис. 167). Из этого уравнения следует, что коническая поверхность является поверхностью второго порядка. (Подробнее о поверхностях второго порядка можно прочитать в «Дополнениях» — в конце этой книги.)
= 0 задаёт коническую поверхность вращения с осью вращения Oz (рис. 167). Из этого уравнения следует, что коническая поверхность является поверхностью второго порядка. (Подробнее о поверхностях второго порядка можно прочитать в «Дополнениях» — в конце этой книги.)
18.2. Сечения конуса
Определение. Сечение конуса плоскостью, проходящей через его ось, называется осевым сечением конуса.

Рис. 168

Рис. 169

Рис. 170
Так как все образующие конуса равны, то его осевым сечением является равнобедренный треугольник, боковыми сторонами которого являются образующие конуса, а основанием — диаметр конуса. При этом все осевые сечения конуса — равные равнобедренные треугольники. На рисунке 168 осевым сечением конуса является треугольник ABP (АР = ВР). Угол АPВ называют углом при вершине осевого сечения конуса.
Конус, в осевом сечении которого правильный треугольник, называется равносторонним конусом.
Если секущая плоскость проходит через вершину конуса, пересекает конус, но не проходит через его ось, то в сечении конуса также получается равнобедренный треугольник (см. рис. 168: △ DCP).
Так как конус — тело вращения, то любое сечение конуса плоскостью, перпендикулярной его оси (т. е. параллельной основанию конуса), есть круг, а сечение боковой поверхности конуса такой плоскостью — окружность этого круга; центром круга (окружности) является точка пересечения оси конуса и секущей плоскости (рис. 169).
Если секущая плоскость не параллельна плоскости основания конуса и не пересекает основание, то сечением боковой поверхности конуса такой плоскостью является эллипс (рис. 170). Поэтому эллипс называют коническим сечением.

Рис. 171
 Если сечением цилиндрической поверхности плоскостью может быть либо окружность, либо эллипс, либо две параллельные прямые, то сечением конической поверхности плоскостью может быть либо окружность (секущая плоскость перпендикулярна оси конической поверхности вращения и не проходит через её вершину, рис. 171, a), либо эллипс (секущая плоскость не перпендикулярна оси конической поверхности и пересекает все её образующие, рис. 171, б), либо парабола (секущая плоскость параллельна только одной образующей конической поверхности, рис. 171, в), либо гипербола (секущая плоскость параллельна оси конической поверхности, рис. 171, г), либо пара пересекающихся прямых (секущая плоскость проходит через вершину конической поверхности, рис. 171, д). Поэтому невырожденные кривые второго порядка — окружность, эллипс, параболу и гиперболу называют коническими сечениями или коротко — кониками.
Если сечением цилиндрической поверхности плоскостью может быть либо окружность, либо эллипс, либо две параллельные прямые, то сечением конической поверхности плоскостью может быть либо окружность (секущая плоскость перпендикулярна оси конической поверхности вращения и не проходит через её вершину, рис. 171, a), либо эллипс (секущая плоскость не перпендикулярна оси конической поверхности и пересекает все её образующие, рис. 171, б), либо парабола (секущая плоскость параллельна только одной образующей конической поверхности, рис. 171, в), либо гипербола (секущая плоскость параллельна оси конической поверхности, рис. 171, г), либо пара пересекающихся прямых (секущая плоскость проходит через вершину конической поверхности, рис. 171, д). Поэтому невырожденные кривые второго порядка — окружность, эллипс, параболу и гиперболу называют коническими сечениями или коротко — кониками.
О конических сечениях можно прочитать в очерках «Элементарная геометрия», «Проективная геометрия» в конце этой книги. 
ЗАДАЧА (3.047). Высота конуса равна радиусу R его основания. Через вершину конуса проведена плоскость, отсекающая от окружности основания дугу: а) в 60°; б) в 90°. Найти площадь сечения.

Решение. Рассмотрим случай а). Пусть плоскость α пересекает поверхность конуса с вершиной Р по образующим РА и РВ (рис. 172); △ АВР — искомое сечение. Найдём площадь этого сечения.
Хорда АВ окружности основания стягивает дугу в 60°, значит, △ AOB — правильный и АВ = R.
Рис. 172
Если точка С — середина стороны АB, то отрезок PC — высота треугольника АВР. Поэтому S△ ABP =  АВ•РC. Имеем: ОР = R (по условию); в △ AOB: ОС =
АВ•РC. Имеем: ОР = R (по условию); в △ AOB: ОС =  ; в △ ОСР: CP =
; в △ ОСР: CP =  =
=  .
.
Тогда S△ ABP =  АВ•РС =
АВ•РС =  .
.
Ответ: а)  .
.
18.3. Касательная плоскость к конусу
Определение. Касательной плоскостью к конусу называется плоскость, проходящая через образующую конуса перпендикулярно осевому сечению, проведённому через эту образующую.

Рис. 173
Говорят, что плоскость α касается конуса по образующей РА (рис. 173): каждая точка образующей РА является точкой касания плоскости α и данного конуса.

Через любую точку боковой поверхности конуса проходит только одна его образующая. Через эту образующую можно провести только одно осевое сечение и только одну плоскость, перпендикулярную плоскости этого осевого сечения. Следовательно, через каждую точку боковой поверхности конуса можно провести лишь одну плоскость, касательную к данному конусу в этой точке.
18.4. Изображение конуса

Рис. 174
Для изображения конуса достаточно построить: 1) эллипс, изображающий окружность основания конуса (рис. 174); 2) центр О этого эллипса; 3) отрезок ОР, изображающий высоту конуса; 4) касательные прямые РА и PB из точки Р к эллипсу (их проводят с помощью линейки на глаз).
Для достижения наглядности изображения невидимые линии изображают штрихами.
Необходимо заметить, что отрезок АВ, соединяющий точки касания образующих и окружности основания конуса, ни в коем случае не является диаметром основания конуса, т. е. этот отрезок не содержит центра О эллипса. Следовательно, △ АBP — не осевое сечение конуса. Осевым сечением конуса является △ ACP, где отрезок AC проходит через точку О, но образующая PC не является касательной к окружности основания.
18.5. Развёртка и площадь поверхности конуса
Пусть l — длина образующей, R — радиус основания конуса с вершиной Р.

Рис. 175

Рис. 176
Поверхность конуса состоит из боковой поверхности конуса и его основания. Если эту поверхность разрезать по одной из образующих, например по образующей PA (рис. 175), и по окружности основания, затем боковую поверхность конуса развернуть на плоскости (рис. 176, a), то получим развёртку поверхности конуса (рис. 176, б), состоящую из: а) кругового сектора, радиус которого равен образующей l конуса, а длина дуги сектора равна длине окружности основания конуса; б) круга, радиус которого равен радиусу R основания конуса. Угол сектора развёртки боковой поверхности конуса называют углом развёртки конуса; его численная величина равна отношению длины окружности основания конуса к его образующей (радиусу сектора развёртки):
α =  .
.
За площадь боковой поверхности конуса принимается площадь её развёртки. Выразим площадь боковой поверхности конуса через длину l его образующей и радиус R основания.
Площадь боковой поверхности — площадь кругового сектора радиуса длины l — вычисляется по формуле
Sбок =  α•l2,(1)
α•l2,(1)
где α — величина угла (в радианах) сектора — развёртки. Учитывая, что α =  , получаем:
, получаем:
Sбок = πRl.(2)
Таким образом, доказана следующая теорема.

Теорема 27. Площадь боковой поверхности конуса равна произведению половины длины окружности основания на образующую. ▼
Площадь полной поверхности конуса равна сумме площадей его боковой поверхности и основания, т. е.
Sкон = πRl + πR2.(3)

Следствие. Пусть конус образован вращением прямоугольного треугольника ABC вокруг катета АС (рис. 177). Тогда Sбок = π•BC•АВ. Если D — середина отрезка АВ, то AB = 2AD, поэтому
Sбок = 2 π ВС•AD.(4)

Рис. 177
Проведём DE ⟂ АB (E ∈ l = AС). Из подобия прямоугольных треугольников ADE и ACB (у них общий угол А) имеем
 =
=  ⇒ BC•AD = DE•АС.(5)
⇒ BC•AD = DE•АС.(5)
Тогда соотношение (4) принимает вид
Sбок = (2π•DE)•AC,(6)
т. е. площадь боковой поверхности конуса равна произведению высоты конуса на длину окружности, радиус которой равен длине серединного перпендикуляра, проведённого из точки на оси конуса к его образующей.
Это следствие будет использовано в п. 19.7.
18.6. Свойства параллельных сечений конуса


Теоремa 28. Если конус пересечён плоскостью, параллельной основанию, то: 1) все образующие и высота конуса делятся этой плоскостью на пропорциональные части; 2) в сечении получается круг; 3) площади сечения и основания относятся, как квадраты их расстояний от вершины.

Рис. 178
Доказательство. 1) Пусть конус с вершиной Р и основанием F пересечён плоскостью α, параллельной плоскости β основания конуса и расположенной между Р и β (рис. 178).
Проведём высоту РО конуса, где точка О — центр круга F. Так как РО ⟂ β, α || β, то α ⟂ РО. Значит, в сечении конуса плоскостью α получается круг с центром в точке O1 = α ∩ РО. Обозначим этот круг F1.
Рассмотрим гомотетию  с центром P, при которой плоскость β основания данного конуса отображается на параллельную ей плоскость α (при гомотетии плоскость, не проходящая через центр гомотетии, отображается на параллельную ей плоскость).
с центром P, при которой плоскость β основания данного конуса отображается на параллельную ей плоскость α (при гомотетии плоскость, не проходящая через центр гомотетии, отображается на параллельную ей плоскость).
Так как при гомотетии её центр является неподвижной точкой, прямая, проходящая через центр гомотетии, отображается на себя, а пересечение двух фигур — на пересечение их образов, то гомотетия  отображает основание F конуса на его параллельное сечение — круг F1, при этом центр О основания отображается на центр О1 круга F1 (почему?). Кроме того, если РХ — произвольная образующая конуса, где Х — точка окружности основания, то при гомотетии
отображает основание F конуса на его параллельное сечение — круг F1, при этом центр О основания отображается на центр О1 круга F1 (почему?). Кроме того, если РХ — произвольная образующая конуса, где Х — точка окружности основания, то при гомотетии  точка X отображается на точку X1 = РX ∩ α. Учитывая, что отношение длин гомотетичных отрезков равно коэффициенту гомотетии, получаем:
точка X отображается на точку X1 = РX ∩ α. Учитывая, что отношение длин гомотетичных отрезков равно коэффициенту гомотетии, получаем:
 =
=  = k,(*)
= k,(*)
где k — коэффициент гомотетии  , т. е. параллельное сечение конуса делит его образующие и высоту на пропорциональные части.
, т. е. параллельное сечение конуса делит его образующие и высоту на пропорциональные части.
А поскольку гомотетия является подобием, то круг F1, являющийся параллельным сечением конуса, подобен его основанию.
Вследствие того что отношение площадей гомотетичных фигур равно квадрату коэффициента гомотетии и k = PO1 : РО, где РO1 и PO — расстояния соответственно параллельного сечения и основания пирамиды от её вершины, то
Sсечен : Sоснов = k2 =  : PO2.
: PO2.
Теорема доказана. ▼
18.7.Вписанные в конус и описанные около конуса пирамиды
Определение. Пирамида называется вписанной в конус, если у них вершина общая, а основание пирамиды вписано в основание конуса. В этом случае конус называется описанным около пирамиды.
Для построения изображения правильной пирамиды, вписанной в конус:
—строят изображение основания пирамиды — правильного многоугольника, вписанного в основание конуса;
—соединяют отрезками прямых вершину конуса с вершинами построенного многоугольника;
—выделяют видимые и невидимые (штрихами) линии изображаемых фигур.
На рисунках 179—182 изображена вписанная в конус пирамида, в основаниях которой лежит:
—прямоугольный треугольник (см. рис. 179);
—правильный треугольник (см. рис. 180);
—квадрат (см. рис. 181);
—правильный шестиугольник (см. рис. 182).

Рис. 179

Рис. 180

Рис. 181

Рис. 182
Определение. Пирамида называется описанной около конуса, если у них вершина общая, а основание пирамиды описано около основания конуса. В этом случае конус называют вписанным в пирамиду (рис. 183).

Рис. 183

Рис. 184
ЗАДАЧА (3.080). В равносторонний конус вписана правильная пирамида. Найти отношение площадей боковых поверхностей пирамиды и конуса, если пирамида: а) треугольная; б) четырёхугольная; в) шестиугольная.
Решение. Рассмотрим случай а). Пусть R — радиус основания равностороннего конуса, РАВС — правильная пирамида, вписанная в этот конус (рис. 184); △ DPE — осевое сечение конуса, CF — медиана △ АBС. Тогда в △ АВС (правильный): АВ = R , OF =
, OF =  R; в △ DPE (правильный): ОР =
R; в △ DPE (правильный): ОР =  = R
= R ; в △ ОРF (∠ FOP = 90°):
; в △ ОРF (∠ FOP = 90°):
PF =  =
=  .
.
Так как CF — медиана △ АВС, то PF — высота равнобедренного треугольника АВР. Поэтому
S△ ABP =  AB•PF =
AB•PF =  R
R •
•  =
=  .
.
Обозначим: S1 — площадь боковой поверхности пирамиды, S2 — площадь боковой поверхности конуса. Тогда
S1 = 3S△ ABP =  ,
,
S
2 = πR•PA = πR•2R = 2πR2.
Следовательно,
S1 : S2 =  : 2πR2 =
: 2πR2 =  .
.
Ответ: а)  .
.


 Во многих пособиях по геометрии за площадь боковой поверхности конуса принимают предел последовательности боковых поверхностей правильных вписанных в конус (или описанных около конуса) п-угольных пирамид при n → +∞. Действительно, Sбок. пов. пирам =
Во многих пособиях по геометрии за площадь боковой поверхности конуса принимают предел последовательности боковых поверхностей правильных вписанных в конус (или описанных около конуса) п-угольных пирамид при n → +∞. Действительно, Sбок. пов. пирам =  •a•Poсн. пирам, где Рoсн. пирам — периметр основания пирамиды, а — апофема боковой грани. Для правильных описанных около конуса пирамид апофема a — постоянная величина, равная образующей l конуса, а предел последовательности периметров правильных многоугольников, описанных около окружности радиуса R основания конуса, равен 2πR — длине этой окружности. Таким образом, мы вновь получаем: Sбок = πRl.
•a•Poсн. пирам, где Рoсн. пирам — периметр основания пирамиды, а — апофема боковой грани. Для правильных описанных около конуса пирамид апофема a — постоянная величина, равная образующей l конуса, а предел последовательности периметров правильных многоугольников, описанных около окружности радиуса R основания конуса, равен 2πR — длине этой окружности. Таким образом, мы вновь получаем: Sбок = πRl. 
18.8. Усечённый конус

Рис. 185
Пусть дан конус с вершиной Р. Проведём плоскость α, параллельную плоскости основания конуса и пересекающую этот конус (рис. 185). Эта плоскость пересекает данный конус по кругу и разбивает его на два тела: одно из них является конусом, а другое (расположенное между плоскостью основания данного конуса и секущей плоскостью) называют усечённым конусом. Таким образом, усечённый конус представляет собой часть полного конуса, заключённую между его основанием и параллельной ему плоскостью. Основание данного конуса и круг, полученный в сечении этого конуса плоскостью α, называются соответственно нижним и верхним основаниями усечённого конуса. Высотой усечённого конуса называется перпендикуляр, проведённый из какой-либо точки одного основания к плоскости другого. Длину этого перпендикуляра также называют высотой усечённого конуса. (Часто за высоту усечённого конуса принимают отрезок, соединяющий центры его оснований.)

Рис. 186

Рис. 187
Часть боковой поверхности данного конуса, ограничивающая усечённый конус, называется боковой поверхностью усечённого конуса, а отрезки образующих конуса, заключённые между основаниями усечённого конуса, называются образующими усечённого конуса. Так как все образующие данного конуса равны и равны все образующие отсечённого конуса, то равны все образующие усечённого конуса.
Построение изображения усечённого конуса следует начинать с изображения того конуса, из которого получился усечённый конус (рис. 186).
На рисунке 187 показана развёртка усечённого конуса.
Из теоремы 28 следует, что основания усечённого конуса — подобные круги.
Определения усечённой пирамиды, вписанной в усечённый конус и описанной около него, аналогичны определениям пирамиды, вписанной в конус и описанной около него.
Заметим, что построение изображений усечённой пирамиды, вписанной в усечённый конус и описанной около него, следует начинать с изображений того конуса или той пирамиды, из которых получены соответственно усечённые конус и пирамида.
Полной поверхностью усечённого конуса называется объединение боковой поверхности этого конуса и двух его оснований. Иногда полную поверхность усечённого конуса называют его поверхностью, а её площадь — площадью поверхности усечённого конуса. Эта площадь равна сумме площадей боковой поверхности и оснований усечённого конуса.
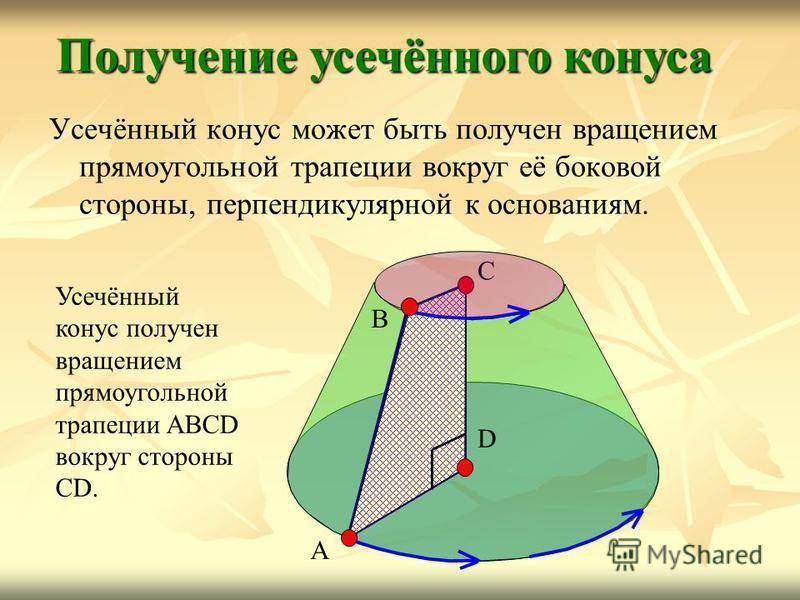
Усечённый конус может быть образован также вращением прямоугольной трапеции вокруг боковой стороны трапеции, перпендикулярной её основанию.

Рис. 188
На рисунке 188 изображён усечённый конус, образованный вращением прямоугольной трапеции ABCD вокруг стороны CD. При этом боковая поверхность усечённого конуса образована вращением боковой стороны АВ, а основания его — вращением оснований AD и ВС трапеции.
18.9. Поверхность усечённого конуса
Выразим площадь Sбок боковой поверхности усечённого конуса через длину l его образующей и радиусы R и r оснований (R > r).

Рис. 189
Пусть точка Р — вершина конуса, из которого получен усечённый конус; точки О, O1 — центры оснований усечённого конуса; AA1 = l — одна из образующих усечённого конуса (рис. 189).
Используя формулу (2) п. 18.5, получаем
Sбок = πR•PA – πr•РA1 =
= πR(РA1 + А1A) – πr•PA1 =
= πR•A1A + π(R – r)•PA1.
Учитывая, что A1A = l, имеем
Sбок = πRl + π(R – r)PA1.(7)
Выразим PA1 через l, R и r. Так как O1A1 || OA и OO1 — высота усечённого конуса, то прямоугольные треугольники POA и PO1A1 подобны. Поэтому АО : А1O1 = PA : PA1 или
R : r = (PA1 + A1A) : PA1, откуда
R•PA1 = r(PA1 + l) ⇒ (R – r)PA1 = rl ⇒ PA1 =  .
.
Подставив это значение РА1 в (7), получаем
Sбок = π(R + r)l.(8)
Таким образом, доказана следующая теорема.

Теорема 29. Площадь боковой поверхности усечённого конуса равна произведению полусуммы длин окружностей оснований на образующую. ▼
Площадь полной поверхности усечённого конуса находится по формуле:
Sполн = π•(R + r)•l + π•R2 + π•r2.

Следствие. Пусть усечённый конус образован вращением прямоугольной трапеции ABCD вокруг её высоты AD (рис. 190). Тогда Sбок = π (АВ + DC)•ВС. Если KЕ — средняя линия трапеции, то АВ + DC = 2KE, поэтому
Sбок = 2π•KE•BC.(9)

Рис. 190
Проведём EF ⟂ ВС. Из подобия прямоугольных треугольников ВСН и EFK имеем
BC : EF = BH : KE ⇒ ⇒ KE•BC = EF•BH.(10)
Тогда равенство (9) принимает вид
Sбок = (2π•EF)•ВH,(11)

т. е. боковая поверхность усечённого конуса равна произведению его высоты на длину окружности, радиус которой равен серединному перпендикуляру, проведённому из точки оси конуса к его образующей.
18.10. Объёмы конуса и усечённого конуса
Найдём объём конуса, высота которого равна h и радиус основания — R. Для этого расположим этот конус и правильную четырёхугольную пирамиду, высота которой равна h и сторона основания — R, так, чтобы их основания находились на одной и той же плоскости α, а вершины — также в одной и той же плоскости β, параллельной плоскости α и удалённой от неё на расстояние h (рис. 191).

Рис. 191
Каждая плоскость, параллельная данным плоскостям и пересекающая конус, пересекает также пирамиду; причём площади сечений, образованных при пересечении обоих тел, относятся к площадям оснований этих тел, как квадраты их расстояний от вершин. А так как секущие плоскости для пирамиды и для конуса равноудалены от их вершин, то  =
=  . Тогда
. Тогда  =
=  =
=  = π, значит, для объёмов этих тел выполняется:
= π, значит, для объёмов этих тел выполняется:
Vкон : Vпир = π : 1 или Vкон :  R2•h = π : 1, откуда
R2•h = π : 1, откуда
Vкон =  πR2 •h.
πR2 •h.

Рис. 192
Самостоятельно рассмотрите усечённые конус и пирамиду, расположенные в соответствии с условиями принципа Кавальери. Тогда вы получите формулу вычисления объёма усечённого конуса:
Vус. кон =  π•h•(R2 + r•R + r2).
π•h•(R2 + r•R + r2).
Эту же формулу вы можете вывести, если используете идею подобия так же, как это сделано в случае с выводом формулы площади боковой поверхности усечённого конуса.

Используя принцип Кавальери, докажите, что объём каждого из тел, на которые конус разбивается его сечением плоскостью, проходящей через вершину (рис. 192), может быть вычислен по формуле V =  •h•Scегм, где h — длина высоты конуса, а Sceгм — площадь соответствующего сегмента основания конуса.
•h•Scегм, где h — длина высоты конуса, а Sceгм — площадь соответствующего сегмента основания конуса.

Конические сечения
Рассмотрим пять возможных случаев расположения секущей плоскости относительно оси конуса и его образующих, определяющих форму линии ее пересечения с поверхностью конуса (математические доказательства не приводятся).
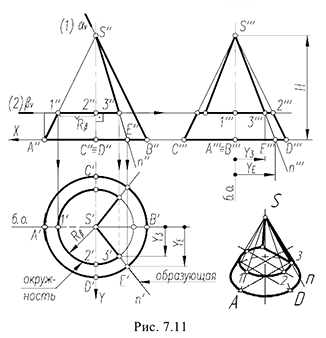
1-й случай. Если секущая плоскость проходит через вершину конуса, то эта плоскость пересекает коническую поверхность по двум образующим 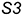 (фронталь-но-проецирующая плоскость
(фронталь-но-проецирующая плоскость 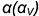 , рис. 7.11).
, рис. 7.11).
2-й случай. Если секущая плоскость расположена перпендикулярно оси конуса, то эта плоскость пересекает коническую поверхность по окружности (горизонтальная плоскость 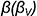 рис. 7.11).
рис. 7.11).
3-й случай. Если секущая плоскость расположена параллельно одной образующей конуса, то эта плоскость пересекает коническую поверхность по параболе (фронтально-проецирующая плоскость 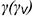 параллельна одной образующей
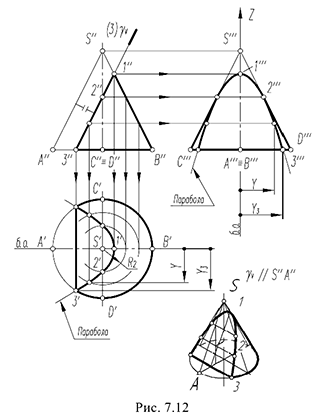
параллельна одной образующей  рис. 7.12).
рис. 7.12).
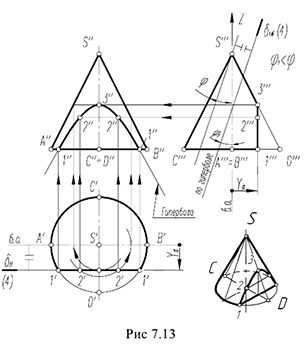
4-й случай. Если секущая плоскость расположена параллельно двум образующим конуса, то эта плоскость пересекает коническую поверхность по гиперболе (фронтальная плоскость 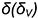 параллельна двум образующим
параллельна двум образующим  и
и  , рис. 7.13).
, рис. 7.13).
5-й случай. Если плоскость пересекает все образующие конуса под углом, отличным от прямого (или иначе не параллельна ни одной образующей конуса), то эта плоскость пересекает коническую поверхность по эллипсу (фронтально-проецирующая плоскость 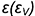 , рис. 7.14).
, рис. 7.14).
Рассмотрим построение на проекциях конуса линий пересечения для всех пяти случаев сечений. 1-й и 2-й случаи. На рис. 7.11 показано построение проекций прямого кругового конуса с вырезом, образованным сечениями конической поверхности фронтально-проецирующей плоскостью 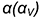 , проходящей через вершину конуса (1-й случай), и горизонтальной плоскостью
, проходящей через вершину конуса (1-й случай), и горизонтальной плоскостью 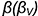 , расположенной перпендикулярно оси конуса (2-й случай).
, расположенной перпендикулярно оси конуса (2-й случай).
Плоскость 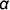 пересекает поверхность конуса по образующим
пересекает поверхность конуса по образующим  , горизонтальные и профильные проекции которых строятся с помощью вспомогательной точки
, горизонтальные и профильные проекции которых строятся с помощью вспомогательной точки 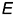 , лежащей на основании конуса.
, лежащей на основании конуса.
Плоскость 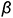 пересекает поверхность конуса по окружности радиуса
пересекает поверхность конуса по окружности радиуса 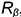 , ограниченной линией 3-3 пересечения плоскостей выреза.
, ограниченной линией 3-3 пересечения плоскостей выреза.
Построение горизонтальной и профильной проекций конуса с вырезом и оформление очерков этих проекций видно из чертежа.
3-й случай. На рис. 7.12 показано построение проекций конуса со срезом фронтально-проецирующей плоскостью 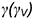 , расположенной параллельно одной образующей конуса
, расположенной параллельно одной образующей конуса  .
.
Плоскость 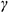 пересекает поверхность конуса по параболе, горизонтальная и профильная проекции которой строятся по отмеченным характерным точкам 1, 2 и 3 и промежуточной точке (не обозначена).
пересекает поверхность конуса по параболе, горизонтальная и профильная проекции которой строятся по отмеченным характерным точкам 1, 2 и 3 и промежуточной точке (не обозначена).
Построение проекций этих точек выполнено по их принадлежности: -точка 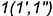 — лежит на проекциях характерной образующей
— лежит на проекциях характерной образующей
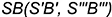
-точки 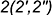 — лежат на проекциях характерных образующих
— лежат на проекциях характерных образующих 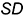 и
и 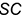 , горизонтальные проекции которых построены с помощью параллели радиусом
, горизонтальные проекции которых построены с помощью параллели радиусом 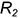 (алгоритм I);
(алгоритм I);
-точки 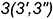 — лежат на окружности основания конуса: горизонтальные проекции этих точек определяются по линии связи на горизонтальной проекции окружности основания, а их профильные проекции построены по координате
— лежат на окружности основания конуса: горизонтальные проекции этих точек определяются по линии связи на горизонтальной проекции окружности основания, а их профильные проекции построены по координате 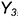
- проекции промежуточной точки построены по ее принадлежности соответствующей параллели (профильные проекции — по координате
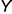 ).
).
Оформление очерков проекций видно из чертежа.
4-й случай. На рис. 7.13 показано построение проекций конуса со срезом фронтальной плоскостью 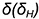 , расположенной параллельно двум образующим конуса
, расположенной параллельно двум образующим конуса  и
и  .
.
Плоскость 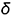 пересекает поверхность конуса по гиперболе, фронтальная проекция которой строится по отмеченным точкам 2 и 3 по их принадлежности параллелям (обратный алгоритм I), а профильная проекция гиперболы проецируется в вертикальную линию и совпадает с вырожденной проекцией плоскости среза
пересекает поверхность конуса по гиперболе, фронтальная проекция которой строится по отмеченным точкам 2 и 3 по их принадлежности параллелям (обратный алгоритм I), а профильная проекция гиперболы проецируется в вертикальную линию и совпадает с вырожденной проекцией плоскости среза 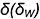
Оформление очерков проекций видно из чертежа
На рис. 7.13 на профильной проекции конуса показано положение секущей плоскости 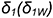 под углом
под углом 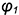 к оси конуса. При
к оси конуса. При 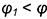 плоскость пересекает поверхность конуса также по гиперболе.
плоскость пересекает поверхность конуса также по гиперболе.
5-й случай. На рис. 7.14 показано построение проекций конуса со срезом фронтально-проецирующей плоскостью 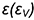 , пересекающей все образующие конуса под углом
, пересекающей все образующие конуса под углом 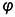 к оси, отличным от прямого.
к оси, отличным от прямого.
Плоскость 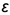 пересекает поверхность конуса по эллипсу, горизонтальная и профильная проекции которого построены по проекциям отмеченных характерных точек 1, 2, 4 я промежуточных точек 3, взятых на середине отрезка 1-4, который является совпадающей проекцией эллипса и его большой оси. Точки 3 определяют проекции малой оси эллипса и построены на горизонтальной проекции конуса по радиусу параллели, а на профильной проекции по координате
пересекает поверхность конуса по эллипсу, горизонтальная и профильная проекции которого построены по проекциям отмеченных характерных точек 1, 2, 4 я промежуточных точек 3, взятых на середине отрезка 1-4, который является совпадающей проекцией эллипса и его большой оси. Точки 3 определяют проекции малой оси эллипса и построены на горизонтальной проекции конуса по радиусу параллели, а на профильной проекции по координате 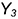 (алгоритм 1).
(алгоритм 1).
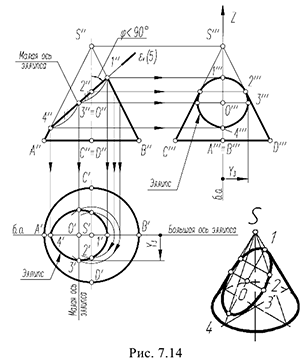
Оформление очерков проекций видно из чертежа. !!! Количество взятых промежуточных точек должно быть минимальным, но достаточным, чтобы построить на проекциях конуса формы кривых второго порядка (параболы, гиперболы и эллипса), которые выполняют на чертеже по построенным характерным и промежуточным точкам с помощью лекала.
Построение проекций прямого конуса со срезами плоскостями частного положения
На рис. 7.15 показан пример построения проекций прямого кругового конуса со срезами фронтально-проецирующей плоскостью 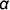 и профильной плоскостью
и профильной плоскостью 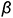
Для построения проекций конуса со срезами следует выполнить графический алгоритм, определяющий порядок действий при решении всех подобных задач.
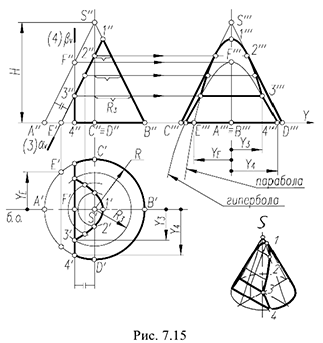
Графический алгоритм: 1-е действие. Построить на чертеже тонкими линиями по заданному радиусу основания 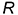 и высоте
и высоте 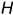 фронтальную, горизонтальную и профильную проекции конуса без срезов, а затем выполнить на его фронтальной проекции заданные срезы фронтально-проецирующей плоскостью
фронтальную, горизонтальную и профильную проекции конуса без срезов, а затем выполнить на его фронтальной проекции заданные срезы фронтально-проецирующей плоскостью 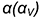 и профильной плоскостью
и профильной плоскостью 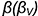 . 2-е действие. Обозначить на фронтальной проекции характерные точки пересечения плоскостей срезов с образующими и основанием конуса и выполнить графический анализ сечений.
. 2-е действие. Обозначить на фронтальной проекции характерные точки пересечения плоскостей срезов с образующими и основанием конуса и выполнить графический анализ сечений.
2.7. Фронтально-проецирующая плоскость 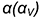 параллельна одной образующей конуса
параллельна одной образующей конуса 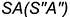 и пересекает его поверхность по участку параболы
и пересекает его поверхность по участку параболы 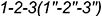 , которая проецируется в отрезок и ограничена вырожденной в точку фронтально-проецирующей линией пересечения
, которая проецируется в отрезок и ограничена вырожденной в точку фронтально-проецирующей линией пересечения 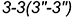 плоскостей срезов
плоскостей срезов 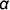 и
и 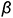 .
.
2.2. Профильная плоскость 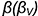 параллельна двум образующим конуса
параллельна двум образующим конуса 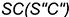 и
и 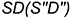 и пересекает его поверхность по участку гиперболы
и пересекает его поверхность по участку гиперболы 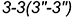 , которая проецируется в отрезок и ограничена вырожденными в точки фронтально-проецирующими линиями пересечения плоскостей срезов
, которая проецируется в отрезок и ограничена вырожденными в точки фронтально-проецирующими линиями пересечения плоскостей срезов 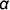 и
и 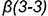 и плоскости
и плоскости 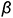 с основанием конуса (4-4).
с основанием конуса (4-4).
3-е действие. Достроить горизонтальную проекцию конуса со срезами, построив проекции плоскостей срезов по горизонтальным проекциям обозначенных точек и определить видимость плоскостей срезов:
3.1. Плоскость среза а определяет видимая горизонтальная проекция участка параболы 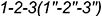 , построенной по горизонтальным проекциям обозначенных точек:
, построенной по горизонтальным проекциям обозначенных точек:
-точка 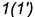 лежит на образующей
лежит на образующей 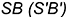 ;
;
-точки 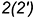 и
и 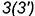 построены по принадлежности соответствующим параллелям (алгоритм I).
построены по принадлежности соответствующим параллелям (алгоритм I).
3.2. Плоскость среза 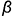 определяет вертикальный видимый отрезок 4′-4′ вырожденной в линию проекции профильной плоскости, точки 4(4′) которой лежат на очерковой окружности основания конуса.
определяет вертикальный видимый отрезок 4′-4′ вырожденной в линию проекции профильной плоскости, точки 4(4′) которой лежат на очерковой окружности основания конуса.
!!! Поскольку горизонтальная проекция имеет вертикальную симметрию, точки обозначены на одной ее половине (нижней).
4-е действие. Выполнить графический анализ построенной горизонтальной проекции конуса для определения ее очерка и внутреннего контура.
4.1. Горизонтальный очерк определяют участок окружности и отрезок 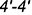 .
.
4.2. Внутренний контур определяет видимый участок параболы 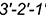 .
.
5-е действие. Достроить профильную проекцию конуса со срезами, построив проекции плоскостей срезов по профильным проекциям обозначенных точек, и определить видимость плоскостей срезов.
5.1. Плоскость среза а определяет видимый участок параболы 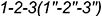 , построенный по профильным проекциям обозначенных точек:
, построенный по профильным проекциям обозначенных точек:
-точки 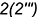 — лежат соответственно на характерных образующих
— лежат соответственно на характерных образующих 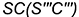 и
и 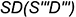 ;
;
5.2. Плоскость среза 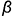 определяют видимые участки гиперболы
определяют видимые участки гиперболы 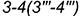 , ограниченные видимым отрезком
, ограниченные видимым отрезком 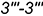 (построен) и видимым отрезком
(построен) и видимым отрезком 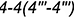 , точки которого построены по координате
, точки которого построены по координате 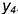 .
.
6-е действие. Выполнить графический анализ построенной профильной проекции конуса для определения ее очерка и внутреннего контура.
6.1. Профильный очерк определяют:
6.2. Внутренний контур определяют:
7-е действие. Оформить чертеж конуса выполнив толстыми сплошными линиями очерки и видимый внутренний контур каждой его проекции (оставить сплошными тонкими линиями полные очерки проекций и линии построения).
Эта теория взята со страницы лекций для 1 курса по предмету «начертательная геометрия»:
Начертательная геометрия для 1 курса
Возможно эти страницы вам будут полезны:

Уклон и Конусность – Определение, обозначение на чертеже, формула расчёта уклона и конусности
Иногда, в задачах по начертательной геометрии или работах по инженерной графике, или при выполнении других чертежей, требуется построить уклон и конус. В этой статье Вы узнаете о том, что такое уклон и конусность, как их построить, как правильно обозначить на чертеже.
Уклон. Уклон это отклонение прямой линии от вертикального или горизонтального положения.Определение уклона. Уклон определяется как отношение противолежащего катета угла прямоугольного треугольника к прилежащему катету, то есть он выражается тангенсом угла а. Уклон можно посчитать по формуле i=AC/AB=tga.
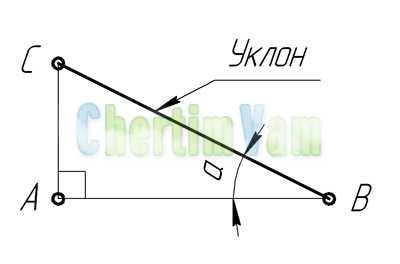
Построение уклона. На примере (рисунок ) наглядно продемонстрировано построение уклона. Для построения уклона 1:1, например, нужно на сторонах прямого угла отложить произвольные, но равные отрезки. Такой уклон, будет соответствовать углу в 45 градусов. Для того чтобы построить уклон 1:2, нужно по горизонтали отложить отрезок равный по значению двум отрезкам отложенным по вертикали. Как видно из чертежа, уклон есть отношение катета противолежащего к катету прилежащему, т. е. он выражается тангенсом угла а.
Обозначение уклона на чертежах. Обозначение уклонов на чертеже выполняется в соответствии с ГОСТ 2.307—68. На чертеже указывают величину уклона с помощью линии-выноски. На полке линии-выноски наносят знак и величину уклона. Знак уклона должен соответствовать уклону определяемой линии, то есть одна из прямых знака уклона должна быть горизонтальна, а другая должна быть наклонена в ту же сторону, что и определяемая линия уклона. Угол уклона линии знака примерно 30°.
Что такое конусность? Формула для расчёта конусности. Обозначение конусности на чертежах.
Конусность. Конусностью называется отношение диаметра основания конуса к высоте. Конусность рассчитывается по формуле К=D/h, где D – диаметр основания конуса, h – высота. Если конус усеченный, то конусность рассчитывается как отношение разности диаметров усеченного конуса к его высоте. В случае усечённого конуса, формула конусности будет иметь вид: К = (D-d)/h.
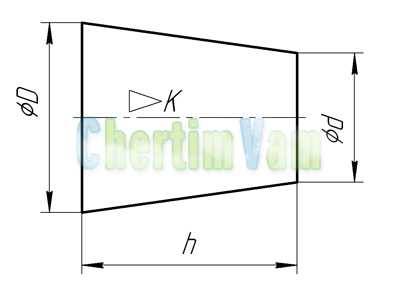
Обозначение конусности на чертежах. Форму и величину конуса определяют нанесением трех из перечисленных размеров: 1) диаметр большого основания D; 2) диаметр малого основания d; 3) диаметр в заданном поперечном сечении Ds , имеющем заданное осевое положение Ls; 4) длина конуса L; 5) угол конуса а; 6) конусность с . Также на чертеже допускается указывать и дополнительные размеры, как справочные.
Размеры стандартизованных конусов не нужно указывать на чертеже. Достаточно на чертеже привести условное обозначение конусности по соответствующему стандарту.
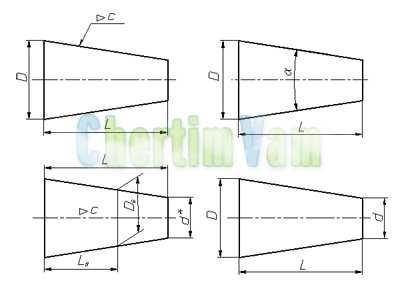
Конусность, как и уклон, может быть указана в градусах, дробью (простой, в виде отношения двух чисел или десятичной), в процентах.
Построение уклона и конусности
Провести построение уклона и конусности достаточно просто, только в некоторых случаях могут возникнуть серьезные проблемы. Среди основных рекомендаций отметим следующее:
- Проще всего отображать нормальные конусности, так как их основные параметры стандартизированы.
- В большинстве случаев вводной информацией при создании конусности становится больший и меньший диаметр, а также промежуточное значение при наличии перепада. Именно поэтому они откладываются первыми с учетом взаимного расположения, после чего проводится соединение. Линия, которая прокладывается между двумя диаметрами и определяет угол наклона.
- С углом наклона при построении возникает все несколько иначе. Как ранее было отмечено, для отображения подобной фигуры требуется построение дополнительных линий, которые могут быть оставлены или убраны. Существенно упростить поставленную задачу можно за счет применения инструментов, которые позволяют определить угол наклона, к примеру, транспортир.
На сегодняшний день, когда компьютеры получили весьма широкое распространение, отображение чертежей также проводится при применении специальных программ. Их преимуществами можно назвать следующее:
- Простоту работы. Программное обеспечение создается для того, чтобы существенно упростить задачу по созданию чертежа. Примером можно назвать отслеживание углов, размеров, возможность зеркального отражения и многое другое. При этом не нужно обладать большим набором различных инструментов, достаточно приобрести требуемую программу и подобрать подходящий компьютер, а также устройство для печати. За счет появления программного обеспечения подобного типа построение конусности и других поверхностей существенно упростилось. Именно поэтому на проведение построений уходит намного меньше времени нежели ранее.
- Высокая точность построения, которая требуется в случае соблюдения масштабов. Компьютер не допускает погрешности, если вся информация вводится точно, то отклонений не будет. Этот момент наиболее актуален в случае создания проектов по изготовлению различных сложных изделий, когда отобразить все основные размеры практически невозможно.
- Отсутствие вероятности допущения ошибки, из-за которой линии будут стерты. Гриф может растираться по поверхности, и созданный чертеж в единственном экземпляре не прослужит в течение длительного периода. В случае использования электронного варианта исполнения вся информация отображается краской, которая после полного высыхания уже больше не реагирует на воздействие окружающей среды.
- Есть возможность провести редактирование на любом этапе проектирования. В некоторых случаях в разрабатываемый чертеж приходится время от времени вносить изменения в связи с выявленными ошибкам и многими другим причинами. В случае применения специального программного обеспечения сделать это можно практически на каждом этапе проектирования.
- Удобство хранения проекта и его передачи. Электронный чертеж не обязательно распечатывать, его можно отправлять в электронном виде, а печать проводится только при необходимости. При этом вся информация может копироваться много раз.
Процедура построения при применении подобных программ характеризуется достаточно большим количеством особенностей, которые нужно учитывать. Основными можно назвать следующее:
- Программа при построении наклонных линий автоматически отображает угол. Проведенные расчеты в этом случае позволяют проводить построение даже в том случае, если нет информации об большом или малом, промежуточном диаметре. Конечно, требуется информация, касающаяся расположения диаметров относительно друг друга.
- Есть возможность использовать дополнительные инструменты, к примеру, привязку для построения нормальной конусности. За счет этого существенно прощается поставленная задача и ускоряется сама процедура. При черчении от руки приходится использовать специальные инструменты для контроля подобных параметров.
- Длина всех линий вводится числовым методом, за счет чего достигается высокая точность. Погрешность может быть допущена исключительно при применении низкокачественного устройства для вывода графической информации.
- Есть возможность провести замер всех показателей при применении соответствующих инструментов.
- Для отображения стандартов используются соответствующие инструменты, которые также существенно упрощают поставленную задачу. Если программа имеет соответствующие настройки, то достаточно выбрать требуемый инструмент и указывать то, какие размеры должны быть отображены. При этом нет необходимости знания стандартов, связанных с отображением стрелок и других линий.
Размеры, мм
Внутренние конусы
Для конусов с лапкой
Для конусов с резьбовым отверстием
| Конус | Метрический | Морзе | Метрический | |||||||||||
| Обозначение конуса | 4 | 6 | 1 | 2 | 3 | 4 | 5 | 6 | 80 | 100 | 120 | 160 | 200 | |
| Конусность | 1 : 20 = 0,05 | 1 : 19,212 = 0,05205 | 1 : 20,047 = 0,04988 | 1 : 20,020 = 0,04995 | 1 : 19,922 = 0,05 | 1 : 19,254 = 0,05194 | 1 : 19,002 = 0,05263 | 1 : 19,180 = 0,05214 | 1 : 20 = 0,05 | |||||
| D | 4 | 6 | 9,045 | 12,065 | 17,780 | 23,825 | 31,267 | 44,399 | 63,348 | 80 | 100 | 120 | 160 | 200 |
| d5 | 3 | 4,6 | 6,7 | 9,7 | 14,9 | 20,2 | 26,5 | 38,2 | 54,6 | 71,5 | 90 | 108,5 | 145,5 | 182,5 |
| d6 | — | — | — | 7 | 11,5 | 14 | 18 | 23 | 27 | 33 | 39 | 52 | ||
| l5 min | 25 | 34 | 52 | 56 | 67 | 84 | 107 | 135 | 188 | 202 | 240 | 276 | 350 | 424 |
| l6 | 21 | 29 | 49 | 52 | 62 | 78 | 98 | 125 | 177 | 186 | 220 | 254 | 321 | 388 |
| g | 2,2 | 3,2 | 3,9 | 5,2 | 6,3 | 7,9 | 11,9 | 15,9 | 19 | 26 | 32 | 38 | 50 | 62 |
| h | 8 | 12 | 15 | 19 | 22 | 27 | 32 | 38 | 47 | 52 | 60 | 70 | 90 | 110 |
1. ГОСТ предусматривает размеры и для конусов инструментальных наружных.
2. Предельные отклонения размеров конусов и допуски формы по ГОСТ 2848-75.
Трубная цилиндрическая резьба
- Единица измерений параметров — дюйм.
- Направление будет левым.
- Класс точности: Класс А в этом случае повышен, а класс В средний.
Почему измерение происходит в дюймах
Дюймовые размеры пришли к нам от западных производителей, так как требования действующего на постсоветском пространстве ГОСТа сформулированы на базе особой резьбы BSW (British Standart Whitworth либо резьба Витворта). Инженер-конструктор Джозеф Фитворт (1803−1887 год) изобрёл в далёком 1841 году и продемонстрировал такой же винтовой профиль для соединений разъёмного типа, и демонстрировал его как совершенно универсальный, надёжный, а также комфортный для использования.
Такой тип осуществления резьбы применяется как в простых трубах, так и в их элементах и соединениях: контргайках, муфтах, угольниках, тройниках.
В сечении профиля можно увидеть равнобедренный треугольник с общим углом в 55 градусов и закруглениями на вершинах и в самих впадинах контура, которые используются для более высокого герметичного соединения.
Нарезка резьбовых соединений должна осуществляться на размере до 6. Все трубы создаются крупными, для особой надёжности и предотвращения процесса разрыва трубы в соединениях стоит фиксировать дополнительной сваркой.
Условные обозначения в стандарте.
- Международная: G.
- Япония: PF.
- Англия: BSPP.
Указания буквы G, а также диаметр отверстия в проходе будут указываться в виде дюймов. Наружный диаметр непосредственно резьбы в обозначении найти нельзя.
Размеры резьбы трубной дюймовой
G ½ — трубы в виде цилиндра наружного типа, внутренний диаметр отверстия равен ½. Наружный диаметр у такой трубы будет равняться 20,995 мм, число шагов по длине — 25,4 мм, что значит около 14 шагов.
Например:
- G ½ -В— резьба трубная цилиндрическая, внутренний диаметр отверстия ½ дюйма, класс точности трубы совпадает с отметкой В.
- G1 ½ LH-B— труба цилиндрического типа, внутренний диаметр отверстия доходит до ½, класс точности В, левая.
Для внутренней цилиндрической трубы стоит использовать отверстие, которое будет полностью соответствовать параметрам.
Как быстро найти шаг в трубе
Можно рассмотреть дополнительные фотографии с англоязычных сайтов, которые смогут наглядно продемонстрировать методику использования и построения конструкции. Трубочная резьба характеризуется в большинстве случаев не общим размером между вершинами профиля, а числом общих витков на 1 дюйм вдоль всей оси поверхности. При помощи простой рулетки, а также линейки прикладываем, отмеряем один дюйм (25,4 мм) и визуально высчитываем количество шагов.
Будет намного проще, если в вашем ящике с инструментами будет находиться резьбомер для дюймового отмера. Таким прибором довольно просто проводить все измерения, но стоит помнить о том, что резьба может различаться углами вершин — 55 и 60 градусов.
Коническая трубная резьба ГОСТ 6211081
Единица измерения всех параметров в этом случае — дюйм.
Форма такой трубы будет соответствовать профилю трубной цилиндрической вырезки с общим углом в 55 градусов Цельсия.
Главные обозначения:
- Международная — R
- Япония — PT.
- Великобритания BSPT.
Для этого стоит указывать букву R и общий номинальный диаметр Dy. Обозначение в виде буквы характеризует наружный тип резьбы, Rc внутренний, а Rp — внутренний цилиндрический. По такому же аналогу с цилиндрической трубой для левой резьбы стоит применять LH.
Примеры:
R1 ½ -это наружная труба конической вырезки, номинальный диаметр которой равен Dy ½ дюйма.
R1 ½ LH — это наружная коническая труба, номинальный диаметр которой Dy будет равняться ½ дюйма.
- Дюймовая вырезка конической формы по ГОСТу 6111−52.
- Единица измерения в этом случае — также дюйм.
- Происходит его изготовление на поверхности с конусностью 1:16.
Обладает общим углом профиля около 60 градусов. Используется в изготовлении трубопроводов (водяных, воздушных, а также топливных) машин и станков с невысоким давлением при работе. Применение такого вида соединений включает в себя особую герметичность и стопорение резьбы без воздействия дополнительных подручных средств (льняных нитей, а также пряжи с суриком).
Главные обозначения
Первой в названии имеется буква К, а после идёт слово ГОСТ.
Пример: К: ½ ГОСТ 6111–52 .
Расшифровывается такая надпись так: резьба коническая дюймовая с наружным, а также внутренним диаметром в основной плоскости, примерно равной наружному либо внутреннему разъёму трубы цилиндрического типа G ½.
Метрически конический тип вырезки. По ГОСт у 25229 -82.
Единицей измерения в этот раз выступает мм.
Процесс создания трубы происходит на поверхностях с общей конусностью в 1:16.
Применяется во время соединения трубопроводов. Угол в самой вершине витка будет доходить до 60. Главная плоскость смещена, если смотреть на торец.
Уклоны и конусность — Техническое черчение
- Уклоном прямой ВС относительно прямой AB (фиг. 57, а) называется отношение:
- i=AC/AB=tga
- Конусностью называется отношение разности диаметров двух поперечных сечений конуса к расстоянию между ними (фиг. 57,б)
- k=(D-d)/l=2tga
- Таким образом,
- k = 2i
- Уклон и конусность могут быть указаны: а) в градусах; б) дробью простой, в виде отношения двух чисел или десятичной; в) в процентах.
- Например: конусность, выраженная в градусах — 11°25’16″; отношением — 1:5; дробью —0,2; в процентах — 20%, и соответственно этому уклон в градусах — 5°42’38″; отношением — 1:10; дробью—0,1; в процентах — 10%.
- Для конусов, применяемых в машиностроении, OCT/BKC 7652 устанавливает следующий ряд нормальных конусностей — 1 :3; 1 :5; 1 :8; 1 : 10; 1 :15; 1:20; 1 :30; 1:50; 1 :100; 1:200, а также 30, 45, 60, 75, 90 и 120°.
- Допускаются в особых случаях также конусности 1:1,5; 1:7; 1:12 и 110°.
Если требуется через точку Л, лежащую на прямой AB (фиг. 57, в), провести прямую с уклоном i=l:n относительно AB, надо отложить от точки А по направлению данной прямой n произвольных единиц; в конце полученного отрезка AB восстановить перпендикуляр ЕС длиной в одну такую же единицу. Гипотенуза AС построенного прямоугольного треугольника определяет искомую прямую.
- Для проведения прямой заданного уклона l:n через точку M, не лежащую на данной прямой AB, можно поступать двояко (фиг. 58):
- 1) построить в стороне прямоугольный треугольник KLN (или KLN1) с отношением катетов l:n, причём катет KL ll AB; затем через точку M провести искомую прямую MD (или MD1) параллельно гипотенузе вспомогательного треугольника KN (или LN1);
2) опустить из точки M перпендикуляр ME на прямую AВ и принять его за единицу. По направлению прямой AB влево или вправо от точки E отложить n таких же отрезков; гипотенузы DM или MD1 построенных таким образом прямоугольных треугольников являются искомыми прямыми.
Построение конусности l:n относительно данной оси сводится к построению уклонов l:n/2 с каждой стороны оси.
Уклон или конусность чаще всего указывается в процентах или отношением единицы к целому числу. Рассмотрим эти способы построения на примерах.
Пример 1. Требуется построить профиль сечения швеллера № 5 ОСТ 10017-39 (фиг. 59, а), если известно, что уклон его полок равен 10%
Размеры для построения берём из ОСТ 10017-39.
Проводим вертикальную прямую ek, равную h = 50 мм. Из точек e и k проводим прямые ec и kf, равные ширине полки b = 37 мм.
Ввиду того, что обе полки швеллера одинаковы, ограничимся построением только одной из них. Откладываем на прямой ec от точки с отрезок cm, равный (b-d)/2.
В точке m на перпендикуляре к прямой ec откладываем отрезок mn, равный t = 7 мм. Через точку n проводим прямую np параллельно ec, равную 50 мм.
- Перпендикулярно к np из точки p проводим отрезок ps, равный по длине десяти процентам отрезка np. Величина его определяется из отношения:
- ps/np=10/100,
- откуда
- ps=10*50/100=5 мм.
Прямая sn является искомой прямой, имеющей уклон 10% по отношению к ec. Дальнейшее построение профиля не представляет затруднений.
Отрезок np можно взять любой длины. Чем больше его величина, тем точнее будет построена прямая уклона. Однако для удобства вычисления следует принимать отрезок np таким, чтобы длина его, выражаемая в миллиметрах, оканчивалась на 0 или 5.
П p и м e p 2. Построить профиль сечения двутавра № 10 ОСТ 10016-39 (фиг. 59, б), если известно, что уклон полок его равен 1:6. Размеры для построения берём из ОСТ 10016-39.
Проводим горизонтальную прямую cc, равную ширине полки b = = 68 мм. Через точку e, являющуюся серединой ширины полки, проводим вертикальную линию. Откладываем от точки с отрезок mс, равный
(b-d)/4. В точке m, перпендикулярно к отрезку cc, проводим прямую и
на ней откладываем отрезок mn, равный t=6,5 мм. Через точку n проводим горизонтальную прямую np, равную 30 мм, которая будет служить катетом прямоугольного треугольника. Чем длиннее катет, тем точнее будет построен уклон. Для удобства принимают длину отрезка np кратной шести, тогда второй катет будет равен целому числу. Величина второго катета определяется из формулы
- i=ps/np=1/6
- где i — заданный уклон.
- Подставив в формулу числовые значения, получим
- ps=30/6=5 мм.
Откладываем в точке p под углом 90° к прямой np вычисленную длину второго катета, получим точку 5. Проводим через точки s и n прямую, которая и будет соответствовать искомой прямой, имеющей уклон 1 :6.
Построение сопряжений такое же, как и для швеллера в предыдущем примере.
Презентация на тему: » Конус Понятие конуса Понятие конуса Площадь поверхности конуса Площадь поверхности конуса Усечённый конус Усечённый конус.» — Транскрипт:
1
Конус Понятие конуса Понятие конуса Площадь поверхности конуса Площадь поверхности конуса Усечённый конус Усечённый конус

2
Понятие конуса Рассмотрим окружность L с центром О и прямую ОР, перпендикулярную к плоскости этой поверхности. Через точку Р и каждую точку окружности проведём прямую. Поверхность, образованная этими прямыми, называется конической поверхностью, а сами прямые – образующими конической поверхности. L О Р

3
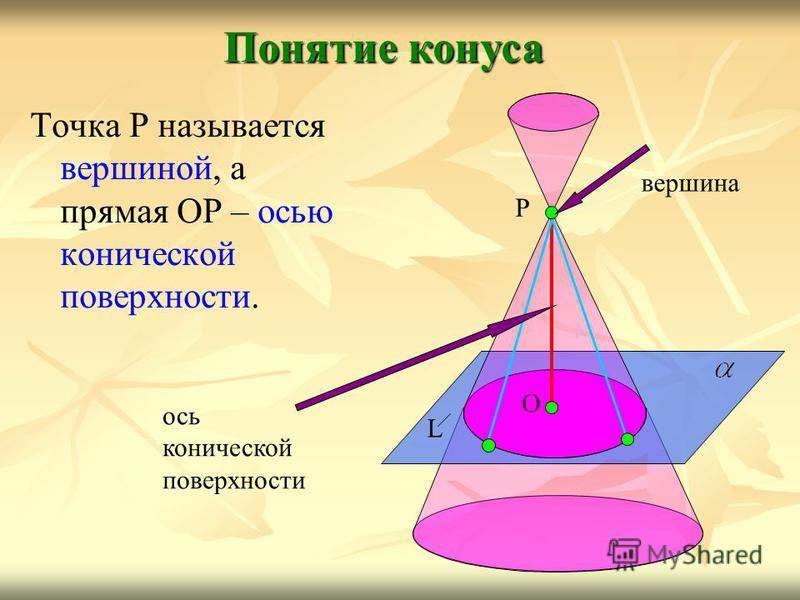
Точка Р называется вершиной, а прямая ОР – осью конической поверхности. Понятие конуса L О Р вершина ось конической поверхности
4
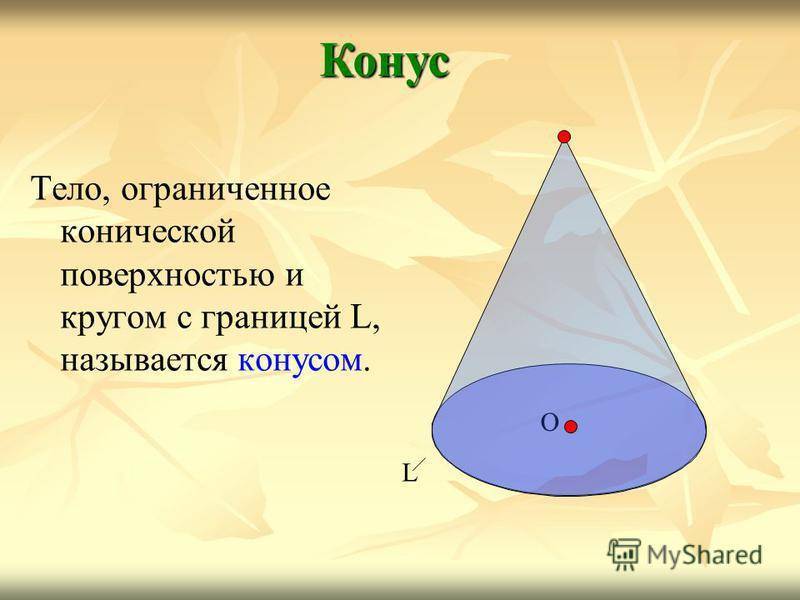
Тело, ограниченное конической поверхностью и кругом с границей L, называется конусом. Конус О L
5
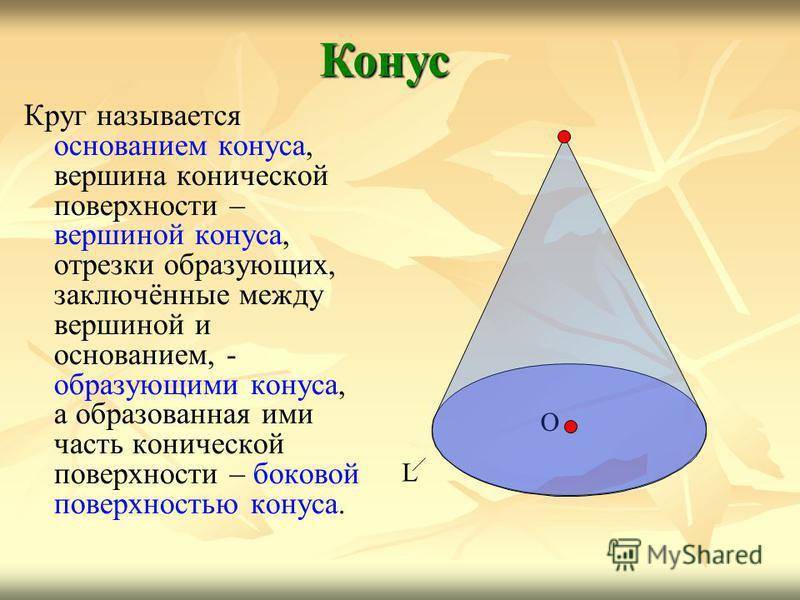
Круг называется основанием конуса, вершина конической поверхности – вершиной конуса, отрезки образующих, заключённые между вершиной и основанием, — образующими конуса, а образованная ими часть конической поверхности – боковой поверхностью конуса. Конус О L
6
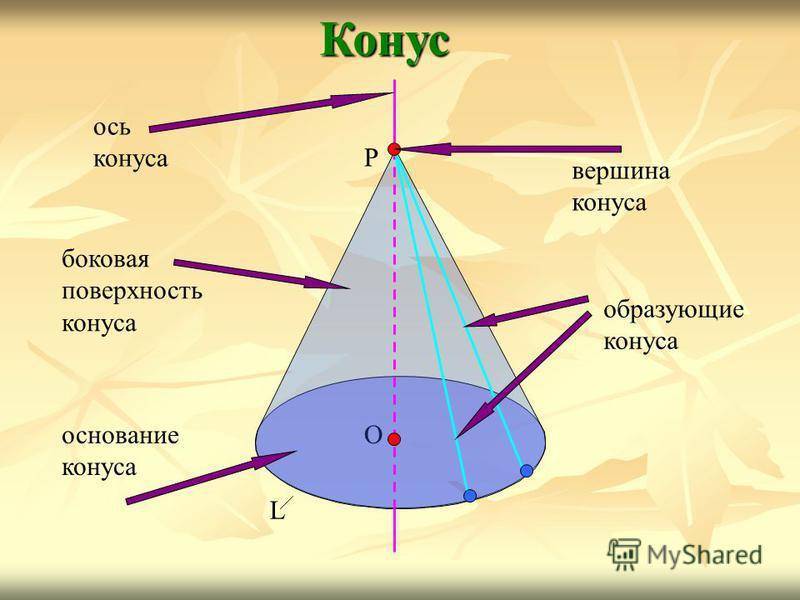
Конус О L Р ось конуса вершина конуса образующие конуса боковая поверхность конуса основание конуса
7
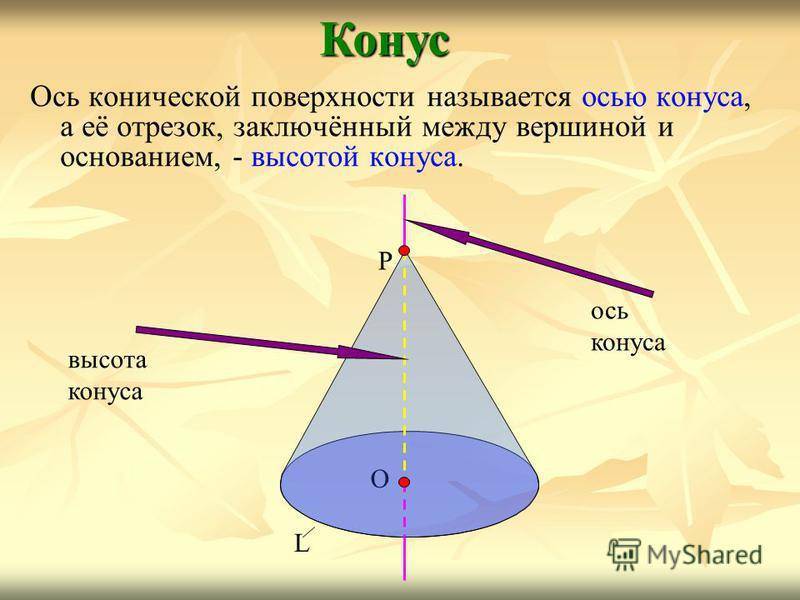
Ось конической поверхности называется осью конуса, а её отрезок, заключённый между вершиной и основанием, — высотой конуса.Конус О L Р ось конуса высота конуса
8
Конус может быть получен вращением прямоугольного треугольника вокруг одного из его катетов. Получение конуса

9
Если секущая плоскость проходит через ось конуса, то сечение представляет собой равнобедренный треугольник, основание которого – диаметр основания конуса, а боковые стороны – образующие конуса. Это сечение называется осевым. Сечение конуса О Р

10
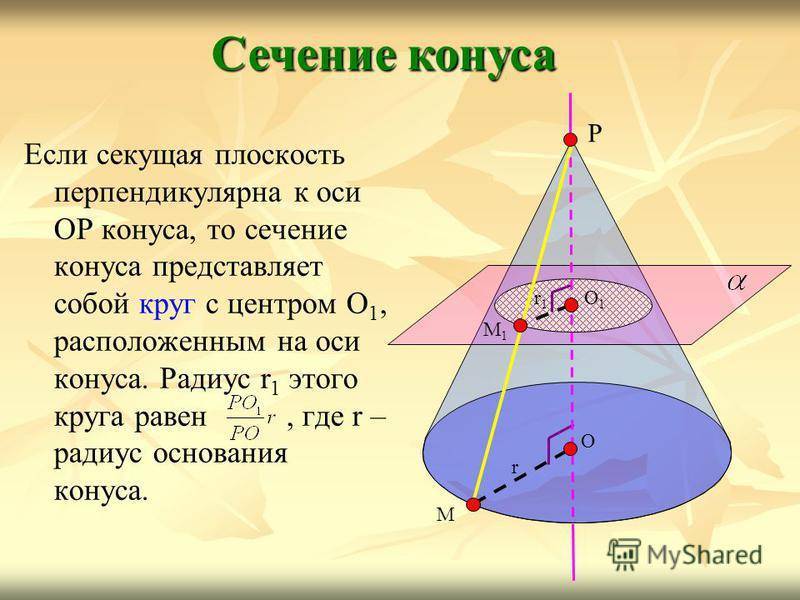
Если секущая плоскость перпендикулярна к оси ОР конуса, то сечение конуса представляет собой круг с центром О 1, расположенным на оси конуса. Радиус r 1 этого круга равен, где r – радиус основания конуса. Сечение конуса Р О М r О1О1 М1М1 r1r1
11
Проводя различные сечения одного и того же кругового конуса, причём любого, можно получить эллипс, параболу и гиперболу. При надлежащем наклоне секущей плоскости удаётся получить все типы конических сечений. Если считать, что конус не заканчивается в вершине, а простирается за неё, тогда у некоторых сечений образуются две ветви. Сечение конуса

12
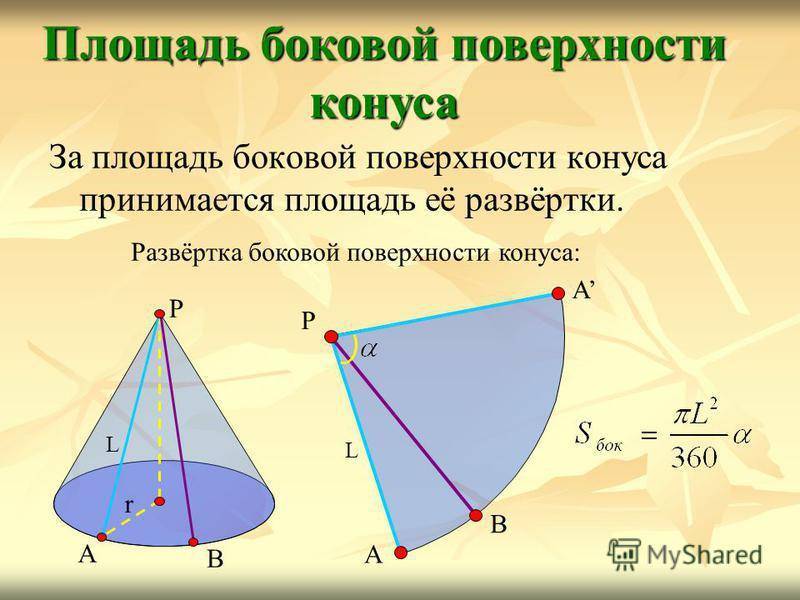
За площадь боковой поверхности конуса принимается площадь её развёртки. Площадь боковой поверхности конуса Развёртка боковой поверхности конуса: А В Р А L А В Р L r
13
Выразим через L и r. Так как длина дуги АВА равна, то, откуда Площадь боковой поверхности конуса А В Р А L Площадь боковой поверхности конуса равна произведению половины длины окружности основания на образующую.

14
Площадью полной поверхности конуса называется сумма площадей боковой поверхности и основания. Площадь полной поверхности конуса А В Р L r S кон = r 2 + rL S кон = r(r + L)

15
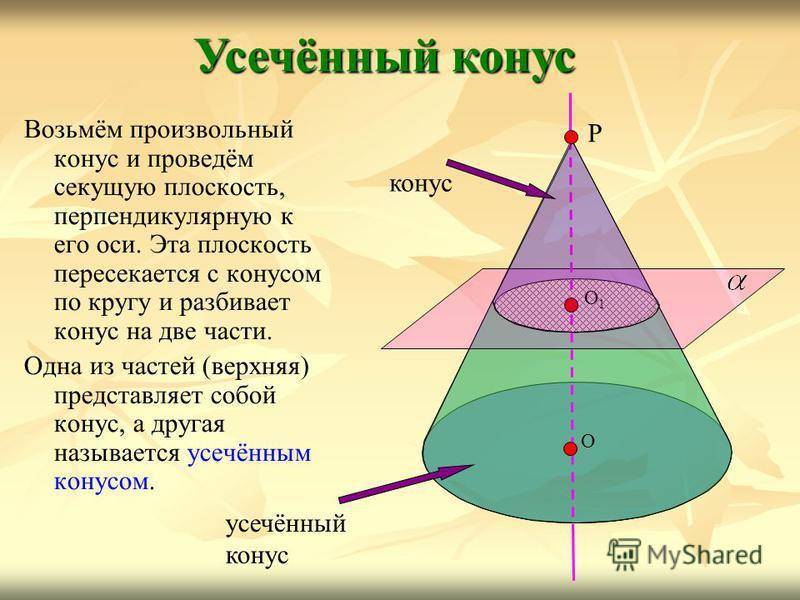
Возьмём произвольный конус и проведём секущую плоскость, перпендикулярную к его оси. Эта плоскость пересекается с конусом по кругу и разбивает конус на две части. Одна из частей (верхняя) представляет собой конус, а другая называется усечённым конусом. Усечённый конус Р О О1О1 конус усечённый конус
16
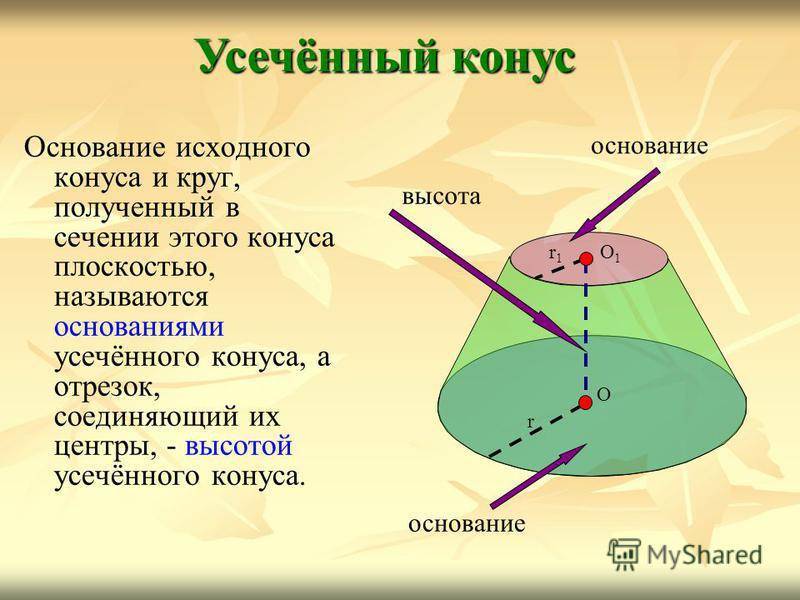
Основание исходного конуса и круг, полученный в сечении этого конуса плоскостью, называются основаниями усечённого конуса, а отрезок, соединяющий их центры, — высотой усечённого конуса. Усечённый конус О1О1 r1r1 r О основание высота
17
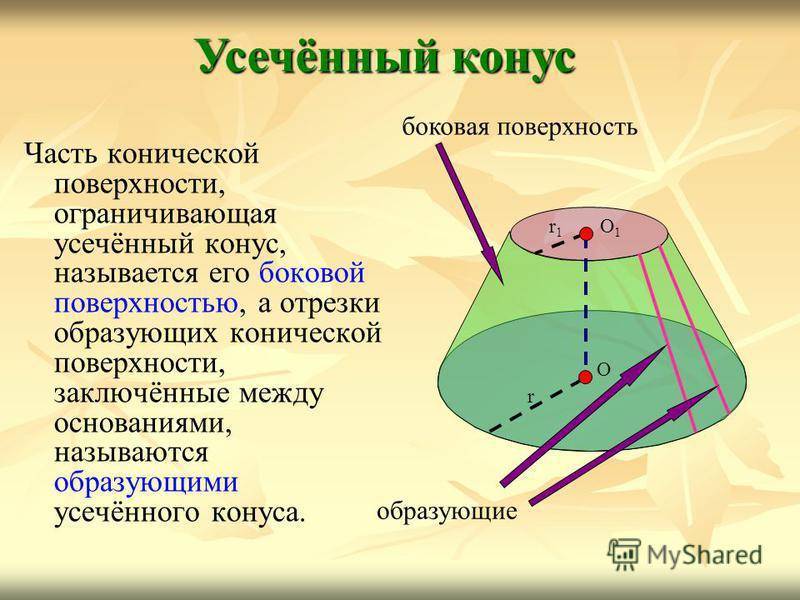
Часть конической поверхности, ограничивающая усечённый конус, называется его боковой поверхностью, а отрезки образующих конической поверхности, заключённые между основаниями, называются образующими усечённого конуса. Усечённый конус О1О1 r1r1 r О боковая поверхность образующие
18
Усечённый конус может быть получен вращением прямоугольной трапеции вокруг её боковой стороны, перпендикулярной к основаниям. Получение усечённого конуса A B C D Усечённый конус получен вращением прямоугольной трапеции ABCD вокруг стороны CD.
19
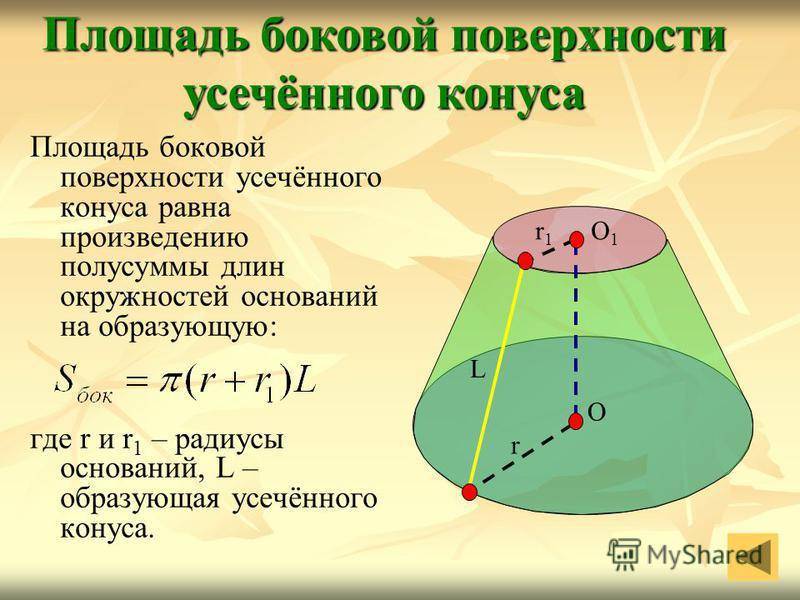
Площадь боковой поверхности усечённого конуса равна произведению полусуммы длин окружностей оснований на образующую: где r и r 1 – радиусы оснований, L – образующая усечённого конуса. Площадь боковой поверхности усечённого конуса О1О1 r1r1 r О L
Задача на определение площади и объема усеченного конуса
Ниже на рисунке изображен усеченный конус и приведены его линейные параметры. Необходимой найти площадь поверхности и объем фигуры.
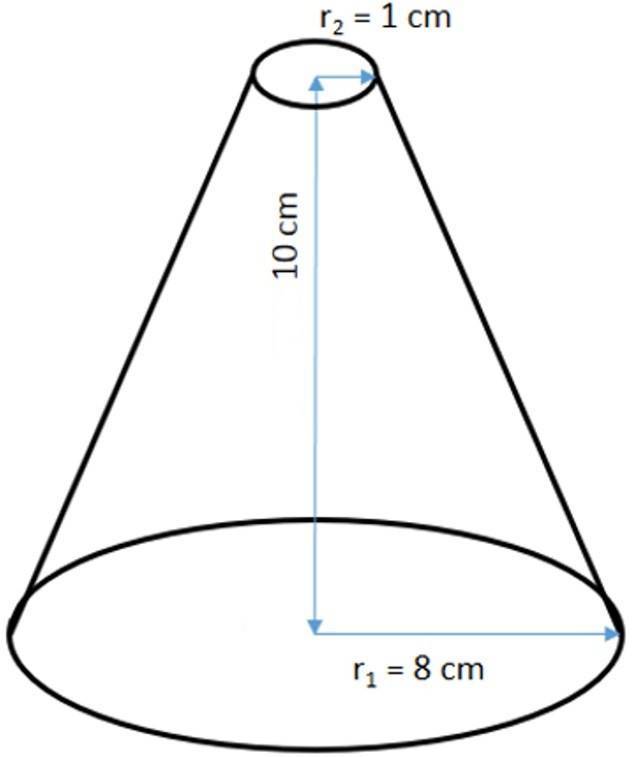
Начнем решать задачу с определения величины V. Ее вычисление не представляет никакого труда, поскольку известны все необходимые параметры. Подставляя их в формулу для V, получаем:
Найденное значение соответствует 0,76 литра.
Чтобы найти площадь поверхности S, следует сначала вычислить длину образующей g фигуры. Она будет равна:
Значение образующей g мы округлили до сотых. Теперь можно воспользоваться формулой для площади S:
Заметим, что формулы для V и S, которые мы использовали при решении задачи, справедливы только для круглого прямого усеченного конуса. В случае наклонной фигуры или же фигуры с некруглыми основаниями этими формулами пользоваться нельзя.
Сечение конуса
Осевым сечением конуса называется плоскость, проходящая по его оси либо высоте. В прямом конусе такое сечение представляет собой равнобедренный треугольник, в котором высотой треугольника является высота тела, его сторонами выступают образующие, а основание – это диаметр основания. В равностороннем геометрическом теле осевое сечение является равносторонним треугольником, так как в этом конусе диаметр основания и образующие равны.
Плоскость осевого сечения в прямом конусе является плоскостью его симметрии. Причиной этому служит то, что его вершина находится над центром его основания, то есть плоскость осевого сечения делит конус на две одинаковые части.
Так как в наклонном объемном теле высота и ось не совпадают, плоскость осевого сечения может не включать в себя высоту. Если осевых сечений в таком конусе можно построить множество, так как для этого необходимо соблюдать лишь одно условие — оно должно проходить только через ось, то осевое сечение плоскости, которому будет принадлежать высота этого конуса, можно провести лишь одно, потому что количество условий увеличивается, а, как известно, две прямые (вместе) могут принадлежать только одной плоскости.
Конусность
Отношение разности диаметров двух поперечных сечений конуса (D-d.) к расстоянию между ними (l) (рис. 6.39, а) называется конусностью (К): К = (D – d)/l.
Рис. 6.39. Построение конусности и нанесение се величины
Например, конический элемент детали с диаметром большего основания 25 мм, диаметром меньшего основания 15 мм, длиной 50 мм будет иметь конусность К = (D – d)/l = (25 – 15)/50 = 1/5 = 1:5.
При проектировании новых изделий применяются величины конусности, установленные ГОСТ 8593–81: 1:3; 1:5; 1:7; 1:8; 1:10; 1:12; 1:15; 1:20; 1:30. Стандартизированы также величины конусности, которые имеют элементы деталей с часто встречающимися углами между образующими конуса: углу 30° соответствует конусность 1:1,866; 45° – 1:1,207; 60° – 1:0,866; 75° – 1:0,652; углу 90° – 1:0,5. В чертежах металлорежущих инструментов часто конусность определяется надписью, указывающей номер конуса Морзе. В этих случаях размеры конических элементов устанавливают по ГОСТ 10079–71 и др.
На чертежах конусность наносят согласно правилам ГОСТ 2.307–2011. Перед размерным числом, определяющим величину конусности, наносят условный знак в виде равнобедренного треугольника, острие которого направлено в сторону вершины конуса.
Знак и цифры, указывающие величину конусности, располагают на чертежах параллельно геометрической оси конического элемента.
Они могут быть проставлены над осью (рис. 6.39, 6) или на полке (рис. 6.39, в). В последнем случае полка соединяется с образующей конуса с помощью линии выноски, заканчивающейся стрелкой.
Плоские поверхности деталей, расположенные наклонно, обозначают на чертеже величиной уклона. Как подсчитать эту величину, покажем на примере. Клин, изображенный на рис. 6.40, я, имеет наклонную поверхность, уклон которой нужно определить. Из размера наибольшей высоты клина вычтем размер наименьшей высоты: 50 – 40 = 10 мм. Разность между этими величинами можно рассматривать как размер катета прямоугольного треугольника, образовавшегося после проведения на чертеже горизонтальной линии (рис. 6.40, б). Величиной уклона будет отношение размера меньшего катета к размеру горизонтальной линии. В данном случае нужно разделить 10 на 100. Величина уклона клина будет 1:10.
Рис. 6.40. Определение величины уклона
На чертеже уклоны указывают знаком и отношением двух чисел, например 1:50; 3:5.
Если требуется изобразить на чертеже поверхность определенного уклона, например 3:20, вычерчивают прямоугольный треугольник, у которого один из катетов составляет три единицы длины, а второй – 20 таких же единиц (рис. 6.41).
Рис. 6.41. Построение уклонов и нанесение их величин
При вычерчивании деталей или при их разметке для построения линии по заданному уклону приходится проводить вспомогательные линии. Например, чтобы провести линию, уклон которой 1:4, через концевую точку вертикальной линии (рис. 6.42), отрезок прямой линии длиной 10 мм следует принять за единицу длины и отложить на продолжении горизонтальной линии четыре такие единицы (т.е. 40 мм). Затем через крайнее деление и верхнюю точку отрезка провести прямую линию.
Рис. 6.42. Построение линии по заданному уклону
Вершина знака уклона должна быть направлена в сторону наклона поверхности детали. Знак и размерное число располагают параллельно направлению, по отношению к которому задан уклон.
Построение уклона и конусности
Провести построение уклона и конусности достаточно просто, только в некоторых случаях могут возникнуть серьезные проблемы. Среди основных рекомендаций отметим следующее:
- Проще всего отображать нормальные конусности, так как их основные параметры стандартизированы.
- В большинстве случаев вводной информацией при создании конусности становится больший и меньший диаметр, а также промежуточное значение при наличии перепада. Именно поэтому они откладываются первыми с учетом взаимного расположения, после чего проводится соединение. Линия, которая прокладывается между двумя диаметрами и определяет угол наклона.
- С углом наклона при построении возникает все несколько иначе. Как ранее было отмечено, для отображения подобной фигуры требуется построение дополнительных линий, которые могут быть оставлены или убраны. Существенно упростить поставленную задачу можно за счет применения инструментов, которые позволяют определить угол наклона, к примеру, транспортир.
На сегодняшний день, когда компьютеры получили весьма широкое распространение, отображение чертежей также проводится при применении специальных программ. Их преимуществами можно назвать следующее:
- Простоту работы. Программное обеспечение создается для того, чтобы существенно упростить задачу по созданию чертежа. Примером можно назвать отслеживание углов, размеров, возможность зеркального отражения и многое другое. При этом не нужно обладать большим набором различных инструментов, достаточно приобрести требуемую программу и подобрать подходящий компьютер, а также устройство для печати. За счет появления программного обеспечения подобного типа построение конусности и других поверхностей существенно упростилось. Именно поэтому на проведение построений уходит намного меньше времени нежели ранее.
- Высокая точность построения, которая требуется в случае соблюдения масштабов. Компьютер не допускает погрешности, если вся информация вводится точно, то отклонений не будет. Этот момент наиболее актуален в случае создания проектов по изготовлению различных сложных изделий, когда отобразить все основные размеры практически невозможно.
- Отсутствие вероятности допущения ошибки, из-за которой линии будут стерты. Гриф может растираться по поверхности, и созданный чертеж в единственном экземпляре не прослужит в течение длительного периода. В случае использования электронного варианта исполнения вся информация отображается краской, которая после полного высыхания уже больше не реагирует на воздействие окружающей среды.
- Есть возможность провести редактирование на любом этапе проектирования. В некоторых случаях в разрабатываемый чертеж приходится время от времени вносить изменения в связи с выявленными ошибкам и многими другим причинами. В случае применения специального программного обеспечения сделать это можно практически на каждом этапе проектирования.
- Удобство хранения проекта и его передачи. Электронный чертеж не обязательно распечатывать, его можно отправлять в электронном виде, а печать проводится только при необходимости. При этом вся информация может копироваться много раз.
История определения конуса
Геометрия как наука появилась из практических требований строительства и наблюдений за природой. Постепенно опытные знания обобщались, а свойства одних тел доказывались через другие. Древние греки ввели понятие аксиом и доказательств. Аксиомой называется утверждение, полученное практическим путем и не требующее доказательств.
В своей книге Евклид привел определение конуса как фигуры, которая получается вращением прямоугольного треугольника вокруг одного из катетов. Также ему принадлежит основная теорема, определяющая объем конуса. А доказал эту теорему древнегреческий математик Евдокс Книдский.
Другой математик древней Греции, Аполлоний Пергский, который был учеником Евклида, развил и изложил теорию конических поверхностей в своих книгах. Ему принадлежит определение конической поверхности и секущей к ней. Школьники наших дней изучают Евклидову геометрию, сохранившую основные теоремы и определения с древних времен.
