Содержание
- Как найти сечение окружности
- Площадь круга: как найти, формулы
- Определение основных понятий
- Формула вычисления площади круга
- Площадь круга через радиус
- Площадь круга через диаметр
- Площадь круга через длину окружности
- Задачи. Определить площадь круга
- Как рассчитать площадь круга
- Расчет площади поперечного сечения круга
- Определение величины
- Область применения
- Способы расчета
- Калькулятор площади круга
- Формула (формулы) площади круга
- По радиусу
- Через диаметр
- Через длину окружности
- Какие термины используются для поиска площади круга?
- Площадь круга и размеры пицц
- Площади усеченных частей круга
- Часто задаваемые вопросы о площади круга?
- Входит ли окружность (периметр) в площадь круга?
- Какие есть ещё калькуляторы для круга у вас на сайте?
- Хватит ли только диаметра, только радиуса или только длинны окружности для расчета площади круга?
- Почему Пи равняется 3,1415926…, а не является «ровным» числом?
- Кто впервые научился вычислять площадь круга?
- Поделитесь в соцсетях
- Есть что добавить?
Как найти сечение окружности
Площадь круга: как найти, формулы

площадь, 6 класс, 9 класс, ЕГЭ/ОГЭ
Определение основных понятий
Прежде чем погрузиться в последовательность расчетов и узнать, чему равна площадь круга, важно выяснить разницу между понятиями окружности и круга.
Окружность — замкнутая плоская кривая, все точки которой равноудалены от центра.
Круг — множество точек на плоскости, которые удалены от центра на расстоянии, не превышающем радиус.
Если говорить простым языком, окружность — это замкнутая линия, как, например, кольцо и шина. Круг — плоская фигура, ограниченная окружностью, как монетка или крышка люка.
Формула вычисления площади круга
Давайте разберем несколько формул расчета площади круга. Поехали!
Площадь круга через радиус
S = π × r 2 , где r — это радиус, π — это константа, которая выражает отношение длины окружности к диаметру, она приблизительно равна 3,14.
Площадь круга через диаметр
S = d 2 : 4 × π, где d — это диаметр.
Площадь круга через длину окружности
S = L 2 : (4 × π), где L — это длина окружности.
Популярные единицы измерения площади:
- квадратный миллиметр (мм 2 );
- квадратный сантиметр (см 2 );
- квадратный дециметр (дм 2 );
- квадратный метр (м 2 );
- квадратный километр (км 2 );
- гектар (га).
Нужно быстро привести знания в порядок перед экзаменом? Записывайтесь на курсы ЕГЭ по математике в Skysmart!
Задачи. Определить площадь круга
Мы разобрали три формулы для вычисления площади круга. А теперь тренироваться — поехали!
Задание 1. Как найти площадь круга по диаметру, если значение радиуса равно 6 см.
Диаметр окружности равен двум радиусам.
Используем формулу: S = π × d 2 : 4.
Подставим известные значения: S = 3,14 × 12 2 : 4.
Задание 2. Найти площадь круга, если известен диаметр, равный 90 мм.
Используем формулу: S = π × d 2 : 4.
Подставим известные значения: S = 3,14 × 90 2 : 4.
Задание 3. Найти длину окружности при радиусе 3 см.
Отношение длины окружности к диаметру является постоянным числом.
Так как диаметр равен двум радиусам, то формула длины окружности примет вид: L = 2 × π × r.
Подставим значение радиуса: L = 2 × 3,14 × 3.
Как рассчитать площадь круга
На данной странице калькулятор поможет рассчитать площадь круга онлайн. Для расчета задайте радиус, диаметр или длину окружности.
Круг – множество точек плоскости, удаленных от заданной точки этой плоскости (центр круг) на расстояние, не превышающее заданное (радиус круга).
Окружность – замкнутая плоская кривая, все точки которой одинаково удалены от данной точки (центра), лежащей в той же плоскости, что и кривая.
Расчет площади поперечного сечения круга
 В инженерной и строительной практике нередко встречаются задачи по расчёту площади поперечного сечения. Если фигуру разрезать по линии, которая перпендикулярна продольной оси предмета, то полученный торец и будет поперечным сечением. Круг — один из наиболее часто встречающихся видов подобного рассечения. Такой срез присущ цилиндру, шару, конусу, тору, эллипсоиду.
В инженерной и строительной практике нередко встречаются задачи по расчёту площади поперечного сечения. Если фигуру разрезать по линии, которая перпендикулярна продольной оси предмета, то полученный торец и будет поперечным сечением. Круг — один из наиболее часто встречающихся видов подобного рассечения. Такой срез присущ цилиндру, шару, конусу, тору, эллипсоиду.
Определение величины
Площадь — это величина, характеризующая размер геометрической фигуры. Её определение — одна из древнейших практических задач. Древние греки умели находить площадь многоугольников: так, каменщикам, чтобы узнать размер стены, приходилось умножать её длину на высоту.
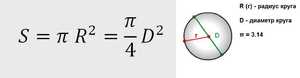
По прошествии долгих лет трудом многих мыслителей был выработан математический аппарат для расчета этой величины практически для любой фигуры.
На Руси существовали особые единицы измерения: копна, соха, короб, верёвка, десятина, четь и другие, так или иначе связанные с пахотой. Две последних получили наибольшее распространение. Однако от древнерусских землемеров нам досталось только само слово — «площадь».
С развитием науки и техники появилось не только множество формул для расчёта площадей любых геометрических фигур, но и приборы, которые делают это за человека. Такие приборы называют планиметрами.
Область применения
Круг — одна из фундаментальных фигур, которые окружают человека повсюду. Трубы, колеса, лампы, конфорки у плиты — всё это имеет форму круга или поперечное сечение в виде круга. Расчёт площади такого сечения может понадобиться в следующих ситуациях:
- Определение объемов емкостей.
- Решение задач по сопротивлению материалов и электротехнике.
- Расчет количества материалов при проектировании, строительстве и ремонте.
- Ведение поливного земледелия.
Стоит обратить внимание на разницу между кругом и окружностью. Окружность — это замкнутая кривая, все точки которой равно удалены от центра, в то время как круг — это часть плоскости (геометрическая фигура), ограниченная окружностью.
Круг имеет ряд характеристик:
- радиус (r/R) — отрезок, соединяющий центр фигуры с его границей;
- диаметр (d/D) — отрезок, который соединяет две точки границы круга и проходит через его центр;
- длина окружности (C/c/L/l).

Теорема гласит: площадь круга (S) равна произведению половины длины окружности и его радиуса. Длина окружности С находится в прямой зависимости от радиуса R с коэффициентом π («пи» = 3,14).
Способы расчета
Чтобы получить круглое поперечное сечение, необходимо разрезать объёмную фигуру перпендикулярно оси вращения. В случае с цилиндром площади всех поперечных сечений будут равны между собой — как, например, кружки колбасы, нарезанные поперек батона, одинаковы.
Шар, по сути, представляет собой напластование блинчиков-кругов различного диаметра от точечного до заданного и обратно до точки. Чтобы найти S какого-либо из блинчиков, необходимо определить его радиус. Принцип его расчёта сводится к решению теоремы Пифагора, где гипотенузой выступает радиус шара, а искомый радиус становится одним из катетов.
При расчёте площади сечений конуса необходимо найти радиус или диаметр каждого из кругов, учитывая, что в продольном разрезе конус — это равнобедренный треугольник.
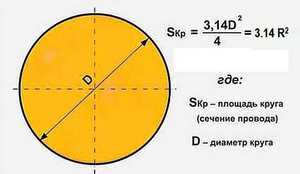
Цилиндр, конус и шар — базовые объемные фигуры. Однако существуют более сложные фигуры, например, тор. Тор, или тороид, при первом приближении являет собой не что иное, как бублик или баранку. Разломив его пополам, на торцах можно увидеть два одинаковых круга. Площадь такого поперечного сечения можно получить, удвоив имеющуюся (на рисунке серая область справа). Если взять нож и рассечь баранку вдоль, на срезе получится кольцо. В случае с такой фигурой необходимо найти площадь круга по внешней окружности и вычесть из нее «дырку от бублика» (показано серым на рисунке слева).
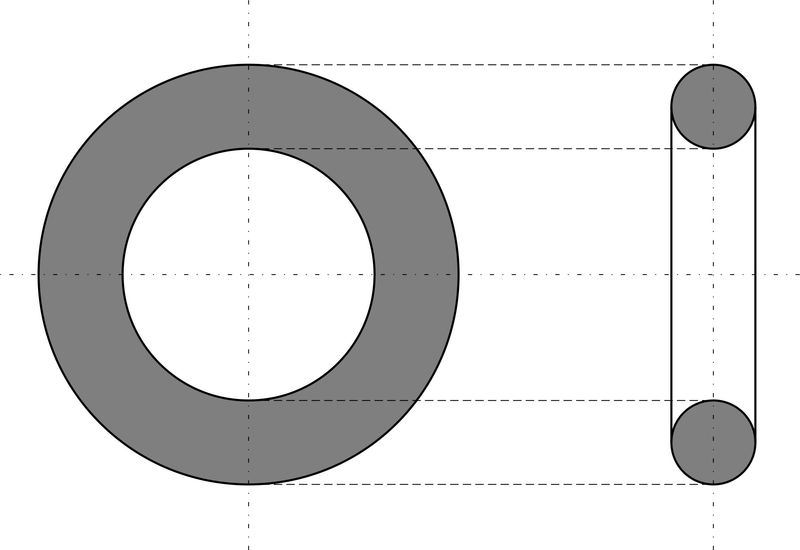
Площадь круглого поперечного сечения рассчитывается исходя из имеющихся характеристик. Она сводится к трем основным формулам. Их можно представить таким образом:

- Самая популярная, легкая в применении и часто используемая формула. Чтобы узнать площадь фигуры, если известен её радиус, нужно возвести это значение в квадрат и умножить на число π. Для бытовых расчетов достаточно двух знаков после запятой, то есть π = 3,14.
- Иногда оперируют диаметром, а не радиусом круга. В этом случае к вычислениям добавляется одна операция: диаметр умножают сам на себя, затем на число π, а произведение делят на 4.
- Если известна длина окружности С и ее радиус R и нужно выяснить площадь круга, ограниченного этой окружностью, не понадобится даже π. Используют следующую формулу: значение С делят пополам и умножают на R. Полученное чисто и будет искомой величиной.
Способов определения того, чему равна площадь круга, достаточно много. Чаще всего, если возникает подобная задача, на ум приходит знакомая еще со школьной скамьи формула «эс равно пи эр квадрат».
Источник
Калькулятор площади круга
Рассчитайте онлайн площадь круга по диаметру, через радиус или длину окружности.
Формула (формулы) площади круга
Найти площадь круга можно разными способами, в зависимости от известных данных.
По радиусу
Если дан только радиус, то площадь составит произведение константы Пи на квадрат радиуса. Расчёт будет по формуле (где r – радиус, а π – константа, равная 3,1415…):
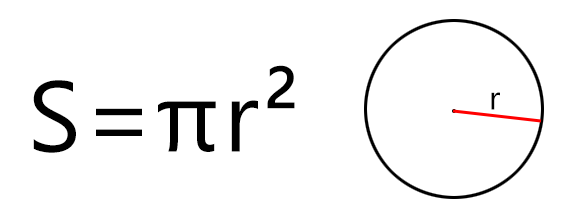
Например, если радиус равен 2 метра, то площадь круг можно вычислить так S = 3,14 × 2 2 = 3,14 × 4 = 12,56 м 2 (квадратных метров).
Через диаметр
Если известен диаметр, то площадь круга будет равняться одной четвёртой произведения Пи и квадрата диаметра. Формула площади круга будет такой (где d — диаметр, а π – константа, равная 3,1415…):
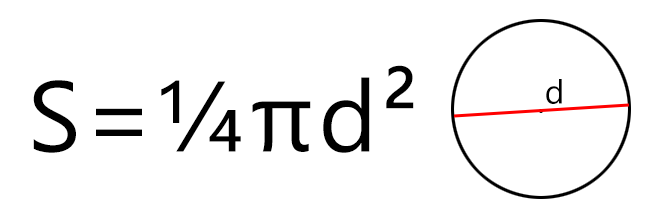
К примеру, если диаметр круга (площадь поверхности пиццы) составляет 35 сантиметров, то площадь такого круга будет равна S = ¼ × 3,14 × 35 2 = ¼ × 3,14 × 1225 = 962 см 2 (квадратных сантиметра).
Через длину окружности
Если мы знаем только длину окружности (периметр круга), то рассчитать площадь фигуры можно по формуле (где L — длина окружности, а π – константа, равная 3,1415…):
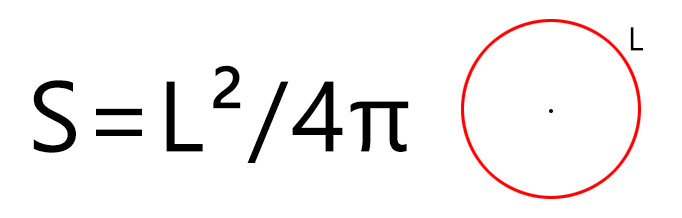
Например, если длинна окружности составляет 120 мм, тогда площадь круга будет равна S = 120 2 / (4 × 3,14) = 14 400 / (4 × 3,14) = 1146,5 мм 2 (квадратных миллиметров).
Какие термины используются для поиска площади круга?
Для вычисления площади круга, в формулах были использованы следующие термины, значение которых нужно знать, чтобы точно понимать принципы расчета.
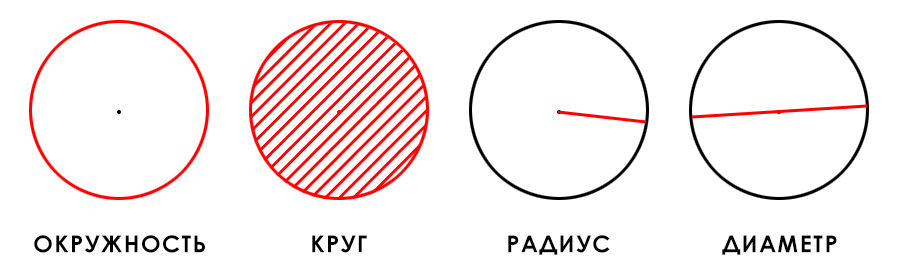
Окружность — замкнутая плоская кривая, все точки которой равноудалены от центра.
Круг — множество точек на плоскости, которые удалены от центра на расстоянии, не превышающем радиус.
Диаметр — отрезок, соединяющий две точки на окружности и проходящий через центр окружности. Диаметр равен двум радиусам.
Радиус — отрезок, который соединяет центр окружности и любую точку на ней.
Число π (пи) — математическая постоянная, равная отношению длины окружности к её диаметру. Пи равняется примерно 3,14.
Площадь круга и размеры пицц
Люди не всегда верно сопоставляют площадь круга и диаметры. К примеру, сможете ли вы ответить:

Что больше: 2 пиццы диаметром 25 см или 1 пицца диаметром 40 см?
Интуитивно кажется, что 2 пиццы, так как в сумме их радиусы дают 50 сантиметров, что больше, чем 40. Однако это неправильный вывод, так как сравнивать нужно не сумму диаметров, а сумму квадратов диаметров. То есть:
- 25 2 + 25 2 = 625 + 625 = 1250
- 40 2 = 1600
Так как ¼π является константой, то можно сравнивать только квадраты диаметров. Получается, что пицца 40 см больше, чем даже 2 пиццы размером 25 см. А вот если диаметр пиццы составляет 35 см, то 35 2 = 1225, и в этом случае 2 пиццы по 25 см будут иметь бОльшую площадь.
Площади усеченных частей круга
А также полезно знать следующие геометрические элементы, связанные с кругами и окружностями:
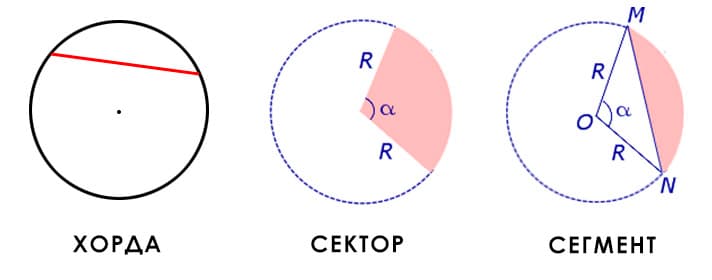
Хорда — отрезок, соединяющий любые две точки окружности.
Сектор — часть круга, ограниченная дугой и двумя радиусами, соединяющими концы дуги с центром круга.
Сектор является частью круга, а его площадь относится к площади круга так же, как и длина окружности сектора к длине всей окружности. Поэтому площадь сектора равна площади круга, умноженной на отношение длинны окружности сектора к длине окружности всего круга.
Но площадь сектора можно вычислить и по более простой формуле. Она равна длине дуги сектора, умноженной на половину радиуса:
где S — площадь сектора, r — радиус круга.
Сегмент — это часть круга, ограниченная дугой и стягивающей её хордой.
Площадь сегмента можно найти по формулам:
где S — площадь сегмента, sinα — синус угла двух между радиусов до концов хорды, r — радиус круга.
Часто задаваемые вопросы о площади круга?
И конечно, стоит ответить на некоторые вопросы, которые возникают во время расчетов.
Входит ли окружность (периметр) в площадь круга?
Да, входит, ведь кругом являются все точки, удаленные от центра круга на расстояние, которое не превышает радиус.
Какие есть ещё калькуляторы для круга у вас на сайте?
У нас есть разнообразные калькуляторы, в частности калькуляторы: длины окружности, диаметра и площади круга. Для последней калькулятор находится на данной странице.
Хватит ли только диаметра, только радиуса или только длинны окружности для расчета площади круга?
Да, хватит чего-то одного, так как все 3 сущности можно вывести одну из другой, например, диаметр равен двум радиусам, а длина окружности – это диаметр, умноженный на число Пи.
Почему Пи равняется 3,1415926…, а не является «ровным» числом?
Число Пи – это отношение длины окружности к диаметру. После его вычисления математики выяснили, что оно является иррациональным числом: то есть его значение не может быть точно выражено в виде дроби m/n, где m — целое число, а n — натуральное. Следовательно, его десятичное представление никогда не заканчивается и не является периодическим. На июнь 2022 года известны первые 100 триллионов знаков числа «пи» после запятой. И получается, что именно с такой точностью можно рассчитать площадь круга. Если у квадрата и треугольника площадь точная, то у круга всегда приблизительная.
Кто впервые научился вычислять площадь круга?
Гиппократ Хиосский (не тот, в честь которого назвали клятву) первым сформулировал, что площадь круга пропорциональна квадрату его диаметра. Евдокс Книдский в IV веке до н. э. строго доказал это утверждение. А Архимед в III веке до н. э. нашёл число Пи и продемонстрировал, что оно чуть меньше, чем 3 и 1/7.
Поделитесь в соцсетях
Если понравилось, поделитесь калькулятором в своих социальных сетях: вам нетрудно, а проекту полезно для продвижения. Спасибо!
Есть что добавить?
Напишите своё мнение, комментарий или предложение.
Источник
Площадь круга: как найти, формулы

О чем эта статья:
площадь, 6 класс, 9 класс, ЕГЭ/ОГЭ
Определение основных понятий
Прежде чем погрузиться в последовательность расчетов и узнать, чему равна площадь круга, важно выяснить разницу между понятиями окружности и круга.
Окружность — замкнутая плоская кривая, все точки которой равноудалены от центра.
Круг — множество точек на плоскости, которые удалены от центра на расстоянии, не превышающем радиус.
Если говорить простым языком, окружность — это замкнутая линия, как, например, кольцо и шина. Круг — плоская фигура, ограниченная окружностью, как монетка или крышка люка.
Формула вычисления площади круга
Давайте разберем несколько формул расчета площади круга. Поехали!
Площадь круга через радиус
S = π × r 2 , где r — это радиус, π — это константа, которая выражает отношение длины окружности к диаметру, она приблизительно равна 3,14.
Площадь круга через диаметр
S = d 2 : 4 × π, где d — это диаметр.
Площадь круга через длину окружности
S = L 2 : (4 × π), где L — это длина окружности.
Популярные единицы измерения площади:
- квадратный миллиметр (мм 2 );
- квадратный сантиметр (см 2 );
- квадратный дециметр (дм 2 );
- квадратный метр (м 2 );
- квадратный километр (км 2 );
- гектар (га).
Нужно быстро привести знания в порядок перед экзаменом? Записывайтесь на курсы ЕГЭ по математике в Skysmart!
Задачи. Определить площадь круга
Мы разобрали три формулы для вычисления площади круга. А теперь тренироваться — поехали!
Задание 1. Как найти площадь круга по диаметру, если значение радиуса равно 6 см.
Диаметр окружности равен двум радиусам.
Используем формулу: S = π × d 2 : 4.
Подставим известные значения: S = 3,14 × 12 2 : 4.
Ответ: 113,04 см 2 .
Задание 2. Найти площадь круга, если известен диаметр, равный 90 мм.
Используем формулу: S = π × d 2 : 4.
Подставим известные значения: S = 3,14 × 90 2 : 4.
Ответ: 6358,5 мм 2 .
Задание 3. Найти длину окружности при радиусе 3 см.
Отношение длины окружности к диаметру является постоянным числом.
Получается: L = d × π.
Так как диаметр равен двум радиусам, то формула длины окружности примет вид: L = 2 × π × r.
Подставим значение радиуса: L = 2 × 3,14 × 3.
Ответ: 18,84 см 2 .
Как рассчитать площадь круга
На данной странице калькулятор поможет рассчитать площадь круга онлайн. Для расчета задайте радиус, диаметр или длину окружности.
Круг – множество точек плоскости, удаленных от заданной точки этой плоскости (центр круг) на расстояние, не превышающее заданное (радиус круга).
Окружность – замкнутая плоская кривая, все точки которой одинаково удалены от данной точки (центра), лежащей в той же плоскости, что и кривая.
Расчет площади поперечного сечения круга
 В инженерной и строительной практике нередко встречаются задачи по расчёту площади поперечного сечения. Если фигуру разрезать по линии, которая перпендикулярна продольной оси предмета, то полученный торец и будет поперечным сечением. Круг — один из наиболее часто встречающихся видов подобного рассечения. Такой срез присущ цилиндру, шару, конусу, тору, эллипсоиду.
В инженерной и строительной практике нередко встречаются задачи по расчёту площади поперечного сечения. Если фигуру разрезать по линии, которая перпендикулярна продольной оси предмета, то полученный торец и будет поперечным сечением. Круг — один из наиболее часто встречающихся видов подобного рассечения. Такой срез присущ цилиндру, шару, конусу, тору, эллипсоиду.
Определение величины
Площадь — это величина, характеризующая размер геометрической фигуры. Её определение — одна из древнейших практических задач. Древние греки умели находить площадь многоугольников: так, каменщикам, чтобы узнать размер стены, приходилось умножать её длину на высоту.
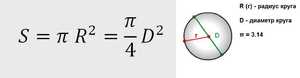
По прошествии долгих лет трудом многих мыслителей был выработан математический аппарат для расчета этой величины практически для любой фигуры.
На Руси существовали особые единицы измерения: копна, соха, короб, верёвка, десятина, четь и другие, так или иначе связанные с пахотой. Две последних получили наибольшее распространение. Однако от древнерусских землемеров нам досталось только само слово — «площадь».
С развитием науки и техники появилось не только множество формул для расчёта площадей любых геометрических фигур, но и приборы, которые делают это за человека. Такие приборы называют планиметрами.
Область применения
Круг — одна из фундаментальных фигур, которые окружают человека повсюду. Трубы, колеса, лампы, конфорки у плиты — всё это имеет форму круга или поперечное сечение в виде круга. Расчёт площади такого сечения может понадобиться в следующих ситуациях:
- Определение объемов емкостей.
- Решение задач по сопротивлению материалов и электротехнике.
- Расчет количества материалов при проектировании, строительстве и ремонте.
- Ведение поливного земледелия.
Стоит обратить внимание на разницу между кругом и окружностью. Окружность — это замкнутая кривая, все точки которой равно удалены от центра, в то время как круг — это часть плоскости (геометрическая фигура), ограниченная окружностью.
Круг имеет ряд характеристик:
- радиус (r/R) — отрезок, соединяющий центр фигуры с его границей;
- диаметр (d/D) — отрезок, который соединяет две точки границы круга и проходит через его центр;
- длина окружности (C/c/L/l).

Теорема гласит: площадь круга (S) равна произведению половины длины окружности и его радиуса. Длина окружности С находится в прямой зависимости от радиуса R с коэффициентом π («пи» = 3,14).
Способы расчета
Чтобы получить круглое поперечное сечение, необходимо разрезать объёмную фигуру перпендикулярно оси вращения. В случае с цилиндром площади всех поперечных сечений будут равны между собой — как, например, кружки колбасы, нарезанные поперек батона, одинаковы.
Шар, по сути, представляет собой напластование блинчиков-кругов различного диаметра от точечного до заданного и обратно до точки. Чтобы найти S какого-либо из блинчиков, необходимо определить его радиус. Принцип его расчёта сводится к решению теоремы Пифагора, где гипотенузой выступает радиус шара, а искомый радиус становится одним из катетов.
При расчёте площади сечений конуса необходимо найти радиус или диаметр каждого из кругов, учитывая, что в продольном разрезе конус — это равнобедренный треугольник.
Цилиндр, конус и шар — базовые объемные фигуры. Однако существуют более сложные фигуры, например, тор. Тор, или тороид, при первом приближении являет собой не что иное, как бублик или баранку. Разломив его пополам, на торцах можно увидеть два одинаковых круга. Площадь такого поперечного сечения можно получить, удвоив имеющуюся (на рисунке серая область справа). Если взять нож и рассечь баранку вдоль, на срезе получится кольцо. В случае с такой фигурой необходимо найти площадь круга по внешней окружности и вычесть из нее «дырку от бублика» (показано серым на рисунке слева).

Площадь круглого поперечного сечения рассчитывается исходя из имеющихся характеристик. Она сводится к трем основным формулам. Их можно представить таким образом:

- Самая популярная, легкая в применении и часто используемая формула. Чтобы узнать площадь фигуры, если известен её радиус, нужно возвести это значение в квадрат и умножить на число π. Для бытовых расчетов достаточно двух знаков после запятой, то есть π = 3,14.
- Иногда оперируют диаметром, а не радиусом круга. В этом случае к вычислениям добавляется одна операция: диаметр умножают сам на себя, затем на число π, а произведение делят на 4.
- Если известна длина окружности С и ее радиус R и нужно выяснить площадь круга, ограниченного этой окружностью, не понадобится даже π. Используют следующую формулу: значение С делят пополам и умножают на R. Полученное чисто и будет искомой величиной.
Способов определения того, чему равна площадь круга, достаточно много. Чаще всего, если возникает подобная задача, на ум приходит знакомая еще со школьной скамьи формула «эс равно пи эр квадрат».
[spoiler title=”источники:”]
http://www.mozgan.ru/Geometry/AreaCircle
http://tokar.guru/hochu-vse-znat/raschet-ploschadi-poperechnogo-secheniya-kruga.html
[/spoiler]
 В инженерной и строительной практике нередко встречаются задачи по расчёту площади поперечного сечения. Если фигуру разрезать по линии, которая перпендикулярна продольной оси предмета, то полученный торец и будет поперечным сечением. Круг — один из наиболее часто встречающихся видов подобного рассечения. Такой срез присущ цилиндру, шару, конусу, тору, эллипсоиду.
В инженерной и строительной практике нередко встречаются задачи по расчёту площади поперечного сечения. Если фигуру разрезать по линии, которая перпендикулярна продольной оси предмета, то полученный торец и будет поперечным сечением. Круг — один из наиболее часто встречающихся видов подобного рассечения. Такой срез присущ цилиндру, шару, конусу, тору, эллипсоиду.
- Определение величины
- Область применения
- Способы расчета
Определение величины
Площадь — это величина, характеризующая размер геометрической фигуры. Её определение — одна из древнейших практических задач. Древние греки умели находить площадь многоугольников: так, каменщикам, чтобы узнать размер стены, приходилось умножать её длину на высоту.
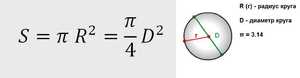
По прошествии долгих лет трудом многих мыслителей был выработан математический аппарат для расчета этой величины практически для любой фигуры.
На Руси существовали особые единицы измерения: копна, соха, короб, верёвка, десятина, четь и другие, так или иначе связанные с пахотой. Две последних получили наибольшее распространение. Однако от древнерусских землемеров нам досталось только само слово — «площадь».
С развитием науки и техники появилось не только множество формул для расчёта площадей любых геометрических фигур, но и приборы, которые делают это за человека. Такие приборы называют планиметрами.
Область применения
Круг — одна из фундаментальных фигур, которые окружают человека повсюду. Трубы, колеса, лампы, конфорки у плиты — всё это имеет форму круга или поперечное сечение в виде круга. Расчёт площади такого сечения может понадобиться в следующих ситуациях:
- Определение объемов емкостей.
- Решение задач по сопротивлению материалов и электротехнике.
- Расчет количества материалов при проектировании, строительстве и ремонте.
- Ведение поливного земледелия.
Стоит обратить внимание на разницу между кругом и окружностью. Окружность — это замкнутая кривая, все точки которой равно удалены от центра, в то время как круг — это часть плоскости (геометрическая фигура), ограниченная окружностью.
Круг имеет ряд характеристик:
- радиус (r/R) — отрезок, соединяющий центр фигуры с его границей;
- диаметр (d/D) — отрезок, который соединяет две точки границы круга и проходит через его центр;
- длина окружности (C/c/L/l).

Теорема гласит: площадь круга (S) равна произведению половины длины окружности и его радиуса. Длина окружности С находится в прямой зависимости от радиуса R с коэффициентом π («пи» = 3,14).
Способы расчета
Чтобы получить круглое поперечное сечение, необходимо разрезать объёмную фигуру перпендикулярно оси вращения. В случае с цилиндром площади всех поперечных сечений будут равны между собой — как, например, кружки колбасы, нарезанные поперек батона, одинаковы.
Шар, по сути, представляет собой напластование блинчиков-кругов различного диаметра от точечного до заданного и обратно до точки. Чтобы найти S какого-либо из блинчиков, необходимо определить его радиус. Принцип его расчёта сводится к решению теоремы Пифагора, где гипотенузой выступает радиус шара, а искомый радиус становится одним из катетов.
При расчёте площади сечений конуса необходимо найти радиус или диаметр каждого из кругов, учитывая, что в продольном разрезе конус — это равнобедренный треугольник.
Цилиндр, конус и шар — базовые объемные фигуры. Однако существуют более сложные фигуры, например, тор. Тор, или тороид, при первом приближении являет собой не что иное, как бублик или баранку. Разломив его пополам, на торцах можно увидеть два одинаковых круга. Площадь такого поперечного сечения можно получить, удвоив имеющуюся (на рисунке серая область справа). Если взять нож и рассечь баранку вдоль, на срезе получится кольцо. В случае с такой фигурой необходимо найти площадь круга по внешней окружности и вычесть из нее «дырку от бублика» (показано серым на рисунке слева).

Площадь круглого поперечного сечения рассчитывается исходя из имеющихся характеристик. Она сводится к трем основным формулам. Их можно представить таким образом:

- Самая популярная, легкая в применении и часто используемая формула. Чтобы узнать площадь фигуры, если известен её радиус, нужно возвести это значение в квадрат и умножить на число π. Для бытовых расчетов достаточно двух знаков после запятой, то есть π = 3,14.
- Иногда оперируют диаметром, а не радиусом круга. В этом случае к вычислениям добавляется одна операция: диаметр умножают сам на себя, затем на число π, а произведение делят на 4.
- Если известна длина окружности С и ее радиус R и нужно выяснить площадь круга, ограниченного этой окружностью, не понадобится даже π. Используют следующую формулу: значение С делят пополам и умножают на R. Полученное чисто и будет искомой величиной.
Способов определения того, чему равна площадь круга, достаточно много. Чаще всего, если возникает подобная задача, на ум приходит знакомая еще со школьной скамьи формула «эс равно пи эр квадрат».
При решении заданий сопротивления материалов в расчетные формулы вводят величины, которые определяют формулу и размеры поперечных сечений, они называются геометрическими характеристиками плоских сечений. Первой такой величиной стоит считать площадь сечения. Рассчитать площадь поперечного сечения можно даже ствола дерева, ведь оно по форме похоже на эллипс или круг. Согласно формуле, площадь поперечного сечения круга, возможно, рассчитать достаточно точно по формуле. Площадь сечения круга или шара можно найти по формуле:
S = πR 2
При этом не стоит забывать о том, что расстояние от плоскости до центра фигуры совпадет с плоскостью, тогда плоскость поперечного сечения шара будет равняться нулю, так как касание им плоскости происходит лишь в одной точке.
Рассмотрим на примере параллелограмма. Прежде всего, для того чтобы найти площадь поперечного сечения, необходимо знать значения высоты и снования параллелограмма. Даже если нам известна только ширина основания и его длина через эти значения возможно найти диагональ, используя теорему Пифагора: квадрат гипотенузы прямоугольного треугольника равняется сумме квадратов катетов. Формула выглядит как:
a 2 + b 2 = c 2
Из нее можно вывести такую формулу:
c = S*q*r*t*(a 2 + b 2 )
Когда у нас известно значение диагонали параллелограмма, то его можно подставить в формулу:
S – площадь поперечного сечения, h это значений высоты параллелограмма. Результат, который получится после исчислений, будет означать площадь поперечного сечения. Такая формула:
используется в тех случаях, когда сечение идет параллельно двум основаниям.
При вычислении площади поперечного сечения цилиндра, которое проходит вдоль его оснований, если одна из сторон данного прямоугольника тождественна радиусу основания, а другая из сторон – высоте цилиндра используется такая формула:
где h – высота цилиндра R – величина радиуса окружности. Если же сечение не проходит сквозь ось цилиндра и одновременно параллельно его основаниям, то это означает, что сторона данного треугольника не равняется диаметру окружности основания.
Для решения этой проблемы необходимо узнать значение неизвестной стороны предварительно нарисовав окружность у основания цилиндра. Расчет производится также по формуле выведенной из теоремы Пифагора. Затем подставляется формула:
где 2а – значение хорды, расчета площади поперечного сечения.
Источник: www.studyguide.ru
Область применения
Круг — одна из фундаментальных фигур, которые окружают человека повсюду. Трубы, колеса, лампы, конфорки у плиты — всё это имеет форму круга или поперечное сечение в виде круга. Расчёт площади такого сечения может понадобиться в следующих ситуациях:
- Определение объемов емкостей.
- Решение задач по сопротивлению материалов и электротехнике.
- Расчет количества материалов при проектировании, строительстве и ремонте.
- Ведение поливного земледелия.
Стоит обратить внимание на разницу между кругом и окружностью. Окружность — это замкнутая кривая, все точки которой равно удалены от центра, в то время как круг — это часть плоскости (геометрическая фигура), ограниченная окружностью.
Круг имеет ряд характеристик:
- радиус (r/R) — отрезок, соединяющий центр фигуры с его границей;
- диаметр (d/D) — отрезок, который соединяет две точки границы круга и проходит через его центр;
- длина окружности (C/c/L/l).

Теорема гласит: площадь круга (S) равна произведению половины длины окружности и его радиуса. Длина окружности С находится в прямой зависимости от радиуса R с коэффициентом π («пи» = 3,14).
Определение величины
Площадь — это величина, характеризующая размер геометрической фигуры. Её определение — одна из древнейших практических задач. Древние греки умели находить площадь многоугольников: так, каменщикам, чтобы узнать размер стены, приходилось умножать её длину на высоту.
По прошествии долгих лет трудом многих мыслителей был выработан математический аппарат для расчета этой величины практически для любой фигуры.
На Руси существовали особые единицы измерения: копна, соха, короб, верёвка, десятина, четь и другие, так или иначе связанные с пахотой. Две последних получили наибольшее распространение. Однако от древнерусских землемеров нам досталось только само слово — «площадь».
С развитием науки и техники появилось не только множество формул для расчёта площадей любых геометрических фигур, но и приборы, которые делают это за человека. Такие приборы называют планиметрами.
Способы расчета
Чтобы получить круглое поперечное сечение, необходимо разрезать объёмную фигуру перпендикулярно оси вращения. В случае с цилиндром площади всех поперечных сечений будут равны между собой — как, например, кружки колбасы, нарезанные поперек батона, одинаковы.
Шар, по сути, представляет собой напластование блинчиков-кругов различного диаметра от точечного до заданного и обратно до точки. Чтобы найти S какого-либо из блинчиков, необходимо определить его радиус. Принцип его расчёта сводится к решению теоремы Пифагора, где гипотенузой выступает радиус шара, а искомый радиус становится одним из катетов.
При расчёте площади сечений конуса необходимо найти радиус или диаметр каждого из кругов, учитывая, что в продольном разрезе конус — это равнобедренный треугольник.
Цилиндр, конус и шар — базовые объемные фигуры. Однако существуют более сложные фигуры, например, тор. Тор, или тороид, при первом приближении являет собой не что иное, как бублик или баранку. Разломив его пополам, на торцах можно увидеть два одинаковых круга. Площадь такого поперечного сечения можно получить, удвоив имеющуюся (на рисунке серая область справа). Если взять нож и рассечь баранку вдоль, на срезе получится кольцо. В случае с такой фигурой необходимо найти площадь круга по внешней окружности и вычесть из нее «дырку от бублика» (показано серым на рисунке слева).
Окружность и круг — в чём отличие?
Часто понятия круг и окружность путают, хотя это разные вещи. Окружность — это замкнутая линия, а круг — это плоская фигура, ограниченная окружностью. Таким образом, гимнастический обруч или колечко — это окружности, а монета или вкусный блин — это круги.
Окружность — замкнутая плоская кривая, все точки которой равноудалены от одной заданной точки — центра окружности.
Круг — бесконечное множество точек на плоскости, которые удалены от заданной точки, называемой центром круга, на значение, не превышающее заданного неотрицательного числа, называемого радиусом этого круга.
Теория. Площадь круга
Формулы для вычисления площади круга:
| ● | S = π r 2 | ||
| ● | S = | 1 | π d 2 |
| 4 |
●S =
где S — площадь круга, r — радиус круга, d — диаметр круга, l — длина окружности, π = 3.141592
Вводить можно числа или дроби (-2.4, 5/7, . ). Более подробно читайте в правилах ввода чисел.
Примеры решения задач
Задача 1
Найдите площадь круга, если известен его радиус см.
Решение: Для определения площади круга используем формулу (1):
см2. Сейчас мы имеем точное значение площади круга. Но если мы возьмем вместо число 3,14, то получим приближенное значение площади круга:
см2.
Ответ: 78,5 см2.
Задача 2
Найдите площадь земельного участка, если известно, что форма участка — круг, а диаметр участка составляет 50 м.
Решение: Чтобы найти площадь земельного участка, мы должны рассчитать площадь круга с диаметром 50 м. Используем формулу (2):
м2.
Ответ: м2.
Уравнение окружности
1. Уравнение окружности с радиусом r и центром в начале декартовой системы координат: r2 = x2 + y2
2. Уравнение окружности с радиусом r и центром в точке с координатами (a, b) в декартовой системе координат:
r2 = (x – a)2 + (y – b)2
3. Параметрическое уравнение окружности с радиусом r и центром в точке с координатами (a, b) в декартовой системе координат:
| { | x = a + r cos t |
| y = b + r sin t |
Длина окружности круга
Множество точек удаленных от центра круга на расстояние, не превышающее радиус круга, называется кругом. Отношение длины любой окружности C
к ее диаметру
d
всегда будет равно одному и тому же числу. Это число – всем известное число
π
(«пи»), которое примерно равно 3,14. Так же, справедлива формула определения числа
π
, как отношение длины окружности
C
к двум ее радиусам
r
. Исходя из этого, выводится формула длины окружности
C
, которая равна произведения числа
π
и диаметра
d
окружности или 2-м ее радиусам
r
.
С=2πr
С=
πd
π=C/d
Для примера
решим простую задачу, где нужно найти длину окружности, у которой известен радиус
r
=2 см.
C= πd
d=2r=4 см
С=4*3,14=12,56
Подставляем известные данные в формулу длины окружности и получаем, что длина окружности примерно равна 12,56 см.
Вычисление площади поперечного сечения
С необходимостью определения площади поперечного сечения проводника сталкивается каждый, кто хоть раз в жизни занимался ремонтом кабельной проводки в квартире, на даче, в гараже или офисе. Нехватка сечения может привести к пожару, так как провод будет сильно нагреваться. Если же сечение, наоборот, подобрано со значительным запасом, то стоимость проводки станет необоснованно высокой. В этой статье рассказывается, о различных методиках определения площади поперечного сечения проводника для круглых, одножильных, многожильных проводов и кабелей.
Чем измерять площадь
Для правильного измерения площади поперечного сечения важно сделать ровный перпендикулярный срез и измерить диаметр металла при помощи высокоточных приборов. В случае с многожильными проводами необходимо выполнить следующие шаги:
- Для точных расчетов нужна одиночная проволока. Из пучка проводов выделяют одну жилку и вычисляют площадь ее сечения.
- Пересчитывают количество жил в проводе.
- Перемножают площадь сечения жилки на их количество.
Полученный результат и будет искомой площадью многожильного проводника.
Дополнительная информация: Для вычисления площади сечения проводника необходимо, в первую очередь, измерить его диаметр, и сделать это лучше всего микрометром, штангенциркулем или, в крайнем случае, высокоточной инженерной линейкой. Так как микрометр – редкость в наборе инструментов электрика, то этот способ мы упустим и остановимся на штангенциркуле и линейке.
Штангенциркуль
Штангенциркуль — высокоточный измерительный инструмент, при помощи которого можно определить линейные размеры любого предмета, диаметры круглых изделий, а также глубину сквозных и глухих отверстий и выемок. Такой инструмент должен быть у каждого домашнего мастера, стоит он не дорого и при правильном обращении может прослужить не одно десятилетие.

Штангенциркули подразделяются на следующие виды:
- Нониусные — имеют классическую конструкцию и высокоточную измерительную шкалу, которая позволяет измерять предметы с точностью до 0.1 – 0.05 мм.
- Со стрелочным отображением результатов измерений — очень удобный для снятия точных показаний инструмент, но его главным недостатком является повышенная хрупкость.
- С электронной индикацией результатов — относительно новая разработка, предназначенная для получения максимальной точности и удобного снятия показаний измерений.
Рассмотрим самый распространенный вид штангенциркуля — нониусный. Из таких инструментов наибольшее распространение получили два вида:
- ШЦ-I с точностью измерений 0,1 мм, такой инструмент есть практически у каждого слесаря.
- ШЦ-II с точностью измерений 0,05 мм, этот штангенциркуль предпочтительнее, так как в результате работы он выдаёт меньшую погрешность.
Для правильного измерения диаметра достаточно оголить сердечник кабеля путём снятия изоляция, после чего прижать раздвижные губки инструмента к его поверхности. Риска на подвижной части штангенциркуля совпадёт с показателем на шкале, который и будет являться диаметром.
Карандаш + линейка
Если под рукой нет точных измерительных инструментов, а определить диаметр провода необходимо в настоящий момент, можно воспользоваться старым проверенным способом. Картинка 5. Метод карандаша.
Для данного способа понадобятся круглый карандаш и линейка. Суть метода состоит в следующем алгоритме:
- Прежде всего необходимо отрезать кусок провода и очистить его от изоляции.
- Далее проволока из металлического сердечника плотно наматывается на карандаш, причём, минимальное количество витков должно быть не меньше 15. Здесь все зависит от толщины провода, и чем он тоньше, тем больше витков необходимо намотать.
- Проводятся вычисления по формуле, приведённой на картинке 6.

Обратите внимание! Для получения точного результата следует наматывать провод на карандаш как можно плотнее. Для этого перед наматыванием его необходимо тщательно выровнять в местах перегибов и образования петель.
Что такое площадь поперечного сеченья
Если провод разрезать строго перпендикулярно его длине, чтобы металлические сердечники имели форму правильного круга, то несложно будет измерить диаметр этих жил и определить их площадь с использованием стандартной формулы.

Важно! До недавнего времени опытные электрики могли определить этот параметр на глаз, но сегодня даже они вынуждены измерять провода, и проводить вычисления. Во времена Советского Союза все провода и кабели выпускались по единому ГОСТу, который и нормировал стандартные сечения. Если это 2.5 мм2, то электрик сразу мог отличить его от близких параметров 2 мм2 или 3 мм2. Сегодня производством кабельной продукции занимаются различные компании, которые могут сознательно уменьшать сечение провода и экономить на этом деньги. Вместо заявленных 2.5 мм2 в продажу может поступить провод 2,2 мм2, а это может иметь серьезные последствия и закончиться выгоранием проводки.
Чему равна площадь
Чему равна площадь поперечного сечения проводника – главный вопрос монтажника. Данный показатель является величиной, которая зависит от формы перпендикулярного среза геометрического тела. Проще всего определить площадь квадрата или прямоугольника, для чего достаточно перемножить между собой длину на ширину. Еще в Древней Греции научились рассчитывать площадь практически любой фигуры. Как правило, большинство проводов имеют круглую форму сечения, которую вычислить несложно по формуле или воспользовавшись справочной таблицей. Для этого нужно знать только диаметр или радиус жилы проводника.
Обратите внимание! Существуют кабели большого сечения, в составе которых расположены секторные провода. Но в конечном итоге, сердечники таких изделий рассчитываются исходя из общего приведённого диаметра всех металлических элементов в пучке. Для определения площади сечения каждой жилы необходимо общий показатель разделить на их количество в кабеле.
Основные свойства касательных к окружности
1. Касательная всегда перпендикулярна к радиусу окружности, проведенного в точке соприкосновения.
2. Кратчайшее расстояние от центра окружности к касательной равна радиусу окружности.
3. Если две касательные, с точками соприкосновения B и C, на одной окружности не параллельны, то они пересекаются в точке A, а отрезок между точкой соприкосновения и точкой пересечения одной касательной равен таком же отрезке на другой касательной:
AB = AC
Также, если провести прямую через центр окружности О и точку пересечения A этих касательных, то углы образованный между этой прямой и касательными будут равны:
∠ОAС = ∠OAB
Определение площади поперечного сечения ствола
Для определения объема ствола или его части нужно знать не только длину ствола, но и площадь сечения g. Поперечное сечение ствола не является правильным кругом, поэтому его диаметр d чаще определяют как среднюю арифметическую величину из двух измерений — наибольшего и наименьшего. Площадь сечения ствола определяют по диаметру, используя формулу:
где d — диаметр ствола, принимаемый за диаметр круга.
Так как сечение ствола не является правильным кругом, то такой способ измерения диаметра приводит к некоторой ошибке при вычислении площади сечения. Кроме того, на величину ошибки вычисления площади сечения в коре влияет строение коры: при гладкой коре ошибка меньше, при трещиноватой ‑ больше.
Влияние ошибки в диаметре на точность вычисления объема и площади сечения.
При измерении толщины ствола или его части исправной мерной вилкой всегда возникает случайная ошибка, которая приводит к неточным вычислениям площади сечения и объема. Процент ошибки в диаметре определяется по обычной формуле процентов, т.е.
Если в диаметре допущена та или иная ошибка, то это приведет к ошибке при определении площади сечения и объема. Эти ошибки выражаются такими формулами:
— процент ошибки в объеме:
— процент ошибки площади сечения:
Из приведенных формул можно сделать следующие выводы:
1. Ошибка в диаметре, выраженная в процентах, вызывает двойную ошибку в объеме и площади сечения с тем же знаком.
2. Тонкие стволы и отрезки нужно измерять с большей точностью, т.е. более мелкими ступенями, так как при одной и той же величине ошибки, полученной при измерении и тонкого и толстого ствола или отрезка, относительная ошибка в диаметре, площади сечения и объеме будет большей.
Для уменьшения величины ошибок при измерении толщины ствола
или его отрезка мерной вилкой необходимо выполнять следующие требования:
1) место измерения необходимо очистить от мха и лишайника;
2) если в месте, где надо измерить диаметр, находятся утолщения, необходимо измерить диаметр выше и ниже на одно и то же расстояние (за зоной влияния утолщения) и из двух измерений взять среднее арифметическое;
3) мерную вилку следует накладывать на ствол или на отрезок при большом растворе подвижной ножки, причем так, чтобы мерная линейка касалась ствола;
4) плоскость, проходящая через мерную линейку и обе ножки, должна быть перпендикулярна оси ствола;
5) отсчет следует делать, не отнимая вилки от ствола.
При решении заданий сопротивления материалов в расчетные формулы вводят величины, которые определяют формулу и размеры поперечных сечений, они называются геометрическими характеристиками плоских сечений. Первой такой величиной стоит считать площадь сечения. Рассчитать площадь поперечного сечения можно даже ствола дерева, ведь оно по форме похоже на эллипс или круг. Согласно формуле, площадь поперечного сечения круга, возможно, рассчитать достаточно точно по формуле. Площадь сечения круга или шара можно найти по формуле:
S = πR 2
При этом не стоит забывать о том, что расстояние от плоскости до центра фигуры совпадет с плоскостью, тогда плоскость поперечного сечения шара будет равняться нулю, так как касание им плоскости происходит лишь в одной точке.
Рассмотрим на примере параллелограмма. Прежде всего, для того чтобы найти площадь поперечного сечения, необходимо знать значения высоты и снования параллелограмма. Даже если нам известна только ширина основания и его длина через эти значения возможно найти диагональ, используя теорему Пифагора: квадрат гипотенузы прямоугольного треугольника равняется сумме квадратов катетов. Формула выглядит как:
a 2 + b 2 = c 2
Из нее можно вывести такую формулу:
c = S*q*r*t*(a 2 + b 2 )
Когда у нас известно значение диагонали параллелограмма, то его можно подставить в формулу:
S – площадь поперечного сечения, h это значений высоты параллелограмма. Результат, который получится после исчислений, будет означать площадь поперечного сечения. Такая формула:
используется в тех случаях, когда сечение идет параллельно двум основаниям.
При вычислении площади поперечного сечения цилиндра, которое проходит вдоль его оснований, если одна из сторон данного прямоугольника тождественна радиусу основания, а другая из сторон – высоте цилиндра используется такая формула:
где h – высота цилиндра R – величина радиуса окружности. Если же сечение не проходит сквозь ось цилиндра и одновременно параллельно его основаниям, то это означает, что сторона данного треугольника не равняется диаметру окружности основания.
Для решения этой проблемы необходимо узнать значение неизвестной стороны предварительно нарисовав окружность у основания цилиндра. Расчет производится также по формуле выведенной из теоремы Пифагора. Затем подставляется формула:
где 2а – значение хорды, расчета площади поперечного сечения.
Источник: www.studyguide.ru
Область применения
Круг — одна из фундаментальных фигур, которые окружают человека повсюду. Трубы, колеса, лампы, конфорки у плиты — всё это имеет форму круга или поперечное сечение в виде круга. Расчёт площади такого сечения может понадобиться в следующих ситуациях:
- Определение объемов емкостей.
- Решение задач по сопротивлению материалов и электротехнике.
- Расчет количества материалов при проектировании, строительстве и ремонте.
- Ведение поливного земледелия.
Стоит обратить внимание на разницу между кругом и окружностью. Окружность — это замкнутая кривая, все точки которой равно удалены от центра, в то время как круг — это часть плоскости (геометрическая фигура), ограниченная окружностью.
Круг имеет ряд характеристик:
- радиус (r/R) — отрезок, соединяющий центр фигуры с его границей;
- диаметр (d/D) — отрезок, который соединяет две точки границы круга и проходит через его центр;
- длина окружности (C/c/L/l).

Теорема гласит: площадь круга (S) равна произведению половины длины окружности и его радиуса. Длина окружности С находится в прямой зависимости от радиуса R с коэффициентом π («пи» = 3,14).
Площадь круга и его частей. Длина окружности и ее дуг
| Справочник по математике | Геометрия (Планиметрия) | Окружность и круг |
| Фигура | Рисунок | Определения и свойства |
| Окружность | Множество точек плоскости, находящихся на одном и том же расстоянии от одной точки – центра окружности | |
| Дуга | Часть окружности, расположенная между двумя точками окружности | |
| Круг | Конечная часть плоскости, ограниченная окружностью | |
| Сектор | Часть круга, ограниченная двумя радиусами | |
| Сегмент | Часть круга, ограниченная хордой | |
| Правильный многоугольник | Выпуклый многоугольник, у которого все стороны равны и все углы равны | |
| Около любого правильного многоугольника можно описать окружность |
| Окружность |
| Множество точек плоскости, находящихся на одном и том же расстоянии от одной точки – центра окружности |
| Дуга |
| Часть окружности, расположенная между двумя точками окружности |
| Круг |
| Конечная часть плоскости, ограниченная окружностью |
| Сектор |
| Часть круга, ограниченная двумя радиусами |
| Сегмент |
| Часть круга, ограниченная хордой |
| Правильный многоугольник |
| Выпуклый многоугольник, у которого все стороны равны и все углы равны
Около любого правильного многоугольника можно описать окружность |
Определение 1. Площадью круга называют предел, к которому стремятся площади правильных многоугольников, вписанных в круг, при неограниченном возрастании числа сторон.
Определение 2. Длиной окружности называют предел, к которому стремятся периметры правильных многоугольников, вписанных в круг, при неограниченном возрастании числа сторон.
Замечание 1. Доказательство того, что пределы площадей и периметров правильных многоугольников, вписанных в круг, при неограниченном возрастании числа сторон действительно существуют, выходит за рамки школьной математики и в нашем справочнике не приводится.
Определение 3. Числом π (пи) называют число, равное площади круга радиуса 1.
Замечание 2. Число π является иррациональным числом, т.е. числом, которое выражается бесконечной непериодической десятичной дробью:
Число π является трансцендентным числом, то есть числом, которое не может быть корнем алгебраического уравнения с целочисленными коэффициентами.
Площадь круга
Рассмотрим две окружности с общим центром (концентрические окружности) и радиусами радиусами 1 и R, в каждую из которых вписан правильный n – угольник (рис. 1).
Обозначим через O общий центр этих окружностей. Пусть внутренняя окружность имеет радиус 1.
Рис.1
Площадь правильного n – угольника, вписанного в окружность радиуса R, равна
Площадь правильного n – угольника, вписанного в окружность радиуса 1, равна
Следовательно,
Поскольку при увеличении n площадь правильного n – угольника, вписанного в окружность радиуса 1, стремится к π, то при увеличении n площадь правильного n – угольника, вписанного в окружность радиуса R, стремится к числу πR2.
Таким образом, площадь круга радиуса R, обозначаемая S, равна
S = πR2.
Длина окружности
Рассмотрим правильный n – угольник B1B2…Bn , вписанный в окружность радиуса радиуса R, и опустим из центраO окружности перпендикуляры на все стороны многоугольника (рис. 2).
Рис.2
Поскольку площадь n – угольника B1B2…Bn равна
то, обозначая длину окружности радиуса R буквой C, мы, в соответствии с определением 2, при увеличении n получаем равенство:
откуда вытекает формула для длины окружности радиуса R:
C = 2πR.
Следствие. Длина окружности радиуса 1 равна 2π.
Длина дуги
Рассмотрим дугу окружности, изображённую на рисунке 3, и обозначим её длину символом L(α), где буквой α обозначена величина соответствующего центрального угла.
Рис.3
В случае, когда величина α выражена в градусах, справедлива пропорция
из которой вытекает равенство:
В случае, когда величина α выражена в радианах, справедлива пропорция
из которой вытекает равенство:
Площадь сектора
Рассмотрим круговой сектор, изображённый на рисунке 4, и обозначим его площадь символом S (α) , где буквой α обозначена величина соответствующего центрального угла.
Рис.4
В случае, когда величина α выражена в градусах, справедлива пропорция
из которой вытекает равенство:
В случае, когда величина α выражена в радианах, справедлива пропорция
из которой вытекает равенство:
Площадь сегмента
Рассмотрим круговой сегмент, изображённый на рисунке 5, и обозначим его площадь символом S (α), где буквой α обозначена величина соответствующего центрального угла.
Рис.5
Поскольку площадь сегмента равна разности площадей кругового сектора MON и треугольника MON (рис.5), то в случае, когда величина α выражена в градусах, получаем
Следовательно,
В случае, когда величина α выражена в в радианах, получаем
Следовательно,
На нашем сайте можно также ознакомиться с разработанными преподавателями учебного учебными материалами для подготовки к ЕГЭ и ОГЭ по математике.
Запись по телефону
Для школьников, желающих хорошо подготовиться и сдать ЕГЭ или ОГЭ по математике или русскому языку на высокий балл, учебный проводит
подготовительные курсы для школьников 8, 9, 10 и 11 классов
У нас также для школьников организованы
индивидуальные занятия с репетиторами по математике и русскому языку
Способы расчета
Чтобы получить круглое поперечное сечение, необходимо разрезать объёмную фигуру перпендикулярно оси вращения. В случае с цилиндром площади всех поперечных сечений будут равны между собой — как, например, кружки колбасы, нарезанные поперек батона, одинаковы.
Шар, по сути, представляет собой напластование блинчиков-кругов различного диаметра от точечного до заданного и обратно до точки. Чтобы найти S какого-либо из блинчиков, необходимо определить его радиус. Принцип его расчёта сводится к решению теоремы Пифагора, где гипотенузой выступает радиус шара, а искомый радиус становится одним из катетов.
При расчёте площади сечений конуса необходимо найти радиус или диаметр каждого из кругов, учитывая, что в продольном разрезе конус — это равнобедренный треугольник.
Цилиндр, конус и шар — базовые объемные фигуры. Однако существуют более сложные фигуры, например, тор. Тор, или тороид, при первом приближении являет собой не что иное, как бублик или баранку. Разломив его пополам, на торцах можно увидеть два одинаковых круга. Площадь такого поперечного сечения можно получить, удвоив имеющуюся (на рисунке серая область справа). Если взять нож и рассечь баранку вдоль, на срезе получится кольцо. В случае с такой фигурой необходимо найти площадь круга по внешней окружности и вычесть из нее «дырку от бублика» (показано серым на рисунке слева).
Калькулятор расчета сечения по диаметру
Для простоты вычислений разработан калькулятор расчета сечения кабеля по диаметру. В его основе лежат формулы, по которым можно найти площадь сечения одножильных и многожильных проводов.
Измерять сечение нужно измеряя жилу без изоляции иначе нечего не получится.
Результат для данного диаметра:
Когда речь идет о вычислении десятков и сотен значений, онлайн-калькулятор способен существенно упростить жизнь электрикам и проектировщикам электрических сетей за счет удобства и повышения скорости расчетов. Достаточно ввести значение диаметра жилы, а при необходимости указать количество проволок, если кабель многожильный, и сервис покажет искомое сечение провода.
Теория. Площадь круга
Формулы для вычисления площади круга:
| ● | S = π r 2 | ||
| ● | S = | 1 | π d 2 |
| 4 |
●S =
где S — площадь круга, r — радиус круга, d — диаметр круга, l — длина окружности, π = 3.141592
Вводить можно числа или дроби (-2.4, 5/7, . ). Более подробно читайте в правилах ввода чисел.
Формула расчета
Вычислить площадь сечения электрического провода можно разными способами в зависимости от его типа. Для всех случаев применяется единая формула расчета сечения кабеля по диаметру. Она имеет следующий вид:
D – диаметр жилы.
Диаметр жилы обычно указывается на оплетке провода или на общем ярлыке с другими техническими характеристиками. При необходимости определить это значение можно двумя способами: с применением штангенциркуля и вручную.
Первым способом измерить диаметр жилы очень просто. Для этого ее необходимо очистить от изоляционной оболочки, после чего воспользоваться штангенциркулем. Значение, которое он покажет, и есть диаметр жилы.
Если провод многожильный, необходимо распустить пучок, пересчитать проволоки и измерить штангенциркулем только одну из них. Определять диаметр пучка целиком смысла нет – такой результат будет некорректным из-за наличия пустот. В этом случае формула расчета сечения будет иметь вид:
D – диаметр жилы;
а – количество проволок в жиле.
При отсутствии штангенциркуля диаметр жилы можно определить вручную. Для этого ее небольшой отрезок необходимо освободить от изоляционной оболочки и намотать на тонкий цилиндрический предмет, например, на карандаш. Витки должны плотно прилегать друг к другу. В этом случае формула вычисления диаметра жилы провода выглядит так:
L – длина намотки проволоки;
N – число полных витков.
Чем больше длина намотки жилы, тем точнее получится результат.
Выбор по таблице
Зная диаметр провода, можно определить его сечение по готовой таблице зависимости. Таблица расчета сечения кабеля по диаметру жилы выглядит таким образом:
| Диаметр проводника, мм | Сечение проводника, мм2 |
| 0.8 | 0.5 |
| 1 | 0.75 |
| 1.1 | 1 |
| 1.2 | 1.2 |
| 1.4 | 1.5 |
| 1.6 | 2 |
| 1.8 | 2.5 |
| 2 | 3 |
| 2.3 | 4 |
| 2.5 | 5 |
| 2.8 | 6 |
| 3.2 | 8 |
| 3.6 | 10 |
| 4.5 | 16 |
Когда сечение известно, можно определить значения допустимых мощности и тока для медного или алюминиевого провода. Таким образом удастся выяснить, на какие параметры нагрузки рассчитана токопроводящая жила. Для этого понадобится таблица зависимости сечения от максимального тока и мощности.
| В воздухе (лотки, короба,пустоты,каналы) | Сечение,кв.мм | В земле | |||||||||
| Медные жилы | Алюминиевые жилы | Медные жилы | Алюминиевые жилы | ||||||||
| Ток. А | Мощность, кВт | Тон. А | Мощность, кВт | Ток, А | Мощность, кВт | Ток. А | Мощность,кВт | ||||
| 220 (В) | 380 (В) | 220(В) | 380 (В) | 220(В) | 380 (В) | 220(В) | |||||
| 19 | 4.1 | 17.5 | 1,5 | 77 | 5.9 | 17.7 | |||||
| 35 | 5.5 | 16.4 | 19 | 4.1 | 17.5 | 7,5 | 38 | 8.3 | 75 | 79 | 6.3 |
| 35 | 7.7 | 73 | 77 | 5.9 | 17.7 | 4 | 49 | 10.7 | 33.S | 38 | 8.4 |
| *2 | 9.7 | 77.6 | 37 | 7 | 71 | 6 | 60 | 13.3 | 39.5 | 46 | 10.1 |
| 55 | 17.1 | 36.7 | 47 | 9.7 | 77.6 | 10 | 90 | 19.8 | S9.7 | 70 | 15.4 |
| 75 | 16.5 | 49.3 | 60 | 13.7 | 39.5 | 16 | 115 | 753 | 75.7 | 90 | 19,8 |
| 95 | 70,9 | 67.5 | 75 | 16.5 | 49.3 | 75 | 150 | 33 | 98.7 | 115 | 75.3 |
| 170 | 76.4 | 78.9 | 90 | 19.8 | 59.7 | 35 | 180 | 39.6 | 118.5 | 140 | 30.8 |
| 145 | 31.9 | 95.4 | 110 | 74.7 | 77.4 | 50 | 775 | 493 | 148 | 175 | 38.5 |
| ISO | 39.6 | 118.4 | 140 | 30.8 | 97.1 | 70 | 775 | 60.5 | 181 | 710 | 46.7 |
| 770 | 48.4 | 144.8 | 170 | 37.4 | 111.9 | 95 | 310 | 77.6 | 717.7 | 755 | 56.1 |
| 760 | 57,7 | 171.1 | 700 | 44 | 131,6 | 170 | 385 | 84.7 | 753.4 | 795 | 6S |
| 305 | 67.1 | 700.7 | 735 | 51.7 | 154.6 | 150 | 435 | 95.7 | 786.3 | 335 | 73.7 |
| 350 | 77 | 730.3 | 770 | 59.4 | 177.7 | 185 | 500 | 110 | 379 | 385 | 84.7 |
Перевод ватт в киловатты
Чтобы правильно воспользоваться таблицей зависимости сечения провода от мощности, важно правильно перевести ватты в киловатты.
1 киловатт = 1000 ватт. Соответственно, чтобы получить значение в киловаттах, мощность в ваттах необходимо разделить на 1000. Например, 4300 Вт = 4,3 кВт.
