Как найти сечение плоскостью по уравнениям

Метод сечений в исследовании уравнений поверхностей

Поверхности второго порядка. Исследование методом сечений

§21. Поверхности второго порядка. Исследование методом сечений.

Общий вид алгебраической поверхности второго порядка представляет собой многочлен второй степени относительно трех переменных:

Одним из наиболее продуктивных методов изучения поверхностей в пространстве является метод сечений. Он заключается в исследовании кривых, получающихся в сечениях поверхности плоскостями, параллельными координатным. Для этого достаточно зафиксировать одну из переменных в уравнении поверхности и получить, тем самым, уравнение кривой в плоскости, параллельной двум другим координатным осям. Этот метод будет использован в последующих параграфах при исследовании поверхностей второго порядка. При этом будут рассматриваться только уравнения, непосредственно сводящиеся к каноническим.

Метод сечений в исследовании уравнений поверхностей

8.4. Построение поверхностей

Мы приступаем к изучению формы поверхностей второго порядка, определённых в предыдущем разделе своими каноническими уравнениями. Напомним, что это вторая из двух основных задач аналитической геометрии: зная уравнение поверхности, изучить её геометрические свойства.

Метод, который мы будем применять, называется методом сечений: пересекая поверхность плоскостями, параллельными координатным плоскостям, будем рассматривать линии пересечения и по их виду делать выводы о форме поверхности.

Каноническое уравнение эллипсоида:

Отметим симметрию поверхности: если точка (x, у, z) лежит на эллипсоиде, то и все точки (±x, ±у, ±z) тоже лежат на эллипсоиде. Значит, поверхность симметрична относительно любой из координатных плоскостей. Пересечём эллипсоид плоскостью z = h. Получим линию

Это эллипс, полуоси которого убывают с увеличением |h|. При h = c эллипс превращается в точку, при h > c плоскость z = h не пересекает эллипсоид. Эллипсы получаются и при сечении эллипсоида плоскостями x = h, у = h. Используя эти данные, изображаем поверхность. Числа a, b, c называются полуосями эллипсоида. Если две полуоси равны, то получается эллипсоид вращения. Например, эллипсоид, образованный при вращении эллипса (лежит в плоскости XOZ) вокруг оси OZ. Если a = b = c, то эллипсоид превращается в сферу.

Поверхности второго порядка

Поверхностью второго порядка называется поверхность S, общее уравнение которой в декартовой прямоугольной системе координат имеет вид:

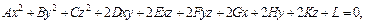(15.22)

где коэффициенты при одночленах второй степени одновременно не равны нулю.

Существует девять типов невырожденных поверхностей, уравнения которых с помощью преобразования координат могут быть приведены к одному из следующих видов. Эти уравнения определяют тип поверхности и называются каноническими уравнениями.

1. Эллипсоид: 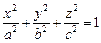(рис. 15.1).

2. Конус второго порядка: 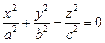(рис. 15.2).

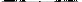
3. Гиперболоиды

4. Параболоиды

5. Цилиндры

3) параболический: 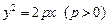(рис. 15.9).

Основным методом исследования формы поверхности является метод параллельных сечений, который состоит в следующем. Поверхность пересекается координатными плоскостями и им параллельными, а затем на основании вида полученных в сечениях линий делается вывод о типе поверхности. Таким образом можно изучать основные геометрические свойства невырожденных поверхностей второго порядка на основе их канонических уравнений.

При этом, когда в общем уравнении поверхности коэффициенты 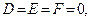приведение к каноническому виду осуществляется с помощью метода выделения полных квадратов.

В определенных случаях уравнение (15.22) поверхности может быть приведено к уравнениям, задающим, так называемые, вырожденные поверхности. Приведем примеры таких случаев:

– пустое множество точек (мнимый эллипсоид);

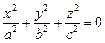– точка (0, 0, 0);

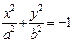– пустое множество точек (мнимый эллиптический цилиндр);

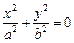– прямая (ось Oz);

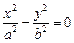– пара пересекающихся плоскостей;

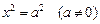– пара параллельных плоскостей;

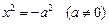– пустое множество точек;

– плоскость (пара совпадающих плоскостей).

Пример 1. Привести уравнение к каноническому виду и определить тип поверхности, которую оно задает:

1)

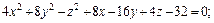
2)

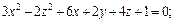
3)

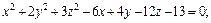
4)

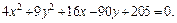
Решение. 1) Воспользуемся методом выделения полных квадратов.

Преобразуем левую часть уравнения:

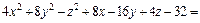
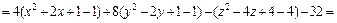
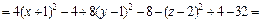
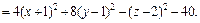
Значит, заданное уравнение равносильно уравнению

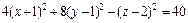или

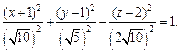
Имеем уравнение однополостного гиперболоида, центр которого находится в точке (–1, 1, 2). Его ось симметрии – прямая, параллельная оси Oz и проходящая через точку (–1, 1, 2).

2) Поскольку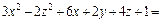

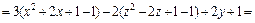
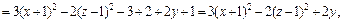
то заданное уравнение равносильно уравнению

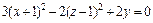или 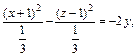что приводит окончательно к уравнению гиперболического параболоида 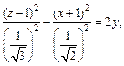смещенного в точку (–1, 0, 1).

3) Выделяем полные квадраты в выражении, стоящем в левой части уравнения:

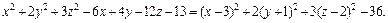
Поэтому заданное уравнение принимает вид:

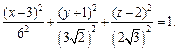
Это уравнение эллипсоида с центром в точке (3, – 1, 2).

4. Методом выделения полных квадратов уравнение 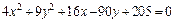приводится к уравнению

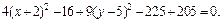т. е.

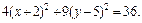
Почленное деление на 36 дает:

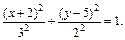
Это уравнение эллиптического цилиндра, смещенного в точку
(–2, 5, 0).

Пример 2. Исследовать поверхность методом сечений и построить ее:

Решение. Для исследования геометрических свойств и формы поверхности используем метод сечений.

Определим сечение поверхности плоскостями где параллельными координатной плоскости Oxy:

Очевидно, что это кривые, проекции которых на ось Oxy задаются уравнением

Уравнение (15.23) при не имеет решений относительно Это означает, что соответствующее сечение есть пустое множество точек, а значит, рассматриваемая поверхность целиком расположена ниже плоскости При уравнение (15.23) определяет эллипс

с полуосями и вырождающийся в точку (0, 0, 1) при Заметим, что все эллипсы, которые получаются в сечениях поверхности плоскостями подобны между собой, причем с уменьшением h их полуоси неограниченно монотонно возрастают.

Дальнейшее уточнение формы можно получить, рассматривая сечения координатными плоскостями Oxz и Oyz:

В первом случае имеем кривую т. е. параболу с параметром вершиной в точке и ветвями, направленными в отрицательную сторону оси Oz. Во втором – параболу с параметром вершиной в точке и аналогичным направлением ветвей.

Выполненное исследование позволяет построить заданную поверхность (рис. 15.10). Это эллиптический параболоид с вершиной в точке (0, 0, 1), направленный в сторону убывания значений z с осью симметрии Oz.

Пример 3. Построить тело, ограниченное поверхностями

Решение. Уравнение задает плоскость. Перейдя к уравнению плоскости «в отрезках», получим:

т. е. плоскость пересекает координатные оси в точках (3, 0, 0), (0, 3, 0) и (0, 0, 3) соответственно.

Уравнение задает круговой цилиндр, осью которого служит Oz. Уравнение определяет координатную плоскость Oxy.

Сделаем рисунок тела (рис. 15.11, 15.12), ограниченного заданными поверхностями.

Источник

Поверхности
второго порядка.
Исследование

поверхностей
методом сечений

Пусть в пространстве задана прямоугольная
декартова система координат.

Определение.  

Поверхностью второго порядка
называется поверхность, определяемая
уравнением
,
где A, B,
C, D,
F, G,
H, K,
L, M
– вещественные числа, причем хотя бы
одно из чисел A, B,
C, D,
F, G
отлично от нуля.

Поверхности второго порядка, за
исключением случаев сильного вырождения,
можно разделить на пять классов:
эллипсоиды, гиперболоиды, параболоиды,
конусы и цилиндры. Для каждой из
поверхностей существует декартова
прямоугольная система координат, в
которой поверхность задается простым
уравнением, называемым каноническим
уравнением. Этот факт будет обоснован
позже.

Сфера

Определение.

Сферой называется геометрическое
место точек пространства, равноудаленных
от фиксированной точки, называемой
центром.

Теорема Сфера радиуса
с
центром в точке

имеет уравнение

.

Пример 1  Построить сферу, заданную
уравнением
.

Решение. Выделив полные квадраты,
получим

.

Следовательно, центром сферы является
точка
,
радиус сферы
.

Для ее изображения построим сечения
сферы плоскостями, проходящими через
центр и параллельными координатным
плоскостям. Каждое такое сечение будет
окружностью радиуса 2 с центром в точке

(рис1).

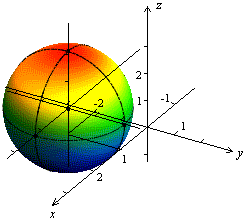
Рис.1.
Рис.2.

Эллипсоид

Определение

Эллипсоидом называется
поверхность, каноническое уравнение
которой имеет вид
,
где

– положительные числа.

Исследуем форму эллипсоида. Из
канонического уравнения эллипсоида
видно, что координаты точек поверхности
ограничены:
.
Эллипсоид обладает тремя плоскостями
симметрии, тремя осями симметрии и
центром симметрии. Ими служат соответственно
координатные плоскости, координатные
оси и начало координат.

Для выяснения формы эллипсоида рассмотрим
его сечения плоскостями. Найдем линию
пересечения эллипсоида с плоскостью.
Так как любая точка плоскости
имеет
нулевую аппликату
,
то координаты точек эллипсоида на
плоскости

удовлетворяют уравнению

Рис.3.Сечение
плоскостью
.

Аналогично, сечение в плоскости

дает эллипс
с
полуосями
и
,
а сечение плоскостью
-эллипс
с
полуосями

и

(рис.4)

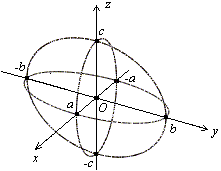
Рис.4.Сечения
эллипсоида координатными плоскостями.

Построенный “каркас” из сечений
уже дает представление об эллипсоиде.
Но чтобы выяснить, как ведет себя
поверхность между нарисованными кривыми,
рассмотрим сечение эллипсоида плоскостью
.
Эта плоскость параллельна плоскости.
Уравнения этой линии пересечения

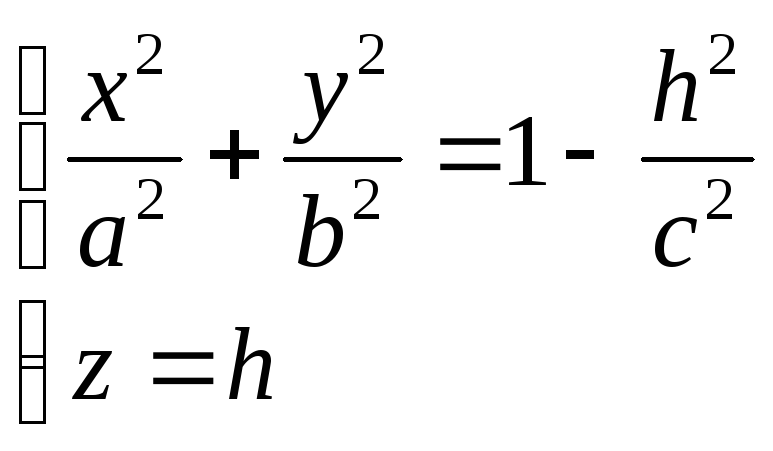
Очевидно, что если
,
то ни одна точка пространства не может
удовлетворять этой системе: в левой
части первого уравнения стоит
неотрицательное число, а в правой –
отрицательное. Если
,
то в сечении получим лишь одну точку

или
в
зависимости от знака
.

Пусть
.
Тогда исходное уравнение преобразуем
к виду

.

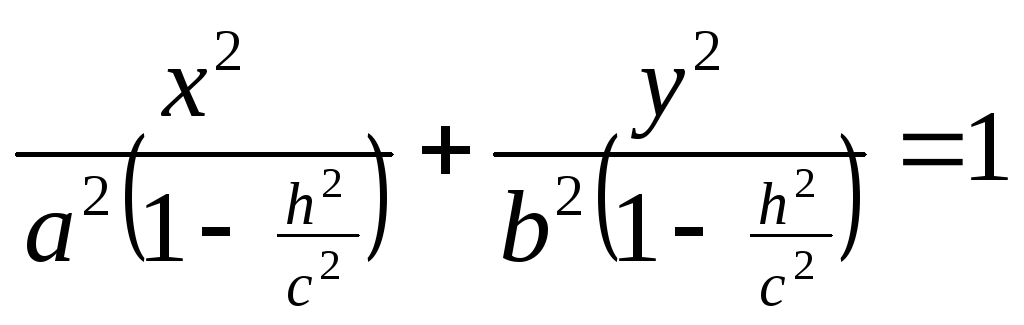Введём обозначения
,

,
тогда уравнение примет вид
.

Данное уравнение является уравнением
эллипса, подобного эллипсу, задаваемому
уравнением, полученным при пересечении
эллипсоида плоскостью
с коэффициентом подобия

и полуосями
и
.
Ясно, что сечение плоскостью
является
таким же эллипсом, расположенным
симметрично первому относительно
плоскости
.
Изобразим эти сечения

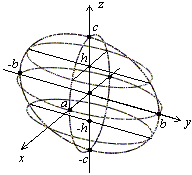
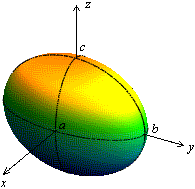
Рис.5.Дополнительные
сечения эллипсоида. Рис.
6. Эллипсоид.

Так же, как для эллипса, точки пересечения
эллипсоида с координатными осями
называются вершинами эллипсоида, центр
симметрии- центром эллипсоида. Числа

называются полуосями. Если полуоси
попарно различны, то эллипсоид называется
трехосным.

Если две полуоси равны друг другу, то
эллипсоид называется эллипсоидом
вращения. Эллипсоид вращения может
быть получен вращением эллипса вокруг
одной из осей. Например, если
,
то все сечения эллипсоида плоскостями
,
,
будут окружностями. Сам эллипсоид может
быть получен из эллипса
,
,
лежащего в плоскости
,
при вращении его вокруг оси

(рис. 7).

Рис.7.Эллипсоид
вращения

Гиперболоиды

Определение.

Однополостным гиперболоидом
называется поверхность, каноническое
уравнение которой имеет вид
,
где
 –
положительные числа.

Исследуем форму однополостного
гиперболоида. Так же, как эллипсоид, он
имеет три плоскости симметрии, три оси
симметрии и центр симметрии. Ими являются
соответственно координатные плоскости,
координатные оси и начало координат.

Для построения гиперболоида найдем его
сечения различными плоскостями. Найдем
линию пересечения с плоскостью
.
На этой плоскости
,
поэтому

Это уравнение на плоскости
задает
эллипс с полуосями
и
.
Найдем линию пересечения с плоскостью
.
На этой плоскости
,
поэтому

.

Это уравнение гиперболы на плоскости
,
где действительная полуось равна
,
а мнимая полуось равна
.
Построим эту гиперболу (рис.8).

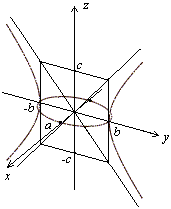
Рис.8.Сечения
однополостного гиперболоида двумя
плоскостями

Сечение плоскостью
также
является гиперболой с уравнением

Изобразим и эту гиперболу, но чтобы не
перегружать чертеж дополнительными
линиями, не будем изображать ее асимптоты
и уберем асимптоты в сечении плоскостью
(рис. 9).

Найдем линии пересечения поверхности
с плоскостями
.
Уравнения этих линий

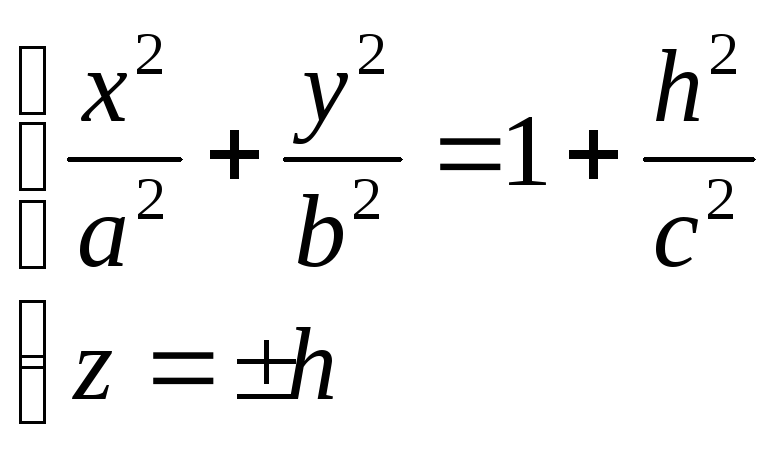
Первое уравнение преобразуем к виду

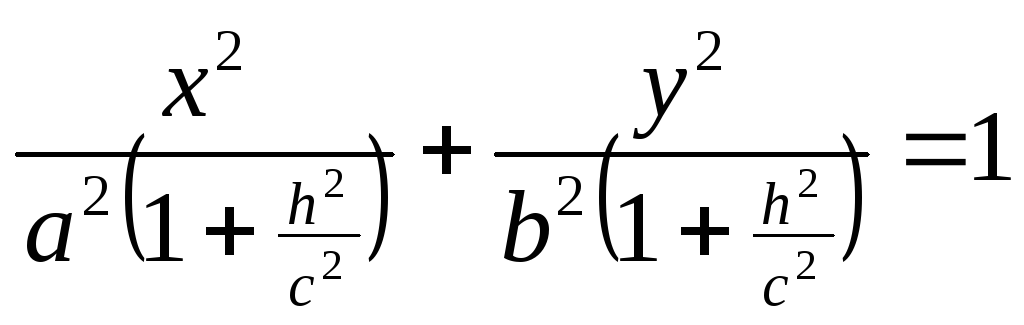
Введём обозначения
,

,
тогда уравнение примет вид

Данное уравнение является уравнением
эллипса, подобного эллипсу в плоскости
,
с коэффициентом подобия
и
полуосями
и
.
Изобразим полученные сечения (рис.9).

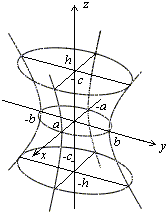
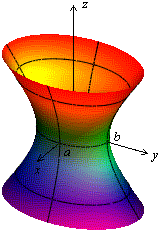
Рис.9.Изображение
однополостного гиперболоида с помощью
сечений

Если в каноническом уравнении гиперболоида
,
то сечения гиперболоида плоскостями,
параллельными плоскости
,
являются окружностями. В этом случае
поверхность называется однополостным
гиперболоидом вращения и может
быть получена вращением гиперболы,
лежащей в плоскости
,
вокруг оси

(рис. 10).

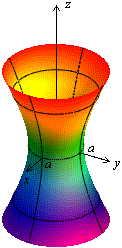
Рис.10.Однополостный
гиперболоид вращения

Определение

Двуполостным гиперболоидом
называется поверхность, каноническое
уравнение которой имеет вид
,
где
 –
положительные числа.

Исследуем форму двуполостного
гиперболоида. Так же, как эллипсоид и
однополостный гиперболоид, он имеет
три плоскости симметрии, три оси симметрии
и центр симметрии. Ими являются
соответственно координатные плоскости,
координатные оси и начало координат.

Для построения гиперболоида найдем его
сечения различными плоскостями. Найдем
линию пересечения с плоскостью
.
На этой плоскости
,
поэтому
.
Координаты ни одной точки плоскости
не
могут удовлетворять данному уравнению.
Следовательно, двуполостный гиперболоид
не пересекает эту плоскость. Найдем
линию пересечения с плоскостью.
На этой плоскости
,
поэтому
.
Это уравнение гиперболы на плоскости
,
где действительная полуось равна
,
а мнимая полуось равна
.
Построим эту гиперболу (рис. 11).

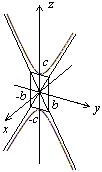
Рис.
11.Сечения
двуполостного гиперболоида плоскостью

Сечение плоскостью
также
является гиперболой, с уравнением
.
Построим гиперболу, но чтобы не перегружать
чертеж дополнительными линиями, не
будем изображать ее асимптоты и уберем
асимптоты в сечении плоскостью
(рис.12).

Найдем линии пересечения поверхности
с плоскостями.
Уравнения этих линий

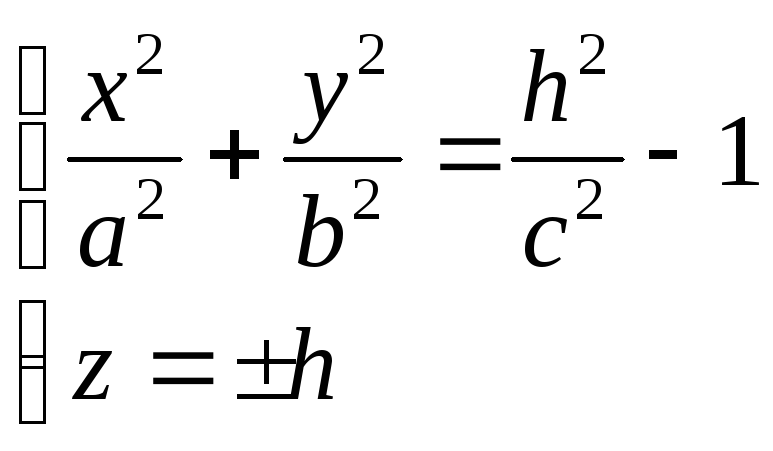
Очевидно, что ни одна точка не может
удовлетворять этим уравнениям, если
.
Если

или
,
то плоскость имеет с исследуемой
поверхностью только одну точку

или
.
Эти точки называются вершинами
гиперболоида.

Пусть
.
Первое уравнение преобразуем к виду

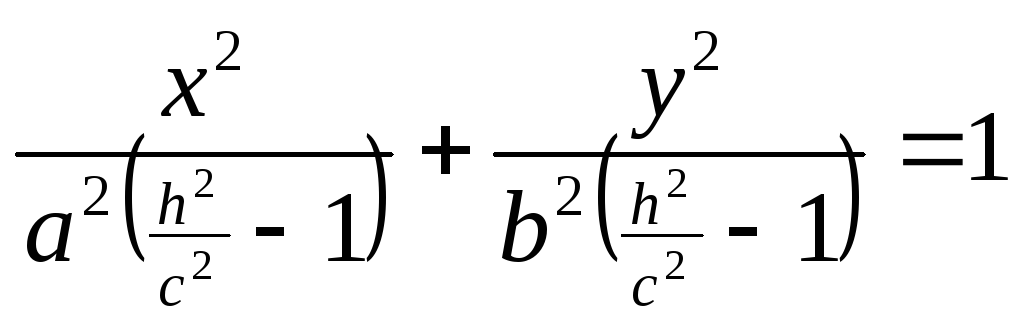
Введём обозначения
,

,
тогда уравнение примет вид

Данное уравнение является уравнением
эллипса, подобного эллипсу в плоскости
,
с коэффициентом подобия
и
полуосями
и
.
Нарисуем полученные сечения (рис. 12).

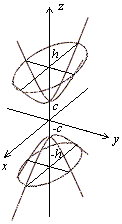
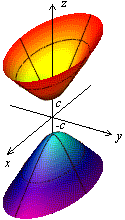
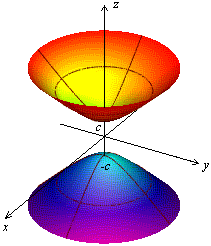
Рис. 12 Изображение
двуполостного. Рис. 13.
Двуполостный
гиперболоид.
Рис. 14
Двуполостный
гиперболоид

гиперболоида с
помощью сечений

вращения

Если в уравнении
,
то сечения гиперболоида плоскостями,
параллельными плоскости
,
являются окружностями. В этом случае
поверхность называется двуполостным
гиперболоидом вращения и может
быть получена вращением гиперболы,
лежащей в плоскости,
вокруг оси

(рис.14).

Конус

Определение

Конусом второго порядка называется
поверхность, уравнение которой в
некоторой декартовой системе координат
имеет вид
,
где
 –
положительные числа.

С математической точки зрения поверхность
лучше определять с помощью уравнения
,
так как в нем меньше параметров, но при
этом, во-первых, теряется аналогия с
уравнениями предыдущих поверхностей,
а во-вторых, если считать, что величины

имеют размерность длины, то в
уравнении размерности правой и левой
части не согласуются.

Для краткости в дальнейшем конус второго
порядка будем называть просто конус.
Исследуем форму конуса. Так же, как
эллипсоид и гиперболоиды, он имеет три
плоскости симметрии, три оси симметрии
и центр симметрии. Ими являются
соответственно координатные плоскости,
координатные оси и начало координат.

Для построения конуса найдем его сечения
различными плоскостями. Найдем линию
пересечения с плоскостью
.
На этой плоскости
,
поэтому
.

Координаты только одной точки плоскости
могут
удовлетворять данному уравнению, а
именно, начала координат. Найдем линию
пересечения с плоскостью.
На этой плоскости
,
поэтому

Это уравнение пары прямых
на
плоскости
.
Построим эти прямые (рис.15). Сечение
плоскостью
также
является парой прямых с уравнением
.

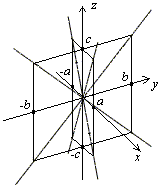
Рис. 15.
Сечения
плоскостями

и
.

Найдем линии пересечения поверхности
с плоскостями
.
Уравнения этих линий

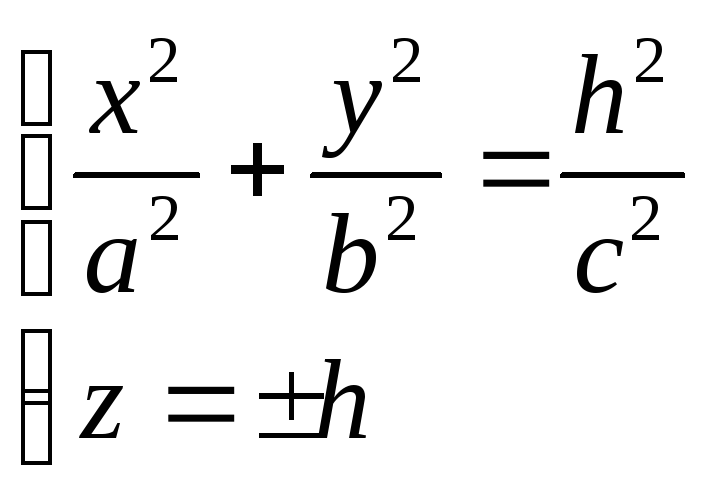
Первое уравнение преобразуем к виду
.
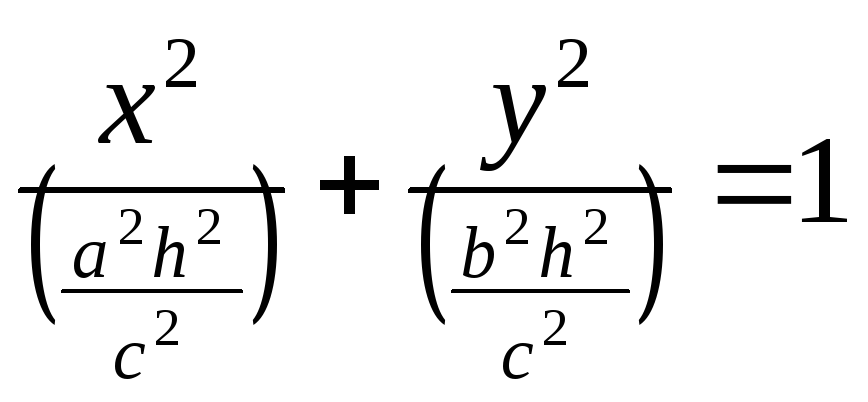Обозначив

и
,
получим

Данное уравнение является уравнением
эллипса. Построим полученные сечения
(рис. 17).

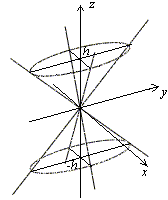
Рис.16.
Дополнительное сечение
Рис.17.
Изображение конуса с помощью сечений

Точка пересечения конуса с плоскостью
называется
вершиной конуса.

Если в каноническом уравнении
,
то сечения конуса плоскостями параллельными
плоскости
являются
окружностями. В этом случае поверхность
называется прямым круговым конусом
и может быть получена вращением прямой,
лежащей в плоскости,
вокруг оси
.

Параболоиды

Определение

Эллиптическим параболоидом
называется поверхность, уравнение
которой в некоторой декартовой системе
координат имеет вид
,
где

и

– положительные числа.

Исследуем
форму эллиптического параболоида. Он
имеет две плоскости симметрии и ось
симметрии. Ими являются соответственно
координатные плоскости
,
и координатная ось
.

Для построения эллиптического параболоида
найдем его сечения различными плоскостями.
Найдем линию пересечения с плоскостью
.
На этой плоскости
,
поэтому
.

Координаты только одной точки плоскости
могут
удовлетворять данному уравнению, а
именно, начала координат. Найдем линию
пересечения с плоскостью
.
На этой плоскости
,
поэтому
.

Это уравнение параболы на плоскости
.
Построим ее (рис. 19). Сечение плоскостью

также является параболой. Найдем линии
пересечения поверхности с плоскостью
.
Уравнения этой линии

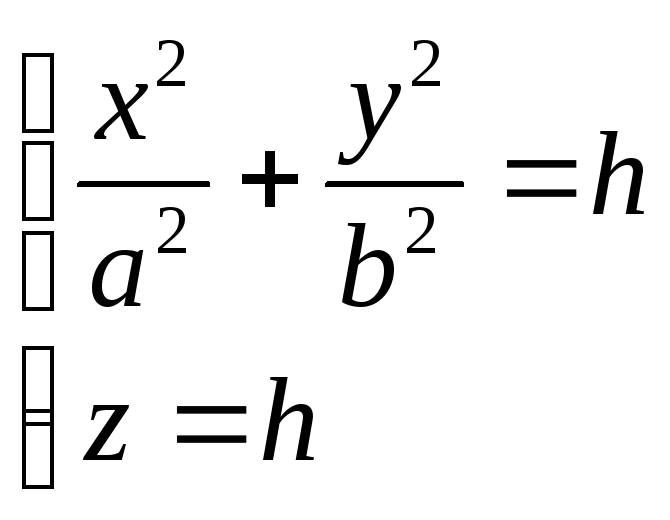
Очевидно, что только одна точка (начало
координат) удовлетворяет этим уравнениям,
если
.
Эта точка называется вершиной
параболоида.

Пусть
.
Первое уравнение преобразуем к виду
,
то есть к виду
,
где
,
.
Полученное уравнение является
уравнением эллипса. Изобразим полученное
сечение (рис.19). При
плоскость поверхность не пересекает.

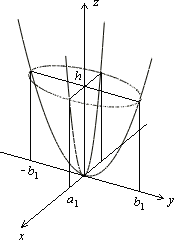
Рис.19.Сечения
эллиптического параболоида координатными
плоскостями

Найдем сечения параболоида плоскостями
,
параллельными плоскости
.
Линии этих сечений удовлетворяют
уравнениям

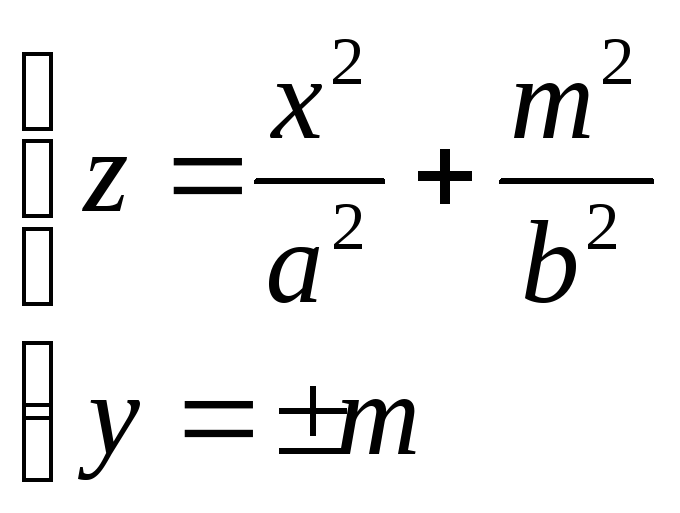
и являются параболами, такими же, как в
плоскости
,
только сдвинутыми вверх на величину
,
их вершины при таком сдвиге лежат на
параболе, получившейся в сечении
плоскостью

(рис. 20).

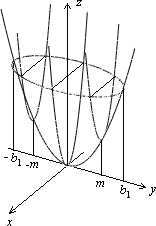
Рис.20
Дополнительное
сечение
Рис.
21.Эллиптический
параболоид Рис.
22.Параболоид
вращения

Следовательно, вся поверхность может
быть получена движением параболы,
лежащей в плоскости
.
Парабола должна двигаться так, чтобы
ее плоскость была параллельна плоскости
,
а вершина скользила по параболе в
плоскости.

Если в уравнении ,
то сечения плоскостями, параллельными
плоскости
,
являются окружностями. В этом случае
поверхность называется параболоидом
вращения и может быть образована
вращением параболы, лежащей в плоскости
,
вокруг оси

(рис. 22).

Соседние файлы в папке модуль2

• #
• #
• #

Для выяснения формы поверхности в пространстве по ее уравнению

Ψ(х, у, z) = 0 (9.10)

часто используют так называемый метод сечений. Он состоит в анализе пересечений поверхности с плоскостями, параллельными координатным плоскостям, например с плоскостями вида z = с, где параметр с пробегает все действительные значения. Для каждого значения с система уравнений

задает соответствующее пересечение. Критерием принадлежности точки M(х; y; z) этому пересечению являются следующие условия: а) z = с; б) координаты x и у ее проекции на координатную плоскость xOy, т.е. координаты точки N(x; у; 0), удовлетворяют уравнению

Ψ(х, у, c) = 0 (9.12)

Зная эти пересечения, т.е. кривые (9.12), можно представить форму поверхности. Отметим, что указанный “рентген” поверхности можно проводить другими плоскостями, но они должны быть параллельными между собой.

Обычно при исследовании формы поверхности методом сечений используют две точки зрения на уравнение (9.12). Первая состоит в том, что его интерпретируют как уравнение проекции на координатную плоскость xOy сечения (9.11). Согласно второй точке зрения предполагают, что в секущей плоскости имеется прямоугольная система координат с началом в точке O’ пересечения секущей плоскости с осью Oz и осями, O’x и O’у, которые проектируются на соответствующие оси Ox и Oy системы координат Oxyz. Это позволяет говорить о (9.12) как об уравнении сечения (9.11) в секущей плоскости.

Пример 9.1. В качестве примера рассмотрим уравнение эллиптического параболоида (9.8) x²/a² + y²/b² = 2z и исследуем его форму методом сечений.

Пересечение этой поверхности с плоскостью z = с описывается уравнением x²/a² + y²/b² = 2c. При с < 0 пересечение пусто, при с = 0 оно совпадает с началом системы координат Oxyz, а при с > 0 представляет собой эллипс x²/(a√(2c))² + y²/(b√(2c))² = 1. Оси этого эллипса с ростом параметра с увеличиваются, и можно представить форму поверхности (рис. 9.16, а). Кстати,

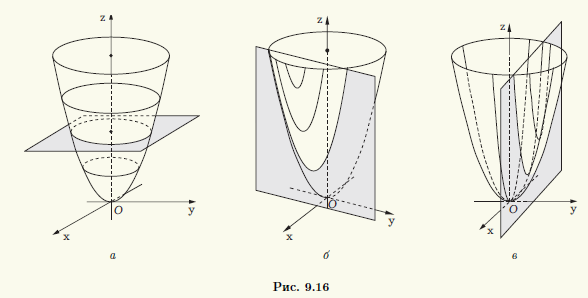
слово “эллиптический” в названии поверхности и указывает на то, что среди ее сечении имеются эллипсы.

Пересечения этоИ же поверхности как с плоскостью x = с (рис. 9.16, б), так и с плоскостью
у = с (рис. 9.16, в) представляют собоq параболы c²/a² + y²/b² = 2z и x²/a² + c²/b² = 2z соответственно.
Параболы в каждом из этих семеИств сечений имеют равные параметры (они не зависят от значения с). Эти сечения позволяют дать еще одно геометрическое построение эллиптического параболоида. Рассмотрим параболу P₁, находящуюся в плоскости у = 0, и аналогичную параболу Р₂ в плоскости x = 0 (рис. 9.17, а). Пусть вторая парабола Р2 перемещается в пространстве так, что:

– вершина параболы Р₂ все время находится на параболе Р₁;

– ось параболы Р₂ параллельна оси параболы Р₁;

– плоскость параболы Р₂ перпендикулярна плоскости параболы Р₁.

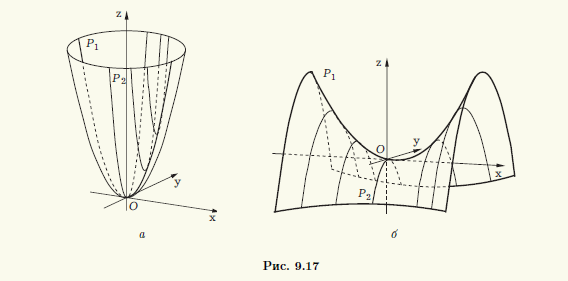
Тогда в результате такого перемещения и образуется эллиптический параболоид. При этом роли парабол Р₁ и Р₂ можно поменять, т. е. перемещать параболу Р₁ , используя параболу Р₂ как направляющую. #

Уравнение

x²/a² – y²/b² = 2z (9.13)

отличается от уравнения (9.8) эллиптического параболоида лишь знаком одного слагаемого и тоже задает поверхность второго порядка. Ее называют гиперболическим параболоидом, а само уравнение (9.13) — каноническим уравнением гиперболического параболоида.

Исследуем вид гиперболического параболоида методом сечений. Его пересечения с плоскостями у = с при любом значении с являются параболами:

x²/a² – c²/b² = 2z.

Пересечения с плоскостями x = с тоже при всех значениях с являются параболами:

c²/a² – y²/b² = 2z.

Обозначим через Р₁ параболу, находящуюся в сечении у = 0, а через Р₂ — аналогичную параболу в сечении x = 0. Перемещая, как и выше, параболу Р₂ по параболе Р₁ (см. рис. 9.17, б), получаем седлообразную поверхность гиперболического параболоида.

Пересечения гиперболического параболоида с плоскостями z = c при c ≠ 0 являются гипер-болами

x²/a² – y²/b² = 2c.

а при c = 0 — парой пересекающихся прямых

x²/a² – y²/b² = 0.

Выбор названия поверхности объясняется характером сечений: горизонтальные сечения гиперболического параболоида — это гиперболы, а два других семейства рассмотренных сечений — параболы.

Поверхности второго порядка: их виды, уравнения, примеры

Общее уравнение поверхности второго порядка и инварианты поворота и переноса декартовой прямоугольной системы координат

Общее уравнение поверхности второго порядка имеет вид

Для определения вида поверхности второго порядка по общему уравнению и приведения общего уравнения к каноническому, нам понадобятся выражения, которые называются инвариантами. Инварианты – это определители и суммы определителей, составленные из коэффициентов общего уравнения, которые не меняются при переносе и повороте системы координат. Эти инварианты следующие:

Следующие два выражения, называемые семиинвариантами, являются инвариантами поворота декартовой прямоугольной системы координат:

В случае, если I 3 = 0 , K 4 = 0 , семиинвариант K 3 будет также и инвариантом переноса; в случае же I 3 = 0 , K 4 = 0 , I 2 = 0 , K 3 = 0 семиинвариант K 2 = 0 будет также и инвариантом переноса.

Виды поверхностей второго порядка и приведение общего уравнения поверхности второго порядка к каноническому

I. Если I 3 ≠ 0 , то общее уравнение поверхности второго порядка при помощи поворота и переноса прямоугольной системы координат может быть приведено к следующему виду:

,

где λ 1 , λ 2 , λ 3 – корни характеристического уравнения

.

В зависимости от того, какие знаки у чисел λ 1 , λ 2 , λ 3 и K 4 /I 3 , определяется вид поверхности второго порядка.

Эллипсоид

Если числа λ 1 λ 2 , λ 3 одного знака, а K 4 /I 3 имеет знак им противоположный, то общее уравнение поверхности второго порядка определяет эллипсоид.

После решения характеристического уравнения общее уравнение можно переписать в следующем виде:

.

Тогда полуоси эллипсоида будут

, , .

Поэтому каноническое уравнение эллипсоида имеет вид

.

Мнимый эллипсоид

Если числа λ 1 λ 2 , λ 3 и K 4 /I 3 одного знака, то общее уравнение поверхности второго порядка определяет мнимый эллипсоид.

После решения характеристического уравнения общее уравнение можно привести к каноническому уравнению мнимого эллипсоида:

,

, , .

Мнимый конус

Если числа λ 1 λ 2 , λ 3 , а K 4 = 0 , то общее уравнение поверхности второго порядка определяет мнимый конус.

После решения характеристического уравнения общее уравнение можно привести к каноническому уравнению мнимого конуса:

,

, , .

Однополостный гиперболоид

Если два корня характеристического уравнения имеют один знак, а третий корень и K 4 /I 3 имеют знак, им противоположный, то общее уравнение поверхности второго порядка определяет однополостный гиперболоид.

Обозначая в этом случае через λ 1 и λ 2 корни характеристического уравнения, имеющие один знак, общее уравнение можно переписать в виде:

.

, , ,

то каноническое уравнение однополостного гиперболоида будет иметь вид

.

Двуполостный гиперболоид

Если два корня характеристического уравнения и K 4 /I 3 имеют один и тот же знак, а третий корень характеристического уравнения им противоположный, то общее уравнение поверхности второго порядка определяет двуполостный гиперболоид.

Обозначая в этом случае через λ 1 и λ 2 корни, имеющие один знак, общее уравнение можно переписать в виде:

.

Последняя запись и есть каноническое уравнение двуполостного гиперболоида.

Конус

Если два корня характеристического уравнения имеют один знак, третий корень имеет знак, им противоположный, а K 4 = 0 , то общее уравнение поверхности второго порядка определяет конус.

Считая, что одинаковый знак имеют корни λ 1 и λ 2 , общее уравнение можно переписать в виде:

,

известном как каноническое уравнение конуса.

II. Если I 3 = 0 , а K 4 ≠ 0 , то общее уравнение поверхности второго порядка при помощи поворота и переноса прямоугольной системы координат может быть приведено к следующему виду:

,

где λ 1 и λ 2 – отличные от нуля корни характеристического уравнения.

Эллиптический параболоид

Если λ 1 и λ 2 имеют один знак, то общее уравнение поверхности второго порядка определяет эллиптический параболоид.

Общее уравнение можно переписать в виде:

.

Выбирая перед корнем знак, противоположный знаку λ 1 и λ 2 , и полагая

,

,

получим каноническое уравнение эллиптического параболоида:

.

Гиперболический параболоид

Если λ 1 и λ 2 имеют разные знаки, то общее уравнение поверхности второго порядка определяет гиперболический параболоид.

Обозначая через λ 1 положительный корень, а через λ 2 – отрицательный и беря перед корнем знак минус, переписываем уравнение в виде:

.

, ,

получим каноническое уравнение гиперболического параболоида:

.

III. Если I 3 = 0 , а K 4 = 0 , I 2 ≠ 0 то общее уравнение поверхности второго порядка при помощи поворота и переноса прямоугольной системы координат может быть приведено к следующему виду:

,

где λ 1 и λ 2 – отличные от нуля корни характеристического уравнения.

Эллиптический цилиндр

Если λ 1 и λ 2 одного знака, а K 3 /I 2 имеет знак, им противоположный, то общее уравнение поверхности второго порядка определяет эллиптический цилиндр.

Переписываем уравнение, получившееся после решения характеристического уравнения, в виде:

.

, ,

получим каноническое уравнение эллиптического цилиндра:

.

Мнимый эллиптический цилиндр

Если λ 1 , λ 2 и K 3 /I 2 одного знака, то общее уравнение поверхности второго порядка определяет мнимый эллиптический цилиндр.

Переписываем уравнение, получившееся после решения характеристического уравнения, в виде:

.

Последняя запись – каноническое уравнение мнимого эллиптического цилиндра.

Мнимые пересекающиеся плоскости

Если λ 1 и λ 2 имеют один знак, а K 3 = 0 , то общее уравнение поверхности второго порядка определяет две мнимые пересекающиеся плоскости.

Переписываем уравнение, получившееся после решения характеристического уравнения, в виде:

.

, ,

получим каноническое уравнение мнимых пересекающихся плоскостей:

.

Гиперболический цилиндр

Если λ 1 и λ 2 имеют разные знаки, а K 3 ≠ 0 , то общее уравнение поверхности второго порядка определяет гиперболический цилиндр.

Переписываем уравнение, получившееся после решения характеристического уравнения, в виде:

,

, .

Таким образом, каноническое уравнение гиперболического цилиндра:

.

Пересекающиеся плоскости

Если λ 1 и λ 2 имеют разные знаки, а K 3 = 0 , то общее уравнение поверхности второго порядка определяет две пересекающиеся плоскости.

Переписываем уравнение, получившееся после решения характеристического уравнения, в виде:

,

, .

Таким образом, пересекающихся плоскостей:

.

IV. Если I 3 = 0 , K 4 = 0 , I 2 = 0 , K 3 ≠ 0 , то общее уравнение поверхности второго порядка при помощи поворота и переноса прямоугольной системы координат может быть приведено к следующему виду:

,

где λ 1 = I 1 – отличный от нуля корень характеристического уравнения.

Параболический цилиндр

Уравнение, получившееся после решения характеристического уравнения, можно переписать в виде:

,

.

Это уравнение параболического цилиндра, в каноническом виде оно записывается так:

.

V. Если I 3 = 0 , K 4 = 0 , I 2 = 0 , K 3 = 0 , то общее уравнение поверхности второго порядка при помощи поворота и переноса прямоугольной системы координат может быть приведено к следующему виду:

,

.

Параллельные плоскости

Если K 2 , то общее уравнение поверхности второго порядка определяет две параллельные плоскости.

,

перепишем его в виде

.

Мнимые параллельные плоскости

Если K 2 > 0 , то общее уравнение поверхности второго порядка определяет две мнимые параллельные плоскости.

,

перепишем его в виде

.

Совпадающие плоскости

Если K 2 = 0 , то общее уравнение поверхности второго порядка определяет две совпадающие плоскости:

.

Решение примеров на определение вида поверхности второго порядка

Пример 1. Определить вид и составить каноническое уравнение поверхности, заданной относительно прямоугольной системы координат общим уравнением

Решение. Найдём I 3 :

(как вычислить определитель).

I 1 = 1 + 5 + 1 = 7 ,

Следовательно, данная поверхность – однополостный гиперболоид.

.

Составляем и решаем характеристическое уравнение:

;

.

,

, , .

Пример 2. Определить вид и составить каноническое уравнение поверхности, заданной относительно прямоугольной системы координат общим уравнением

Решение. Найдём I 3 :

.

.

Следовательно, общее уравнение определяет эллиптический параболоид.

.

I 1 = 2 + 2 + 3 = 7 .

Решаем характеристическое уравнение:

.

.

,

, .

Пример 3. Определить вид и составить каноническое уравнение поверхности, заданной относительно прямоугольной системы координат общим уравнением

,

,

,

I 1 = 5 + 2 + 5 = 12 .

Так как I 3 = К 4 = 0 , I 2 > 0 , I 1 K 3 , то данное общее уравнение определяет эллиптический цилиндр.

.

.

Определить вид поверхности второго порядка самостоятельно, а затем посмотреть решение

Пример 4. Определить вид и составить каноническое уравнение поверхности, заданной относительно прямоугольной системы координат общим уравнением

Как находить уравнения сечения поверхностей

Глава 46. Поверхности второго порядка

Эллипсоидом называется поверхность, которая в некоторой системе декартовых прямоугольных координат определяется уравнением

(1).

Уравнение (1) называется каноническим уравнением эллипсоида. Величины a, b, c суть полуоси эллипсоида (рис. 1). Если все они различны, эллипсоид называется трехосным; в случае, когда какие-нибудь две из них одинаковы, эллипсоид называется вытянутым, при a=b>c – сжатым. В случае, когда a=b=c , эллипсоид представляет собой сферу.

Гиперболоидами называются поверхности, которые в некоторой системе декартовых прямоугольных координат определяются уравнениями

, (2)

. (3)

Гиперболоид, определяемый уравнением (2), называется однополостным (рис. 2); гиперболоид, определяемый уравнением (3), – двуполостным (рис. 3); уравнения (2) и (3) называются каноническими уравнениями соответствующих гиперболоидов. Величины a, b, c называются полуосями гиперболоида. В случае однополостного гиперболоида, заданного уравнением (2), только первые из них (а и b ) показаны на рис. 2. В случае двуполостного гиперболоида, заданного уравнением (3), одна из них (именно, с) показана на рис. 3. Гиперболоиды, определяемые уравнениями (2) и (3), при a=b являются поверхностями вращения.

Параболоидами называются поверхности, которые в некоторой системе декартовых прямоугольных координат определяются уравнениями

, (4)

, (5)

где p и q – положительные числа, называемые параметрами параболоида. Параболоид, определяемый уравнением (4), называется эллиптическим (рис. 4); параболоид, определяемый уравнением (5), – гиперболическим (рис. 5). Уравнения (4) и (5) называют каноническими уравнениями соответствующих параболоидов. В случае, когда p=q , параболоид, определяемый уравнением (4), является поверхностью вращения (вокруг Oz).

Рассмотрим теперь преобразование пространства, которое называется равномерным сжатием (или равномерным растяжением).

Выберем какую-нибудь плоскость; обозначим ее буквой . Зададим, кроме того, некоторое положительное число q . Пусть М – произвольная точка пространства, не лежащая на плоскости , – основание перпендикуляра, опущенного на плоскость из точки М. Переместим точку М по прямой в новое положение так, чтобы имело место равенство

и чтобы после перемещения точка осталась с той же стороны от плоскости , где она была первоначально (рис. 6). Точно так же мы поступим со всеми точками пространства, не лежащими на плоскости ; точки, которые расположены на плоскости , оставим на своих местах. Таким образом, все точки пространства, за исключением тех, что лежат на плоскости , переместятся; при этом расстояние от каждой точки до плоскости изменится в некоторое определенное число раз, общее для всех точек. Описываемое сейчас перемещение точек пространства называется его равномерным сжатием к плоскости ; число q носит название коэффициента сжатия.

Пусть дана некоторая поверхность F ; при равномерном сжатии пространства точки, которые ее составляют, переместятся и в новых положениях сотавят поверхность F ’. Будем говорить, что поверхность F ’ получено из F в результате равномерного сжатия пространства. Оказывается, что многие поверхности второго порядка (все, кроме гиперболического параболоида) можно получить в результате равномерного сжатия из поверхностей вращения).

ПРИМЕР. Доказать, что произвольный трехосный эллипсоид

может быть получен из сферы

в результате двух последовательных равномерных сжатий пространства к координатным плоскостям: к плоскости Oxy с коэффициентом сжатия и к плоскости Oxz с коэффициентом сжатия .

ДОКАЗАТЕЛЬСТВО. Пусть производится равномерное сжатие пространства к плоскости Oxy с коэффициентом и пусть – точка, в которую переходит при этом точка . Выразим координаты x’, y’, z ’ точки М’ через координаты x, y, z точки М. Так как прямая MM ’ перпендикулярна к плоскости Oxy , то x’=x, y’=y . С другой стороны, так как расстояние от точки М’ до плоскости Oxy равно расстоянию от точки М до этой плоскости, умноженному на число , то .

Таким образом, мы получаем искомые выражения:

, , (6)

, , (7)

Предположим, что M(x; y; z ) – произвольная точка сферы

.

Заменим здесь x, y, z их выражениями (7); получим

,

.

Следовательно, точка M’(x’; y’; z ’) лежит на эллипсоиде вращения. Аналогично, мы должны осуществить сжатие пространства к плоскости Oxz по формулам

, , ;

тогда получим трехосный эллипсоид и именно тот, уравнение которого дано в условии задачи.

Отметим еще, что однополостный гиперболоид и гиперболический параболоид суть линейчатые поверхности, то есть они состоят из прямых; эти прямые называются прямолинейными образующими указанных поверхностей.

имеет две системы прямолинейных образующих, которые определяются уравнениями:

, ;

, ,

где и – некоторые числа, не равные одновременно нулю. Гиперболический параболоид

также имеет две системы прямолинейных образующих, которые определяются уравнениями

, ;

, .

Конической поверхностью, или конусом, называется поверхность, которая описывается движущейся прямой (образующей) при условии, что эта прямая проходит через постоянную точку S и пересекает некоторую определенную линию L . Точка S называется вершиной конуса; линия L – направляющей.

Цилиндрической поверхностью, или цилиндром, называется поверхность, которая описывается движущейся прямой (образующей) при услвоии, что эта прямая имеет постоянное направление и пересекает некоторую определенную линию L (направляющую).

Как находить уравнения сечения поверхностей

С помощью векторов мы ввели понятие пространства и его размерности, в частности трехмерного. Рассмотрим в нем поверхности, которые “похожи” на поверхности, образованные вращением кривой второго порядка вокруг ее оси симметрии. Например, сфера может быть получена вращением окружности вокруг диаметра. Поверхность, описываемая некоторой линией, вращающейся вокруг неподвижной прямой d, называется поверхностью вращения с осью вращения d. Наряду с такими поверхностями мы встретимся и с более сложными случаями.

Пусть в пространстве задана прямоугольная декартова система координат.

Поверхность второго порядка – геометрическое место точек, декартовы прямоугольные координаты которых, удовлетворяют уравнению вида

в котором хотя бы один из коэффициентов отличен от нуля. Уравнение (2.48) называется общим уравнением поверхности второго порядка.

Уравнение (2.48) может и не определять действительного геометрического образа, но для сохранения общности в таких случаях говорят, что оно определяет мнимую поверхность второго порядка. В зависимости от значений коэффициентов общего уравнения (2.48) оно может быть преобразовано с помощью параллельного переноса и поворота системы координат к одному из канонических видов, каждому из которых соответствует определённый класс поверхностей второго порядка. Среди них выделяют пять основных классов поверхностей: эллипсоиды, гиперболоиды, параболоиды, конусы и цилиндры. Для каждой из этих поверхностей существует декартова прямоугольная система координат, в которой поверхность задается простым уравнением, называемым каноническим уравнением.

Перечисленные поверхности второго порядка относятся к так называемым нераспадающимся поверхностям второго порядка. Можно говорить о случаях вырождения – распадающихся поверхностях второго порядка, к которым относятся: пары пересекающихся плоскостей, пары мнимых пересекающихся плоскостей, пары параллельных плоскостей, пары мнимых параллельных плоскостей, пары совпадающих плоскостей.

Наша цель – указать канонические уравнения для поверхностей второго порядка и показать, как выглядят эти поверхности.

Поверхность, задаваемая в некоторой прямоугольной декартовой системе координат уравнением

называется эллипсоидом (рис. 2.22) .

1. Эллипсоид – ограниченная поверхность, поскольку из его уравнения следует, что .

2. Эллипсоид обладает

· центральной симметрией относительно начала координат,

· осевой симметрией относительно координатных осей,

· плоскостной симметрией относительно начала координат.

3. В сечении эллипсоида плоскостью, перпендикулярной любой из координатных осей, получается эллипс (см. рис. 2.22).

Так же, как для эллипса, точки пересечения эллипсоида с координатными осями называются вершинами эллипсоида, центр симметрии – центром эллипсоида. Числа а, b , с называются полуосями. Если полуоси попарно различны, то эллипсоид называется трехосным.

Если две полуоси равны друг другу, то эллипсоид называется эллипсоидом вращения. Эллипсоид вращения может быть получен вращением эллипса вокруг одной из осей.

Примечание. Сфера является частным случаем эллипсоида при а= b =с. Тогда все равные полуоси обозначают R и уравнение (2.49) после умножения на R 2 принимает вид .

Поверхность, задаваемая в некоторой прямоугольной декартовой системе координат уравнением

называется эллиптическим параболоидом (рис. 2.23) .

1. Эллиптический параболоид – неограниченная поверхность, поскольку из его уравнения следует, что z ≥ 0 и принимает сколь угодно большие значения.

2. Эллиптический параболоид обладает

· осевой симметрией относительно оси 0z ,

· плоскостной симметрией относительно координатных осей 0xz и 0yz .

3. В сечении эллиптического параболоида плоскостью, ортогональной оси 0z , получается эллипс, а плоскостями, ортогональными осям 0x и 0y –парабола. (см. рис. 2.23).

Можно получить эллиптический параболоид симметричный относительно оси 0х или 0у, для чего нужно в уравнении (2.50) поменять между собой переменные х и z или у и z соответственно.

Если полуоси равны a = b , то параболоид называется параболоидом вращения и может быть получен вращением параболы вокруг ее оси симметрии. При этом в сечении параболоида вращения плоскостью, перпендикулярной оси 0z , получается окружность.

Поверхность, задаваемая в некоторой прямоугольной декартовой системе координат уравнением

называется гиперболическим параболоидом (рис . 2.24).

Свойства гиперболического параболоида.

1. Гиперболический параболоид – неограниченная поверхность, поскольку из его уравнения следует, что z – любое число.

2. Гиперболический параболоид обладает

· осевой симметрией относительно оси 0z ,

· плоскостной симметрией относительно координатных плоскостей 0xz и 0yz .

4. Гиперболический параболоид может быть получен поступательным перемещением в пространстве параболы так, что ее вершина перемещается вдоль другой параболы, ось которой параллельна оси первой параболы, а ветви направлены противоположно, причем их плоскости взаимно перпендикулярны.

5. Поверхность, задаваемая в некоторой прямоугольной декартовой системе координат уравнением

называется однополостным гиперболоидом (рис. 2.25) .

Свойства однополостного гиперболоида.

1. Однополостный гиперболоид – неограниченная поверхность, поскольку из его уравнения следует, что z – любое число.

2. Однополостный гиперболоид обладает

· центральной симметрией относительно начала координат,

· осевой симметрией относительно всех координатных осей,

· плоскостной симметрией относительно всех координатных плоскостей.

3. В сечении однополостного гиперболоида плоскостью, перпендикулярной оси координат 0z , получается эллипс, а плоскостями, ортогональными осям 0x и 0y, – гипербола (см. рис. 2.25).

Если в уравнении (2.52) a = b , то сечения однополостного гиперболоида плоскостями, параллельными плоскости х0у, являются окружностями. В этом случае поверхность называется однополостным гиперболоидом вращения.

Поверхность, задаваемая в некоторой прямоугольной декартовой системе координат уравнением

называется двуполостным гиперболоидом (рис. 2.26) .

1. Двуполостный гиперболоид – неограниченная поверхность, поскольку из его уравнения следует, что | z |≥ c и неограничен сверху.

2. Двуполостный гиперболоид обладает

· центральной симметрией относительно начала координат,

· осевой симметрией относительно всех координатных осей,

· плоскостной симметрией относительно всех координатных плоскостей.

3. В сечении однополостного гиперболоида плоскостью, перпендикулярной оси координат 0z , при | z |> c получается эллипс, при | z |= c – точка, а в сечении плоскостями, перпендику­лярными осям 0x и 0y , – гипербола (см. рис. 2.26).

Если в уравнении (2.53) a = b , то сечения двуполостного гиперболоида плоскостями, параллельными плоскости х0у, являются окружностями. В этом случае поверхность называется двуполостным гиперболоидом вращения.

Примечание. Если уравнение поверхности в прямоугольной системе координат имеет вид: F ( x 2 + y 2 ; z )=0, то эта поверхность – поверхность вращения с осью вращения 0z. Аналогично: F ( x 2 + z 2 ; y )=0 – поверхность вращения с осью вращения 0у, F ( z 2 + y 2 ; x )=0 – с осью вращения 0х

С учетом данного примечания могут быть записаны уравнения для рассмотренных выше поверхностей вращения, если осью вращения являются оси 0х или 0у.

Цилиндрическая поверхность образуется движением прямой линии, скользящей по некоторой неподвижной замкнутой или незамкнутой кривой и остающейся параллельной своему исходному положению. Множество прямолинейных образующих представляет собой непрерывный каркас цилиндрической поверхности. Через каждую точку поверхности проходит одна прямолинейная образующая. Неподвижная кривая, по которой скользит образующая, называется направляющей. Если направляющая линия является кривой второго порядка, то и цилиндрическая поверхность – второго порядка.

Если уравнение поверхности не содержит в явном виде какой–либо переменной, то это уравнение определяет в пространстве цилиндрическую поверхность с образующими, параллельными оси отсутствующего переменного и направляющей, которая в плоскости двух других переменных имеет то же самое уравнение.

Достаточно нарисовать на плоскости х0у направляющую, уравнение которой на этой плоскости совпадает с уравнением самой поверхности, и затем через точки направляющей провести образующие параллельно оси 0z. Для наглядности следует построить также одно–два сечения плоскостями, параллельными плоскости х0у. В каждом таком сечении получим такую же кривую, как и исходная направляющая. Аналогично поступают, рассматривая направляющую в плоскости х0z или у0z.

Цилиндрическая поверхность является бесконечной в направлении своих образующих. Часть замкнутой цилиндрической поверхности, заключенная между двумя плоскими параллельными сечениями, называется цилиндром, а фигуры сечения – его основаниями. Сечение цилиндрической поверхности плоскостью, перпендикулярной ее образующим, называется нормальным. В зависимости от формы нормального сечения цилиндры бывают:

1) эллиптические – нормальное сечение представляет собой эллипс (рис. 2.27а), каноническое уравнение

2) круговые – нормальное сечение круг, при a = b = r уравнение

3) гиперболические – нормальное сечение гипербола (рис. 2.27б), каноническое уравнение

4) параболические – нормальное сечение парабола (рис. 2.27в), каноническое уравнение

5) общего вида – нормальное сечение кривая случайного вида.

Если за основание цилиндра принимается его нормальное сечение, цилиндр называют прямым (рис. 2.27). Если за основание цилиндра принимается одно из косых сечений, цилиндр называют наклонным. Например, наклонные сечения прямого кругового цилиндра являются эллипсами. Наклонные сечения прямого эллиптического цилиндра в общем случае – эллипсы. Однако его всегда можно пересечь плоскостью, наклонной к его образующим, таким образом, что в сечении получится круг.

Конической поверхностью называется поверхность, производимая движением прямой, перемещающейся в пространстве так, что она при этом постоянно проходит через неподвижную точку и пересекает данную линию. Данная прямая называется образующей, линия – направляющей, а точка – вершиной конической поверхности (рис. 2.28).

Конусом называется тело, ограниченное частью конической поверхности, расположенной по одну сторону от вершины, и плоскостью, пересекающей все образующие по ту же сторону от вершины. Часть конической поверхности, ограниченная этой плоскостью, называется боковой поверхностью, а часть плоскости, отсекаемая боковой поверхностью, – основанием конуса. Перпендикуляр, опущенный из вершины на плоскость основания, называется высотой конуса.

Конус называется прямым круговым, если его основание есть круг, а высота проходит через центр основания. Такой конус можно рассматривать как тело, происходящее от вращения прямоугольного треугольника, вокруг катета как оси. При этом гипотенуза описывает боковую поверхность, а катет – основание конуса.

В курсе геометрии общеобразовательной школы рассматривается только прямой круговой конус, который для краткости называется просто конусом.

Если вершина конуса расположена в начале координат, направляющая кривая — эллипс с полуосями а и b, плоскость которого находится на расстоянии с от начала координат, то уравнение эллиптического конуса имеет вид:

( a >0, b >0, c >0). (2.58)

При а = b конус становится круговым.

Примечание. По аналогии с коническими сечениями (аналогично теореме 2.1) существуют и вырожденные поверхности второго порядка. Так, уравнением второго порядка x 2 = 0 описывается пара совпадающих плоскостей, уравнением x 2 = 1 – пара параллельных плоскостей, уравнением x 2 – y 2 = 0 – пара пересекающихся плоскостей. Уравнение x 2 + y 2 + z 2 = 0 описывает точку с координатами (0;0;0). Существуют и другие вырожденные случаи. Полная теория поверхностей второго порядка рассматривается в курсе аналитической геометрии

[spoiler title=”источники:”]

http://a-geometry.narod.ru/problems/problems_46.htm

http://www.sites.google.com/site/vyssaamatem/kupit-ucastok/ii-10-poverhnosti-vtorogo-poradka

[/spoiler]

Исследование поверхностей второго порядка

(методом сечений)

Эллипсоид

— поверхность второго порядка, которая в некоторой декартовой системе координат задается уравнением вида = 1 (*) (где a > 0, b > 0, c > 0).

Уравнение (*) называется каноническим уравнением эллипсоида, и именно по этому уравнению мы будем исследовать форму эллипсоида.

1) По уравнению (*) видно, что эллипсоид симметричен относительно координатных плоскостей, координатных осей и начала координат.

Действительно, если точка M(x,y,z) принадлежит эллипсоиду, то есть ее координаты удовлетворяют уравнению (*), то и точки M₁(-x,y,z), M₂(x,-y,z), M₃(x,y,-z), M₄(-x,-y,z), M₅(-x,y,-z), M₆(x,-y,-z) и M₇(-x,-y,-z) принадлежат эллипсоиду, так как их координаты удовлетворяют уравнению (*).

2) По уравнению (*) видно, что для координат точек эллипсоида справедливы неравенства: | x | £ a, | y | £ b, | z | £ c, то есть эллипсоид рассоложен внутри прямоугольного параллелепипеда, заданного системой неравенств .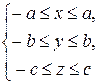

3) Сечения плоскостями z = z₀.

Согласно пунктам 1,2 достаточно рассмотреть случай 0 £ z₀ £ c.

z = 0 (плоскость (xOy)):

— эллипс с полуосями a и b;

z = c (плоскость параллельная плоскости (xOy)):

— точка с координатами (0,0,c);

z = z₀ , 0 0, l 2 = ) —

— эллипс с полуосями la и lb.

При этом, чем ближе значение z₀ к c, тем ближе l к нулю, то есть тем меньше полуоси la и lb эллипса, который мы получаем в сечении.

4) Сечения плоскостями x = x₀.

Согласно пунктам 1,2 достаточно рассмотреть случай 0 £ x₀ £ a.

x = 0 (плоскость (yOz)):

— эллипс с полуосями b и с;

x = a (плоскость параллельная плоскости (yOz)):

— точка с координатами (a,0,0);

x = x₀ , 0 0, l 2 = ) —

— эллипс с полуосями lb и lc.

При этом, чем ближе значение x₀ к a, тем ближе l к нулю, то есть тем меньше полуоси lb и lc эллипса, который мы получаем в сечении.

5) Сечения плоскостями y = y₀.

Согласно пунктам 1,2 достаточно рассмотреть случай 0 £ y₀ £ b.

y = 0 (плоскость (xOz)):

— эллипс с полуосями a и с;

y = b (плоскость параллельная плоскости (xOz)):

— точка с координатами (0,b,0);

y = y₀ , 0 0, l 2 = ) —

— эллипс с полуосями la и lc.

При этом, чем ближе значение y₀ к b, тем ближе l к нулю, то есть тем меньше полуоси la и lc эллипса, который мы получаем в сечении.

Замечания.

1) При a = b = c эллипсоид — это сфера с центром в начале координат и радиусом a.

2) При a = с эллипсоид является эллипсоидом вращения, получается вращением эллипса 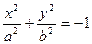, лежащего в плоскости (xOy), вокруг оси (Oy).

Случаи a = b, b = c аналогичны.

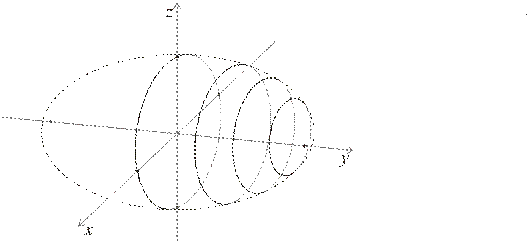
Эллиптический цилиндр

— поверхность второго порядка, которая в некоторой декартовой системе координат задается уравнением вида (**) (где a > 0, b > 0).

1) По уравнению (**) видно, что эллиптический цилиндр симметричен относительно координатных плоскостей, координатных осей и начала координат.

2) По уравнению (**) видно, что для координат точек эллиптического цилиндра справедливы неравенства: | x | £ a, | y | £ b.

3) Сечения плоскостями z = z₀ (z₀ — константа).

Согласно пунктам 1,2 достаточно рассмотреть случай z₀ ³ 0.

(плоскость (xOy) или плоскость параллельная плоскости (xOy)):

— эллипс с полуосями a и b.

То есть во всех плоскостях параллельных плоскости (xOy) и в самой плоскости (xOy) сечением эллиптического цилиндра являются равные эллипсы с полуосями a и b, центры которых лежат на оси (Oz).

4) Сечения плоскостями x = x₀ (x₀ — константа).

Согласно пунктам 1,2 достаточно рассмотреть случай 0 £ x₀ £ a.

x = 0 (плоскость (yOz)):

Û — две параллельные прямые;

x = a (плоскость параллельная плоскости (yOz)):

Û — прямая;

x = x₀ , 0 0, l 2 = ) — две параллельные прямые.

Заметим, что в сечении мы получаем прямые параллельные оси (Oz), то есть все эти прямые попарно параллельны (принадлежат одному параллельному пучку).

5) Сечения плоскостями y = y₀ (случай аналогичен предыдущему).

РИС. 51 эллиптический цилиндр

Замечания.

1) При a = b эллиптический цилиндр является эллиптическим цилиндром вращения, получается вращением прямой, лежащей в плоскости (yOz) и параллельной оси (Oz), вокруг оси (Oz).

2) Сечения плоскостями x = const и y = const — прямые из одного параллельного пучка, эти прямые называют прямолинейные образующими эллиптического цилиндра.

Гиперболический цилиндр

— поверхность второго порядка, которая в некоторой декартовой системе координат задается уравнением вида 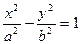(***) (где a > 0, b > 0).

1) По уравнению (***) видно, что гиперболический цилиндр симметричен относительно координатных плоскостей, координатных осей и начала координат.

2) По уравнению (***) видно, что для координат точек гиперболического цилиндра справедливы неравенства: | x | ³ a.

3) Сечения плоскостями z = z₀ (z₀ — константа).

Согласно пунктам 1,2 достаточно рассмотреть случай z₀ ³ 0.

(плоскость (xOy) или плоскость параллельная плоскости (xOy)):

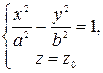— гипербола с действительной полуосью a и мнимой полуосью b.

То есть во всех плоскостях параллельных плоскости (xOy) и в самой плоскости (xOy) сечением гиперболического цилиндра являются равные гиперболы.

4) Сечения плоскостями x = x₀ (x₀ — константа).

Согласно пунктам 1,2 достаточно рассмотреть случай x₀ ³ a.

x = a (плоскость параллельная плоскости (yOz)):

Û — прямая;

x = x₀ , x₀ > a (плоскость параллельная плоскости (yOz)):

Û (где l > 0, l 2 = ) — две параллельные прямые.

Заметим, что в сечении мы получаем прямые параллельные оси (Oz), то есть все эти прямые попарно параллельны (принадлежат одному параллельному пучку).

5) Сечения плоскостями y = y₀ (y₀ — константа).

Согласно пунктам 1,2 достаточно рассмотреть случай y₀ ³ 0.

y = 0 (плоскость (xOz)):

Û — две параллельные прямые;

y = y₀ , (плоскость параллельная плоскости (xOz)):

Û (где l > 0, l 2 = ) — две параллельные прямые.

Заметим, что в сечении мы получаем прямые параллельные оси (Oz), то есть все эти прямые попарно параллельны (принадлежат одному параллельному пучку).

РИС. 52 гиперболический цилиндр

Замечание.

Сечения плоскостями x = const и y = const — прямые из одного параллельного пучка, эти прямые называют прямолинейные образующими гиперболического цилиндра.

Параболический цилиндр

— поверхность второго порядка, которая в некоторой декартовой системе координат задается уравнением вида 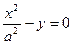(***) (где a > 0).

1) По уравнению (***) видно, что параболический цилиндр симметричен относительно координатной плоскости (yOz) и координатной оси (Oy).

2) По уравнению (***) видно, что для координат точек параболического цилиндра справедливо неравенство: y ³ 0, то есть параболический цилиндр расположен не левее плоскости (xOz).

3) Сечения плоскостями z = z₀ (z₀ — константа).

Согласно пунктам 1,2 достаточно рассмотреть случай z₀ ³ 0.

(плоскость (xOy) или плоскость параллельная плоскости (xOy)):

— парабола.

То есть во всех плоскостях параллельных плоскости (xOy) и в самой плоскости (xOy) сечением параболического цилиндра являются равные параболы, вершины которых лежат на оси (Oz).

4) Сечения плоскостями x = x₀ (x₀ — константа).

Согласно пунктам 1,2 достаточно рассмотреть случай x₀ ³ 0.

x = 0 (плоскость (yOz)):

— прямая — ось (Oz);

x = x₀ (плоскость параллельная плоскости (yOz)):

— прямая параллельная оси (Oz)/

5) Сечения плоскостями y = y₀ (y₀ — константа).

Согласно пункту 2 достаточно рассмотреть случай y₀ ³ 0.

y = 0 (плоскость (xOz)):

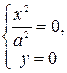Û — прямая — ось (Oz);

y = y₀ , y₀ > 0 (плоскость параллельная плоскости (xOz)):

Û — две прямые, параллельные оси (Oz).

РИС. 53 параболический цилиндр

Замечание.

Сечения плоскостями x = const и y = const — прямые из одного параллельного пучка, эти прямые называют прямолинейные образующими параболического цилиндра.

Конус

— поверхность второго порядка, которая в некоторой декартовой системе координат задается уравнением вида = 0 (ð) (где a > 0, b > 0, c > 0).

Уравнение (ð) называется каноническим уравнением конуса.

1) По уравнению (ð) видно, что конус симметричен относительно координатных плоскостей, координатных осей и начала координат.

2) Сечения плоскостями z = z₀ (z₀— константа).

Согласно пункту 1 достаточно рассмотреть случай z₀ ³ 0.

z = 0 (плоскость (xOy)):

— точка (0,0,0) — начало координат;

z = z₀ , z₀ > 0(плоскость параллельная плоскости (xOy)):

Û (где l > 0, l 2 = ) — эллипс с полуосями la и lb.

При этом чем больше значение z₀, тем больше значение l, то есть тем больше полуоси la и lb эллипса, который мы получаем в сечении.

3) Сечения плоскостями x = x₀ (x₀— константа)..

Согласно пункту 1 достаточно рассмотреть случай x₀ ³ 0.

x = 0 (плоскость (yOz)):

— две пересекающиеся в начале координат прямые y = в плоскости (yOz);

x = x₀ , x₀ > 0 (плоскость параллельная плоскости (yOz)):

Û (где l > 0, l 2 = ) — гипербола с действительной полуосью lb и мнимой полуосью lc (асимптоты гиперболы — это прямые z = y в плоскости x = x₀).

При этом, чем больше значение x₀, тем больше значение l, то есть тем больше полуоси lb и lc гиперболы, тем дальше вершины гиперболы друг от друга.

4) Сечения плоскостями y = y₀ (случай аналогичен п. 3, рассмотреть самостоятельно)

Замечания.

1) При a = b конус является конусом вращения (сечения, рассмотренные в п 2, будут окружностями), и получается вращением прямой y = z, лежащей в плоскости (yOz), вокруг оси (Oz).

2) Через каждую точку конуса проходит ровно одна прямая, которая лежит на конусе (докажите самостоятельно) Прямую, лежащую на конусе, называют прямолинейной образующей конуса.

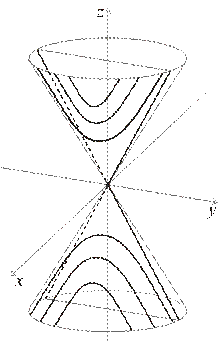
Однополостный гиперболоид

— поверхность второго порядка, которая в некоторой декартовой системе координат задается уравнением вида = 1 (ðð) (где a > 0, b > 0, c > 0).

1) По уравнению (ðð) видно, что однополостный гиперболоид симметричен относительно координатных плоскостей, координатных осей и начала координат.

2) Сечения плоскостями z = z₀ (z₀— константа).

Согласно пункту 1 достаточно рассмотреть случай z₀ ³ 0.

z = 0 (плоскость (xOy)):

— эллипс с полуосями a и b;

z = z₀ , z₀ > 0(плоскость параллельная плоскости (xOy)):

Û (где l > 0, l 2 = 1 + ) — эллипс с полуосями la и lb.

При этом чем больше значение z₀, тем больше значение l, то есть тем больше полуоси la и lb эллипса, который мы получаем в сечении.

Итак, в сечении однополостного гиперболоида плоскостями параллельными плоскости (xOy) или самой плоскостью (xOy) мы получаем эллипсы, при этом в сечении плоскостью (xOy) получаем эллипс с наименьшими полуосями, этот эллипс будем называть горловым эллипсом однополостного гиперболоида.

3) Сечения плоскостями x = x₀ (x₀— константа)..

Согласно пункту 1 достаточно рассмотреть случай x₀ ³ 0.

x = 0 (плоскость (yOz)):

— гипербола с действительной полуосью b и мнимой полуосью c (асимптоты гиперболы — это прямые z = y в плоскости (yOz));

x = x₀ , 0 0, l 2 = 1 — ) — гипербола с действительной полуосью lb и мнимой полуосью lc (асимптоты гиперболы — это прямые z = y в плоскости x = x₀).

При этом, чем ближе значение x₀ к a, тем меньше значение l, то есть тем меньше полуоси lb и lc гиперболы, тем ближе вершины гиперболы друг к другу.

x₀ = a(плоскость параллельная плоскости (yOz)):

— две пересекающиеся в точке (a,0,0) прямые z = y в плоскости x = a.

x = x₀ , x₀ > a (плоскость параллельная плоскости (yOz)):

Û (где l > 0, l 2 = — 1) — гипербола с действительной полуосью lc и мнимой полуосью lb (асимптоты гиперболы — это прямые z = y в плоскости x = x₀).

При этом, чем больше значение x₀, тем больше значение l, то есть тем больше полуоси lc и lb гиперболы, тем дальше вершины гиперболы друг от друга.

4) Сечения плоскостями y = y₀ (случай аналогичен п. 3, рассмотреть самостоятельно)

РИС. 57 однополостный гиперболоид

Замечание.

При a = b однополостный гиперболоид является гиперболоидом вращения, получается вращением гиперболы , лежащей в плоскости (yOz), вокруг оси (Oz).

Двуполостный гиперболоид

— поверхность второго порядка, которая в некоторой декартовой системе координат задается уравнением вида = -1 (ððð) (где a > 0, b > 0, c > 0).

1) По уравнению (ððð) видно, что двуполостный гиперболоид симметричен относительно координатных плоскостей, координатных осей и начала координат.

2) По уравнению (ððð) видно, что для координат точек двуполостного гиперболоида справедливо неравенство | z | ³ c.

3) Сечения плоскостями z = z₀ (z₀— константа).

Согласно пунктам 1 и 2 достаточно рассмотреть случай z₀ ³ c.

z = c (плоскость параллельная плоскости (xOy)):

— точка на оси (Oz) с координатами (0,0,c);

z = z₀ , z₀ > c (плоскость параллельная плоскости (xOy)):

Û (где l > 0, l 2 = — 1) — эллипс с полуосями la и lb.

При этом чем больше значение z₀, тем больше значение l, то есть тем больше полуоси la и lb эллипса, который мы получаем в сечении.

4) Сечения плоскостями x = x₀ (x₀ — константа)..

Согласно пункту 1 достаточно рассмотреть случай x₀ ³ 0.

x = 0 (плоскость (yOz)):

— гипербола с действительной полуосью c и мнимой полуосью b (асимптоты гиперболы — это прямые z = y в плоскости (yOz));

x = x₀ , x₀ > 0 (плоскость параллельная плоскости (yOz)):

Û (где l > 0, l 2 = 1+ ) — гипербола с действительной полуосью lc и мнимой полуосью lb (асимптоты гиперболы — это прямые z = y в плоскости x = x₀).

При этом, чем больше значение x₀, тем больше значение l, то есть тем больше полуоси lc и lb гиперболы, тем дальше вершины гиперболы друг от друга.

5) Сечения плоскостями y = y₀ (случай аналогичен п. 4, рассмотреть самостоятельно)

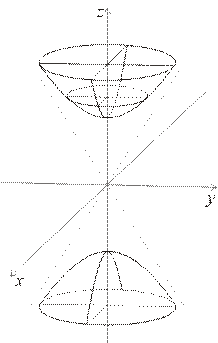
РИС. 58 двуполостный гиперболоид

Замечание.

При a = b двуполостный гиперболоид является гиперболоидом вращения, получается вращением гиперболы , лежащей в плоскости (yOz), вокруг оси (Oz).

Введем следующее обозначение: F(x,y,z) = . Тогда уравнения F(x,y,z) = 0, F(x,y,z) = 1, F(x,y,z) = — 1 задают (соответственно) конус, однополостный и двуполостный гиперболоиды. При этом при достаточно больших по модулю значениях переменных x и y, значения переменных z для точек, лежащих на конусе и гиперболоидах, отличаются мало (Пусть M(x,y,z) — точка на конусе, M’(x,y,z’) — точка на однополостном гиперболоиде, M’’(x,y,z’’) — точка на двуполостном гиперболоиде, тогда при x ® ¥, y ® ¥ |z — z’| ® 0 и | z — z’’| ® 0). Конус, который задается уравнением F(x,y,z) = 0, будем называть асимптотическим для гиперболоидов, которые задаются уравнениями F(x,y,z) = ± 1.

рис.59 гиперболоиды и асимптотический конус

Эллиптический параболоид

— поверхность второго порядка, которая в некоторой декартовой системе координат задается уравнением вида 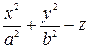= 0 (°) (где a > 0, b > 0).

Уравнение (°) называется каноническим уравнением эллиптического параболоида.

1) По уравнению (°) видно, что эллиптический параболоид симметричен относительно координатных плоскостей (xOz) и (yOz) и координатной оси (Oz).

2) По уравнению (°) видно, что для координат точек эллиптического параболоида справедливо неравенство z ³ 0, то есть эллиптический параболоид весь расположен по одну сторону от плоскости (xOy).

3) Сечения плоскостями z = z₀, z₀ ³ 0.

z = 0 (плоскость (xOy)):

— точка (0,0,0) — начало координат;

z = z₀ , z₀ > 0(плоскость параллельная плоскости (xOy)):

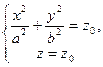Û (где l > 0, l 2 = z₀) — эллипс с полуосями la и lb.

При этом чем больше значение z₀, тем больше значение l, то есть тем больше полуоси la и lb эллипса, который мы получаем в сечении.

4) Сечения плоскостями x = x₀ (x₀— константа)..

Согласно пункту 1 достаточно рассмотреть случай x₀ ³ 0.

x = 0 (плоскость (yOz)):

— парабола с вершиной в начале координат, ветви которой направлены «вверх» (относительно положительной полуоси (Oz));

x = x₀ , x₀ > 0 (плоскость параллельная плоскости (yOz)):

— парабола с вершиной в точке , ветви которой направлены «вверх» (относительно положительной полуоси (Oz)).

Заметим, что от значения x₀, не зависит форма параболы, в сечении плоскостями параллельными плоскости (yOz) мы получаем равные параболы, вершины которых с ростом значения x₀ смещаются вверх вдоль оси (Oz).

5) Сечения плоскостями y = y₀ (случай аналогичен п. 4, рассмотреть самостоятельно)

РИС. 60 эллиптический параболоид

Замечание.

При a = b конус является конусом вращения (сечения, рассмотренные в п. 3, будут окружностями), и получается вращением параболы вокруг свое оси (вокруг оси (Oz)).

Исследовать методом сечений поверхность заданную уравнением

8.4. Построение поверхностей

Мы приступаем к изучению формы поверхностей второго порядка, определённых в предыдущем разделе своими каноническими уравнениями. Напомним, что это вторая из двух основных задач аналитической геометрии: зная уравнение поверхности, изучить её геометрические свойства.

Метод, который мы будем применять, называется методом сечений: пересекая поверхность плоскостями, параллельными координатным плоскостям, будем рассматривать линии пересечения и по их виду делать выводы о форме поверхности.

Каноническое уравнение эллипсоида:

Отметим симметрию поверхности: если точка (x, у, z) лежит на эллипсоиде, то и все точки (±x, ±у, ±z) тоже лежат на эллипсоиде. Значит, поверхность симметрична относительно любой из координатных плоскостей. Пересечём эллипсоид плоскостью z = h. Получим линию

Это эллипс, полуоси которого убывают с увеличением |h|. При h = c эллипс превращается в точку, при h > c плоскость z = h не пересекает эллипсоид. Эллипсы получаются и при сечении эллипсоида плоскостями x = h, у = h. Используя эти данные, изображаем поверхность. Числа a, b, c называются полуосями эллипсоида. Если две полуоси равны, то получается эллипсоид вращения. Например, эллипсоид, образованный при вращении эллипса (лежит в плоскости XOZ) вокруг оси OZ. Если a = b = c, то эллипсоид превращается в сферу.

Поверхности второго порядка

Поверхностью второго порядка называется поверхность S, общее уравнение которой в декартовой прямоугольной системе координат имеет вид:

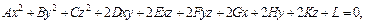(15.22)

где коэффициенты при одночленах второй степени одновременно не равны нулю.

Существует девять типов невырожденных поверхностей, уравнения которых с помощью преобразования координат могут быть приведены к одному из следующих видов. Эти уравнения определяют тип поверхности и называются каноническими уравнениями.

1. Эллипсоид: 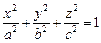(рис. 15.1).

2. Конус второго порядка: 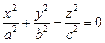(рис. 15.2).

3. Гиперболоиды

Рис. 15.3 Рис. 15.4

4. Параболоиды

Рис. 15.5 Рис. 15.6

5. Цилиндры

Рис. 15.7 Рис. 15.8

3) параболический: 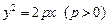(рис. 15.9).

Основным методом исследования формы поверхности является метод параллельных сечений, который состоит в следующем. Поверхность пересекается координатными плоскостями и им параллельными, а затем на основании вида полученных в сечениях линий делается вывод о типе поверхности. Таким образом можно изучать основные геометрические свойства невырожденных поверхностей второго порядка на основе их канонических уравнений.

При этом, когда в общем уравнении поверхности коэффициенты 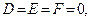приведение к каноническому виду осуществляется с помощью метода выделения полных квадратов.

В определенных случаях уравнение (15.22) поверхности может быть приведено к уравнениям, задающим, так называемые, вырожденные поверхности. Приведем примеры таких случаев:

– пустое множество точек (мнимый эллипсоид);

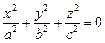– точка (0, 0, 0);

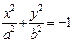– пустое множество точек (мнимый эллиптический цилиндр);

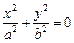– прямая (ось Oz);

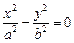– пара пересекающихся плоскостей;

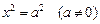– пара параллельных плоскостей;

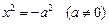– пустое множество точек;

– плоскость (пара совпадающих плоскостей).

Пример 1. Привести уравнение к каноническому виду и определить тип поверхности, которую оно задает:

1)

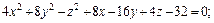
2)

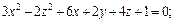
3)

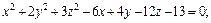
4)

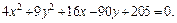
Решение. 1) Воспользуемся методом выделения полных квадратов.

Преобразуем левую часть уравнения:

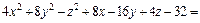
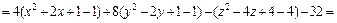
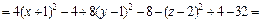
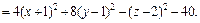
Значит, заданное уравнение равносильно уравнению

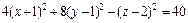или

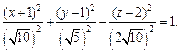
Имеем уравнение однополостного гиперболоида, центр которого находится в точке (–1, 1, 2). Его ось симметрии – прямая, параллельная оси Oz и проходящая через точку (–1, 1, 2).

2) Поскольку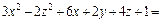

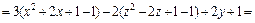
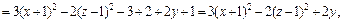
то заданное уравнение равносильно уравнению

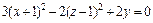или 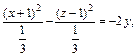что приводит окончательно к уравнению гиперболического параболоида 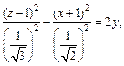смещенного в точку (–1, 0, 1).

3) Выделяем полные квадраты в выражении, стоящем в левой части уравнения:

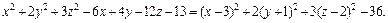
Поэтому заданное уравнение принимает вид:

или (после деления на 36)

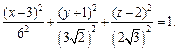
Это уравнение эллипсоида с центром в точке (3, – 1, 2).

4. Методом выделения полных квадратов уравнение 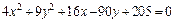приводится к уравнению

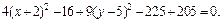т. е.

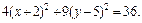
Почленное деление на 36 дает:

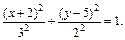
Это уравнение эллиптического цилиндра, смещенного в точку
(–2, 5, 0).

Пример 2. Исследовать поверхность методом сечений и построить ее:

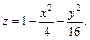
Решение. Для исследования геометрических свойств и формы поверхности используем метод сечений.

Определим сечение поверхности плоскостями 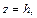где параллельными координатной плоскости Oxy:

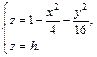
Очевидно, что это кривые, проекции которых на ось Oxy задаются уравнением

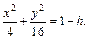(15.23)

Уравнение (15.23) при не имеет решений относительно Это означает, что соответствующее сечение есть пустое множество точек, а значит, рассматриваемая поверхность целиком расположена ниже плоскости При 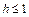уравнение (15.23) определяет эллипс

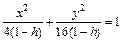
с полуосям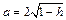и и 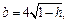вырождающийся в точку (0, 0, 1) при 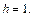Заметим, что все эллипсы, которые получаются в сечениях поверхности плоскостями 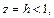подобны между собой, причем с уменьшением h их полуоси неограниченно монотонно возрастают.

Дальнейшее уточнение формы можно получить, рассматривая сечения координатными плоскостями Oxz и Oyz:

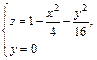и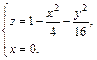

В первом случае имеем кривую 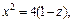т. е. параболу с параметром 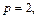вершиной в точке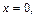 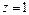и ветвями, направленными в отрицательную сторону оси Oz. Во втором – параболу 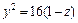с параметром 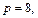вершиной в точке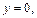 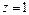и аналогичным направлением ветвей.

Выполненное исследование позволяет построить заданную поверхность (рис. 15.10). Это эллиптический параболоид 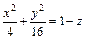с вершиной в точке (0, 0, 1), направленный в сторону убывания значений z с осью симметрии Oz.

Пример 3. Построить тело, ограниченное поверхностями

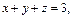
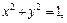
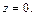
Решение. Уравнение 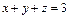задает плоскость. Перейдя к уравнению плоскости «в отрезках», получим:

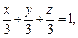
т. е. плоскость пересекает координатные оси в точках (3, 0, 0), (0, 3, 0) и (0, 0, 3) соответственно.

Уравнение 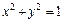задает круговой цилиндр, осью которого служит Oz. Уравнение 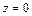определяет координатную плоскость Oxy.

Сделаем рисунок тела (рис. 15.11, 15.12), ограниченного заданными поверхностями.