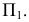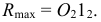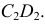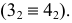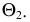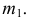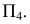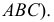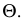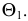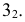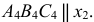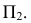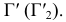При пересечении поверхности или какой-либо геометрической фигуры плоскостью получается плоская фигура, которую называют сечением.
Сечение поверхности плоскостью в общем случае представляет собой кривую (или прямую, если пересекаются плоскости), принадлежащую секущей плоскости.
Определение проекций линий сечения следует начинать с построения опорных точек – точек, расположенных на очерковых образующих поверхности (точки, определяющие границы видимости проекций кривой); точек, удаленных на экстремальные (максимальное и минимальное) расстояния от плоскостей проекций. После этого определяют произвольные точки линии сечения.
Если произвольные точки определяются с помощью одного и того же приема, то для нахождения опорных точек, как правило, приходится пользоваться различными способами.
В дальнейшем при построении сечения поверхности и линии пересечения поверхностей будет показано нахождение как опорных так и произвольных точек сечения.
А. Построение сечения многогранников.
Многогранником называют пространственную фигуру, ограниченную замкнутой поверхностью, состоящей из отсеков плоскостей, имеющих форму многоугольников (в частном случае треугольников).
Стороны многоугольников образуют ребра, а плоскости многоугольников – грани многогранника.
Проекциями сечения многогранников, в общем случае, являются многоугольники, вершины которых принадлежат ребрам, а стороны – граням многогранника*. Поэтому задачу по определению сечения многогранника можно свести к многократному решению задачи по определению точки встречи прямой (ребер многогранника) с плоскостью или к задаче по нахождению линии пересечения двух плоскостей (грани многогранника и секущей плоскости).
Первый путь решения называют способом ребер, второй – способом граней. Какому из способов следует отдать предпочтенение, надо решать в каждом конкретном случае.
ПРИМЕР 1. Определить сечение четырехгранной призмы ABCDEFGH (рис. 189) плоскостью α(а || b).
РЕШЕНИЕ. Решаем эту задачу способом ребер. Для этого заключаем ребра в горизонтально проецирующие плоскости γ1, γ2, γ3, γ4: γ1 ⊃ (АЕ); γ2 ⊃ (BF); γ3 ⊃ (CG); γ4 ⊃ (DH).
Находим проекции линий пересечения этих плоскостей с плоскостью α (прямые 1, 2; 3, 4; 5, 6; 7, 8). Отмечаем точки пересечения полученных прямых с соответствующими ребрами призмы К = (1, 2) ∩ (АЕ); L = (3, 4) ∩ (BF); М = (5, 6) ∩ (CG); N= (7,8) ∩ (DH). Четырехугольник KLMN – искомое сечение.
Решение задачи значительно упрощается, если секущая плоскость или плоскости граней (если многогранник относится к призмам) занимает проецирующее положение.
ПРИМЕР 2. Определить сечение трехгранной пирамиды SABC горизонтально проецирующей плоскостью α (рис. 190).
Для получения ответа на посталвенную задачу не требуется никаких дополнительных построений. На основании инвариантного свойства 2г (§ 6) горизонтальная проекция сечения пирамиды плоскостью а должна принадлежать следу плоскости h0α. Поэтому достаточно отметить точки М’ , N’, L’, в которых горизонтальный след h0α секущей плоскос-
* В частном случае многоугольник сечения может проецироваться в отрезок прямой (см. инвариантное свойство 2г, § 6).
ти α пересекает горизонтальные проекции ребер пирамиды.
Фронтальные проекции вершин треугольника сечения определяются по их горизонтальным проекциям. Для этого достаточно из точек М’, N’, L’ провести линии связи – вертикальные прямые и отметить точки их пересечения с фронтальными проекциями ребер пирамиды.
ПРИМЕР 3. Определить сечение пятигранной призмы ABCDE, ребра которой перепендикулярны горизонтальной плоскости проекции, секущая плоскость α – общего положения (рис. 191).
Так как ребра призмы перпендикулярны плоскости π1, то горизонтальные проекции точек пересечения этих ребер с плоскостью α(1′, 2′, 3′, 4′, 5′) совпадают с горизонтальными проекциями ребер, т. е. точками А’, В’, С, D’, Е’.
Фронтальные проекции точек встречи определяем из условия принадлежности этих точек плоскости α. Решение сводится к нахождению недостающей проекции точки, принадлежащей плоскости, если известна хотя бы одна из ее проекций (см. §40, пример 3, рис. 171). На рис. 191 фронтальные проекции точек 1″, 2″, 3″, 4″, 5″ найдены с помощью фронтальной плоскости α.
Б. Построение сечения поверхности вращения.
Так как для рассматриваемого круга задач в алгоритме l = (L1 ∪ L2 ∪ L3 ∪ … ∪ Ln); [Lj = (γj ∩ α) ∩ (γj ∩ β) ] α – поверхность вращения, а β – плоскость, то для нахождения общих точек Lj, … , принадлежащих как поверхности α, так и плоскости β, целесообразно в качестве вспомогательных секущих поверхностей γj принять плоскости, перпендикулярные к оси вращения; в этом случае плоскости γj будут пересекать поверхность α по окружностям, а плоскость β по линиям уровня *. Определение точек Lj сводится к нахождению точек пересечения прямой с окружностью.
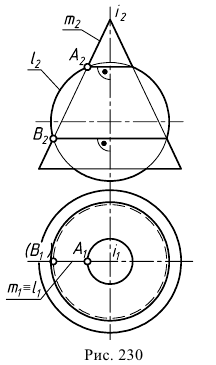
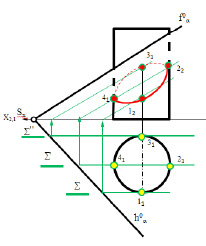
ПРИМЕР. Определить сечения поверхности сферы а плоскостью общего положения β (рис. 192).
РЕШЕНИЕ. При сечении поверхности сферы плоскостью получается окружность. Если секущая плоскость общего положения, то эта окружность проецируется на плоскости проекций в виде эллипсов.
Построения начнем с определения опорных точек. Для нахождения низшей А и высшей В точки кривой сечения проводим через центр сферы О вспомогательную секущую плоскость γ1 ⊥ h0β. Точки А и В принадлежат линии пересечения плоскостей γ1 и β. Эти точки находят в результате пересечения прямой (1, 2) = γ1 ∩ β с поверхностью α. А и В = (1, 2) ∩ α. Для их определения воспользуемся способом замены плоскостей проекции. Перейдем от системы xπ2/π1 к x1π3/π1. Ось x1 проводим перпендикулярно h0β. По отношению к π3 плоскость β занимает проецирующее положение, поэтому точки А”1 и В”1, в которых след f0β1, пересекает новую фронтальную проекцию очерка сферы α”1, будут вспомогательными проекциями искомых точек. Обратными построениями определяем положение горизонтальных А’, В’, а затем и фронтальных А”. В” проекций искомых точек.
[А’В’] является малой осью (диаметром) горизонтальной проекции эллипса. Для определения большого диаметра этого эллипса [ D’ Е’ ] достаточно из вспомогательной проекции центра сферы
О”1 провести прямую, перпендикулярную к отрезку [А”1В”1]. Точка С”1(С’, С”), в которой перпендикуляр пересекает [A”1, В”1], является центром эллипса, через который пройдет сопряженный (большой) диаметр эллипса DE.
DE принадлежит горизонтали плоскости β. Для определения точек D и Е вводим вспомогательную секущую плоскость γ2, проходящую через точку С и параллельную плоскости проекций π1. Эта плоскость пересекает поверхность сферы по окружности с, которая проецируется на плоскость π1 без искажения в окружность радиуса R = [ 6″ 7″], проведенную из центра О’. Пересечение этой окружности с горизонтальной проекцией горизонтали h2 определяет положение горизонтальных проекций точек D’ и Е’. Для нахождения точек F и G, являющихся граничными точками видимости для фронтальной проекции эллипса, воспользуемся плоскостью γ3 || π2 . Эта плоскость пересечет поверхность сферы по главному меридиану, который проецируется на π2 во фронтальную проекцию очерка сферы, а плоскость β по фронтали f3 (f’3 f”3 ). Пересечение f”3 с фронтальной проекции очерка сферы укажет положение точек F” и G”.
Для нахождения точек М и N, указывающих границы видимости на горизонтальной проекции сечения, проводим плоскость γ4 || π1 (γ4 ∋ О).
Плоскость γ4 ∩ β = h4 , а поверхность сферы – по окружности, которая проецируется на плоскость π1 в горизонтальную проекцию очерка сферы.
* Имеется в виду, что ось поверхности вращения перпендикулярна плоскости проекции.
Пересечение h’4 с горизонтальным очерком сферы α’ определяет положение искомых горизонтальных проекций точек M’ и N’
Для определения произвольных точек L1 и L2, принадлежащих линии сечения, как правило, целесообразно в качество вспомогательной секущей плоскости использовать плоскости уровня
На рис 192 показано построение точек L1 и L2 , с помощью горизонтальной плоскости γ5. Проведя плоскости γj || π1 мы каждый раз будем получать окружность в результате пересечения γj с α и прямую – горизонталь при пересечении γj с β. Пересечения окружностей и прямых укажут положение горизонтальных проекций точек , принадлежащих горизонтальной проекции линии сечения
Если задана произвольная поверхность вращения, то ход решения задачи и последовательность выполнения геометрических построении ничем не отличается от случая, рассмотренного на рис. 192.
На рис. 193 показано построение сечения произвольной поверхности вращения α плоскостью общего положения β. Как и в предыдущем примере, вначале определены опорные точки: низшая A и высшая B: точки С, I) – границы видимости на фронтальной и точки Е. F – на горизонтальной проекциях. На рис. 193 показано также построение произвольных точек L1 и L2.
Решение задачи но определению сечения поверхности вращения α плоскостью значительно упрощается, если секущая плоскость занимает проецирующее положение. В этом случае одна из проекций сечения – отрезок примой, принадлежит следу плоскости.
Задача по определению второй проекции линии сечения сводится к многократному решению ранее рассмотренной задачи по нахождению второй проекции точки, принадлежащей плоскости, если известна хотя бы одна ее проекции (см. § 40, пример 3, рис. 171).
Рис. 194 дает представление о таком частном случае решения задачи. Из чертежа видно, что оно проще решении, рассмотренных на рис:. 192 и 193. Потому целесообразно при решении задач на определение сечения поверхности плоскостью предварительно перевести секущую плоскость в проецирующее положение.
В. Построение сечения поверхности прямого кругового конуса.
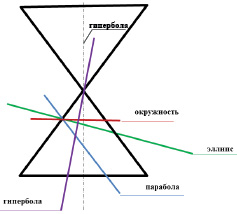
Поверхность прямого кругового конуса относится к поверхностям вращения, но мы рассматриваем ее отдельно, гак как она занимает особое место среди других поверхностей вращения. Эта поверхность н своем роде уникальна, она служит носителем замечательных кривых второго порядка: окружности, зллипса, параболы и гиперболы. Роль и области использования лих кривых в науке и, особенно, технике невозможно переоценить.
Все перечисленные кривые являются плоскими и, следовательно, могут быть получены в результате сечения конической поверхности плоскостью. В связи с этим перечисленные кривые называют также коническими сечениями. В частных случаях при определенном положении секущих плоскостей α3, β2, γ1, (см. рис. 195, 196, 197) кривые
второго порядка распадаются на две прямые (действительные или мнимые *).
Прежде чем говорить о построении ортогональных проекций сечения поверхности прямого кругового конуса, отметим существование теоремы, которой будем пользоваться при построении кривых второго порядка.
Т е о р е м а: ортогональная проекция плоского сечения поверхности прямого конуса на плоскость, перпендикулярную к его оси, представляет собой кривую второго порядка и имеет одним из своих фокусов ортогональную проекцию на эту плоскость вершины конической поверхности.
Условия, которые должны быть выполнены, чтобы получить ту или иную кривую второго порядка, при сечении конической поверхности плоскостью могут быть установлены из свойств кривых второго порядка.
Известно, что эллипс представляет кривую второго порядка, не имеющую бесконечно удаленных (несобственных) точек. Поэтому, чтобы получить в сечении конической поверхности эллипс, надо выбрать такую плоскость, которая пересекает все прямолинейные образующие этой поверхности. В частном случае, когда диаметры эллипса равны (секущая плоскость перпендикулярна к оси конической поверхности) , в сечении получается окружность.
Из аффинной геометрии известно, что параболой называется кривая второго порядка, касающаяся несобственной прямой, или, что то же самое, кривая, имеющая одну несобственную точку. В связи с этим для получения параболы необходимо, чтобы секущая плоскость была параллельно одной образующей конической поверхности. В пределе, когда секущая плоскость переходит в касательную к поверхности, две симметричные дуги параболы преобразуются в две полупрямые, принадлежащие одной прямой.
* Плоскость α3 (рис. 195) пересекает коническую поверхность по двум мнимым прямым, пересекающимся в собственной точке.
И, наконец, гипербола с аффинной точки прения представляет собой кривую второго порядка, пересекающую несобственную прямую, или, иначе, гипербола – кривая второго порядка, имеющая две несобственные точки, т. е. чтобы получить гиперболу, нужно секущую плоскость взять параллельной двум прямолинейным образующим. В частном случае, когда секущая плоскость проходит через вершину конической поверхности, гипербола распадается на две пересекающиеся прямые.
На рис. 195 показаны положение секущей плоскости для получения эллипса (плоскость α1 ) и окружности (плоскость α2) и одна из плоскостей, принадлежащих связке, проходящей через вершину конической поверхности, и пересекающих эту поверхность по двум мнимым прямым, пересекающимся в действительной точке (плоскость α3) . На рис. 196 показаны положение секущей плоскости для получения параболы (плоскость β1 ) и плоскость β2, имеющая с конической поверхностью общую прямую (точнее две совпавшие прямые). На рис. 197 изображены плоскость γ1 , пересекающая коническую поверхность по гиперболе, и плоскость γ2, в сечении которой образуются две пересекающиеся прямые.
На рис. 198 приведены фронтальные проекции поверхности прямого кругового конуса, следы фронтально проецирующих секущих плоскостей и указан вид получаемой в сечении кривой. По рис. 198 можно установить признаки, обеспечивающие получение в сечении той или иной кривой второго порядка. Так, если обозначить угол наклона образующей конической поверхности к его оси через φ°, а угол между секущей плоскостью и той же осью через ψ°, то можно утверждать, что при 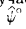


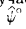
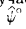

Проследим па примерах характер графических построений, которые должны быть выполнены для построения сечения поверхности прямою кругового конуса.
ПРИМЕР 1. Построить проекции сечения поверхности прямого кругового конуса ω плоскостью α (рис. 199)
РЕШЕНИЕ. Плоскость α фронтально проецирующая. Угол между секущем плоскостью и осью конической поверхности ψ° больше угла наклона образующей конической поверхности к его оси, поэтому в сечении получим эллипс, большая ось которого [AB] будет проецироваться на плоскость π2 без искажения в [A”B”], а малая ось эллипса CD спроецируется на плоскость π2 в точку С” D”, расположенную в середине оотрезка [A”B”]. Величина мамой оси [CD] определяется на условия (C, D) ∈ α. Проводим через С”D” фрональную проекцию параллели поверхности α – h”. Дли построении ее горизтотальной проекции из горизонтальной проекции фокуса эллипса S’ проводим окружность радиусом |1″2″| и отмечаем точки ее пересечени С” и D” с перпендикуляром, востановленным в середине |A’B’| –
горизонтальной проекции большой оси эллипса. Зная большой и малый диаметры эллипса, известным способом строим эллипс.
ПРИМЕР 2. На рис. 200 показаны проекции поверхности прямого кругоного конуса ω и фрнтально проецирующей плоскости β. Построить проекции липни сечении.
РЕШЕНИЕ. Угол наклона секущей плоскости β к оси конической понерхности ранен yглу наклона прямолинейной образующей к этой оси 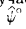

ПРИМЕР 3.Построить проекции сечения поверхности прямого кругового конуса ω плоскостью γ (рис 20 I).
РЕШЕНИЕ. Так как / ψ° наклона секу щей плоскости γ к оси конической поверхности меньше угла наклона образущей конической поверхности / φ°, то плоскость γ пересечет поверхность ω по гиперболе. Фокусы и вершины горизонтальной проекции ее ветвей определяются непосредственно из чертежа .С помощью фокусов и вершин строим асимптоты горизонтальной проекции гиперболы. Зная положение вершин, фокусов и асимптот, можно построить любое число точек, принадлежащих ветвям гиперболы
В рассмотренных примерах пересекающая коническую поверхность плоскость занимала проецирующее положение. Если секущая плоскость общего положения, то целесообразно с помощью способов преобразования перевести ее в проецирующее положение. Это позволит свести задачу к простейшей – одному из рассмотренных случаев (рис. 199 … 201).
ПРИМЕР 4. Построить проекции сечения конической поверхности ω плоскостью α (рис. 202).
РЕШЕНИЕ. Чтобы упростить решение задачи, осуществим замену плоскости π2 новой плоскостью π3. Плоскость π3 выбираем так, чтобы по отношению к ней секущая плоскость α заняла проецирующее положение. Спроецируем на плоскость π3 коническую поверхность ω. Выполненные преобразования позволили свести решение к случаю, рассмотренному ранее (см. пример 1, рис. 199) .
Для построения фронтальной проекции зллипса сечения на рис. 202, кроме точек А, В и С, D, на вспомогательной проекции взяты точки Е, F и М, N, горизонтальные и фронтальные проекции этих точек определены с помощью горизонталей h2 и h3. Кроме опорных точек А и В, являющихся высшей (B) и низшей (A) точками сечения, на рис. 202 показаны точки Р и L, принадлежащие фронтальным проекциям очерковых образуещих конической поверхности ω. Эти точки служат границей видимости для фронтальной проекции сечения. Для нахождения точек Р” и L” пользуемся фронталью f.

Цель – выработать навыки построения линий сечения поверхностей плоскостями частного положения, определить величину и форму сечения.
Для решения задания необходимо вспомнить общий алгоритм решения задачи о пересечении поверхностей (α и β) .
1. Вводим вспомогательную поверхность γi .
2. Определяем линии пересечения поверхности γi с поверхностями α и β: (mi ) = γi ∩α; (ni ) = γi ∩β.
3.Определяем точку (точки пересечения) линий пересечения mi и ni : Li = mi ∩ni .
4.Повторяем записанные операции n раз и определяем n точек L . Соединив их плавной кривой получаем искомую кривую l :
(l) = L1 L2 L3…Ln .
Если одна из фигур – плоскость, а вторая – линейчатая поверхность, то решение сводится к нахождению точек пересечения образующих поверхности с секущей плоскостью, т.е. к нахождению точки пересечения прямой с плоскостью. При построении сечения многогранника задача может быть так же сведена к многократному решению задачи по определению пересечения двух плоскостей – грани многогранника и секущей плоскости. Задача существенно упрощается, если секущая плоскость проецирующая. В этом случае задача сводится к построению второй проекции сечения; одна его проекция, лежащая в секущей плоскости, уже есть. Для этого следует воспользоваться условиями принадлежности. Истинная величина и форма сечения находятся методами преобразования чертежа.
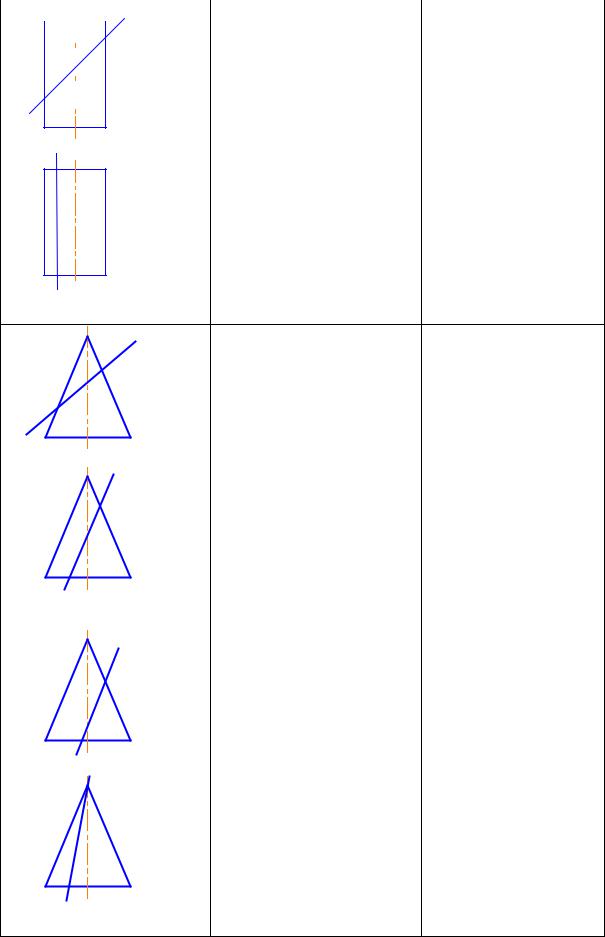
Линии пересечения плоскостей с поверхностями, наклонные сечения часто встречаются в реальных конструкциях. Часто на чертежах различных деталей (отливок, поковок) требуется строить проекции кривых линий, по которым плоскости пересекаются с различными телами вращения. Такие линии называются линиями среза (рис. 16). Каждую деталь можно рассматривать как комбинацию простых геометрических элементов, поэтому полезно напомнить форму сечения простых поверхностей вращения плоскостью (табл. 1).
Т а б л и ц а 1.1
|
Поверхность вращения |
Положение секущей плоскости |
Линия сечения |
Произвольное Окружность
v
Сфера
28
|
Окончание табл. 1 |
||||||
|
Поверхность вращения |
Положение секущей плоскости |
Линия сечения |
||||
|
Наклонно относительно оси вра- |
Эллипс |
|||||
|
щения |
||||||
v
|
Параллельно оси вращения |
Две прямые |
|
(образующие) |
v
Цилиндр
|
Пересекает все образующие под |
Эллипс |
|
наклоном к оси вращения |
v
v
|
Параллельно образующей |
Парабола |
v
|
Параллельно двум образующим |
Гипербола |
|
Проходит через вершину конуса |
Две прямые |
|
(образующие) |
v
Конус
29

При вычерчивании проекций реальных деталей приходится выполнять всевозможные сопряжения. При построении линии среза часто необходимо вычертить сопряжение дуги окружности и прямой с помощью заданного радиуса. Сначала определяют множество возможных по-
ложений центров дуг сопряжения заданного радиуса R1 (рис. 16,а), для чего на расстоянии R1 от прямой a проводят параллельную ей прямую m .
|
а) |
a) |
+R |
||||||
|
R |
1 |
|||||||
|
R |
R |
|||||||
|
O |
1 |
|||||||
|
б) |
б) |
E |
C |
О |
||||
|
О |
||||||||
|
O |
2 |
O |
||||||
|
2 |
||||||||
|
R |
||||||||
|
D |
R-R |
|||||||
|
B |
||||||||
|
1 |
||||||||
|
в)в) |
C |
E |
||||||
|
R |
||||||||
|
= |
||||||||
|
R |
O |
|||||||
|
2O |
||||||||
|
1 |
O |
O |
||||||
|
R |
2 |
|||||||
|
+ |
||||||||
|
R |
B |
|||||||
|
D |
||||||||
|
Рис. 16 |
O1 m
R 1
a
C
C1
R1
O1
B1
B1
R1
O1
C1
Из центра O радиусом R + R1 проводят концентрические окружности. Точка O1 будет цен-
тром дуги сопряжения. Точка сопряжения C получена на перпендикуляре, проведенном из точки O к прямой a , а точка B – на прямой, соединяющей точки O и O1 . Сопряжение дуг двух
окружностей при помощи прямой линии сводится к построению внешней или внутренней касательной к этим окружностям. Для проведения внешней касательной, сопрягающей две окружно-
сти радиусами R и R1 (рис. 16,б), сначала соединяют центры окружностей, затем отрезок делят точкой O2 пополам, а из точки O проводят окружность радиусом, равным разности радиусов
30

|
заданных окружностей |
R −R1 . |
На этой окружности радиусом |
O2 O засекают точки E и D . |
|||||||||||||||||||||||
|
Продлив отрезки OE и OD до пересечения с окружностью радиусом R , |
получают точки со- |
|||||||||||||||||||||||||
|
пряжения C и B . Соединяют точки E и D с центром O1 . Из точки C и B параллельно пря- |
||||||||||||||||||||||||||
|
мым O1E и O1D проводят прямые, сопрягающие две окружности. Такие сопряжения на окруж- |
||||||||||||||||||||||||||
|
ности радиусом R1 |
можно получить, проведя из точки O1 |
прямые, |
перпендикулярные прямым |
|||||||||||||||||||||||
|
O1E и O1D . Построение касательных, сопрягающих окружности R и R1 , аналогично предыду- |
||||||||||||||||||||||||||
|
щему (16,в). |
Деталь образуется снятием материала заготовки по плоскости α (рис. 17). |
|||||||||||||||||||||||||
|
П р и м е р 1. |
||||||||||||||||||||||||||
|
Построить горизонтальную проекцию детали, найти истинную величину сечения. |
||||||||||||||||||||||||||
|
‘ |
||||||||||||||||||||||||||
|
31 |
||||||||||||||||||||||||||
|
‘ |
5′1 |
|||||||||||||||||||||||||
|
91 |
‘ |
|||||||||||||||||||||||||
|
‘ |
‘ |
11 |
||||||||||||||||||||||||
|
31 |
||||||||||||||||||||||||||
|
1 |
61 |
|||||||||||||||||||||||||
|
‘ |
8′1 |
|||||||||||||||||||||||||
|
51 |
||||||||||||||||||||||||||
|
1 |
||||||||||||||||||||||||||
|
‘ |
‘ |
|||||||||||||||||||||||||
|
71 |
||||||||||||||||||||||||||
|
1 |
11 |
|||||||||||||||||||||||||
|
3′1 |
5 |
|||||||||||||||||||||||||
|
2 |
‘ |
|||||||||||||||||||||||||
|
‘ |
π |
|||||||||||||||||||||||||
|
81 |
||||||||||||||||||||||||||
|
41 |
1 |
|||||||||||||||||||||||||
|
2 |
‘ |
X1 |
||||||||||||||||||||||||
|
1 |
||||||||||||||||||||||||||
|
21 |
2 |
|||||||||||||||||||||||||
|
7″≡8″ |
π |
|||||||||||||||||||||||||
|
сь |
ии |
‘ |
‘ |
aH |
||||||||||||||||||||||
|
141 |
||||||||||||||||||||||||||
|
о |
р |
21 |
||||||||||||||||||||||||
|
ет |
a |
2 |
||||||||||||||||||||||||
|
имм |
4″≡5″≡6″ |
|||||||||||||||||||||||||
|
с |
||||||||||||||||||||||||||
|
10″≡11″ |
1″≡2″≡3″ |
|||||||||||||||||||||||||
|
9″ |
Tv1 |
Tv |
||||||||||||||||||||||||
|
15″ |
r1 |
1 |
2 |
|||||||||||||||||||||||
|
12″≡13“≡14″ r2 |
||||||||||||||||||||||||||
|
16″≡17″≡18″ |
π2 |
|||||||||||||||||||||||||
|
24″23″ |
19″≡20″≡21″≡22″ |
2 |
Х |
|||||||||||||||||||||||
|
π1 |
||||||||||||||||||||||||||
|
17′ |
16′ |
10′ |
7′ |
2′ |
||||||||||||||||||||||
|
24′ |
15′ |
9′ |
4′ |
3′ |
ось |
|||||||||||||||||||||
|
a |
23′ |
18′ |
13′ |
6′ |
симметрии |
|||||||||||||||||||||
|
.Н |
a |
21′ |
11′ |
|||||||||||||||||||||||
|
8′ |
1′ |
|||||||||||||||||||||||||
|
22′ |
14′ |
|||||||||||||||||||||||||
|
Рис. 17 |
Анализ данных. Деталь представляет собой сочетание пяти цилиндрических (три из них – отверстия) и одной конической поверхности, оси которых перпендикулярны горизонтальной плоскости проекции. Плоскость α фронтально-проецирующая.
Анализ решения. Первая часть задачи сводится к построению линий пересечения фронталь- но-проецирующей плоскостью α поверхностей, на которые можно расчленить деталь. Как явствует из приведенной выше табл. 1, линии сечения всех рассматриваемых поверхностей – эллипсы. Так как цилиндрические поверхности являются проецирующими на плоскость H , то на горизонтальной проекции линии их сечения совпадут с проекциями поверхностей. Горизонтальную проекцию линии сечения конической части удобно построить с помощью вспомогательных секущих плоскостей, параллельных H .
Для решения второй части задачи следует воспользоваться одним из способов преобразования чертежа – сделать так, чтобы сечение спроецировалось на одну из плоскостей проекций в натуральную величину.
31

Алгоритм решения.
1. Строим горизонтальную проекцию линии сечения конической части детали с помощью вспомогательных плоскостей Ti // π1 . Линия пересечения плоскости α с верхним основанием
усеченного конуса – прямая 1–2.
2.Линия пересечения верхнего основания цилиндра I с плоскостью α – прямая 12–14.
3.Линии пересечения верхнего основания цилиндра II с α прямые – [19–20], [21–22].
|
4. Переходим от системы X |
π2 |
к X |
π2 |
. При этом |
X |
// α |
V |
. Строим новую горизонталь- |
|
|
π |
1 π |
5 |
1 |
||||||
|
1 |
ную проекцию сечений детали плоскостью α , помня, что координаты y для π1 и π5 неизменны. Отсчет координат удобно вести от осей симметрии (см. точки 22′ и 221′).
П р и м е р 2. Построить линию среза детали, образованной из заготовки (тело вращения), срезанной плоскостями γ , параллельными фронтальной плоскости проекций (рис. 18).
|
ЦилиндрI |
ТорI |
Сфера |
ТорII |
Цилиндр |
|||||
|
α |
αv4 |
α |
βv |
αv |
v2 |
||||
|
v1 |
1 |
5 |
|||||||
|
v3 |
α |
||||||||
|
r4 |
A |
C |
R |
B |
|||||
|
1” |
2” |
||||||||
|
r |
6” |
r2 |
|||||||
|
r3 |
c |
||||||||
|
r1 |
r5 |
3” |
|||||||
|
4” |
|||||||||
|
R |
5” |
||||||||
II
|
γw 1 |
γw 2 |
|||
|
1”’ |
r1 |
r2 |
|
|
6”’ |
|||
|
3”’ |
r3 |
r5 |
|
|
4”’ |
r4 |
||
|
5”’ |
Рис. 18
Анализ данных. Как ви дно из чертежа, заготовка образована из сферы и двух цилиндров, которые сопрягаются между собой с помощью поверхностей вращения – торов. Правый цилиндр завершается полусферой. Установить участки поверхностей вращения, ограничивающих рассматриваемую деталь, можно при помощи точек сопряжения, найденных на линиях центров или на перпендикулярах к образующим.
Анализ решения. Решение задачи сводится к построению сечения плоскостью частного положения тел вращения, образующих заготовку. Из чертежа видно, что цилиндр I плоскостями не рассекается. Согласно табл. 1 в сечении цилиндра II получим две прямые линии, в сечении сферы и полусферы – окружности, а в сечении торовых поверхностей – кривые более высокого
порядка, которые можно построить, используя вспомогательные плоскости, параллельные π3 .
Решение следует начать с нахождения характерных точек линии среза, которые определяются с помощью вспомогательных секущих плоскостей αi // π3 , проведенных через точки сопря-
жений.
32
Алгоритм решения.
1. Находим точки сопряжения A, B,C на очерковых образующих детали и проводим через них плоскости α1,α2 и β, параллельные π3 . Плоскость α1 рассекает поверхность по окружности радиусом r1 . На плоскость π3 эта окружность проецируется в истинную величину.
2.Определяем профильную проекцию I′′′ точки I – пересечения окружности радиуса r1 и профильного следа γW1 секущей плоскости γ .
3.Определяем фронтальную проекцию I′′ точки I .
4.Аналогично находим проекции точки 3.
5.Строим линию среза на сфере – окружности радиуса rc от точки I′′ до точки 2′′ пересе-
чения окружности радиуса rc с фронтальным следом βV1 .
6. Определим положение крайней левой точки линии среза – точки 4. Для этого проводим плоскость α3 // π3 так, чтобы она рассекала поверхность детали по окружности радиусом r3 ,
которая касается плоскости среза γ .
|
7. Для построения линии среза тора I проведем плоскость α4 |
// π3 и найдем точку 5. |
|
8. Для построения среза тора II проведем плоскость α5 // π3 |
и найдем точку 6. Для более |
точного построения линии среза следует взять несколько промежуточных вспомогательных секущих плоскостей.
9.Строим линию среза на цилиндре II . Для этого проводим прямую из точки 3”, параллельно оси детали до пересечения с βV 2 в точке 7”.
10.Точка 7” определяет величину радиуса окружности линии среза на полусфере.
11.Достраиваем линию среза до полной пользуясь тем, что она симметрична оси детали.
Варианты задания № 4
Варианты 1–12. Построить чертеж детали, получаемой обработкой изображенной на чертеже заготовки, так, чтобы проецирующими плоскостями отсекалась ее часть; следы указаны на чертеже. Показать истинную величину сечения заготовки плоскостью α . Линии невидимого контура можно на чертеже не изображать.
Варианты 13–24. Закончить изображение фронтальной проекции детали (построить фронтальную проекцию линии среза), получаемой заготовки (тело вращения) путем срезания по
плоскостям α1 и α2 параллельно оси вращения. Указать границы перехода одной поверхности в
другую. Все построения по определению центров радиусов сопряжения, точек сопряжения и прочие на чертеже должны быть сохранены (рис. 18).
33
Содержание:
Задачи на нахождение общих точек у прямой и поверхности, построение линии пересечения плоскости с поверхностью, двух поверхностей определяют взаимное положение геометрических образов и относятся к классу позиционных.
Пересечение поверхности плоскостью
Линия пересечения поверхности с плоскостью представляет собой, в общем случае, плоскую кривую или ломаную линию, все точки которой одновременно принадлежат поверхности и секущей плоскости.
Аналитически для определения уравнения линии пересечения плоскости с поверхностью необходимо решить следующую систему уравнений:
где
Для графического построения точек линии пересечения поверхности с плоскостью используется общий способ нахождения точек, принадлежащих двум геометрическим образам – способ вспомогательных секущих поверхностей. В качестве секущих поверхностей используют вспомогательные плоскости.
На рис. 203 показана поверхность 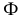
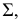
- заданные геометрические образы рассекают вспомогательной секущей плоскостью
которую выбирают так, чтобы она пересекла поверхность по графически простым линиям (прямым или окружностям);
- находят линии
и
пересечения вспомогательной секущей плоскости
с поверхностью
и плоскостью
соответственно;
- определяют точки
и
взаимного пересечения линий
и
лежащих в секущей плоскости
Точки
и
принадлежат обоим геометрическим образам, т.е. искомой линии пересечения
- последовательно выбирают ряд секущих плоскостей, построения при этом остаются теми же;
- полученные точки искомой линии пересечения соединяют с учетом видимости.
До начала построений необходимо сделать анализ взаимного расположения геометрических образов и искомой линии их пересечения, рационально выбрать вспомогательные секущие плоскости.
При анализе искомой линии пересечения и данных геометрических образов пользуются следующими основными положениями:
- Плоскость, пересекающая поверхность, может занимать как общее, так и частное положение относительно плоскостей проекций.
- Линия пересечения криволинейной поверхности с секущей плоскостью в общем случае – кривая линия.
- При пересечении сферы любой плоскостью в сечении всегда получается окружность.
- Сечение поверхности вращения плоскостью всегда будет фигурой симметричной, ось симметрии которой располагается в общей плоскости симметрии двух пересекающихся геометрических образов. Плоскостью симметрии секущей плоскости является любая плоскость, перпендикулярная ей. Плоскость симметрии поверхности вращения всегда проходит через ее ось. Таким образом, общая плоскость симметрии должна удовлетворять обоим условиям – проходить через ось вращения поверхности и быть перпендикулярной секущей плоскости.
- При пересечении линейчатой поверхности плоскостью точки искомой кривой находятся как точки пересечения образующих поверхности с данной секущей плоскостью.
- Линия пересечения многогранной поверхности с секущей плоскостью в общем случае – ломаная линия, вершинами которой служат точки пересечения ребер многогранной поверхности с секущей плоскостью, а сторонами – отрезки прямых пересечения граней поверхности с той же плоскостью.
- При пересечении прямого кругового конуса получается семейство различных кривых второго порядка (конические сечения) или прямые линии (образующие).
- При пересечении прямого кругового цилиндра могут получаться окружности, образующие или эллипсы.
- У цилиндрических, конических и призматических поверхностей выделяются так называемые нормальные сечения. Нормальным называется сечение цилиндра или призмы, перпендикулярное образующим. Нормальное сечение конуса – это сечение, перпендикулярное его оси симметрии.
- При пересечении поверхности открытого тора (кругового кольца) (рис. 204, а) с плоскостью получаются алгебраические кривые четвертого порядка. Их общее название – кривые Персея. На рис. 204 показаны сечения поверхности открытого тора различными плоскостями, которые расположены на расстоянии
от оси тора.
В зависимости от величин 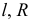
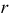
- – две окружности (см. рис. 204, б)
- – овалы с одной осью симметрии (см. рис. 204, в);
- – двухлепестковую кривую с узловой точкой в начале координат (см. рис. 204, г);
- – волнообразную кривую (см. рис. 204, д);
- – овал с двумя осями симметрии (см. рис. 204, е).
Построение искомой линии пересечения следует начинать с опорных точек кривой. Опорными точками кривой называют такие, которые выделяются особым расположением по отношению к плоскостям проекций или занимают особое место на кривой.
Опорными точками являются:
- – экстремальные точки линии пересечения, позволяющие судить, в каких пределах следует строить линию пересечения. К экстремальным относятся самая дальняя и самая ближняя точки, самая левая и самая правая, наивысшая и наинизшая точки линии пересечения, которые всегда располагаются в общей плоскости симметрии двух пересекающихся геометрических образов;
- – точки линии пересечения, лежащие на очерках поверхности и называемые точками изменения видимости. Проекции этих точек делят проекцию линии пересечения на видимую и невидимую части. Видимость линии пересечения определяется по видимости поверхности, на которой она лежит. Видима всегда та часть поверхности, которая ближе к наблюдателю;
- – характерные точки закономерных кривых – это вершины гиперболы или параболы, большая и малая оси эллипса.
Остальные точки линии пересечения называются промежуточными. Следует помнить, что приведенная классификация опорных точек условна. Экстремальные и характерные точки одновременно могут являться и точками изменения видимости. Характерные точки могут определять экстремальные положения линии пересечения.
Приведенный выше анализ задачи на пересечение поверхности с плоскостью дает наиболее общие закономерности, используемые при решении. Особенно следует выделить задачи построения нормальных сечений, сечений прямых круговых конуса и цилиндра, сечений линейчатых и нелинейчатых поверхностей, сечений плоскостями общего и частного положения.
Сечение поверхности проецирующей плоскостью
В случае, когда секущая плоскость является проецирующей, построение линии пересечения ее с поверхностью значительно упрощается.
Из рис. 203 видно, что линию 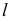
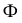
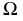
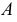
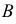
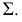
На рис. 205, а горизонтально проецирующая плоскость 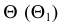
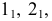
На рис. 205, б приведена схема нахождения точек линии пересечения поверхности вращения с фронтально-проецирующей плоскостью 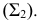
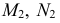
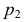
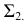
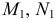
Построение сечения наклонного эллиптического конуса с круговым основанием горизонтально-проецирующей плоскостью 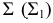
Горизонтальная проекция сечения совпадает с горизонтальным следом плоскости 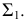
Наивысшая точка искомой кривой находится в общей плоскости симметрии двух пересекающихся г.о. Эта плоскость общего положения проходит через центровую линию 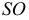
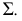
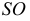
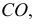
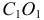
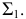
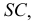
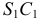
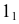
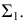
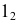
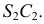
Самые низкие точки кривой располагаются на основании конуса. На горизонтальной проекции отмечаются точки 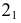
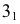
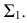
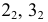
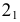
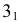
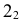
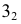
Горизонтальная проекция крайней правой точки 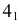
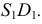
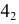
Точки изменения видимости располагаются на образующих, дающих фронтальный очерк поверхности, это образующие 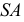
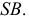
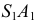
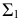
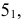
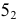
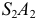
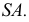
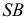
Для получения плавной кривой необходимо построить ряд промежуточных точек, таких как точка 6. Натуральная величина сечения находится проецированием на дополнительную плоскость проекций
Сечение поверхности плоскостью общего положения
В случае, когда секущая плоскость занимает общее положение, схема построения точек линии пересечения совпадает с приведенным выше алгоритмом решения задачи, проиллюстрированным на рис. 203.
В соответствии с этим алгоритмом на рис. 207 показано нахождение точек линии пересечения поверхности вращения с плоскостью общего положения 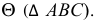
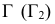
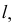
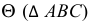
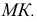
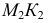
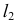
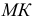
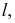
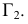
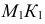
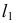
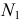
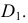
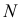
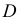
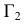
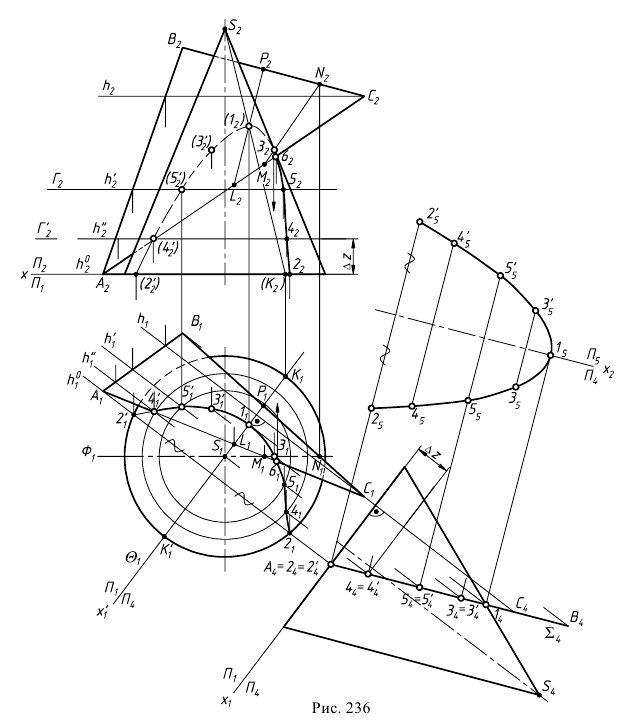
Полное решение задачи на пересечение поверхности конуса с плоскостью общего положения приведено ниже (рис. 236).
Рассмотрим применение способа вспомогательных секущих плоскостей для построения линии сечения цилиндра плоскостью. На рис. 208 заданы прямой круговой цилиндр и плоскость 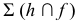
Плоскость 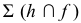
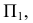
Построение линии пересечения начинают с опорных точек.
Высшая и низшая точки искомой кривой располагаются в общей плоскости симметрии пересекающихся геометрических образов. Такой плоскостью является горизонтально-проецирующая плоскость 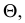
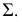
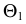
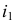
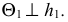
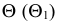
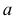
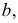
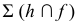
Горизонтальные проекции 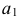
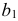
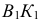
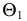
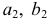
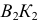
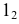
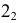
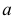
Точки изменения видимости линии пересечения всегда располагаются на очерке поверхности. Фронтальный очерк цилиндра определяют образующие 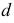
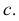
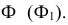
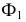
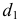
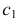
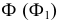
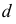
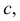
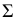
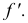
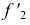
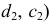
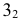
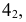
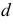
Точки изменения видимости 3 и 4 одновременно являются самой левой и самой правой точками искомой линии пересечения.
Для определения самой дальней 5 и самой ближней 6 точек эллипса проводятся вспомогательные секущие плоскости уровня 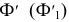
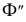
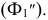
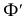
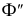
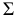
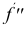
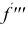
Для получения плавной кривой строятся промежуточные точки при помощи горизонтальных плоскостей уровня, которые рассекают цилиндр по окружностям, а данную плоскость по горизонталям. На рис. 208 построены промежуточные точки эллипса 7 и 8, лежащие в секущей плоскости 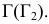
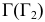
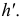
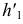
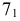
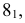
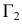
Полученные точки эллипса соединяют плавной кривой с учетом видимости. На фронтальной плоскости проекций видимой будет линия на передней половине цилиндра до образующих 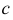
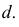
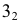
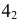
Ранее было показано, что построение линии пересечения поверхности с проецирующей плоскостью значительно проще, чем с плоскостью общего положения. Используя методы преобразования эпюра, можно секущую плоскость общего положения преобразовать в проецирующую и построить линию пересечения поверхности с плоскостью частного положения.
Пример такого преобразования приведен на рис. 209. Условие задачи соответствует задаче пересечения цилиндра с плоскостью общего положения (см. рис. 208).
Секущая плоскость общего положения в новой системе плоскостей проекций преобразована так, что она стала проецирующей. На новой плоскости проекций 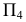
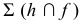
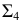
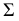
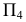
Если известна проекция линии пересечения на плоскости 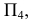
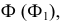
Конические сечения
Из многообразия конических поверхностей выделяют поверхность прямого кругового конуса, так как она обладает особыми свойствами. Коническая поверхность, кроме прямых линий (образующих), несет на себе семейства различных кривых второго порядка: эллипсов, окружностей, парабол и гипербол. Эти кривые получаются как конические сечения, то есть являются линиями пересечения поверхности конуса с плоскостями.
На рис. 210 показаны сечения прямого кругового конуса. В том случае, когда плоскость 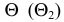
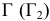
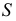
Если секущая плоскость 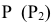
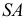
В том случае, когда секущая плоскость 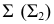
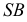
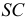
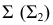
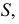
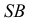
Построение линии пересечения прямого кругового конуса с плоскостью частного положения аналогично рассмотренным ранее задачам. Полное решение такой задачи с нахождением натуральной фигуры сечения приведено ниже (рис. 236).
В случае, когда рассматривается пересечение конической поверхности второго порядка и секущей плоскости общего положения, также можно определить вид линии пересечения. Для этого через вершину конической поверхности проводится плоскость, параллельная заданной, и определяется вид вырожденного сечения (примеры построения не приводятся).
Нормальные сечения
Нормальным называется сечение цилиндра или призмы плоскостью, перпендикулярной образующим. Нормальное сечение конуса – это сечение, перпендикулярное его оси симметрии. Любой конус или цилиндр называется всегда по нормальному сечению. Если нормальное сечение – окружность, то конус или цилиндр называются круговыми. Если нормальным сечением является эллипс, то поверхность называется эллиптической.
Пример построения нормального сечения призмы приведен на рис. 211. Ребра трехгранной призмы являются фронталями, поэтому плоскость, им перпендикулярная, будет фронтально-проецирующей 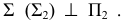
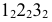
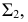
Для конической поверхности (рис. 212) при построении нормального сечения необходимо определить ось конуса, как линию пересечения двух плоскостей симметрии 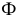
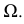
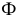
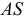
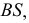
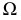
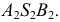
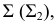
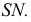
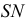
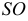
На рис. 213 показано построение нормального сечения призмы, у которой ребра занимают общее положение. Плоскость, перпендикулярная прямой общего положения, должна быть также общего положения относительно плоскостей проекций. Такую плоскость можно было бы задать горизонталью и фронталью, перпендикулярным ребрам призмы, а затем три раза решать задачу на пересечение прямой с плоскостью общего положения.
Однако в данном случае приведено решение, которое проецированием на дополнительную плоскость проекций сведено к частному, показанному на рис. 211. Новая плоскость проекций 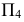
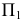
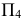
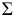
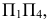
Нормальное сечение 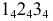
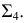
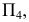
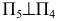
Плоскость, касательная к поверхности
Положение плоскости 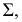
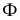
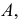
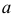
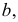
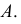
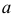
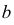
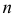
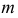
Плоскость может касаться поверхности либо в точке, либо по линии (прямой или плоской кривой). Касаясь поверхности в данной точке, плоскость может пересекать поверхность по одной или двум линиям. На поверхности могут быть точки, в которых нельзя провести касательную плоскость. Такие точки называются особыми. К их числу относятся точки самопересечения поверхности, точки ребра возврата, заостренные вершины поверхностей вращения (когда образующая пересекает ось вращения не под прямым углом).
Точки, в которых можно провести единственную касательную плоскость, называют обыкновенными.
Плоскость, касательная к линейчатой поверхности в произвольной точке на данной образующей, проходит через эту образующую. Сказанное объясняется тем, что каждая образующая является своей собственной касательной.
Задача построения касательной плоскости в точке 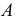
Однополосный гиперболоид вращения – поверхность дважды линейчатая. Через каждую точку этой поверхности можно провести две прямолинейные образующие. Они и определят искомую плоскость.
Касаясь поверхности в данной точке, эта плоскость пересекает гиперболоид по двум прямым. Горизонтальные проекции прямолинейных образующих построены как касательные к горловой окружности, проведенные из 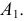
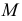
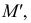
При построении касательной плоскости к нелинейчатой поверхности необходимо через заданную точку провести на поверхности две кривые. Касательные к ним определят искомую плоскость.
На рис. 215, б построена касательная плоскость к поверхности вращения в данной на ней точке
В качестве кривых, проходящих по поверхности через точку 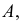
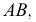
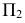
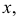
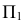
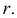
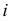
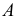
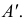
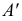
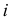
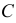
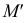
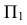
Теперь остается перевести меридиан и построенную касательную в первоначальное положение. Соединяя точку 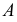
- Заказать чертежи
Пересечение прямой линии с поверхностью
Аналитически для определения координат точек пересечения прямой линии с поверхностью необходимо решить следующую систему уравнений:
где 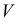
Графическое решение задачи на определение точек пересечения прямой линии с поверхностью аналогично задаче нахождения точки пересечения прямой линии с плоскостью. Точки пересечения прямой линии с поверхностью определяются способом вспомогательных секущих плоскостей. Алгоритм решения задачи следующий:
- через прямую
проводится вспомогательная плоскость
(рис.216);
- находится линия пересечения
вспомогательной плоскости
с данной поверхностью
- на пересечении полученной линии пересечения
с заданной прямой а найдутся искомые точки
и
- определяется видимость прямой.
Через прямую можно провести сколько угодно различных плоскостей, однако для упрощения решения задачи надо выбирать такую вспомогательную плоскость, в пересечении которой с данной поверхностью получились бы простые линии (прямые или окружности). Вспомогательная плоскость 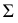
На рис. 217, а задана горизонтально-проецирующая прямая 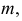
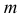
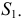
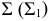
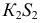
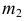
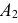
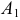
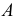
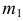
На рис. 217, б решена задача на пересечение горизонтали 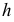
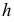
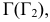
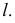
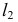
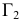
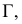
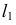
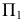
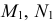
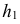
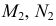
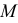
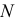
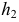
На горизонтальной плоскости проекции точки 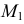
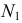
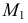
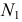
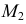
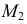
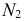
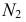
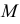
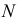
На рис. 218 приведена задача на построение точек пересечения прямой с поверхностью вращения. В качестве вспомогательной секущей плоскости выбрана горизонтально-проецирующая плоскость 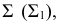
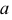
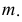
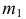
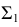
Для построения фронтальной проекции 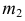
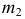
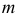
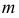
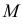
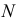
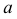
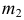
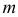
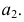
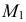
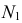
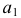
На горизонтальной плоскости проекций точки 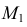
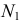
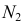
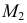
Во всех приведенных выше задачах вспомогательная секущая плоскость занимает частное положение. Вспомогательную плоскость общего положения удобно использовать в задачах при пересечении прямой линии с конической или цилиндрической поверхностью. При пересечении цилиндрической поверхности прямой линией вспомогательную плоскость проводят через данную прямую параллельно образующим цилиндра. В этом случае в сечении плоскости с цилиндром получаются прямые линии.
Пример решения задачи на пересечение прямой с цилиндром приведен на рис. 219. Задан наклонный цилиндр с круговыми основаниями. Для построения точек пересечения поверхности цилиндра с прямой линией 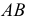
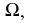
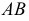
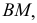
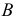
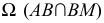
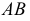
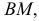
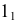
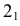
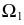
Горизонтальный след 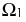
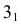
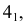
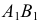
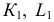
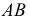
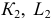
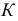
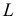
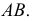
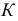
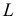
При решении задачи на пересечение поверхности прямой линией может оказаться, что данная прямая не пересекает, а лишь касается данной поверхности. В этом случае прямая является касательной к данной поверхности (рис. 220). На этом рисунке через горизонтальную проекцию 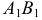
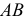
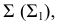
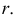
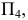
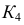
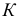
Пересечение поверхностей
Геометрическое место точек, принадлежащее одновременно двум поверхностям, называют линией пересечения (или линией перехода) данных поверхностей.
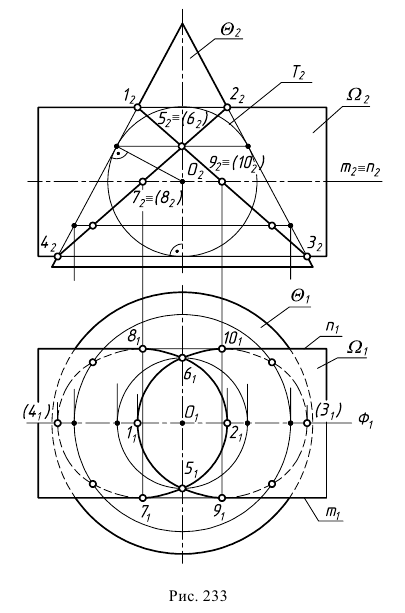
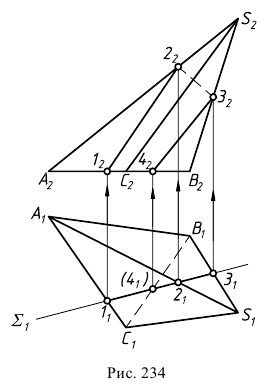
Линия пересечения двух поверхностей в общем случае представляет собой пространственную кривую. При частичном пересечении поверхностей (одна из поверхностей как бы «врезается» в другую) будет одна замкнутая линия пересечения (рис. 221). При полном пересечении поверхностей (одна из поверхностей пересекает другую насквозь) получаются две замкнутые линии пересечения (рис. 222). В случае двух многогранных поверхностей линия их пересечения является ломаной линией (рис. 223). Если одна из поверхностей кривая, а другая – гранная, то линия их пересечения состоит из участков представляющих собой плоские кривые линии, принадлежащие граням (рис. 224).
Обычно линию пересечения двух поверхностей строят по ее отдельным точкам, которые аналитически определяются при решении системы уравнений
В начертательной геометрии задачи на пересечение двух поверхностей решают путем введения вспомогательных секущих поверхностей-посредников. В качестве поверхностей-посредников применяют плоскости или сферы, поэтому различают способ вспомогательных секущих плоскостей и способ вспомогательных секущих сфер. Последний имеет разновидности: способ концентрических сфер и способ эксцентрических сфер. Применение того или иного способа зависит от типа данных поверхностей, их взаимного расположения, и расположения относительно плоскостей проекций.
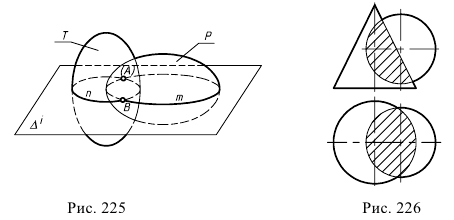
Построение общих точек, принадлежащих линии перехода поверхностей, поясняется на рис. 225 и осуществляется по общему для всех способов решения алгоритму:
- выбирают секущие поверхности-посредники
относительно данных поверхностей
такими, чтобы в пересечении получались графически простые линии (прямые, окружности), и проекции этих линий легко строились на эпюре;
- строят линии
и
по которым посредник пересечет обе поверхности;
- находят общие точки
и
пересечения линий
и
Эти точки принадлежат одному посреднику и одновременно двум данным поверхностям;
- применив последовательно несколько раз посредники и выявив ряд общих точек, соединяют их линией (последняя на рис. 225 не показана).
Каким бы способом не производилось построение линии пересечения поверхностей, при нахождении точек этой линии необходимо соблюдать определенную последовательность. У линии пересечения двух поверхностей так же, как и у линии пересечения поверхности с плоскостью (см. раздел VII. 1), различают опорные и промежуточные точки.
В первую очередь определяют экстремальные точки, так как они всегда позволяют видеть, в каких пределах расположены проекции линии пересечения, и где между ними имеет смысл строить промежуточные точки.
Далее определяют точки изменения видимости, которые отделяют видимую часть линии пересечения от невидимой. Эти точки всегда находятся на очерке той поверхности, которая расположена ближе к наблюдателю.
Строят точки на очерке другой поверхности. В точках, расположенных на очерках, проекции линии пересечения касаются очерковых линий пересекающихся поверхностей.
Для более точного построения линии пересечения данных поверхностей определяют промежуточные точки.
Следует иметь в виду, что проекции линии пересечения всегда располагаются в пределах заштрихованного контура наложения проекций двух пересекающихся поверхностей (рис. 226).
В случае, если одна из поверхностей является проецирующей, то строят проекцию линии пересечения только на одной плоскости проекций, к которой поверхность не перпендикулярна. На другой же плоскости проекция искомой линии совпадает с вырожденной проекцией поверхности (см. пример на рис. 240).
Способ вспомогательных секущих плоскостей
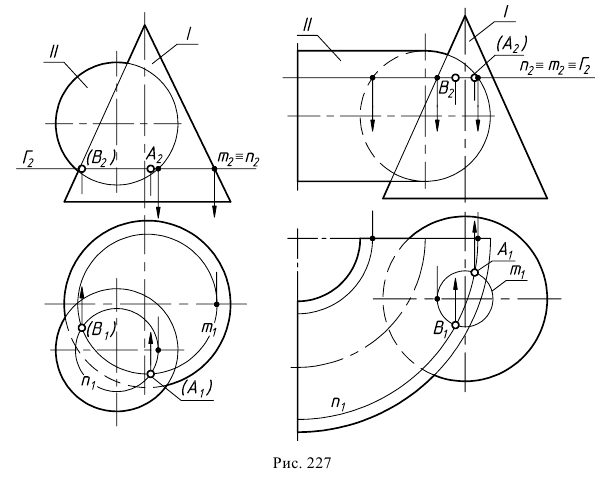
Способ вспомогательных секущих плоскостей частного положения (способ плоскостей общего положения в данном разделе не рассматривается) следует применять тогда, когда обе поверхности возможно пересечь по графически простым линиям некоторой совокупностью плоскостей уровня. Такие плоскости используют для нахождения промежуточных точек (рис. 227) после того, как найдены экстремальные точки.
Экстремальные точки располагаются в общей для двух поверхностей плоскости симметрии, которая проходит через оси этих поверхностей. Общая плоскость симметрии задана горизонтальным следом 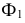
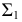
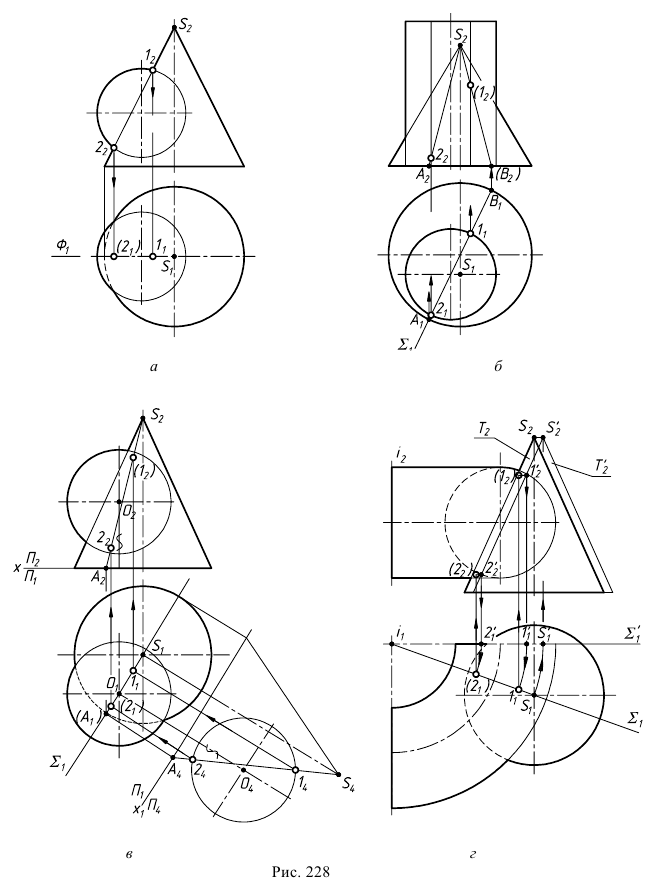
Если общая плоскость симметрии является плоскостью уровня (см. рис. 228, а), то фронтальные проекции высшей – 1 и низшей – 2 точек будут находиться на пересечении фронтальных очерков поверхности. Если общая плоскость симметрии не является плоскостью уровня, то возможны два варианта построения этих точек – без применения (см. рис. 228, б) и с применением (см. рис. 228, в, г) преобразования чертежа.
Так, на рис. 228, в сначала строят очерки поверхностей на дополнительную плоскость проекций 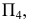
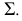
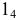
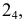
Для нахождения экстремальных точек можно воспользоваться также способом вращения вокруг проецирующей прямой. За ось вращения принимают ось одной из поверхностей. Вокруг нее поворачивают другую поверхность так, чтобы общая плоскость симметрии 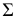
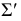
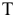
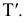
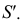
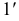
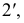
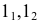
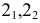
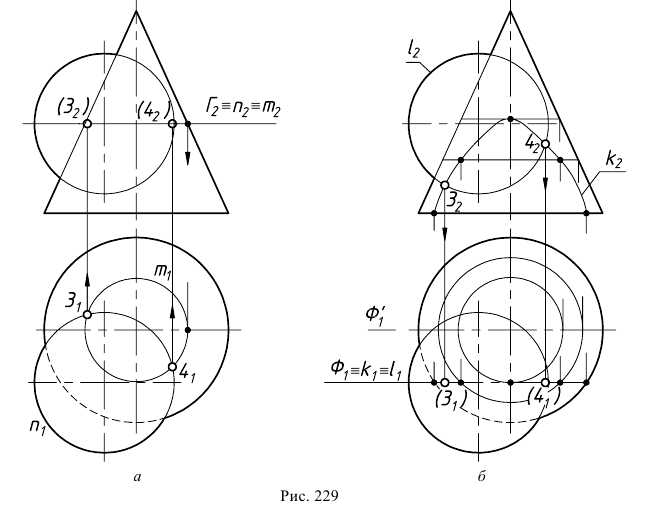
Как уже отмечалось, для определения точек изменения видимости плоскость проводят через очерк той поверхности, которая определяет видимость на соответствующей плоскости проекций. Так, на рис. 229 а, для нахождения точек изменения видимости на 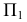
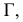
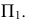
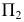
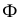
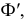
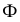
Пересечение многогранников
Линия пересечения двух многогранников может быть определена точками пересечения ребер одного многогранника с поверхностью другого и ребер второго с поверхностью первого способом вспомогательных секущих плоскостей.
Найденные точки пересечения соединяют в определенном порядке прямыми линиями, в результате чего получается замкнутая ломаная линия, звенья которой представляют собой линии пересечения граней обоих многогранников. Эта ломаная линия и будет являться линией пересечения.
При построении такой линии надо выполнять правило: соединять прямыми только те точки, которые лежат на одних и тех же гранях первого и второго многогранников. При определении видимости частей линии пересечения следует иметь в виду, что она будет видимой на проекциях только тех граней, которые видимы на данной проекции.
В зависимости от взаимного расположения пересекающихся поверхностей линия пересечения может представлять собой или одну замкнутую ломаную линию, или две. Построение линии пересечения двух многогранников на чертеже приведено ниже (VII.4., задача 7).
Способ вспомогательных секущих сфер
Для построения линии пересечения двух поверхностей вращения можно воспользоваться свойством, присущим поверхностям вращения: две соосные поверхности (т.е. поверхности с общей осью) пересекаются друг с другом по параллелям (окружностям), причем число последних равно числу точек пересечения меридианов поверхностей.
Действительно, пусть коническая поверхность образуется вращением образующей 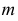
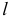
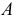
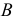
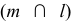
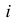
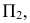
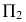
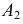
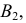
Аналогично, если расположить центр сферы на оси любой поверхности вращения, то сфера рассечет эту поверхность по окружностям, перпендикулярным оси вращения. Эти окружности (параллели) спроецируются на плоскость проекций в виде отрезков прямых, перпендикулярных проекции оси, только если ось рассекаемой поверхности вращения параллельна данной плоскости проекций.
С помощью вспомогательных поверхностей (сфер) сравнительно просто решаются задачи на построение линий пересечения двух произвольных поверхностей вращения, имеющих общую плоскость симметрии, при этом возможны два случая:
- – если оси поверхностей пересекаются, то для определения линии пересечения поверхностей используют семейство концентрических сфер, центр которых находится в точке пересечения осей поверхностей;
- – если оси не пересекаются, применяют эксцентрические сферы, центры которых перемещаются по оси одной из поверхностей.
Рассмотрим каждый случай в отдельности.
Построение линии пересечения двух поверхностей вращения с помощью концентрических сфер
Метод вспомогательных концентрических сфер можно применить при наличии следующих условий:
- пересекающиеся поверхности должны быть поверхностями вращения, так как сфера рассекает соосную с ней поверхность вращения по параллелям (окружностям);
- оси поверхностей вращения должны пересекаться, так как через точку пересечения осей можно провести сферу, соосную обеим данным поверхностям вращения;
- оси поверхностей вращения должны быть параллельны плоскости проекций, так как в этом случае параллели пересечения вспомогательной секущей сферы с данными поверхностями вращения будут проецироваться на эту плоскость проекций в виде отрезков прямых. Точки, общие для данных поверхностей, находятся как точки пересечения полученных параллелей (в виде отрезков прямых).
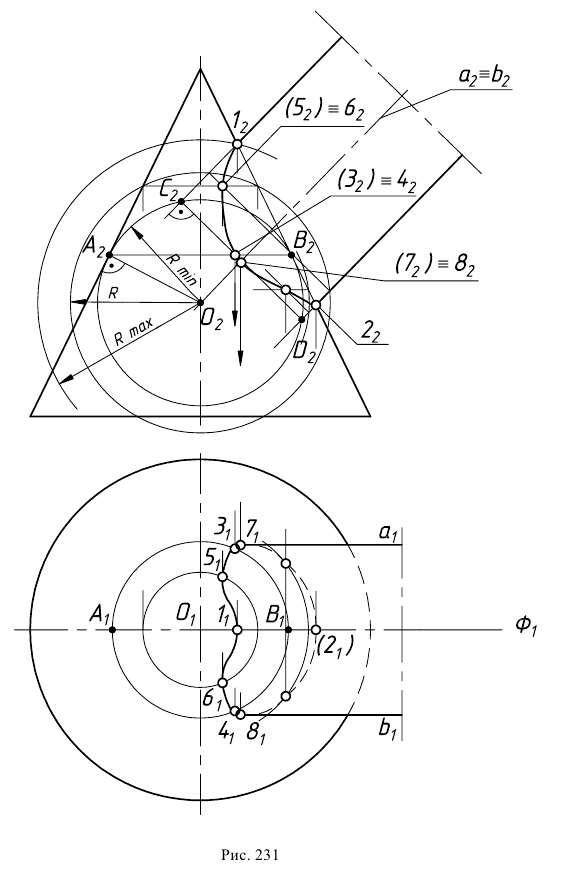
Рассмотрим основные этапы построения линии пересечения двух поверхностей – конуса и цилиндра вращения способом концентрических сфер (рис. 231).
Опорные точки 1 и 2, лежащие в плоскости симметрии 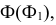
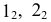
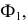
Далее выполняют следующие построения. Определяют центр 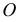
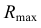
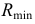
Радиус 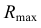
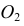
Радиус 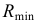
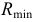
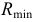
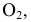
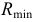
Сфера, как соосная с конусом и цилиндром, пересечет их по окружностям диаметрами 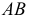
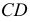
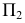
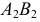
Рассмотрим взаимное расположение полученных линий пересечения (окружностей диаметрами 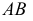
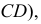
По линии проекционной связи находят горизонтальные проекции 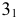
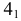
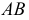
Проводя из точки 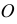
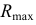
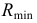
Точки изменения видимости 7 и 8 линии пересечения относительно плоскости 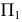
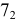
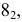
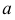
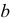
Построение линии пересечения двух поверхностей вращения с помощью эксцентрических сфер
Метод эксцентрических сфер применяется при построении линии пересечения поверхностей вращения с поверхностью, несущей на себе непрерывное множество окружностей. При этом обе поверхности должны иметь общую плоскость симметрии.
Вспомогательные эксцентрические сферы пересекаются с данными поверхностями по окружностям, которые проецируются на плоскость проекций, параллельную плоскости симметрии, в виде отрезков прямых.
Пример построения линии пересечения двух поверхностей вращения способом эксцентрических сфер рассмотрен на рис. 232, где кольцо 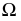
Круговые сечения конуса вращения получаются при сечении его плоскостями уровня. Кольцо имеет три системы круговых сечений, двумя из них мы воспользуемся в решении задачи. Одна система круговых сечений тора находится в плоскостях, перпендикулярных оси тора. Другая система находится в меридиональных плоскостях.
При построении линии пересечения прежде всего определяют точки 1 и 2, лежащие в общей плоскости симметрии заданных поверхностей. Затем через ось вращения тора проводим фронтально проецирующую плоскость 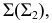
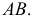
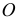
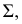
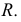
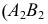
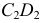
Аналогично определяем другие промежуточные точки линии пересечения поверхностей. Вспомогательные сферы имеют различные центры, находящиеся на оси конуса вращения.
По фронтальной проекции линии пересечения строят ее горизонтальную проекцию, используя принадлежности точек этой линии любой из поверхностей.
Частные случаи построения линии пересечения поверхностей. Теорема Монжа
Теорема. Если две поверхности второго порядка описаны (или вписаны) около третьей поверхности второго порядка, то они пересекаются между собой по двум плоским кривым второго порядка.
Пример построения линии пересечения поверхностей конуса 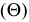
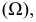
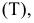
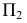
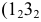
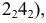
Имея фронтальные проекции линии пересечения поверхностей, можно легко построить их горизонтальные проекции (рис. 233).
Примеры решения задач
Задача 1. Построить линию пересечения пирамиды с горизонтально-проецирующей плоскостью 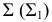
При пересечении пирамиды плоскостью получается ломаная линия.
Горизонтальная проекция линии пересечения совпадает с горизонтальным следом 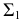
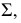
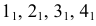
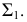
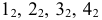
Видимость линии пересечения определяется в соответствии с видимостью граней пирамиды. Стороны линии пересечения, лежащие на видимых гранях, будут видимыми, а лежащие на невидимых гранях – невидимы.
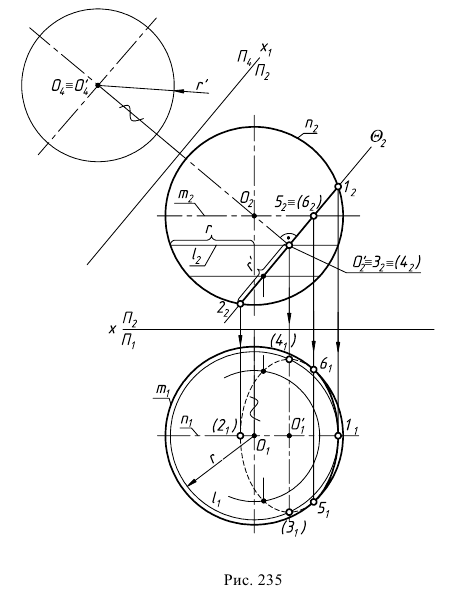
Задача 2. Построить линию пересечения сферы с фронтально-проецирующей плоскостью (рис. 235).
При пересечении сферы плоскостью 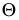
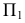
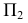
Для построения малой оси эллипса 12 на плоскости 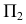
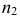
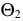
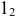
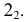
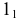
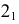
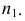
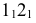
Большая и малая оси эллипсов перпендикулярны и делятся точкой пересечения пополам. Для построения большой оси эллипса отрезок 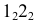
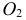
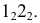
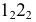
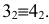
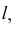
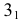
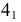
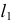
Точки изменения видимости искомой линии на 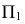
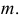
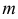
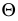
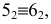
Для построения плавной кривой находятся промежуточные точки линии пересечения, как точки на соответствующих параллелях сферы.
Полученные точки линии пересечения соединяются с учетом видимости. На горизонтальной проекции линии пересечения будут видны точки, лежащие выше экватора в верхней половине сферы. Видимость поменяется на противоположную в точках 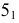
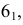
Натуральная величина сечения представляет собой окружность радиусом 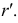
Задача 3. Построить сечение прямого кругового конуса плоскостью общего положения 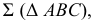
Анализ заданных геометрических образов показывает, что сечение поверхности вращения плоскостью является фигурой симметричной. Ось симметрии искомой линии пересечения лежит в плоскости 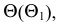
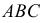
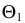
Кривая сечения строится по точкам способом вспомогательных секущих плоскостей. Построения начинаются с опорных точек.
Высшая и низшая точки, как правило, лежат в общей плоскости симметрии двух пересекающихся геометрических образов. Плоскость 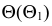
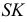
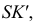
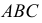
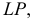
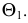
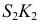
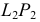
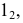
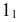
Низшие точки в данном примере располагаются на основании конуса в плоскости 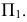
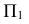
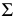
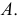
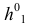
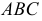
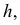
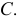
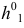
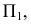
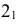
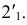
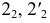
Точки изменения видимости строятся при помощи фронтальной плоскости уровня 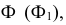
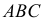
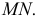
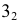
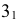
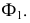
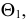
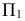
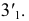
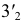
Промежуточные точки линии пересечения строятся при помощи вспомогательных плоскостей уровня 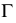
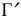
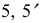
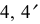
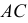
Для определения вида кривой, получающейся в сечении, выполняется перемена плоскостей проекций. Плоскость 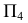
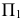
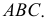
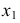
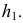
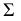
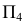
Натуральная величина сечения построена проецированием на дополнительную плоскость 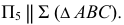
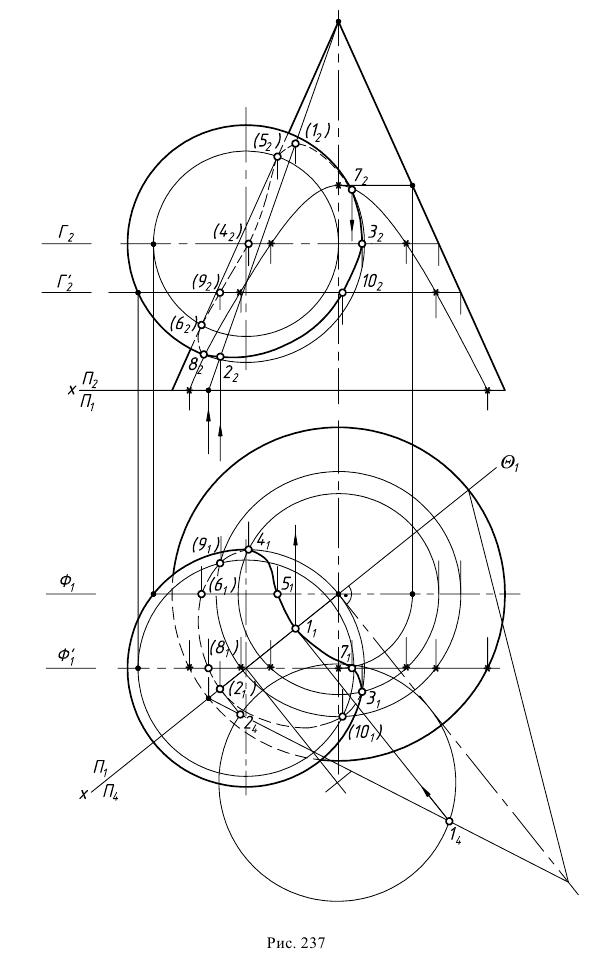
Задача 4. Построить линию пересечения сферы и прямого кругового конуса; проанализировать характерные точки линии; показать видимость линии пересечения и очерков поверхностей (рис. 237).
Анализ заданных г.о. показывает, что общая плоскость симметрии поверхностей 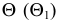
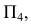
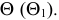
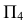
Для построения остальных точек искомой линии пересечения применяют способ вспомогательных секущих плоскостей.
Точки, лежащие на экваторе сферы (точки изменения видимости на 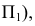
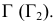
Точки искомой линии пересечения, лежащие на фронтальном очерке конуса, определяют при помощи фронтальной плоскости уровня Ф (i), проходящей через ось конуса. При пересечении фронтальной проекции очерка конуса с соответствующей параллелью сферы получают точки 5 и 6.
Для определения точек линии пересечения, принадлежащих фронтальному очерку сферы, вводят секущую плоскость 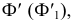
Промежуточные точки искомой линии пересечения строят при помощи секущей плоскости 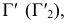
Построенные точки соединяют с учетом видимости поверхностей. На плоскости проекций 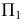
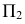
Искомая линия пересечения представляет собой пространственную кривую линию, расположенную на заданных поверхностях. Ее проекции на комплексном чертеже – плавные кривые линии, при этом на 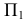
Задача 5. Построить линию пересечения конической поверхности и четверти торовой поверхности; проанализировать линию пересечения и ее проекции (рис. 238).
Решение задачи выполняем в следующей последовательности.
Сначала строим точки, расположенные в общей плоскости симметрии 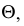
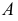
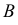
Затем находим точки изменения видимости на 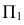
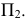
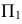
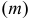
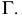
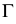
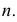
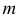
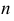
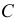
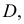
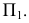
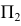
Предполагаемые точки изменения видимости могут принадлежать фронтальному очерку либо конической поверхности, либо торовой. С помощью плоскости 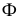
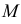
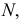
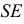
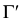
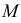
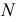
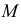
Промежуточные точки (см. рис. 227) определяем при помощи горизонтальных плоскостей уровня, рассекающих данные поверхности по параллелям. На рис. 238 обозначены проекции промежуточных точек 3 и 4, найденных с помощью плоскости 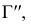
Все построенные точки соединяем с учетом видимости тех частей поверхностей, которым они принадлежат. Показываем видимость проекций очерков: толстой линией – видимые очерки, тонкой штриховой линией – невидимые очерки, очерки поверхностей, пропадающие друг в друге -тонкой сплошной линией. Построенная линия представляет собой симметричную замкнутую кривую линию четвертого порядка.
Проекции искомой линии являются плоскими кривыми (второго порядка), при этом горизонтальная проекция линии перехода симметрична относительно следа 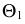
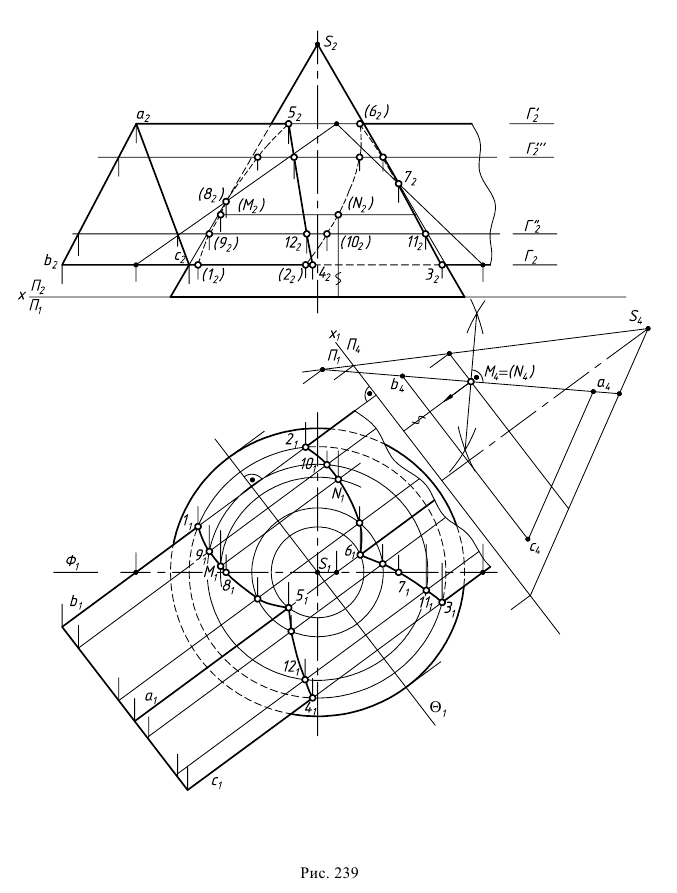
Задача 6. Построить линию пересечения трехгранной призмы и прямого кругового конуса (рис. 239).
Анализ заданных геометрических образов показывает, что грани призмы пересекают коническую поверхность по кривым 2-го порядка.
Вид этих кривых определяют переменой плоскостей проекций, выбирая вспомогательную плоскость проекций так, чтобы грани призмы заняли проецирующее положение. Плоскость проекций 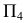
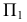
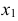
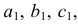
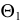
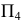
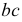
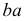
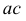
Для построения искомой линии пересечения целесообразно применять способ вспомогательных секущих плоскостей частного положения.
Линия пересечения грани 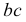
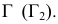
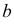
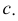
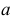
Для построения точек, лежащих на фронтальном очерке конуса, вводят секущую плоскость 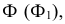
Вершины эллипса 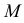
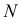
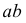
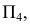
Промежуточные точки искомой линии пересечения строят при помощи вспомогательных горизонтальных плоскостей уровня, рассекающих конус по параллелям, а призму – по образующим. На рис. 239 обозначены проекции промежуточных точек 9, 10, 11, 12, найденных с помощью плоскости 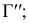
Построенные точки соединяют с учетом видимости тех частей поверхностей, которым они принадлежат. На плоскости проекций 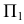
После построения проекций линии пересечения показывают видимость очерков поверхностей.
Задача 7. Построить линию пересечения многогранников: шестигранной горизонтально-проецирующей призмы I и трехгранной наклонной призмы II (рис. 240).
Точки (1, 2, 3, 4, 5, 6), принадлежащие линии пересечения многогранников, получаем непосредственно без вспомогательных построений, как точки, в которых боковые ребра 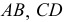
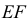
Далее находим точки пересечения ребер 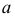
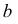
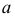
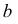
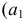
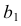
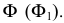
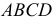
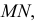
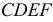
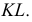
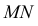
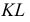
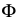
Точки пересечения ребер 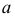
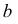
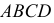
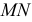
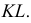
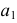
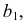
Точки 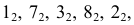
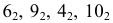
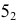
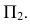
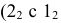
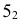
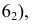
Точки 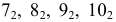
Горизонтальные проекции линий пересечения совпадают с горизонтальными следами тех боковых граней призмы I, которым отрезки ломаной линии соответственно принадлежат.
После построения линии пересечения обводим ребра обоих многогранников, учитывая их видимость относительно друг друга.
- Развертки поверхностей
- Способы преобразования проекций
- Взаимное положение прямой и плоскости
- Решение метрических задач
- Взаимное расположение геометрических образов и фигур
- Преобразование чертежа
- Кривые линии
- Образование и задание поверхности на чертеже
Скачать материал

Скачать материал




- Сейчас обучается 274 человека из 65 регионов


- Сейчас обучается 393 человека из 62 регионов


Описание презентации по отдельным слайдам:
-
1 слайд
Лекция 6 Сечение поверхности плоскостью
-
2 слайд
Алгоритм решения задачи
1. Объекты ( и ) рассекают вспомогательной секущей плоскостью Г
2. Находят линию пересечения вспомогательной плоскости с каждым из объектов
4. Выбирают следующую секущую плоскость и повторяют алгоритм
5. Полученные точки соединяют с учетом видимости искомой линии пересечения
Г Ю b
Г Ю а ;
a b Ю A,B
3. На полученных линиях пересечения определяют общие точки, принадлежащие заданным поверхностям
Г
а
b
А
B -
3 слайд
Методические указания
Плоскость, пересекающая поверхность, может занимать общее и частное положение относительно плоскостей проекций
В общем случае вид сечения – кривая линия
Сечение поверхности вращения плоскостью является фигурой симметричной. Ось симметрии фигуры сечения лежит в плоскости общей симметрии заданной поверхности и плоскости, при условии:
– проходит через ось вращения поверхности;
– перпендикулярности секущей плоскости
Сечением многогранной поверхности является ломаная линия, вершины которой лежат на ребрах поверхности -
4 слайд
2
1
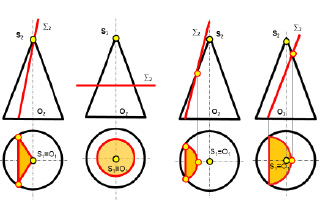
При рассечении прямого кругового цилиндра плоскостями можно получить:
1- окружность, 2- эллипс, 3 – прямые линииСечения прямого кругового цилиндра
3
2
1
3 -
5 слайд
Сечение сферы
Любая плоскость пересекает сферу по окружности. Окружность на плоскость проекций может проецироваться в натуральную величину (плоскость уровня), в виде отрезка, равного диаметру (проецирующая плоскость) и в виде эллипса (плоскость общего положения) -
6 слайд
Ф1
Q2
О1
О2
(11 )
12
21
22
При построении линии сечения сферы плоскостью частного положения Q(Q2) прежде всего находим на П2 проекции экстремальных точек. Это точки пересечения следа Q2 с очерком сферы – 12 и 22. На П1 проекции 11 и 21 располагаем на следе плоскости Ф1 с учетом их видимости.
3 ПО. -
7 слайд
С помощью плоскости Г(Г2) зафиксируем совпадающие проекции точек (32 и 42) на пересечении Г2 со следом заданной плоскости Q2. Проекции 31 и 41 располагаем на горизонтальном очерке сферы – экваторе. Это будут точки изменения видимости линии сечения на П1.
Ф1
Q2
О1
О2
31
(42)
32
Г2
41
(11 )
21
12
22 -
8 слайд
Экстремальные точки эллипса (высшую и низшую) находим, разделив пополам отрезок 12 22 перпендикуляром, опущенным из точки О2. В осно- вании перпендикуляра фиксируем две совпадающие проекции точек (52 и 62). На П1 проекции 51 и 61 располагаем на параллели b1 как невидимые.
Ф1
Q2
О1
О2
(11 )
12
21
31
(42)
32
Г2
41
b2
41
b1
22
(51 )
(61 )
(62)
52
-
9 слайд
с1
Для уточнения формы кривой – эллипса находим промежуточные точки
( на чертеже не обозначены). Совпадающие точки фиксируем произвольно на следе Q2 и переносим их на П1с помощью параллели с.Ф1
Q2
О2
(11 )
12
(61 )
21
Г2
b2
(51 )
(62)
52
b1
22
с2
31
41
О1
(42)
32
-
10 слайд
Объединяем все построенные на П1 точки в линию (эллипс) с учетом ее видимости относительно сферы. Видимость линии будет меняться в точках 31 и 41, построенных заранее в соответствии с алгоритмом решения задачи.
Ф1
Q2
с1
О2
(11 )
12
(61 )
21
Г2
b2
(51 )
(62)
52
b1
22
с2
31
41
(42)
32
О1 -
11 слайд
На П1 дополняем построенную проекцию эллипса большой осью, проходящей через экстремальные точки 51 и 61. Показать натуральную линию сечения можно, применив преобразование чертежа – замену плоскости проекций
Ф1
Q2
с1
О2
(11 )
(61 )
21
Г2
b2
(51 )
b1
22
с2
31
41
(42)
32
О1
П2
x1
П4
П1
П2
x
(62)
52
12
О4 -
12 слайд
Rc
На дополнительной плоскости проекций П4 линия сечения – окружность проецируется в натуральную величину.
Ф1
Q2
с1
О2
(11 )
(61 )
21
Г2
b2
(51 )
b1
22
с2
31
41
(42)
32
О1
П2
x1
П4
П1
П2
x
О4
(62)
52
Rc
12 -
13 слайд
1
Сечения прямого кругового конуса
При пересечении прямого кругового конуса с плоскостью в зависимости от ее расположения получаются:
1 – окружность; 2 – эллипс; 3 – парабола; 4 – гипербола; 5 – прямые линии
1
2
3
4
5
2
3
4
5 -
14 слайд
В сечении конической поверхности вращения плоскостью могут быть получены различные геометрические образы
В плоскости Г – точка,
Δ – окружность,
Θ – эллипс,
Σ – гипербола,
Ф – парабола,
Ψ – одна прямая,
Ω – две прямые. -
15 слайд
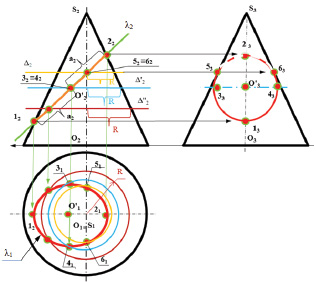
13
(43)
Сечения конической поверхности вращения плоскостями
S3
S2
Г2
Δ2
Ф2
2
Ψ2
Σ1
Ω1
S1
= m2
23
33
11
41
21
31
12
22
32
42 -
16 слайд
Анализ расположения следа секущей плоскости относительно
очерка конуса показывает, что линией сечения будет кривая 2-го порядка гипербола.
2 ПО. -
17 слайд
Точки пересечения следа плоскости с фронтальным очерком являются экстремальными точками линии сечения, определяемыми плоскостями Г и Ф. Строим их на П3.
2 ПО. -
18 слайд
Точки линии сечения 4 и 5, лежащие на профильном очерке конуса, являются точками изменения видимости на П3 и промежуточными на П1.
2 ПО. -
19 слайд
Промежуточные точки (без обозначения) линии сечения строим с помощью плоскостей Г’’ и Г’’’. На П1 объединяем все точки в проекцию линии сечения.
2 ПО. -
20 слайд
При объединении точек параболы на П3 следует учитывать её видимость относительно конуса. Видимость линии изменяется в точках 4 и 5, построенных в соответствии с алгоритмом решения.
2 ПО.
Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:
6 255 295 материалов в базе
- Выберите категорию:
- Выберите учебник и тему
- Выберите класс:
-
Тип материала:
-
Все материалы
-
Статьи
-
Научные работы
-
Видеоуроки
-
Презентации
-
Конспекты
-
Тесты
-
Рабочие программы
-
Другие методич. материалы
-
Найти материалы
Другие материалы
- 12.12.2020
- 97
- 0
- 06.12.2020
- 133
- 0
- 21.11.2020
- 233
- 2
- 12.11.2020
- 164
- 0
- 06.11.2020
- 128
- 0
- 26.10.2020
- 114
- 1
- 23.09.2020
- 211
- 0
- 02.09.2020
- 287
- 0
Вам будут интересны эти курсы:
-
Курс профессиональной переподготовки «Маркетинг: теория и методика обучения в образовательной организации»
-
Курс повышения квалификации «Методика написания учебной и научно-исследовательской работы в школе (доклад, реферат, эссе, статья) в процессе реализации метапредметных задач ФГОС ОО»
-
Курс повышения квалификации «Организация практики студентов в соответствии с требованиями ФГОС педагогических направлений подготовки»
-
Курс профессиональной переподготовки «Организация менеджмента в туризме»
-
Курс повышения квалификации «Финансы: управление структурой капитала»
-
Курс профессиональной переподготовки «Разработка эффективной стратегии развития современного вуза»
-
Курс профессиональной переподготовки «Политология: взаимодействие с органами государственной власти и управления, негосударственными и международными организациями»
-
Курс повышения квалификации «Финансовые инструменты»
-
Курс повышения квалификации «Международные валютно-кредитные отношения»
-
Курс профессиональной переподготовки «Организация маркетинговой деятельности»
-
Курс профессиональной переподготовки «Технический контроль и техническая подготовка сварочного процесса»
8.2. Пересечение поверхностей плоскостью
Определение взаимного положения плоскости и поверхности – задача позиционная, для решения которой применяется метод вспомогательных секущих плоскостей. В качестве вспомогательных секущих плоскостей используются проецирующие плоскости – плоскости перпендикулярные плоскостям проекций, поэтому основу метода вспомогательных секущих плоскостей составляет алгоритм решения задачи по нахождению проекций линии пересечения поверхности с проецирующей плоскостью.
Для определения проекций линии сечения следует найти проекции точек, принадлежащих этой линии.
В этом случае нужно выполнить анализ положений поверхности и плоскости относительно плоскостей проекций. Если секущая плоскость – общего положения, то необходимо её привести в проецирующее положение. Затем необходимо представить какого вида линия должна получиться в сечении и определить:
1) проекции опорных точек – точек расположенных на очерковых образующих поверхности (эти точки определяют границы видимости проекции кривой);
2) проекции экстремальных точек, удаленных на минимальные и максимальные расстояния от плоскостей проекций;
3) проекции произвольных (промежуточных) точек линии сечения.
В зависимости от положения плоскости по отношению к плоскостям проекций, сложность решения позиционной задачи, по определению линии пересечения ее с поверхностью существенно меняется. Наиболее простым представляется случай, когда плоскость проецирующая, а поверхность гранная. Решение подобной задачи рассмотрено на рис. 8.4.
Алгоритм решения таких задач однотипный. Рассмотрим задачи по определению линий сечения некоторых поверхностей.
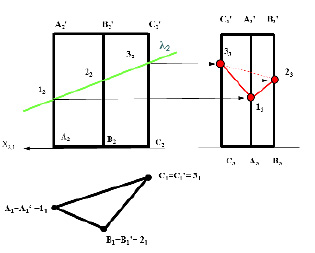
Задача 1. Определить проекции линии сечения поверхности трёхгранной призмы с фронтально-проецирующей плоскостью λ (рис. 8.11).
Рис. 8.11. Пример определения натуральной величины линии сечения
гранной поверхности проецирующей плоскостью
Многогранником называется пространственная фигура, ограниченная замкнутой поверхностью, состоящей из отсеков плоскостей, имеющих форму многоугольников. Стороны многоугольников образуют рёбра, а плоскости многоугольников – грани многогранника. Поэтому задачу по определению линии пересечения поверхности многогранника плоскостью можно свести к многократному решению задачи по нахождению: а) линии пересечения двух плоскостей (граней многогранника и секущей плоскости); б) точки встречи прямой (рёбер многогранника) с секущей плоскостью.
Если происходит пересечение многогранника, то в сечении должна получиться ломаная замкнутая кривая. В рассматриваемой задаче использован вариант а. Рассмотрим второй вариант.
Задача 2. Определить линию сечения пирамиды (рис. 8.12) плоскостью способом рёбер.
Рис. 8.12. Пример определения линии пересечения пирамиды с плоскостью
Для определения линии пересечения использованы вспомогательные проецирующие плоскости. Во фронтальной плоскости проекций через фронтальную проекцию ребра S2A2 проводится вспомогательная фронтально-проецирующая плоскость α, которая пересечёт фронтальные проекции сторон плоскости D2E2F2 в точках 12 22. По принадлежности определяются горизонтальные проекции 1121 этих точек и горизонтальная проекция точки K1 пересечения этой плоскости с ребром пирамиды S2A2. Фронтальная проекция К2 находится по принадлежности ребру S2A2. Аналогичными построениями находятся проекции точек L и M. Точка L находится с помощью плоскости β. Точка М находится с помощью вспомогательной горизонтально-проецирующей плоскости γ.
Особое место занимают задачи по нахождению линии пересечения плоскости с конической поверхностью. В зависимости от положения секущей плоскости линией пересечения может быть окружность, эллипс, парабола, гипербола (рис. 8.13).
Рис. 8.13. Возможные линии сечения поверхности конуса плоскостью
Рассмотрим примеры пересечения поверхности конуса фронтально- проецирующими плоскостями.
Задача 3. Найти линию сечения поверхности конуса фронтально-проецирующей плоскостью (рис. 8.14).
Во фронтальной плоскости проекций фронтально-проецирующая плоскость λ, при пересечении обеих образующих поверхности конуса, даёт в сечении плоскую линию эллипса (рис. 8.14).
Рис. 8.14. Пример пересечения поверхности конуса
фронтально-проецирующей плоскостью
Для определения проекций этой линии сечения необходимо найти опорные точки, к которым относятся очерковые 12 и 22 (самая низкая и самая высокая), которые расположены на образующих конусной поверхности и представляют собой одну из проекций осей эллипса. В горизонтальной плоскости проекций проекции этих точек 11 и 21 расположены на осевой линии конуса. Вторая ось эллипса находится на середине оси 12 22 в точке О’2(12О’2 = О’222 = а). Эта ось определяет вторую пару опорных точек.
Одна из этих точек (41) является самой близкой. А вторая (31) – самой далёкой. Величина второй оси эллипса определяется с помощью вспомогательной плоскости уровня Δ’2, в сечении которой находится окружность радиуса R. Величина диаметра этой окружности 3141 и представляет величину второй оси этого эллипса. Последовательное соединение проекций, полученных точек, даёт возможность для определения проекций линии сечения поверхности плоскостью. Для определения добавочных (промежуточных) точек для построения линии сечения можно воспользоваться добавочными вспомогательными плоскостями. На рисунке 8.14. построения выделены цветными линиями.
При построении третьей проекции линии сечения нужно учесть, что проекции точек для построения определяются по принадлежности, а профильные проекции точек (53 63) являются точками смены видимости для проекции линии сечения в профильной плоскости проекций.
а б в г
Рис. 8.15. Примеры возможных линий сечений поверхности конуса:
а – треугольник; б – окружность; в – гипербола; г – парабола
Рассмотрим пример сечения конуса плоскостью, проходящей через вершину конуса и другие варианты сечений поверхности конуса.
При сечении конуса плоскостью, проходящей через вершину конуса, в сечении получится фигура треугольника (рис. 8.15 а).
В сечении конуса плоскостью, перпендикулярной оси конуса получится фигура окружности (рис. 8.15 б).
Если секущая плоскость наклонена к оси вращения конуса и не проходит через его вершину, то в сечении получатся линии: эллипса (рис. 8.15 б), параболы (рис.8.15 г) и гиперболы (рис. 8.15 в).
Если плоскость ∑ параллельна одной образующей поверхности конуса, то линией пересечения является парабола (рис.8.15 г). В частном случае (плоскость касательная к поверхности конуса) сечение вырождается впрямую.
Если плоскость ∑ параллельна двум образующим поверхности конуса (в частном случае параллельна оси конуса), то линия сечения будет гиперболой. В случае прохождения плоскости через вершину конической поверхности фигурой сечения могут быть сами образующие, т.е. гипербола вырождается в две пересекающие прямые.
Задача 4. Найти линию сечения поверхности сферы фронтально-проецирующей плоскостью (рис. 8.16).
Окружность, по которой плоскость α пересекает сферу, проецируется на плоскости П1 и П3 в виде эллипса, а на плоскость П2 в прямую линию, ограниченную очерком сферы.
Охарактеризуем выбранные для построения точки:
1, 2 – две вершины эллипса, определяющие положение малой оси на горизонтальной и профильной проекциях, их фронтальные проекции определяют пересечение следа плоскости ∑ с очерком сферы. Эти точки являются соответственно высшей и низшей точками сечения.
3, 4 – фронтальные проекции этих точек лежат на горизонтальной оси сферы, т.е. принадлежат экватору сферы, их горизонтальные проекции лежат на очерке сферы и определяют зону видимости при построении эллипса на П1.
5, 6 – фронтальные проекции этих точек лежат на вертикальной оси сферы, а профильные проекции лежат на очерке сферы и определяют зону видимости при построении эллипса на П3.
7, 8 – две вершины эллипса, определяющие положение его большой оси на горизонтальной и профильной проекциях.
Рис. 8.16. Изображение пересечения поверхности сферы
проецирующей плоскостью
Положение их фронтальных проекций определяет перпендикуляр, опущенный из центра сферы к следу плоскости ∑.
Линия пересечения плоскости ∑ и сферы на фронтальной плоскости проекций совпадает со следом плоскости ∑, и на ней находятся точки 12 и 22. Горизонтальные проекции этих точек 11 и 21определяются с помощью линий связи на горизонтальной оси сферы в горизонтальной плоскости проекций.
Для определения промежуточных точек линии сечения, в общем случае, можно использовать вспомогательные секущие плоскости (Δ – горизонтальные плоскости уровня).
Например, через точки 52, 62, можно провести след плоскости Δ2 , на горизонтальной плоскости проекций линией пересечения вспомогательной плоскости сферы будет окружность радиуса R1. Горизонтальные проекции этих точек будут лежать на пересечении линии связи с полученной линией сечения. Для определения других промежуточных точек нужно выполнять аналогичные построения с использованием вспомогательных плоскостей (см. точки 71 и 81). Для определения точек 33и 43 удобно использовать вспомогательную плоскость λ. Эти проекции точек будут находиться на пересечении проекции линии сечения (окружность радиуса R2) cлиниями связи. Так могут находиться все проекции точек линии сечения.
Задача 5. Найти линию сечения поверхности цилиндра плоскостью, заданной следами (рис. 8.17).
Задача решается с помощью вспомогательных плоскостей ∑, проведённых через опорные точки поверхности цилиндра.
а б
Рис. 8.17. Пример определения линии сечения цилиндра плоскостью:
а – алгоритм определения; б – пример возможного результата определения
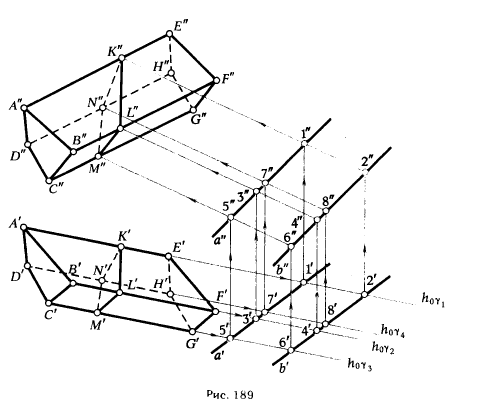
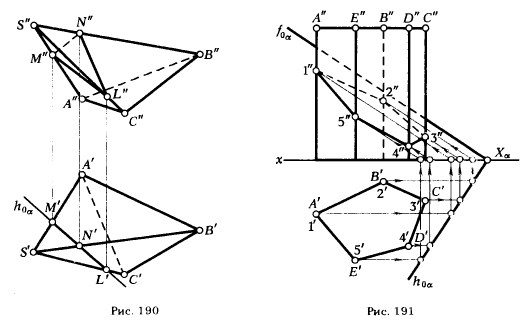

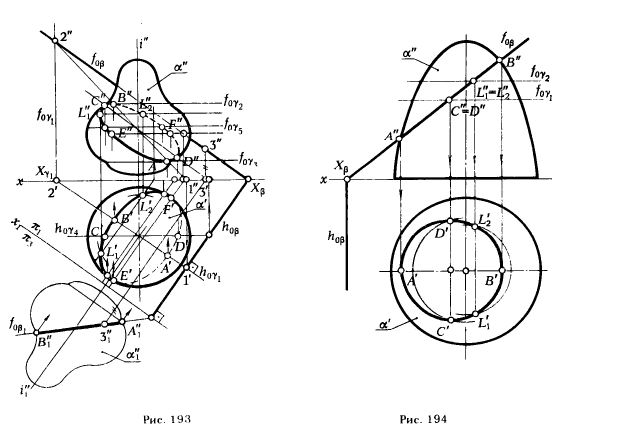
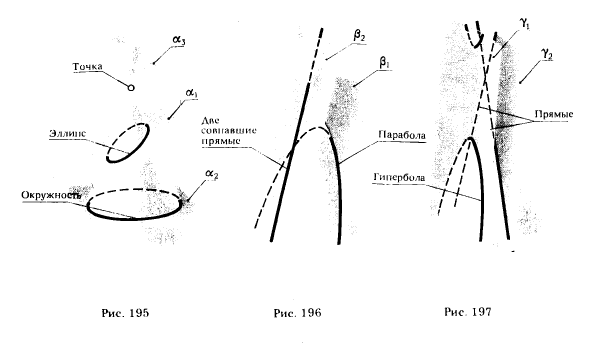
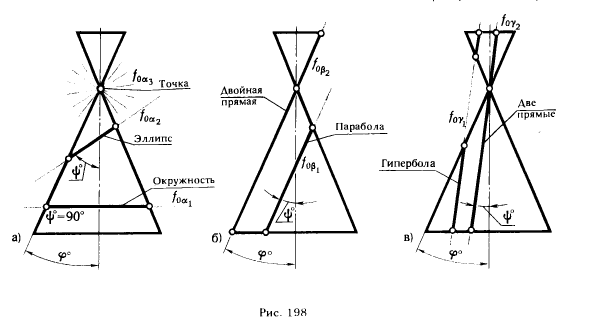
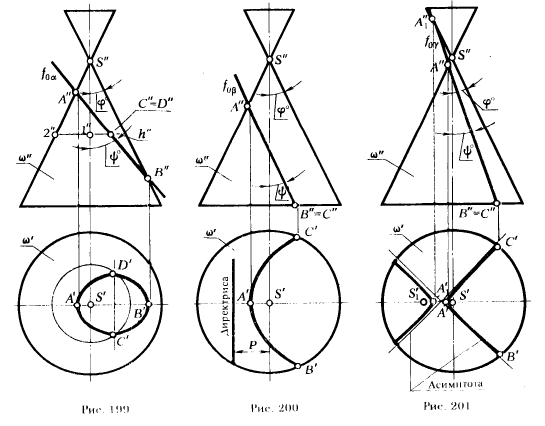
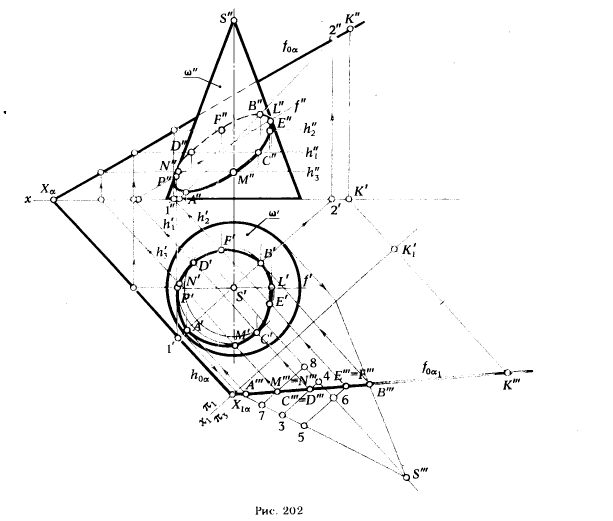

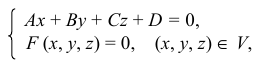
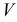
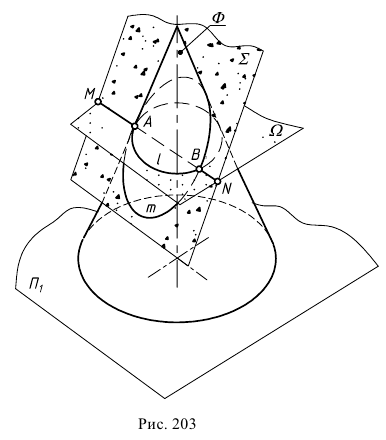
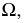 которую выбирают так, чтобы она пересекла поверхность по графически простым линиям (прямым или окружностям);
которую выбирают так, чтобы она пересекла поверхность по графически простым линиям (прямым или окружностям);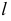 и
и 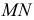 пересечения вспомогательной секущей плоскости
пересечения вспомогательной секущей плоскости 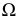 с поверхностью
с поверхностью 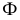 и плоскостью
и плоскостью 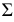 соответственно;
соответственно;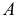 и
и 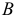 взаимного пересечения линий
взаимного пересечения линий 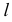 и
и 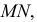 лежащих в секущей плоскости
лежащих в секущей плоскости 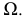 Точки
Точки 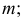
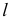 от оси тора.
от оси тора.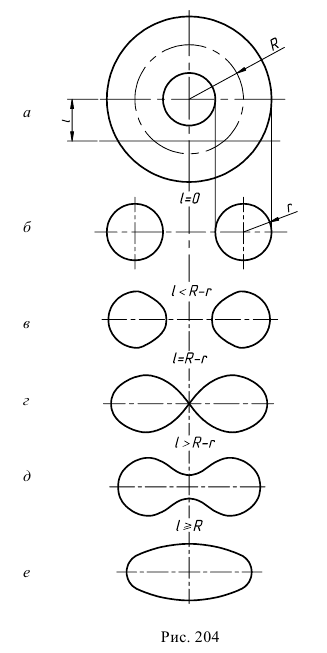
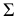
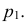
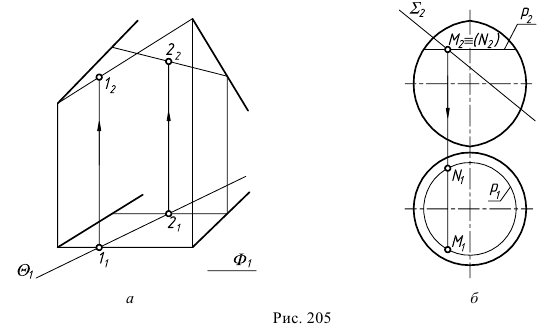
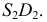
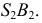
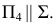
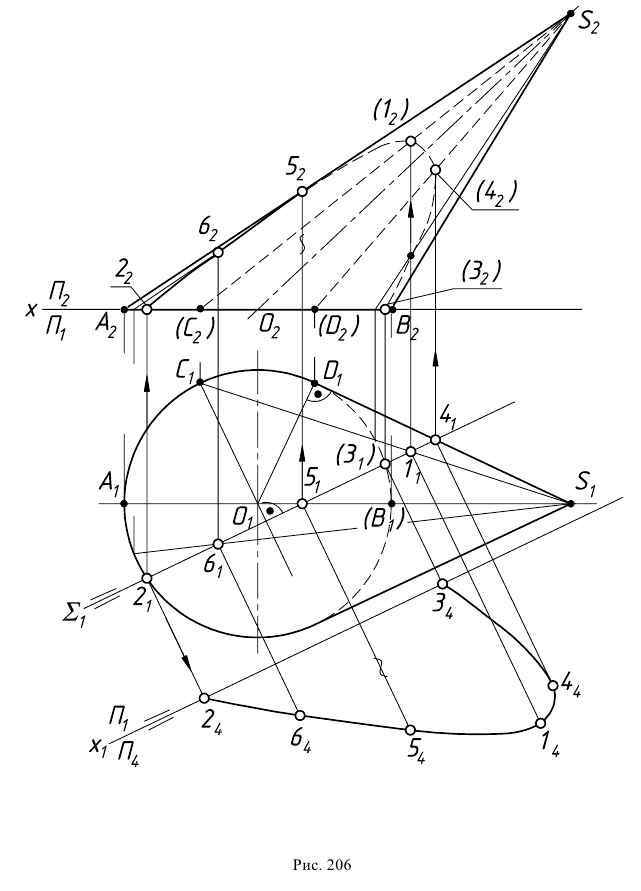
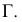
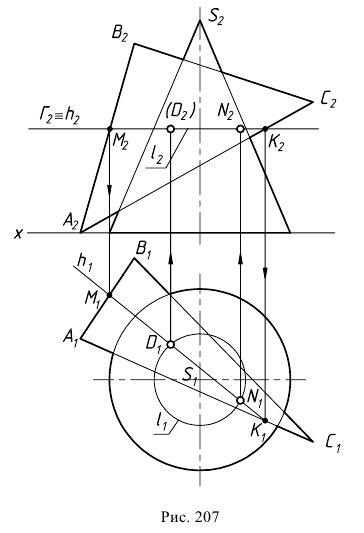
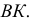
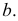
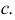
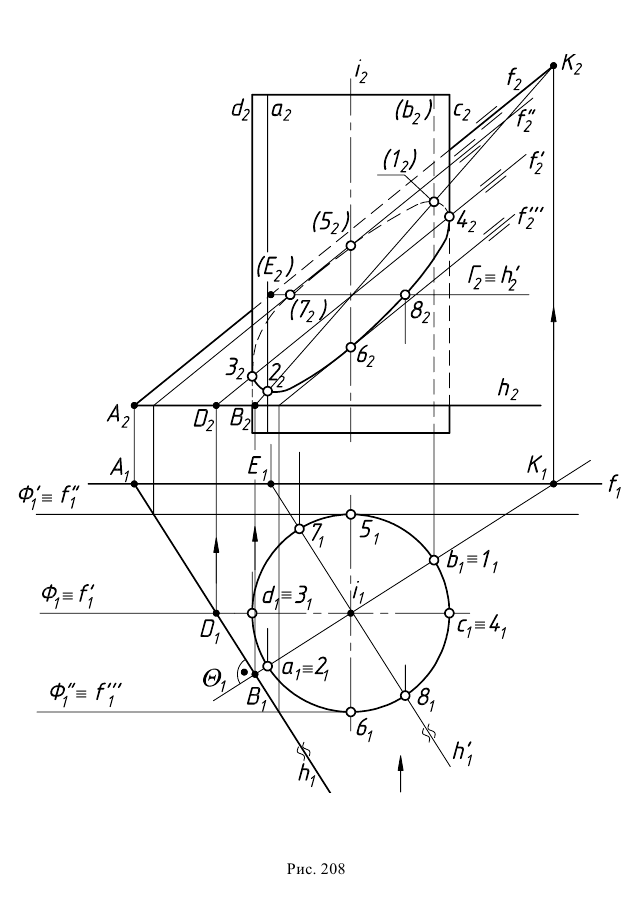
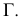
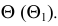
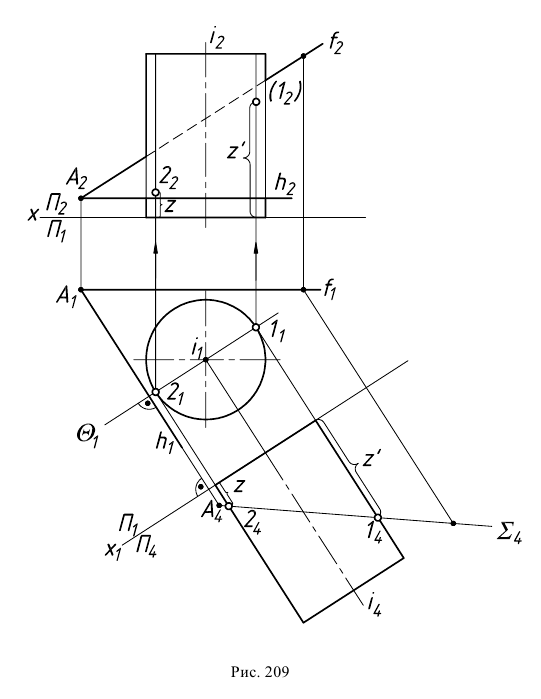
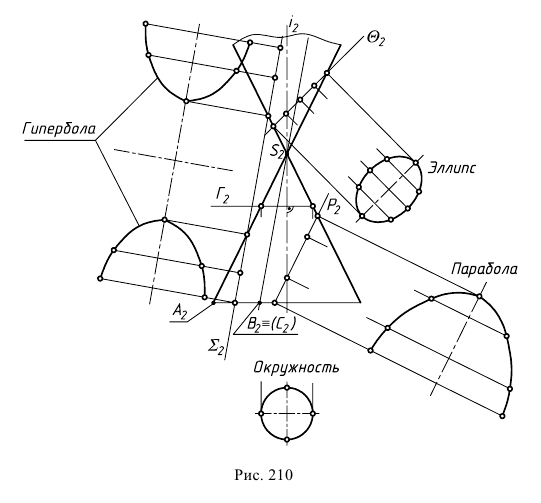
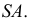
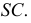
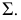
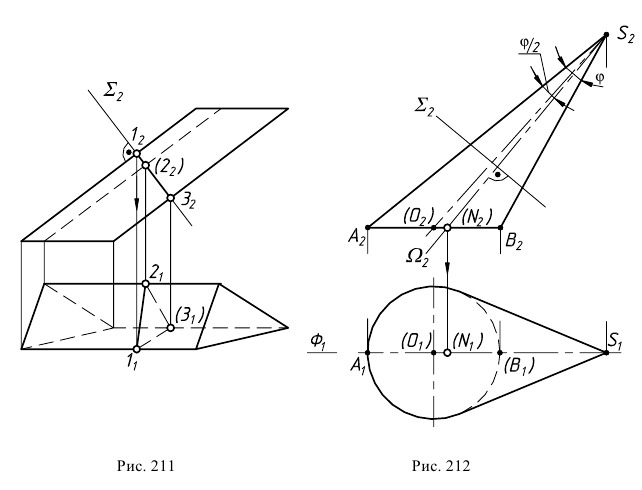
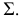
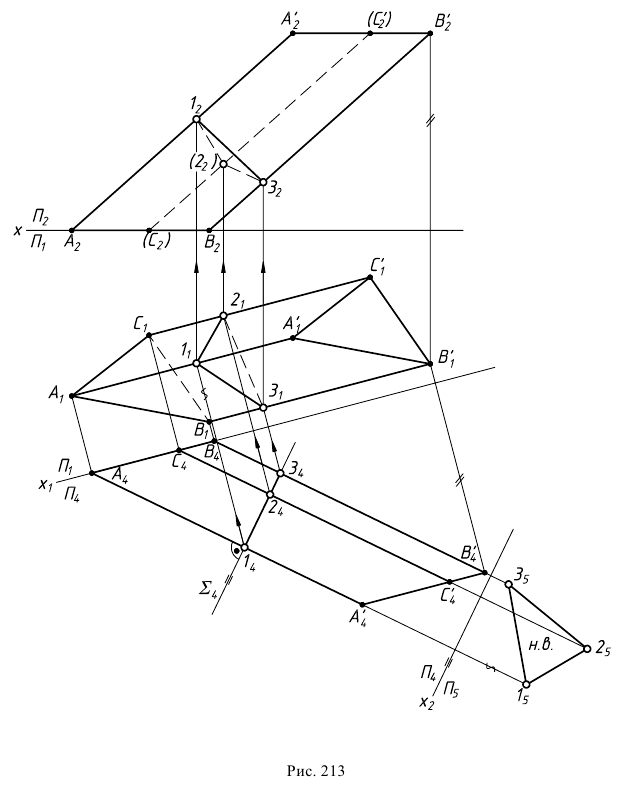
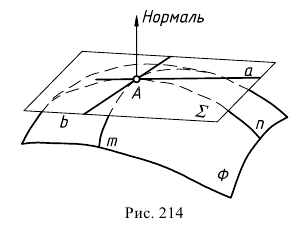
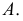
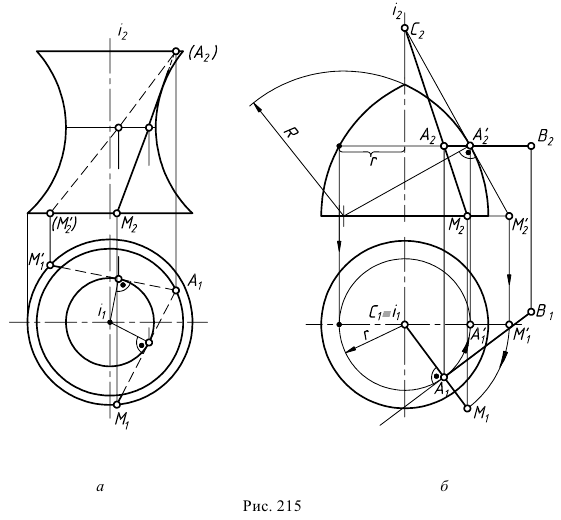
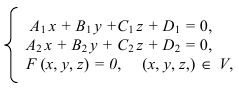
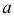 проводится вспомогательная плоскость
проводится вспомогательная плоскость 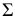 (рис.216);
(рис.216);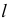 вспомогательной плоскости
вспомогательной плоскости 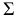 с данной поверхностью
с данной поверхностью 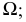
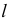 с заданной прямой а найдутся искомые точки
с заданной прямой а найдутся искомые точки 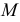 и
и 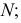
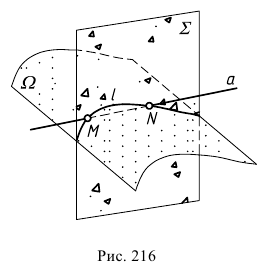
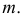
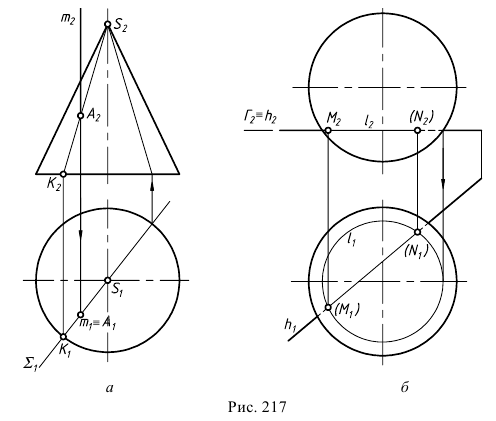
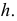
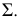
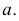
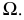
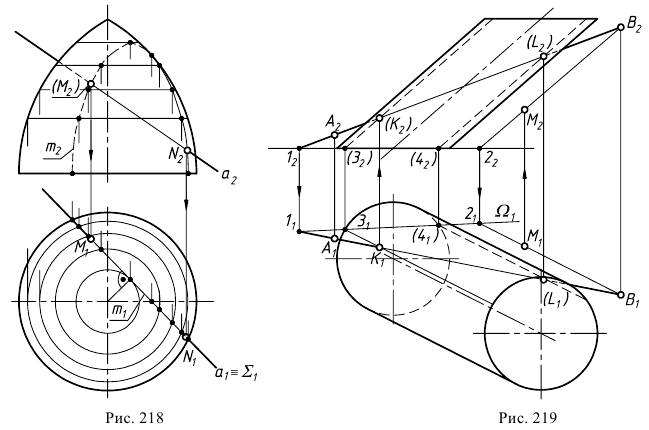
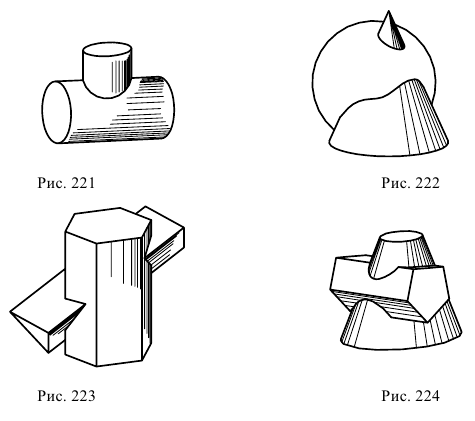
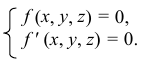
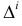 относительно данных поверхностей
относительно данных поверхностей 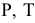 такими, чтобы в пересечении получались графически простые линии (прямые, окружности), и проекции этих линий легко строились на эпюре;
такими, чтобы в пересечении получались графически простые линии (прямые, окружности), и проекции этих линий легко строились на эпюре;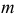 и
и 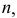 по которым посредник пересечет обе поверхности;
по которым посредник пересечет обе поверхности;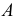 и
и 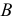 пересечения линий
пересечения линий 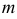 и
и 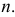 Эти точки принадлежат одному посреднику и одновременно двум данным поверхностям;
Эти точки принадлежат одному посреднику и одновременно двум данным поверхностям;