Обычно в инженерной
практике проверку прочности балок
производят по нормальным наибольшим и
касательным напряжениям [2]. Нормальные
напряжения σ зависят от величины
изгибавшего момента, а касательные
τ – от величины поперечной силы.
Касательные напряжения в сечениях балки
обычно не играют существенной роли,
поэтому размеры сечения балок определяют
из условия прочности по нормальным
максимальным напряжениям:
 ,
,
где Мmax
–
наибольший (по абсолютной величине)
изгибающий момент, известный из эпюры
изгибающих моментов (![]() ).
).
Сечение балки
подбирается по моменту сопротивления
относительно нейтральной оси:
 .
.
(3.10)
Для балки
прямоугольного сечения
![]() .
.
Числовые значения
моментов сопротивления стандартных
профилей проката указаны в соответствующих
государственных стандартах на прокат,
а на балки двутавровые приведены в
таблицах приложения Г. Следует подбирать
номер профиля, имеющий большее стандартное
ближайшее значение. Допустимо принимать
и меньшее ближайшее значение WхСТ,
однако оно должно удовлетворять условию:
![]() .
.
Момент сопротивления
при изгибе

Подходит швеллер
№ 8 (Wx=22,4
см3,
площадь сечения А=8,98 см2).
Определим
прямоугольное сечение (рисунок 3.10) при
![]()

Рисунок 3.10 –
Сечение швеллера и прямоугольное сечение
![]()
![]()
![]()
Площадь
прямоугольного сечения
![]()
A=bh=16,27
см2
≈
в 2 раза больше площади швеллера.
3.4 Совместное действие изгиба и кручения
Сочетание деформаций
изгиба и кручения испытывает большинство
валов, которые обычно представляют
собой прямые брусья круглого или
кольцевого сечения.
Возникающие от
изгиба нормальные напряжения достигают
максимального значения в волокнах,
наиболее удаленных от нейтральной оси:
![]() ,
,
где М – максимальный
изгибающий момент, Нм;
W
– осевой момент сопротивления сечения,
м3.
Для вала круглого
сечения
![]()
Максимальные
касательные напряжения при кручении
возникают в точках контура поперечного
сечения:
![]()
где Wp
– полярный момент сопротивления сечения
(Wp=2W),
м3;
Т
– крутящий момент, Нм.
Таким образом, при
сочетании изгиба и кручения опасными
будут точки (для конкретного поперечного
сечения), наиболее удаленные от нейтральной
оси.
Применив третью
теорию прочности, получим
 .
.
Расчетная формула
для круглых валов принимает вид:
 ,
,
где М
экв.
– эквивалентный момент, Нм;
[σ]
– допускаемое
напряжение на растяжение для материала
вала, Па.
Если величина и
направление нагрузки во время работы
вращающегося вала остаются неизменными,
то напряжения изгиба в теле вала будут
изменяться во времени по симметричному
циклу – I циклу
нагружения (рисунок 3.11).

Рисунок 3.11 – График
изменения во времени напряжения изгиба
I
цикл
При действии на
вал нагрузок в разных плоскостях силы
раскладывают на две взаимно перпендикулярные
плоскости, за одну из которых выбирают
плоскость действия одной из сил.
Суммарный изгибающий
момент определится как геометрическая
сумма моментов, действующих во взаимно
перпендикулярных плоскостях
рассматриваемого сечения:
![]()
где Мiв
и Мiгор
– изгибающие
моменты в i
– м сечении,
действующие в вертикальной и в
горизонтальной плоскостях соответственно.
Эквивалентный
момент определится по формуле:
![]() ,
,
Диаметр вала в
опасном сечении
рассчитывается из условия прочности:
 .
.
Примечание –
При решении задач все необходимые
вычисления следует сначала проделать
в общем виде, обозначая все данные и
искомые величины буквами, после чего
вместо буквенных обозначений подставить
их числовые значения и найти результат.
На расчетных эскизах размеры должны
быть проставлены теми же буквами, какие
имеются в расчетных формулах.
Пример 4.
Построить
эпюры изгибающих, крутящего, суммарного
изгибающего моментов и определить
диаметр вала (рисунок 3.12) в опасном
сечении.
Т = 0,2 кНм, F
= 2 кН, q
= 4 кН/м, a
= 0,2м, b
=1,2а = 0,24м,
с = 0,8а = 0,16м, [σ]
= 110МПа.
Решение:
Плоскость yz:
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Плоскость хz:
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Из условия прочности
наиболее нагруженного сечения А определим
диаметр вала.
![]()
![]()
![]()

Рисунок 3.12 –
Расчетная
схема и эпюры вала
ПРИЛОЖЕНИЕ А
ЗАДАЧА 1
Расчет бруса на
осевое растяжение (сжатие)
Сечение бруса
квадратное. Материал – сталь. Допускаемое
напряжение [σ]
= 100 МПа. Модуль продольной упругости Е
= 2·105
МПа. Исходные данные к расчету см. в
таблице + рисунок.
ИСХОДНЫЕ ДАННЫЕ
|
Вариант |
F1 |
F2 |
F3 |
l1 |
l2 |
l3 |
|
кН |
м |
|||||
|
1 |
32 |
18 |
24 |
0,7 |
0,4 |
0,8 |
|
2 |
28 |
16 |
12 |
0,6 |
0,5 |
0,7 |
|
3 |
22 |
8 |
26 |
0,5 |
0,6 |
0,9 |
|
4 |
19 |
24 |
15 |
0,8 |
0,6 |
0,5 |
|
5 |
30 |
12 |
16 |
0,4 |
0,9 |
0,6 |
|
6 |
27 |
15 |
10 |
0,6 |
0,7 |
0,8 |
|
7 |
24 |
14 |
8 |
0,3 |
0,8 |
0,7 |
|
8 |
26 |
16 |
11 |
0,7 |
0,9 |
0,4 |
|
9 |
25 |
12 |
18 |
0,5 |
0,5 |
0,9 |
|
10 |
31 |
26 |
14 |
0,7 |
0,3 |
0,5 |
|
11 |
18 |
15 |
12 |
0,6 |
0,6 |
0,8 |
|
12 |
23 |
25 |
12 |
0,8 |
0,4 |
0,7 |
|
13 |
16 |
8 |
12 |
0,4 |
0,7 |
0,9 |
|
14 |
18 |
10 |
14 |
0,6 |
0,5 |
0,8 |
|
15 |
22 |
12 |
14 |
0,5 |
0,6 |
0,7 |
|
16 |
20 |
9 |
12 |
0,7 |
0,4 |
0,8 |
|
17 |
24 |
16 |
12 |
0,9 |
0,3 |
0,6 |
|
18 |
18 |
10 |
14 |
0,8 |
0,2 |
0,7 |
|
19 |
25 |
18 |
14 |
0,7 |
0,6 |
0,9 |
|
20 |
19 |
11 |
10 |
0,8 |
0,5 |
0,6 |
|
21 |
30 |
13 |
10 |
0,4 |
0,8 |
0,5 |
|
22 |
27 |
15 |
12 |
0,6 |
0,9 |
0,4 |
|
23 |
22 |
11 |
10 |
0,7 |
0,7 |
0,6 |
|
24 |
20 |
9 |
10 |
0,5 |
0,9 |
0,7 |
|
25 |
24 |
12 |
14 |
0,7 |
0,4 |
0,9 |
|
26 |
19 |
10 |
11 |
0,8 |
0,3 |
0,6 |
|
27 |
25 |
13 |
13 |
0,4 |
0,7 |
0,8 |
|
28 |
21 |
16 |
12 |
0,5 |
0,5 |
0,7 |
|
29 |
22 |
20 |
10 |
0,8 |
0,6 |
0,8 |
|
30 |
23 |
15 |
11 |
0,7 |
0,3 |
0,9 |
Расчетные схемы


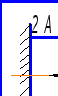
ПРИЛОЖЕНИЕ Б
ЗАДАЧА 2 РАСЧЕТ
ВАЛА НА КРУЧЕНИЕ
Сечение вала
круглое, сплошное и кольцевое. Допускаемое
напряжение кручения [τ]=25
МПа. Модуль сдвига G=8∙104
МПа
|
Вариант |
Т1, |
Т2, |
Т3, |
Т4, |
l1, |
l2, |
l3, |
l4, |
l5, |
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
1 |
200 |
300 |
400 |
0,8 |
0,7 |
0,4 |
0,6 |
0,3 |
|
|
2 |
300 |
500 |
500 |
0,7 |
0,6 |
0,5 |
0,8 |
0,4 |
|
|
3 |
400 |
400 |
300 |
0,9 |
0,5 |
0,6 |
0,3 |
0,2 |
|
|
4 |
100 |
200 |
300 |
0,5 |
0,8 |
0,9 |
0,4 |
0,3 |
|
|
5 |
300 |
400 |
100 |
0,6 |
0,4 |
0,6 |
0,5 |
0,4 |
|
|
6 |
100 |
100 |
500 |
0,8 |
0,6 |
0,7 |
0,3 |
0,2 |
|
|
7 |
300 |
200 |
200 |
0,7 |
0,3 |
0,8 |
0,4 |
0,3 |
|
|
8 |
500 |
600 |
500 |
0,4 |
0,7 |
0,9 |
0,5 |
0,4 |
|
|
9 |
600 |
800 |
700 |
0,9 |
0,5 |
0,5 |
0,3 |
0,2 |
|
|
10 |
400 |
200 |
300 |
0,5 |
0,7 |
0,8 |
0,2 |
0,3 |
|
|
11 |
300 |
500 |
600 |
0,8 |
0,6 |
0,6 |
0,4 |
0,3 |
|
|
12 |
100 |
200 |
200 |
0,7 |
0,8 |
0,4 |
0,3 |
0,4 |
|
|
13 |
700 |
500 |
200 |
0,9 |
0,4 |
0,7 |
0,2 |
0,3 |
|
|
14 |
800 |
400 |
300 |
0,8 |
0,6 |
0,5 |
0,3 |
0,3 |
|
|
15 |
900 |
600 |
400 |
0,7 |
0,5 |
0,6 |
0,4 |
0,4 |
|
|
16 |
100 |
200 |
300 |
0,8 |
0,7 |
0,4 |
0,2 |
0,5 |
|
|
17 |
200 |
800 |
100 |
0,6 |
0,9 |
0,3 |
0,3 |
0,6 |
|
|
18 |
300 |
800 |
100 |
0,7 |
0,8 |
0,2 |
0,4 |
0,7 |
|
|
19 |
400 |
500 |
300 |
200 |
0,9 |
0,7 |
0,6 |
0,2 |
|
|
20 |
500 |
500 |
200 |
300 |
0,6 |
0,8 |
0,5 |
0,3 |
|
|
21 |
600 |
900 |
400 |
100 |
0,5 |
0,4 |
0,8 |
0,4 |
|
|
22 |
700 |
800 |
300 |
200 |
0,4 |
0,6 |
0,9 |
0,2 |
|
|
23 |
800 |
700 |
100 |
400 |
0,6 |
0,7 |
0,7 |
0,3 |
|
|
24 |
900 |
600 |
200 |
300 |
0,7 |
0,5 |
0,9 |
0,4 |
|
|
25 |
100 |
500 |
300 |
200 |
0,9 |
0,7 |
0,4 |
0,2 |
|
|
26 |
200 |
300 |
500 |
300 |
0,6 |
0,8 |
0,3 |
0,4 |
|
|
27 |
300 |
300 |
400 |
200 |
0,8 |
0,4 |
0,7 |
0,3 |
|
|
28 |
400 |
200 |
600 |
100 |
0,7 |
0,5 |
0,5 |
0,2 |
|
|
29 |
500 |
100 |
700 |
200 |
0,8 |
0,8 |
0,6 |
0,3 |
|
|
30 |
600 |
200 |
800 |
300 |
0,9 |
0,7 |
0,3 |
0,4 |
Расчетные схемы



ПРИЛОЖЕНИЕ В
ЗАДАЧА 3
РАСЧЕТ НА ПРОЧНОСТЬ ДВУХОПОРНОЙ БАЛКИ
ПРИ ИЗГИБЕ
Для данной балки подобрать сечения
двутавра и прямоугольника (h/b=2).
Допускаемое напряжения изгиба [σ]=160
МПа
|
Вариант |
М,K |
F, |
q, |
l1, |
l2, |
l3, |
l4, |
l5, |
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
|
1 |
18 |
26 |
14 |
2 |
2 |
5 |
1 |
1 |
|
2 |
24 |
18 |
10 |
2 |
3 |
2 |
3 |
2 |
|
3 |
16 |
34 |
12 |
2 |
3 |
3 |
2 |
2 |
|
4 |
30 |
24 |
16 |
2 |
4 |
4 |
1 |
2 |
|
5 |
20 |
12 |
8 |
1,8 |
2,2 |
1 |
5 |
1 |
|
6 |
22 |
16 |
10 |
1,6 |
1 |
1,4 |
6 |
2 |
|
7 |
18 |
22 |
14 |
2,2 |
2 |
1,8 |
5 |
1 |
|
8 |
16 |
24 |
12 |
2,5 |
1 |
1,5 |
5 |
2 |
|
9 |
16 |
24 |
12 |
2,5 |
1 |
1,5 |
5 |
2 |
|
10 |
14 |
15 |
8 |
1,6 |
2 |
1,4 |
4 |
3 |
|
11 |
10 |
23 |
12 |
2 |
2 |
2 |
4 |
2 |
|
12 |
18 |
17 |
10 |
1,8 |
3 |
1,2 |
5 |
1 |
|
13 |
16 |
25 |
15 |
2 |
2 |
4 |
2 |
2 |
|
14 |
24 |
16 |
10 |
2 |
3 |
4 |
2 |
1 |
|
15 |
1 |
22 |
12 |
1,6 |
2,4 |
3,5 |
2,5 |
2 |
|
16 |
20 |
18 |
14 |
1,8 |
2,2 |
4,5 |
2,5 |
2 |
|
17 |
22 |
24 |
8 |
2 |
2 |
4 |
3 |
1 |
|
18 |
16 |
26 |
6 |
2 |
2 |
3,5 |
3,5 |
1 |
|
19 |
18 |
20 |
10 |
1,5 |
2,5 |
4,2 |
1,8 |
8 |
|
20 |
28 |
18 |
16 |
1,8 |
2,2 |
4,5 |
2,5 |
3 |
|
21 |
17 |
25 |
12 |
2 |
2 |
1 |
5 |
2 |
|
22 |
15 |
30 |
10 |
1,5 |
2,5 |
2 |
4 |
1 |
|
23 |
26 |
22 |
8 |
2 |
2 |
2 |
3 |
2 |
|
24 |
30 |
18 |
14 |
1,6 |
3,0 |
2 |
4 |
1 |
|
25 |
24 |
26 |
15 |
1,5 |
2,5 |
6 |
1 |
1 |
|
26 |
22 |
13 |
2,5 |
1,5 |
5 |
2 |
2 |
|
|
27 |
20 |
12 |
2,0 |
1,5 |
5,5 |
3 |
2 |
|
|
28 |
18 |
28 |
10 |
2,0 |
1,5 |
4,5 |
2 |
2 |
|
29 |
30 |
20 |
8 |
1,8 |
3,2 |
1 |
2 |
1 |
|
30 |
28 |
18 |
15 |
2 |
2,5 |
1,5 |
5 |
2 |
Расчетные схемы
задачи 3



ПРИЛОЖЕНИЕ Г
Сталь прокатная
– балки двутавровые (ГОСТ 8239-83)
h
– высота профиля;
b
– ширина;
d
– толщина;
t
– средняя толщина;
R
и r
– внутренний и наружный радиусы
скруглений;
J
– момент инерции;
W
– момент сопротивления;
i
– радиус инерции;
S
– статический момент полусечения

|
Номер профиля |
Масса |
Размеры, |
Площадь сечения, |
Jx, см4 |
Wx, см3 |
ix, см |
Sx, см3 |
Jy, см4 |
Wy, см3 |
iy, см |
|||||
|
h |
b |
d |
t |
R |
r |
||||||||||
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
15 |
16 |
|
10 |
9,46 |
100 |
55 |
4,5 |
7,2 |
7 |
2,5 |
12 |
198 |
39,7 |
4,06 |
23 |
17,9 |
6,49 |
1,22 |
|
12 |
11,45 |
120 |
64 |
4,8 |
7,3 |
7,5 |
3 |
14,7 |
350 |
58,4 |
4,88 |
33,7 |
27,9 |
8,72 |
1,38 |
|
14 |
13,7 |
140 |
73 |
4,9 |
7,5 |
8 |
3 |
17,4 |
572 |
81,7 |
5,73 |
46,8 |
41,9 |
11,5 |
1,55 |
|
16 |
15,9 |
160 |
81 |
5,0 |
7,8 |
8,5 |
3,5 |
20,2 |
873 |
109,0 |
6,57 |
62,3 |
58,6 |
14,5 |
1,7 |
|
18 |
18,4 |
180 |
90 |
5,1 |
8,1 |
9,0 |
3,5 |
23,4 |
1290 |
143,0 |
7,42 |
81,4 |
82,6 |
18,4 |
1,88 |
|
18а |
19,9 |
180 |
100 |
5,1 |
8,3 |
9,0 |
3,5 |
25,4 |
1430 |
159,0 |
7,51 |
89,8 |
114,0 |
22,8 |
2,12 |
|
20 |
21,0 |
200 |
100 |
5,2 |
8,4 |
9,5 |
4,0 |
26,8 |
1840 |
184,0 |
8,28 |
104,0 |
115,0 |
23,1 |
2,07 |
|
20а |
22,7 |
200 |
110 |
5,2 |
8,6 |
9,5 |
4,0 |
28,9 |
2030 |
203,0 |
8,37 |
114,0 |
155,0 |
28,2 |
2,32 |
|
22 |
24,0 |
220 |
110 |
5,4 |
8,7 |
10,0 |
4,0 |
30,6 |
2550 |
232,0 |
9,13 |
131,0 |
157,0 |
28,6 |
2,27 |
|
22а |
25,8 |
220 |
120 |
5,4 |
8,9 |
10,0 |
4,0 |
32,6 |
2790 |
254,0 |
9,22 |
143,0 |
106,0 |
34,3 |
2,5 |
|
24 |
27,3 |
240 |
115 |
5,6 |
9,5 |
10,5 |
4,0 |
34,8 |
3460 |
289 |
9,97 |
163 |
198 |
34,5 |
2,37 |
|
24а |
29,4 |
240 |
125 |
5,6 |
9,8 |
20,5 |
4,0 |
37,5 |
3800 |
317 |
10,1 |
178 |
260 |
41,6 |
2,63 |
|
27 |
31,5 |
270 |
125 |
6,0 |
9,8 |
11,0 |
4,5 |
40,2 |
5010 |
371 |
11,2 |
210 |
260 |
41,5 |
2,54 |
|
27а |
33,9 |
270 |
135 |
6,0 |
10,2 |
11,0 |
4,5 |
43,2 |
5500 |
407 |
11,3 |
229 |
337 |
50,0 |
2,8 |
|
30 |
36,5 |
300 |
135 |
6,5 |
10,2 |
12,0 |
5 |
46,5 |
7080 |
472 |
12,3 |
268 |
337 |
49,9 |
2,69 |
|
30а |
39,2 |
300 |
145 |
6,5 |
10,7 |
12,0 |
5 |
49,9 |
7780 |
518 |
12,5 |
292 |
436 |
60,1 |
2,95 |
|
33 |
42,2 |
330 |
140 |
7,0 |
11,2 |
13,0 |
5 |
53,8 |
9840 |
597 |
13,5 |
339 |
419 |
59,1 |
3,79 |
|
36 |
48,6 |
360 |
145 |
7,5 |
12,3 |
14,0 |
6 |
61,9 |
13380 |
743 |
14,7 |
423 |
516 |
71,1 |
2,89 |
|
40 |
57,0 |
400 |
155 |
8,3 |
13,0 |
15,0 |
6 |
72,6 |
19062 |
953 |
16,2 |
545 |
667 |
86,1 |
3,08 |
|
45 |
66,5 |
450 |
160 |
9,0 |
14,2 |
16,0 |
7 |
84,7 |
27696 |
1231 |
18,1 |
708 |
808 |
101,0 |
3,09 |
|
50 |
78,5 |
500 |
170 |
10,0 |
15,2 |
17,0 |
7 |
100 |
39727 |
1589 |
19,9 |
919 |
1043 |
123,0 |
3,23 |
|
60 |
108,0 |
600 |
190 |
12,0 |
17,8 |
20,0 |
8 |
138 |
76806 |
2560 |
23,6 |
1491 |
1725 |
182,0 |
3,54 |
|
60б |
120,0 |
650 |
200 |
12,0 |
19,2 |
22,0 |
9 |
153 |
101400 |
3120 |
25,8 |
1800 |
2170 |
217,0 |
3,77 |
|
70 |
138,0 |
700 |
210 |
13,0 |
20,8 |
24,0 |
10 |
176 |
134600 |
3840 |
27,7 |
2230 |
2730 |
260,0 |
3,94 |
|
70а |
168,0 |
700 |
210 |
15,0 |
24,0 |
24,0 |
10 |
202 |
152700 |
4360 |
27,5 |
2550 |
3240 |
309,0 |
4,01 |
|
70б |
184,0 |
700 |
210 |
17,5 |
28,2 |
24,0 |
10 |
234 |
175770 |
5010 |
27,4 |
2940 |
3910 |
373,0 |
4,09 |
ПРИЛОЖЕНИЕ Д
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #

Пример решения задачи по подбору номера двутаврового сечения балки, обеспечивающего её необходимую прочность.
Задача
Для заданной стальной балки подобрать двутавровое сечение по условию прочности.
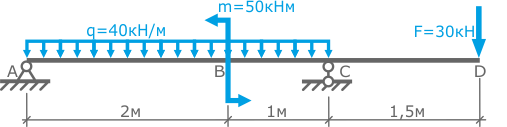
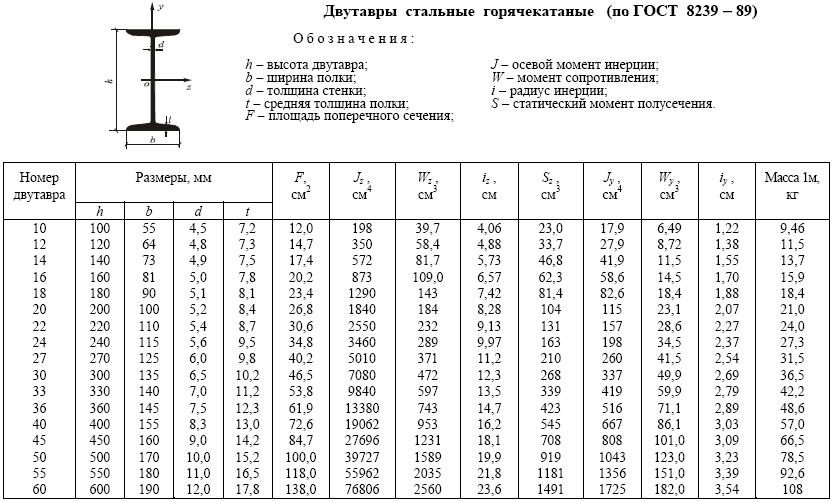
Двутавр стальной горячекатаный ГОСТ 8239-89.
Допустимые напряжения для материала балки [σ]=160МПа.
Другие примеры решений >
Помощь с решением задач >
Решение
Предыдущие пункты решения задачи:
- Определение опорных реакций.
- Построение эпюр внутренних поперечных сил и изгибающих моментов.
- Расчет момента сопротивления сечения балки по условию прочности.
Как было показано ранее, для обеспечения необходимой прочности балки момент сопротивления Wx сечения балки должен быть не менее 297,5 см3
Другие видео
В данном случае нагружения двутавровое сечение, очевидно, необходимо расположить «вертикально».
Номер двутавра обеспечивающий прочность балки определим по сортаменту прокатной стали для двутавров ГОСТ 8232.
Для этого в графе Wx таблицы находим ближайшее к расчетному (297,5 см3) в сторону увеличения значение момента сопротивления.
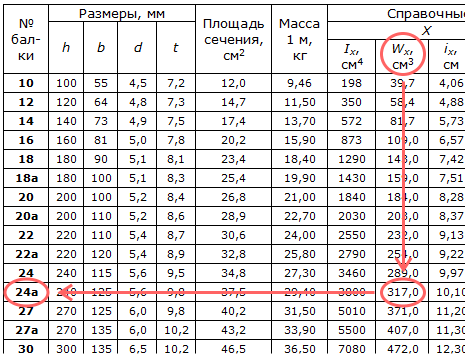
Ближайшим в большую сторону значением является 317 см3.
На этой же строке в первом столбце указан соответствующий номер двутаврового сечения.
Искомый номер двутавра – 24a.
Номер швеллера для балки подбирается аналогично, по сортаменту швеллеров.
Оценка экономичности сечений >
Другие примеры решения задач >
Сохранить или поделиться с друзьями
Вы находитесь тут:
На нашем сайте Вы можете получить решение задач и онлайн помощь
Подробнее
Решение задач и лекции по технической механике, теормеху и сопромату
Проверка прочности балки и подбор поперечных сечений
Балка проверяется на прочность по наибольшим нормальным напряжениям, возникающие в поперечном сечении балки, где на эпюре 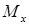 наибольший по абсолютному значению изгибающий момент. При поперечном изгибе в балке возникают и касательные напряжения, но они невелики, и при расчете на прочность учитываются только для двутавровых балок.
наибольший по абсолютному значению изгибающий момент. При поперечном изгибе в балке возникают и касательные напряжения, но они невелики, и при расчете на прочность учитываются только для двутавровых балок.
Условие прочности при изгибе по нормальным напряжениям: 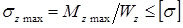 ,
,
где допускаемое напряжение 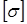 принимается, как и при растяжении (сжатии) стержня из такого же материала.
принимается, как и при растяжении (сжатии) стержня из такого же материала.
Формула условия прочности при изгибе по нормальным напряжениям позволяет осуществить подбор сечения балки при заданном материале и максимальном абсолютном значении изгибающего момента. Требуемый момент сопротивления балки при изгибе определяется из условия: 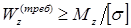 .
.
При изменении положения сечения по отношению к действующей нагрузке прочность балки существенно изменяется, хотя площадь сечения и остается неизменной. Например, для балки прямоугольного поперечного сечения с отношением сторон 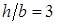 , расположенной таким образом, что высота прямоугольника h перпендикулярна нейтральной оси x, прочнее той же самой балки повернутой на
, расположенной таким образом, что высота прямоугольника h перпендикулярна нейтральной оси x, прочнее той же самой балки повернутой на 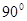 , в три раза, так как
, в три раза, так как 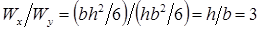 . В выражении для осевого момента сопротивления балки прямоугольного поперечного сечения при изгибе в квадрате стоит тот ее размер, который перпендикулярен нейтральной оси. Следовательно, сечение балки необходимо располагать таким образом, чтобы силовая плоскость совпадала с той из главных центральных осей, относительно которой момент инерции минимален ( ось, относительно которой главный момент инерции поперечного сечения максимален, является нейтральной осью). Это обстоятельство лишний раз подчеркивает важность темы «Определение положения главных центральных осей инерции поперечного сечения стержня».
. В выражении для осевого момента сопротивления балки прямоугольного поперечного сечения при изгибе в квадрате стоит тот ее размер, который перпендикулярен нейтральной оси. Следовательно, сечение балки необходимо располагать таким образом, чтобы силовая плоскость совпадала с той из главных центральных осей, относительно которой момент инерции минимален ( ось, относительно которой главный момент инерции поперечного сечения максимален, является нейтральной осью). Это обстоятельство лишний раз подчеркивает важность темы «Определение положения главных центральных осей инерции поперечного сечения стержня».
Проверка прочности двутавров
Для тонкостенных балок, например балок двутаврового профиля, проверка прочности производится следующим образом:
в наиболее удаленных от нейтральной оси точках прочность проверяется по формуле 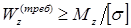 ;
;
в точках, где полка соединяется со стенкой прочность определяется по главным напряжениям.
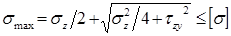
в точках, расположенных на нейтральной оси, прочность определяется по наибольшим касательным напряжениям:
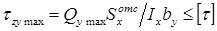
Подбор сечения металлической балки
Расчет металлической балки перекрытия
Бывают случаи, когда деревянные балки для междуэтажных или чердачных перекрытий использовать экономически не выгодно. Например, когда пролет слишком большой и поэтому для его перекрытия требуются деревянные балки большого сечения. Или когда у Вас есть хороший знакомый, который торгует не пиломатериалом, а металлопрокатом.
В любом случае не лишним будет знать во сколько может обойтись перекрытие, если использовать металлические балки, а не деревянные. И в этом Вам поможет данный калькулятор. С его помощью можно рассчитать требуемые момент сопротивления и момент инерции, которые для подбора металлических балок для перекрытия по сортаментам из условия прочности и прогиба.
Рассчитывается балка перекрытия на изгиб как однопролетная шарнирно-опертая балка.
Помощь в расчете
Нет желания и времени разбираться в калькуляторе и сборе нагрузок. И в то же время хочется быть уверенным на 100% в результате. Буду рад помочь.
Стоимость расчета балок и других строительных конструкций:
- от 1 000 руб. — без предоставления подробного письменного отчета;
- от 1 500 руб. — с отчетом.
А также, если проект не предполагается, но есть масса вопросов по выбору материалов, конструкциям и архитектуре. Обращайтесь, помогу.
- Консультации от 1 000 руб.
Контакт для связи, e-mail: Этот адрес электронной почты защищен от спам-ботов. У вас должен быть включен JavaScript для просмотра.
С уважением, Игорь.
Калькулятор
 Калькуляторы по теме:
Калькуляторы по теме:
Инструкция к калькулятору
Исходные данные
Длина пролета (L) — расстояние между двумя внутренними гранями стен. Другими словами, пролет, который перекрывают рассчитываемые балки.
Шаг балок (Р) — шаг по центру балок, через который они укладываются.
Вид перекрытия — в случае, если на последнем этаже Вы жить не будете, и он не будет сильно захламляться милыми Вашему сердцу вещами, то выбирается «Чердачное», в остальных случаях — «Междуэтажное».
Длина стены (Х) — длина стены, на которую опираются балки.
Длина балки (А) — самый большой размер балки.
Вес 1 п.м. — данный параметр используется как бы во втором этапе (после того, как Вы уже подобрали нужную балку).
Расчетное сопротивление Ry — данный параметр зависит от марки стали. Например, если марка стали:
- С235 — Ry = 230 МПа;
- С255 — Ry = 250 МПа;
- С345 — Ry = 335 МПа;
Но обычно в расчете используется Ry = 210 МПа для того, чтобы обезопасить себя от разного рода «форс-мажерных» ситуаций. Все-таки в России живем — привезут металлопрокат из стали не той марки и все.
Модуль упругости Е — этот параметр зависит от вида металла. Для самых распространенных его значение равно:
- сталь — Е = 200 000 МПа;
- алюминий — Е = 70 000 МПа.
Значения нормативной и расчетной нагрузок указываются после их сбора на перекрытие.
Цена за 1 т — стоимость 1 тонны металлопроката.
Результат
Расчет по прочности:
Wтреб — требуемый момент сопротивления профиля. Находится по сортаменту (есть ГОСТах на профили). Направление (х-х, y-y) выбирается в зависимости от того, как будет лежать балка. Например, для швеллера и двутавра, если Вы хотите их поставить (т.е. больший размер направлен вверх — [ и Ι), нужно выбирать «x-x».
Расчет по прогибу:
Jтреб — минимально допустимый момент инерции. Выбирается по тем же сортаментам и по тем же принципам, что и Wтреб.
Количество балок — общее количество балок, которое получается при укладки их по стене X с шагом P.
Общая масса — вес всех балок длиной А.
Стоимость — затраты на покупку металлических балок перекрытия.
Эти примеры помогут сделать расчет металлической балки без напряга

Металлические балки двутавровые
Кроме повсеместно ведущегося строительства многоэтажных зданий с большим числом квартир, широкое распространение получило сооружение частных домов, причем не только небольших одноэтажных, но и довольно крупных, с двумя и более этажами, иногда и с мансардой наверху или обитаемым чердаком. Для таких домов уже не подходит каркасный метод; материалом часто служит, вместо дерева, кирпич или железобетон. Возведение крупных частных домов должно вестись по всем правилам строительной науки, так как ошибки при проектировании или воплощении проекта могут привести к нежелательным последствиям.
Если строящийся дом представляет собой капитальное здание – из бетона, кирпича, шлакоблока, то для потолочных перекрытий, межэтажных и чердачных, целесообразно применить железобетонные плиты. Наиболее подходящий тип каркаса, способный выдержать вес таких перекрытий, – это каркас, элементом которого является металлическая балка двутаврового профиля.
Именно этот вид проката, установленный своей стенкой вертикально, обладает наибольшей несущей способностью. Естественно, фундамент и стены дома при этом должны быть достаточной прочности, чтобы выдерживать дополнительный вес от 0,5 до 1 тонны – столько металла, в зависимости от количества балок и номера профиля может понадобиться для потолочного перекрытия.
Чтобы избежать лишних затрат и лишнего веса каркаса потолка, а также не допустить обрушения или значительного прогиба балок, необходимо заранее рассчитать их параметры и по результатам расчета подобрать нужный прокат. Расчет сводится к вычислению следующих величин: требуемого момента сопротивления и минимального момента инерции сечения балки, а исходя из последнего – максимального относительного прогиба.
Расчет ведется по двум характеристикам – на прочность и на жесткость. По полученным значениям момента сопротивления и момента инерции в таблицах ГОСТ находят требуемый номер проката.
Исходные данные для расчетов
Для каркаса потолочных перекрытий малогабаритных частных домов обычно используется двутавр 10 – 20 номеров. Характеристики этих профилей приводятся в ГОСТ 8239-72 – их линейные размеры, площади сечения, максимальные моменты сопротивления по вертикали Wy и минимальные моменты инерции Jy.
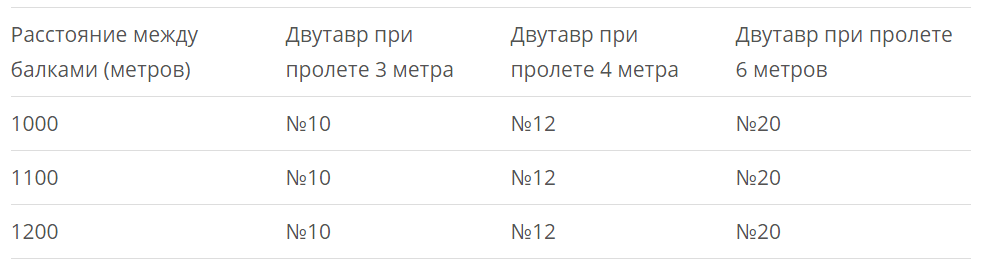
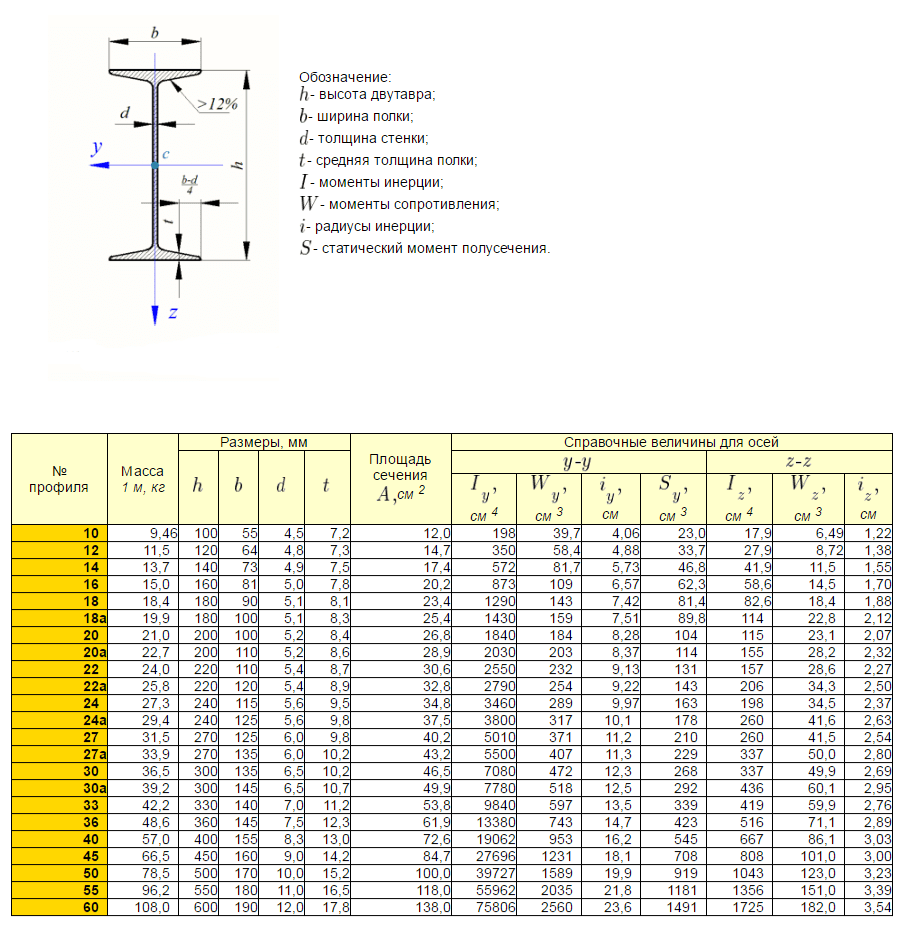
Необходимо знать тип плит, которые будут опираться на балочный каркас, а также размеры несущего периметра дома. Можно применить пустотные железобетонные плиты ПК-12-10-8 (1180 х 990 мм, масса 380 кг), а размеры дома взять 4,5 х 6 м. Балки укладываются вдоль короткой стены; шаг укладки при таком размере плит равен 1000 мм (стыки плит совпадают с продольными осями балок, при минимальном зазоре 1 см). Это потребуется для расчета распределенной нагрузки, и исходя из нее – линейной нагрузки на балку, вес самой балки по сравнению с распределенной нагрузкой мал, и при вычислении линейной нагрузки им можно пренебречь.
Распределенная нагрузка при таком типе плит будет равна 325 кгс / м 2 . К этому надо добавить нагрузку возможных перегородок на верхней стороне перекрытия (75 кгс / м 2 ) и возможную временную нагрузку (200 кгс / м 2 ). В итоге нагрузка, распределенная по площади:
Q = 325 + 75 + 200 = 600 кгс / м 2 ,
а линейная нагрузка
q = Q * p = 600 кгс / м = 6 кгс / см.
Эта величина используется в дальнейших расчетах.
Расчет на прогиб
Изгибающий момент для каждой балки вычисляется, исходя из величины линейной нагрузки q, шага укладки балок p и длины перекрываемого пролета L. Так как балки укладываются вдоль короткой стороны, то L = 4,5 м = 450 см (конечно, сами балки длиннее – около 5 м, так как опираются на стены, но шарнирными опорами для них служат именно внутренние края стен).
Искомая величина момента, в таком случае:
My = (q * L 2 ) / 8 = 6 * 450 2 / 8 = 151875 кгс * см.
Максимальный момент сопротивления сечения балки можно рассчитать, разделив изгибающий момент на расчетное сопротивление стали – например, марки С235, равное 2150 кгс / см 2 :
Wy = 151875 / 2150 = 70,6 см 3 .
Это полученное значение надо сравнить с величиной момента сопротивления сечения двутавровой балки. Из таблицы ГОСТ 8239-72 видно, что вычисленный показатель примерно соответствует (с запасом) моменту сопротивления для профиля 14 (81,7 см 3) . Следовательно, этот номер проката будет удовлетворять требованиям к прочности балок.
Как правильно произвести расчеты металлической балки?
Несмотря на бушующий в мире экономический кризис, который, к сожалению, затронул и нашу страну, строительство объектов различной важности продолжает производиться. При этом, в последнее время получило новый толчок развития именно промышленное строительство, однако, потребность жителей страны в жилых квадратных метрах не уменьшилось.

- Описание ↓
- Область применения ↓
- Расчет ↓
- Онлайн ↓
- Пример расчета ↓
Сегодня в строительстве промышленных и гражданских объектов повсеместно применяются металлические балки перекрытия, которые повышают несущую способность всей конструкции.
Описание
 Стальные балки перекрытия представляют собой металлический брус определённой длины и определённой формы поперечного сечения. Как правило, металлические балки исполняются из высокопрочной стали марки Ст 5 с формой поперечного сечения типа двутавр и швеллер.
Стальные балки перекрытия представляют собой металлический брус определённой длины и определённой формы поперечного сечения. Как правило, металлические балки исполняются из высокопрочной стали марки Ст 5 с формой поперечного сечения типа двутавр и швеллер.
Балки производятся именно в таких формах поперечного сечения, потому что расчёт показывает, что такая форма является более экономически выгодной по сравнению с другими геометрическими фигурами.
Кроме того, расчёты показывают, что балка именно двутаврогого сечения лучше всего воспринимает давление и такие нагрузки, как изгиб, кручение и их совместное действие.
Продолжая перечислять преимущества двутавровых балок, можно отметить немаловажный факт того, что такая форма сечения помогает уменьшить вес конструкции.
Это помогает снизить нагрузку, например, на стены и фундамент здания, если в межэтажном перекрытии использовать металлические балки перекрытия. Также, из преимуществ можно отметить простоту монтажа любой конструкции из балок, скорость выполнения работ.
Все значения площадей и массы профиля представлены в таблицах ГОСТ 8239-72. Чтобы её произвести, необходимо произвести расчёт профиля по прочностным характеристикам и вычислить подходящую площадь. Точная методика представлена ниже.
Таким образом, видно, что в качестве бруса перекрытия стоит использовать именно стальные балки, так как они во многом выигрывают по сравнению с конкурирующими материалами.
Область применения

Чаще всего, двутавровые балки применяются в промышленном строительстве, а именно, в случае возведения зданий с большими пролётами между опорами.
Благодаря своим механическим характеристикам и стойкости к динамическим воздействиям, металлический брус используют при возведении дорог и мостов и в других случаях необходимости возведения конструкций, выдерживающих большие нагрузки подобного характера.
В последнее время, стальные двутавровые балки стали применять в качестве элемента декора в квартирах и офисах. После покраски, металлическая балка может выглядеть эстетично и иметь практическое применение в бытовом хозяйстве.
Расчет
 Чтобы произвести выбор металлического бруса для той или иной конструкции, которая будет нести определённую нагрузку, необходимо произвести расчёт балки на прочность при изгибе. Это можно сделать, рассчитав все параметры самостоятельно по известной методике или воспользоваться онлайн-калькулятором.
Чтобы произвести выбор металлического бруса для той или иной конструкции, которая будет нести определённую нагрузку, необходимо произвести расчёт балки на прочность при изгибе. Это можно сделать, рассчитав все параметры самостоятельно по известной методике или воспользоваться онлайн-калькулятором.
Для выбора балки перекрытия, делают проверку из условия на прочность, где максимальная прочность стали должна быть больше суммы отношений максимального изгибающего момента в точке действия той или иной нагрузки к осевому моменту, и поперечных сил и площади поперечного сечения в максимально нагруженной точке.
Для определения всех неизвестных параметров этого условия, вычисления проводят поочерёдно.
Сначала определяют максимально нагруженный участок балки. Для этого, строят эпюру поперечных сил и изгибающих моментов. Чтобы построить эпюру, необходимо вычислить все суммарные изгибающие моменты и поперечные силы, действующие на балку, по участкам.
Как правило, в случае металлического бруса перекрытия, расчётную схему заменяют балкой, лежащей на двух шарнирных опорах. В этих опорах возникают реакции сопротивления, у которых необходимо определить их условия:
Когда реакции определены, балку разбивают на участки по опорам. Первый участок находится от одного конца балки до опоры, второй участок располагается между опорами, третий за последней опорой и так далее. Необходимо знать, что если на одном участке имеется точка изменения нагрузки, то её нужно выделить в отдельный участок.
После того, как участки определены, строятся эпюры поперечных сил и изгибающий моментов, и определяется нагруженный участок. Далее, вычисляется осевой момент сопротивления сечения:
По вычисленному параметру производят выбор номера двутавра из сортамента. На этом расчёт балки считается оконченным.
Онлайн
Рассчитывать металлическую балку и производить её выбор вручную довольно трудоёмко и занимает время, которое не всегда можно выделить занятому человеку. Поэтому, стоит довериться расчётам профессионалов.
Но, если заказчик строительства сомневается в экономической целесообразности произведённого строителями расчёта, можно произвести быстрый автоматический расчёт при помощи сайтов, предлагающих данный товар.
Одним из примеров такого калькулятора может быть портал http://svoydomtoday.ru/building-onlayn-calculators/111-raschet-metallicheskoy-balki-perekritiya.html, который предлагает, находясь на сайте, рассчитать расход материала и выбрать балку из сортамента.
Данный калькулятор требует введения следующих исходных данных:
- Сначала нужно ввести условия эксплуатации металлической балки.
- После этого характеристики предварительно выбранной металлической балки.
- Указать нормативную и расчётную нагрузку на балку и произвести расчёт.
В результате, получается минимально возможный при заданных условиях момент сопротивления балки. Из полученного момента можно выбрать балку по таблице сортамента.
Пример расчета

Металлической балки перекрытия:
Предварительно подбираем профиль балки №12, у которого масса 1 м.п. составляет 11,5 кг, длина балки – 6 м, расчётное сопротивление принимаем равным 210 МПа, а модуль Юнга 200000 МПа. Нормативную нагрузку примем согласно СНиП «Нагрузки и воздействия» равной 240 кг/кв.м., расчётная будет равна 300 кг/кв.м. Стоимость одной тонны металлического фасонного профиля в среднем составляет 25000 рублей.
Итоговый результат можно увидеть на рисунке выше.
Полученные результаты показывают, что в таких условиях эксплуатации двутавровая балка сортамента №12 не подойдёт. Исходя из полученного момента инерции, выбираем профиль №18.
Расчет несущей способности:
- Чтобы рассчитать несущую способность одной балки нужно из таблицы сортамента выбрать момент осевого сопротивления и по формуле вычислить максимально допустимый изгибающий момент:
- Отсюда можно вычислить максимально допустимую равнораспределённую нагрузку на однопролётную балку.
Расчет сечения металлических балок:
- Для расчёта необходимого сечения металлической балки можно воспользоваться формулой расчёта момента сопротивления сечения.
- После вычисления результата, определить площадь сечения нужно по сортаменту фасонного профиля, выбрав при этом номер двутавра с ближайшим большим значением момента сопротивления.
При расчёте металлической балки пролёта необходимо отнестись ко всему ответственно и внимательно, потому что от расчёта зависит срок эксплуатации здания и его возможная нагрузка. Здания, построенные по ошибочным расчётам, могут разрушиться в любой момент, унеся за собой много жизней.
buildingbook.ru
Информационный блог о строительстве зданий
- Home
- /
- Стальные конструкции
- /
- Расчет балки
Расчет балки
При расчете стальных балок необходимо руководствоваться СП 16.13330 «Стальные конструкции».
В данном обзоре я рассмотрю расчет балок 1-го класса напряженно-деформированного состояния (напряжения по всей площади напряжения не превышают расчетного сопротивления стали). Расчёт подкрановых, бистальных, защемленных и многопролетных балок будет рассмотрен отдельно.
Элементы конструкции должны иметь запас прочности по 1-му и 2-му предельному состоянию.
По 1-му предельному состоянию проверяется прочность элементов. Нагрузки для расчета по 1-му предельному состоянию выше, чем по 2-му предельному состоянию т.к. используются коэффициенты запаса для нагрузок.
По 2-му предельному состоянию проверяются деформации конструкции.
Расчеты по 1-му предельному состоянию:
- Расчет на прочность при действии изгибающего момента
- Расчет на прочность при действии поперечной силы
- Расчет на прочность стенки балки при действии сосредоточенной силы
- Расчет на прочность в опорном сечении
- Расчет на общую устойчивость
- Расчет на устойчивость стенок и поясных листов балки
Расчеты по 2-му предельному состоянию:
- Расчет прогиба балки
1. Расчет на прочность при действии изгибающего момента
В первую очередь необходимо подобрать балку по изгибающему моменту.
Прочность стальной балки на изгиб проверяется по следующей формуле (п.8.2.1 СП 16.13330.2011 или 5.12 СНиП II-23-81*):
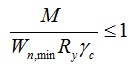
где M – максимальный момент, возникающий в балке (находится по эпюре моментов);
Wn,min – момент сопротивления сечения (находится по таблице или вычисляется для данного профиля), у сечения обычно 2-а момента сопротивления сечения, в расчетах используется Wx если нагрузка перпендикулярна оси х-х профиля или Wy если нагрузка перпендикулярна оси y-y;
Ry – расчетное сопротивление стали при изгибе (задается в соответствии с выбором стали);
γc – коэффициент условий работы (данный коэффициент можно найти в таблице 1 СП 16.13330.2011 Стальные конструкции либо таблице 6* СНиП II-23-81) для балок сплошного сечения коэффициент равен 0,9, при расчете по сечению, ослабленному отверстиями 1,1.
Из этой формулы можно вычислить минимально требуемый момент сопротивления сечения.
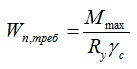
Вначале вычисляем максимальный момент от нагрузок. На этом этапе мы еще не знаем массу балки и ее можно не учитывать при предварительном расчете.
Далее выбираем марку стали. При выборе марки стали необходимо учитывать класс конструкции и климатические условия эксплуатации – если конструкция эксплуатируется в холодном климате в неотапливаемом здании, то марка стали не должна быть хрупкой. Прочность стали выбирается исходя из экономического расчета – несмотря на то, что с увеличением марки стали ее стоимость увеличивается, сечение балки из более прочной стали может быть меньше и соответственно будут меньше нагрузки. Для того, чтобы выбрать оптимальную марку стали необходимо сделать несколько расчетов и оценить их.
После того, как мы предварительно рассчитали минимальный момент сопротивления сечения (Wn) подбираем из сортамента профиль, имеющий W не много выше чем требуемый и имеющий наименьшую массу. Для балок оптимальным профилем является двутавр, швеллер. Возможно использование составного сечения из листов. При расчете важно правильно учесть положение профиля – Wx используется, если ось x-x перпендикулярна направлению приложения нагрузки. Соответственно профиль необходимо располагать так, чтобы момент сопротивления сечения был максимальным (от того как расположить профиль многое зависит).
После выбора сечения необходимо прибавить к изгибающему моменту момент, создаваемый массой балки и вновь проверить сечение.
Если балка расположена под углом, то расчет прочности при изгибе производят по следующей формуле:
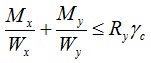
где требуется разложить силу на направляющие по оси х-х и у-у и отдельно вычислить максимальные моменты Mx и My вокруг оси х-х и у-у соответственно.
В СП 16.13330.2011 дополнительно требуют учитывать бимомент, формула выглядит следующим образом:
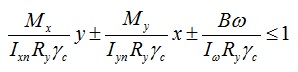
x и y — расстояния от главных осей до рассматриваемой точки;
Ixn,Iyn — моменты инерции сечения, находятся по таблице согласно ГОСТ-у на выбранный профиль;
Iω — секториальный момент инерции сечения, можно найти в приложении 3 руководства по подбору сечений стальных конструкций;
ω — секториальная площадь.
Здесь рассматриваются несколько точек, как правило 4 крайние точки профиля и для них проверяют условия, знаки подбирают согласно эпюрам напряжения. Подробно расчет профилей с учетом бимомента расписано в книге Д.В.Бычкова Строительная механика стержневых тонкостенных конструкций.
Для прогонов наклонной кровли из швеллера для упрощения расчета бимомент можно не учитывать т.к. он разгружает профиль на 10-15%, и это будет запасом прочности. В других случаях рекомендуется принимать конструктивные меры препятствующие возникновению закручивающего момента.
2. Расчет на прочность при действии поперечной силы
Далее необходимо проверить профиль на действие касательных (поперечных) сил по формуле:
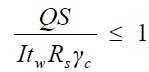
где Q – наибольшая поперечная сила (можно определить согласно эпюре Q), для балки наибольшее значение получается на опорах;
S – статический момент сдвигаемой части сечения (определяется по таблице для выбранного профиля);
I – момент инерции сечения (определяется по таблице для выбранного профиля);
tw – толщина стенки балки;
Rs — расчетное сопротивление стали сдвигу, равно 0,58 от Ry согласно Таблице 2 СП 16.13330.2011;
γc – коэффициент условий работы (данный коэффициент можно найти в таблице 1 СП Стальные конструкции) для балок сплошного сечения коэффициент равен 0,9, при расчете по сечению, ослабленному отверстиями 1,1.
Если профиль не удовлетворяет условию, то необходимо увеличить сечение.
3. Расчет на прочность стенки балки при действии сосредоточенной силы
Расчет на прочность стенки балки, не укрепленной ребрами жесткости, при действии сосредоточенной силы и в опорных сечениях определяют по формуле:
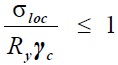
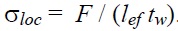
здесь F – расчетное значение нагрузки;
lef – условная длина распределения нагрузки;
tw – толщина стенки балки.
Условную длину распределения нагрузки можно определить по формуле

для следующих случаев:
для прокатной балки:
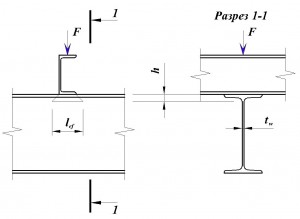
где b – ширина полки швеллера
h – сумма толщины верхней полки и радиуса закругления
для сварной балки:
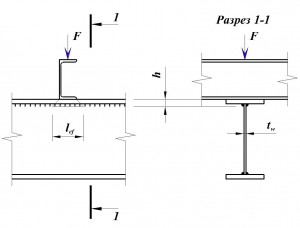
где h – сумма толщины верхней полки и катета сварного шва.
4. Расчет на прочность в опорном сечении
Расчет на прочность в опорном сечении балки (при Mx=0 и My=0) следует определять по формулам:
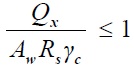
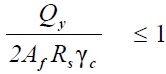
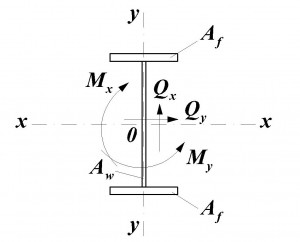
где Aw– площадь сечения стенки,
Af– площадь сечения полки,
Rs–расчетное сопротивление стали сдвигу.
При ослаблении стенки отверстиями для болтов левую часть формулы необходимо умножить на коэффициент α, который находиться по формуле: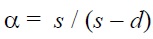
где s – шаг отверстий в одном ряду;
d – диаметр отверстия.
Расчет на прочность для защемленных и неразрезных балок мы рассмотрим отдельно.
5. Расчет на общую устойчивость
Далее необходимо проверить балку на устойчивость.
Данный расчет можно не выполнять:
а) при передаче нагрузки через сплошной жесткий настил (плиты железобетонные, плоский или профилированный металлический настил, волнистая сталь и т.п.), непрерывно опирающийся на сжатый пояс балки и надежно с ним связанный (с помощью сварки, болтов, самонарезающих винтов), при этом силы трения учитывать не стоит;
б) если условная гибкость сжатого пояса балки меньше предельных значений. Условная гибкость вычисляется по формуле:
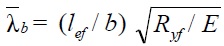
Предельное значение гибкости пояса вычисляется по формулам:
при приложении нагрузке к верхнему поясу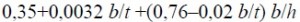
при приложении нагрузке к нижнему поясу
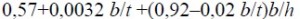
независимо от уровня приложения нагрузки при расчете участка балки между связями или при чистом изгибе
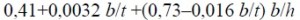
где b – ширина сжатого пояса;
t – толщина сжатого пояса;
h – расстояние (высота) между осями поясных листов.
-
Значения предельной гибкости определены при 1≤ h/b ≤6 и 15≤ b/t ≤35; для балок с отношением b/t Построение эпюр балки
Как правильно закрепить балку на колонне читайте в статье Опорные узлы балки
Как рассчитать балку в SCAD и подобрать сечение читайте в статье Расчет балки в SCAD
Балка металлическая
Расчет стальных балок
Проектирование металлических конструкций любого сечения, обоснование принятия меньшего сечения (облегченние) проверками согласно СНиП (СП) металлоконструкций. Детальный расчет стальных балок, монтажных узлов и стыков всех основных видов:
- Переменного под длине сечения
- Подкрановые или кран-балки
- Балки перекрытий и покрытий
- Стальные перемычки над проёмами
- Стропильные конструкции
- Обрешётка по ограждающие конструкции
Проектирование металлических балок включает в себя:
- Рассмотрение конструктивной схемы:
- принятие расчётной схемы работы (разрезная, неразрезная)
- определение связей из плоскости изгиба
- Определение вида сечения балки
- Задание марки стали
- Проверка сечения — собственно сам расчёт расчет стальной балки
- Конструирование узлов опирания
Конструктивные схемы работы балок
Основные сечения стальных балок
| Сечение конструкции | Название / описания работы |
|---|---|
 |
Профильная труба Примеряется в качестве обрешетки, ветровых прогонов |
 |
Швеллер Самый распространённый вид балки, экономично применять при профилированном настиле, который скрепляет её |
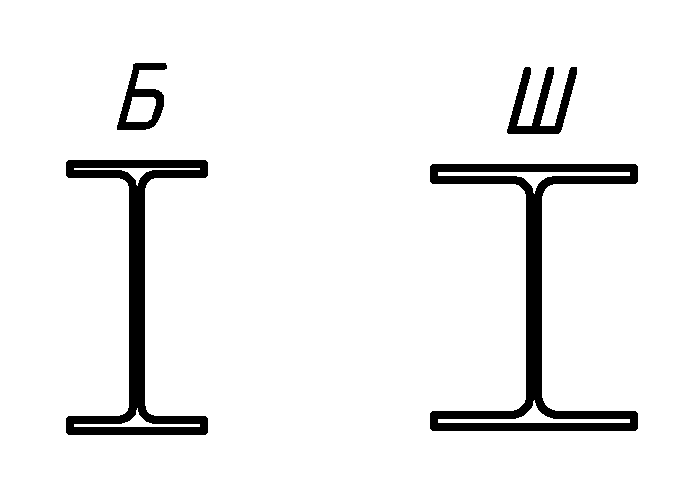 |
Двутавр Балочный — хорошо работает когда сосредоточенная нагрузка на балку передается через балку, которая является связью. Профиль дорогой но устойчивый. Применяется что бы уменьшить высоту перекрытия. Широкополочный — тяжелый вариант балки, применяется когда есть потребность уменьшить высоту балки по архитектурным соображениям |
 |
ЛСТК Хорошо применять при пролётах до 2,0м. Нет программ для расчёта, сложный расчёт по СП 260.1325800.2016 Конструкции стальные тонкостенные |
 |
Балка с перфорированной стенкой Минус — требуется изготовление балки на заводе (увеличивается стоимость) Плюс — при пролётах 9-13м, при относительно небольшой нагрузки (снеговая) и при больших объемах можно получается экономический эффект |
 |
С гибкой стенкой балка применяется балка при пролётах 12-18м Легче балка по сравнению с устойчивой стенкой |
| Балка с устойчивой стенкой применяется балка при пролётах 12-18м. |
|
| Бистальная балка с устойчивой стенкой применяется балка при пролётах 12-18м при увеличенных нагрузках. Суть балки -пояса изготавливаются из высококачественной стали, а стенка из обычной |
В общем расчет стальных балок из прокатного профиля, расположенного вертикально — самый простой алгоритм. Тут справляется простые программы. Но как дело доходит до сварных конструкций, то тут и передовой софт отстаёт. Нет множество проверок устойчивости стенки и пояса и при этом нет предупреждений явных. Так же к прогонам, расхоложенных на наклонной плоскости, при отсутствии профнастила, также требует хорошего понимания его работы.
Расчет балки на прогиб — формулы, параметры и примеры решения
Расчет балки на прогиб нужно проводить практически для любой конструкции, чтобы проверить ее надежность и прочность. Под влиянием внешних, внутренних факторов, природных явлений балка подвержена деформации.
Балку сравнивают со стержнем, закрепленным на опорах. Чем больше опор, тем сложнее провести расчет самостоятельно. Основная нагрузка считается путем сложения сил, перпендикулярно направленных к сечению.
Данный расчет – основы сопромата, помогает определить наивысшую деформацию. Значения показателей должны входить в рамки допустимых величин.
Виды балок
При возведении зданий используется балки разных конфигураций, размеров, профиля, характера сечения. Их изготавливают из металла и дерева. Для любого вида используемого материала нужен индивидуальный расчёт изгиба.
Деревянные — их используют в основном при строительстве индивидуальных построек. Они применяются при возведении полов, потолков, несущих перекрытий. Дерево – капризный материал и подвержено деформации. Для определения максимального изгиба, существенны такие параметры: используемый профиль, размер, нагрузка, характер поперечного сечения.
Металлические — такие балки изготавливают из сплава металлов и сечение у них сложное. Поэтому особое внимание уделяется жесткости, а также прочности соединений. Балки из металла применяются в возведении многоэтажек, сооружений, требующих высокой прочности.
Прочность и жесткость балки
При проектировании следует учесть изгиб балок, чтобы конструкция была надежная, качественная, прочная и практичная.
На эти параметры влияют следующие факторы:
величина наружных нагрузок, их положение;
параметры, характер, нахождение поперечного сечения;
число опор, метод их закрепления.
Выделяют 2 метода исчисления: простой – применяется увеличительный коэффициент, и точный – дополнительно включает пограничные подсчеты.
Построение эпюр балки
Эпюра распределения величины нагрузки на объект:
Расчет на жесткость
В формуле обозначены:
M – max момент, возникающий в брусе;
Wn,min – момент сопротивления сечения (табличный показатель);
Ry – сопротивление на изгиб (расчётный показатель);
γc – показатель условий труда (табличный показатель).
Такой расчет не трудоемок, но для более верного значения требуется следующее:
рабочий план объекта;
определение характеристик балки, характер сечения;
определение max нагрузки, воздействующей на брус;
оценка точки max прогиба;
проверка прочности max изгибающего момента.
Расчет моментов инерции и сопротивления сечения
J – момент инерции сечения;
W – момент сопротивления.
Для определения данных параметров необходимо учитывать сечение по грани разреза. Если момент инерции возрастает, величина жесткости также возрастает.
Нахождение максимальной нагрузки и прогиба
Формула для вычисления:
q – нагрузка равномерно-распределенная;
E – гибкость (табличный показатель);
I – момент инерции сечения.
Нагрузки учитываются статические и периодические.
Расчет на прогиб и его особенности
Он необходим для всех перекрытий при высоких эксплуатационных нагрузках.
При применении соответствующих коэффициентов, придерживаются следующего:
балка, держащаяся на одной жесткой и одной шарнирной опоре, подвергающаяся воздействию сосредоточенной нагрузки;
балка, держащаяся на жесткой и шарнирной опоре, подвергающаяся воздействию распределенной нагрузки;
нагрузка консольного типа;
воздействие комплексной нагрузки.
Пример расчет балки на прогиб
Рассмотрим задачу из курса сопромата.
Дано: балка четырехугольного сечения 20 на 30 см; поперечная сила Q = 19 кН; изгибающий момент М = 28 кНм.
Необходимо рассчитать напряжение: нормальное и в пределе К, отдаленной на 11 см от оси, узнать прочность бруса из дерева, при [σ] = 10 МПа, [τ] = 3 МПа.
Чтобы узнать σ(К), τ(К), σmax, τmax определяем значение осевого момента инерции общего сечения IН.О., осевого момента сопротивления WН.О., статического момента отсеченного ряда и статического момента середины сечения Smax:
Из этого следует:
Определение прочности по нормальному напряжению:
Определение прочности по касательному напряжению:
При проектировании конструкций важно соблюдать все физико-механические вычисления на прочность. Удобно и качественно произвести расчеты может онлайн, что существенно сократит временные сроки.
Калькулятор выполняет подробный подсчет на основе формул, эпюр усилий, подбирает номер сечения металлической балки из прокатных профильных, двутавровых материалов, а также из металлических труб.
26 августа 2019
3863
Подбор сечения двутавра – критерии выбора, правила и секреты

Балка двутавровая или просто двутавр – один из наиболее широко применяемых видов черного фасонного металлопроката. Главное его отличие – сечение в форме буквы «Н». Зачастую возникает необходимость выполнить подбор сечения двутавра. Как это сделать правильно? Читайте далее в нашей статье.
Начнем с общих параметров, чтобы определить основные критерии выбора сечения. Сначала нужно понять что такое двутавр и каковы его основные характеристики. Итак, двутавр это вид изделий, состоящий из двух полок и соединяющей их стенки. Стенку называют шейкой, полки располагаются параллельно друг другу. Именно шейка и полки образуют профиль сечения двутавра, о котором и идет речь. Думаем, понятно.
Несколько важных моментов влияющих на выбор сечения двутавра. Первый – материал изготовления и технология производства. Двутавр может изготавливаться из различных материалов, в статье поговорим о металлопрокате. Второй – технология производства, либо сварная, либо горячекатаная двутавровая балка. И третий – предназначение изделий (нагружаемые или ненагружаемые конструкции).

Подбор сечения двутавра – сортамент, ключевые моменты
Исходя из того что двутавр – две полки, соединенные шейкой, определяются размеры сечения по таким параметрам как:
- общая высота профиля (включая длину шейки и толщину двух полок);
- высота стенки двутавра;
- общая ширина каждой из полок;
- ширина одной части полки от шейки к краю, называется свесом;
- толщина шейки (стенки);
- толщина полки проката с гранями, расположенными параллельно;
- средняя толщина полки проката с уклоном внутренних граней;
- радиус закругления перехода от полки к стенке, он же радиус сопряжения, внутреннего закругления;
- радиус закругления полки (ее кромки).
Вот эти значения и определяют подбор сечения двутавра. Ряд из них указан в маркировке, об этом ниже.
Отметим один важный, ключевой момент. Выбор сечения двутавра напрямую зависит от государства, на территории которого будет применяться двутавровая балка.
Немного истории
Не нам судить, но на территории России возникла интересная, парадоксальная ситуация. Суть вопроса в том что двутавр по наклону внутренних граней подразделяется на две группы. Первая – с параллельными внутренними гранями. Вторая – с уклоном внутренних граней. Характеристики (площадь сечения, масса и другие) и эксплуатационные параметры, предназначение зачастую совершенно разные.
Во времена Советского Союза сортамент первой группы определял ГОСТ 26020-83. Сортамент второй группы устанавливался ГОСТ 8239-89 (еще ранее ГОСТ 8239-72). С мая 2018 года в России действует свой национальный стандарт – ГОСТ Р 57837-2017. Он определяет технические условия, а вот тут внимательно, для двутавра с параллельными гранями полок. И что вполне естественно, заменяет ГОСТ 26020-83. Приказ Росстандарта от 30.11.2018 N 1047-ст. Пункт первый четко указывает что ГОСТ 8239-89 заменен на ГОСТ Р 57837-2017.
В результате двутавр с уклоном внутренних граней в России оказался вне закона, нет такого и все. На рынке такой прокат есть, а использовать в строительстве официально нельзя. Других ГОСТов для двутавра с уклоном внутренних граней в России нет. Если не считать специальный прокат (ГОСТ 19428-74) и изделия из цветного проката. Но ГОСТ Р 57837-2017 – это российский национальный стандарт. В ряде государств СНГ ГОСТ 26020-83 и ГОСТ 8239-89 действуют.
Выбор сечения двутавра – основные расчеты
Помимо сортамента, о нем поговорим детальнее далее, выбор сечения двутавра должен основываться на расчетах. Тут два важных определяющих критерия. Первый – действующие СНиП. Второй – такая наука как «Сопротивление материалов», сокращенно сопромат. Сечение двутавра рассчитывается исходя из его предназначения и предполагаемых статических и динамических нагрузок. То есть тех нагрузок, которые будут воздействовать на конструкцию. Учитывается развитие пластических деформаций в наиболее нагруженном сечении. Лекцию по сопромату читать не будем. Остановимся на основных моментах.
Величина сопротивления
Сечение двутавра зависит от величины нужного момента его сопротивления. Многое находится в зависимости от марки стали, ее расчетного сопротивления и корректирующего коэффициента. Рассчитываются такие параметры как:
- высота сечения, в зависимости от пролета балки, условий наименьшего расхода стали, обеспечения требуемой жесткости;
- толщина стенки;
- геометрические характеристики сечения, исходя из момента сопротивления и момента инерции.
Толщина стенки
Под обеспечением требуемой жесткости следует понимать расчеты с учетом полного использования несущей способности материала. Отталкиваться надо от условий обеспечения предельного прогиба. Толщина стенки рассчитывается с использованием различных методик, включая:
- эмпирическую формулу;
- исходя из условий прочности шейки на срез;
- исходя из условий обеспечения местной устойчивости шейки, без укрепления ее дополнительным продольным ребром жесткости.
Обязательно нужно выполнять проверку сечения двутавра. Наиболее важно на прочность по нормальным напряжениям, возникающим в поперечном сечении балки, и на жесткость. Инженерного образования нет, сопромат – темный лес, требуется выбрать сечение двутавра для несущих, нагружаемых конструкций? Воспользуйтесь услугами квалифицированного инженера или специальным программным обеспечением, введя все исходные данные. Если конструкции ненагружаемые, то при выборе сечения двутавра расчет нагрузок не так критичен.

Сортамент и сечение двутавра – ГОСТ Р 57837-2017
Не будем затрагивать тему двутавра с уклоном внутренних граней полок. Раз уж так повелось на Руси использовать только ГОСТ Р 57837-2017, пусть будет ГОСТ Р 57837-2017. Отметим лишь одно. В прайсах помимо него могут быть указаны все те же ГОСТ 26020-83 и ГОСТ 8239-89. Ах да, есть еще и СТО АСЧМ 20-93, на него тоже ссылаются. Но он отменен на основании информационного письма ТК375/ГР-57837 от 11.04.2018 года.
Разговор у нас пойдет о выборе сечения для горячекатаного двутавра с параллельными гранями полок. Возьмем за основу сортамент этого вида фасонного черного металлопроката. Но прежде о маркировке двутавра. Она состоит из букв и цифр. Первая цифра обозначает высоту профиля в сантиметрах. Этот параметр называется номером, цифра от 10 до 100. Следом идет буква. Она указывает на тип в зависимости от условий работы и соотношение размеров. Именно соотношение размеров в полной мере влияет на сечение двутавра. Оттого на типах двутавра остановимся детальнее далее. И еще в маркировке встречается цифра после буквы. Она указывает на профилеразмер в данной серии (по толщине стенки и полки). Это тоже влияет на сечение.
В качестве примера маркировки 12Б1. Двутавр высотой 12 сантиметров, балочный нормальный, первого профилеразмера.
Какие существуют типы двутавра
О профилеразмерах, соотношении толщины полки и балки, говорить не будем. Это очень важный параметр при выборе сечения двутавра. Но у одного производителя их бывает до 200 и постоянно количество растет. Все зависит от настроек и характеристик прокатного стана. Описать все в рамках одной статьи невозможно. Это каталожные данные, причем по каждому металлургическому предприятию в отдельности.
Теперь о типе двутавра и характерных особенностях сечения. Он делится на несколько групп:
- балочный (о нем ниже);
- колонный, характерная черта сечения – высота равна или близка ширине полок, толщина полок увеличенная;
- свайный, сечение с высотой равной или близкой ширине полок, толщина стенки и полки равны.
Теперь о балочном типе двутавра, их два. Первый – нормальный. Характерная черта сечения – ширина полок меньше чем высота профиля. Толщина стенок минимальная. Второй – широкополочный, с увеличенной шириной полок.
Выбор сечения двутавра – другие виды изделий
Подбор сечения профиля для специального горячекатаного профиля будет отличаться. Во многом это определяется уклоном внутренних граней полок. ГОСТ 19425-74 еще ГОСТом Р 57837-2017 заменить гениальная мысль не пришла в головы (шутка). Если кратко, то существует два основных вида специальной двутавровой балки. Первый – М (подвесная, монорельсовая). Соотношение основания двутавра к ширине полок примерно 2/1 или 3/1. С – для армирования стволов шахт. Сечение отличается значительным уклоном внутренних граней полок.
Обращайте внимание что все еще есть на рынке и двутавровая балка У. Буква указывает на то что это узкополочный прокат. Характерная черта сечения – узкие полки.
И последний тип горячекатаного двутавра – Д. Это обозначает дополнительный. По ГОСТ Р 57837-2017 маркируется как ДК и ДБ. Изготавливается по требованиям заказчика. Какое нужно сечение, такое и сделают под заказ. Особенно актуально когда стоит сложная, нетривиальная инженерная задача при проектировании уникальных металлоконструкций. Среди характерных черт сечения – ширина полки. Она меньше чем ширина полки у широкополочного двутавра. Но при этом ширина полки двутавра Д меньше чем ширина полки у двутавра нормального типа. Хотя бывают и исключения.

Подводя итог скажем так. Подбор сечения двутавра определяется сложными расчетами. Форма профиля зависит от основных параметров проката и определяет его тип. Иногда характеристики типа определяют вид сечения. С особой тщательностью надо выполнять выбор сечения двутавра для нагруженных конструкций. Остались вопросы? Требуется двутавровая балка? Обращайтесь!
