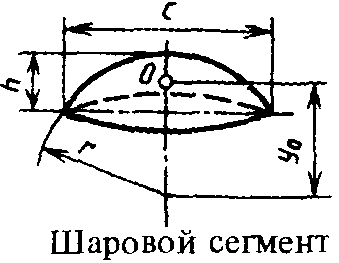
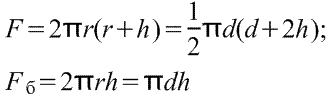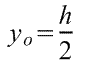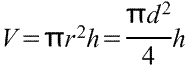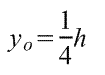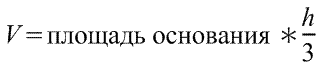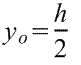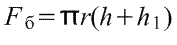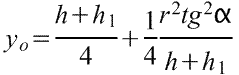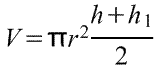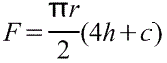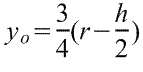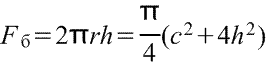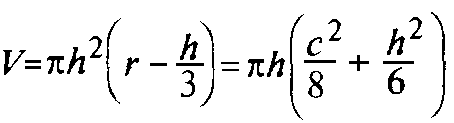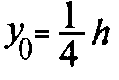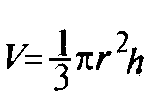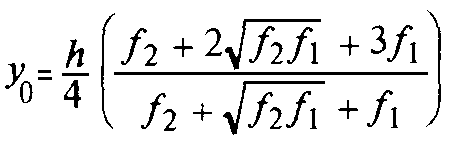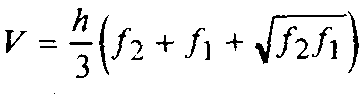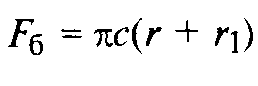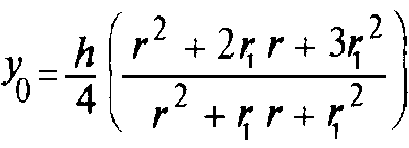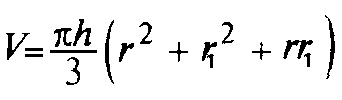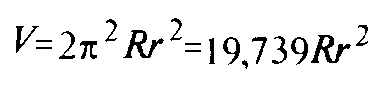Объём части цилиндра
- Главная
- /
- Математика
- /
- Геометрия
- /
- Объём части цилиндра
Чтобы посчитать объём части цилиндра воспользуйтесь нашим очень удобным онлайн калькулятором:
Онлайн калькулятор

Для того чтобы найти объём части цилиндра (Vчц) необходимо знать радиус r или диаметр d цилиндра, его высоту h и угол между двумя плоскостями, ограничивающими эту часть (∠α).
Чему равен объём части цилиндра Vчц если:
=
Угол α = °
Высота цилиндра h =
Ответ: Vчц =
0
Просто подставьте данные и получите ответ.
Теория
Чему равен объём части цилиндра Vчц если радиус цилиндра r, высота цилиндра h, а угол между плоскостями части цилиндра α?
Формула
Vчц = α/360 ⋅ π ⋅ r² ⋅ h
через диаметр:
Vчц = α/360 ⋅ π ⋅ (d/2)² ⋅ h
Пример
К примеру найдём чему равен объём части цилиндра с радиусом r = 5см, высотой h = 10см и углом между ограничивающими часть плоскостями ∠α = 30°:
Vчц = 30/360 ⋅ 3.14 ⋅ 5² ⋅ 10 ≈ 0.262 ⋅ 25 ⋅ 10 ≈ 65.5 см³
См. также
Наш пользователь попросил написать калькулятор объема сегмента цилиндра. Сегмент цилиндра я себе представляю так — см. картинку.
Соответственно, задаем четыре параметра, получаем объем сегмента. Если внутренний радиус указать 0, а число градусов 360, то будет объем цилиндра, ну и так далее.
Формула проста — разность площадей сегментов, получаемых по первому и второму радиусу, умножается на высоту.
Площадь сегмента
![]()
Объем сегмента цилиндра
Наружний радиус
Внутренний радиус
Угол сегмента в градусах
Высота цилиндра
Точность вычисления
Знаков после запятой: 2
Объем сегмента
 Главная
Главная  Учёба
Учёба  Площадь части цилиндра и полого цилиндра
Площадь части цилиндра и полого цилиндра
Площадь части цилиндра и полого цилиндра
Онлайн калькуляторы, формулы для вычисления площадей части цилиндра и полого цилиндра.
Площадь части цилиндра
Укажите радиус основания (r), высота цилиндра (h) и угол между плоскостями части цилиндра (α°).
Формула полной поверхности цилиндра: S = 2*(α°/360)*pi*r2+(α°/360)*2*pi*r*h+2*r*h
Формула внутренней и внешней боковой поверхности цилиндра: S = (α°/360)*2*pi*r*h+2*r*h
Формула основания цилиндра: S = (α°/360)*pi*r2
Понравилась страница? Поделитесь ссылкой в социальных сетях. Поддержите проект!
Нет комментариев.
Цилиндр, конус, шар
Цилиндр – тело, ограниченное цилиндрической поверхностью и двумя кругами с границами $М$ и $М_1$. Цилиндрическая поверхность называется боковой поверхностью цилиндра, а круги – основаниями цилиндра.
Образующие цилиндрической поверхности называются образующими цилиндра, на рисунке образующая $L$.
Цилиндр называется прямым, если его образующие перпендикулярны основаниям.
Осевое сечение цилиндра – это прямоугольник, у которого одна сторона равна диаметру основания, а вторая – высоте цилиндра.
Основные понятия и свойства цилиндра:
- Основания цилиндра равны и лежат в параллельных плоскостях.
- Все образующие цилиндра параллельны и равны.
- Радиусом цилиндра называется радиус его основания ($R$).
- Высотой цилиндра называется расстояние между плоскостями оснований (в прямом цилиндре высота равна образующей).
- Осью цилиндра называется отрезок, соединяющий центры оснований ($ОО_1$).
- Если радиус или диаметр цилиндра увеличить в n раз, то объем цилиндра увеличится в $n^2$ раз.
- Если высоту цилиндра увеличить в m раз, то объем цилиндра увеличится в то же количество раз.
- Если призму вписать в цилиндр, то ее основаниями будут являться равные многоугольники, вписанные в основание цилиндра, а боковые ребра – образующими цилиндра.
- Если цилиндр вписан в призму, то ее основания – равные многоугольники, описанные около оснований цилиндра. Плоскости граней призмы касаются боковой поверхности цилиндра.
- Если в цилиндр вписана сфера, то радиус сферы равен радиусу цилиндра и равен половине высоты цилиндра.
$R_{сферы}=R_{цилиндра}={h_{цилиндра}}/{2}$
Площадь поверхности и объем цилиндра.
Площадь боковой поверхности цилиндра равна произведению длины окружности основания на высоту.
$S_{бок.пов.}=2πR·h$
Площадь поверхности цилиндра равна сумме двух площадей оснований и площади боковой поверхности.
$S_{полной.пов.}=2πR^2+2πR·h=2πR(R+h)$
Объем цилиндра равен произведению площади основания на высоту.
$V=πR^2·h$
Объем части цилиндра, в основании которого лежит сектор: $V={πR^2·n°·h}/{360}$, где $n°$ – это градусная мера центрального угла, отсекающего заданный сектор.
Пример:
Цилиндр описан около шара. Объём цилиндра равен $30$. Найдите объём шара.
Решение:
Если в цилиндр вписан шар, то радиус цилиндра равен радиусу шара, а высота цилиндра в два раза больше радиуса шара.
$R_{цилиндр}=R_{шар}; h_{цилиндр}=2R_{шар}$
Распишем формулы объема цилиндра и шара.
$V_{цилиндра}=πR_{цилиндр}^2·h_{цилиндр}=πR_{шар}^2·2R_{шар}=2πR_{шар}^3$
$V_{шара}={4π·R_{шар}^3}/{3}$
Далее надо сравнить во сколько раз объем цилиндра больше объема шара, для этого разделим объемы друг на друга.
${V_{цилиндра}}/{V_{шара}}={2πR_{шар}^3·3}/{4π·R_{шар}^3}={3}/{2}=1.5$
Объем цилиндра больше объема шара в $1.5$ раза, следовательно, чтобы найти объем шара, надо объем цилиндра разделить на $1.5$.
$V_{шара}=30:1.5=20$
Ответ: $20$
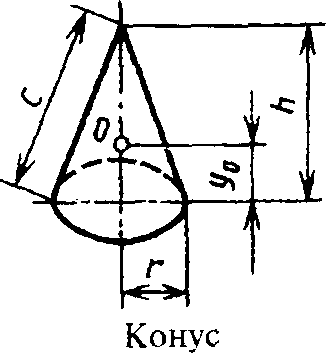
Конусом (круговым конусом) называется тело, которое состоит из круга, точки, не лежащей в плоскости этого круга, и всех отрезков, соединяющих заданную точку с точками круга.
Отрезки, соединяющие вершину конуса с точками окружности основания, называются образующими и обозначаются (l).
$l=SA$
Высотой конуса называется перпендикуляр, опущенный из его вершины на плоскость основания. Ось прямого конуса и его высота равны.
$SО$ – высота и ось конуса.
Свойства конуса:
- Все образующие конуса равны.
- Осевым сечением конуса является равнобедренный треугольник, основание которого равно двум радиусам, а боковые стороны равны образующим конуса.
- Если боковая поверхность конуса – полукруг, то осевым сечением является равносторонний треугольник, угол при вершине равен $60°$.
- Если радиус или диаметр конуса увеличить в n раз, то его объем увеличится в $n^2$ раз.
- Если высоту конуса увеличить в m раз, то объем конуса увеличится в то же количество раз.
Площадь поверхности и объем конуса.
Площадь боковой поверхности конуса равна произведению половины длины окружности основания на образующую.
$S_{бок.пов.}=πR·l$
Площадь поверхности конуса равна сумме площади основания и площади боковой поверхности.
$S_{полной.пов.}=πR^2+πR·l=πR(R+l)$
Объем конуса равен трети произведения площади основания на высоту.
$V={πR^2·h}/{3}$
Объем части конуса, в основании которого лежит сектор: $V={πR^2·n°·h}/{360·3}$, где $n°$ – это градусная мера центрального угла, отсекающего заданный сектор.
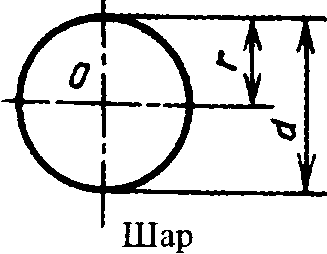
Сферой называется поверхность, состоящая из всех точек пространства, расположенных на данном расстоянии ($R$) от данной точки (центра сферы $О$).
Тело, ограниченное сферой, называется шаром.
Осевое сечение шара это круг, радиус которого равен радиусу шара. Осевым сечением является самый большой круг шара.
Площадь поверхности сферы: $S_{п.п}=4π·R^2=π·d^2$, где $R$ – радиус сферы, $d$ – диаметр сферы
Объем шара: $V={4π·R^3}/{3}={π·d^3}/{6}$, где $R$ – радиус шара, $d$ – диаметр шара.
Если радиус или диаметр шара увеличить в n раз, то площадь поверхности увеличится в $n^2$ раз, а объем в $n^3$ раз.
Теорема Пифагора
В прямоугольном треугольнике сумма квадратов катетов равна квадрату гипотенузы.
$АС^2+ВС^2=АВ^2$
Соотношение между сторонами и углами в прямоугольном треугольнике:
В прямоугольном треугольнике $АВС$, с прямым углом $С$:
Для острого угла $В: АС$ – противолежащий катет; $ВС$ – прилежащий катет.
Для острого угла $А: ВС$ – противолежащий катет; $АС$ – прилежащий катет.
- Синусом ($sin$) острого угла прямоугольного треугольника называется отношение противолежащего катета к гипотенузе.
- Косинусом ($cos$) острого угла прямоугольного треугольника называется отношение прилежащего катета к гипотенузе.
- Тангенсом ($tg$) острого угла прямоугольного треугольника называется отношение противолежащего катета к прилежащему катету.
Значения тригонометрических функций некоторых углов:
| $α$ | $30$ | $45$ | $60$ |
| $sinα$ | ${1}/{2}$ | ${√2}/{2}$ | ${√3}/{2}$ |
| $cosα$ | ${√3}/{2}$ | ${√2}/{2}$ | ${1}/{2}$ |
| $tgα$ | ${√3}/{3}$ | $1$ | $√3$ |
| $ctgα$ | $√3$ | $1$ | ${√3}/{3}$ |
Признаки подобия треугольников:
- Если два угла одного треугольника соответственно равны двум углам другого треугольника, то такие треугольники подобны.
- Если две стороны одного треугольника пропорциональны двум сторонам другого треугольника и углы, заключенные между ними равны, то такие треугольники подобны.
- Если три стороны одного треугольника пропорциональны трем сторонам другого треугольника, то такие треугольники подобны. Периметры подобных треугольников и их линейные величины (медианы, биссектрисы, высоты) относятся друг к другу как коэффициент подобия $k$. Отношение площадей двух подобных треугольников равно квадрату коэффициента подобия.
Таблицы DPVA.ru – Инженерный Справочник
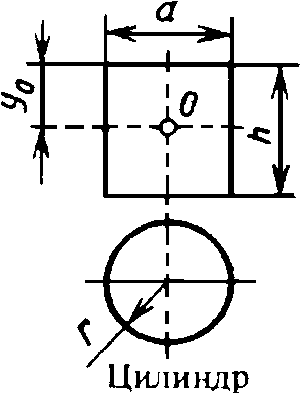
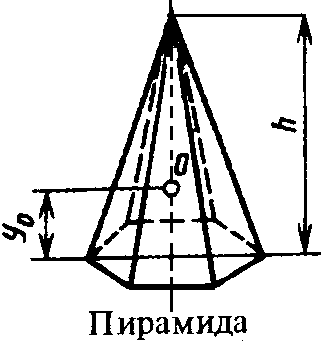
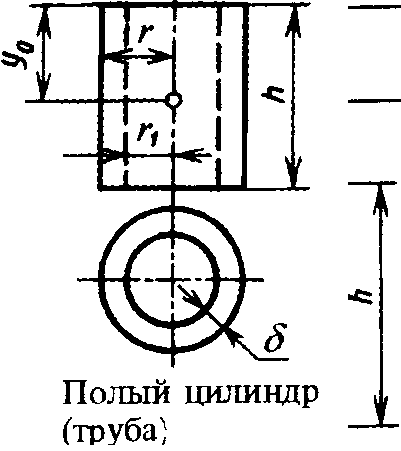
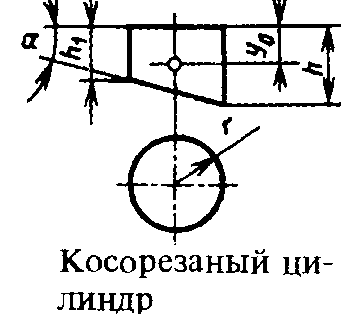
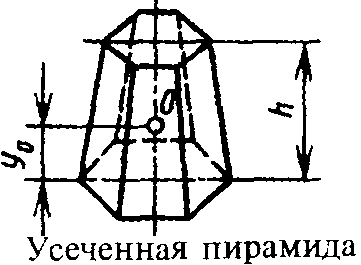
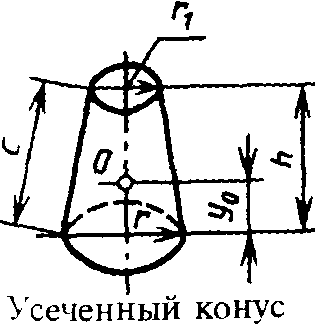
Адрес этой страницы (вложенность) в справочнике dpva.ru:  главная страница / / Техническая информация / / Математический справочник / / Геометрические фигуры. Свойства, формулы: периметры, площади, объемы, длины. Треугольники, Прямоугольники и т.д. Градусы в радианы. / / Вычисление поверхностей, боковых поверхностей, расстояний до центров тяжести и объемов Цилиндра, Пирамиды, Полого цилиндра (трубы), Косорезанного цилиндра, Шара, Шарового сектора, Шарового сегмента, Конуса, Усеченной пирамиды, Усеченного конуса, Тора.
главная страница / / Техническая информация / / Математический справочник / / Геометрические фигуры. Свойства, формулы: периметры, площади, объемы, длины. Треугольники, Прямоугольники и т.д. Градусы в радианы. / / Вычисление поверхностей, боковых поверхностей, расстояний до центров тяжести и объемов Цилиндра, Пирамиды, Полого цилиндра (трубы), Косорезанного цилиндра, Шара, Шарового сектора, Шарового сегмента, Конуса, Усеченной пирамиды, Усеченного конуса, Тора.
Вычисление поверхностей, боковых поверхностей, расстояний до центров тяжести и объемов Цилиндра, Пирамиды, Полого цилиндра (трубы), Косорезанного цилиндра, Шара, Шарового сектора, Шарового сегмента, Конуса, Усеченной пирамиды, Усеченного конуса, Тора.
Вычисление поверхностей, площадей боковых поверхностей, расстояний (положений) до центров тяжести и объемов Цилиндра, Пирамиды, Полого цилиндра (трубы), Косорезанного цилиндра, Шара, Шарового сектора, Шарового сегмента, Конуса, Усеченной пирамиды, Усеченного конуса, Тора.(Исправлена опечатка 17 мая 2016 года)
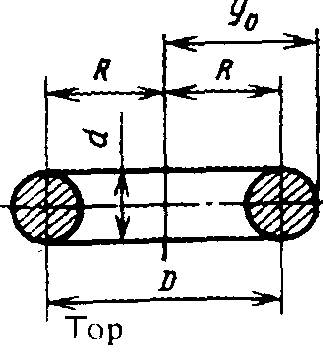
*Тор – кольцо, оринг. |
||||||||||||||||||||||||||||||||||||||||||||||||||
|
Поиск в инженерном справочнике DPVA. Введите свой запрос: |
Поиск в инженерном справочнике DPVA. Введите свой запрос:
Если Вы не обнаружили себя в списке поставщиков, заметили ошибку, или у Вас есть дополнительные численные данные для коллег по теме, сообщите , пожалуйста.
Вложите в письмо ссылку на страницу с ошибкой, пожалуйста.
Коды баннеров проекта DPVA.ru
Начинка: KJR Publisiers
Консультации и техническая
поддержка сайта: Zavarka Team
Free xml sitemap generator
![]()