Как найти сектор круга если известен угол

В данной публикации мы рассмотрим формулы, с помощью которых можно вычислить площадь сектора круга, а также разберем примеры решения задач для демонстрации их практического применения.

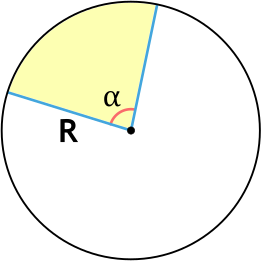
Определение сектора круга

Сектор круга – это часть круга, образованная двумя его радиусами и дугой между ними. На рисунке ниже сектор закрашен зеленым цветом.

• AB – дуга сектора;
• R (или r) – радиус круга;
• α – это угол сектора, т.е. угол между двумя радиусами. Также его иногда называют центральным углом.

Формулы нахождения площади сектора круга

Через длину дуги и радиус круга

Площадь (S) сектора круга равняется одной второй произведения длины дуги сектора (L) и радиуса круга (r).

Через угол сектора (в градусах) и радиус круга

Площадь (S) сектора круга равняется площади круга, умноженной на угол сектора в градусах (α°) и деленной на 360°.

Через угол сектора (в радианах) и радиус круга

Площадь (S) сектора круга равняется половине произведения угла сектора в радианах (a_рад) и квадрата радиуса круга.

Примеры задач

Задание 1
Дан круг радиусом 6 см. Найдите площадь сектора, если известно, что длина его дуги составляет 15 см.

Решение
Воспользуемся первой формулой, подставив в нее заданные значения:

Задание 2
Найдите угол сектора, если известно, что его площадь равна 78 см², а радиус круга – 8 см.

Решение
Выведем формулу для нахождения центрального угла из второй формулы, рассмотренной выше:

Здесь вы можете рассчитать площадь сектора круга с помощью удобного онлайн калькулятора по двум формулам. Для этого необходимо ввести известные вам параметры фигуры:

• радиус круга и угол,
• длину дуги и радиус.

Формула площади сектора круга через радиус и угол

Формула площади сектора круга через радиус и длину дуги

Примеры задач на нахождение площади сектора круга

Круговой сегмент — часть круга ограниченная дугой и секущей (хордой).

На рисунке:
L — длина дуги сегмента
c — хорда
R — радиус
a — угол сегмента
h — высота

Первый калькулятор рассчитывает параметры сегмента, если известен радиус и угол по следующим формулам:

Формулы вычисления параметров сегмента

Площадь сегмента:
[1]
Длина дуги:

Длина хорды:

Высота сегмента:

Однако, как справедливо заметил наш пользователь:«на практике часто случается, что как радиус дуги, так и угол неизвестны» (см. длина дуги ). Для этого случая для расчета площади сегмента и длины дуги можно использовать следующий калькулятор:

Калькулятор вычисляет радиус круга по длине хорды и высоте сегмента по следующей формуле:

Далее, зная радиус и длину хорды, легко найти угол сегмента по формуле:

Остальные параметры сегмента вычисляются аналогично первому калькулятору, по формулам, приведенным в начале статьи.

Следующий калькулятор вычисляет площадь сегмента по высоте и радиусу:

Этот калькулятор вычисляет угол из высоты и радиуса по следующей формуле:

далее используется формула [1] для получения площади.

15 вычислений по сегменту круга в одной программе

Последний калькулятор включает в себя все оставшиеся вычисления параметров кругового сегмента:

• длина дуги
• угол
• хорда
• высота
• радиус
• площадь

Выберите два известных аргумента и калькулятор выдаст вам все оставшиеся.

Площадь круга и его частей. Длина окружности и ее дуг

Основные определения и свойства

Множество точек плоскости, находящихся на одном и том же расстоянии от одной точки – центра окружности

Часть окружности, расположенная между двумя точками окружности

Конечная часть плоскости, ограниченная окружностью

Часть круга, ограниченная двумя радиусами

Часть круга, ограниченная хордой

Выпуклый многоугольник, у которого все стороны равны и все углы равны

Около любого правильного многоугольника можно описать окружность

Фигура	Рисунок	Определения и свойства
Окружность
Дуга
Круг
Сектор
Сегмент
Правильный многоугольник

Окружность

Множество точек плоскости, находящихся на одном и том же расстоянии от одной точки – центра окружности

Дуга

Часть окружности, расположенная между двумя точками окружности

Круг

Конечная часть плоскости, ограниченная окружностью

Сектор

Часть круга, ограниченная двумя радиусами

Сегмент

Часть круга, ограниченная хордой

Правильный многоугольник

Выпуклый многоугольник, у которого все стороны равны и все углы равны

Около любого правильного многоугольника можно описать окружность

Определение 1 . Площадью круга называют предел, к которому стремятся площади правильных многоугольников, вписанных в круг, при неограниченном возрастании числа сторон.

Определение 2 . Длиной окружности называют предел, к которому стремятся периметры правильных многоугольников, вписанных в круг, при неограниченном возрастании числа сторон.

Замечание 1 . Доказательство того, что пределы площадей и периметров правильных многоугольников, вписанных в круг, при неограниченном возрастании числа сторон действительно существуют, выходит за рамки школьной математики и в нашем справочнике не приводится.

Определение 3 . Числом π (пи) называют число, равное площади круга радиуса 1.

Замечание 2 . Число π является иррациональным числом, т.е. числом, которое выражается бесконечной непериодической десятичной дробью:

Число π является трансцендентным числом, то есть числом, которое не может быть корнем алгебраического уравнения с целочисленными коэффициентами.

Формулы для площади круга и его частей

,

где R – радиус круга, D – диаметр круга

,

если величина угла α выражена в радианах

,

если величина угла α выражена в градусах

,

если величина угла α выражена в радианах

,

если величина угла α выражена в градусах

Числовая характеристика	Рисунок	Формула
Площадь круга
Площадь сектора
Площадь сегмента

Площадь круга

,

где R – радиус круга, D – диаметр круга

Площадь сектора

,

если величина угла α выражена в радианах

,

если величина угла α выражена в градусах

Площадь сегмента

,

если величина угла α выражена в радианах

,

если величина угла α выражена в градусах

Формулы для длины окружности и её дуг

где R – радиус круга, D – диаметр круга

если величина угла α выражена в радианах

,

если величина угла α выражена в градусах

Длина окружности

где R – радиус круга, D – диаметр круга

Длина дуги

если величина угла α выражена в радианах

,

если величина угла α выражена в градусах

Площадь круга

Рассмотрим две окружности с общим центром ( концентрические окружности ) и радиусами радиусами 1 и R , в каждую из которых вписан правильный n – угольник (рис. 1).

Обозначим через O общий центр этих окружностей. Пусть внутренняя окружность имеет радиус 1 .

Поскольку при увеличении n площадь правильного n – угольника, вписанного в окружность радиуса 1 , стремится к π , то при увеличении n площадь правильного n – угольника, вписанного в окружность радиуса R , стремится к числу πR 2 .

Таким образом, площадь круга радиуса R , обозначаемая S , равна

Длина окружности

то, обозначая длину окружности радиуса R буквой C , мы, в соответствии с определением 2, при увеличении n получаем равенство:

откуда вытекает формула для длины окружности радиуса R :

Следствие . Длина окружности радиуса 1 равна 2π.

Длина дуги

Рассмотрим дугу окружности, изображённую на рисунке 3, и обозначим её длину символом L(α), где буквой α обозначена величина соответствующего центрального угла.

В случае, когда величина α выражена в градусах, справедлива пропорция

из которой вытекает равенство:

В случае, когда величина α выражена в радианах, справедлива пропорция

из которой вытекает равенство:

Площадь сектора

Рассмотрим круговой сектор, изображённый на рисунке 4, и обозначим его площадь символом S (α) , где буквой α обозначена величина соответствующего центрального угла.

В случае, когда величина α выражена в градусах, справедлива пропорция

из которой вытекает равенство:

В случае, когда величина α выражена в радианах, справедлива пропорция

из которой вытекает равенство:

Площадь сегмента

Рассмотрим круговой сегмент, изображённый на рисунке 5, и обозначим его площадь символом S (α), где буквой α обозначена величина соответствующего центрального угла.

Поскольку площадь сегмента равна разности площадей кругового сектора MON и треугольника MON (рис.5), то в случае, когда величина α выражена в градусах, получаем

В случае, когда величина α выражена в в радианах, получаем

Сегмент круга

Вычисляет площадь, длину дуги, длину хорды, высоту и периметр сегмента круга. Описывается несколько вариантов расчета по параметрам сегмента – по углу, по хорде, по радиусу, по высоте и длине дуги.

Сегмент круга

Круговой сегмент — часть круга ограниченная дугой и секущей (хордой).

На рисунке:
L — длина дуги сегмента
c — хорда
R — радиус
a — угол сегмента
h — высота

Первый калькулятор рассчитывает параметры сегмента, если известен радиус и угол по следующим формулам:

Формулы вычисления параметров сегмента

Площадь сегмента:
[1]
Длина дуги:

Как найти фрагмент окружности

Сегмент круга

Вычисляет площадь, длину дуги, длину хорды, высоту и периметр сегмента круга. Описывается несколько вариантов расчета по параметрам сегмента — по углу, по хорде, по радиусу, по высоте и длине дуги.

Сегмент круга

Круговой сегмент — часть круга ограниченная дугой и секущей (хордой).

На рисунке:
L — длина дуги сегмента
c — хорда
R — радиус
a — угол сегмента
h — высота

Первый калькулятор рассчитывает параметры сегмента, если известен радиус и угол по следующим формулам:

Формулы вычисления параметров сегмента

Площадь сегмента:
[1]
Длина дуги:

Площадь круга и его частей. Длина окружности и ее дуг

Основные определения и свойства

Фигура	Рисунок	Определения и свойства
Окружность

Множество точек плоскости, находящихся на одном и том же расстоянии от одной точки — центра окружности

Дуга

Часть окружности, расположенная между двумя точками окружности

Круг

Конечная часть плоскости, ограниченная окружностью

Сектор

Часть круга, ограниченная двумя радиусами

Сегмент

Часть круга, ограниченная хордой

Правильный многоугольник

Выпуклый многоугольник, у которого все стороны равны и все углы равны

Около любого правильного многоугольника можно описать окружность

Окружность

Множество точек плоскости, находящихся на одном и том же расстоянии от одной точки — центра окружности

Дуга

Часть окружности, расположенная между двумя точками окружности

Круг

Конечная часть плоскости, ограниченная окружностью

Сектор

Часть круга, ограниченная двумя радиусами

Сегмент

Часть круга, ограниченная хордой

Правильный многоугольник

Выпуклый многоугольник, у которого все стороны равны и все углы равны

Около любого правильного многоугольника можно описать окружность

Определение 1 . Площадью круга называют предел, к которому стремятся площади правильных многоугольников, вписанных в круг, при неограниченном возрастании числа сторон.

Определение 2 . Длиной окружности называют предел, к которому стремятся периметры правильных многоугольников, вписанных в круг, при неограниченном возрастании числа сторон.

Замечание 1 . Доказательство того, что пределы площадей и периметров правильных многоугольников, вписанных в круг, при неограниченном возрастании числа сторон действительно существуют, выходит за рамки школьной математики и в нашем справочнике не приводится.

Определение 3 . Числом π (пи) называют число, равное площади круга радиуса 1.

Замечание 2 . Число π является иррациональным числом, т.е. числом, которое выражается бесконечной непериодической десятичной дробью:

Число π является трансцендентным числом, то есть числом, которое не может быть корнем алгебраического уравнения с целочисленными коэффициентами.

Формулы для площади круга и его частей

Числовая характеристика	Рисунок	Формула
Площадь круга

,

где R – радиус круга, D – диаметр круга

Площадь сектора

,

если величина угла α выражена в радианах

,

если величина угла α выражена в градусах

Площадь сегмента

,

если величина угла α выражена в радианах

,

если величина угла α выражена в градусах

Площадь круга

,

где R – радиус круга, D – диаметр круга

Площадь сектора

,

если величина угла α выражена в радианах

,

если величина угла α выражена в градусах

Площадь сегмента

,

если величина угла α выражена в радианах

,

если величина угла α выражена в градусах

Формулы для длины окружности и её дуг

Числовая характеристика	Рисунок	Формула
Длина окружности

где R – радиус круга, D – диаметр круга

Длина дуги

если величина угла α выражена в радианах

,

если величина угла α выражена в градусах

Длина окружности

где R – радиус круга, D – диаметр круга

Длина дуги

если величина угла α выражена в радианах

,

если величина угла α выражена в градусах

Площадь круга

Рассмотрим две окружности с общим центром ( концентрические окружности ) и радиусами радиусами 1 и R , в каждую из которых вписан правильный n – угольник (рис. 1).

Обозначим через O общий центр этих окружностей. Пусть внутренняя окружность имеет радиус 1 .

Поскольку при увеличении n площадь правильного n – угольника, вписанного в окружность радиуса 1 , стремится к π , то при увеличении n площадь правильного n – угольника, вписанного в окружность радиуса R , стремится к числу πR 2 .

Таким образом, площадь круга радиуса R , обозначаемая S , равна

Длина окружности

то, обозначая длину окружности радиуса R буквой C , мы, в соответствии с определением 2, при увеличении n получаем равенство:

откуда вытекает формула для длины окружности радиуса R :

Следствие . Длина окружности радиуса 1 равна 2π.

Длина дуги

Рассмотрим дугу окружности, изображённую на рисунке 3, и обозначим её длину символом L(α), где буквой α обозначена величина соответствующего центрального угла.

В случае, когда величина α выражена в градусах, справедлива пропорция

из которой вытекает равенство:

В случае, когда величина α выражена в радианах, справедлива пропорция

из которой вытекает равенство:

Площадь сектора

Рассмотрим круговой сектор, изображённый на рисунке 4, и обозначим его площадь символом S (α) , где буквой α обозначена величина соответствующего центрального угла.

В случае, когда величина α выражена в градусах, справедлива пропорция

из которой вытекает равенство:

В случае, когда величина α выражена в радианах, справедлива пропорция

из которой вытекает равенство:

Площадь сегмента

Рассмотрим круговой сегмент, изображённый на рисунке 5, и обозначим его площадь символом S (α), где буквой α обозначена величина соответствующего центрального угла.

Поскольку площадь сегмента равна разности площадей кругового сектора MON и треугольника MON (рис.5), то в случае, когда величина α выражена в градусах, получаем

В случае, когда величина α выражена в в радианах, получаем

Как найти фрагмент окружности

Круг — это часть плоскости, ограниченная окружностью. Центр данной окружности называется центром круга, а расстояние от центра до любой точки окружности — радиусом круга:

O — центр круга, OA — радиус круга.

Площадь круга

Площадь круга равна произведению числа π на квадрат радиуса. Формула нахождения площади круга:

где S — площадь круга, а r — радиус круга.

Так как диаметр круга равен удвоенному радиусу, то радиус равен диаметру, разделённому на 2:

Следовательно, формула нахождения площади круга через диаметр будет выглядеть так:

S = π(	D	) 2 = π	D 2	= π	D 2	.
2	2 2	4

Сектор круга. Площадь сектора

Сектор — это часть круга, ограниченная двумя радиусами и дугой. Два радиуса разделяют круг на два сектора:

Чтобы найти площадь сектора, дуга которого содержит n°, надо площадь круга разделить на 360 и полученный результат умножить на n.

Формула площади сектора:

S =	πr 2	· n =	πr 2 n	,
360	360

где S — площадь сектора. Выражение

можно представить в виде произведения

πr 2 n	= n ·	πr	·	r	,
360	180	2

где	nπr	— это длина дуги сектора.
180

Следовательно, площадь сектора равна длине дуги сектора, умноженной на половину радиуса:

где S — это площадь сектора, s — длина дуги данного сектора, r — радиус круга.

Сегмент. Площадь сегмента

Сегмент — это часть круга, ограниченная дугой и стягивающей её хордой. Любая хорда делит круг на два сегмента:

Площадь сегмента равна половине радиуса, умноженной на разность между дугой сегмента и половиной хорды двойной дуги.

Площадь сегмента AMB будет вычисляться по формуле:

где S — это площадь сегмента, r — радиус круга, s — длина дуги AB, а BC — длина половины хорды двойной дуги.

[spoiler title=”источники:”]

http://planetcalc.ru/1421/

http://b4.cooksy.ru/articles/kak-nayti-fragment-okruzhnosti

[/spoiler]

Информация по назначению калькулятора

Сектор круга – это часть окружности внутри круга, состоящая из дуги вместе с ее двумя радиусами. Часть окружности (также известная как дуга) и 2 радиуса окружности встречаются в обеих конечных точках дуги, образуя сектор. Форма сектора круга выглядит как кусочек пиццы или пирога. В геометрии круг – одна из самых совершенных фигур. Форма сектора окружности – самая простая форма в геометрии. У него есть свои собственные различные части. Например, диаметр, радиус, окружность, сегмент, сектор.

Круг разделен на два сектора, и разделенные части известны как второстепенные сектора и главные сектора.

Большая часть круга является основным сектором, в то время как меньшая часть является второстепенным сектором.

В случае полукругов окружность делится на два сектора одинакового размера.

2 радиуса встречаются в части окружности круга, известной как дуга, образуя сектор окружности.

Онлайн калькулятор предназначен для нахождения параметров сектора круга, таких как:

• Площадь сектора

– это объем пространства, занимаемого в пределах границы сектора круга. Сектор всегда начинается с центра круга. Полукруг также является сектором круга, в данном случае круг имеет два сектора одинакового размера.
Можно найти зная радиус и центральный угол в градусах (Ssek = ( α / 360° ) * πr²)

• Длина дуги

– находится путем умножения радиуса на центральный угол сектора в радианах (L = r * α)

• Радиус
• Периметр сектора

– равен сумме длины дуги и двум радиусам (Psek = L + r + r)

• Центральный угол сектора в градусах и радианах