В данной публикации мы рассмотрим формулы, с помощью которых можно вычислить площадь сектора круга, а также разберем примеры решения задач для демонстрации их практического применения.
- Определение сектора круга
-
Формулы нахождения площади сектора круга
- Через длину дуги и радиус круга
-
Через угол сектора (в градусах) и радиус круга
- Через угол сектора (в радианах) и радиус круга
- Примеры задач
Определение сектора круга
Сектор круга – это часть круга, образованная двумя его радиусами и дугой между ними. На рисунке ниже сектор закрашен зеленым цветом.

- AB – дуга сектора;
- R (или r) – радиус круга;
- α – это угол сектора, т.е. угол между двумя радиусами. Также его иногда называют центральным углом.
Формулы нахождения площади сектора круга
Через длину дуги и радиус круга
Площадь (S) сектора круга равняется одной второй произведения длины дуги сектора (L) и радиуса круга (r).
![]()
Через угол сектора (в градусах) и радиус круга
Площадь (S) сектора круга равняется площади круга, умноженной на угол сектора в градусах (α°) и деленной на 360°.

Через угол сектора (в радианах) и радиус круга
Площадь (S) сектора круга равняется половине произведения угла сектора в радианах (aрад) и квадрата радиуса круга.

Примеры задач
Задание 1
Дан круг радиусом 6 см. Найдите площадь сектора, если известно, что длина его дуги составляет 15 см.
Решение
Воспользуемся первой формулой, подставив в нее заданные значения:
![]()
Задание 2
Найдите угол сектора, если известно, что его площадь равна 78 см2, а радиус круга – 8 см.
Решение
Выведем формулу для нахождения центрального угла из второй формулы, рассмотренной выше:
![]()
Нахождение площади сектора круга
В данной публикации мы рассмотрим формулы, с помощью которых можно вычислить площадь сектора круга, а также разберем примеры решения задач для демонстрации их практического применения.
Определение сектора круга
Сектор круга – это часть круга, образованная двумя его радиусами и дугой между ними. На рисунке ниже сектор закрашен зеленым цветом.

- AB – дуга сектора;
- R (или r) – радиус круга;
- α – это угол сектора, т.е. угол между двумя радиусами. Также его иногда называют центральным углом.
Формулы нахождения площади сектора круга
Через длину дуги и радиус круга
Площадь (S) сектора круга равняется одной второй произведения длины дуги сектора (L) и радиуса круга (r).

Через угол сектора (в градусах) и радиус круга
Площадь (S) сектора круга равняется площади круга, умноженной на угол сектора в градусах ( α°) и деленной на 360°.

Через угол сектора (в радианах) и радиус круга
Площадь (S) сектора круга равняется половине произведения угла сектора в радианах (aрад) и квадрата радиуса круга.

Примеры задач
Задание 1
Дан круг радиусом 6 см. Найдите площадь сектора, если известно, что длина его дуги составляет 15 см.
Решение
Воспользуемся первой формулой, подставив в нее заданные значения:

Задание 2
Найдите угол сектора, если известно, что его площадь равна 78 см 2 , а радиус круга – 8 см.
Решение
Выведем формулу для нахождения центрального угла из второй формулы, рассмотренной выше:
Как рассчитать площадь сектора круга
На данной странице калькулятор поможет рассчитать площадь сектора круга онлайн. Для расчета задайте радиус, длину дуги или угол сектора круга.
Сектор круга – это часть круга, окружности ограниченная дугой и двумя радиусами, проведенными к концам дуги.
Через длину дуги и радиус
Формула для нахождения площади сектора круга:
Через угол и радиус
Формула для нахождения площади сектора круга:
Площадь круга и его частей. Длина окружности и ее дуг

Основные определения и свойства
Множество точек плоскости, находящихся на одном и том же расстоянии от одной точки – центра окружности
Часть окружности, расположенная между двумя точками окружности
Конечная часть плоскости, ограниченная окружностью
Часть круга, ограниченная двумя радиусами
Часть круга, ограниченная хордой
Выпуклый многоугольник, у которого все стороны равны и все углы равны
Около любого правильного многоугольника можно описать окружность
| Фигура | Рисунок | Определения и свойства |
| Окружность |  |
|
| Дуга |  |
|
| Круг |  |
|
| Сектор |  |
|
| Сегмент |  |
|
| Правильный многоугольник |  |
|
 |
| Окружность |
 |
Множество точек плоскости, находящихся на одном и том же расстоянии от одной точки – центра окружности
Дуга

Часть окружности, расположенная между двумя точками окружности
Круг

Конечная часть плоскости, ограниченная окружностью
Сектор

Часть круга, ограниченная двумя радиусами
Сегмент

Часть круга, ограниченная хордой
Правильный многоугольник

Выпуклый многоугольник, у которого все стороны равны и все углы равны

Около любого правильного многоугольника можно описать окружность
Определение 1 . Площадью круга называют предел, к которому стремятся площади правильных многоугольников, вписанных в круг, при неограниченном возрастании числа сторон.
Определение 2 . Длиной окружности называют предел, к которому стремятся периметры правильных многоугольников, вписанных в круг, при неограниченном возрастании числа сторон.
Замечание 1 . Доказательство того, что пределы площадей и периметров правильных многоугольников, вписанных в круг, при неограниченном возрастании числа сторон действительно существуют, выходит за рамки школьной математики и в нашем справочнике не приводится.
Определение 3 . Числом π (пи) называют число, равное площади круга радиуса 1.
Замечание 2 . Число π является иррациональным числом, т.е. числом, которое выражается бесконечной непериодической десятичной дробью:

Число π является трансцендентным числом, то есть числом, которое не может быть корнем алгебраического уравнения с целочисленными коэффициентами.
Формулы для площади круга и его частей
 ,
,
где R – радиус круга, D – диаметр круга
 ,
,
если величина угла α выражена в радианах
 ,
,
если величина угла α выражена в градусах
 ,
,
если величина угла α выражена в радианах
 ,
,
если величина угла α выражена в градусах
| Числовая характеристика | Рисунок | Формула |
| Площадь круга |  |
|
| Площадь сектора |  |
|
| Площадь сегмента |  |
| Площадь круга |
 |
 ,
,
где R – радиус круга, D – диаметр круга
Площадь сектора

 ,
,
если величина угла α выражена в радианах
 ,
,
если величина угла α выражена в градусах
Площадь сегмента

 ,
,
если величина угла α выражена в радианах
 ,
,
если величина угла α выражена в градусах
Формулы для длины окружности и её дуг
где R – радиус круга, D – диаметр круга
если величина угла α выражена в радианах
 ,
,
если величина угла α выражена в градусах
| Длина окружности |
 |
где R – радиус круга, D – диаметр круга
Длина дуги

если величина угла α выражена в радианах
 ,
,
если величина угла α выражена в градусах
Площадь круга
Рассмотрим две окружности с общим центром ( концентрические окружности ) и радиусами радиусами 1 и R , в каждую из которых вписан правильный n – угольник (рис. 1).
Обозначим через O общий центр этих окружностей. Пусть внутренняя окружность имеет радиус 1 .






Поскольку при увеличении n площадь правильного n – угольника, вписанного в окружность радиуса 1 , стремится к π , то при увеличении n площадь правильного n – угольника, вписанного в окружность радиуса R , стремится к числу πR 2 .
Таким образом, площадь круга радиуса R , обозначаемая S , равна
Длина окружности



то, обозначая длину окружности радиуса R буквой C , мы, в соответствии с определением 2, при увеличении n получаем равенство:

откуда вытекает формула для длины окружности радиуса R :
Следствие . Длина окружности радиуса 1 равна 2π.
Длина дуги
Рассмотрим дугу окружности, изображённую на рисунке 3, и обозначим её длину символом L(α), где буквой α обозначена величина соответствующего центрального угла.

В случае, когда величина α выражена в градусах, справедлива пропорция

из которой вытекает равенство:

В случае, когда величина α выражена в радианах, справедлива пропорция

из которой вытекает равенство:

Площадь сектора
Рассмотрим круговой сектор, изображённый на рисунке 4, и обозначим его площадь символом S (α) , где буквой α обозначена величина соответствующего центрального угла.

В случае, когда величина α выражена в градусах, справедлива пропорция

из которой вытекает равенство:

В случае, когда величина α выражена в радианах, справедлива пропорция

из которой вытекает равенство:

Площадь сегмента
Рассмотрим круговой сегмент, изображённый на рисунке 5, и обозначим его площадь символом S (α), где буквой α обозначена величина соответствующего центрального угла.

Поскольку площадь сегмента равна разности площадей кругового сектора MON и треугольника MON (рис.5), то в случае, когда величина α выражена в градусах, получаем



В случае, когда величина α выражена в в радианах, получаем
[spoiler title=”источники:”]
http://www.mozgan.ru/Geometry/AreaSectorCircle
http://www.resolventa.ru/demo/diaggia6.htm
[/spoiler]
Как найти площадь сектора круга Если известна площадь всего круга и центральный угол
Ученик
(25),
закрыт
4 года назад
Dimitry Zinkovsky
Мыслитель
(5320)
5 лет назад
Ну, смотри: площадь всего круга – это сектор с центральным углом в 360 градусов (или 2pi, если угол искомого сектора дан в радианах). Соответственно, площадь сектора с центральным углом в 1 градус (или в 1 радиан), будет равен площади целой окружности, деленной на 360 (или на 2pi соответственно).
Для того, чтобы найти площадь сектора с заданным центральным углом, нужно площадь сектора в 1 градус (1 радиан), умножить на величину центрального угла искомого сектора в градусах (или радианах):
Sсектора=(Sокр/360)*@ – для центрального угла @ сектора заданного в градусах
Sсектора=(Sокр/2pi)*@ – для центрального угла @ сектора заданного в радианах
Здесь вы можете рассчитать площадь сектора круга с помощью удобного онлайн калькулятора по двум формулам. Для этого необходимо ввести известные вам параметры фигуры:
- радиус круга и угол,
- длину дуги и радиус.
Сектор круга или окружности – это его(её) часть, ограниченная дугой и двумя радиусами, соединяющими концы дуги с центром круга (окружности).
Содержание:
- калькулятор площади сектора круга
- формула площади сектора круга через радиус и угол
- формула площади сектора круга через радиус и длину дуги
- примеры задач
Формула площади сектора круга через радиус и угол
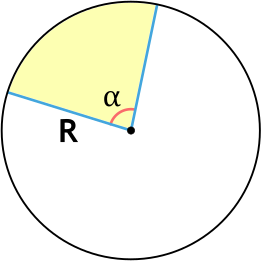
S = pi R^2 dfrac{alpha °}{360°}
S = dfrac{alpha}{2} R^2
R – радиус сектора
α° – угол сектора (в градусах)
α – угол сектора (в радианах)
Формула площади сектора круга через радиус и длину дуги

S = dfrac{1}{2}LR
L – длина дуги сектора
R – радиус сектора
Примеры задач на нахождение площади сектора круга
Задача 1
Найдите площадь сектора круга радиуса 1 длина дуги которого равна 2.
Решение
Для решения задачи нам подойдет вторая формула.
S = dfrac{1}{2}LR = dfrac{1}{2} cdot 2 cdot 1 = dfrac{1}{2} cdot 2 = 1 : см^2
Ответ: 1 : см^2
Давайте проверим ответ с помощью калькулятора .
Задача 2
Найдите площадь сектора круга радиуса 24 длина дуги которого равна 3.
Решение
Задача аналогична предыдущей.
S = dfrac{1}{2}LR = dfrac{1}{2} cdot 3 cdot 24 = dfrac{1}{2} cdot 72 = 36 : см^2
Ответ: 36 : см^2
Проверка .
Задача 3
Найдите площадь кругового сектора если радиус круга равен 3, а угол сектора равен 120°.
Решение
Для решения этой задачи нам потребуется первая формула, в которой угол указывается в градусах.
S = pi R^2 dfrac{alpha °}{360°} = pi cdot 3^2 cdot dfrac{120°}{360°} = pi cdot 9 cdot dfrac{1}{3} = 3 pi : см^2 approx 9.42478 : см^2
Ответ: 3 pi : см^2 approx 9.42478 : см^2
Проверка .
В этом простом онлайн-калькуляторе для нахождения величин сектора круга можно быстро определить длину дуги сектора, зная площадь, периметр или центральный угол сектора. Для этого нужно заполнить по одному пустующему слота в калькуляторах окружности и сектора окружности, после чего нажать на кнопку “Рассчитать”. В результате высветятся все недостающие значения вместе с формулами.
Калькулятор окружности:
Достаточно заполнить только одну ячейку — остальное калькулятор посчитает сам.
Периметр или длина окружности (P)
Калькулятор сектора окружности:
Достаточно ввести только одно значение и указать радиус окружности — остальное калькулятор посчитает сам.
Центральный угол сектора в градусах (α)
Площадь сектора окружности (S1)
Калькулятор сегмента окружности:
Достаточно ввести только одно* значение и указать радиус окружности — остальное калькулятор посчитает сам.
Исключения:
* – при известном периметре (P2) нужно дополнительно указать длину дуги (l1) или хорды (c).
* – при известной площади (S2) нужно дополнительно указать длину хорды (c) или высоты (h).
Угол сегмента в градусах (α1)
Площадь сегмента окружности (S2)
Округление:
* – обязательно заполнить
