-
Скорость истечения
Чтобы
найти скорость истечения газа через
сопло, нужно проинтегрировать уравнение:
![]() ;
;
![]() ,
,
где
w
1 и w
2 –
значения скорости в конце и начале
процесса.
Для
случаев, когда , w
2
w
1, то
членом 1
можно
пренебречь, получаем:
![]() ,
,
(9.17)
но
т.к. l0
связано
с параметрами
![]() ,
,
можно записать:
 ,
,
или
![]() (9.18)
(9.18)
Из
последних формул видно, что скорость
истечения определяется параметрами
газа
![]()
на входе
в сопло и его давлением P2
на
выходе, или
разностью энтальпий h0
на входе и
выходе из сопла.
При
истечении газа в вакуум (P2
= 0) скорость
истечения будет максимальная.
![]() .
.
(9.19)
-
Секундный расход идеального газа через сопло
Массовый
расход газа через сопло определяется
по уравнению неразрывности
![]() ,
,
где
F2
– площадь выходного сечения; v2
– удельный объем. v2
можно определить из соотношения
параметров в адиабатном процессе:
 .
.
Подставляя
значения удельного объема v2
и скорость
истечения
в уравнение
неразрывности, получаем:
 ,
,
или
 .
.
Таким
образом, массовый секундный расход газа
зависит от площади выходного сечения
сопла F2,
параметров газа на входе
![]()
и степени
его расширения.
-
Истечение газа из сосуда неограниченной емкости
Рассмотрим
истечение газа из бесконечно большого
резервуара (рис. 9.4), в котором параметры
газа
![]() ;
;
параметры на срезе сопла
![]() ;
;
параметры окружающей среды
![]() .
.
Начальную скорость в резервуаре принимаем
равной нулю (![]() =
=
0).

Рис.
9.4. Истечение газа из резервуара через
суживающееся сопло
Если
истечение является обратимым адиабатным,
то
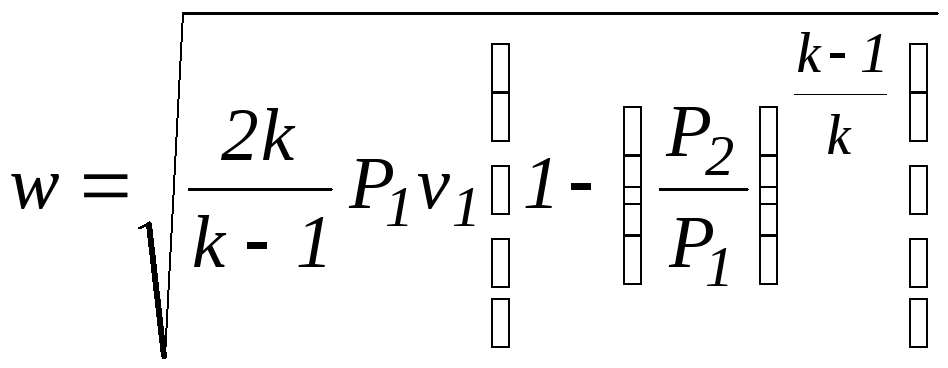
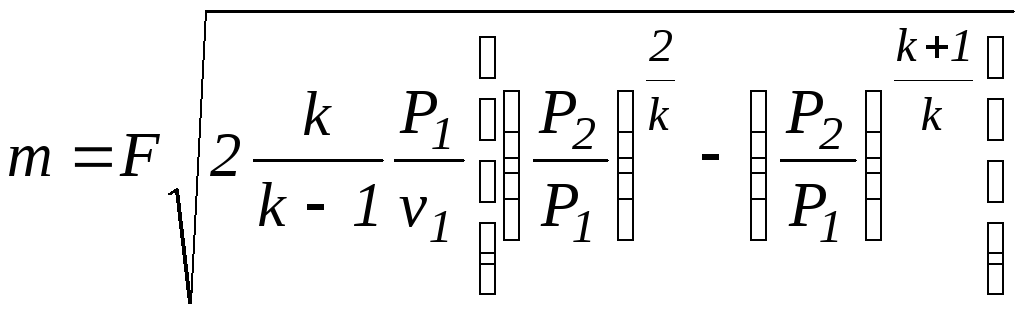
Таким
образом, для данного газа и заданных
параметров газа
![]()
и
![]() скоростьw
скоростьw
и расход газа m
зависят только от отношения давления
![]() ,
,
т.е. от давления во внешнем пространстве,
куда истекает газ. Анализ показывает,
что при![]() ,
,
когда
= 1, скорость
истечения газа равна нулю, с уменьшением
скорость
все время возрастает и при
![]() 0,
0,
когда
= 0
оно достигает максимального значения.
Расход газа
m
становится равным нулю при![]() ,
,
когда
= 1,
и при
![]() 0,
0,
когда
= 0.
Между
этими граничными значениями
расход m
больше нуля, а при некотором определенном
отношении давлений
![]() расход
расход
газа m
и скорость
истечения
становятся
максимальными. В точке максимума
производная расхода m
по
превращается
в ноль. Давление
![]() ,
,
при которомm
= mmax
и w
=
w
max,
называется критическим
![]() .
.
Для определения критического отношения
давлений![]() возьмем
возьмем
первую производную от последней
зависимости, которая стоит в квадратных
скобках под корнем и приравняем ее к
нулю.
 ,
,
отсюда
![]()
(9.20)
Критическое
отношение давлений зависит только от
показателя адиабаты k,
т.е. от физических свойств газа. Для
одноатомного газа k
= 1,66, кр
= 0,49; для
двухатомного: k
= 1,41, кр
= 0,528; для
трехатомного: k
= 1,33, кр
= 0,546. С учетом
изложенного можно записать:
![]() ,
,
(9.21)
т.е.
критическое давление равно начальному
давлению, умноженному на коэффициент
кр.

Рис.
9.5. Зависимость расхода газа (а) от
скорости истечения (б) и удельного объема
(в)
при
истечении от отношения давлений![]()
Из
рисунка 9.5 видно, что при уменьшении
перепада давлений от
=
1
до
=
кр
расход газа m
возрастает от m
=
0 при
=
1 до
m
=
mmax
=
mкр
при
=
кр,
т.е. на срезе сопла наступает такой режим
течения, когда расход газа m,
скорость
и
удельный объем v
достигают
своего предельного значения. При
дальнейшем понижении давления до
кр,
изменение расхода газа m
соответствуют
участки кривой bc
и
bo.
Участок bo
получен по теоретической зависимости.
Действительное же изменение расхода
происходит по линии bс.
Соседние файлы в папке Термодинамика
- #
- #
- #
- #
- #
- #
- #
- #
Секундный массовый расход
Cтраница 1
Секундный массовый расход через сопло Лаваля, так же как и в случае чисто конфузорного сопла, не может превзойти своего максимального значения, равного тому расходу, который пройдет сквозь сопло, если в наиболее узком его сечении будет достигнута местная скорость звука. Но в отличие от конфузорного сопла скорость на выходе из сопла Лаваля при сверхзвуковом режиме превосходит скорость звука и может быть подбором формы и длины сопла сделана тем больше, чем меньше противодавление.
[1]
Секундный массовый расход т одинаков для всех сечений, поэтому изменение площади сечения F вдоль сопла ( по координате х) определяется соотношением интенсивностей возрастания удельного объема газа v и его скорости с.
[2]
Секундный массовый расход т через сопло Лаваля, так же как и п случае чисто конфузорного сопла, не может превзойти своего максимального значения, равного тому расходу, который пройдет сквозь сопло, если в наиболее узком его сечении, на границе между конфузорной и диффузорной частями, будет достигнута местная скорость звука. Но в отличие от конфузорного сопла скорость на выходе из сопла Лаваля превосходит соответствующую выходу скорость звука и может быть подбором длины сопла сделана тем больше, чем меньше противодавление.
[3]
Секундный массовый расход через сопло Лаваля, так же как и в случае чисто конфузорпого сопла, не может превзойти своего максимального значения, равного тому расходу, который пройдет сквозь сопло, если в наиболее узком его сечении будет достигнута местная скорость звука. Но в отличие от конфузорного сопла скорость на выходе из сопла Лаваля при сверхзвуковом режиме превосходит скорость звука и может быть подбором формы и длины сопла сделана тем больше, чем меньше противодавление.
[4]
Секундный массовый расход через сопло Лаваля, так же как и в случае чисто конфузорного сопла, не может превзойти своего максимального значения, равного тому расходу, который пройдет сквозь сопло, если в наиболее узком его сечении будет достигнута местная скорость звука. Но в отличие от конфузорного сопла скорость на выходе из сопла Лаваля при сверхзвуковом режиме превосходит скорость звука и может быть подбором формы и длины сопла сделана тем больше, чем меньше противодавление.
[5]
При ркр секундный массовый расход достигает максимальной величины Мтах.
[6]
Вс – секундный массовый расход, кг / сек; рм – плотность протекающего топлива, кг / м3; F – площадь поперечного сечения, м2; d – диаметр трубопровода, м; w – скорость протекания, м / сек.
[7]
Таким образом, секундный массовый расход газа, вытекающего из сопла, зависит от отношения p / Pi – Так как k i, то при p – iipi I M – мнимое число. Физически это означает, что истечение газа при / – 2 pt ( из среды с меньшим давлением в среду с большим давлением) невозможно.
[8]
Величину Gc называют секундным массовым расходом жидкости.
[9]
Величину Сс называют секундным массовым расходом жидкости.
[10]
Формула (1.3) дает значение секундного массового расхода газа через любое сечение струйки при условии, что скорость и, следовательно, плотность газа в каждой точке сечения остаются постоянными.
[12]
Последнее равенство выражает закон постоянства секундного массового расхода вдоль трубки тока.
[13]
Термический КПД монотонно растет с ростом секундного массового расхода рабочего тела. С точки зрения достижения максимальных значений КПД выгодно увеличивать массовый расход вплоть до значений, при которых начинается неустойчивое горение.
[15]
Страницы:
1
2
3
5.2. Критическое давление и скорость. Сопло Лаваля
Если перемещение газа по каналу происходит его
расширение с уменьшением давления и увеличением скорости, то такой канал
называется
соплом
.
Если в канале происходит сжатие рабочего тела с увеличением его давления и
уменьшением скорости, то такой канал называют
диффузором.
В каналах при небольшой разности давлений газа и внешней среды скорость течения
рабочего тела достаточно большая. В большинстве случаев длина канала небольшая
и процесс теплообмена между стенкой и газом незначителен, поэтому процесс
истечения газа можно считать адиабатным.
Скорость истечения (на выходе канала) определяется из уравнения:w = w2 =
v 2(h1 – h2) . (5.6)
или
w = v 2Ö/(g
– 1)·P1·х 1 [1 – (P2/P1)(g-1)/g].
(5.7)
Массовый секундный расход
газа, [кг/с]:
m = f·w/х 2 , (5.8)
где: f – площадь сечения
канала на выходе.
Так как процесс истечения адиабатный, то:
m = f·Ö 2g/(g
– 1)·P1/х 1·[(P2/P1)2/g
– (P2/P1)(g+1)/g].
(5.9)
Массовый секундный расход идеального газа зависит от
площади выходного канала, начального состояния газа и степени его расширения.
Критическим давлением
называется
такое давление на выходном сечении канала, при котором достигается максимальный
расход газа и определяется следующим выражением:
PК = P2
= bК·P1
, (5.10)
где: PК = (2/(g
+ 1))г/(г-1) .
для одноатомных газов:
g =1,66 q bК
= 0,49 ;
для двухатомных газов:
g =1,4 q bК
= 0,528 ;
для трехатомных газов:
g =1,3 q bК
= 0,546 .
Критической скоростью
называется скорость газа в выходном сечении канала, при давлении равном или
меньшем критического – PК.
wК = Ö
2(g/(g + 1))·P1·х
1 . (5.11)
Критическая скорость зависит при истечении идеального
газа только от начальных параметров, его природы и равна скорости звука газа (а) при критических параметрах.
wК = а
= Ö g·PК·хК
. (5.12)
Комбинированное сопло Лаваля предназначено для
использования больших перепадов давления и для порлучения скоростей истечения,
превышающих критическую или скорость звука. Сопло Лаваля состоит из короткого
суживающегося участка и расширяющейсяя конической насадки (Рис.5.1).
Опыты показывают, что угол конусности расширяющейся части должен быть равен a = 8-12о.
При больших углах наблюдается отрыв струи от стенок канала.
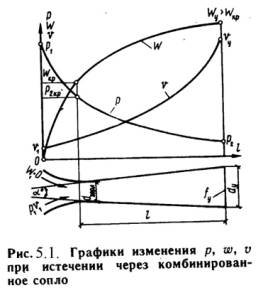
Скорость истечения и секундный расход идеального газа определяются по формулам
(5.7) и (5.9).
Длину расширяющейся части сопла можно определить по уравнению:
l = (D – d) / 2·tg(j/2) , (5.13)
где: j
– угол конусности сопла;
D – диаметр выходного отверстия;
d – диаметр сопла в минимальном сечении.
