Как найти секущую окружности зная радиус - Сайт, где вы сможете решить свои вопросы

Как найти секущую окружности

Касательная к окружности

О чем эта статья:

Касательная к окружности, секущая и хорда — в чем разница

В самом названии касательной отражается суть понятия — это прямая, которая не пересекает окружность, а лишь касается ее в одной точке. Взглянув на рисунок окружности ниже, несложно догадаться, что точку касания от центра отделяет расстояние, в точности равное радиусу.

Касательная к окружности — это прямая, имеющая с ней всего одну общую точку.

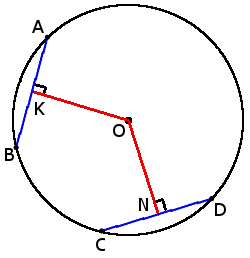
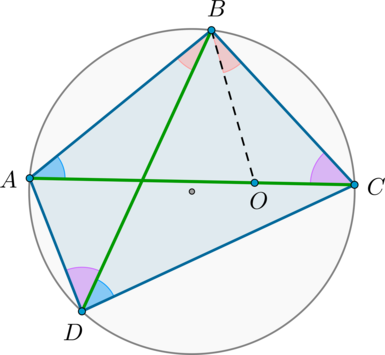
Если мы проведем прямую поближе к центру окружности — так, чтобы расстояние до него было меньше радиуса — неизбежно получится две точки пересечения. Такая прямая называется секущей, а отрезок, расположенный между точками пересечения, будет хордой (на рисунке ниже это ВС ).

Секущая к окружности — это прямая, которая пересекает ее в двух местах, т. е. имеет с ней две общие точки. Часть секущей, расположенная внутри окружности, будет называться хордой.

Свойства касательной к окружности

Выделяют четыре свойства касательной, которые необходимо знать для решения задач. Два из них достаточно просты и легко доказуемы, а вот еще над двумя придется немного подумать. Рассмотрим все по порядку.

Касательная к окружности и радиус, проведенный в точку касания, взаимно перпендикулярны.

Не будем принимать это на веру, попробуем доказать. Итак, у нас даны:

окружность с центральной точкой А;
прямая а — касательная к ней;
радиус АВ, проведенный к касательной.

Докажем, что касательная и радиус АВ взаимно перпендикулярны, т.е. а ⟂ АВ.

Пойдем от противного — предположим, что между прямой а и радиусом АВ нет прямого угла и проведем настоящий перпендикуляр к касательной, назвав его АС.

В таком случае наш радиус АВ будет считаться наклонной, а наклонная, как известно, всегда длиннее перпендикуляра. Получается, что АВ > АС. Но если бы это было на самом деле так, наша прямая а пересекалась бы с окружностью два раза, ведь расстояние от центра А до нее — меньше радиуса. Но по условию задачи а — это касательная, а значит, она может иметь лишь одну точку касания.

Итак, мы получили противоречие. Делаем вывод, что настоящим перпендикуляром к прямой а будет вовсе не АС, а АВ.

Курсы подготовки к ОГЭ по математике от Skysmart придадут уверенности в себе и помогут освежить знания перед экзаменом.

Задача

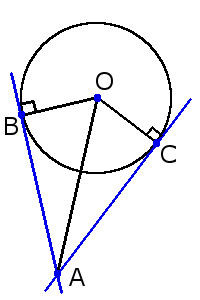
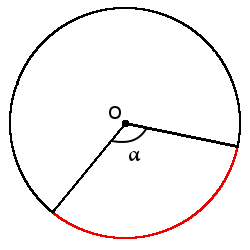
У нас есть окружность, центр которой обозначен О. Из точки С проведена прямая, и она касается этой окружности в точке А. Известно, что ∠АСО = 28°. Найдите величину дуги АВ.

Мы знаем, что касательная АС ⟂ АО, следовательно ∠САО = 90°.

Поскольку нам известны величины двух углов треугольника ОАС, не составит труда найти величину и третьего угла.

∠АОС = 180° — ∠САО — ∠АСО = 180° — 90° — 28° = 62°

Поскольку вершина угла АОС лежит в центре окружности, можно вспомнить свойство центрального угла — как известно, он равен дуге, на которую опирается. Следовательно, АВ = 62°.

Если провести две касательных к окружности из одной точки, лежащей вне этой окружности, то их отрезки от этой начальной точки до точки касания будут равны.

Докажем и это свойство на примере. Итак, у нас есть окружность с центром А, давайте проведем к ней две касательные из точки D. Обозначим эти прямые как ВD и CD . А теперь выясним, на самом ли деле BD = CD.

Для начала дополним наш рисунок, проведем еще одну прямую из точки D в центр окружности. Как видите, у нас получилось два треугольника: ABD и ACD . Поскольку мы уже знаем, что касательная и радиус к ней перпендикулярны, углы ABD и ACD должны быть равны 90°.

Итак, у нас есть два прямоугольных треугольника с общей гипотенузой AD. Учитывая, что радиусы окружности всегда равны, мы понимаем, что катеты AB и AC у этих треугольников тоже одинаковой длины. Следовательно, ΔABD = ΔACD (по катету и гипотенузе).. Значит, оставшиеся катеты, а это как раз наши BD и CD (отрезки касательных к окружности), аналогично равны.

Важно: прямая, проложенная из стартовой точки до центра окружности (в нашем примере это AD), делит угол между касательными пополам.

Задача 1

У нас есть окружность с радиусом 4,5 см. К ней из точки D, удаленной от центра на 9 см, провели две прямые, которые касаются окружности в точках B и C. Определите градусную меру угла, под которым пересекаются касательные.

Решение

Для этой задачи вполне подойдет уже рассмотренный выше рисунок окружности с радиусами АВ и АC. Поскольку касательная ВD перпендикулярна радиусу АВ , у нас есть прямоугольный треугольник АВD. Зная длину его катета и гипотенузы, определим величину ∠BDA.

∠BDA = 30° (по свойству прямоугольного треугольника: угол, лежащий напротив катета, равного половине гипотенузы, составляет 30°).

Мы знаем, что прямая, проведенная из точки до центра окружности, делит угол между касательными, проведенными из этой же точки, пополам. Другими словами:

∠BDC = ∠BDA × 2 = 30° × 2 = 60°

Итак, угол между касательными составляет 60°.

Задача 2

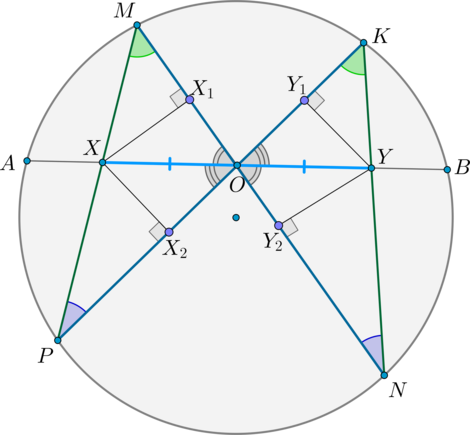
К окружности с центром О провели две касательные КМ и КN. Известно, что ∠МКN равен 50°. Требуется определить величину угла ∠NМК.

Решение

Согласно вышеуказанному свойству мы знаем, что КМ = КN. Следовательно, треугольник МNК является равнобедренным.

Углы при его основании будут равны, т.е. ∠МNК = ∠NМК.

∠МNК = (180° — ∠МКN) : 2 = (180° — 50°) : 2 = 65°

Соотношение между касательной и секущей: если они проведены к окружности из одной точки, лежащей вне окружности, то квадрат расстояния до точки касания равен произведению длины всей секущей на ее внешнюю часть.

Данное свойство намного сложнее предыдущих, и его лучше записать в виде уравнения.

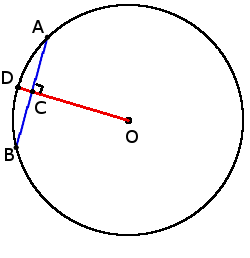
Начертим окружность и проведем из точки А за ее пределами касательную и секущую. Точку касания обозначим В, а точки пересечения — С и D. Тогда CD будет хордой, а отрезок AC — внешней частью секущей.

Задача 1

Из точки М к окружности проведены две прямые, пусть одна из них будет касательной МA, а вторая — секущей МB. Известно, что хорда ВС = 12 см, а длина всей секущей МB составляет 16 см. Найдите длину касательной к окружности МA.

Решение

Исходя из соотношения касательной и секущей МА 2 = МВ × МС.

Найдем длину внешней части секущей:

МС = МВ — ВС = 16 — 12 = 4 (см)

МА 2 = МВ × МС = 16 х 4 = 64

Задача 2

Дана окружность с радиусом 6 см. Из некой точки М к ней проведены две прямые — касательная МA и секущая МB . Известно, что прямая МB пересекает центр окружности O. При этом МB в 2 раза длиннее касательной МA . Требуется определить длину отрезка МO.

Решение

Допустим, что МО = у, а радиус окружности обозначим как R.

В таком случае МВ = у + R, а МС = у – R.

Поскольку МВ = 2 МА, значит:

МА = МВ : 2 = (у + R) : 2

Согласно теореме о касательной и секущей, МА 2 = МВ × МС.

(у + R) 2 : 4 = (у + R) × (у — R)

Сократим уравнение на (у + R), так как эта величина не равна нулю, и получим:

Поскольку R = 6, у = 5R : 3 = 30 : 3 = 10 (см).

Ответ: MO = 10 см.

Угол между хордой и касательной, проходящей через конец хорды, равен половине дуги, расположенной между ними.

Это свойство тоже стоит проиллюстрировать на примере: допустим, у нас есть касательная к окружности, точка касания В и проведенная из нее хорда AВ. Отметим на касательной прямой точку C, чтобы получился угол AВC.

Задача 1

Угол АВС между хордой АВ и касательной ВС составляет 32°. Найдите градусную величину дуги между касательной и хордой.

Решение

Согласно свойствам угла между касательной и хордой, ∠АВС = ½ АВ.

АВ = ∠АВС × 2 = 32° × 2 = 64°

Задача 2

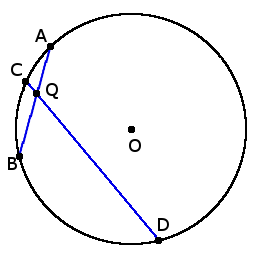
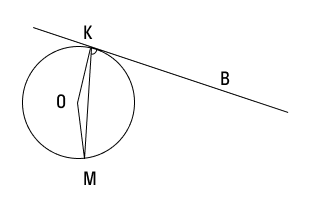
У нас есть окружность с центром О, к которой идет прямая, касаясь окружности в точке K. Из этой точки проводим хорду KM, и она образует с касательной угол MKB, равный 84°. Давайте найдем величину угла ОMK.

Решение

Поскольку ∠МКВ равен половине дуги между KM и КВ, следовательно:

КМ = 2 ∠МКВ = 2 х 84° = 168°

Обратите внимание, что ОМ и ОK по сути являются радиусами, а значит, ОМ = ОК. Из этого следует, что треугольник ОMK равнобедренный.

∠ОКМ = ∠ОМК = (180° — ∠КОМ) : 2

Так как центральный угол окружности равен угловой величине дуги, на которую он опирается, то:

∠ОМК = (180° — ∠КОМ) : 2 = (180° — 168°) : 2 = 6°

Хорда, секущая, касательная

Определения

Хорда – отрезок, соединяющий две точки окружности.

В частности, хорда, проходящая через центр окружности, называется диаметром .

Секущей к окружности называется прямая, которая пересекает окружность в двух различных точках.

Касательная к окружности — прямая, имеющая с окружностью единственную общую точку.

Свойства

Радиус, проведенный в точку касания, перпендикулярен касательной

Отрезки касательных, проведенных к окружности из одной точки, равны.

Отрезки пересекающихся хорд связаны соотношением:

Произведения отрезков секущих, проведенных из одной точки, равны:

Квадрат отрезка касательной равен произведению отрезков секущей, проведенной из той же точки:

Если две окружности касаются внешним образом, то длина отрезка общей внешней касательной равна удвоенному среднему пропорциональному их радиусов Видеодоказательство

Чтобы не потерять страничку, вы можете сохранить ее у себя:

Отрезки и прямые, связанные с окружностью. Теорема о бабочке

Отрезки и прямые, связанные с окружностью

Свойства хорд и дуг окружности

Теоремы о длинах хорд, касательных и секущих

Доказательства теорем о длинах хорд, касательных и секущих

Теорема о бабочке

Отрезки и прямые, связанные с окружностью

Фигура	Рисунок	Определение и свойства
Окружность

Множество точек плоскости, находящихся на одном и том же расстоянии от одной точки — центра окружности

Круг

Конечная часть плоскости, ограниченная окружностью

Радиус

Отрезок, соединяющий центр окружности с любой точкой окружности

Хорда

Отрезок, соединяющий две любые точки окружности

Диаметр

Хорда, проходящая через центр окружности.

Диаметр является самой длинной хордой окружности

Касательная

Прямая, имеющая с окружностью только одну общую точку.

Касательная перпендикулярна к радиусу окружности, проведённому в точку касания

Секущая

Прямая, пересекающая окружность в двух точках

Множество точек плоскости, находящихся на одном и том же расстоянии от одной точки — центра окружности

Круг

Конечная часть плоскости, ограниченная окружностью

Радиус

Отрезок, соединяющий центр окружности с любой точкой окружности

Хорда

Отрезок, соединяющий две любые точки окружности

Диаметр

Хорда, проходящая через центр окружности.

Диаметр является самой длинной хордой окружности

Касательная

Прямая, имеющая с окружностью только одну общую точку.

Касательная перпендикулярна к радиусу окружности, проведённому в точку касания

Секущая

Прямая, пересекающая окружность в двух точках

Свойства хорд и дуг окружности

Фигура	Рисунок	Свойство
Диаметр, перпендикулярный к хорде		Диаметр, перпендикулярный к хорде, делит эту хорду и стягиваемые ею две дуги пополам.
Диаметр, проходящий через середину хорды	Диаметр, проходящий через середину хорды, перпендикулярен к этой хорде и делит стягиваемые ею две дуги пополам.
Равные хорды		Если хорды равны, то они находятся на одном и том же расстоянии от центра окружности.
Хорды, равноудалённые от центра окружности	Если хорды равноудалены (находятся на одном и том же расстоянии) от центра окружности, то они равны.
Две хорды разной длины		Большая из двух хорд расположена ближе к центру окружности.
Равные дуги		У равных дуг равны и хорды.
Параллельные хорды		Дуги, заключённые между параллельными хордами, равны.

Диаметр, перпендикулярный к хорде

Диаметр, перпендикулярный к хорде, делит эту хорду и стягиваемые ею две дуги пополам.

Диаметр, проходящий через середину хорды

Диаметр, проходящий через середину хорды, перпендикулярен к этой хорде и делит стягиваемые ею две дуги пополам.

Равные хорды

Если хорды равны, то они находятся на одном и том же расстоянии от центра окружности.

Хорды, равноудалённые от центра окружности

Если хорды равноудалены (находятся на одном и том же расстоянии) от центра окружности, то они равны.

Две хорды разной длины

Большая из двух хорд расположена ближе к центру окружности.

Равные дуги

У равных дуг равны и хорды.

Параллельные хорды

Дуги, заключённые между параллельными хордами, равны.

Теоремы о длинах хорд, касательных и секущих

Фигура	Рисунок	Теорема
Пересекающиеся хорды

Произведения длин отрезков, на которые разбита каждая из хорд, равны:

Касательные, проведённые к окружности из одной точки

Если к окружности из одной точки проведены две касательных, то длины отрезков касательных от этой точки до точек касания с окружностью равны.

Касательная и секущая, проведённые к окружности из одной точки

Секущие, проведённые из одной точки вне круга

Произведения длин отрезков, на которые разбита каждая из хорд, равны:

Пересекающиеся хорды

Касательные, проведённые к окружности из одной точки

Касательная и секущая, проведённые к окружности из одной точки

Секущие, проведённые из одной точки вне круга

Произведения длин отрезков, на которые разбита каждая из хорд, равны:

Касательные, проведённые к окружности из одной точки

Касательная и секущая, проведённые к окружности из одной точки

Секущие, проведённые из одной точки вне круга

Доказательства теорем о длинах хорд, касательных и секущих

Теорема 1 . Предположим, что хорды окружности AB и CD пересекаются в точке E (рис.1).

Тогда справедливо равенство

Доказательство . Заметим, что углы BCD и BAD равны как вписанные углы, опирающиеся на одну и ту же дугу. Углы BEC и AED равны как вертикальные. Поэтому треугольники BEC и AED подобны. Следовательно, справедливо равенство

откуда и вытекает требуемое утверждение.

Теорема 2 . Предположим, что из точки A , лежащей вне круга, к окружности проведены касательная AB и секущая AD (рис.2).

Точка B – точка касания с окружностью, точка C – вторая точка пересечения прямой AD с окружностью. Тогда справедливо равенство

Доказательство . Заметим, что угол ABC образован касательной AB и хордой BC , проходящей через точку касания B . Поэтому величина угла ABC равна половине угловой величины дуги BC . Поскольку угол BDC является вписанным углом, то величина угла BDC также равна половине угловой величины дуги BC . Следовательно, треугольники ABC и ABD подобны (угол A является общим, углы ABC и BDA равны). Поэтому справедливо равенство

откуда и вытекает требуемое утверждение.

Теорема 3 . Предположим, что из точки A , лежащей вне круга, к окружности проведены секущие AD и AF (рис.3).

Точки C и E – вторые точки пересечения секущих с окружностью. Тогда справедливо равенство

Доказательство . Проведём из точки A касательную AB к окружности (рис. 4).

Точка B – точка касания. В силу теоремы 2 справедливы равенства

откуда и вытекает требуемое утверждение.

Теорема о бабочке

Теорема о бабочке . Через середину G хорды EF некоторой окружности проведены две произвольные хорды AB и CD этой окружности. Точки K и L – точки пересечения хорд AC и BD с хордой EF соответственно (рис.5). Тогда отрезки GK и GL равны.

Доказательство . Существует много доказательств этой теоремы. Изложим доказательство, основанное на теореме синусов, которое, на наш взгляд, является наиболее наглядным. Для этого заметим сначала, что вписанные углы A и D равны, поскольку опираются на одну и ту же дугу. По той же причине равны и вписанные углы C и B . Теперь введём следующие обозначения:

Воспользовавшись теоремой синусов, применённой к треугольнику CKG , получим

Воспользовавшись теоремой синусов, применённой к треугольнику AKG , получим

Воспользовавшись теоремой 1, получим

Воспользовавшись равенствами (1) и (2), получим

Проводя совершенно аналогичные рассуждения для треугольников BGL и DGL , получим равенство

откуда вытекает равенство

что и завершает доказательство теоремы о бабочке.

Отрезки и прямые, связанные с окружностью. Теорема о бабочке

Отрезки и прямые, связанные с окружностью

Свойства хорд и дуг окружности

Теоремы о длинах хорд, касательных и секущих

Доказательства теорем о длинах хорд, касательных и секущих

Теорема о бабочке

Отрезки и прямые, связанные с окружностью

Множество точек плоскости, находящихся на одном и том же расстоянии от одной точки – центра окружности

Конечная часть плоскости, ограниченная окружностью

Отрезок, соединяющий центр окружности с любой точкой окружности

Отрезок, соединяющий две любые точки окружности

Хорда, проходящая через центр окружности.

Диаметр является самой длинной хордой окружности

Прямая, имеющая с окружностью только одну общую точку.

Касательная перпендикулярна к радиусу окружности, проведённому в точку касания

Прямая, пересекающая окружность в двух точках

Фигура	Рисунок	Определение и свойства
Окружность
Круг
Радиус
Хорда
Диаметр
Касательная
Секущая

Множество точек плоскости, находящихся на одном и том же расстоянии от одной точки – центра окружности

Круг

Конечная часть плоскости, ограниченная окружностью

Радиус

Отрезок, соединяющий центр окружности с любой точкой окружности

Хорда

Отрезок, соединяющий две любые точки окружности

Диаметр

Хорда, проходящая через центр окружности.

Диаметр является самой длинной хордой окружности

Касательная

Прямая, имеющая с окружностью только одну общую точку.

Касательная перпендикулярна к радиусу окружности, проведённому в точку касания

Секущая

Прямая, пересекающая окружность в двух точках

Свойства хорд и дуг окружности

Фигура	Рисунок	Свойство
Диаметр, перпендикулярный к хорде		Диаметр, перпендикулярный к хорде, делит эту хорду и стягиваемые ею две дуги пополам.
Диаметр, проходящий через середину хорды	Диаметр, проходящий через середину хорды, перпендикулярен к этой хорде и делит стягиваемые ею две дуги пополам.
Равные хорды		Если хорды равны, то они находятся на одном и том же расстоянии от центра окружности.
Хорды, равноудалённые от центра окружности	Если хорды равноудалены (находятся на одном и том же расстоянии) от центра окружности, то они равны.
Две хорды разной длины		Большая из двух хорд расположена ближе к центру окружности.
Равные дуги		У равных дуг равны и хорды.
Параллельные хорды		Дуги, заключённые между параллельными хордами, равны.

Диаметр, перпендикулярный к хорде

Диаметр, перпендикулярный к хорде, делит эту хорду и стягиваемые ею две дуги пополам.

Диаметр, проходящий через середину хорды

Равные хорды

Если хорды равны, то они находятся на одном и том же расстоянии от центра окружности.

Хорды, равноудалённые от центра окружности

Если хорды равноудалены (находятся на одном и том же расстоянии) от центра окружности, то они равны.

Две хорды разной длины

Большая из двух хорд расположена ближе к центру окружности.

Равные дуги

У равных дуг равны и хорды.

Параллельные хорды

Дуги, заключённые между параллельными хордами, равны.

Теоремы о длинах хорд, касательных и секущих

Произведения длин отрезков, на которые разбита каждая из хорд, равны:

Фигура	Рисунок	Теорема
Пересекающиеся хорды
Касательные, проведённые к окружности из одной точки
Касательная и секущая, проведённые к окружности из одной точки
Секущие, проведённые из одной точки вне круга

Произведения длин отрезков, на которые разбита каждая из хорд, равны:

Пересекающиеся хорды

Касательные, проведённые к окружности из одной точки

Касательная и секущая, проведённые к окружности из одной точки

Секущие, проведённые из одной точки вне круга

Произведения длин отрезков, на которые разбита каждая из хорд, равны:

Касательные, проведённые к окружности из одной точки

Касательная и секущая, проведённые к окружности из одной точки

Секущие, проведённые из одной точки вне круга

Доказательства теорем о длинах хорд, касательных и секущих

Теорема 1 . Предположим, что хорды окружности AB и CD пересекаются в точке E (рис.1).

Тогда справедливо равенство

откуда и вытекает требуемое утверждение.

Теорема 3 . Предположим, что из точки A , лежащей вне круга, к окружности проведены секущие AD и AF (рис.3).

Точки C и E – вторые точки пересечения секущих с окружностью. Тогда справедливо равенство

Доказательство . Проведём из точки A касательную AB к окружности (рис. 4).

Точка B – точка касания. В силу теоремы 2 справедливы равенства

откуда и вытекает требуемое утверждение.

Теорема о бабочке

Воспользовавшись теоремой синусов, применённой к треугольнику CKG , получим

Воспользовавшись теоремой синусов, применённой к треугольнику AKG , получим

Воспользовавшись теоремой 1, получим

Воспользовавшись равенствами (1) и (2), получим

Проводя совершенно аналогичные рассуждения для треугольников BGL и DGL , получим равенство

откуда вытекает равенство

что и завершает доказательство теоремы о бабочке.

Хорда, секущая, касательная

Определения

Хорда – отрезок, соединяющий две точки окружности.

В частности, хорда, проходящая через центр окружности, называется диаметром .

Секущей к окружности называется прямая, которая пересекает окружность в двух различных точках.

Касательная к окружности — прямая, имеющая с окружностью единственную общую точку.

Свойства

Радиус, проведенный в точку касания, перпендикулярен касательной

Отрезки касательных, проведенных к окружности из одной точки, равны.

Отрезки пересекающихся хорд связаны соотношением:

Произведения отрезков секущих, проведенных из одной точки, равны:

Квадрат отрезка касательной равен произведению отрезков секущей, проведенной из той же точки:

Чтобы не потерять страничку, вы можете сохранить ее у себя:

[spoiler title=”источники:”]

http://www.resolventa.ru/demo/training.htm

Хорда, секущая, касательная

[/spoiler]

Источник

Окружность, круг, сегмент, сектор. Формулы и свойства

Окружность – определение
Круг – определение
Радиус и диаметр окружности
Основные свойства окружности
Формулы длины окружности и площади круга
Уравнение окружности
Касательная окружности и ее свойства
Секущая окружности и ее свойства
Хорда окружности и ее свойства
Центральный угол, вписанный угол и их свойства
Дуга, длина дуги, градусная мера дуги
Полуокружность и полукруг
Сектор, площадь сектора
Сегмент, площадь сегмента
Концентрические окружности
Кольцо

Определение. Окружность — это совокупность всех точек на плоскости, которые находятся на одинаковом расстоянии от заданной точки О, которая называется центром окружности.

Определение. Единичная окружность – окружность, радиус которой равен единице.

Определение. Круг – часть плоскости, ограничена окружностью.

Определение. Радиус окружности R – расстояние от центра окружности О до любой точки окружности.

Определение. Диаметр окружности D – отрезок, который соединяет две точки окружности и проходит через ее центр.

Основные свойства окружности

1. Диаметр окружности равен двум радиусам.

D = 2r

2. Кратчайшее расстояние от центра окружности к секущей (хорде) всегда меньше радиуса.

3. Через три точки, которые не лежат на одной прямым, можно провести только одну окружность.

4. Среди всех замкнутых кривых с одинаковой длиной, окружность имеет наибольшую площадь.

5. Если две окружности соприкасаются в одной точке, то эта точка лежит на прямой, что проходит через центры этих окружностей.

Формулы длины окружности и площади круга

Формулы длины окружности

1. Формула длины окружности через диаметр:

L = πD

2. Формула длины окружности через радиус:

L = 2πr

Формулы площади круга

1. Формула площади круга через радиус:

S = πr²

2. Формула площади круга через диаметр:

S = πD²4

Уравнение окружности

1. Уравнение окружности с радиусом r и центром в начале декартовой системы координат:

r² = x² + y²

2. Уравнение окружности с радиусом r и центром в точке с координатами (a, b) в декартовой системе координат:

r² = (x – a)² + (y – b)²

3. Параметрическое уравнение окружности с радиусом r и центром в точке с координатами (a, b) в декартовой системе координат:

{	x = a + r cos t
y = b + r sin t

Касательная окружности и ее свойства

Определение. Касательная окружности – прямая, которая касается окружности только в одной точке.

Основные свойства касательных к окружности

1. Касательная всегда перпендикулярна к радиусу окружности, проведенного в точке соприкосновения.

2. Кратчайшее расстояние от центра окружности к касательной равна радиусу окружности.

3. Если две касательные, с точками соприкосновения B и C, на одной окружности не параллельны, то они пересекаются в точке A, а отрезок между точкой соприкосновения и точкой пересечения одной касательной равен таком же отрезке на другой касательной:

AB = AC

Также, если провести прямую через центр окружности О и точку пересечения A этих касательных, то углы образованный между этой прямой и касательными будут равны:

∠ОAС = ∠OAB

Секущая окружности и ее свойства

Определение. Секущая окружности – прямая, которая проходит через две точки окружности.

Основные свойства секущих

1. Если с точки вне окружности (Q) выходят две секущие, которые пересекают окружность в двух точках A и B для одной секущей и C и D для другой секущей, то произведения отрезков двух секущих равны между собою:

AQ ∙ BQ = CQ ∙ DQ

2. Если из точки Q вне окружности выходит секущая прямая, что пересекает окружность в двух точках A и B, и касательная с точкой соприкосновения C, то произведение отрезков секущей равна квадрату длины отрезка касательной:

AQ ∙ BQ = CQ²

Хорда окружности ее длина и свойства

Определение. Хорда окружности – отрезок, который соединяет две точки окружности.

Длина хорды

1. Длина хорды через центральный угол и радиус:

AB = 2r sin α2

2. Длина хорды через вписанный угол и радиус:

AB = 2r sin α

Основные свойства хорд

1. Две одинаковые хорды стягивают две одинаковые дуги:

если хорды AB = CD, то

дуги ◡ AB = ◡ CD

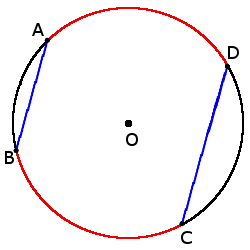
2. Если хорды параллельные, то дуги между ними будут одинаковые:

если хорды AB ∣∣ CD, то

◡ AD = ◡ BC

3. Если радиус окружности перпендикулярен к хорде, то он разделяет хорду пополам в точке их пересечения:

если OD ┴ AB, то

AC = BC

4. Если две хорды AB и CD пересекаются в точке Q, то произведение отрезков, что образовались при пересечении, одной хорды равны произведению отрезков другой хорды:

AQ ∙ BQ = DQ ∙ QC

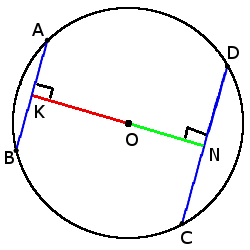
5. Хорды с одинаковой длиной находятся на одинаковом расстоянии от центра окружности.

если хорды AB = CD, то

ON = OK

6. Чем больше хорда, тем ближе она к центру.

если CD > AB, то

ON < OK

Центральный угол, вписанный угол и их свойства

Определение. Центральный угол окружности – угол, вершиной которого есть центр окружности.

Определение. Угол вписанный в окружность – угол, вершина которого лежит на окружности, а стороны угла пересекают окружность.

Основные свойства углов

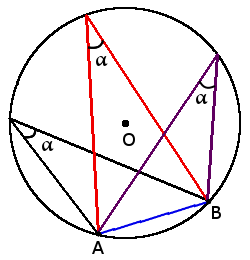
1. Все вписанные углы, которые опираются на одну дугу – равны.

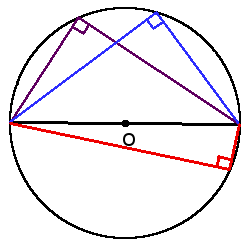
2. Вписанный угол, который опирается на диаметр будет прямым (90°).

3. Вписанный угол равен половине центрального угла, что опирается на ту же дугу

β = α2

4. Если два вписанных угла опираются на одну хорду и находятся по различные стороны от нее, то сумма этих углов равна 180°.

α + β = 180°

Определение. Дуга окружности (◡) – часть окружности, которая соединяет две точки на окружности.

Определение. Градусная мера дуги – угол между двумя радиусами, которые ограничивают эту дугу. Градусная мера дуги всегда равна градусной мере центрального угла, который ограничивает эту дугу своими сторонами.

Формула длины дуги через центральный угол (в градусах):

l = πr180°∙ α

Определение. Полуокружность – дуга в которой концы соединены диаметром окружности.

Определение. Полукруг (◓) – часть круга, которая ограничена полуокружностью и диаметром.

Определение. Сектор (◔) – часть круга, которая ограничена двумя радиусами и дугой между этими радиусами.

Формула. Формула площади сектор через центральный угол (в градусах)

S = πr²360°∙ α

Определение. Сегмент – часть круга, которая ограничена дугой и хордой, что соединяет ее концы.

Определение. Концентрические окружности – окружности с различными радиусами, которые имеют общий центр.

Определение. Кольцо – часть плоскости ограниченная двумя концентрическими окружностями.

Источник

Секущая и хорда окружности

Зачем что-то знать о секущих и хордах в окружности?

Как обычно, знание свойств и закономерностей сильно облегчает жизнь.

Зная свойства секущих и хорд в окружности и закономерности (формулы), мы сможем решить многие задачи на ЕГЭ!

Поехали!

Секущая и хорда окружности — коротко о главном

Секущая окружности

Здесь ( displaystyle AC) – секущая окружности – начинается снаружи окружности и пересекает её в двух точках.

Хорда окружности

Здесь ( displaystyle BC) – хорда окружности – отрезок, соединяющий две точки на окружности.

Длина хорды

Пусть ( displaystyle AB) – хорда, ( displaystyle R) – радиус, ( displaystyle angle AСB) – любой вписанный угол, опирающийся на хорду ( displaystyle AB). Тогда:

( displaystyle AB=2Rsin alpha).

Произведение длин отрезков хорд и секущих

Для любых двух хорд, проходящих через некоторую точку ( displaystyle A), выполняется:

( displaystyle ABcdot AC=ADcdot AE).

Теорема о секущей и касательной

Для любых секущей и касательной, проходящих через точку ( A), верно:

( displaystyle A{{C}^{2}}=ADcdot AE).

А теперь подробнее…

Определения секущей и хорды окружности

Давай прежде всего вспомним, что такое секущая и хорда. Смотри на картинки.

Здесь ( displaystyle AC) – секущая окружности – начинается снаружи окружности и пересекает её в двух точках.

Здесь ( displaystyle BC) – хорда окружности – отрезок, соединяющий две точки на окружности.

Кстати, заметил ли ты, что на первом рисунке хорда ( displaystyle BC) является кусочком секущей ( displaystyle AC)?

Вот так всегда и бывает: если есть секущая, то один её кусок – хорда, а второй называется внешняя часть, ну, как у нас ( displaystyle AB) – она же снаружи, верно?

Что же мы должны знать о секущей и хорде окружности?

Всего-то 2-3-4 утверждения. Давай начнём с того, что ты, возможно, уже читал в разделе «Теорема синусов» и «Теорема косинусов» — с длины хорды в окружности.

Длина хорды окружности

Пусть ( displaystyle AB) – хорда, ( displaystyle R) – радиус, ( displaystyle angle ACB) – любой вписанный угол, опирающийся на хорду ( displaystyle AB).

Тогда ( Largefrac{AB}{sin alpha }=2R)

Узнал теорему синусов?

Значит, длину хорды окружности можно найти по формуле:

Произведение длин отрезков хорд и секущих

Сейчас мы сформулируем очень важное, пожалуй, даже основное свойство хорд и секущих окружности.

Словами это свойство формулировать неудобно – получается длинно и некрасиво, поэтому ограничимся буквами.

Произведение длин отрезков хорд окружности

Для любых двух хорд окружности, проходящих через некоторую точку ( displaystyle A), выполняется: ( displaystyle ABcdot AC=ADcdot AE)

Произведение длин отрезков секущих окружности

Для любых двух секущих, проходящих через некоторую точку ( displaystyle A), выполняется: ( displaystyle ABcdot AC=ADcdot AE)

Вопрос первый: Почему мы сформулировали утверждения друг под другом столбиком?

Ответ: Утверждения очень похожи – если закрыть картинки и слова, то получится просто одно и то же – удивительно, не правда ли? Ну, и это сходство гораздо лучше видно, когда утверждения стоят рядом.

Вопрос второй: Как не перепутать, что на что умножать?

Произведение длин отрезков хорд окружности — доказательство

Повторим формулировку.

Для любых двух хорд, проходящих через некоторую точку ( displaystyle A), выполняется: ( ABcdot AC=ADcdot AE)

А теперь докажем.

Рассмотрим ( triangle ABD) и ( triangle AEC). У них углы ( displaystyle A) равны как вертикальные и ( angle DBC=angle DEC), потому что они опираются на одну дугу ( displaystyle DC).

Значит, ( displaystyle triangle ABDsim triangle AEC) по двум углам (вспоминаем признаки подобия треугольников).

Запишем, что же нам даёт это подобие (и откроем маленький секрет!).

Произведение длин отрезков секущих окружности — доказательство

Еще раз формулировку…

Для любых двух секущих, проходящих через некоторую точку ( displaystyle A), выполняется: ( ABcdot AC=ADcdot AE)

Снова рассмотрим ( displaystyle triangle ABD) и ( displaystyle triangle AEC).

У них есть общий ( angle A);
Четырехугольник ( BCED) — вписанный (срочно повторяем или читаем тему «Окружность. Вписанный угол»).

sekushie iz odnoj tochki dokazatelstvo 2

Значит, ( angle 1+angle 2=180{}^circ ) (сумма противоположных углов вписанного четырехугольника равна ( 180{}^circ )). Но ( angle 2+angle 3=180{}^circ ) — как смежные углы (смотри на картинку).

Что же получилось?

( left{ begin{array}{l}angle 1+angle 2=180{}^circ \angle 2+angle 3=180{}^circ end{array} right.Rightarrow angle 1=angle 3)

То есть ( underbrace{angle ACE}_{в triangle AEC}=underbrace{angle ADB}_{в triangle ABD }).

Из всего этого следует, что ( triangle AECsim triangle ABD) по двум углам (( angle A) – общий и ( angle ACE=angle ADB)).

Снова запишем отношение соответствующих сторон:

Теорема о секущей и касательной (секретное оружие)

А сейчас «секретное» оружие — теорема о секущей и касательной. Почему секретное?

Потому что множество задач ОГЭ и ЕГЭ можно решить с помощью этой теоремы. А акцент на ней в учебнике не делается. То есть ее как бы нет…

В предыдущем пункте мы выяснили, что ( ABcdot AC=ADcdot AE)

Но возникает вопрос: а что будет, если секущая ( AC) и «превратится» в касательную?

Видишь: осталось всего три зелёных точки? Оказывается, ничего страшного, всё почти так же. Формулируем:

Для любых секущей и касательной, проходящих через точку ( A), верно: ( Large A{{C}^{2}}=ADcdot AE).

Тут точки ( B) и ( C) как бы слились в одну – и на рисунке, и в формуле. Заметил?

Самые бюджетные курсы по подготовке к ЕГЭ на 90+

Алексей Шевчук — ведущий мини-групп

математика, информатика, физика

+7 (905) 541-39-06 — WhatsApp/Телеграм для записи

alexei.shevchuk@youclever.org — email для записи

тысячи учеников, поступивших в лучшие ВУЗы страны
автор понятного всем учебника по математике ЮКлэва (с сотнями благодарных отзывов);
закончил МФТИ, преподавал на малом физтехе;
репетиторский стаж — c 2003 года;
в 2021 году сдал ЕГЭ (математика 100 баллов, физика 100 баллов, информатика 98 баллов — как обычно дурацкая ошибка:);
отзыв на Профи.ру: «Рейтинг: 4,87 из 5. Очень хвалят. Такую отметку получают опытные специалисты с лучшими отзывами».

Источник

В данной публикации мы рассмотрим определение и свойства одного из основных геометрических объектов – окружности. Также приведем формулы, с помощью которых можно найти ее радиус, диаметр и длину.

Определение окружности

Окружность – это замкнутая кривая на плоскости, состоящая из точек, равноудаленных от определенной точки. Данная точка называется центром окружности.

Радиус окружности (R) – это отрезок, соединяющий любую точку, лежащую на окружности, с ее центром.

Диаметр окружности (d) – это линия (хорда), проходящая через центр окружности и соединяющая две противоположные точки, лежащие на ней.

Примечание: Не стоит путать окружность с кругом, т.к. круг – это множество точек плоскости, ограниченных окружностью (т.е. лежащих внутри окружности).

Свойства окружности

Свойство 1

Через три точки на плоскости, не лежащие на одной прямой, можно провести окружность, причем только одну.

Свойство 2

Точка касания двух окружностей (C) лежит на одной прямой (AB), которая проходит через их центры.

Свойство 3

Изопериметрическое неравенство: Из всех замкнутых кривых одинаковой длины окружность ограничивает область с самой большой площадью.

Формулы

1. Диаметр окружности (d):

2. Длина окружности (С):

3. Радиус окружности (R):

Эта статья содержит минимальный набор сведений об окружности, необходимый для успешной сдачи ЕГЭ по математике.

Окружностью называется множество точек, расположенных на одинаковом расстоянии от данной точки, которая называется центром окружности.

Для любой точки , лежащей на окружности выполняется равенство OL=R ( Длина отрезка равна радиусу окружности.

Отрезок, соединяющий две точки окружности называется хордой.

Хорда, проходящая через центр окружности называется диаметром окружности (). D=2R

Длина окружности:

Площадь круга:

$S={pi}R^2$

Дуга окружности:

Часть окружности, заключенная между двумя ее точками называется дугой окружности. Две точки окружности определяют две дуги. Хорда стягивает две дуги: CMD и CLD . Равные хорды стягивают равные дуги.

Угол между двумя радиусами называется центральным углом:

Чтобы найти длину дуги , составляем пропорцию:

а) угол alpha дан в градусах:

$2{pi}R~~~~~360^{circ}$

$x~~~~~~~{alpha}^{circ}$

Отсюда $x={{pi}R{alpha}^{circ}}/{180^{circ}}$

б) угол alpha дан в радианах:

Отсюда

Диаметр, перпендикулярный хорде, делит эту хорду и дуги, которые она стягивает пополам:

Если хорды 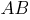и окружности пересекаются в точке , то произведения отрезков хорд, на которые они делятся точкой равны между собой:

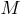
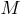
Касательная к окружности.

Прямая, имеющая с окружностью одну общую точку называется касательной к окружности. Прямая, имеющая с окружностью две общие точки называется секущей.

Касательная к окружности перпендикулярна радиусу, проведенному к точке касания.

Если из данной точки проведены к окружности две касательные, то отрезки касательных равны между собой и центр окружности лежит на биссектрисе угла с вершиной в этой точке:

AC=CB

Если из данной точки проведены к окружности касательная и секущая, то квадрат длины отрезка касательной равен произведению всего отрезка секущей на его внешнюю часть:

Следствие: произведение всего отрезка одной секущей на его внешнюю часть равно произведению всего отрезка другой секущей на его внешнюю часть:

Углы в окружности.

Градусная мера центрального угла равна градусной мере дуги, на которую он опирается:

∠ COD= ⌣ $CD={alpha}^{circ}$

Угол, вершина которого лежит на окружности, а стороны содержат хорды, называется вписанным углом. Вписанный угол измеряется половиной дуги, на которую он опирается:

∠ AOB=2 ∠ ADB

Вписанный угол, опирающийся на диаметр, прямой:

∠ CBD= ∠ CED= ∠ $CAD=90^{circ}$

Вписанные углы, опирающиеся на одну дугу, равны:

∠ ADB= ∠ AEB= ∠ AFB

Вписанные углы, опирающиеся на одну хорду равны или их сумма равна $180^{circ}$

∠ ADB+ ∠ $AKB=180^{circ}$

∠ ADB= ∠ AEB= ∠ AFB

Вершины треугольников с заданным основанием и равными углами при вершине лежат на одной окружности:

Угол между двумя хордами (угол с вершиной внутри окружности) равен полусумме угловых величин дуг окружности, заключенных внутри данного угла и внутри вертикального угла.

∠ DMC= ∠ ADM+ ∠ DAM=1/2 ( ⌣ DmC+ ⌣ AlB )

Угол между двумя секущими (угол с вершиной вне окружности) равен полуразности угловых величин дуг окружности, заключенных внутри угла.

∠ ∠ CBD- ∠( ⌣ DmC- ⌣ AlB )

Вписанная окружность.

Окружность называется вписанной в многоугольник, если она касается его сторон. Центр вписанной окружности лежит в точке пересечения биссектрис углов многоугольника.

Не во всякий многоугольник можно вписать окружность.

Площадь многоугольника, в который вписана окружность можно найти по формуле

S=pr ,

здесь — полупериметр многоугольника, — радиус вписанной окружности.

Отсюда радиус вписанной окружности равен r=S/p

Если в выпуклый четырехугольник вписана окружность, то суммы длин противоположных сторон равны. Обратно: если в выпуклом четырехугольнике суммы длин противоположных сторон равны, то в четырехугольник можно вписать окружность:

В любой треугольник можно вписать окружность, притом только одну. Центр вписанной окружности лежит в точке пересечения биссектрис внутренних углов треугольника.

Радиус вписанной окружности равен r=S/p . Здесь

Описанная окружность.

Окружность называется описанной около многоугольника, если она проходит через все вершины многоугольника. Центр описанной окружности лежит в точке пересечения серединных перпендикуляров сторон многоугольника. Радиус вычисляется как радиус окружности, описанной около треугольника, определенного любыми тремя вершинами данного многоугольника:

Около четырехугольника можно описать окружность тогда и только тогда, когда сумма его противоположных углов равна $180^{circ}$ .

∠+∠=∠+∠ $D=180^{circ}$

Около любого треугольника можно описать окружность, притом только одну. Ее центр лежит в точке пересечения серединных перпендикуляров сторон треугольника:

Радиус описанной окружности вычисляется по формулам:

Где — длины сторон треугольника, — его площадь.

Теорема Птолемея

Во вписанном четырехугольнике произведение диагоналей равно сумме произведений его противоположных сторон:

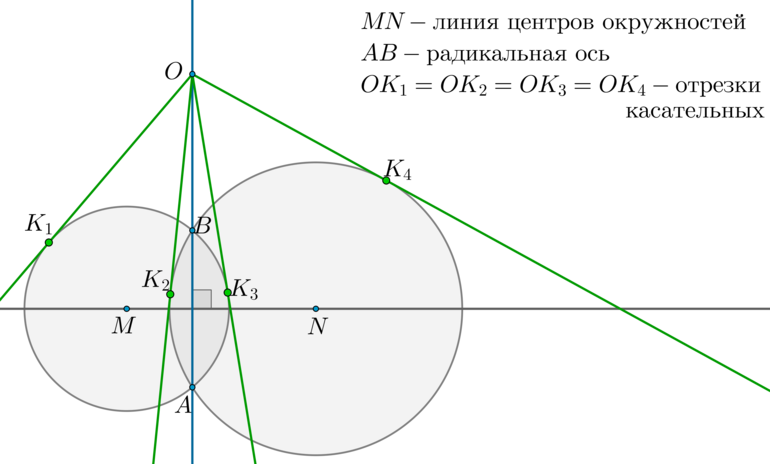
Радикальная ось — прямая, проходящая через точки пересечения двух окружностей.
Линия центров окружностей — прямая, проходящая через центры двух окружностей.

Теорема 1.

1) Радикальная ось перпендикулярна линии центров окружностей.
2) Отрезки касательных, проведенных из любой точки радикальной оси к этим окружностям, равны.

Доказательство:

1) Рассмотрим (triangle BMN) и (triangle AMN): они равны по трем сторонам ((BM=AM=R_1, BN=AN=R_2) — радиусы первой и второй окружностей соответственно). Таким образом, (angle BNM=angle ANM), следовательно, (MN) — биссектриса в равнобедренном (triangle ANB), следовательно, (MNperp AB).

2) Отметим произвольную точку (O) на радикальной оси и проведем касательные (OK_1, OK_3) к первой окружности и (OK_2, OK_4) ко второй окружности. Т.к. квадрат отрезка касательной равен произведению секущей на ее внешнюю часть, то (OK_1^2=OK_2^2=OK_3^2=OK_4^2=OBcdot OA).

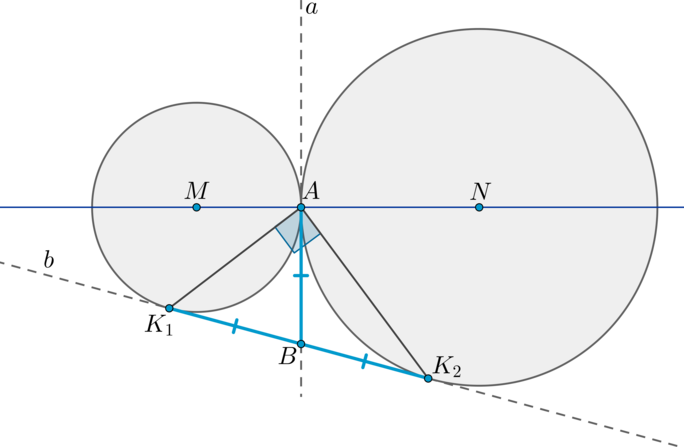
Теорема 2.

Пусть две окружности с центрами (M) и (N) касаются внешним образом в точке (A). Две общие касательные (внутренняя и внешняя) (a) и (b) этих окружностей пересекаются в точке (B). Точки касания — точки (A, K_1, K_2) (как показано на рисунке). Тогда [(1) {large{K_1B=AB=K_2B}}] [(2) {large{angle K_1AK_2=90^circ}}]

Доказательство:

1) Т.к. (BA) и (BK_1) — две касательные, проведенные к первой окружности из одной точки, то отрезки касательных равны: (BA=BK_1). Аналогично, (BA=BK_2). Таким образом, (BA=BK_1=BK_2).

2) Значит, (BA) — медиана в (triangle K_1AK_2), равная половине стороны, к которой она проведена. Значит, (angle A=90^circ).

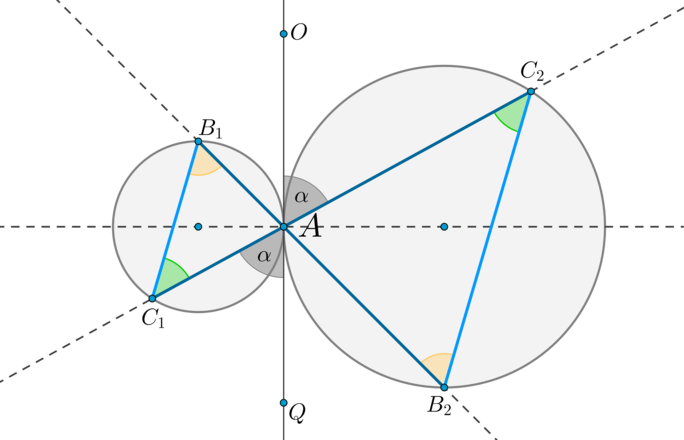
Теорема 3.

Пусть две окружности касаются внешним образом в точке (A). Через точку (A) проведены две прямые (B_1B_2) и (C_1C_2), пересекающие каждую окружность в двух точках, как показано на рисунке. Тогда: [(1) {large{triangle AB_1C_1 sim triangle AB_2C_2}}] [(2) {large{B_1C_1parallel B_2C_2}}]

Доказательство:

1) Проведем через точку (A) общую касательную этих окружностей (OQ). (angle OAC_2=angle QAC_1=alpha) как вертикальные. Т.к. угол между касательной и хордой, проведенной через точку касания, равен половине дуги, заключенной между ними, то (angle
OAC_2=frac12buildrelsmileover{AC_2}), (angle
QAC_1=frac12buildrelsmileover{AC_1}). Следовательно, (buildrelsmileover{AC_1}=buildrelsmileover{AC_2}=2alpha). Таким образом, (angle AB_1C_1=angle AB_2C_2=alpha). Значит, по двум углам (triangle AB_1C_1sim triangle AB_2C_2).

2) Т.к. (angle AB_1C_1=angle AB_2C_2), то прямые (B_1C_1parallel
B_2C_2) по накрест лежащим углам при секущей (B_1B_2).

Теорема Птолемея

Во вписанном четырехугольнике произведение диагоналей равно сумме произведений противоположных сторон: [ACcdot BD=ABcdot CD+BCcdot AD]

Доказательство

Пусть для определенности (angle ABD<angle CBD). Проведем отрезок (BO) так, чтобы (O) лежала на (AC) и (angle ABD=angle CBO):

Т.к. (angle ACB=angle ADB) (опираются на одну и ту же дугу), то по двум углам (triangle OBCsim triangle ABD). Значит: [dfrac{OC}{AD}=dfrac{BC}{BD} Rightarrow ADcdot BC=OCcdot BDphantom{00000000000} (1)]

Т.к. (angle BAC=angle BDC) (опираются на одну и ту же дугу), (angle ABO=angle CBD) (состоят из равных по построению (оранжевых) углов и общего угла (angle DBO)), то по двум углам (triangle
ABOsim triangle BDC). Значит: [dfrac{AO}{DC}=dfrac{AB}{BD} Rightarrow ABcdot CD=AOcdot BD phantom{00000000000} (2)]

Сложим равенства ((1)) и ((2)): (ADcdot BC+ABcdot CD=OCcdot
BD+AOcdot BD=ACcdot BD), чтд.

Формула Эйлера:

Пусть (R) — радиус описанной около треугольника (ABC) окружности, (r) — радиус вписанной окружности. Тогда расстояние (d) между центрами этих окружностей вычисляется по формуле: [{large{d^2=R^2-2Rr}}]

Доказательство:

а) Предположим, что (dne 0). Пусть (O, Q) — центры описанной и вписанной окружности соответственно. Проведем диаметр описанной окружности (PS) через точку (Q). Проведем также биссектрисы углов (angle A, angle B) — (AA_1, BB_1) соответственно (заметим, что они пересекутся в точке (Q), т.к. центр вписанной окружности лежит на пересечении биссектрис). Хорды (PS) и (BB_1) пересекаются, следовательно, отрезки этих хорд равны: (PQcdot QS=BQcdot QB_1).

Т.к. (OP=OS=R, OQ=d), то последнее равенство можно переписать в виде ((R-d)(R+d)=BQcdot QB_1 (*)).

Заметим, что т.к. (AA_1, BB_1) — биссектрисы, то (buildrelsmileover{AB_1}=buildrelsmileover{B_1C}=x,
buildrelsmileover{CA_1}=buildrelsmileover{A_1B}=y). Т.к. угол между хордами равен полусумме дуг, заключенных между ними, то:
(angle AQB_1=frac12(x+y)).

С другой стороны, (angle
B_1AA_1=frac12big(buildrelsmileover{B_1C}+buildrelsmileover{CA_1}big)=frac12(x+y))

Таким образом, (angle AQB_1=angle B_1AA_1). Следовательно, (triangle QB_1A) — равнобедренный и (B_1Q=B_1A). Значит, равенство ((*)) можно переписать как:
(R^2-d^2=BQcdot AB_1 (**)).

Проведем еще один диаметр описанной окружности (B_1B_2). Тогда (triangle B_1AB_2) — прямоугольный ((angle A) опирается на диаметр). Пусть также вписанная окружность касается стороны (AB) в точке (K). Тогда (triangle BKQ) — прямоугольный.
Заметим также, что (angle KBQ=angle AB_2B_1) (т.к. они опираются на одну и ту же дугу).
Значит, (triangle B_1AB_2sim triangle BKQ) по двум углам, следовательно:

(dfrac{KQ}{AB_1}=dfrac{BQ}{B_1B_2} Rightarrow
dfrac{r}{AB_1}=dfrac{BQ}{2R} Rightarrow BQcdot AB_1=2Rr).

Подставим это в ((**)) и получим:

(R^2-d^2=2Rr Rightarrow d^2=R^2-2Rr).

б) Если (d=0), т.е. центры вписанной и описанной окружностей совпадают, то (AK=BK=sqrt{R^2-r^2} Rightarrow AB=2sqrt{R^2-r^2}). Аналогично (AC=BC=AB=sqrt{R^2-r^2}), т.е. треугольник равносторонний. Следовательно, (angle A=60^circ Rightarrow angle
KAO=30^circ Rightarrow r=frac12R Rightarrow R=2r) или (0=R^2-2Rr) (т.е. в этом случае формула также верна).

Теорема о бабочке:

Пусть через середину хорды (AB) — точку (O), проведены две хорды (MN) и (KP). Пусть (MPcap AB=X, KNcap AB=Y). Тогда [{large{OX=OY}}]

Доказательство:

Проведем перпендикуляры (XX_1, YY_2perp
MN, XX_2, YY_1perp KP).
Следующие углы равны, т.к. опираются на одну и ту же дугу: (angle
PMO=angle NKO, angle MPO=angle KNO).
Следующие углы равны, т.к. вертикальные: (angle XOX_1=angle YOY_2,
angle XOX_2=angle YOY_1).

Следующие прямоугольные треугольники подобны:

1) (triangle XX_1Osim triangle YY_2O Rightarrow
dfrac{XO}{YO}=dfrac{XX_1}{YY_2})

2) (triangle XX_2Osim triangle YY_1O Rightarrow
dfrac{XO}{YO}=dfrac{XX_2}{YY_1})

3) (triangle MXX_1sim triangle KYY_1 Rightarrow
dfrac{XX_1}{YY_1}=dfrac{MX}{KY})

4) (triangle PXX_2sim triangle NYY_2 Rightarrow
dfrac{XX_2}{YY_2}=dfrac{PX}{NY})

Из 1) и 2) следует, что

(dfrac{XO^2}{YO^2}=dfrac{XX_1cdot XX_2}{YY_1cdot YY_2})

Из 3) и 4) следует, что

(dfrac{XX_1cdot XX_2}{YY_1cdot YY_2}=dfrac{MXcdot PX}{KYcdot
NY})

Совместив последние два равенства, получим:

(dfrac{XO^2}{YO^2}=dfrac{MXcdot PX}{KYcdot NY})

Заметим, что для пересекающихся хорд (AB) и (MP): (AXcdot
XB=MXcdot PX). Аналогично (AYcdot YB=KYcdot NY). Значит:

(dfrac{XO^2}{YO^2}==dfrac{AXcdot XB}{AYcdot YB})

Обозначим (OX=x, OY=y, OA=OB=t Rightarrow)

(dfrac{x^2}{y^2}=dfrac{(t-x)(t+x)}{(t+y)(t-y)}=dfrac{t^2-x^2}{t^2-y^2}
Rightarrow x^2t^2-x^2y^2=y^2t^2-x^2y^2 Rightarrow x^2=y^2
Rightarrow x=y).

Касательная к окружности, секущая и хорда — в чем разница

Касательная к окружности — это прямая, имеющая с ней всего одну общую точку.

Свойства касательной к окружности

Касательная к окружности и радиус, проведенный в точку касания, взаимно перпендикулярны.

Не будем принимать это на веру, попробуем доказать. Итак, у нас даны:

окружность с центральной точкой А;
прямая а — касательная к ней;
радиус АВ, проведенный к касательной.

Докажем, что касательная и радиус АВ взаимно перпендикулярны, т.е. а ⟂ АВ.

Итак, мы получили противоречие. Делаем вывод, что настоящим перпендикуляром к прямой а будет вовсе не АС, а АВ.

Задача

Решение:

Мы знаем, что касательная АС ⟂ АО, следовательно ∠САО = 90°.

∠АОС = 180° — ∠САО — ∠АСО = 180° — 90° — 28° = 62°

Поскольку вершина угла АОС лежит в центре окружности, можно вспомнить свойство центрального угла — как известно, он равен дуге, на которую опирается. Следовательно,

АВ = 62°.

Ответ:

АВ = 62°.

Задача 1

Решение

∠BDC = ∠BDA × 2 = 30° × 2 = 60°

Итак, угол между касательными составляет 60°.

Ответ: ∠BDA = 60°.

Задача 2

Решение

Углы при его основании будут равны, т.е. ∠МNК = ∠NМК.

∠МNК = (180° — ∠МКN) : 2 = (180° — 50°) : 2 = 65°

Ответ: ∠NМК = 65°.

Данное свойство намного сложнее предыдущих, и его лучше записать в виде уравнения.

AB² = AD × AC

Задача 1

Решение

Исходя из соотношения касательной и секущей МА ² = МВ × МС.

Найдем длину внешней части секущей:

МС = МВ — ВС = 16 — 12 = 4 (см)

МА² = МВ × МС = 16 х 4 = 64

МА = √
64= 8 (см)

Ответ: MA = 8 см.

Задача 2

Решение

Допустим, что МО = у, а радиус окружности обозначим как R.

В таком случае МВ = у + R, а МС = у – R.

Поскольку МВ = 2 МА, значит:

МА = МВ : 2 = (у + R) : 2

Согласно теореме о касательной и секущей, МА² = МВ × МС.

Значит:

(у + R)² : 4 = (у + R) × (у — R)

Сократим уравнение на (у + R), так как эта величина не равна нулю, и получим:

(у + R) : 4 = (у — R)

у = 5R : 3

Поскольку R = 6, у = 5R : 3 = 30 : 3 = 10 (см).

Ответ: MO = 10 см.

∠АВС = ½

АВ

Задача 1

Решение

Согласно свойствам угла между касательной и хордой, ∠АВС = ½

АВ.

АВ = ∠АВС × 2 = 32° × 2 = 64°

Ответ:

АВ = 64°.

Задача 2

Решение

Поскольку ∠МКВ равен половине дуги между KM и КВ, следовательно:

КМ = 2 ∠МКВ = 2 х 84° = 168°

∠ОКМ = ∠ОМК = (180° — ∠КОМ) : 2

Так как центральный угол окружности равен угловой величине дуги, на которую он опирается, то:

∠КОМ =

КМ = 168°

∠ОМК = (180° — ∠КОМ) : 2 = (180° — 168°) : 2 = 6°

Ответ: ∠ОМК = 6°.

2 марта 2019

В закладки

Обсудить

Жалоба

Как решать задачи на вписанную окружность с формулами и без? В этом видео будет рассказано об основных свойствах, используемых для решения задач, и примеры с решениями.

→ Теорема о двух касательных 00:01
→ Окружность в треугольнике 2:57
→ Окружность в правильном треугольнике 9:00
→ Окружность в равнобедренном треугольнике 11:27
→Окружность в прямоугольном треугольнике 17:47
→ Окружность в четырехугольнике 23:28

Тест «Виды потребления»

Проверочная работа по обществознанию.

Источник

Основные определения

Хорды

Касательные и секущие

Касание двух окружностей

Углы в окружности

Длина окружности и дуги

Площадь круга и его частей

Основные определения
	Окружностью называется замкнутая плоская кривая, все точки которой одинаково удалены от данной точки (центра окружности), которая лежит в той же плоскости, что и кривая. Отрезок R, который соединяет центр окружности с любой её точкой (а также длина этого отрезка), называется радиусом. Отрезок DE, который соединяет какие-либо две точки окружности, называется хордой. Хорда BC, проходящая через центр окружности, называется диаметром. Диаметр – наибольшая хорда данной окружности. Наименьшей хорды окружности не существует.
	Дуга, ∪AB,– это часть окружности, расположенная между двумя её точками. Вписанным углом, α, называется угол, образованный двумя хордами, имеющими общий конец. Центральным углом, β, называется угол, образованный двумя радиусами.
Хорды
	Параллельные хорды отсекают на окружности равные дуги: AB\|\|CD ⇒ ∪AC = ∪BD.
	Диаметр, проходящий через середину хорды, перпендикулярен ей: AC = BC ⇒ OC⊥AB.
	Хорды окружности равны тогда и только тогда, когда они равноудалены от её центра: AB = CD ⇔ OK = OL. Хорды окружности равны тогда и только тогда, когда они стягивают равные дуги: AB = CD ⇔ ∪AB = ∪CD. Большая из двух хорд окружности расположена ближе к её центру: AB > EF ⇔ OK < OM.
	Угол, составленный двумя хордами, измеряется полусуммой дуг, заключённых между его сторонами, продолженными в обе стороны: α = ½·(∪AC + ∪BD). Если хорды AB и CD пересекаются в точке М, то AM·MB = CM·MD.
Касательные и секущие
	Прямая (a), которая лежит в одной плоскости с окружностью и имеет с ней только одну общую точку (B), называется касательной к этой окружности. Прямая (a), которая перпендикулярна диаметру окружности (АВ) и проходит через его конец (В), является касательной к этой окружности. Касательная окружности перпендикулярна диаметру и радиусу, проведённым в точку касания.
	Отрезки касательных, проведённые из одной точки, равны: АВ = АС. Углы, образованные касательными, проведёнными из одной точки, и прямой, проходящей через центр окружности и эту точку, равны: ∠ВАО = ∠САО.
	Прямая, которая пересекает окружность в двух различных точках, называется секущей. Если через точку М вне окружности проведена секущая к ней, то произведение расстояний от точки М до точек пересечения с окружностью равно квадрату длины отрезка касательной, проведённой из точки М к окружности: МВ·МС = МА², и ∠М = ½·(∪AC – ∪АВ).
	Угол, образованный двумя секущими, равен полуразности дуг, заключенных между его сторонами: ∠А = ½·(∪CD – ∪BE) и AB·AC = AE·AD.
Касание двух окружностей
Для двух окружностей с центрами О₁ и О₂, и радиусами R и r: при внешнем касании: О₁О₂ = R + r; при внутреннем касании: О₁О₂ = R – r.
Углы в окружности
Радиан – угол, который соответствует дуге, длина которой равна радиусу окружности. Один радиан содержит приближённо 57°17’44,8’’. Радиан принимается за единицу измерения углов при так называемом круговом, или радианном, измерении углов. Если радианная мера угла равна α, то угол содержит (180·α)/π градусов. Если градусная мера угла составляет п°, то круговая – πп/180 радиан. Так углам в 1°, 10°, 30°, 60°, 90°, 135°, 180°, 360° соответствуют углы, содержащие π/180, π/18, π/6, π/3, π/2, 3π/4, π, 2π радиан.
	Угловой величиной дуги называется величина соответствующего ей центрального угла: ∪АС = ∠АОС. Угловая величина дуги обладает следующими свойствами: Угловая величина дуги неотрицательна. Равные дуги имеют равные угловые величины. Если две дуги одной окружности (или равных окружностей) имеют равные угловые величины, то они равны. Вписанный угол измеряется половиной дуги, на которую он опирается, и равен половине центрального угла, опирающегося на ту же дугу: ∠АВС = ½·∪АС = ½·∠АОС. Вписанные углы, опирающиеся на одну и ту же дугу, равны: ∠ABC=∠ADC=∠AEC.
	Вписанный угол, опирающийся на полуокружность (диаметр), является прямым: ∠ACВ= ½·∪АВ=½·180°=90°.
Длина окружности и дуги
	Длиной окружности называется общая граница периметров вписанных и описанных правильных многоугольников при неограниченном увеличении числа их сторон. Отношение длины окружности к длине её диаметра одинаково для всех окружностей и обозначается греческой буквой π. π = 3,1415926535… . Длина окружности: L = 2πR. Длина дуги окружности, выраженной в радианной мере, равна произведению числа её радиан на радиус окружности: l = α·R.
Площадь круга и его частей

Площадь круга: S = π·R².	Площадь сектора: S = ½·α·R².	Площадь сегмента: S = ½·(α–sin α)·R².