Как найти секущую параллелепипеда

Пошаговое построение сечения параллелепипеда

Построение сечения методом следов – это поэтапное отыскание точек, принадлежащих одной и той же плоскости грани и одновременно плоскости сечения, то есть прямым, проходящим через точки, принадлежащие сечению. Метод подходит для использования тогда, когда следы секущей плоскости и прямые граней многогранника пересекаются в области чертежа, то есть если сечение параллельно или почти параллельно основанию, этот метод построения не подойдет.

Задача 1.

Построить сечение параллелепипеда плоскостью, проходящей через точки  .

Шаг 1. Чезез точки и , которые принадлежат одной грани, и, следовательно, одной плоскости, проводим прямую. Точки этой прямой все принадлежат секущей плоскости. Точка лежит в плоскости основания, поэтому неплохо бы найти найти точку прямой , которая также принадлежала бы основанию. Для этого проводим прямую , и находим точку ее пересечения с прямой – .

Шаг 2. Проводим прямую , принадлежащую плоскости основания. Находим точку пересечения этой прямой ребра – .

Шаг 3. Точка лежит в задней грани, поэтому надо бы найти точку прямой , которая принадлежала бы плоскости задней грани. Для этого проведем прямую , которая принадлежит как плоскости основания, так и плоскости задней грани, и найдем точку ее пересечения с прямой – . Через две точки задней грани проводим прямую , и находим место пересечения этой прямой с ребром – .

Шаг 4. Окончание построения. Соединяем полученные точки отрезками, и строим многоугольник сечения.

Задача 2.

Построить сечение параллелепипеда плоскостью, проходящей через точки 

Шаг 1. Точки и лежат в одной плоскости, можно соединить их прямой. Прямая пересечет ребро в точке .

Шаг 2. Точки и также лежат в одной плоскости. Соединяем их прямой и отыскиваем точку пересечения ею ребра – .

Шаг 3. Найдем точку секущей плоскости, принадлежащую передней грани, чтобы затем через эту точку и точку можно было бы тоже провести след секущей плоскости. Для того, чтобы найти такую точку, проведем луч и найдем его пересечение с прямой – ведь обе эти прямые принадлежат плоскости верхней грани. Точка пересечения – точка . Точки и можно соединить отрезком.

Шаг 4. Находим точку пересечения отрезком ребра – точку .

Шаг 5. После этого соединяем отрезками полученные точки и закрашиваем многоугольник сечения.

Задача 3.

Построить сечение параллелепипеда плоскостью, проходящей через точки 

Шаг 1. Построим прямую , это можно сделать, так как обе точки принадлежат одной грани. Точка принадлежит грани основания, поэтому нужна точка в этой плоскости.

Шаг 2. Для того, чтобы найти точку, одновременно принадлежащую и секущей плоскости, и плоскости нижней грани, продолжим прямую и найдем точку ее пересечения с прямой – .

Шаг 3. Проводим прямую и находим точку пересечения этой прямой с ребром – точка .

Шаг 4. Теперь надо найти точку в плоскости передней  грани, потому что в этой плоскости у нас уже есть точка – точка . Для того, чтобы найти такую точку, продлим прямую  и найдем пересечение этой прямой с прямой – точка .

Шаг 5. Проводим прямую , отыскиваем точки пересечения ею ребер – точку , и ребра – точку .

Шаг 6. Соединяем точки и получаем многоугольник сечения.

Окончательный вид сечения с другого ракурса:

Задача 4.

Построить сечение параллелепипеда плоскостью, проходящей через точки  . Точка в задней грани.

Шаг 1.  Проводим прямую через две точки одной плоскости – и .  Определяем точку пересечения данной прямой ребра – .

Шаг 2. Продолжение прямой пересечется с продолжением прямой – так как обе прямые принадлежат плоскости задней грани. Точка также принадлежит задней грани, но также и боковой. А в боковой грани у нас есть точка , и тогда можно провести прямую .

Шаг 3. Точка – точка пересечения прямой ребра . Продлим также ребро и найдем пересечение прямой и прямой – точку , которая принадлежит плоскости основания.

Шаг 4. Соединяем Точки и плоскости основания, определяем точку пересечения данной прямой с ребром – точку . Соединяем полученные точки отрезками. Штрихуем полученный многоугольник сечения.

Окончательный вид сечения с другого ракурса:

12 комментариев

Сечение параллелепипеда: как рассчитать его площадь

Масса задач составлена на основе свойств многогранников. Грани объёмных фигур, как и конкретные точки на них, лежат в разных плоскостях. Если одну из таких плоскостей под определённым углом провести сквозь параллелепипед, то часть плоскости, лежащая в пределах многогранника и разделяющая его на части, будет его сечением.

Вам понадобится

• – линейка
• – карандаш

Инструкция

Постройте параллелепипед. Помните, что его основание и каждая из граней должны представлять собой параллелограмм. Это означает, что вам надо построить многогранник так, чтобы все противоположные рёбра параллельны. Если в условии сказано построить сечение прямоугольного параллелепипеда, то его грани сделайте прямоугольными. У прямой параллелепипед прямоугольные только 4 боковые грани. Если боковые грани параллелепипеда не перпендикулярны основанию, то такой многогранник называют наклонным. Если вы хотите построить сечение куба, изначально начертите прямоугольный параллелепипед с равными размерами. Тогда все шесть его граней будут представлять собой квадраты. Назовите все вершины для удобства обозначения.

Обозначьте две точки, которые будут принадлежать плоскости сечения. Иногда их положение указано в задаче: расстояние от ближайшей вершины, конец отрезка, проведённого по определенным условиям. Теперь проведите прямую через точки, лежащие в одной плоскости.

Найдите прямые на пересечении секущей плоскости с гранями параллелепипеда. Для выполнения этого шага найдите точки, в которых прямая, лежащая в плоскости сечения параллелепипеда, пересекается с прямой линией, принадлежащей грани параллелепипеда. Эти прямые должны находиться в одной плоскости.

Достройте сечение параллелепипеда. При этом помните, что ее плоскость должна пересекать параллельные грани параллелепипеда по параллельным прямым.

Стройте секущую плоскость в соответствии с исходными данными в задаче. Существует несколько возможностей построения плоскости сечения, проходящей:
– перпендикулярно заданной прямой линии через заданную точку;
– перпендикулярно заданной плоскости через заданную прямую;
– параллельно двум скрещивающимся прямым через заданную точку;
– параллельно другой заданной прямой через другую заданную прямую;
– параллельно заданной плоскости через заданную точку.
По таким исходным данным стройте сечение по принципу, описанному выше.

Видео по теме

Обратите внимание

Чтобы построить сечение параллелепипеда, нужно определить точки пересечения плоскости сечения с ребрами параллелепипеда, а затем соединить данные точки отрезками. Учтите, что соединять только те точки, которые лежат в плоскости одной грани. Параллельные грани параллелепипеда пересекайте секущей плоскостью по параллельным отрезкам. Если в плоскости грани только одна точка принадлежит плоскости сечения, постройте дополнительную такую точку. Для этого найдите точки пересечения построенных прямых с теми прямыми, которые лежат в нужных гранях.

Полезный совет

Параллелепипед имеет 6 граней. В его сечениях могут получиться треугольники, четырёхугольники, пятиугольники и фигуры с шестью углами. Плоскость, в том числе и секущая, определяется:
– тремя точками;
– прямой линией и одной точкой;
– двумя линиями, параллельными друг другу;
– двумя прямыми, пересекающимися между собой.

Войти на сайт

или

Забыли пароль?
Еще не зарегистрированы?

Рассмотрим задачу на построение сечения параллелепипеда. На рёбрах параллелепипеда даны точки K,L,M. Построить сечение параллелепипеда плоскостью KLM. Построим данный параллелепипед и отметим указанные точки. Так как точки L и M принадлежат грани АА₁D₁D и секущей плоскости, значит прямая LM их линия пересечения, а отрезок LM след от сечения грани АА₁D₁D секущей плоскостью. Аналогично в грани DD₁C₁C построим прямую MK и выделим отрезок MK. В грани А₁B₁C₁D₁ есть только одна точка L, для построения второй точки продлим до пересечения прямые D₁C₁ и MK. Отметим их общую точку H. Точка H принадлежит секущей плоскости, так принадлежит прямой MK. И принадлежит грани A₁B₁C₁D₁, так как принадлежит прямой D₁C₁. Проведем прямую LH. Отметим точку T точку пересечения прямой с ребром B₁C₁. Выделим отрезок LT это будет след от сечения плоскость. Так как точки T и К принадлежат секущей плоскости и грани ВВ₁С₁С, то отрезок ТК будет следом от сечения в этой грани. Выделим получившийся четырехугольник KMLT. Это искомое сечение. Рассмотренные задачи относятся к классу задач на построение и имеют свои этапы решения: анализ, построение, доказательство. Мы рассмотрели только этап построения, так как наша цель– научиться строить искомое сечение. На экране текст: На рёбрах CC₁,A₁D₁, DD₁ параллелепипеда АВСDA₁B₁C₁D₁ отмечены точки K,L,M соответственно. Построить сечение параллелепипеда плоскостью KLM. 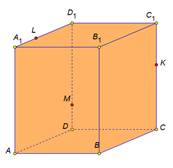На экране изображение: На экране изображение:

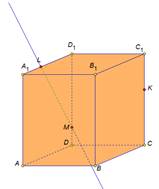Решение: 1) Провести прямую LM, выделить отрезок LM.

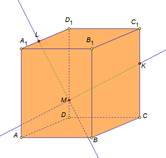
На экране изображение и и текст:

Решение: 1) Провести прямую LM, выделить отрезок LM. 2) Провести прямую MK, выделить отрезок MK

На экране изображение и текст:

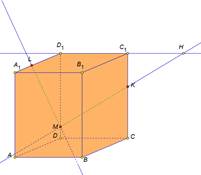Решение: 1) Провести прямую LM, выделить отрезок LM. 2) Провести прямую MK, выделить отрезок MK 3) Провести прямые D1C1 и MK, отметить точку Н.

На экране изображение и текст:

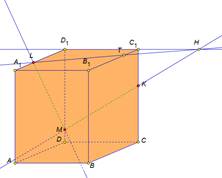Решение: 1) Провести прямую LM, выделить отрезок LM. 2) Провести прямую MK, выделить отрезок MK 3) Провести прямые D1C1 и MK, отметить точку Н. 4) Провести прямую LH, отметить точку Т, выделить отрезок LT.

На экране изображение:

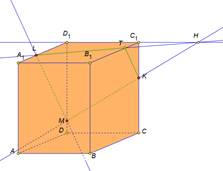Решение: 1) Провести прямую LM, выделить отрезок LM. 2) Провести прямую MK, выделить отрезок MK 3) Провести прямые D1C1 и MK, отметить точку Н. 4) Провести прямую LH, отметить точку Т, выделить отрезок LT. 5) Провести и выделить отрезок ТК.

На экране изображение:

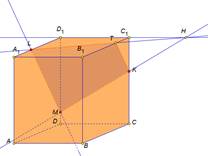Решение: 1) Провести прямую LM, выделить отрезок LM. 2) Провести прямую MK, выделить отрезок MK 3) Провести прямые D1C1 и MK, отметить точку Н. 4) Провести прямую LH, отметить точку Т, выделить отрезок LT. 5) Провести и выделить отрезок ТК. 6) Четырехугольник KMLT-искомое сечение.

Комментарий: задачи разобраны очень подробно, оформлены, четко структурированы. были небольшие опечатки по ходу решения.

Задачи на построение сечений в параллелепипеде

Этот видеоурок доступен по абонементу

У вас уже есть абонемент? Войти

В ходе урока все желающие смогут получить представление о теме « Задачи на построение сечений в параллелепипеде». Вначале мы повторим четыре основные опорные свойства параллелепипеда. Затем, используя их, решим некоторые типовые задачи на построение сечений в параллелепипеде и на определение площади сечения параллелепипеда.

Сечения параллелепипеда различными плоскостями могут быть : а) шестиугольниками б)пятиугольниками в) треугольниками г) четырехугольниками 1)а, в, г 2)в, г 3)б, в, г 4)а, б, в, г?

Геометрия | 10 – 11 классы

Сечения параллелепипеда различными плоскостями могут быть : а) шестиугольниками б)пятиугольниками в) треугольниками г) четырехугольниками 1)а, в, г 2)в, г 3)б, в, г 4)а, б, в, г.

3 выриант если что обращайтесь.

Постройте сечение данного параллелепипеда плоскостью abc?

Постройте сечение данного параллелепипеда плоскостью abc.

Постройте сечение параллелепипеда ABCDA1B1C1D1 плоскостью, проходящей через точки P, F и М – середины ребер AA1, A1B1 и DC?

Постройте сечение параллелепипеда ABCDA1B1C1D1 плоскостью, проходящей через точки P, F и М – середины ребер AA1, A1B1 и DC.

Дан параллелепипед АВСДА1В1С1Д1?

Дан параллелепипед АВСДА1В1С1Д1.

Точка Р лежит в плоскости грани ВСС1 В1 и не принадлежит ребру ВС.

Постойте сечение паралепипеда плоскостью проходящей через точку Р параллельно плоскости С1СД.

Постройте сечение данного параллелепипеда плоскостью ABC?

Постройте сечение данного параллелепипеда плоскостью ABC.

Построить сечение параллелепипеда?

Построить сечение параллелепипеда.

СРОЧНО?

Постройте сечение параллелепипеда плоскостью, проходящей через точки E и F и параллельной прямой a.

АВСДА1В1С1Д1 – прямоугольный параллелепипед, СС1 = 9 ?

АВСДА1В1С1Д1 – прямоугольный параллелепипед, СС1 = 9 .

Точка К лежит на СС1 , причем СК : КС1 = 1 : 2.

Периметр сечения параллелепипеда плоскостью АДК = 22.

Найдите боковую площадь параллелепипеда.

Постройте сечение данного параллелепипеда плоскостью MNK?

Постройте сечение данного параллелепипеда плоскостью MNK.

50 баллов за решение геометрии с фоткой сечений?

50 баллов за решение геометрии с фоткой сечений!

С подробным объяснением или хотя бы как провести сечения и двугранные углы!

В правильной 4 – угольной призме авсда1в1с1д1 со стороной основания 4 и высотой 7 на ребре АА1 взята точка М, АМ = 2.

На ребре ВВ1 точка К, В1К = 2.

Построить сечение плоскостью Д1МК, найти угол между этой плоскостью и плоскостью СС1Д1.

Через прямую ВД1 проведена плоскость а, параллельная АС.

Сечение параллелепипеда плоскостью а – ромб.

Докажите, что АВСД – квадрат

Найти угол между плоскостью а и плоскостью ВСС1, если АА1 : АВ = 3 : 2.

Через середины M и N ребер AD и CC1 параллелепипедаABCDA1 B1 C1 D1 проведена плоскость параллельно диагонали DB1 ?

Через середины M и N ребер AD и CC1 параллелепипеда

ABCDA1 B1 C1 D1 проведена плоскость параллельно диагонали DB1 .

Постройте сечение параллелепипеда этой плоскостью.

В каком отношении она делит ребро BB1 ?

Вы перешли к вопросу Сечения параллелепипеда различными плоскостями могут быть : а) шестиугольниками б)пятиугольниками в) треугольниками г) четырехугольниками 1)а, в, г 2)в, г 3)б, в, г 4)а, б, в, г?. Он относится к категории Геометрия, для 10 – 11 классов. Здесь размещен ответ по заданным параметрам. Если этот вариант ответа не полностью вас удовлетворяет, то с помощью автоматического умного поиска можно найти другие вопросы по этой же теме, в категории Геометрия. В случае если ответы на похожие вопросы не раскрывают в полном объеме необходимую информацию, то воспользуйтесь кнопкой в верхней части сайта и сформулируйте свой вопрос иначе. Также на этой странице вы сможете ознакомиться с вариантами ответов пользователей.

Дано ABCD – четырёхугольник Окр (O ; R) вписана : ab + cd = 15 дм P = ? Решение Т. К. ABCD описанный четырехугольник следовательно. Ab + cd = ad + bc т. Е. ad + dc = 15см 2)p = ab + cd + bc + ad = 30 дм.

Можно решить и другим способом : sinА = R / 2R = 12 ⇒∠А = 30°.

В результате вращения образуется фигура – цилиндр с радиусом 6 см и высотой 6 см V = πR² * H = π6² * 6 = 216π см³ Sп = 2πR * H + 2πR² = π(2 * 6 * 6 + 2 * 6²) = 144π см².

Уже сам разберись в записях.

2 * (х + х + 3) = 48 2х + 3 = 48÷ 2 2х + 3 = 24 2х = 24 – 3 2х = 21 х = 10, 5 см 10, 5 + 3 = 13, 5 см.

5) все углы по 60 градусов, т. К. треугольник равносторонний 9) т. К. внешний угол угла М = 130, то угол М = 50 градусов. А т. к. Треугольник равнобедренный, то угол К = 50, а угол N = 80 6) т. К. угол Е = 90, а угол К = 60, то угол Р = 30 7) тр..

BK – высота, медиана, биссектриса ▲АВK.

1) если высоты провести из вершины острого угла, то несложно доказать, что угол между высотами будет равен тупому углу параллелограмма. К этому условию задачи этот вариант не подходит)) 2) если высоты провести из вершины тупого угла, то несложно док..

Из того, что АС = AD ; AE = AB ; и угол А – общий уже следует равенство треугольников АСЕ и ADB (по двум сторонам и углу между ними) (и в этом случае не важно чему именно равен угол А))) из равенства треугольников последует равенство всех остальных с..

Один угол х, второй 2х. Так как треуг. Прямоугольный, то сумма двух этих углов 90 градусов х + 2х = 90 3х = 90 х = 30 2х = 60 градусов – больший угол.

[spoiler title=”источники:”]

http://interneturok.ru/lesson/geometry/10-klass/parallelnost-pryamyh-i-ploskostej/zadachi-na-postroenie-secheniy-v-parallelepipede

http://geometria.my-dict.ru/q/6151712_secenia-parallelepipeda-razlicnymi-ploskostami-mogut-byt/

[/spoiler]

Как построить сечение параллелепипеда плоскостью ? Секущая плоскость может рассекать параллелепипед по-разному, из-за чего сечением может являться 1) треугольник, 2) четырехугольник, 3) пятиугольник, 4) шестиугольник. Рассмотрим случай, когда сечением параллелепипеда оказывается пятиугольник. При построении сечения руководствуемся правилом, согласно которому отрезки, по которым секущая плоскость пересекает параллелепипед, параллельны. Конкретный вид сечения всегда зависит от расположения точек, задающих секущую плоскость. Рассмотрим случай расположения точек А, B и С на рёбрах параллелепипеда (рис.1). Для построения сечения проводим отрезки AB и ВС. Далее пользуемся вышеуказанным правилом и проводим две прямые: 1) прямую, параллельную ВС, проводим через точку А – в плоскости передней грани параллелепипеда и 2) прямую, параллельную АВ, проводим через точку С – в плоскости боковой грани параллелепипеда. Таким образом, получаем точки Е и D на рёбрах нижней грани параллелепипеда (рис.2). Для завершения построения пятиугольного сечения соединяем точки E и D. модератор выбрал этот ответ лучшим Tangr­am [176K] 9 лет назад  Прежде чем приступать к построению сечений параллелепипеда, следует вспомнить правило: отрезки, по которым секущая плоскость пересекает две противоположные грани параллелепипеда, параллельны. Также следует учесть, что секущая плоскость может рассекать параллелепипед по-разному: сечением параллелепипеда может являться треугольник, четырехугольник, пятиугольник, шестиугольник. Рассматривать следует все эти четыре случая. Случай первый (самый простой): сечение – треугольник. Дан параллелепипед ABCDA1B1C1D1. Точки KMN располагаются на рёбрах A1B1, A1D1 и AA1 соответственно. Строим сечение параллелепипеда плоскостью KMN. Точки M и N одновременно находятся в двух плоскостях: в плоскости AA1D1 и в секущей плоскости. Следовательно, MN – линия пересечения двух указанных плоскостей. Точно так же получаем MK и KN. То есть искомым сечением будет являться треугольник MKN. Этот и три другие более сложные случаи подробно, доходчиво и в разных вариантах исполнения изложены в ролике урока “Построение сечений в параллелограмме”. Смотрим с конца второй минуты и до конца ролика, а лучше – с самого начала, чтобы повторить свойства параллелепипеда. Полезно также прочитать объяснения после ролика. Успехов в построениях! Zolot­ynka [551K] 6 лет назад  1) Нарисуем две точки на задней поверхности и проведем через них линию, будем вести ее до тех пор, пока она не “встретится” с правой вертикальной стороной задней поверхности параллелепипеда, и поставим там зеленую точку. 2) Проведем параллельную линию, проходящую через точку на передней поверхности; отметим пересечение красной точкой, а затем продлим линию вниз и поставим там синюю точку. 3) Соединяем точки как показано на рисунке параллельными линиями: 4) Соединяем точки между собой и получаем шестиугольник. Наш шестиугольник и будет представлять собой сечение параллелепипеда плоскостью, см. ниже: morel­juba [62.5K] 6 лет назад  Прежде чем построить сечение параллелепипеда необходимо определиться с теми точками. через которые проходит плоскость. Далее важно помнить, что те линии плоскости, которые пересекают параллельные стороны также будут проходить параллельно друг другу. Также важно при построении понимать, что искомое сечение может быть представлено и треугольником – и шестиугольником. А вот пример построения:

Практическое занятие : «Параллелепипед. Построение сечений параллелепипеда ».

1. Цель практической работы: . Закрепить знания теоретического материала о многогранниках, навыки решения задач на построение сечений, умения анализировать чертеж.

2.Дидактическое оснащение практической работы: АРМ, модели и развёртки многогранников, измерительные инструменты, ножницы, клей, плотная бумага.

Время:2 часа

Задания к работе:

Задание 1

Построить сечение параллелепипеда ABCDA₁B₁C₁D₁ плоскостью, проходящей через точки M, N, P, лежащие, на прямых, соответственно, A₁ B_1, АD, DC

Образец и последовательность решения задачи:

1.Точки N и P лежат в плоскости сечения и в плоскости нижнего основания параллелепипеда. Построим прямую, проходящую через эти точки. Эта прямая является следом секущей плоскости на плоскость основания параллелепипеда.

2.Продолжим прямую, на которой лежит сторона AB параллелепипеда. Прямые AB и NP пересекутся в некоторой точке S. Эта точка принадлежит плоскости сечения.

3.Так как точка M также принадлежит плоскости сечения и пересекает прямую АА₁ в некоторой точке Х.

4.Точки X и N лежат в одной плоскости грани АА₁D₁D, соединим их и получим прямую XN.

5.Так как плоскости граней параллелепипеда параллельны, то через точку M можно провести прямую в грани A₁B₁C₁D₁, параллельную прямой NP. Эта прямая пересечет сторону В₁С₁ в точке Y.

6.Аналогично проводим прямую YZ, параллельно прямой XN. Соединяем Z с P и получаем искомое сечение – MYZPNX.

Задание 2

Вариант1. Построить сечение параллелепипеда АВСDА1В1С1D1 плоскостью, заданной следующими точками M, N и P

 1 Уровень: Все три точки лежит на рёбрах, выходящих из вершиныА

2 Уровень. M лежит в грани AA1D1D, N лежит в грани АА1В1В, P лежит в грани СС1D1D.

3 Уровень. M лежит на диагонали B1D, N лежит на диагонали АС1, P лежит на ребре С1D1.

Вариант2. Построить сечение параллелепипеда АВСDА1В1С1D1 плоскостью, проходящей через прямую DQ, где точка Q лежит на ребре СС1 и точку Р, заданную следующим образом

 1 Уровень: Все три точки лежит на рёбрах, выходящих из вершиныС

 2 Уровень: М лежит на продолжении ребра А1В1, причем точка А1 находится между точками В1 и Р.

 3 Уровень: Р лежит на диагонали В1D

Порядок выполнения работы:

1.Изучите теоретический материал по темам:

Параллелепипед.

Прямой параллелепипед.

Наклонный параллелепипед.

Противолежащие грани параллелепипеда.

Свойства диагоналей параллелепипеда.

Понятие секущей плоскости и правила её построения.

Какие виды многоугольников получаются в сечении куба и параллелепипеда.

2. Постройте параллелепипед ABCDA₁B₁C₁D₁

3.Разберите решение задачи № 1

4.Последовательно постройте сечение параллелепипеда ABCDA₁B₁C₁D₁ плоскостью, проходящей через точки P, Q, R задачи № 1.

5.Постройте ещё три параллелепипеда и выделите на них сечения к задачам 1, 2, и 3 уровней

Критерии оценивания:

Литература: Атанасян Л.С. Геометрия: Учебник для 10-11 кл. общеобразоват. учреждений. Л.С. Атанасян, В.Ф. Бутузов, С.Б. Кодомцев и др. – М.: Просвещение, 2010г Зив Б.Г. Задачи по геометрии: Пособие для учащихся 7-11 кл. общеобразоват. учреждений. / Б.Г. Зив, В.М. Мейлер, А.Г. Баханский. – М.: Просвещение, 2010. В. Н. ЛитвиненкоЗадачи на развитие пространственных представлений. Книга для учителя. – М.: Просвещение, 2010г

Дидактический материал к заданию практического занятия

К задаче № 1:

Некоторые возможные сечения:

Построить сечения параллелепипеда плоскостью, проходящей через данные точки

Ответы к практической работе.