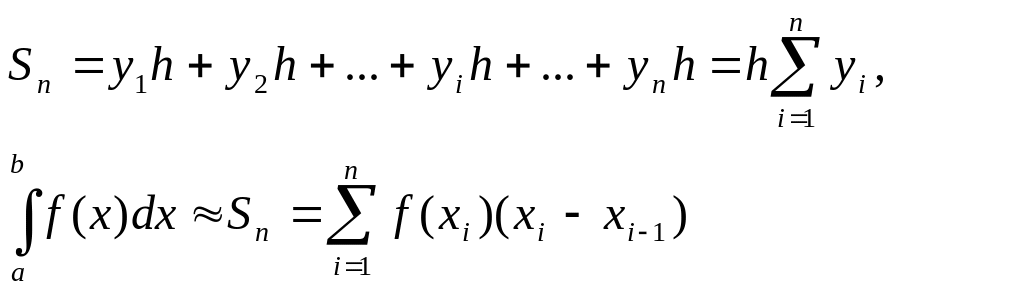Как найти секущую прямоугольника

Прямоугольник

Частным видом параллелограмма является прямоугольник.

Прямоугольником называют параллелограмм, у которого все углы прямые

ABCD – прямоугольник.

Особое свойство прямоугольника

Диагонали прямоугольника равны

Доказательство

Дано: ABCD – прямоугольник

Доказать: AC = DB

Доказательство:

Рассмотрим ABD иACB: ABCD – прямоугольник, А и B – прямые, ABD иACB – прямоугольные. AD = CB (по свойству параллелограмма). AB – общий катет, ABD =ACB (по двум катетам). А в равных треугольниках против соответственно равных углов лежат равные стороны, значит, AC = DB, что и требовалось доказать.

Теорема

Если в параллелограмме диагонали равны, то этот параллелограмм – прямоугольник

Доказательство

Дано: ABCD – параллелограмм, AC = DB

Доказать: ABCD – прямоугольник

Доказательство:

Рассмотрим ABD иACB:

AC = DB (по условию), AD = BC (по свойству параллелограмма), AB – общая, ABD =ACB (по трем сторонам). А в равных треугольниках против соответственно равных сторон лежат равные углы, A = B. А в параллелограмме противоположные углы равны, значит A = C и В = D, A = В = C = D (1). A + В + C + D = 360 0 (2)(т.к. параллелограмм выпуклый четырёхугольник). Следовательно, из (2), учитывая (1), получаем, что A = В = C = D = 90 0 , ABCD – прямоугольник, что и требовалось доказать.

Теорема

Если один из углов параллелограмма прямой, то этот параллелограмм – прямоугольник

Доказательство

Дано: ABCD – параллелограмм, A = 90 0

Доказать: ABCD – прямоугольник

Доказательство:

Если две параллельные прямые пересечены секущей, то сумма односторонних углов равна 180 0 , т.е. A + В = 180 0 , В = 180 0 – A = 180 0 – 90 0 = 90 0

Противолежащие углы параллелограмма равны, A = C = 90 0 и В = D = 90 0

Итак: ABCD – параллелограмм (по условию), и все его углы прямые (по доказанному выше), ABCD – прямоугольник (по определению), что и требовалось доказать.

Две теоремы, доказанные выше, называют признаками прямоугольника.

Поделись с друзьями в социальных сетях:

Параллельность прямых

О чем эта статья:

10 класс, ЕГЭ/ОГЭ

Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).

Определение параллельности прямых

Начнем с главного — определимся, какие прямые параллельны согласно евклидовой геометрии. Мы недаром упомянули Евклида, ведь именно в его трудах, написанных за 300 лет до н. э., до нас дошли первые упоминания о параллельности.

Параллельными называются прямые в одной плоскости, не имеющие точек пересечения, даже если их продолжать бесконечно долго. Обозначаются они следующим образом: a II b.

Казалось бы, здесь все просто, но со времен Евклида над определением параллельных прямых и признаками параллельности прямых бились лучшие умы. Особый интерес вызывал 5-й постулат древнегреческого математика: через точку, которая не относится к прямой, в той же плоскости можно провести только одну прямую, параллельную первой. В XIX веке российский математик Н. Лобачевский смог опровергнуть постулат и указать на условия, при которых возможно провести как минимум 2 параллельные прямые через одну точку.

Впрочем, поскольку школьная программа ограничена евклидовой геометрией, вышеуказанное утверждение мы принимаем как аксиому.

На плоскости через любую точку, не принадлежащую некой прямой, можно провести единственную прямую, которая была бы ей параллельна.

Курсы по математике в онлайн-школе Skysmart помогут подтянуть оценки, подготовиться к контрольным, ВПР и экзаменам.

Свойства и признаки параллельных прямых

Есть ряд признаков, по которым можно определить, что одна прямая параллельна другой. К счастью, свойства и признаки параллельности прямых тесно связаны, поэтому не придется запоминать много информации.

Начнем со свойств. Для этого проведем третью прямую, пересекающую параллельные прямые — она будет называться секущей. В результате у нас образуется 8 углов.

Если секущая проходит через две параллельные прямые, то:

два внутренних односторонних угла образуют в сумме 180°:

∠4 + ∠6 = 180°; ∠3 + ∠5 = 180°.

два внутренних накрест лежащих угла равны между собой:

два соответственных угла равны между собой:

∠1 = ∠5, ∠3 = ∠7, ∠4 = ∠8, ∠2 = ∠6.

Если секущая образует перпендикуляр с одной из параллельных прямых, то она будет перпендикулярна и другой.

Вышеуказанные свойства являются одновременно признаками, по которым мы можем сделать вывод о параллельности прямых. Причем достаточно установить и доказать лишь один признак — остальные будут к нему прилагаться.

А сейчас посмотрим, как все это помогает решать задачи и практиковаться в определении параллельности двух прямых.

Задача 1

Прямые MN и KP пересекают две другие прямые, образуя несколько углов. Известно, что ∠1 = 73°; ∠3 = 92°; ∠2 = 73°. Требуется найти величину ∠4.

Решение

Поскольку ∠1 и ∠2 являются соответственными, их равенство говорит о том, что MN II KP. Следовательно, ∠3 = ∠MPK = 92°.

Согласно другому свойству параллельных прямых ∠4 + ∠MPK = 180°.

Задача 2

Две параллельные прямые а и b удалены друг от друга на расстояние 27 см. Секущая к этим прямым образует с одной из них угол в 150°. Требуется найти величину отрезка секущей, расположенного между а и b.

Решение

Поскольку а II b, значит ∠MKD + ∠KDN = 180°.

Соответственно, ∠MKD = 180° – ∠KDN = 180° – 150° = 30°.

Теперь рассмотрим треугольник KDM. Мы знаем, что отрезок DM представляет собой расстояние между прямыми а и b, а значит, DM ┴ b и наш треугольник является прямоугольным.

Поскольку катет, противолежащий углу в 30°, равен ½ гипотенузы, DM = 1/2DK.

Геометрия. 7 класс

Конспект урока

Признаки параллельности прямых

Перечень рассматриваемых вопросов:

• Параллельные прямые.
• Накрест лежащие, соответственные, односторонние углы.
• Признаки параллельности прямых.
• Решение задач на доказательство параллельности прямых.

Две прямые на плоскости называются параллельными, если они не пересекаются.

Признаки параллельности двух прямых:

1. Если при пересечении двух прямых секущей, накрест лежащие углы равны, то прямые параллельны.

2. Если при пересечении двух прямых секущей, соответственные углы равны, то прямые параллельны.

3. Если при пересечении двух прямых секущей, сумма односторонних углов равна 180°, то прямые параллельны.

1. Атанасян Л. С. Геометрия: 7–9 класс. // Атанасян Л. С., Бутузов В. Ф., Кадомцев С. Б. – М.: Просвещение, 2017. – 384 с.

1. Атанасян Л. С. Геометрия: Методические рекомендации 7 класс. // Атанасян Л. С., Бутузов В. Ф., Глазков Ю. А. и др. – М.: Просвещение, 2019. – 95 с.
2. Зив Б. Г. Геометрия: Дидактические материалы 7 класс. // Зив Б. Г., Мейлер В. М. – М.: Просвещение, 2019. – 127 с.
3. Мищенко Т. М. Дидактические материалы и методические рекомендации для учителя по геометрии 7 класс. // Мищенко Т. М., – М.: Просвещение, 2019. – 160 с.
4. Атанасян Л. С. Геометрия: Рабочая тетрадь 7 класс. // Атанасян Л. С., Бутузов В. Ф., Глазков Ю. А., Юдина И. И. – М.: Просвещение, 2019. – 158 с.
5. Иченская М. А. Геометрия: Самостоятельные и контрольные работы 7–9 классы. // Иченская М. А. – М.: Просвещение, 2019. – 144 с.

Теоретический материал для самостоятельного изучения.

Вы уже знаете, что при пересечении двух прямых секущей образуются углы:

• накрест лежащие: 3 и 6, 4 и 5.
• односторонние: 3 и 5, 4 и 6.
• соответственные: 1 и 5, 3 и 7, 2 и 6; 4 и 8.

Прямая c называется секущей по отношению к прямым a и b, если она пересекает их в двух точках.

Рассмотрим и докажем признаки параллельности прямых.

Если при пересечении двух прямых секущей, накрест лежащие углы равны, то прямые параллельны.

Дано: прямые a и b, секущая AB, ∠ 1 = ∠ 2 накрест лежащие.

В этом случае две прямые, перпендикулярные к третьей не пересекаются, т. е. параллельны.

2 случай: ∠ 1= ∠ 2 ≠ 90°

1) Из середины O отрезка AB проведём перпендикуляр OH к прямой а. На прямой b от точки B отложим отрезок BH₁, равный отрезку AH и проведем отрезок OH₁.

2) AO = OB т. к. O середина AB; AH = BH₁ по построению; ∠1 = ∠2 по условию. Тогда ΔOHA = ΔOH₁B по первому признаку равенства треугольников.

Далее следует из равенства треугольников: ∠3 = ∠4 и ∠5 = ∠6.

3) Из равенства углов ∠3 и ∠4 следует, что точка H₁ лежит на продолжении луча OH. Это значит, что точки H₁, O, H лежат на одной прямой.

4) Из равенства ∠5 и ∠6 следует, что ∠6 = 90°. Это значит, что прямые a и b перпендикулярны к третьей НН₁, а значит, по теореме о двух прямых, перпендикулярных к третьей, не пересекаются, т. е. параллельны.

Если при пересечении двух прямых секущей, соответственные углы равны, то прямые параллельны.

Дано: прямые a и b, секущая AB, ∠1 = ∠2 соответственные.

∠1 = ∠2 – по условию и ∠2 = ∠3 – по свойству вертикальных углов.

Значит, ∠1 = ∠3, это накрест лежащие углы, следовательно, a║b по теореме 1.

Если при пересечении двух прямых секущей, сумма односторонних углов равна 180°, то прямые параллельны.

Прямые a и b, секущая AB, ∠1 + ∠2 = 180° ‑ односторонние.

∠3 +∠2 = 180°– по свойству смежных углов, откуда ∠3 = 180° – ∠2.

∠1 + ∠2 = 180 ° по условию, откуда ∠1 = 180° – ∠2.

Тогда ∠1 = ∠3, это накрест лежащие углы, следовательно, a║b по теореме 1.

Разбор заданий тренировочного модуля.

Дано: ∠1= 60°, ∠2 = 120°.

1. ∠2 и ∠3 смежные, ∠3 = 180° – 120° = 60° по свойству смежных углов;
2. ∠3 = ∠1, это накрест лежащие углы;
3. Значит, прямые a и b параллельны по 1 признаку параллельности прямых.

Ответ: прямые a и b параллельны по 1 признаку параллельности прямых.

Дано: ΔABC – равнобедренный, ∠А = 60°. CD – биссектриса ∠BCK.

Докажите: AB ║ CD.

1. ∠A = ∠C = 60° – углы при основании равнобедренного Δ–ка равны.
2. ∠BCK и ∠С смежные. ∠BCK = 180° – 60°= 120° – по свойству смежных углов.
3. ∠BCD = ∠CDK = 60° т. к. CD – биссектриса делит угол пополам.
4. Значит, ∠A = ∠DCK = 60° ‑ соответственные, следовательно, AB║CD по 2 признаку параллельности прямых.

Ответ: AB║CD по 2 признаку параллельности прямых.

[spoiler title=”источники:”]

http://skysmart.ru/articles/mathematic/parallelnost-pryamyh

http://resh.edu.ru/subject/lesson/7298/conspect/

[/spoiler]

1. Главная
2. Справочники
3. Справочник по геометрии 7-9 класс
4. Четырехугольники
5. Прямоугольник

Советуем посмотреть:

Многоугольник

Выпуклый многоугольник

Четырехугольник

Параллелограмм

Признаки параллелограмма

Трапеция

Ромб и квадрат

Осевая и центральная симметрии

Четырехугольники

Правило встречается в следующих упражнениях:

7 класс

Задание 411,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник

Задание 428,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник

Задание 446,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник

Задание 455,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник

Задание 774,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник

Задание 986,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник

Задание 1023,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник

Задание 1152,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник

Задание 1174,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник

Задание 1179,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник

---

Идея
формулы прямоугольников заключается
в том, что на малом отрезке [x₀;
x₀+h]
площадь
криволинейной трапеции, как показано
на рис.2.1, приближенно равна площади
прямоугольника с основанием [x₀;
x₀+h]
и высотой,
равной ординате в какой-то точке

.

Рисунок
2.1 – Вычисление площади элементарной

криволинейной
трапеции на отрезке h

Таким образом,

.

В
зависимости от того, какую точку отрезка
[x₀;
x₀+h]
выбирают в
качестве

,
и получают разновидности формулы
прямоугольников.

Разобьем
отрезок [a;
b] на n
равных частей точками

a=x₀,
x₁=x₀+h,
x₂=x₁+h,
… , x_i=x_i-1+h,
… , x_n=x_n-1+h=b,
где

.

На
каждом частичном отрезке [x_i-1;
x_i]
заменим
соответствующую криволинейную трапецию
на прямоугольник, высоту которого можно
выбрать по-разному.

1.1 Формула «левых» прямоугольников

Если
выбрать в качестве высоты прямоугольника
на каждом из отрезков [x_i-1;
x_i],
(

),
ординату в
левом конце, т. е. y_i-1=f(x_i-1),
то криволинейная трапеция заменится
на ступенчатую фигуру, площадь S_n
которой можно принять за площадь
трапеции. Верхняя граница этой ступенчатой
фигуры изображена на рис. 2.2 сплошными
линиями.

Рисунок
2.2 – Приближенное вычисление площади

криволинейной
трапеции на отрезке [a; b]

Следовательно,

(1)

Полученную
формулу называют формулой «левых»
прямоугольников.

1.2 Формула «правых» прямоугольников

Если
в качестве высоты прямоугольника выбрать
ординату правого конца частичного
отрезка, т. е. считать, что высота
прямоугольника на отрезке [x_i-1;
x_i]
равна y_i=f(x_i),
(

),
то для приближенного вычисления интеграла
получим формулу «правых»
прямоугольников:

(2)

(на
рис. 2.2 штрихпунктирной линией обозначена
ступенчатая фигура, составленная из
«правых» прямоугольников).

1.3 Формула «средних» прямоугольников

Часто
используется еще при расчетах так
называемая формула «средних»
прямоугольников
или просто формула
прямоугольников.
Высотой прямоугольника, построенного
на частичном отрезке, считают ординату,
взятую в средней точке отрезка, т. е.

(получаемая
ступенчатая фигура на рис. 2.2 заштрихована).
Тогда

(3)

Формулы
(1)—(3) можно использовать при аналитическом
или графическом способе задания функции
у = f (х),
а формулы (1), (2) и при задании функции в
виде таблицы с равноотстоящими узлами.

Формулу
(3) можно записать в другом виде, более
удобном для составления программ.

1.4 Случай неравноотстоящих узлов

Рассмотрим
использование метода прямоугольников
в случае, когда функция задана таблицей
с неравноотстоящими узлами:

Таблица
1 – Задание функции с неравноотстоящими
узлами

i	0	1	2	…	i	…	n
xi	a=x0	x1	x2	…	xi	…	xn=b
yi	y0	y1	y2	…	yi	…	yn

Обозначим
h₁=x_l
– x₀,
h₂=x₂
– x₁,
…, h_i=x_i
– x_i-1,
… ,h_n
= x_n
– х_n-1,
причем не все h_i,
(
),
равны между
собой. Для вычисления определенного
интеграла по методу прямоугольников в
этом случае легко получить формулы
(1.1) и (2.1), аналогичные формулам (1) и (2):

(1.1)

— формула
«левых» прямоугольников;

(2.1)

— формула
«правых» прямоугольников.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

Теорема

(Свойство секущих)

Для каждой из секущих, проведённых из одной точки, произведение длины секущей на длину её внешней части есть величина постоянная.

Дано: окружность (O; R), AB и AC — секущие,

AB∩окр. (O; R)=F, AC∩окр. (O; R)=K

Доказать:

AB ∙ AF=AC ∙ AK

Доказательство:

I способ

Рассмотрим треугольники ABK и ACF.

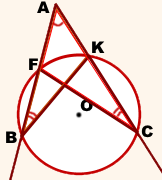
∠A — общий угол;

∠ABK=∠ACF (как вписанные углы, опирающиеся на одну дугу FK).

Следовательно, треугольники ABK и ACF подобны (по двум углам).

Из подобия треугольников следует пропорциональность соответствующих сторон:

   

По основному свойству пропорции:

   

Что и требовалось доказать.

II способ

1) Проведём отрезки FK и BC.

2) Так как четырёхугольник BFKC — вписанный в окружность, то сумма его противолежащих углов равна 180º:

∠BCK+∠BFK=180º. Следовательно, ∠BFK=180º-∠BCK.

3) ∠AFK+∠BFK=180º (как смежные). Отсюда,

∠AFK=180º-∠BFK=180º-(180º-∠BCK)=180º-180º+∠BCK=∠BCK,

то есть ∠AFK=∠BCK.

4) Рассмотрим треугольники ABC и AKF.

У них ∠ACB=∠AFK (так как ∠AFK=∠BCK по доказанному), ∠A — общий угол. Следовательно, треугольники ABC и AKF — подобны (по двум углам).

Отсюда,

   

Что и требовалось доказать.

При решении задач будем использовать свойство секущих, а также запомним полученные в ходе доказательства теоремы факты о подобии треугольников, образованных секущими. Причем подобие треугольников ABC и AKF можно доказывать как приведённым выше способом, так и опираясь на свойство секущих.

Прямоугольник, свойства, признаки и формулы.

Прямоугольник – это четырехугольник, у которого все углы прямые (каждый из углов равен 90 градусам).

Прямоугольник (понятие, определение)

Видеоурок “Прямоугольник“

Свойства прямоугольника

Признаки прямоугольника

Формулы прямоугольника

Прямоугольник (понятие, определение):

Прямоугольник – это четырехугольник, у которого все углы прямые (каждый из углов равен 90 градусам).

Прямоугольник – это четырехугольник, у которого каждый угол является прямым.

Прямоугольник – это четырехугольник, у которого две противоположные стороны равны между собой и все четыре угла равны между собой и каждый из них составляет 90 градусов.

Рис. 1. Прямоугольник

В свою очередь четырёхугольник (греч. τετραγωνον) – это геометрическая фигура (многоугольник), состоящая из четырёх точек (вершин), никакие три из которых не лежат на одной прямой, и четырёх отрезков (сторон), последовательно соединяющих эти точки.

Длинную сторону прямоугольника называют длиной прямоугольника, а короткую – шириной прямоугольника.

@ https://youtu.be/_EVDcbOydAI

Свойства прямоугольника:

1. Прямоугольник является параллелограммом – его противоположные стороны попарно параллельны.

Рис. 2. Прямоугольник

AB || CD,   BC || AD

2. Противоположные стороны прямоугольника равны.

Рис. 3. Прямоугольник

AB = CD,  BC = AD

3. Стороны прямоугольника являются его высотами.

4. Прилегающие стороны прямоугольника всегда перпендикулярны.

Рис. 4. Прямоугольник

AB ┴ BC,   BC ┴ CD,   CD ┴ AD,   AD ┴ AB

5. Каждый угол прямоугольника прямой и равен 90 градусам. Сумма всех углов прямоугольника составляет 360 градусов.

Рис. 5. Прямоугольник

∠ABC = ∠BCD = ∠CDA = ∠DAB = 90°,

∠ABC + ∠BCD + ∠CDA + ∠DAB = 360°

6. Диагонали прямоугольника равны.

Рис. 6. Прямоугольник

AC = BD

7. Каждая диагональ прямоугольника делит его на два одинаковых прямоугольных треугольника.

Рис. 7. Прямоугольник

△ABD = △BCD, △ABC = △ACD

8. Квадрат диагонали прямоугольника равен сумме квадратов двух его смежных сторон (что вытекает из теоремы Пифагора).                                   

Рис. 8. Прямоугольник

AC² ​= AD​²​​+ CD​²

9. Диагонали прямоугольника делятся точкой пересечения пополам.

Рис. 9. Прямоугольник

AO = BO = CO = DO = АС / 2 = BD / 2

10. Около любого прямоугольника можно описать окружность. Диагональ прямоугольника является диаметром описанной окружности.

Рис. 10. Прямоугольник

АС и BD – диаметр описанной окружности и диагональ прямоугольника

11. Точка пересечения диагоналей называется центром прямоугольника и является центром описанной окружности.

12. Прямоугольник может содержать вписанную окружность и только одну, если все его стороны равны, т.е. он является квадратом.

Рис. 11. Квадрат

AВ = ВC = AD = CD

Признаки прямоугольника: 

– если диагонали параллелограмма равны, то он является прямоугольником;

– если квадрат диагонали параллелограмма равен сумме квадратов смежных сторон, то он (параллелограмм) является прямоугольником;

– если углы параллелограмма равны, то он является прямоугольником. 

Формулы прямоугольника:

Пусть a – длина прямоугольника, b – ширина прямоугольника, d – диагональ и диаметр описанной окружности прямоугольника, R – радиус описанной окружности прямоугольника, P – периметр прямоугольника, S – площадь прямоугольника.

Формула стороны прямоугольника (длины и ширины прямоугольника):

,

,

,

. 

Формула диагонали прямоугольника:

,              

d = 2R.

Формулы периметра прямоугольника:

P = 2a + 2b,

P = 2(a + b). 

Формулы площади прямоугольника:

S = a · b. 

Формула радиуса окружности, описанной вокруг прямоугольника:

.

Прямоугольник

Прямоугольный треугольник

Равнобедренный треугольник

Равносторонний треугольник

Примечание: © Фото https://www.pexels.com, https://pixabay.com

Видео https://youtu.be/_EVDcbOydAI

Коэффициент востребованности
5 376