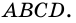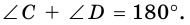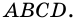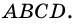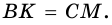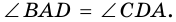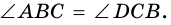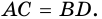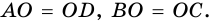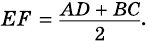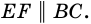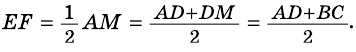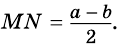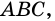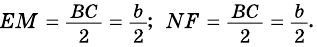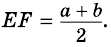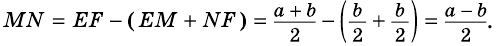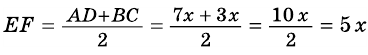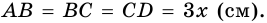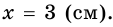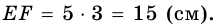Трапеция и ее свойства с определением и примерами решения
Содержание:
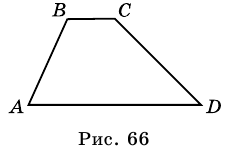
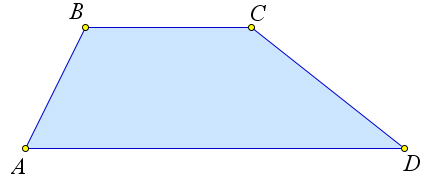
Трапецией называют четырехугольник, у которого две стороны параллельны, а две другие не параллельны.
На рисунке 66 изображена трапеция
Свойства трапеции
Рассмотрим некоторые свойства трапеции.
1. Сумма углов трапеции, прилежащих к боковой стороне, равна 180°.
Так как 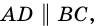
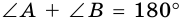
2. Трапеция является выпуклым четырехугольником.
Поскольку 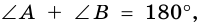
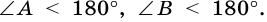
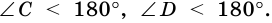
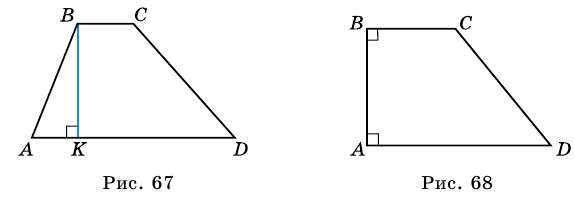
Высотой трапеции называют перпендикуляр, проведенный из любой точки основания трапеции к прямой, содержащей другое ее основание.
Как правило, высоту трапеции проводят из ее вершины. На рисунке 67 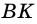
Трапецию называют прямоугольной, если один из ее углов -прямой. На рисунке 68 – прямоугольная трапеция 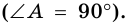
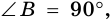
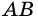
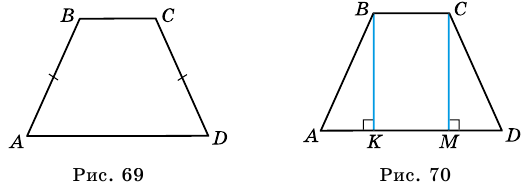
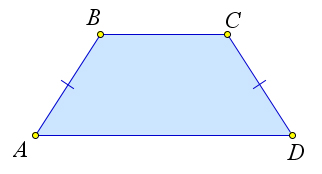
Трапецию называют равнобокой, если ее боковые стороны равны. На рисунке 69 – равнобокая трапеция
Свойства равнобокой трапеции
Рассмотрим некоторые важные свойства равнобокой трапеции.
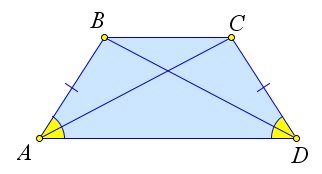
1. В равнобокой трапеции углы при основании равны.
Доказательство:
1) Пусть в трапеции 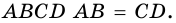
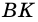
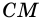
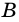
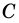
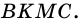
2) 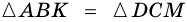
3) Также 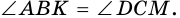
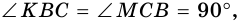
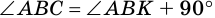
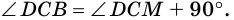
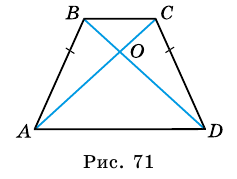
2. Диагонали равнобокой трапеции равны.
Доказательство:
Рассмотрим рисунок 71. 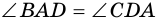
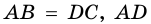
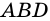
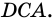
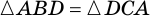
Пример:
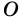
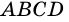
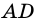
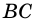
Доказательство:
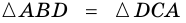
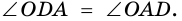
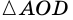
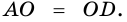
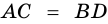
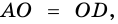
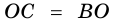
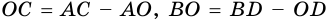
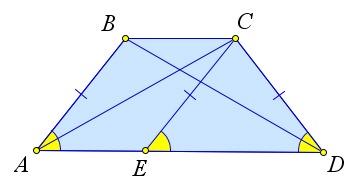
Теорема (признак равнобокой трапеции). Если в трапеции углы при основании равны, то трапеция — равнобокая.
Доказательство:
1) Пусть в 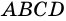
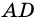
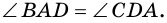
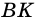
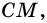
2) Тогда 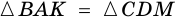
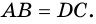
Термин «трапеция» греческого происхождения (по-гречески «трапед-зион» означает «столик», в частности столик для обеда; слова «трапеция» и «трапеза» – однокоренные).
В «Началах» Евклид под термином «трапеция» подразумевал любой четырехугольник, не являющийся параллелограммом. Большинство математиков Средневековья использовали термин «трапеция» с тем же смыслом.
Трапеция в современной трактовке впервые встречается у древнегреческого математика Посидония (I в.), но начиная только с XVIII в. этот термин стал общепринятым для четырехугольников, у которых две стороны параллельны, а две другие – не параллельны.
Свойство средней линии трапеции
Средней линией трапеции называют отрезок, соединяющий середины ее боковых сторон.
Рассмотрим свойство средней линии трапеции.
Теорема (свойство средней линии трапеции). Средняя линия трапеции параллельна основаниям и равна их полусумме.
Доказательство:
Пусть 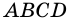
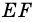
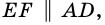
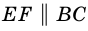
1) Проведем луч 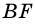
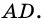
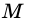
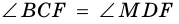
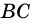
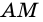
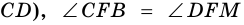
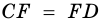
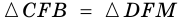
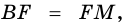
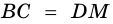
2) Поскольку 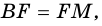
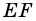
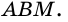
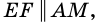
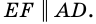
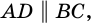
3) Кроме того,
Пример:
Докажите, что отрезок средней линии трапеции, содержащийся между ее диагоналями, равен полуразности оснований.
Доказательство:
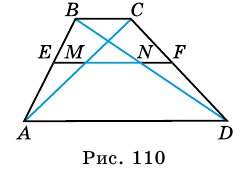
Пусть 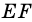
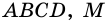
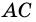
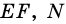
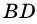
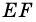
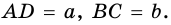
1) Так как 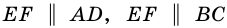
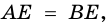
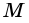
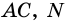
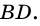
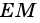
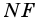
Тогда
2) 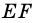
3)
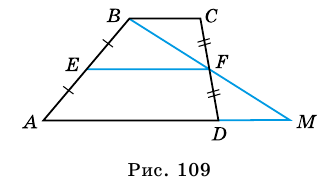
Пример:
В равнобокой трапеции диагональ делит острый угол пополам. Найдите среднюю линию трапеции, если ее основания относятся как 3 : 7, а периметр трапеции – 48 см.
Решение:
Пусть 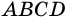
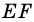
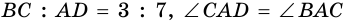
1) Обозначим 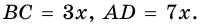
2) 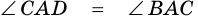
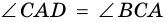
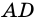
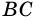
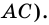
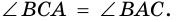
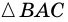
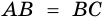
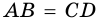
3) Учитывая, что 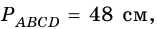
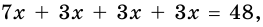
4) Тогда
То, что средняя линия трапеции равна полусумме оснований, было известно еще древним египтянам; эту информацию содержал папирус Ахмеса (примерно XVII в. до н. э.).
О свойстве средней линии трапеции знали также и вавилонские землемеры; это свойство упоминается и в трудах Герона Александрийского (первая половина I в. н. э.).
| Рекомендую подробно изучить предметы: |
|
| Ещё лекции с примерами решения и объяснением: |
- Площадь трапеции
- Центральные и вписанные углы
- Углы и расстояния в пространстве
- Подобие треугольников
- Площадь параллелограмма
- Прямоугольник и его свойства
- Ромб и его свойства, определение и примеры
- Квадрат и его свойства
При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org
Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи
Сайт пишется, поддерживается и управляется коллективом преподавателей
Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.
Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.
Трапеция. Свойства трапеции
Трапеция – четырехугольник, у которого только одна пара сторон параллельна (а другая пара сторон не параллельна).
Параллельные стороны трапеции называются основаниями. Другие две — боковые стороны .
Если боковые стороны равны, трапеция называется равнобедренной .
Трапеция, у которой есть прямые углы при боковой стороне, называется прямоугольной .
Отрезок, соединяющий середины боковых сторон, называется средней линией трапеции .
Свойства трапеции
1. Средняя линия трапеции параллельна основаниям и равна их полусумме.
2. Биссектриса любого угла трапеции отсекает на её основании (или продолжении) отрезок, равный боковой стороне.
3. Треугольники и , образованные отрезками диагоналей и основаниями трапеции, подобны.
Коэффициент подобия –
Отношение площадей этих треугольников есть .
4. Треугольники и , образованные отрезками диагоналей и боковыми сторонами трапеции, имеют одинаковую площадь.
5. В трапецию можно вписать окружность, если сумма оснований трапеции равна сумме её боковых сторон.
6. Отрезок, соединяющий середины диагоналей, равен полуразности оснований и лежит на средней линии.
7. Точка пересечения диагоналей трапеции, точка пересечения продолжений её боковых сторон и середины оснований лежат на одной прямой.
8. Если сумма углов при любом основании трапеции равна 90°, то отрезок, соединяющий середины оснований, равен их полуразности.
Свойства и признаки равнобедренной трапеции
1. В равнобедренной трапеции углы при любом основании равны.
2. В равнобедренной трапеции длины диагоналей равны.
3. Если трапецию можно вписать в окружность, то трапеция – равнобедренная.
4. Около равнобедренной трапеции можно описать окружность.
5. Если в равнобедренной трапеции диагонали перпендикулярны, то высота равна полусумме оснований.
Вписанная окружность
Если в трапецию вписана окружность с радиусом и она делит боковую сторону точкой касания на два отрезка — и , то
Площадь
или где – средняя линия
Смотрите хорошую подборку задач с трапецией (входят в ГИА и часть В ЕГЭ) здесь и здесь.
Чтобы не потерять страничку, вы можете сохранить ее у себя:
Трапеция. Определение, виды, свойства
Определения
Определение 1. Трапецией называется четырехугольник, у которого две стороны параллельны а две другие − нет.
На Рис.1 четырехугольники ABCD и EFGH являются трапециями.
Параллельные стороны трапеции называются основаниями трапеции, а непараллельные стороны − боковыми сторонами (Рис.2).
В трапеции ABCD (Рис.1) углы A и B называют углами при основании AB, а углы C и D называют углами при основании CD.
Определение 2. Высотой трапеции называется перпендикуляр, отпущенный из любой точки прямой, проходящей через один из оснований трапеции, на прямую, проходящую через другое основание.
На Рис.3 отрезки DM, ON, QP являются вершинами трапеции ABCD. Поскольку величина каждой из этих отрезков является расстоянием между параллельными прямыми, проходящими через основания трапеции, то они равны друг другу.
Определение 3. Средней линией трапеции называется отрезок, соединяющий средние точки боковых сторон.
На рисунке Рис.4 ( small MN ) является средней линией трапеции ( small ABCD, ) причем ( small AM=MD,;; BN=NC. )
Виды трапеций
Если боковые стороны трапеции равны, то трапеция называется равнобокой или равнобедренной (Рис.5).
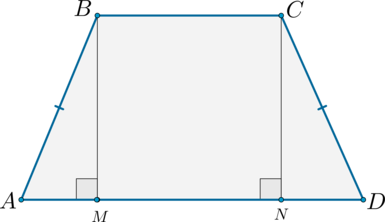
Трапеция называется прямоугольной, если одна из боковых сторон перпендикуляна основаниям трапеции (Рис.6).
Трапеция называется разносторонней, если длина всех сторон разные (т.е. если трапеция не прямоульная и не равнобедренная)(Рис.7).
Свойства трапеции
Свойство 1. Средняя линия трапеции параллельна основаниям и равна половине их суммы.
Доказательство. Пусть MN средняя линия трапеции ABCD (Рис.8). Докажем, что ( small MN || AB, ) ( small MN=frac12 (AB+CD). )
Проведем прямую DN и обозначим точку ее пересечения с прямой AB точкой P. Так как MN является средней линией трапеции ABCD, то
Углы 1 и 2 вертикальные , следовательно
| ( small angle 1=angle 2. ) | (2) |
Углы 3 и 4 являются накрест лежащими, при рассмотрении параллельных прямых BP и CD пересеченные секущей CB, тогда (теорема 1 статьи Теоремы об углах, образованных двумя параллельными прямыми и секущей).
| ( small angle 3=angle 4. ) | (3) |
Исходя из равенств (1),(2) и (3) получим, что треугольники CND и NPC равны, по второму признаку равенства треугольников. Тогда BP = DC, DN = NP. Из равенств AM = MD и DN = NP следует, что MN является средней линией треугольника ADP. Тогда ( small MN || AP ) ( или ( small MN || AB )) и ( small MN =frac 12 AP ). Но ( small AP=AB +BP=AB+CD ). Тогда ( small MN =frac 12 (AB+CD).)
Свойство 2. Сумма углов трапеции, прилежащих к одной боковой стороне равна 180°.
Доказательство. Рассмотрим трапецию ABCD (Рис.9).
Углы A и D являутся односторонними углами, при рассмотрении параллельных прямых AB и CD пересеченные секущей AD (теорема 3 статьи Теоремы об углах, образованных двумя параллельными прямыми и секущей). Тогда ( small angle A+ angle D=180°.)
Свойство 3. Отрезок, слединяющий середины диагоналей трапеции лежит на средней линии трапеции и равен половине разности оснований.
Доказательство. Рассмотрим трапецию ABCD (Рис.10).
Поскольку точки P и Q являются средними точками диагоналей AC и BD, соответственно, то:
MP − является средней линией треугольника ADC, так как , . Тогда
QN − является средней линией треугольника BCD, так как , Тогда
Из и следует, что P находится на прямой, проходящей через среднюю линию MN, поскольку из точки M можно провести только одну прямую, параллельно CD (Аксиома 1 статьи Аксиома параллельных прямых).
Аналогично, из и следует, что Q находится на прямой, проходящей через среднюю линию MN, поскольку из точки N можно провести только одну прямую, параллельно CD.
Далее, учитывая (4) и (5), получим:
Далее, учитывая свойство 1, получим:
Свойства равнобокой (равнобедренной) трапеции
Свойсво 1′. В равнобокой трапеции углы при каждом основании равны.
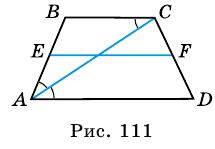
Доказательство. Рассмотрим равнобедренную (равнобокую) трапецию ABCD, где AD = BC (Рис.11).
Проведем высоты DM и CN. Поскольку DM = CN и AD = BC, то прямоугольники ADM и NCB равны гипотенузе и катету (см. статью Прямоугольный треугольник. Свойства, признаки равенства). Тогда ( small angle A=angle B. ) Докажем, далее, что ( small angle ADC=angle DCB. ) ( small angle A +angle ADC=180° ) поскольку углы A и ADC являются односторонними углами, при рассмотрении параллельных прямых AB и CD пересеченные секущей AD (теорема 3 статьи Теоремы об углах, образованных двумя параллельными прямыми и секущей). Аналогично ( small angle B +angle DCB=180°. ) Учитывая, что ( small angle A=angle B ), получим ( small angle ADC=angle DCB. )
Свойсво 2′. В равнобокой трапеции диагонали равны.
Доказательство. Рассмотрим треугольники ADC и DCB (Рис.12). Имеем CD общая сторона для обеих треугольников, AD = CB, ( small angle ADC=angle DCB. ) Тогда треугольники равны по двум сторонам и углу между ними. Следовательно диагонали AC и DB трапеции ABCD равны.
Свойсво 3′. В равнобокой трапеции высота, приведенная из вершины тупого угла на основание, делит основание трапеции на отрезки, больший из которых равен половине суммы оснований, а меньший равен половине разности оснований.
Доказательство. Рассмотрим четырехугольник DMNC (Рис.11). Имеем:
Тогда четырехугольник DMNC является прямоугольником. Следовательно DC = MN. Поскольку треугольники ADM и NCB равны (см. доказательство следствия 1), то AM = NB. Следовательно:
[spoiler title=”источники:”]
http://matworld.ru/geometry/trapeciya.php
[/spoiler]
Свойства трапеции
Итак, что ты должен знать о свойствах трапеции…
Сумма углов при каждой боковой стороне трапеции равна 180°. (у нас на рисунке ( displaystyle angle 1+angle 2=180{}^circ ) и ( displaystyle angle 3+angle 4=180{}^circ ))
Почему так?
Ну, конечно, просто потому, что основания – параллельны, а боковая сторона – секущая.
Вот и получается, что ( displaystyle angle 1) и ( displaystyle angle 2) – внутренние односторонние углы при параллельных ( displaystyle AD) и ( displaystyle BC) и секущей ( displaystyle AB).
Поэтому ( displaystyle angle 1+angle 2=180{}^circ ).
И точно так же ( displaystyle angle 3) и ( displaystyle angle 4) – внутренние односторонние углы при тех же параллельных ( displaystyle AD) и ( displaystyle BC), но секущая теперь – ( displaystyle CD).
Видишь: главное, что играет роль – это параллельность оснований. Давай разберем еще некоторые свойства трапеции.
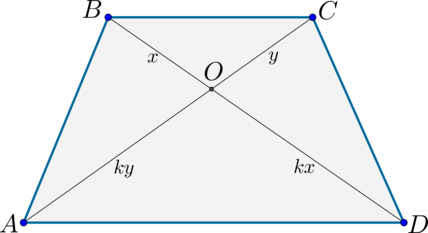
Как у всякого четырехугольника, у трапеции есть диагонали. Их две – посмотри на рисунки:
Снова порассуждаем об углах:
Опять ( displaystyle AD) и ( displaystyle BC) – параллельные, а диагональ ( displaystyle AC) – секущая. Поэтому ( displaystyle angle 1=angle 2).
А теперь рассмотрим сразу 2 диагонали и 4 угла:
( displaystyle angle 1=angle 2)
( displaystyle angle 3=angle 4)
Что из этого может следовать?
Очень важный факт:
Треугольники ( displaystyle BOC) и ( displaystyle AOD) – подобны по двум углам.
Их коэффициент подобия равен отношению оснований: ( displaystyle K=frac{a}{b}).
[{Large{text{Произвольная трапеция}}}]
Определения
Трапеция – это выпуклый четырехугольник, у которого две стороны параллельны, а две другие стороны не параллельны.
Параллельные стороны трапеции называются её основаниями, а две другие стороны – боковыми сторонами.
Высота трапеции – это перпендикуляр, опущенный из любой точки одного основания к другому основанию.
Теоремы: свойства трапеции
1) Сумма углов при боковой стороне равна (180^circ).
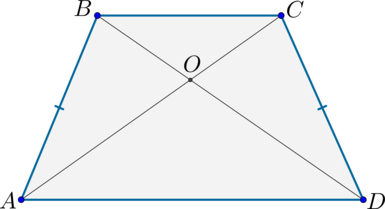
2) Диагонали делят трапецию на четыре треугольника, два из которых подобны, а два другие – равновелики.
Доказательство
1) Т.к. (ADparallel BC), то углы (angle BAD) и (angle ABC) – односторонние при этих прямых и секущей (AB), следовательно, (angle
BAD
+angle ABC=180^circ).
2) Т.к. (ADparallel BC) и (BD) – секущая, то (angle DBC=angle
BDA) как накрест лежащие.
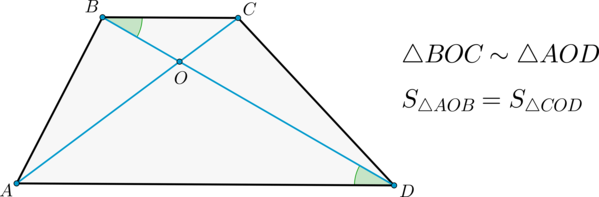
Также (angle BOC=angle AOD) как вертикальные.
Следовательно, по двум углам (triangle BOC sim triangle AOD).
Докажем, что (S_{triangle AOB}=S_{triangle COD}). Пусть (h) – высота трапеции. Тогда (S_{triangle ABD}=frac12cdot hcdot
AD=S_{triangle ACD}). Тогда: [S_{triangle AOB}=S_{triangle ABD}-S_{triangle AOD}=S_{triangle ACD}-S_{triangle AOD}=S_{triangle
COD}]
Определение
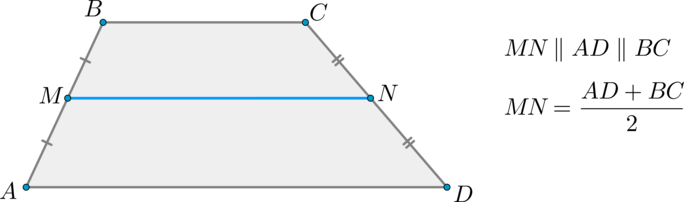
Средняя линия трапеции – отрезок, соединяющий середины боковых сторон.
Теорема
Средняя линия трапеции параллельна основаниям и равна их полусумме.
Доказательство*
С доказательством рекомендуется ознакомиться после изучения темы “Подобие треугольников”.
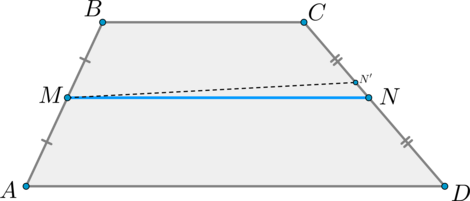
1) Докажем параллельность.
Проведем через точку (M) прямую (MN’parallel AD) ((N’in CD)). Тогда по теореме Фалеса (т.к. (MN’parallel ADparallel BC, AM=MB)) точка (N’) — середина отрезка (CD). Значит, точки (N) и (N’) совпадут.
2) Докажем формулу.
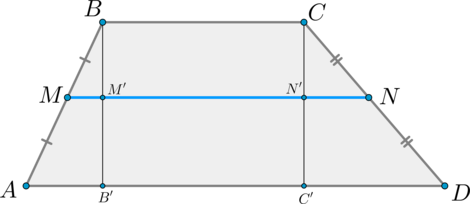
Проведем (BB’perp AD, CC’perp AD). Пусть (BB’cap MN=M’, CC’cap
MN=N’).
Тогда по теореме Фалеса (M’) и (N’) — середины отрезков (BB’) и (CC’) соответственно. Значит, (MM’) – средняя линия (triangle
ABB’), (NN’) — средняя линия (triangle DCC’). Поэтому: [MM’=dfrac12 AB’, quad NN’=dfrac12 DC’]
Т.к. (MNparallel ADparallel BC) и (BB’, CC’perp AD), то (B’M’N’C’) и (BM’N’C) – прямоугольники. По теореме Фалеса из (MNparallel AD) и (AM=MB) следует, что (B’M’=M’B). Значит, (B’M’N’C’) и (BM’N’C) – равные прямоугольники, следовательно, (M’N’=B’C’=BC).
Таким образом:
[MN=MM’+M’N’+N’N=dfrac12 AB’+B’C’+dfrac12 C’D=] [=dfrac12 left(AB’+B’C’+BC+C’Dright)=dfrac12left(AD+BCright)]
Теорема: свойство произвольной трапеции
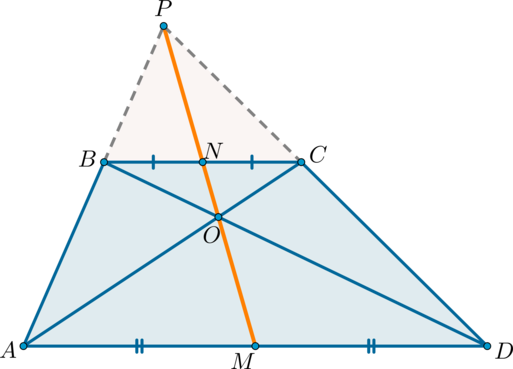
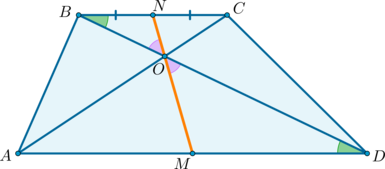
Середины оснований, точка пересечения диагоналей трапеции и точка пересечения продолжений боковых сторон лежат на одной прямой.
Доказательство*
С доказательством рекомендуется ознакомиться после изучения темы “Подобие треугольников”.
1) Докажем, что точки (P), (N) и (M) лежат на одной прямой.
Проведем прямую (PN) ((P) – точка пересечения продолжений боковых сторон, (N) – середина (BC)). Пусть она пересечет сторону (AD) в точке (M). Докажем, что (M) – середина (AD).
Рассмотрим (triangle BPN) и (triangle APM). Они подобны по двум углам ((angle APM) – общий, (angle PAM=angle PBN) как соответственные при (ADparallel BC) и (AB) секущей). Значит: [dfrac{BN}{AM}=dfrac{PN}{PM}]
Рассмотрим (triangle CPN) и (triangle DPM). Они подобны по двум углам ((angle DPM) – общий, (angle PDM=angle PCN) как соответственные при (ADparallel BC) и (CD) секущей). Значит: [dfrac{CN}{DM}=dfrac{PN}{PM}]
Отсюда (dfrac{BN}{AM}=dfrac{CN}{DM}). Но (BN=NC), следовательно, (AM=DM).
2) Докажем, что точки (N, O, M) лежат на одной прямой.
Пусть (N) – середина (BC), (O) – точка пересечения диагоналей. Проведем прямую (NO), она пересечет сторону (AD) в точке (M). Докажем, что (M) – середина (AD).
(triangle BNOsim triangle DMO) по двум углам ((angle OBN=angle
ODM) как накрест лежащие при (BCparallel AD) и (BD) секущей; (angle BON=angle DOM) как вертикальные). Значит: [dfrac{BN}{MD}=dfrac{ON}{OM}]
Аналогично (triangle CONsim triangle AOM). Значит: [dfrac{CN}{MA}=dfrac{ON}{OM}]
Отсюда (dfrac{BN}{MD}=dfrac{CN}{MA}). Но (BN=CN), следовательно, (AM=MD).
[{Large{text{Равнобедренная трапеция}}}]
Определения
Трапеция называется прямоугольной, если один из ее углов – прямой.
Трапеция называется равнобедренной, если ее боковые стороны равны.
Теоремы: свойства равнобедренной трапеции
1) У равнобедренной трапеции углы при основании равны.
2) Диагонали равнобедренной трапеции равны.
3) Два треугольника, образованные диагоналями и основанием, являются равнобедренными.
Доказательство
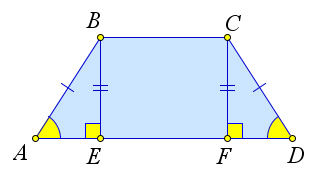
1) Рассмотрим равнобедренную трапецию (ABCD).
Из вершин (B) и (C) опустим на сторону (AD) перпендикуляры (BM) и (CN) соответственно. Так как (BMperp AD) и (CNperp AD), то (BMparallel CN); (ADparallel BC), тогда (MBCN) – параллелограмм, следовательно, (BM = CN).
Рассмотрим прямоугольные треугольники (ABM) и (CDN). Так как у них равны гипотенузы и катет (BM) равен катету (CN), то эти треугольники равны, следовательно, (angle DAB = angle CDA).
2)
Т.к. (AB=CD, angle A=angle D, AD) – общая, то по первому признаку (triangle ABD=triangle ACD). Следовательно, (AC=BD).
3) Т.к. (triangle ABD=triangle ACD), то (angle BDA=angle CAD). Следовательно, треугольник (triangle AOD) – равнобедренный. Аналогично доказывается, что и (triangle BOC) – равнобедренный.
Теоремы: признаки равнобедренной трапеции
1) Если у трапеции углы при основании равны, то она равнобедренная.
2) Если у трапеции диагонали равны, то она равнобедренная.
Доказательство
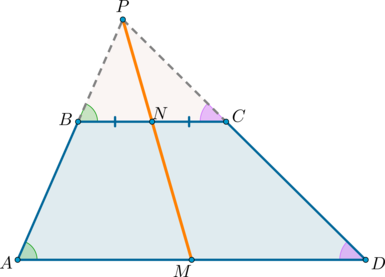
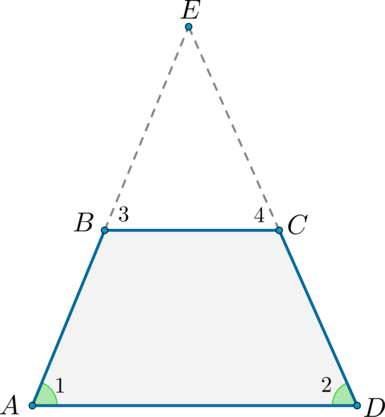
Рассмотрим трапецию (ABCD), такую что (angle A = angle D).
Достроим трапецию до треугольника (AED) как показано на рисунке. Так как (angle 1 = angle 2), то треугольник (AED) равнобедренный и (AE
= ED). Углы (1) и (3) равны как соответственные при параллельных прямых (AD) и (BC) и секущей (AB). Аналогично равны углы (2) и (4), но (angle 1 = angle 2), тогда (angle 3 = angle 1 = angle 2 =
angle 4), следовательно, треугольник (BEC) тоже равнобедренный и (BE = EC).
В итоге (AB = AE – BE = DE – CE = CD), то есть (AB = CD), что и требовалось доказать.
2) Пусть (AC=BD). Т.к. (triangle AODsim triangle BOC), то обозначим их коэффициент подобия за (k). Тогда если (BO=x), то (OD=kx). Аналогично (CO=y Rightarrow AO=ky).
Т.к. (AC=BD), то (x+kx=y+ky Rightarrow x=y). Значит (triangle AOD) – равнобедренный и (angle OAD=angle ODA).
Таким образом, по первому признаку (triangle ABD=triangle ACD) ((AC=BD, angle OAD=angle ODA, AD) – общая). Значит, (AB=CD), чтд.
25
Июл 2013
Категория: Справочные материалы
Трапеция. Свойства трапеции
2013-07-25
2016-06-15
Трапеция – четырехугольник, у которого только одна пара сторон параллельна (а другая пара сторон не параллельна).
Параллельные стороны трапеции называются основаниями. Другие две — боковые стороны.
Если боковые стороны равны, трапеция называется равнобедренной.
Трапеция, у которой есть прямые углы при боковой стороне, называется прямоугольной.
Отрезок, соединяющий середины боковых сторон, называется средней линией трапеции.
Свойства трапеции
1. Средняя линия трапеции параллельна основаниям и равна их полусумме.
2. Биссектриса любого угла трапеции отсекает на её основании (или продолжении) отрезок, равный боковой стороне.
3. Треугольники и
, образованные отрезками диагоналей и основаниями трапеции, подобны.
Коэффициент подобия –
Отношение площадей этих треугольников есть .
4. Треугольники и
, образованные отрезками диагоналей и боковыми сторонами трапеции, имеют одинаковую площадь.
5. В трапецию можно вписать окружность, если сумма оснований трапеции равна сумме её боковых сторон.
6. Отрезок, соединяющий середины диагоналей, равен полуразности оснований и лежит на средней линии.
7. Точка пересечения диагоналей трапеции, точка пересечения продолжений её боковых сторон и середины оснований лежат на одной прямой.
8. Если сумма углов при любом основании трапеции равна 90°, то отрезок, соединяющий середины оснований, равен их полуразности.
Свойства и признаки равнобедренной трапеции
1. В равнобедренной трапеции углы при любом основании равны.
2. В равнобедренной трапеции длины диагоналей равны.
3. Если трапецию можно вписать в окружность, то трапеция – равнобедренная.
4. Около равнобедренной трапеции можно описать окружность.
5. Если в равнобедренной трапеции диагонали перпендикулярны, то высота равна полусумме оснований.
Вписанная окружность
Если в трапецию вписана окружность с радиусом и она делит боковую сторону точкой касания на два отрезка —
и
, то
Площадь
или
где
– средняя линия
Смотрите хорошую подборку задач с трапецией (входят в ГИА и часть В ЕГЭ) здесь и здесь.
Смотрите также площадь трапеции.
Автор: egeMax |
комментарий 431
Печать страницы
math-public:trapeciya
Содержание
Трапеция
Определение
Трапецией называется четырехугольник, у которого две стороны
параллельны, а две другие не параллельны.
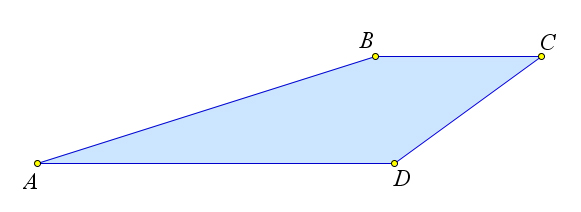
Замечание
Сумма углов при боковой стороне трапеции равна $180^circ$.
Доказательство
Действительно, так как основания трапеции параллельны, а боковая
сторона является секущей, то углы при боковой стороне являются
внутренними односторонними углами при параллельных прямых, и,
следовательно, их сумма равна $180^circ$.
Определение
-
Трапеция называется равнобедренной, если ее боковые стороны равны.
-
Трапеция называется прямоугольной, если один из ее углов равен $90^circ$.
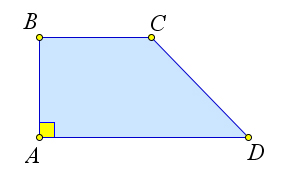
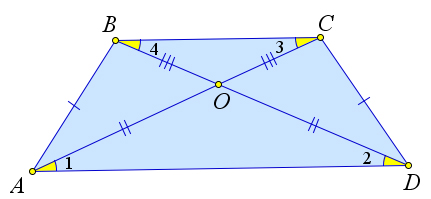
Свойства равнобедренной трапеции
-
Углы при основании равнобедренной трапеции равны.
-
Диагонали равнобедренной трапеции равны.
-
Диагонали равнобедренной трапеции, пересекаясь, образуют два равных и два равнобедренных треугольника.
-
Проекция боковой стороны равнобедренной трапеции на основание равна полуразности оснований, а проекция диагонали – полусумме оснований.
Доказательство
Докажем первый пункт теоремы.
Рассмотрим равнобедренную трапецию $ABCD$, $AB=CD$.
Докажем, что $angle A=angle D$.
Проведем из точек $B$ и $C$ высоты $BE$ и $CF$.
Треугольники $triangle ABE$ и $triangle CFD$ равны по катету и гипотенузе ($AB=CD,
BE=CF$).
Следовательно, $angle A=angle D$.
Докажем второй пункт теоремы.
В равнобедренной трапеции $ABCD$ рассмотрим треугольники $triangle ABD$ и $triangle ACD$.
Они равны по первому признаку ($AB=CD$, $AD$ – общая, $angle A=angle D$ по
первому пункту).
Следовательно, $AC=BD$.
Докажем третий пункт теоремы.
Пусть диагонали равнобедренной трапеции $ABCD$ пересекаются в точке $O$. Докажем, что треугольники $triangle AOD$ и $triangle BOC$ – равнобедренные, а треугольники $triangle AOB$ и $triangle COD$ равны.
Действительно, во втором пункте уже было доказано, что $triangle ABD=triangle ACD$.
Следовательно, $angle 1=angle 2$, а так как они накрест лежащие с углами $angle 3$ и $angle 4$ соответственно, то $angle 3=angle 4$, что
и означает, что треугольники $triangle AOD$ и $triangle BOC$ – равнобедренные.
Тогда $AO=OD$ и $BO=OC$, и как следствие, $triangle AOB=triangle COD$ по
третьему признаку равенства треугольников.
Докажем четвертый пункт теоремы.
Так как $triangle AEB=triangle CFD$ (по катету и
гипотенузе), то $AE=FD$.
Кроме того, $EF=BC$, следовательно, $AE=dfrac{AD-BC}{2}$ и
$AF=dfrac{AD-BC}{2}+BC=dfrac{AD+BC}{2}$.
Признаки равнобедренной трапеции
-
Если углы при основании трапеции равны, то она равнобедренная.
-
Если диагонали трапеции равны, то она равнобедренная.
Доказательство
Докажем первый пункт теоремы.
Рассмотрим трапецию $ABCD$, в которой $angle A=angle D$.
Докажем, что тогда $AB=CD$, то есть трапеция равнобедренная.
Проведем из вершины $C$ отрезок $CE$ параллельный стороне $AB$.
Тогда $angle A=angle CED$, как соответственные углы.
Следовательно, $angle CED=angle D$, а тогда $triangle CED$ – равнобедренный.
А поскольку $AB=CE$ ($ABCE$ – параллелограмм), то $AB=CD$.
Докажем второй пункт теоремы.
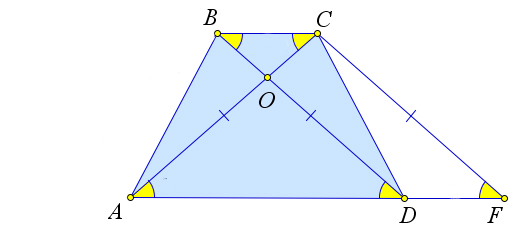
Рассмотрим трапецию $ABCD$, у которой $AC=BD$.
Докажем, что тогда $AB=CD$.
Построим из точки $C$ прямую, параллельный диагонали $BD$. Пусть она пересекает прямую $AD$ в точке $F$.
Тогда $BD=CF$, так как $BCFD$ – параллелограмм по определению.
Тогда $triangle ACF$ – равнобедренный, так как $AC=CF$.
Следовательно $angle OAD=angle ODA$, и $triangle AOD$ – равнобедренный.
Тогда $AO=OD$ и $BO=OC$.
Следовательно, $triangle BOA=triangle COD$ по первому признаку ($angle BOA=angle COD$ – как вертикальные).
Следовательно, $AB=CD$.
Теорема (о равнобедренной трапеции с перпендикулярными диагоналями)
В равнобедренной трапеции со взаимно перпендикулярными диагоналями
высота равна средней линии.
Доказательство
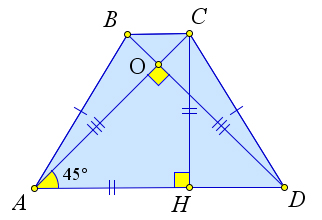
Рассмотрим равнобедренную трапецию $ABCD$, в которой $ACperp BD$.
Докажем, что в такой трапеции высота $CH$ равна средней линии то есть полусумме оснований.
Действительно, $triangle AOD$ – равнобедренный и прямоугольный, следовательно, $angle OAD = 45^circ$. Тогда $triangle AHC$ – равнобедренный, то есть $AH=CH$.
Но отрезок $AH$ равен полусумме оснований.
· Последнее изменение: 2016/04/13 23:56 —
labreslav