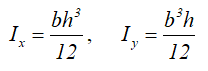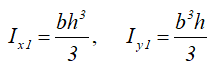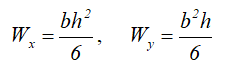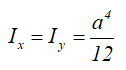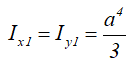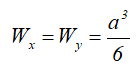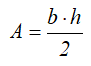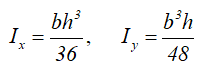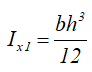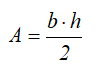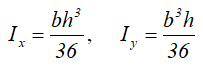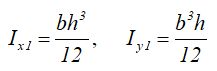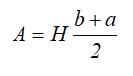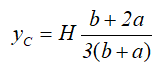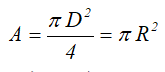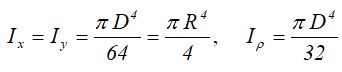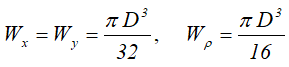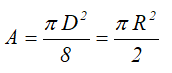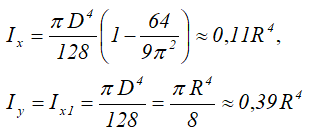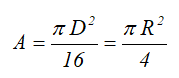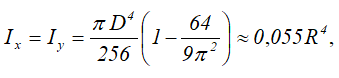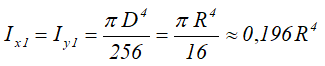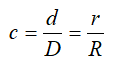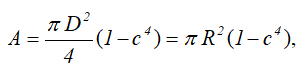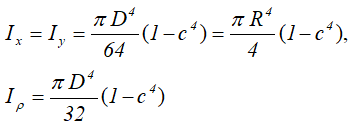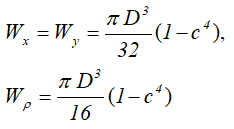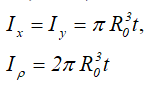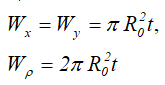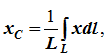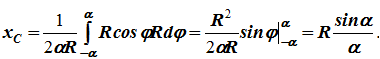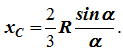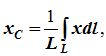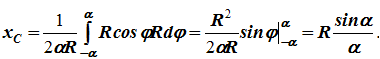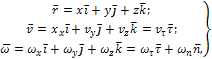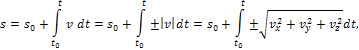Как найти середин полукруга

Можно проинтегрировать, но это долго объяснять. В данном случае можно воспользоваться второй теоремой Паппа — Гульдина: Объём тела, образованного вращением плоской фигуры вокруг оси, расположенной в той же плоскости и не пересекающей фигуру, равен площади фигуры, умноженной на длину окружности, радиусом которой служит расстояние от оси вращения до центра масс фигуры

В нашем случае объём тела вращения – объём шара: (4/3)pi*R^3; расстояние от оси вращения: l (значит длина окружности 2pi*l); площадь фигуры – половина круга: (pi*R^2)/2.

Таким образом: (4/3)pi*R^3 = (2pi*l)*(pi*R^2)/2 <=> l = 4R/3pi

ПоршМастер (1757)

2 года назад

Речь идет не о шаре, а о полуКРУГЕ. А ты вообще посчитала объема шара, из которого вырезали шар поменьше. Полукруга нет даже в разрезе. В разрезе будет круг из которого вырезали круг

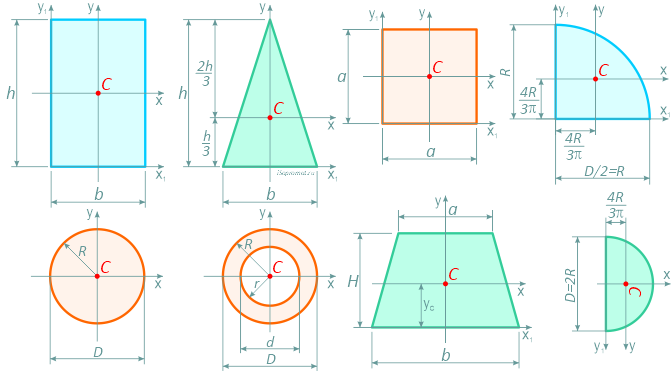
Формулы площадей, центров тяжести, осевых и полярных моментов инерции, моментов сопротивления и других геометрических характеристик основных простых фигур: прямоугольника, квадрата, равнобедренного и прямоугольного треугольника, круга, полукруга, четверти круга, кольцевого и тонкостенного сечений.

Обозначения в формулах:
C — положение центра тяжести фигуры;
A — площадь сечения;
I_x , I_y — осевые моменты инерции сечения относительно главных осей;
I_x1 , I_y1 — осевые моменты инерции относительно вспомогательных (смещённых) осей;
I_ρ — полярный момент инерции сечения;
W_x , W_y — осевые моменты сопротивления;
W_ρ — полярный момент сопротивления

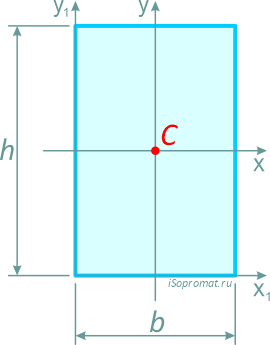
Прямоугольник

Прямоугольник высотой h и шириной b.

Центр тяжести прямоугольника в точке пересечения его диагоналей, на расстоянии половины высоты (h/2) по вертикали и половины ширины (b/2) по горизонтали.

Площадь

Центральные осевые моменты инерции прямоугольника

Моменты инерции относительно смещенных осей, проходящих через нижнюю левую точку

Осевые моменты сопротивления прямоугольного сечения

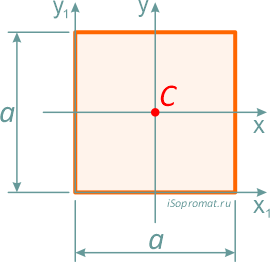
Квадрат

Квадрат — это частный случай прямоугольника, у которого высота равна ширине, т.е. h=b=a.

Центр тяжести квадрата находится так же на пересечении диагоналей — на расстоянии половины стороны (a/2) по высоте и ширине.

Площадь

Центральные осевые моменты инерции квадрата

Моменты инерции относительно смещенных осей, проходящих через нижнюю левую точку

Осевой момент сопротивления квадратного сечения

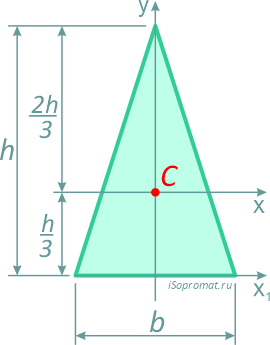
Треугольник равнобедренный

Равнобедренный треугольник высотой h и шириной основания b.

Центр тяжести треугольника располагается в точке пересечения его медиан на расстоянии 1/3 высоты от основания и 2/3 высоты от его вершин.

Площадь

Центральные осевые моменты инерции треугольника

Момент инерции относительно смещенной оси x₁, проходящей через его основание

Прямоугольный треугольник

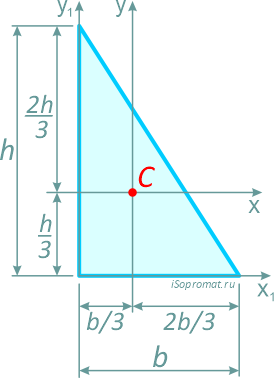
Прямоугольный треугольник высотой h и шириной основания b.

Центр тяжести прямоугольного треугольника располагается аналогично, на пересечении медиан на расстоянии 1/3 высоты от основания и 2/3 высоты от вершины.

Площадь

Центральные осевые моменты инерции прямоугольного треугольника

Моменты инерции относительно смещенных осей x₁ и y₁, проходящих через точку, соединяющую его катеты

Трапеция

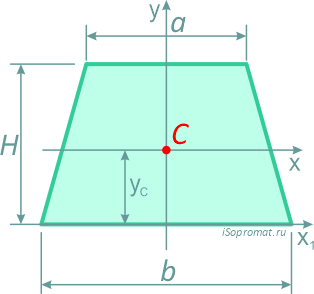
Равнобокая трапеция высотой H и шириной оснований: малого a и большого b.

Площадь трапеции

Центр тяжести на линии, соединяющей середины оснований трапеции, на высоте, определяемой по формуле:

Круг

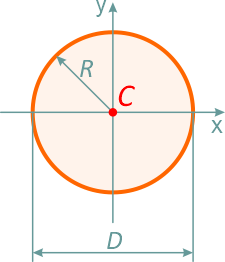
Круг диаметром D (d) или радиусом R (r)

Площадь круга через его диаметр и радиус

Центральные осевые и полярный моменты инерции круга

Осевые и полярный моменты сопротивления

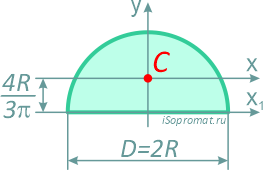
Полукруг

Половина круга диаметром D (d) или радиусом R (r)

Площадь

Осевые моменты инерции полукруга

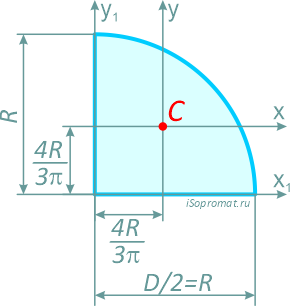
Четверть круга

Четверть круга диаметром D (d) или радиусом R (r)

Площадь

Центральные осевые моменты инерции четверти круга

Моменты инерции относительно смещенных осей x₁ и y₁

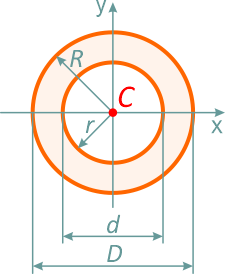
Кольцо

Кольцо с внешним диаметром D и внутренним d, (радиусами: внешним R и внутренним r)

Отношение внутреннего диаметра (радиуса) к внешнему обозначается буквой c.

Площадь

Центральные осевые и полярный моменты инерции кольца

Осевые и полярный моменты сопротивления

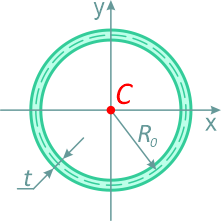
Тонкостенное сечение (труба)

Тонкостенный профиль (сечение трубы) средним радиусом R₀ и толщиной стенки трубы t при R₀>>t

Площадь

Центральные осевые и полярный моменты инерции трубного сечения

Осевые и полярный моменты сопротивления

Пример определения координат центра тяжести сложной фигуры:

Другие видео

Смотрите также:
Определение координат центра тяжести сложных фигур
Геометрические характеристики сечений

Сохранить или поделиться с друзьями

Вы находитесь тут:

На нашем сайте Вы можете получить решение задач и онлайн помощь

Подробнее

iSopromat.ru

Формулы для расчета координат положения центра тяжести треугольника, дуги окружности и кругового сегмента.

Центр тяжести треугольника

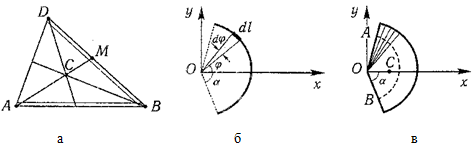
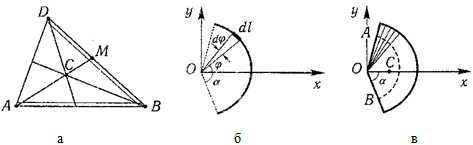
Центр тяжести площади треугольника совпадает с точкой пересечения его медиан (рисунок 1.10, а).

Центр тяжести дуги окружности

Дуга имеет ось симметрии (рисунок 1.10, б). Центр тяжести лежит на этой оси, т.е. y_C = 0.

dl – элемент дуги, dl = Rdφ, R – радиус окружности, x = Rcosφ, L = 2αR,

Центр тяжести кругового сектора

Сектор радиуса R с центральным углом 2α имеет ось симметрии Ox, на которой находится центр тяжести (рисунок 1.10, в).

Разбиваем сектор на элементарные секторы, которые можно считать треугольниками. Центры тяжести элементарных секторов располагаются на дуге окружности радиуса (2/3)R.

Центр тяжести сектора совпадает с центром тяжести дуги AB:

Уважаемые студенты!
На нашем сайте можно получить помощь по техническим и другим предметам:
✔ Решение задач и контрольных
✔ Выполнение учебных работ
✔ Помощь на экзаменах

Тема 1.5. Центр тяжести тела

§1. Центр тяжести однородного тела.

Рассмотрим твердое тело весом P и объемом V в системе координат Oxyz , где оси x и y связаны с поверхностью земли, а ось z направлена в зенит.

Если разбить тело на элементарные части объемом ∆V_i , то на каждую его часть будет действовать сила притяжения ∆P_i, направленная к центру Земли. Предположим, что размеры тела значительно меньше размеров Земли, тогда систему сил, приложенных к элементарным частям тела можно считать не сходящейся, а параллельной (рис.1), и к ней применимы все выводы предыдущей главы.

Рис.1. Параллельная система сил

Центром тяжести твердого тела называется центр параллельных сил тяжести элементарных частей этого тела.

При определении центра тяжести полезны несколько теорем.

1) Если однородное тело имеет плоскость симметрии, то центр тяжести его находится в этой

2) Если однородное тело имеет ось симметрии, то центр тяжести тела находится на этой оси.

3) Если однородное тело имеет центр симметрии, то центр тя­жести тела находится в этой точке.

§2. Способы определения координат центра тяжести.

1. Симметрия. Если однородное тело имеет плоскость, ось или центр симметрии (рис.2), то его центр тяжести лежит соответственно в плоскости симметрии, оси симметрии или в центре симметрии.

Рис.2. Центр тяжести тел, имеющих ось симметрии

2. Разбиение. Тело разбивается на конечное число частей (рис.3), для каждой из которых положение центра тяжести и площадь известны.

Рис.3. Центр тяжести сплошной

сложной геометрической фигуры

– центр тяжести и площадь первой фигуры;

– центр тяжести и площадь второй фигуры;

– координата центра тяжести сплошной сложной геометрической фигуры по оси x;

– координата центра тяжести сплошной сложной геометрической фигуры по оси y;

3. Метод отрицательных площадей. Частный случай способа разбиения (рис.4). Он применяется к телам, имеющим вырезы, если центры тяжести тела без выреза и вырезанной части известны. Тело в виде пластинки с вырезом представляют комбинацией сплошной пластинки (без выреза) с площадью S₁ и площади вырезанной части S₂ .

Рис.4. Центр тяжести сложной геометрической фигуры,

– центр тяжести и площадь первой фигуры;

– центр тяжести и площадь второй фигуры;

– координата центра тяжести сложной геометрической фигуры по оси x;

– координата центра тяжести сложной геометрической фигуры по оси y;

§3. Координаты центра тяжести некоторых простых фигур.

1. Центр тяжести тре­угольника. Центр тяжести треугольника лежит в точке пересечения его медиан (рис.5). Координаты центра тяжести треугольника представляют собой среднее арифметическое из координат его вершин: x_c =1/3(x₁+x₂+x₃) ; y_c =1/3(y₁+y₂+y₃).

Рис.5. Центр тяжести треугольника

2. Центр тяжести прямоугольника. Центр тяжести прямоугольника лежит в точке пересечения его диагоналей (рис.6). Координаты центра тяжести прямоугольника рассчитываются по формулам: x_c =b/2 ; y_c =h/2.

Рис. 6. Центр тяжести треугольника

3. Центр тяжести полукруга. Центр тяжести полукруга лежит на оси симметрии (рис.7). Координаты центра тяжести полукруга рассчитываются по формулам: x_c =D/2 ; y_c =4R/3π.

Рис. 7. Центр тяжести полукруга

4. Центр тяжести круга. Центр тяжести круга лежит в центре (рис.8). Координаты центра тяжести круга рассчитываются по формулам: x_c =R ; y_c =R.

Рис. 8. Центр тяжести круга

Вопросы для самопроверки:

– Что называется центром параллельных сил?

– Что называется центром тяжести тела?

– Почему силы притяжения Земле, действующие на точку тела, можно принять за систему параллельных сил?

– Запишите формулу для определения положения центра тяжести неоднородных и однородных тел, формулу для определения положения центра тяжести плоских сечений?

– Запишите формулу для определения положения центра тяжести простых геометрических фигур: прямоугольника, квадрата, трапеции и половины круга?

– Как используются свойства симметрии при определении центров тяжести тел?

– В чем состоит сущность способа отрицательных площадей?

– Каким графическим построением можно найти центр тяжести треугольника?

– Запишите формулу, определяющую центр тяжести треугольника.

Техническая механика

Методы нахождения центра тяжести

Наиболее часто для нахождения центра тяжести тела или фигуры применяют следующие методы:

• метод симметрии;
• метод разбиения;
• метод отрицательных масс.

Рассмотрим приемы, применяемые в каждом из перечисленных методов.

Метод симметрии

Представим себе однородное тело, которое имеет плоскость симметрии. Выберем такую систему координат, чтобы оси x и z лежали в плоскости симметрии (см. рисунок 1) .

В этом случае каждой элементарной частице силой тяжести G_i с абсциссой y_i = +a соответствует такая же элементарная частица с абсциссой y_i = -a , тогда:

Отсюда вывод: если однородное тело имеет плоскость симметрии, то центр тяжести тела лежит в этой плоскости.

Аналогично можно доказать и следующие положения:

• Если однородное тело имеет ось симметрии, то центр тяжести тела лежит на этой оси;
• Если однородное тело имеет две оси симметрии, то центр тяжести тела находится в точке их пересечения;
• Центр тяжести однородного тела вращения лежит на оси вращения.

Метод разбиения

Этот метод заключается в том, что тело разбивают на наименьшее число частей, силы тяжести и положение центров тяжести которых известны, после чего применяют приведенные ранее формулы для определения общего центра тяжести тела.

Допустим, что мы разбили тело силой тяжести G на три части G’ , G” , G”’ , абсциссы центров тяжести этих частей x’_C, x”_C, x”’_C известны.
Формула для определения абсциссы центра тяжести всего тела:

Перепишем ее в следующем виде:

Последнее равенство запишем для каждой из трех частей тела отдельно:

Сложив левые и правые части этих трех равенств, получим:

Но правая часть последнего равенства представляет собой произведение Gx_C , так как

Следовательно, x_C = (G’x’_C + G”x”_C + G”’x”’_C)/G , что и требовалось доказать.
Аналогично определяются координаты центра тяжести на координатных осях y и z :

Полученные формулы аналогичны формулам для определения координат цента тяжести, выведенные выше. Поэтому в исходные формулы можно подставлять не силы тяжести элементарных частиц G_i , а силы тяжести конечных частей; под координатами x_i , y_i , z_i понимают координаты центров тяжести частей, на которые разбито тело.

Метод отрицательных масс

Этот метод заключается в том, что тело, имеющее свободные полости, считают сплошным, а массу свободных полостей – отрицательной. Вид формул для определения координат центра тяжести тела при этом не меняется.

Таким образом, при определении центра тяжести тела, имеющего свободные полости, следует применять метод разбиения, но считать массу полостей отрицательной.

Практические методы определения центра тяжести тел

На практике для определения центра тяжести плоских тел сложной формы часто применяют метод подвешивания , который заключается в том, что плоское тело подвешивают на нити за какую-нибудь точку. Прочерчивают вдоль нити линию, и тело подвешивают за другую точку, не находящуюся на полученной линии.
Затем вновь проводят линию вдоль нити.
Точка пересечения двух линий и будет являться центром тяжести плоского тела.

Еще один способ определения центра тяжести, применяемый на практике, называется метод взвешивания . Этот метод часто применяется для определения центра тяжести крупных машин и изделий – автомобилей, самолетов, колесных тракторов и т. п., которые имеют сложную объемную форму и точечную опору на грунт.
Метод заключается в применении условий равновесия, исходя из того, что сумма моментов всех сил, действующих на неподвижное тело равна нулю.
Практически это осуществляется взвешиванием одной из опор машины (задние или передние колеса устанавливаются на весы), при этом показания весов, по сути, являются реакцией опоры, которая учитывается при составлении уравнения равновесия относительно второй точки опоры (находящейся вне весов).
По известной массе (соответственно – весу) тела, показанию весов в одной из точек опоры, и расстоянию между точками опоры можно определить расстояние от одной из точек опоры до плоскости, в которой расположен центр тяжести.
Чтобы найти подобным образом линию (ось), на которой расположен центр тяжести машины, необходимо произвести два взвешивания по принципу, изложенному выше для метода подвешивания (см. рис. 1а) .

Положение центра тяжести некоторых фигур

Прямоугольник. Так как прямоугольник имеет две оси симметрии, то центр тяжести его площади находится в точке пересечения этих осей, иначе говоря, в точке пересечения диагоналей прямоугольника.

Треугольник. Пусть дан треугольник АBD (см. рисунок 2) .
Разобьем его на элементарные (бесконечно узкие) полоски, параллельные стороне AD . Центр тяжести каждой полоски будет лежать на медиане Bd (т. е. в середине каждой полоски) , следовательно, на этой медиане будет лежать и центр тяжести всей площади треугольника. Разбив треугольник на элементарные полоски, параллельные стороне AB , увидим, что искомый центр тяжести лежит и на медиане aD .
Проделав аналогичное действие с треугольником относительно стороны ВD , получим тот же результат – центр тяжести находится на соответствующей медиане.
Следовательно, центр тяжести всей площади треугольника лежит на точке пересечения его медиан, поскольку эта точка является единственной общей точкой для всех трех медиан данной геометрической фигуры.

Из геометрии известно, что медианы треугольника пересекаются в одной точке и делятся в соотношении 1:2 от основания. Следовательно, центр тяжести треугольника расположен на расстоянии одной трети высоты от каждого основания.

Дуга окружности. Возьмем дугу окружности АВ радиусом R с центральным углом 2α (см. рисунок 3) . Систему координат выберем так, чтобы начало координат было в центре окружности, а ось x делила дугу пополам, тогда y_C = 0 вследствие симметрии дуги относительно оси x . Определим координату центра тяжести x_C .

Разобьем дугу АВ на элементарные части l_i , одна из которых изображена на рисунке. Тогда, согласно сделанным выше выводам,

Дугу l_i вследствие малости примем за отрезок прямой. Из подобия треугольника OD_iC_i и элементарного треугольника S (на рисунке заштрихован) получим:

поскольку RΣΔy_i = AB , а Σl_i = l – длина дуги АВ . Но АВ = 2R sinα , а l = 2Rα , следовательно,

При α = π/2 рад (полуокружность) , x_C = 2R/π .

Круговой сектор. Возьмем сектор радиусом R с центральным углом 2α (см. рисунок 3а) . Проведем оси координат, как показано на рисунке (ось x направлена вдоль оси симметрии сектора), тогда y_C = 0 .

Определим x_C , для чего разобьем сектор на ряд элементарных секторов, каждый из которых из-за малости дуги l_i можно принять за равнобедренный треугольник с высотой R . Тогда центр тяжести каждого элементарного сектора будет находиться на дуге радиуса 2R/3 и задача определения центра тяжести сектора сводится к определению центра тяжести этой дуги.
Очевидно, что

При α = π/2 рад (полукруг) : x_C = 4R/(3π) .

Пример решения задачи на определение центра тяжести

Задача:
Определить положение центра тяжести сечения, составленного из двутавра № 22 и швеллера № 20, как показано на рисунке 4 .

Решение.
Из курса инженерной графики известно, что номер проката соответствует наибольшему габаритному размеру его сечения, выраженного в сантиметрах.

Так как сечение, составленное из двутавра и швеллера, представляет собой фигуру, симметричную относительно оси y , то центр тяжести такого сечения лежит на этой оси, т. е. x_C = 0 .
По справочнику определим площади и координаты центров тяжести двутавра 1 и швеллера 2.

Для двутаврового сечения: А₁ = 15,2 см 2 ; y₁ = 22/2 = 11 см.
Для швеллерного сечения: А₂ = 12 см 2 ; y₂ = 22 + d – z₀ = 22 + 0,32 – 1,25 = 21,07 см ,
где d – толщина стенки швеллера; z₀ – размер, определяющий положение центра тяжести швеллера.

Применим формулу для определения координаты центра тяжести всего сечения:

[spoiler title=”источники:”]

http://www.sites.google.com/site/tehmehprimizt/lekcii/teoreticeskaa-mehanika/statika/centr-tazesti

http://k-a-t.ru/tex_mex/11-statika_center_tj2/

[/spoiler]

На этой странице представлена справочная информация с формулами для вычисления площадей простых фигур (сечений) с указанием положения их центров тяжестей.

Эта страничка будет полезна при расчёте более сложных фигур (составных поперечных сечений): определении положения центра тяжести, а также общей площади.

Центры тяжести

Для всех фигур, положение центра тяжести в статье обозначается буквой – C, это наиболее используемый вариант. Также иногда центр тяжести обозначают буквой – O.

Формулы для расчёта площадей

В сопромате площадь поперечного сечения обозначается буквой – A, однако, в некоторой литературе ты можешь встретить обозначения с буквой – F.

Другую справочную информацию, размещённую на сайте – ssopromat.ru, можешь найти, перейдя по указанной ссылке.

Центр
тяжести дуги окружности

Дуга
имеет ось симметрии. Центр тяжести лежит
на этой оси, т.е.  y_C =
0.

dl  –
элемент дуги,  dl = Rdφ,
 R –
радиус окружности,  x
= Rcosφ,  L
= 2αR,

Следовательно:

 x_C =
R(sinα/α).

Центр
тяжести кругового сектора

Сектор
радиуса  R с
центральным углом  2α имеет
ось симметрии  Ox,
на которой находится центр тяжести. 

Разбиваем
сектор на элементарные секторы, которые
можно считать треугольниками. Центры
тяжести элементарных секторов
располагаются на дуге окружности радиуса
 (2/3)R. 

Центр
тяжести сектора совпадает с центром
тяжести дуги  AB:

Полукруг:

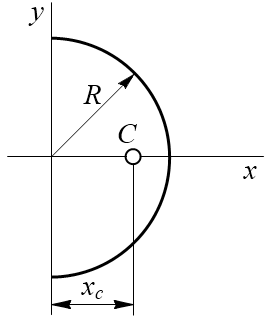
37. Кинематика. Кинематика точки. Способы задания движения точки.

Кинематика –
раздел механики, в котором изучаются
движение материальных тел с геометрической
точки зрения, без учета массы и действующих
на них сил. Способы задания движения
точки: 1) естественный, 2) координатный,
3) векторный.

Кинема́тика
точки  —
раздел кинематики,
изучающий математическое описание движения
материпльных точек.
Основной задачей кинематики является
описание движения при помощи математического
аппарата без выяснения причин, вызывающих
это движение.

Естественный
сп.
указывается траектория точки, закон ее
движения по этой траектории, начало и
направление отсчета дуговой
координаты: s=f(t)
– закон
движения точки. При прямолинейном
движении: х=f(t).

Координатный
сп.
положение точки в пространстве
определяется тремя координатами, изменения
которых определяют закон движения
точки: x=f₁(t),
y=f₂(t),
z=f₃(t).

Если
движение в плоскости, то два уравнения
движения. Уравнения движения описывают
уравнение траектории в параметрической
форме. Исключив из уравнений параметр t,
получаем уравнение траектории в обычном
виде:f(x,y)=0 (для
плоск-ти).

Векторный
сп.
положение точки определяется ее
радиус-вектором , проведенным из
какого-либо центра. Кривая, которая
вычерчивается концом какого-либо
вектора, назыв. годографом этого
вектора. Т.е. траектория – годограф
радиус-вектора.

38.Связь между координатным и векторным, координатным и естественным способами задания движения точки.

СВЯЗЬ
ВЕКТОРНОГО СПОСОБА С КООРДИНАТНЫМ И
ЕСТЕСТВЕННЫМ выражается
соотношениями:

где  –
орт касательной к траектории в данной
точке, направленный в сторону отсчета
расстояний, –
орт нормали к траектории в данной точке,
направленный в сторону центра кривизны
(см. рис. 3).

СВЯЗЬ
КООРДИНАТНОГО СПОСОБА С ЕСТЕСТВЕННЫМ.
Уравнение траектории f(x, y)=z; f₁(x,
z)=y получается из уравнений движения в
координатной форме посредством исключения
времени t. Дополнительным анализом
значений, которые могут принимать
координаты точки, определяется тот
участок кривой ,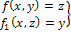
который является траекторией. Например,
если движение точки задано уравнениями:
x=sin t; y=sin²t=x²,
то траекторией точки является тот
участок параболы у=х²,
для которого -1≤x≤+1, 0≤x≤1. Начало и
направление отсчета расстояний выбираются
произвольно, этим в дальнейшем определяется
знак скорости и величина и знак начального
расстояния s₀.

Закон движения
определяется зависимостью:

знак + или –
определяется в зависимости от принятого
направления отсчета расстояний.

39

Скорость
точки –
это кинематическая мера ее движения,
равная производной по времени от
радиус-вектора этой точки в рассматриваемой
системе отсчета. Вектор скорости
направлен по касательной к траектории
точки в сторону движения

Вектор
скорости (v) —
это расстояние, которое тело проходит
в определенном направлении за единицу
времени. Обратите внимание, что
определение вектора
скорости очень
похоже на определение скорости, за
исключением одного важного различия:
скорость тела не указывает направление
движения, а вектор скорости тела указывает
и скорость, и направление движения.
Следовательно, необходимы две переменные,
которые описывают вектор скорости тела:
скорость и направление. Физические
величины, у которых есть значение и
направление, называют векторными
величинами.

Вектор
скорости тела
может время от времени изменяться. Если
или его скорость, или направление
изменяются, скорость тела также меняется.
Постоянный вектор скорости подразумевает
неизменную скорость и неизменное
направление, тогда как термин «постоянная
скорость» подразумевает только неизменное
значение, не принимая во внимание
направление. Термин «вектор скорости»
часто используется попеременно с
термином «скорость». Они оба выражают
расстояние, которое тело проходит в
единицу времени

40

Ускорение
точки –
это мера изменения ее скорости, равная
производной по времени от скорости этой
точки или второй производной от
радиус-вектора точки по времени. Ускорение
характеризует изменение вектора скорости
по величине и направлению и направлено
в сторону вогнутости траектории.

Вектор ускорения

это отношение
изменения скорости к промежутку времени,
за который это изменении произошло.
Определить среднее ускорение можно
формулой:

где  – вектор
ускорения.

Направление
вектора ускорения совпадает с направлением
изменения скорости Δ =  – ₀ (здесь ₀ –
это начальная скорость, то есть скорость,
с которой тело начало ускоряться).

В
момент времени t1 (см. рис 1.8) тело имеет
скорость ₀.
В момент времени t2 тело имеет скорость .
Согласно правилу вычитания векторов
найдём вектор изменения скорости
Δ =  – ₀.
Тогда определить ускорение можно так:

41

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #