Серединный перпендикуляр – определение, свойства и формулы
Общие сведения
Серединным перпендикуляром отрезка называют прямую, которая проходит под прямым углом через среднюю точку, т. е. середину отрезка. Для полного понимания материала следует остановиться на базовых элементах геометрии.
Точка — единица, при помощи которой строятся прямые, отрезки, лучи и фигуры. Прямая — простая фигура в форме бесконечной линии, состоящей из множества точек, лежащих в одной плоскости. Луч — базовая геометрическая фигура в виде бесконечной линии с одной стороны и точки-ограничителя — с другой. Иными словами, луч имеет начало, но не имеет конца. Отрезок — некоторая часть прямой (луча или другого отрезка), ограниченная двумя точками.
Кроме того, в геометрии серединный перпендикуляр встречается в треугольниках. Из определения можно сделать вывод, что им может быть прямая, отрезок и даже луч.
Аксиомы геометрии Евклида
Евклидовой геометрией называется наука о фигурах на плоскости, основанная на аксиомах и теоремах. Аксиома — базовое утверждение, не требующее доказательства. Оно используется для доказательства каких-либо теорем. Математики выделяют пять аксиом:
- Принадлежности.
- Порядка.
- Конгруэнтности.
- Параллельности прямых.
- Непрерывности.
Формулировка первой имеет такой вид: если существует в геометрическом пространстве плоскость, состоящая из множества точек, то через любые из них можно провести только одну прямую. Иными словами, можно взять произвольные две точки и провести через них одну прямую. Чтобы начертить еще одну прямую, следует взять две другие точки.
Следующее утверждение называется аксиомой порядка. Она гласит, что существует точка, которая лежит между двумя другими на прямой. Значение слова “конгруэнтность” не совсем понятно для новичка, однако нужно постепенно привыкать к терминологии. Оно обозначает “равенство”. Третий геометрический факт формулируется таким образом: когда два отрезка или угла конгруэнтны третьему, тогда они равны между собой. Аксиома касается только отрезков и углов.
Чтобы убедиться в ее правильности, нужно разобрать следующий пример: длина первого отрезка составляет 10 см, второго — тоже, а третий равен первому. Необходимо доказать, что они равны между собой. Это делается очень просто:
- Вводятся обозначения: первый — MN, второй — OP и третий — RS.
- Устанавливаются значения по условию: MN = 10 см, ОР = 10 см, а RS = MN.
- Доказательство строится таким образом: MN = RS = 10 (см). Следовательно, отрезки равны, поскольку MN = ОР = RS = 10 (см).
Следует отметить, что данные действия оказались лишними — было потрачено время на понимание простой “истины”. Параллельность прямых является также аксиомой и формулируется таким образом: если существует некоторая прямая на плоскости и точка, не лежащая на ней, то через последнюю можно провести только одну параллельную ей прямую.
И последняя аксиома называется Архимедовой. Ее формулировка имеет такой вид: для произвольных отрезков, лежащих на одной прямой, существует некоторая последовательность базовых элементов (точек), лежащих на одном и другом отрезках, таких, что заданные их части равны между собой. Иными словами, на одной прямой могут быть расположены равные между собой отрезки.
Информация о треугольниках
Треугольником является любая фигура, состоящая из трех вершин (точек) соединенных отрезками (сторонами), причем точки не лежат на одной прямой в одной плоскости. Они классифицируются по такому типу:
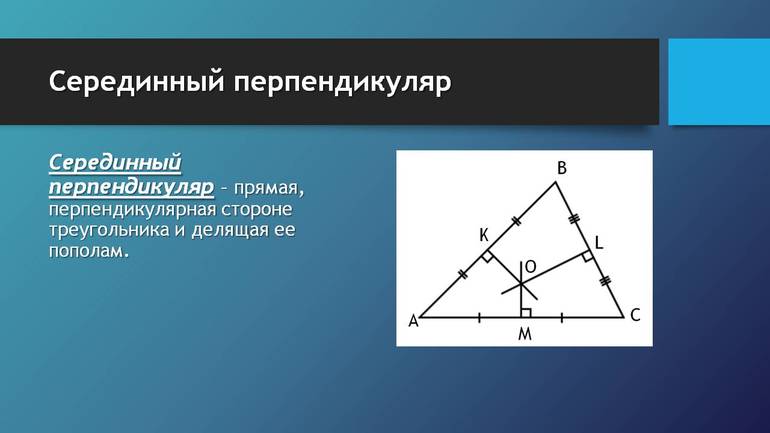
В первом случае фигуры делятся на остроугольные, тупоугольные и прямоугольные. Остроугольным называется треугольник, у которого все углы острые (меньше 90 градусов). У тупоугольного — один угол тупой (> 90), а в прямоугольном — один из углов равен 90 градусам. Следует отметить, что сумма градусных мер углов любого треугольника эквивалентна 180.
Когда стороны у треугольника неравны между собой, тогда его называют разносторонним. При равенстве двух боковых сторон он считается равнобедренным, у которого третья сторона — основание. Если все стороны равны, то значит, фигура является равносторонней или правильной.
У треугольника есть еще и другие параметры. Их называют медианой, биссектрисой и высотой. Первый параметр является отрезком, который проводится из любой вершины на среднюю точку стороны. Высота — часть прямой, которая проводится из произвольной вершины и перпендикулярна противоположной стороне. Биссектрисой называется прямая, делящая угол на две равные части.
Медиана, высота и биссектриса, проведенные из вершины к основанию, совпадают и эквивалентны серединному перпендикуляру в треугольниках равнобедренного и равностороннего типов. Это очень важно при решении задач. Еще одним признаком, по которому выполняется классификация — подобность треугольников. У них могут быть равными только углы и некоторые стороны. Они отличаются между собой по определенному параметру, который называется коэффициентом подобия. Последний влияет только на размерность сторон. Говорят, что фигуры подобны по определенному признаку (их всего три).
Основные теоремы
Теорема — гипотеза (предположение), которую нужно доказать. Они применяются для оптимизации расчетов и вычисления отдельных параметров заданной фигуры. Кроме того, существуют следствия, полученные при доказательстве таких научных предположений. Эти аспекты упрощают и автоматизируют вычисления. Например, при вычислении площади треугольника нет необходимости выводить формулу, достаточно воспользоваться уже готовой.
Математики выделяют всего три теоремы о СП, которые могут значительно упростить расчеты. К ним можно отнести следующие:
- Прямая.
- Обратная.
- Пересечение в треугольнике.
Первая теорема называется прямой о СП. Она показывает, каким свойством обладают точки серединного перпендикуляра. Ее формулировка следующая: произвольная точка, которая взятая на перпендикуляре, удалена на равные расстояния от конечных точек отрезка, ограничивающих его на плоскости.
Для доказательства следует рассмотреть два прямоугольных треугольника с общей вершиной (искомая точка), общей стороной — катетом и равными катетами (по определению). Фигуры равны по одному из признаков равенства треугольников. Следовательно, их гипотенузы (стороны, равенство которых нужно доказать), равны между собой. Первая теорема доказана.
Следующая теорема — обратная: если точка удалена на равные расстояния от концов отрезка, то значит, она лежит на СП. В этом случае следует рассматривать равнобедренный треугольник, вершиной которого она является. Удалена точка на одинаковые расстояния от вершин основания по условию. Следовательно, этот факт доказывает, что полученный треугольник является равнобедренным, а в нем медиана, проведенная к основанию, является биссектрисой и высотой. Значит, она лежит на серединном перпендикуляре. Утверждение доказано.
Следующую теорему нет необходимости доказывать, поскольку известно, что в равнобедренном и равностороннем треугольниках высоты (медианы и биссектрисы) имеют общую точку пересечения. Они являются также и СП. Следовательно, это утверждение справедливо для них.
Важные свойства
Иногда трех теорем недостаточно для решения какой-либо сложной задачи. В этом случае необходимо знать еще и некоторые свойства СП:
- Центр описанной окружности вокруг треугольника соответствует точке их пересечения.
- Точка, взятая на СП, равноудалена от конечных точек отрезка и образует равнобедренный или равносторонний треугольник.
- В треугольниках равнобедренного и равностороннего типов им является высота, медиана и биссектриса.
В первом случае все зависит от типа треугольника. Если он является остроугольным, то центр лежит внутри него. Для тупоугольного — во внешнем пространстве, а в прямоугольном — на середине гипотенузы.
Следует отметить, что есть формулы для его расчета. Если предположить, что существует некоторый произвольный треугольник со сторонами а, b и с. Кроме того, для них выполняется условие a >= b >= c. Исходя из полученных данных, можно записать формулы перпендикуляров (Р), проведенных к определенной стороне:
- а: Pa = (2 * а * S) / (a^2 + b^2 – c^2).
- b: Pb = (2 * b * S) / (a^2 + b^2 – c^2).
- c: Pc = (2 * c * S) / (a^2 – b^2 + c^2).
Иными словами, Р является отношением удвоенного произведения стороны на площадь треугольника к сумме квадратов смежных сторон без квадрата противоположной. Кроме того, справедливы неравенства: Pa >= Pb и Pс >= Pb. Стороны — известные параметры, а вот площадь находится по некоторым соотношениям, которые выглядят следующим образом:
- Основание и высоту, проведенную к нему: S = (1/2) * a * Ha = (1/2) * b * Hb = (1/2) * c * Hc.
- Через радиус вписанной окружности: S = (1/2) * r * (a + b + c).
- Формулу Герона через полупериметр (р) и без него: S = [p * (p – a) * (p – b) * (p – c)]^(1/2) и S = 1/4 * [(a + b + c) * (b + c – a) * (а + c – b) * (a + b – c)]^(1/2).
В основном по таким соотношениям и нужно определить площадь. Полупериметр вычисляется таким образом: р = (а + b + с) / 2.
Бывают задачи, в которых необходимо просто подставить значения в формулу. Они называются простейшими. Однако встречаются и сложные. К ним относятся все виды без некоторых промежуточных параметров фигуры.
Пример решения задачи
В интернете попадаются примеры решения простых задач, а сложные приходится решать самостоятельно, просить помощи у кого-нибудь или покупать на сайтах готовое решение. Для примера нужно решить задание с такими данными:
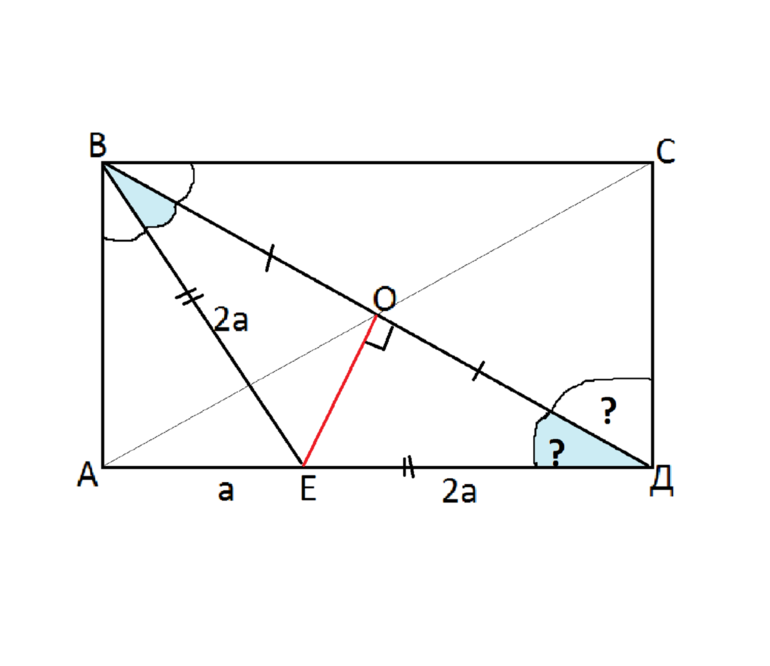
- Прямоугольник, изображенный на рисунке 1 с диагональю равной d.
- Серединный перпендикуляр, проведенный к диагонали прямоугольника.
- Точка Е делит сторону на отрезки а и 2а.
Нужно найти: углы, указанные на рисунке, стороны и ОЕ. Кроме того, дополнительные данные можно узнать из чертежа, который используется для решения задачи (рис. 1). К любому заданию нужно делать графическое представление, поскольку оно позволяет избежать ошибок при вычислении
Рисунок 1. Чертеж для решения задачи.
Числовых значений нет, тогда необходимо решать в общем виде. Углы можно найти по такому алгоритму:
- Нужно рассмотреть треугольник ВДЕ. Он является равнобедренным, поскольку ОЕ — СП, а диагональ — отрезок. Следовательно, ВЕ = ДЕ = 2а.
- Необходимо найти угол ЕВО. Сделать это проблемно. Рекомендуется обратить внимание на треугольник АВЕ.
- При помощи тригонометрической функции синуса можно вычислить значение угла АBE: sin(АBE) = a/2а = 0,5. Следовательно, arcsin(0,5) = 30 (градусов).
- Угол СВЕ вычисляется следующим образом: 90 – 30 = 60 (градусов).
- Следовательно, искомый угол равен 30, поскольку 90 – 30 – 30 = 30.
- В равнобедренном треугольнике углы при основании равны между собой: ЕДО = ЕВО = 30 (градусов).
Для нахождения сторон нужно составить уравнение в общем виде, обозначив неизвестную величину АВ литерой “х”. Рассмотрев прямоугольный треугольник АВЕ, по теореме Пифагора можно вычислить АВ: x = [4a^2 + a^2]^(1/2) = a * [5]^(1/2). Следовательно, АВ = a * [5]^(1/2) и ВС = 3а. ОЕ находится по формуле: ОЕ = (2 * 2 * а * S) / (8 * a^2 – d^2). Можно править соотношение таким образом через прямоугольный треугольник ДОЕ: ОЕ = [4 * a^2 – (d^2) / 4]^(1/2).
Таким образом, нахождение серединного перпендикуляра позволяет значительно уменьшить объемы вычислений. Однако для этого нужно знать не только основные теоремы, но и его свойства.
Серединный перпендикуляр
Что такое серединный перпендикуляр к отрезку? Что можно сказать о пересечении серединных перпендикуляров к сторонам треугольника? К сторонам многоугольника?
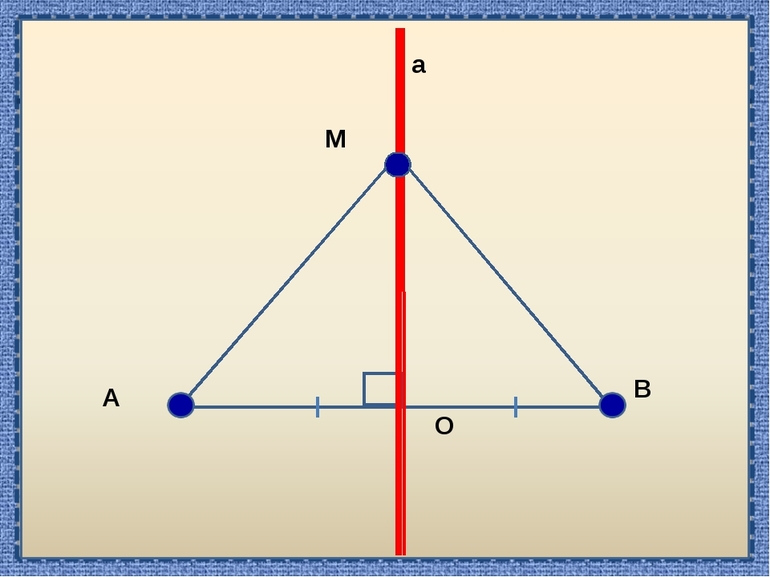
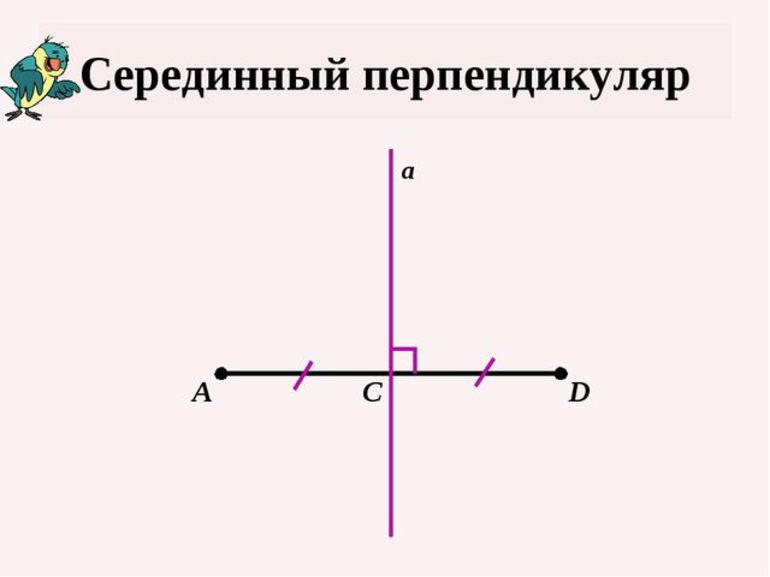
Серединный перпендикуляр к отрезку — это прямая, перпендикулярная данному отрезку и проходящая через его середину.
m — серединный перпендикуляр к отрезку AB, если
точка C — середина отрезка AB,
Чтобы построить серединный перпендикуляр к данному отрезку с помощью угольника, нужно:
1) найти середину отрезка;
2) провести через эту точку прямую, перпендикулярную данному отрезку (для этого угольник прикладываем прямым углом к середине отрезка так, чтобы она сторона угольника проходила через отрезок, а через другую сторону проводим прямую):
Свойства серединного перпендикуляра.
1) Геометрическое место точек, равноудаленных от двух данных точек, есть серединный перпендикуляр к отрезку, соединяющему эти точки.
Например, прямая m — геометрическое место точек, равноудаленных от точек A и B (рисунок 1).
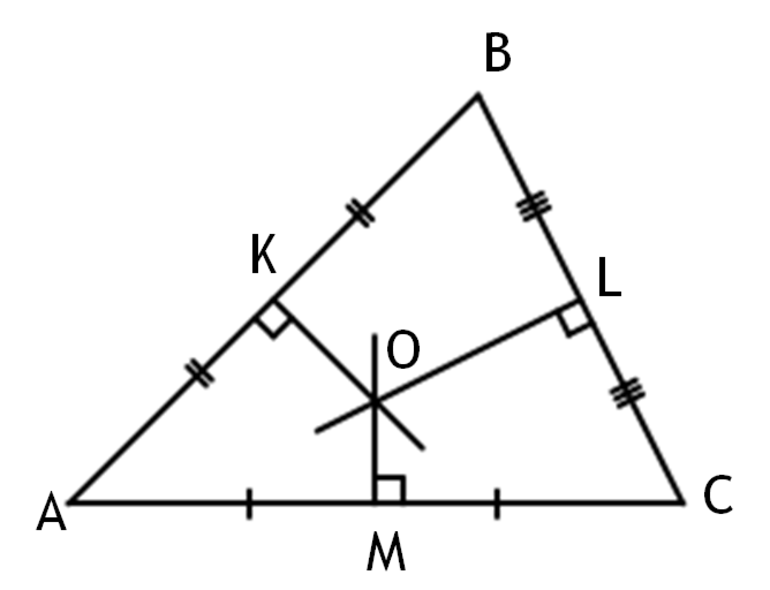
2) Серединные перпендикуляры к сторонам треугольника пересекаются в одной точке. Эта точка является центром описанной около треугольника окружности.
3) Если около многоугольника можно описать окружность, то центр этой описанной окружности является точкой пересечения серединных перпендикуляров к сторонам многоугольника.
Серединные перпендикуляры к сторонам треугольника
Теорема 1. Серединные перпендикуляры к сторонам треугольника пересекаются в одной точке.

Доказательство. Пусть ( small m ) и ( small n ) серединные перпендикуляры сторон ( small AB ) и ( small BC ) треугольника ( small ABC, ) соответственно (Рис.1). Покажем, сначала, что они пересекаются. Предположим, что ( small m ) и ( small n ) параллельны. Тогда прямая ( small AB, ) которая перпендикулярна к прямой ( small m, ) перпендикулярна и к прямой ( small n.) Получается, что через точку ( small B ) проходят две прямые ( small AB ) и ( small BC, ) которые перпендикулярны к прямой ( small n. ) Но это невозможно. Следовательно прямые ( small m ) и ( small n ) пересекаются в некоторой точке ( small O. )
Поскольку точка ( small O ) находится на серединном перпендикуляре к отрезку ( small AB ,) то равноудалена от точек ( small A ) и ( small B. ) Тогда ( small AO=BO. ) Аналогично ( small BO=CO. ) Следовательно ( small AO=CO, ) то есть точка ( small O ) находится на серединном перпендикуляре отрезка ( small AC. ) Получили, что все три серединных перпендикуляра ( small m, n, p ) пересекаются в точке ( small O. )
[spoiler title=”источники:”]
http://matworld.ru/geometry/seredinny-perpendikulyar-treugolnika.php
[/spoiler]
Обновлено: 18.05.2023
Определение и формулы для расчета серединного перпендикуляра треугольника
Серединный перпендикуляр треугольника – это перпендикуляр, проведенный к середине стороны треугольника.

Три срединных перпендикуляра треугольника пересекаются в одной точке, являющейся центром описанной окружности.
Точка пересечения серединных перпендикуляров в остроугольном треугольнике лежит внутри треугольника; в тупоугольном – вне треугольника; в прямоугольном – на середине гипотенузы.
Свойства срединных перпендикуляров треугольника:
- Любая точка серединного перпендикуляра к стороне равноудалена от концов этой стороны.
- Любая точка, равноудаленная от концов стороны, лежит на серединном перпендикуляре к ней.
- Точка пересечения серединных перпендикуляров, проведенных к сторонам треугольника, является центром окружности, описанной около этого треугольника.
Примеры решения задач

![]()

![]()
По свойству серединного перпендикуляра точка равноудалена от концов стороны , т.е. . Из прямоугольного треугольника по теореме Пифагора найдем :
![]()

Треугольник – это геометрическая фигура, которая состоит из трёх точек, не лежащих на одной прямой (вершин треугольника) и трёх отрезков с концами в этих точках (сторон треугольника).
Углами (внутренними углами) треугольника называются три угла, каждый из которых образован тремя лучами, выходящими из вершин треугольника и проходящими через две другие вершины.
Внешним углом треугольника называется угол, смежный внутреннему углы треугольника.
Сумма углов треугольника равна 180°:

Внешний угол равен сумме двух внутренних углов, не смежных с ним, и больше любого внутреннего, с ним не смежного:

Длина каждой стороны треугольника больше разности и меньше суммы длин двух других сторон:

В треугольнике против большего угла лежит большая сторона, против большей стороны лежит больший угол:

Средней линией треугольника называется отрезок, который соединяет середины двух его сторон.
Средняя линия треугольника параллельна одной из его сторон и равна её половине:

Треугольники называются равными, если у них соответствующие стороны равны и соответствующие углы равны:

У равных треугольников все соответствующие элементы равны (стороны, углы, высоты, медианы, биссектрисы, средние линии и т.д.)
В равных треугольниках против равных сторон лежат равные углы, а против равных углов – равные стороны.
Первый признак равенства треугольников.
Если две стороны и угол между ними одного треугольника равны соответственно двум сторонам и углу между ними другого треугольника, то такие треугольники равны:

Второй признак равенства треугольников.
Если сторона и прилежащие к ней углы одного треугольника равны соответственно стороне и прилежащим к ней углам другого треугольника, то такие треугольники равны:

Третий признак равенства треугольников.
Если три стороны одного треугольника равны соответственно трём сторонам другого треугольника, то такие треугольники равны:

Подобными называются треугольники, у которых соответствующие стороны пропорциональны.
Коэффициент пропорциональности называется коэффициентом подобия:

Два треугольника подобны, если:
- Два угла одного треугольника равны двум углам другого треугольника.
- Две стороны одного треугольника пропорциональны двум сторонам другого, и углы, образованные этими сторонами, равны.
- Стороны одного треугольника пропорциональны сторонам другого.
У подобных треугольников соответствующие углы равны, а соответствующие отрезки пропорциональны:

Отношение периметров подобных треугольников равно коэффициенту подобия.
Отношение площадей подобных треугольников равно квадрату коэффициента подобия.
Прямая, пересекающая две стороны треугольника, и параллельная третьей, отсекает треугольник, подобный данному:

Три средние линии треугольника делят его на четыре равных треугольника, подобные данному, с коэффициентом подобия ½:

Медианой треугольника называется отрезок, который соединяет вершину треугольника с серединой противолежащей стороны.
Три медианы треугольника пересекаются в одной точке, делящей медианы в отношении 2:1, считая от вершины:

- Медиана делит треугольник на два равновеликих (с равными площадями) треугольника.
- Три медианы треугольника делят его на шесть равновеликих треугольников:

Длины медиан, проведённых к соответствующим сторонам треугольника, равны:

Биссектрисой треугольника, проведённой из данной вершины, называется отрезок биссектрисы угла треугольника, соединяющий эту вершину с точкой на противолежащей стороне.
Биссектрисы внутренних углов треугольника пересекаются в одной точке, находящейся внутри треугольника, равноудалённой от трёх его сторон, которая является центром окружности, вписанной в данный треугольник.
Биссектриса внутреннего угла треугольника делит противолежащую углу сторону на отрезки, пропорциональные двум другим сторонам:

Длина биссектрисы угла А :

Биссектрисы внутреннего и смежного с ним внешнего угла перпендикулярны.
Биссектриса внешнего угла треугольника делит (внешне) противолежащую сторону на отрезки, пропорциональные двум другим сторонам.
BL – биссектриса угла В ;
ВЕ – биссектриса внешнего угла СВК :

Высотой треугольника называется перпендикуляр, опущенный из любой вершины треугольника на противолежащую сторону или на продолжение стороны.
Высоты треугольника пересекаются в одной точке, которая называется ортоцентром треугольника.
Высоты треугольника обратно пропорциональны его сторонам:

Длина высоты, проведённой к стороне а :

Серединный перпендикуляр – это прямая, которая проходит через середину стороны треугольника перпендикулярно к ней.
Три серединных перпендикуляра треугольника пересекаются в одной точке, которая является центром окружности, описанной около данного треугольника.
Точка пересечения биссектрисы угла треугольника с серединным перпендикуляром противолежащей стороны лежит на окружности, описанной около данного треугольника.
Окружность называется вписанной в треугольник, если она касается всех его сторон.
Точки касания вписанной окружности сторон треугольника отсекают от его сторон три пары равных между собой отрезков:

Радиус вписанной в треугольник окружности – расстояние от её центра до сторон треугольника:

Окружность называется описанной около треугольника, если она проходит через все его вершины.
Радиус описанной окружности:

Треугольник называется равнобедренным, если у него две стороны равны. Равные стороны называют боковыми сторонами, а третью – основанием равнобедренного треугольника.
В равнобедренном треугольнике углы при основании равны: ∠ A = ∠ C.
В равнобедренном треугольнике медиана, проведённая к основанию, является и биссектрисой, и высотой: BL – медиана, биссектриса, высота.
Основные формулы для равнобедренного треугольника:

Треугольник у которого все стороны равны называется равносторонним или правильным треугольником.
Центры вписанной и описанной окружностей правильного треугольника совпадают.
Все углы равностороннего треугольника равны:
Каждая медиана равностороннего треугольника совпадает с биссектрисой и высотой, которые проведены из той же вершины:

Основные соотношения для элементов равностороннего треугольника

Треугольник называется прямоугольным, если у него есть прямой угол.
Стороны, прилежащие к прямому углу, называются катетами, противолежащая прямому углу – гипотенузой.
Прямоугольные треугольники равны если у них равны:
- два катета;
- катет и гипотенуза;
- катет и прилежащий острый угол;
- катет и противолежащий острый угол;
- гипотенуза и острый угол.
- одному острому углу;
- из пропорциональности двух катетов;
- из пропорциональности катета и гипотенузы.

Косинусом острого угла прямоугольного треугольника называется отношение прилежащего катета к гипотенузе:

Синусом острого угла прямоугольного треугольника называется отношение противолежащего катета к гипотенузе:

Тангенсом острого угла прямоугольного треугольника называется отношение противолежащего катета к прилежащему:

Котангенсом острого угла прямоугольного треугольника называется отношение прилежащего катета к противолежащему:

Катет прямоугольного треугольника есть среднее пропорциональное между гипотенузой и проекцией этого катета на гипотенузу:

Высота прямоугольного треугольника, проведённая из вершины прямого угла, есть среднее пропорциональное между проекциями катетов на гипотенузу:

Высота прямоугольного треугольника, проведённая из вершины прямого угла, может быть определена через катеты и их проекции на гипотенузу:

Медиана, проведённая из вершины прямого угла, равна половине гипотенузы:

Высота прямоугольного треугольника, проведённая из вершины прямого угла, делит данный треугольник на два треугольника, подобные данному:

Площадь прямоугольного треугольника можно определить

через катеты:

через катет и острый угол:

через гипотенузу и острый угол:
Центр описанной окружности совпадает с серединой гипотенузы.
Радиус описанной окружности:

Радиус вписанной окружности:

Три окружности, каждая из которых касается одной стороны (снаружи) и продолжений двух других сторон треугольника, называются вневписанными.
Центр вневписанной окружности лежит не пересечении биссектрисы одного внутреннего угла и биссектрис внешних углов при двух других вершинах.
Так точка О1 , центр одной из вневписанных окружностей Δ ABC , лежит на пересечении биссектрисы ∠ A треугольника ABC и биссектрис BО1 и C О1 внешних углов Δ ABC при вершинах B и C .
Таким образом, шесть биссектрис треугольника – три внутренние и три внешние – пересекаются по три в четырёх точках – центрах вписанной и трёх вневписанных окружностей.
Δ ABC является ортоцентричным в Δ О1О2О3 (точки A , B и C – основания высот в Δ О1О2О3 ).
В Δ ABC углы равны 180°–2 О1 , 180°–2 О2 , 180°–2 О3 .
Радиус окружности, описанной около Δ О1О2О3 , равен 2 R , где R – радиус окружности, описанной около Δ ABC .
Δ ABC имеет наименьший периметр среди всех треугольников, вписанных в Δ О1О2О3 .
Если ra , rb , rс – радиусы вневписанных окружностей в Δ ABC , то в Δ ABC верно:

для r –

для R –

для S –

для самих ra , rb , rс –
Теорема косинусов. Квадрат любой стороны треугольника равен сумме квадратов двух других сторон без удвоенного произведения этих сторон на косинус угла между ними:


- если c 2 > a 2 +b 2 , то угол γ – тупой ( cos γ
- если c 2 2 +b 2 , то угол γ – острый ( cos γ > 0 );
- если c 2 = a 2 +b 2 , то угол γ – прямой ( cos γ = 0 ).

Теорема синусов. Стороны треугольника пропорциональны синусам противолежащих углов. Коэффициент пропорциональности равен диаметру описанной окружности:
Треугольники: равные, равнобедренные. Первый, второй и третий признаки равенства треугольников. Перпендикуляр, высота, медиана, биссектриса, основание, вершина, боковая сторона. Свойства и признаки равнобедренного треугольника. Серединный перпендикуляр, геометрическое место точек, первая замечательная точка. Подробные доказательства теорем.

Треугольник — одна из самых замечательных и самых важных фигур в геометрии. Все знают, как он выглядит. Но что же такое треугольник? Допустим, что треугольник — это замкнутая ломаная из трех звеньев. Можно представить себе треугольник, сделанный из проволоки. Но известно, что у него есть площадь. Поэтому треугольник — это трехзвенная замкнутая ломаная вместе с частью плоскости, которую она ограничивает. Представьте себе треугольник, сделанный из фанеры или вырезанный из картона.
Очень важным моментом при решении геометрических задач является нахождение равных треугольников. Очевидно, что если у двух треугольников все стороны и углы окажутся соответственно равными, то и треугольники будут равны. На практике равные треугольники определяют, прикладывая их друг к другу. Если треугольники совпадут при наложении, значит, они равны. Этот способ и позволяет дать определение равных треугольников.

Треугольник — это трехзвенная замкнутая ломаная вместе с частью плоскости, которую она ограничивает. Сумма длин всех трех сторон треугольника называется периметром. Треугольники называются равными, если совпадают при наложении. Если равные треугольники наложить так, что они совпадут, то окажется, что в равных треугольниках против равных сторон лежат равные углы, а против равных углов лежат равные стороны.
Первый признак равенства треугольников. Если две стороны и угол между ними одного треугольника соответственно равны двум сторонам и углу между ними другого треугольника, то такие треугольники равны. Действительно, если наложить треугольники друг на друга равными углами, то совпадут и равные стороны. Значит, совпадут и оставшиеся две вершины.
Второй признак равенства треугольников. Если сторона и два прилежащих к ней угла одного треугольника соответственно равны стороне и двум прилежащим к ней углам другого треугольника, то такие треугольники равны.
Если наложить треугольники друг на друга равными сторонами, то совпадут углы, прилежащие к этим сторонам. Значит, совпадут и третьи вершины.
Перпендикуляром, опущенным из данной точки на данную прямую, называется отрезок прямой, перпендикулярной данной, проходящей через данную точку, с концами в данной точке и в точке пересечения с данной прямой. Точка пересечения называется основанием перпендикуляра.
Высотой треугольника называется перпендикуляр, опущенный из вершины треугольника на противоположную сторону или ее продолжение.
Медианой треугольника называется отрезок, соединяющий вершину треугольника с серединой противоположной стороны.
Биссектрисой треугольника называется отрезок биссектрисы угла треугольника, заключенный между вершиной и точкой пересечения биссектрисы угла и стороны треугольника.
Свойства равнобедренного треугольника. 1. В равнобедренном треугольнике углы при основании равны. 2. Биссектриса равнобедренного треугольника, проведенная из вершины к основанию, является высотой и медианой.
Признак равнобедренного треугольника (по двум углам). Если в треугольнике два угла равны, то он равнобедренный.
Есть еще три признака равнобедренного треугольника. Треугольник является равнобедренным, если:
- высота треугольника является и медианой;
- высота треугольника является и биссектрисой;
- медиана треугольника является и биссектрисой (доказывается продлением медианы на ее длину).
Третий признак равенства треугольников. Если три стороны одного треугольника соответственно равны трем сторонам другого треугольника, то такие треугольники равны.
Серединным перпендикуляром к отрезку называется прямая, перпендикулярная этому отрезку и проходящая через его середину.
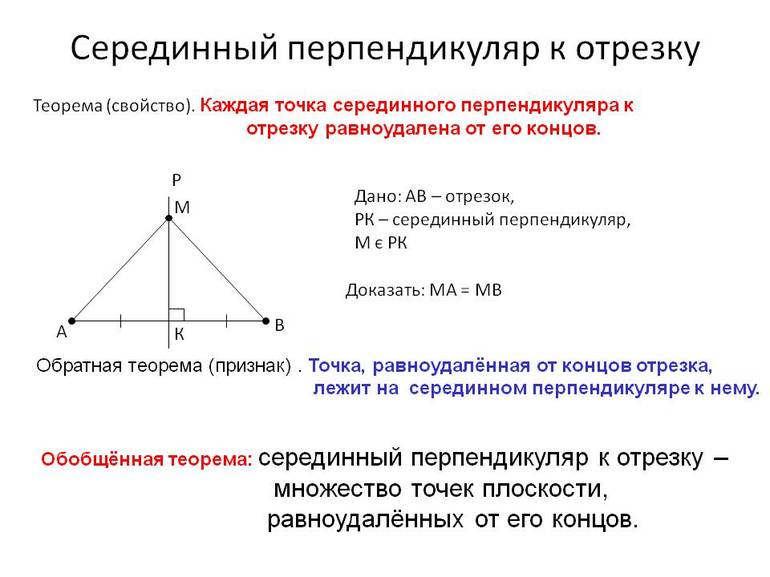
Свойство точек серединного перпендикуляра. Любая точка серединного перпендикуляра равноудалена от концов отрезка. Если точка равноудалена от концов отрезка, то она лежит на серединном перпендикуляре к этому отрезку.
Геометрическое место точек (ГМТ) — это множество всех точек плоскости, обладающих общим свойством. Например, все точки серединного перпендикуляра равноудалены от концов отрезка, и все точки плоскости, равноудаленные от концов отрезка, лежат на серединном перпендикуляре.
Первая замечательная точка. Все три серединных перпендикуляра к сторонам треугольника пересекаются в одной точке — центре описанной окружности.
Возьмем прямую и точку А, не лежащую на этой прямой. Соединим точку А с точкой Н, лежащей на прямой (Рис.1).

Отрезок АН называется перпендикуляром, проведенным из точки А к прямой , если прямые АН и перпендикулярны.
Теорема
Из точки, не лежащей на прямой, можно провести перпендикуляр к этой прямой, и притом только один.
Доказательство:
1. Существование перпендикуляра.
Пусть точка А не лежит на прямой ВС. Проведем луч ВА. Затем от луча ВС отложим угол СВD, равный углу АВС. На луче ВD отложим отрезок ВК, равный отрезку ВА (Рис.2).

Проведем прямую АК, пусть Н – точка пересечения прямых ВС и АК (Рис.3).

АВН = КВН по первому признаку равенства треугольников: ВН – общая сторона, ВА = ВК, АВН =КBН (по построению), ВНА =ВНD. Но ВНА и ВНD – смежные углы, тогда по свойству смежных углов ВНА +ВНD = 180 0 , следовательно, каждый из смежных улов прямой, т.е. ВНА =ВНD = 90 0 , а значит АНВС.
2. Единственность перпендикуляра.

Предположим, что через точку А можно провести еще один перпендикуляр АН1 к прямой ВС, тогда получим, что две прямые АН и АН1, перпендикулярные к прямой ВС пересекаются в точке А (Рис.4). Но по свойству перпендикулярных прямых, прямые АН и АН1 пересекаться не могут, значит, наше предположение неверно и через точку А можно провести только один перпендикуляр к прямой ВС. Теорема доказана.
Проведение перпендикуляра из точки к прямой
Для проведения перпендикуляра из точки к прямой, используют чертежный угольник (Рис.5). Чертежный угольник прикладывают так, чтобы одна из его сторон, образующих прямой угол угольника, располагалась вдоль прямой, к которой нужно провести перпендикуляр. Вдоль второй стороны, образующей прямой угол угольника, проводим прямую так, чтобы она проходила через точку, из которой нужно провести перпендикуляр к прямой. Отрезок, соединяющий точку на прямой, к которой нужно провести перпендикуляр, и точку, из которой нужно провести перпендикуляр, и есть перпендикуляр проведенный из данной точки к данной прямой. На Рис.5 АН.
В геометрии одна задача может скрывать в себе множество подзадач, требующих от решающего их человека наличия большого количества знаний. Так для операций с треугольниками, нужно знать о соотношениях между медианами, биссектрисами и сторонами, уметь разными способами вычислять площадь фигур, а также находить перпендикуляр.

- Как найти перпендикуляр в треугольнике
- Как провести перпендикуляр
- Как найти точку пересечения высот треугольника
Обратите внимание на то, что перпендикуляр в треугольнике необязательно должен лежать внутри фигуры. Высота, опущенная на основание, может оказаться и на продолжении стороны, как это происходит в том случае, если один из углов больше девяноста градусов, или совпадать со стороной, если треугольник прямоугольный.
Воспользуйтесь формулой для вычисления высоты треугольника, если задача содержит все требуемые для этого данные. Для нахождения перпендикуляра составьте дробь, в числителе которой удвоенный квадратный корень из следующего произведения: р*(р-а)(р-в)(р-с), где а, в и с – стороны треугольника, а р – его полупериметр. В знаменателе дроби должна стоять длина того основания, на которое опущен перпендикуляр.
Найдите высоту треугольника, воспользовавшись формулой для вычисления площади этой фигуры: для этого достаточно удвоенную площадь поделить на длину основания. Для нахождения площади используйте другие формулы: например, найти эту величину можно через полупроизведение двух сторон треугольника на синус угла между ними.
Запомните основное соотношение между высотами треугольника: оно обратно пропорционально отношению оснований. Также выучите стандартные формулы, позволяющие быстро найти перпендикуляр в равностороннем и равнобедренном треугольнике. В первом случае высота являет собой произведение стороны треугольника на синус угла в 60 градусов (как следствие формулы для вычисления площади), во втором – удвоенному корню из разности квадрата двойной длины боковой стороны и квадрата основания.
Посчитайте перпендикуляр треугольника, введя данные в графы онлайн-калькулятора. Для этого вам необходимо знать длины сторон данной фигуры, так как расчет проводится по первой указанной выше формуле, использующей полупериметр.
Читайте также:
- Подготовительная группа по физкультуре в школе нормативные документы как оценивается
- Школа россии проект говорите правильно 4 класс русский язык
- Чему учил христос кратко
- Общеобразовательная политехническая трудовая средняя школа с производственной деятельностью
- Как сделать пенек своими руками для детского сада
Подготовка к профильному уровню единого государственного экзамена по математике. Полезные материалы по планиметрии, видеоразборы задач и подборка заданий прошлых лет.
Полезные материалы
Подборки видео
- Все ролики с заданием 16
- Все ролики по планиметрии
- Мини-курс “Вписанные углы”
Как прокачать геометрию
Если с планиметрией у вас всё совсем плохо, а нужно ее «затащить», и вы готовы потратить на это значительное время, то есть хорошая книжка — Гордин. Планиметрия. Работать с ней нужно так. По каждой теме:
- читаете теорию (обычно, пара абзацев);
- изучаете разобранные примеры;
- пробуете решать последние 3-5 задач «второго» уровня;
- если они получились, то переходите к следующей теме («третий» уровень смотреть необязательно);
- если они не решаются, то пробуете решить задачи из начала «второго» уровня;
- если получается, то решаете все задачи «второго» уровня (если их много, то можно идти через одну-две);
- если почти все получается, то переходите к следующей теме;
- если многие задачи непонятно как решать, то отрешиваете весь «первый» уровнь (там совсем простые одноходовые задачи, но решение таких задач позволит вам узнать основные идеи решения задач по этой теме).
Важно! Читать решения в конце книжки можно только в двух случаях. Либо вы решили задачу и хотите узнать авторское решение, либо вы долго пытались и у вас совсем нет никаких идей. Долго — это подумать над задачей минимум полчаса, отложить, вернуться через день-два, подумать еще минимум полчаса. И так 3-4 раза, параллельно отрешивая простые задачи на ту же тему. Если вы будете смотреть решение задачи сразу, не пытаясь ее решать, толку от этого не будет.
Всё про прямоугольный треугольник
Теорема Менелая
Замечательные точки треугольника
Теоремы синусов и косинусов
Формула Герона
Как найти длину биссектрисы, медианы и высоты
Видеоразборы задач
Две окружности касаются внешним образом в точке $K$. Прямая $AB$ касается первой окружности в точке $A$, а второй — в точке $B$. Прямая $BK$ пересекает первую окружность в точке $D$, прямая $AK$ пересекает вторую окружность в точке $C$.
а) Докажите, что прямые $AD$ и $BC$ параллельны.
б) Найдите площадь треугольника $AKB$, если известно, что радиусы окружностей равны 4 и 1.
Окружность высекает на всех сторонах трапеции ABCD равные отрезки.
а) Докажите, биссектрисы всех углов трапеции пересекаются в одной точке.
б) Пусть окружность пересекает боковую сторону $AB$ в точках $K$ и $L$ так, что $AK = 23$, $KL = 4$ и $LB = 2$. Найдите высоту трапеции.
В выпуклом четырёхугольнике $ABCD$ известны стороны и диагональ: $AB = 3$, $BC = CD = 5$, $AD = 8$, $AC = 7$.
а) Докажите, что вокруг этого четырёхугольника можно описать окружность.
б) Найдите $BD$.
В треугольнике $ABC$ угол $B$ тупой, $H$ — точка пересечения высот, угол $AHC$ равен $60^{circ}$.
а) Докажите, что угол $ABC$ равен $120^{circ}$.
б) Найдите $BH$, если $AB = 7$, $BC = 8$.
Точка $M$ — середина гипотенузы $AB$ треугольника $ABC$. Серединный перпендикуляр к гипотенузе пересекает катет $BC$ в точке $N$.
а) Докажите, что $angle CAN = angle CMN$.
б) Найдите отношение радиусов окружностей, описанных около треугольников $ANB$ и $CBM$, если $mathrm{tg} angle BAC = dfrac43$.
В треугольнике $ABC$ точки $A_1$, $B_1$ и $C_1$ — середины сторон $BC$, $AC$ и $AB$ соответственно, $AH$ — высота, $angle BAC = 60^{circ}$, $angle BCA = 45^{circ}$.
а) Докажите, что точки $A_1$, $B_1$, $C_1$ и $H$ лежат на одной окружности.
б) Найдите $A_1H$, если $BC = 2 sqrt3$.
Квадрат $ABCD$ вписан в окружность. Хорда $CE$ пересекает его диагональ $BD$ в точке $K$.
а) Докажите, что $CK cdot CE = AB cdot CD$.
б) Найдите отношение $CK$ и $KE$, если $angle ECD = 15^{circ}$.
В треугольнике $ABC$ проведены высоты $AK$ и $CM$. На них из точек $M$ и $K$ опущены перпендикуляры $ME$ и $KH$ соответственно.
а) Докажите, что прямые $EH$ и $AC$ параллельны;
б) Найдите отношение $EH : AC$, если угол $ABC$ равен $30^{circ}$.
Подборка задач
- Точки $M$ и $N$ — середины соответственно боковых сторон $AB$ и $CD$ трапеции $ABCD$. Окружность проходящая через точки $B$ и $C$ пересекает отрезки $MB$ и $CN$ в точках $P$ и $Q$ соответственно.
а) Докажите, что $M$, $P$, $Q$ и $N$ лежат на одной окружности.
б) Найдите длину отрезка $QN$. Если $BC=4{,}5$, $AD=21{,}5$, $AB=26$, $CD=25$, а угол $CPD$ — прямой. (ЕГЭ-2019, досрочная волна) - В треугольнике $ABC$ угол $B$ тупой, $H$ — точка пересечения высот, угол $AHC$ равен $60^{circ}$.
а) Докажите, что угол $ABC$ равен $120^{circ}$.
б) Найдите $BH$, если $AB = 7$, $BC = 8$. (ЕГЭ-2018, досрочная волна) - Точка $O$ — центр окружности, описанной около остроугольного треугольника $ABC$, а $BH$ — высота этого треугольника.
а) Докажите, что углы $ABH$ и $CBO$ равны.
б) Найдите $BH$, если $AB = 16$, $BC = 18$, $BH = BO$. (ЕГЭ-2018, основная волна, резервный день) - В выпуклом четырёхугольнике $ABCD$ известны стороны и диагональ: $AB = 3$, $BC = CD = 5$, $AD = 8$, $AC = 7$.
а) Докажите, что вокруг этого четырёхугольника можно описать окружность.
б) Найдите $BD$. (ЕГЭ-2018, досрочная волна, резервный день) - В трапеции $ABCD$ с основаниями $BC$ и $AD$ углы $ABD$ и $ACD$ прямые.
а) Докажите, что $AB = CD$.
б) Найдите $AD$, если $AB = 2$, $BC = 7$. (ЕГЭ-2018, основная волна) - Четырёхугольник $ABCD$ вписан в окружность радиуса 8. Известно, что
а) Докажите, что прямые $BC$ и $AD$ параллельны.
б) Найдите $AD$. (ЕГЭ-2018, основная волна) - Окружность с центром $O_1$ касается оснований $BC$ и $AD$ и боковой стороны $AB$ трапеции $ABCD$. Окружность с центром $O_2$ касается сторон $BC$, $CD$ и $AD$. Известно, что $AB = 10$, $BC = 9$, $CD = 30$, $AD = 39$.
а) Докажите, что прямая $O_1O_2$ параллельна основаниям трапеции $ABCD$.
б) Найдите $O_1O_2$. (ЕГЭ-2018, основная волна) - Окружность высекает на всех сторонах трапеции $ABCD$ равные отрезки.
а) Докажите, биссектрисы всех углов трапеции пересекаются в одной точке.
б) Пусть окружность пересекает боковую сторону $AB$ в точках $K$ и $L$ так, что $AK = 23$, $KL = 4$ и $LB = 2$. Найдите высоту трапеции. (ЕГЭ-2018, основная волна) - Точка $E$ — середина стороны $BC$ квадрата $ABCD$. Серединные перпендикуляры к отрезкам $AE$ и $EC$ пересекаются в точке $O$.
а) Докажите, что $angle AOE = 90^{circ}$.
б) Найдите $BO : OD$. (ЕГЭ-2018, основная волна, резервный день) - Точка $M$ — середина гипотенузы $AB$ треугольника $ABC$. Серединный перпендикуляр к гипотенузе пересекает катет $BC$ в точке $N$.
а) Докажите, что $angle CAN = angle CMN$.
б) Найдите отношение радиусов окружностей, описанных около треугольников $ANB$ и $CBM$, если $mathrm{tg} angle BAC = dfrac43$. (ЕГЭ-2017) - В треугольнике $ABC$ точки $A_1$, $B_1$ и $C_1$ — середины сторон $BC$, $AC$ и $AB$ соответственно, $AH$ — высота, $angle BAC = 60^{circ}$, $angle BCA = 45^{circ}$.
а) Докажите, что точки $A_1$, $B_1$, $C_1$ и $H$ лежат на одной окружности.
б) Найдите $A_1H$, если $BC = 2 sqrt3$. (ЕГЭ-2017) - Точка $E$ — середина боковой стороны $CD$ трапеции $ABCD$. На стороне $AB$ взяли точку $K$, так, что прямые $CK$ и $AE$ параллельны. Отрезки $CK$ и $BE$ пересекаются в точке $O$.
а) Докажите, что $CO = KO$.
б) Найти отношение оснований трапеции $BC$ и $AD$, если площадь треугольника $BCK$ составляет $0,009$ площади трапеции $ABCD$. (ЕГЭ-2017) - Две окружности с центрами $O_1$ и $O_2$ пересекаются в точках $A$ и $B$, причем точки $O_1$ и $O_2$ лежат по разные стороны от прямой $AB$. Продолжения диаметра $CA$ первой окружности и хорды $CB$ этой окружности пересекают вторую окружности в точках $D$ и $E$ соответственно.
а) Докажите, что треугольники $CBD$ и $O_1AO_2$ подобны.
б) Найдите $AD$, если $angle DAE = angle BAC$, радиус второй окружности втрое больше радиуса первой и $AB = 3$. (ЕГЭ-2017) - В прямоугольном треугольнике $ABC$ проведена высота $CH$ из вершины прямого угла. В треугольники $ACH$ и $BCH$ вписаны окружности с центрами $O_1$ и $O_2$ соответственно, касающиеся прямой $CH$ в точках $M$ и $N$ соответственно.
а) Докажите, что прямые $AO_1$ и $CO_2$ перпендикулярны.
б) Найдите площадь четырехугольника $MO_1NO_2$, если $AC = 20$ и $BC = 15$. (ЕГЭ-2017) - Точки $E$ и $K$ — соответственно середины сторон $CD$ и $AD$ квадрата $ABCD$. Прямая $BE$ пересекается с прямой $CK$ в точке $O$.
а) Докажите, что вокруг четырехугольника $ABOK$ можно описать окружность.
б) Найдите $AO$, если сторона квадрата равна 1. (ЕГЭ-2017) - Точка $O$ — центр окружности, описанной около остроугольного треугольника $ABC$, $I$ — центр вписанной в него окружности, $H$ — точка пересечения высот. Известно, что $angle BAC = angle OBC + angle OCB$.
а) Докажите, что точка $I$ лежит на окружности, описанной около треугольника $BOC$.
б) Найдите угол $OIH$, если $angle ABC = 55^{circ}$. (ЕГЭ-2016) - В треугольнике $ABC$ проведены высоты $AK$ и $CM$. На них из точек $M$ и $K$ опущены перпендикуляры $ME$ и $KH$ соответственно.
а) Докажите, что прямые $EH$ и $AC$ параллельны;
б) Найдите отношение $EH : AC$, если угол $ABC$ равен $30^{circ}$. (ЕГЭ-2016) - В треугольнике $ABC$ угол $ABC$ равен $60^{circ}$. Окружность, вписанная в треугольник, касается стороны $AC$ в точке $M$.
а) Докажите, что отрезок $BM$ не больше утроенного радиуса вписанной в треугольник окружности.
б) Найдите $sin angle BMC$ если известно, что отрезок $BM$ в 2,5 раза больше радиуса вписанной в треугольник окружности. (ЕГЭ-2016) - Квадрат $ABCD$ вписан в окружность. Хорда $CE$ пересекает его диагональ $BD$ в точке $K$.
а) Докажите, что $CK cdot CE = AB cdot CD$.
б) Найдите отношение $CK$ и $KE$, если $angle ECD = 15^{circ}$. (ЕГЭ-2016) - В прямоугольном треугольнике $ABC$ точки $M$ и $N$ — середины гипотенузы $AB$ и катета $BC$ соответственно. Биссектриса угла $BAC$ пересекает прямую $MN$ в точке $L$.
а) Докажите, что треугольники $AML$ и $BLC$ подобны.
б) Найдите отношение площадей этих треугольников, если $cos angle BAC = dfrac{7}{25}$. (ЕГЭ-2016) - Окружность касается стороны $AC$ остроугольного треугольника $ABC$ и делит каждую из сторон $AB$ и $BC$ на три равные части.
а) Докажите, что треугольник $ABC$ равнобедренный.
б) Найдите, в каком отношении высота этого треугольника делит сторону $BC$. (ЕГЭ-2016) - В прямоугольном треугольнике $ABC$ с прямым углом $C$ точки $M$ и $N$ — середины катетов $AC$ и $BC$ соответственно, $CH$ — высота.
а) Докажите, что прямые $MH$ и $NH$ перпендикулярны.
б) Пусть $P$ — точка пересечения прямых $AC$ и $NH$, а $Q$ — точка пересечения прямых $BC$ и $MH$. Найдите площадь треугольника $PQM$, если $AH = 4$ и $BH = 2$. (ЕГЭ-2016) - На катетах $AC$ и $BC$ прямоугольного треугольника $ABC$ как на диаметрах построены окружности, второй раз пересекающиеся в точке $M$. Точка $Q$ лежит на меньшей дуге $MB$ окружности с диаметром $BC$. Прямая $CQ$ второй раз пересекает окружность с диаметром $AC$ в точке $P$.
а) Докажите, что прямые $PM$ и $QM$ перпендикулярны.
б) Найдите $PQ$, если $AM = 1$, $BM = 3$, а $Q$ — середина дуги $MB$. (ЕГЭ-2016) - Две окружности касаются внутренним образом. Третья окружность касается первых двух и их линии центров.
а) Докажите, что периметр треугольника с вершинами в центрах трех окружностей равен диаметру наибольшей из этих окружностей.
б) Найдите радиус третьей окружности, если известно, что радиусы первых двух равны 6 и 2. - Хорды $AD$, $BE$ и $CF$ окружности делят друг друга на три равные части.
а) Докажите, что эти хорды равны.
б) Найдите площадь шестиугольника $ABCDEF$, если точки $A$, $B$, $C$, $D$, $E$ последовательно расположены на окружности, а радиус окружности равен $2sqrt{21}$. - Дан равнобедренный треугольник $ABC$ с основанием $AC$. Вписанная в него окружность с центром $O$ касается боковой стороны $BC$ в точке $P$ и пересекает биссектрису угла $B$ в точке $Q$.
а) Докажите, что отрезки $PQ$ и $OC$ параллельны.
б) Найдите площадь треугольника $OBC$, если точка $O$ делит высоту $BD$ треугольника в отношении $BO : OD = 3 : 1$ и $AC = 2$.
Что такое серединный перпендикуляр к отрезку? Что можно сказать о пересечении серединных перпендикуляров к сторонам треугольника? К сторонам многоугольника?
Определение.
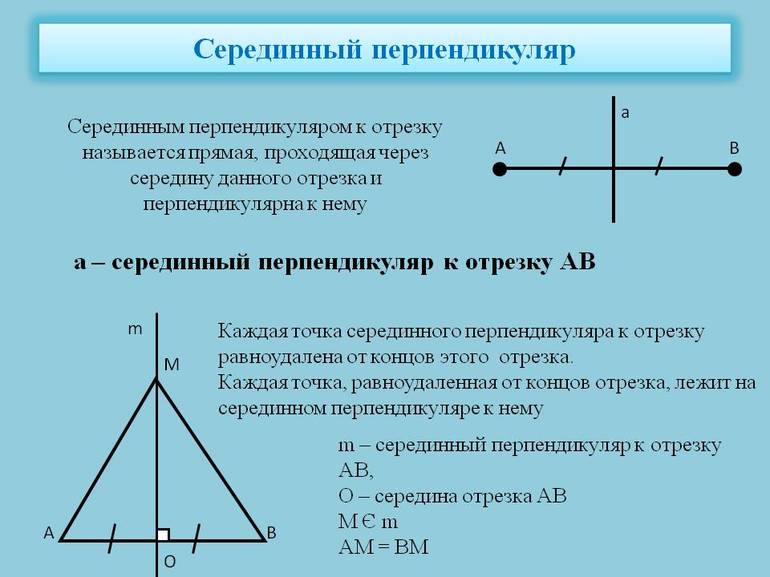
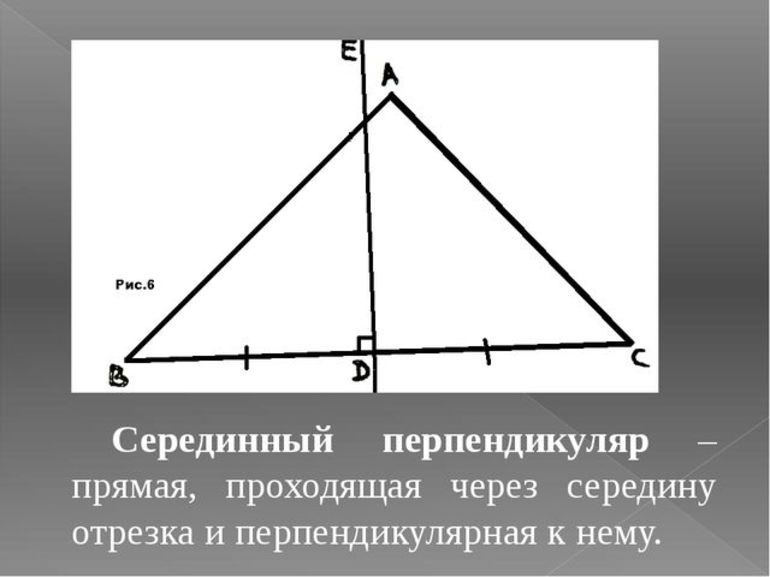
Серединный перпендикуляр к отрезку — это прямая, перпендикулярная данному отрезку и проходящая через его середину.
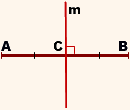
рисунок 1
m — серединный перпендикуляр к отрезку AB, если
точка C — середина отрезка AB,
![]()
![]()
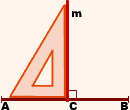
Чтобы построить серединный перпендикуляр к данному отрезку с помощью угольника, нужно:
1) найти середину отрезка;
2) провести через эту точку прямую, перпендикулярную данному отрезку (для этого угольник прикладываем прямым углом к середине отрезка так, чтобы она сторона угольника проходила через отрезок, а через другую сторону проводим прямую):

Свойства серединного перпендикуляра.
1) Геометрическое место точек, равноудаленных от двух данных точек, есть серединный перпендикуляр к отрезку, соединяющему эти точки.
Например, прямая m — геометрическое место точек, равноудаленных от точек A и B (рисунок 1).
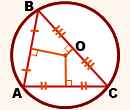
2) Серединные перпендикуляры к сторонам треугольника пересекаются в одной точке. Эта точка является центром описанной около треугольника окружности.
3) Если около многоугольника можно описать окружность, то центр этой описанной окружности является точкой пересечения серединных перпендикуляров к сторонам многоугольника.
скажите пожалуйста , как провести серединные перпендикуляры в прямоугольном треугольнике ! или такого быть не может?
Знаток
(408),
на голосовании
11 лет назад
Дополнен 11 лет назад
а если нужно провести серединный перпендикуляр в тупоугольном треугольнике к сторонам прилежащим к тупому углу, то перпендикуляр же выйде за пределы и он бдет не серединным
Голосование за лучший ответ
Иван Небогатых
Гуру
(2552)
11 лет назад
Чтобы провести серединный перпендикуляр к стороне, нужно найти её середину, а затем из этой точки нарисовать отрезок, перпендикулярный этой стороне. Отрезок нужно провести внутрь треугольника, а не наружу. Вести его нужно до тех пор, пока он не пересечётся с какой-то другой стороной (или даже вершиной) треугольника. 3 стороны, значит, 3 серединных перпендикуляра.
