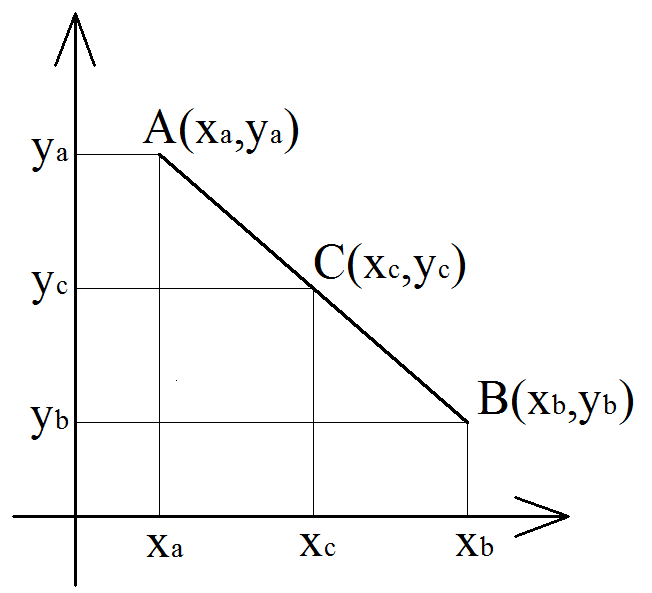Онлайн калькулятор. Середина отрезка
Предлагаю вам воспользоваться онлайн калькулятором для вычисления середины отрезка AB.
Воспользовавшись онлайн калькулятором, вы получите детальное решение вашей задачи, которое позволит понять алгоритм решения задач на вычисление координат середины отрезка и закрепить пройденный материал.
Калькулятор для вычисления координат середины отрезка AB
Выберите необходимую вам размерность:
Размерность:
Введите координаты точек.
Вводить можно числа или дроби (-2.4, 5/7, …). Более подробно читайте в правилах ввода чисел.
Середина отрезка: онлайн-калькулятор
Середина отрезка – это точка, принадлежащая этому отрезку и находящаяся на равном расстоянии от его концов. Координаты середины отрезка, который имеет концы A(xa,ya) и B(xb,yb), рассчитывается по формулам:
xc=xa+xb2,
yc=xb+yb2.
Чтобы найти середину отрезка по координатам онлайн:
- введите данные координат точек A и B в соответствующие поля;
- для получения решения нажмите на кнопку «Рассчитать».
Найти координаты середины отрезка онлайн
С помощью сервиса Zaochnik школьники и студенты могут находить середину отрезка онлайн. Эта возможность сокращает время на подготовку к занятиям. Самостоятельно полученный ответ легко сверить с решением на сайте. Подробные вычисления в случае нестыковки помогут выявить и исправить неточности.
Расчет середины отрезка по координатам онлайн имеет ряд преимуществ:
- нет надобности искать необходимую формулу для вычислений – она уже заложена в программе;
- набор действий выполняется за один раз и подробно отображается в решении;
- исключены неточности в вычислениях, которые возникают при расчетах на бумаге;
- сервис не ограничивает число запросов на расчет от пользователя;
- за использование калькулятора не требуется платить.
Если у вас возникли вопросы при самостоятельном изучении этой или других тем, напишите консультанту. Наш специалист оперативно предложит вам выгодные условия сотрудничества по решению задач.
Интервалы используются в математике по разным причинам. Интервал – это определенный сегмент набора данных. Например, интервал может быть от 4 до 8. Интервалы используются в статистике и в исчислении при получении интегралов. Интервалы также используются при попытке найти среднее из частотных таблиц. Средняя точка каждого интервала необходима для завершения этого процесса и определения среднего значения.
Найти верхний и нижний предел интервала. Например, интервал от 4 до 8 будет иметь 4 в качестве нижнего предела и 8 в качестве верхнего предела.
Суммируйте верхний и нижний предел. В примере 4 + 8 = 12.
Разделите сумму верхнего и нижнего пределов на 2. Результат – средняя точка интервала. В этом примере 12, деленное на 2, дает 6 как среднюю точку между 4 и 8.
Как найти абсолютное значение числа в математике
Распространенной задачей в математике является вычисление того, что называется абсолютным значением данного числа. Как правило, мы используем вертикальные полосы вокруг числа, чтобы отметить это, как видно на рисунке. Мы будем читать левую часть уравнения как абсолютное значение -4. Компьютеры и калькуляторы часто используют формат …
Как рассчитать размер выборки из доверительного интервала
Когда исследователи проводят опросы общественного мнения, они рассчитывают необходимый размер выборки на основе того, насколько точными они хотят, чтобы их оценки были. Размер выборки определяется уровнем достоверности, ожидаемой пропорцией и доверительным интервалом, необходимым для обследования. Доверительный интервал представляет запас …
Как найти середину координат
Средняя точка двух координат – это точка, которая находится точно посередине между двумя точками, или среднее значение двух точек. Вместо того, чтобы пытаться визуально определить полпути крутой линии, проведенной на координатной плоскости, вы можете использовать формулу средней точки. Формула средней точки – [(x1 + x2) / 2, (y1 + y2) / 2] – …

Как найти середину интервала
При статистической обработке результатов исследований самого разного рода полученные значения часто группируются в последовательность интервалов. Для расчета обобщающих характеристик таких последовательностей иногда приходится вычислять середину интервала – «центральную варианту». Методы ее расчета достаточно просты, но имеют некоторые особенности, вытекающие как из используемой для измерения шкалы, так и из характера группировки (открытые или закрытые интервалы).

Инструкция
Если интервал является участком непрерывной числовой последовательности, то для нахождения ее середины используйте обычные математические методы вычисления среднеарифметического значения. Минимальное значение интервала (его начало) сложите с максимальным (окончанием) и разделите результат пополам – это один из способов вычисления среднеарифметического значения. Например, это правило применимо, когда речь идет о возрастных интервалах. Скажем, серединой возрастного интервала в диапазоне от 21 года до 33 лет будет отметка в 27 лет, так как (21+33)/2=27.
Иногда бывает удобнее использовать другой метод вычисления среднеарифметического значения между верхней и нижней границами интервала. В этом варианте сначала определите ширину диапазона – отнимите от максимального значения минимальное. Затем поделите полученную величину пополам и прибавьте результат к минимальному значению диапазона. Например, если нижняя граница соответствует значению 47,15, а верхняя – 79,13, то ширина диапазона составит 79,13-47,15=31,98. Тогда серединой интервала будет 63,14, так как 47,15+(31,98/2) = 47,15+15,99 = 63,14.
Если интервал не является участком обычной числовой последовательности, то вычисляйте его середину в соответствии с цикличностью и размерностью используемой измерительной шкалы. Например, если речь идет об историческом периоде, то серединой интервала будет являться определенная календарная дата. Так для интервала с 1 января 2012 года по 31 января 2012 серединой будет дата 16 января 2012.
Кроме обычных (закрытых) интервалов статистические методы исследований могут оперировать и «открытыми». У таких диапазонов одна из границ не определена. Например, открытый интервал может быть задан формулировкой «от 50 лет и старше». Середина в этом случае определяется методом аналогий – если все остальные диапазоны рассматриваемой последовательности имеют одинаковую ширину, то предполагается, что и этот открытый интервал имеет такую же размерность. В противном случае вам надо определить динамику изменения ширины интервалов, предшествующих открытому, и вывести его условную ширину, исходя из полученной тенденции изменения.
Источники:
- что такое открытый интервал
Войти на сайт
или
Забыли пароль?
Еще не зарегистрированы?
This site is protected by reCAPTCHA and the Google Privacy Policy and Terms of Service apply.
Координаты точки середины отрезка на плоскости онлайн
Калькулятор рассчитывает координаты середины отрезка на плоскости по координатам конца отрезка с подробным порядком вычислений. В поля можно вводить целые или десятичные числа.
Введите координаты точки A
Введите координаты точки B
Определение середины отрезка
Середина отрезка – это точка которая лежит на отрезке, делит этот отрезок пополам и находится на равном расстоянии от начала и конца отрезка.
Формула расчёта координаты середины отрезка на плоскости
Каждая координата середины отрезка равна полусумме соответствующих координат его концов.
xc=(xa+xb)/2
yc=(ya+yb)/2
A(xa, ya), B(xb, yb) – координаты концов отрезка
C(xc, yc) – координаты середины отрезка
Задачи на вычисление координат середины отрезка
Найдите координаты точки C – середины отрезка AB заданного точками A(2,3), B(8,9)
По формулам нахождения координыты середины отрезка найдём координаты точки C.
xc=(2+8)/2=5
yc=(3+9)/2=6
Координаты точки C(5, 6)
Найдите координаты середины отрезка AB, если A(1,1), B(5,5)
xc=(1+5)/2=3
yc=(1+5)/2=3
Координаты точки середины отрезка C(3, 3)
Найти координаты середины отрезка AB если A(-5, -6), B(6, -4).
Найти координаты середины отрезка AB если A(6, -2), B(-2, 7).
Найти координаты середины отрезка AB если A(7, -4), B(5, -6).
Найти координаты середины отрезка AB если A(-4, -7), B(1, 7).
Найти координаты середины отрезка AB если A(7, 7), B(7, 2).
Похожие калькуляторы