Как найти середину многоугольника

В математике барице́нтр, или геометри́ческий центр, двумерной фигуры — это среднее арифметическое положений всех точек данной фигуры. Определение распространяется на любой объект в n-мерном пространстве. Радиус-вектор барицентра в трёхмерном случае вычисляется как

,

где интегрирование выполняется по объёму тела. Другое название барицентра в этом значении — центроид.

Неформально, геометрический барицентр есть точка равновесия фигуры, вырезанной из картона, в предположении, что картон имеет постоянную плотность, а внешнее гравитационное поле однородно.

В физике термин «барицентр» — синоним понятия «центр масс», используемый, в основном, в задачах космической механики. Центр масс объекта является средним арифметическим всех его точек с учётом локальной плотности массы. Для физических объектов с постоянной плотностью центр масс совпадает с барицентром фигуры той же формы.

Ниже барицентр рассматривается в математическом (геометрическом) смысле, о барицентре в физике см. статью Центр масс.

Свойства[править | править код]

Геометрический барицентр выпуклого объекта всегда лежит внутри объекта. Невыпуклый объект может иметь барицентр, лежащий вне фигуры. Барицентр кольца или миски, например, лежат вне фигуры.

Если барицентр известен, он является фиксированной точкой группы изометрии симметрий фигуры. Барицентр объекта лежит на пересечении всех его гиперплоскостей симметрии. Барицентры многих фигур (правильного многоугольника, правильного многогранника, цилиндра, прямоугольника, ромба, окружности, сферы, эллипса, эллипсоида, суперэллипса, суперэллипсоида и т. д.) можно найти исходя исключительно из этого принципа.

В частности, барицентром треугольника является точка пересечения его медиан (см. рисунок). Барицентром параллелограмма является точка пересечения его диагоналей, но это неверно для других четырёхугольников.

Барицентр объекта с трансляционной симметрией не определён (или лежит вне пространства фигуры), поскольку сдвиг не имеет фиксированной точки.

Центроид треугольника[править | править код]

• Барицентр треугольника называется центроидом и лежит на пересечении трёх медиан, также лежит на прямой Эйлера (проходящей и через другие ключевые точки, включая ортоцентр и центр описанной окружности)^[1][2].

• Если в вершины треугольника поместить равные массы, то центр масс (барицентр) полученной системы будет совпадать с центроидом. Более того, центр масс треугольника с равномерно распределённой массой также находится в центроиде.

^[3].

• Сумма квадратов сторон треугольника равна утроенной сумме квадратов расстояний от центроида до вершин треугольника:

^[3].

• Центр масс сторон треугольника совпадает с центром вписанной окружности дополнительного треугольника (треугольника с вершинами, расположенными в серединах сторон данного треугольника). Эту точку называют центром Шпикера. Если стороны треугольника сделать из тонкой проволоки одинакового сечения, то центр масс (барицентр) полученной системы будет совпадать с инцентром дополнительного треугольника, или с центром Шпикера.
• О других свойствах центроида треугольника смотрите ниже.

Минимаксные свойства центроида треугольника[править | править код]

• Центроид или точка пресечения медиан треугольника является единственной точкой треугольника такой, что проведенные через неё три чевианы разделяют своими концами стороны треугольника на шесть отрезков. При этом произведение длин трёх из этих шести отрезков, не имеющих общих концов, максимально^[4].
• Центроид или точка пересечения трёх медиан является точкой, для которой сумма квадратов расстояний до вершин треугольника принимает наименьшее значение (теорема Лейбница).

Центроид четырёх точек (вершин четырёхугольника)[править | править код]

Центроид (барицентр или центр масс) вершин произвольного четырёхугольника лежит в точке пересечения 3-х отрезков: 1-й отрезок соединяет середины диагоналей, два другие — середины противолежащих сторон. Точка пересечения делит все три отрезка пополам.

Четыре отрезка, каждый из которых соединяет вершину четырёхугольника с центроидом треугольника, образованного оставшимися тремя вершинами, пересекаются в одной точке (центроиде вершин четырёхугольника) и делятся ею в отношении 3:1, считая от вершины.

Центр масс вершин четырёхугольника не обязан совпадать с центром масс самого четырёхугольника как плоской фигуры.

Определение местоположения барицентра[править | править код]

Определение местоположения барицентра однородной плоской фигуры методом отвеса[править | править код]

Барицентр однородной плоской фигуры, такой как фигура (a) на рисунке, можно найти экспериментально с использованием отвеса и булавки путём нахождения центра масс тонкой пластины однородной плотности, имеющей ту же форму. Пластина удерживается булавкой, вставленной ближе к периметру так, чтобы пластина могла свободно вращаться. Отмечаем на пластине прямую, которую образует отвес, прикреплённый к булавке (b). Проделываем то же самое с другим положением булавки. Пересечение двух прямых даст барицентр (c).

Этот метод можно распространить (в теории) на вогнутые фигуры, когда барицентр лежит вне их, а также тела (постоянной плотности), но положение линии отвеса придётся отмечать каким-то иным способом.

Определение местоположения барицентра выпуклой двумерной фигуры методом балансировки[править | править код]

Барицентр выпуклой двумерной фигуры можно найти путём балансировки на меньшей фигуре, например, на вершине узкого цилиндра. Барицентр будет находиться где-то внутри области контакта этих фигур. В принципе, последовательным уменьшением диаметра цилиндра можно получить местоположение барицентра с любой точностью. На практике потоки воздуха делают это невозможным, однако используя наложение областей балансировки и усреднение, можно получить нужную точность.

Определение местоположения барицентра для конечного множества точек[править | править код]

Барицентр конечного множества из точек в находится по формуле

^[5].

Полученная точка такая, что сумма квадратов расстояний между ней и точками множества является минимальной.

Определение местоположения барицентра с помощью геометрического разложения[править | править код]

Барицентр плоской фигуры можно вычислить, разделив её на конечное число более простых фигур , найдя положение барицентров и площадей каждой части, а затем вычислив

Дыры в фигуре , наложения частей, или части, выступающие за фигуру, можно рассматривать как фигуры с отрицательной площадью . А именно, знак площади нужно выбирать так, чтобы сумма знаков для всех частей, включающих точку , была равна 1, если принадлежит , и 0 в противном случае.

Например, фигуру (a) на рисунке легко разделить на квадрат и треугольник с положительным знаком, круглое отверстие с отрицательным (b).

Барицентр каждой части легко найти в любом списке барицентров простых фигур (c). Затем вычисляется барицентр фигуры, как средневзвешенное трёх точек. Горизонтальное положение барицентра, считая от левого края фигуры, равно

Вертикальное положение вычисляется аналогично.

Та же формула применима для любого трёхмерного объекта, только обозначают уже объёмы частей тела , а не площади. Формула верна также для пространства любой размерности при замене площади -мерными мерами частей.

Определение местоположения барицентра интегрированием[править | править код]

Барицентр подмножества X пространства можно вычислить с помощью интеграла

где интегрирование ведётся по всему пространству , а g является характеристической функцией подмножества, принимающей 1 внутри X и 0 вне его^[6]. Заметим, что знаменатель равен мере множества X. Формула неприменима к множеству нулевой меры, а также к множествам, для которых интеграл расходится.

Другая формула для вычисления координат барицентра:

где G_k является k-й координатой G, а S_k(z) — мера пересечения X с гиперплоскостью, определяемой уравнением x_k = z. Снова знаменатель — это мера множества X.

Для плоской фигуры координатами барицентра будут

где A — площадь фигуры X, S_y(x) — длина пересечения^{[неизвестный термин]} X с вертикальной прямой с абциссой x, S_x(y) — аналогичная величина при обмене осей.

Определение местоположения барицентра для области, ограниченной графиками непрерывных функций[править | править код]

Координаты барицентра области, ограниченной графиками непрерывных функций и , таких что на интервале , , задаются выражениями

^[6].

^[7]

где  — площадь области (вычисляемая по формуле )^[8][9].

Определение местоположения барицентра объекта, имеющего форму буквы L[править | править код]

Метод нахождения барицентра фигуры, имеющей форму буквы L.

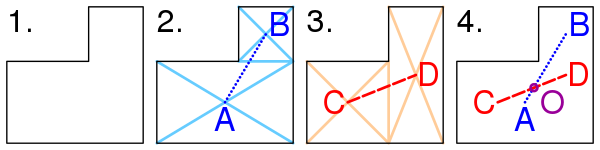
1. Фигуру делят на два прямоугольника (см. фигуру (2) на рисунке). Находят барицентры A и B этих двух прямоугольников как пересечение диагоналей. Рисуют отрезок AB, соединяющий барицентры. Барицентр фигуры должен лежать на этом отрезке AB.
2. Делят фигуру на два прямоугольника другим способом (см. фигуру (3) на рисунке). Находят барицентры C и D этих двух прямоугольников. Проводят отрезок CD, соединяющий барицентры. Барицентр фигуры должен лежать на отрезке CD.
3. Поскольку барицентр должен лежать как на отрезке AB, так и на отрезке CD, очевидно, что он является точкой пересечения этих двух отрезков — точкой O. Точка O не обязана лежать внутри фигуры.

Барицентры треугольника и тетраэдра[править | править код]

Барицентр треугольника совпадает с пересечением медиан. Барицентр разбивает каждую медиану в отношении 2:1, то есть барицентр находится на расстоянии ⅓ от стороны до противоположной вершины (см. рисунок). Его декартовыми координатами является среднее координат трёх вершин. То есть, если вершинами треугольника являются , и , то координаты барицентра вычисляются по формуле

.

Таким образом, барицентр имеет барицентрические координаты .

В трилинейных координатах барицентр можно получить одним из эквивалентных способов^[10]:

Барицентр является также физически центром масс треугольника, сделанного из однородного листового материала, а также, если вся масса сконцентрирована в вершинах и одинаково разделена между ними. Если же масса распределена равномерно вдоль периметра, то центр масс лежит в точке Шпикера (инцентре серединного треугольника), который (в общем случае) не совпадает с центроидом всего треугольника.

Площадь треугольника равна 3/2 длины любой стороны, умноженной на расстояние от центроида до стороны^[11].

Центроид треугольника лежит на прямой Эйлера между его ортоцентром и центром его описанной окружности , ровно вдвое ближе ко второму, чем к первому:

.

Кроме того, для инцентра и центра девяти точек , мы имеем

,

,

,

,

.

Аналогичными свойствами обладает тетраэдр — его барицентр является пересечением отрезков, соединяющих вершины с барицентрами противоположных граней. Эти отрезки делятся барицентром в отношении 3:1. Результат может быть обобщён на любой -мерный симплекс. Если вершины симплекса обозначить и рассматривать вершины как вектора, центроид равен

.

Геометрический барицентр совпадает с центром масс, если масса равномерно распределена по всему симплексу или сосредоточена в вершинах как равных масс.

Изогональным сопряжением центроида треугольника является точка пересечения его симедиан.

Барицентр тетраэдра[править | править код]

Тетраэдр является телом в трёхмерном пространстве, имеющим четыре треугольника в качестве граней. Отрезок, соединяющий вершину тетраэдра с барицентром противоположной грани, называется медианой, а отрезок, соединяющий середины двух противоположных сторон, называется бимедианой. Таким образом, имеется четыре медианы и две бимедианы. Эти шесть отрезков пересекаются в барицентре тетраэдра^[12]. Барицентр тетраэдра лежит посередине между точкой Монжа и центром описанной сферы. Эти точки задают прямую Эйлера тетраэдра, являющуюся аналогом прямой Эйлера треугольника.

Барицентр многоугольника[править | править код]

Барицентром самонепересекающегося замкнутого многоугольника, заданного вершинами , , , , является точка , где

;

и где является площадью многоугольника (со знаком):

^[13].

В этой формуле предполагается, что вершины пронумерованы вдоль периметра многоугольника. Кроме того, вершина считается той же самой, что и .
Заметим, что если точки пронумерованы по часовой стрелке, площадь , вычисленная выше, будет отрицательной, но координаты барицентра подкорректируют этот случай.

Барицентры конуса и пирамиды[править | править код]

Барицентр конуса или пирамиды расположен на отрезке, соединяющем вершину тела с барицентром основания. Для целого конуса или пирамиды барицентр находится на расстоянии 1/4 от основания к вершине. Для поверхности конуса или пирамиды (боковая поверхность без внутренности и без основания) центроид находится на 1/3 расстояния от основания до вершины.

См. также[править | править код]

• Центр масс
• Центроид треугольника
• Центр тяжести
• Центр Чебышева^[en]
• Среднее Фреше^[en]
• k-means
• Список барицентров
• Теоремы Паппа — Гульдина
• Замечательные точки треугольника

Примечания[править | править код]

Литература[править | править код]

• Зетель, С. И. Новая геометрия треугольника. Пособие для учителей. — 2-е изд/. — М. : Учпедгиз, 1962. — С. 12.
• Leung Kam-tim, Suen Suk-nam. Vectors, matrices and geometry. — Hong Kong University Press, 1994.

• Nathan Altshiller-Court. College Geometry: An Introduction to the Modern Geometry of the Triangle and the Circle. — 2nd. — New York: Barnes & Noble, 1925.
• Paul Bourke. Calculating the area and centroid of a polygon. — 1997.
• Roger A. Johnson. Advanced Euclidean Geometry. — Dover, 2007.
• David C. Kay. College Geometry. — New York: Holt, Rinehart and Winston, 1969.
• Roland E. Larson, Robert P. Hostetler, Bruce H. Edwards. Calculus of a Single Variable. — 6th. — Houghton Mifflin Company, 1998.
• Murray H. Protter, Charles B. Morrey Jr. College Calculus with Analytic Geometry. — 2nd. — Reading: Addison-Wesley, 1970.

Ссылки[править | править код]

• Characteristic Property of Centroid at cut-the-knot
• Barycentric Coordinates at cut-the-knot
• Interactive animations showing Centroid of a triangle and Centroid construction with compass and straightedge
• Experimentally finding the medians and centroid of a triangle at Dynamic Geometry Sketches, an interactive dynamic geometry sketch using the gravity simulator of Cinderella.

На карте отобразил условный контур и теперь хотел бы в него вывести балун. Создать балун не проблема, не поместить его в центр полигона — проблема.

В математике есть довольно сложные формулы для расчёта центра масс многоугольника, ими я не умею пользоваться. но в яндекс апи есть poly.geometry.getBounds(), который берёт максимально большой контур и находит центр. У меня тоже не получается его применить потому что полигон я создал не стандартным способом( new ymaps.Polygon()), а через map.geoObjects.add(objectManager);

Помогите пожалуйста получить координаты центра полигона.

Если нужно, то вот фиддл, который демонстрирует getBounds().

Медиана треугольника есть диаметр, делящий пополам хорды, параллельные основанию, поэтому на ней лежит центр тяжести (п° 217) площади треугольника. Следовательно, три медианы треугольника, пересекаясь, определяют центр тяжести площади треугольника.

Элементарные соображения показывают, что медианы треугольника пересекаются в точке, отстоящей на две трети длины каждой из них от соответствующей вершины. Поэтому центр тяжести площади треугольника лежит на любой его медиане на расстоянии двух третей ее длины от вершины.

219. Четырехугольник.

Центр тяжести площади четырехугольника определяется пересечением двух прямых, которые мы получаем, применяя распределительное свойство центров тяжести (п° 213).

Сначала делим четырехугольник диагональю на два треугольника. Центр тяжести четырехугольника лежит на прямой, соединяющей центры тяжести этих треугольников. Эта прямая и есть первая из двух искомых прямых.

Вторую прямую получим таким же способом, разбивая четырехугольник на два треугольника (отличных от предыдущих) посредством другой диагонали.

220. Многоугольник.

Мы знаем способы нахождения центров тяжести площади треугольника и четырехугольника. Чтобы определить центр тяжести площади многоугольника с произвольным числом сторон, предположим, что мы умеем находить центр тяжести площади многоугольника с меньшим числом сторон.

Тогда можно поступить так же, как в случае четырехугольника. Площадь данного многоугольника делят на две части двумя разными способами проведением диагоналей. В каждом из двух случаев соединяют прямой центры тяжести отдельных частей. Эти две прямые пересекаются в искомом центре тяжести.

221. Дуга окружности.

Пусть требуется определить центр тяжести дуги окружности АВ длины s. Отнесем окружность к двум взаимно перпендикулярным диаметрам ОХ и OY, из которых первый проходит через середину С дуги АВ. Центр тяжести лежит на оси ОХ, являющейся осью симметрии. Достаточно поэтому определить 5. Для этого имеем формулу:

Пусть будут: а — радиус окружности, с — длина хорды АВ, — угол между осью ОХ и радиусом, проведенным к элементу значения , соответствующие концам дуги АВ. Имеем:

Тогда, принимая В за переменную интегрирования и выполняя интегрирование вдоль дуги АВ, получим:

Следовательно, центр тяжести дуги окружности лежит на радиусе, проведенном через середину дуги, в точке, расстояние которой от центра окружности есть четвертая пропорциональная длины дуги, радиуса и хорды.

222. Круговой сектор.

Сектор, заключенный между дугой окружности и двумя радиусами ОА и ОВ, может быть разложен промежуточными радиусами на бесконечно малые равные между собою секторы. Эти элементарные секторы можно рассматривать как бесконечно узкие треугольники; центр тяжести каждого из них, по предыдущему, лежит на радиусе, проведенном через середину элементарной дуги этого сектора, на расстоянии двух третей длины радиуса от центра окружности. Равные между собою массы всех элементарных треугольников, сосредоточенные в их центрах тяжести, образуют однородную дугу окружности, радиус которой равен двум третям радиуса дуги сектора. Рассматриваемый случая приводится, таким образом, к отысканию центра тяжести этой однородной дуги, т. е. к задаче, решенной в предыдущем п°.

223. Тетраэдр.

Определим центр тяжести объема тетраэдра. Плоскость, проходящая через одно из ребер и через середину противоположного ребра, есть диаметральная плоскость, которая делит пополам хорды, параллельные этому последнему ребру: она содержит поэтому центр тяжести объема тетраэдра. Следовательно, шесть плоскостей, тетраэдра, из которых каждая проходит через одно из ребер и через середину противоположного ребра, пересекаются в одной точке, представляющей собой центр тяжести объема тетраэдра.

Рассмотрим тетраэдр ABCD (фиг. 37); соединим вершину А с центром тяжести I основания BCD; прямая AI есть пересечение диаметральных плоскостей, проходящих

через ребра АВ и поэтому она содержит искомый центр тяжести. Точка находится на расстоянии двух третей медианы ВН от вершины В. Точно так же возьмем на медиане АН точку К на расстоянии двух третей ее длины от вершины . Прямая В К пересечет прямую А в центре тяжести тетраэдра. Проведем из подобия треугольников АВН и ЮН видно, что IK есть третья часть АВ) далее, из подобия треугольников и ВГА заключаем, что есть третья часть .

Следовательно, центр тяжести объема тетраэдра лежит на отрезке, соединяющем любую вершину тетраэдра с центром тяжести противоположной грани, на расстоянии трех четвертей длины этого отрезка от вершины.

Заметим еще, что прямая, соединяющая середины Я и L двух противоположных ребер (фиг. 38) есть пересечение диаметральных плоскостей, проходящих через эти ребра, она также проходит через центр тяжести тетраэдра. Таким образом, три прямые, соединяющие середины противоположных ребер тетраэдра, пересекаются в его центре тяжести.

Пусть Н и — середины одной пары противоположных ребер (фиг. 38) и М, N — середины двух других противоположных ребер. Фигура HNLM есть параллелограм, стороны которого соответственно параллельны остальным

двум ребрам. Прямые HL и MN, соединяющие середины двух противоположных ребер, суть диагонали этого параллелограма, а значит, они в точке пересечения делятся пополам. Таким образом, центр тяжести тетраэдра лежит в середине отрезка, соединяющего середины двух противоположных ребер тетраэдра.

224. Пирамида с многоугольным основанием.

Центр тяжести пирамиды лежит на отрезке, соединяющем вершину пирамиды с центром тяжести основания на расстоянии трех четвертей длины этого отрезка от вершины.

Чтобы доказать эту теорему, разложим пирамиду на тетраэдры плоскостями, проведенными через вершину пирамиды и через диагонали основания ABCD (например BD на фиг. 39).

Проведем плоскость пересекающую ребра на расстоянии трех четвертей их длины от вершины. Эта плоскость содержит центры тяжести тетраэдров, а следовательно, и пирамиды. Массы тетраэдров, которые мы предполагаем сосредоточенными в их центрах тяжести, пропорциональны их объемам, следовательно и площадям из оснований (фиг. 39) или также площадям треугольников bad, bed. подобных предыдущим и расположенным в секущей плоскости abcd. Таким образом, искомый центр тяжести совпадает с центром тяжести многоугольника abcd. Последний же лежит на прямой, соединяющей вершину S пирамиды с центром тяжести (подобно расположенным) многоугольника основания.

225. Призма. Цилиндр. Конус.

На основании симметрии, центры тяжести призмы и цилиндра лежат на середине отрезка, соединяющего центры тяжести оснований.

Рассматривая конус, как предел вписанной в него пирамиды с той же вершиной, убеждаемся, что центр тяжести конуса лежит на отрезке, соединяющем вершину конуса с центром тяжести основания, на расстоянии трех четвертей длины этого отрезка от вершины. Можно также сказать, что центр тяжести конуса совпадает с центром тяжести сечения конуса плоскостью, параллельной основанию и проведенной на расстоянии одной четверти высоты конуса от основания.

Понятие “центр тяжести многоугольника” можно интерпретировать тремя различными способами:

1. Масса находится только в вершинах, причем каждая вершина “весит” одинаково
2. Масса равномерно распределена по границе многоугольника
3. Масса равномерно распределена по области, ограниченной многоугольником.

Рассмотрим все три интерпретации в порядке возрастания сложности алгоритма.

1. Масса находится только в вершинах, причем каждая вершина весит одинаково

В этом случае координаты центра тяжести выражаются по формулам:

Таким образом для нашего частного случая имеем:

2. Масса равномерно распределена по границе многоугольника

В этом случае масса ребра пропорциональна его длине. Таким образом каждое ребро мы можем заменить на точечную массу (пропорциональную длине ребра). Затем применяя те же формулы для определения центра тяжести получаем:

Ниже представлена программа, реализующая описанный алгоритм:

3. Масса равномерно распределена по области, ограниченной многоугольником.

Этот случай уже не является столь тривиальным, как два предыдущих. Для построения алгоритма понадобится следующий факт:

Предложение 1
Пусть фигура Ф есть объединение двух других фигур Ф1 и Ф2 (пересекающихся только по границе).
Тогда центр тяжести фигуры Ф выражается так:

(Это утверждение очевидно следует из определения центра тяжести произвольной фигуры и свойства аддитивности интеграла)

Кроме того для треугольника центр тяжести определяется так:

Разобьем наш многоугольник на треугольники. Для каждого треугольника найдем его центр тяжести (Xci, Yci) и площадь (Si). После этого, согласно Предложению 1, координаты центра тяжести многоугольника можно найти следующим образом:

Остается вопрос, как разбить многоугольник на треугольники. Если многоугольник выпуклый, а вершины перечислены в порядке обхода по или против часовой стрелки, то достаточно просто найти одну точку внутри многоугольника (Xm,Ym), а затем разбить многоугольник на N следующих треугольников:

Если же многоугольник выпуклый, но вершины перечислены не в порядке обхода, то их придется упорядочить. Сделать это можно, например, отсортировав вершины по углу между положительной полуосью ОХ и вектором (Xi-Xm, Yi-Ym).

Невыпуклый многоугольник всегда можно разбить на несколько выпуклых. А затем, применив описанный алгоритм для каждой выпуклой части, и используя Предложение 1, найти центр тяжести всего многоугольника. Задача о разбиении произвольного многоугольника на выпуклые части является самостоятельной задачей, которая рассмотрена в соответствующем разделе. Поэтому представленная ниже реализация алгоритма работает только для выпуклых многоугольников.

Ниже представлен пример реализации описанного алгоритма на языке С для нахождения центра тяжести выпуклого многоугольника, вершины которого перечислены в порядке обхода по или против часовой стрелки:

Как найти центр окружности описанной около многоугольника

Ключевые слова: многоугольник, правильный многоугольник, сторона, угол, вписанная, описанная окружность

Выпуклый многоугольник называется правильным, если у него все стороны равны и все углы равны.

Центром правильного многоугольника называется точка, равноудаленная от всех его вершин и всех его сторон.

Центральным углом правильного многоугольника называется угол, под которым видна сторона из его центра.

См. также:
Вписанная окружность, Описанная окружность, Выпуклый четырёхугольник, Произвольный выпуклый многоугольник

Центр описанной окружности

Где находится центр описанной около треугольника окружности? Что можно сказать о центре окружности, описанной около многоугольника?

Центр описанной около треугольника окружности является точкой пересечения серединных перпендикуляров к сторонам треугольника.

окружность (O;R) — описанная около ∆ ABC.

O — точка пересечения серединных перпендикуляров к сторонам ∆ ABC.

Соединим отрезками точки O и A, O и C.

OA=OC (как радиусы), следовательно, треугольник AOC — равнобедренный с основанием AC (по определению).

По свойству равнобедренного треугольника, высота и медиана, проведенные к основанию AC, совпадают):

Следовательно, центр описанной окружности — точка O — лежит на прямой, перпендикулярной стороне AC и проходящей через ее середину, то есть на серединном перпендикуляре к AC.

Аналогично доказывается, что точка O лежит на серединном перпендикуляре к стороне AB.

Так как серединные перпендикуляры к сторонам треугольника пересекаются в одной точке, то точка O — центр описанной около треугольника ABC окружности.

Что и требовалось доказать.

Аналогичные рассуждения можно применить и для многоугольника, около которого можно описать окружность.

Центр описанной около многоугольника окружности является точкой пересечения серединных перпендикуляров к сторонам этого многоугольника.

2 Comments

на мой взгляд у вас опечатка — «Соединим отрезками точки O и A, O и C.

OA=OB( написано ОВ вместо ОС) (как радиусы), следовательно, треугольник AOB — равнобедренный с основанием AC (по определению).»

Описанная окружность

Окружность описанная около многоугольника – это окружность, на которой лежат все вершины многоугольника. Вписанный в окружность многоугольник – это многоугольник, все вершины которого лежат на окружности. На рисунке 1 четырехугольник АВСD вписан в окружность с центром О, а четырехугольник АЕСD не является вписанным в эту окружность, так как вершина Е не лежит на окружности.

Теорема

Около любого треугольника можно описать окружность.

Доказательство

Дано: произвольный АВС.

Доказать: около АВС можно описать окружность.

Доказательство:

1. Проведем серединные перпендикуляры к сторонам АВС, которые пересекутся в точке О (по свойству серединных перпендикуляров треугольника). Соединим точку О с точками А, В и С (Рис. 2).

Точка О равноудалена от вершин АВС (по теореме о серединном перпендикуляре), поэтому ОА = ОВ = ОС. Следовательно, окружность с центром О радиуса ОА проходит через все три вершины треугольника, значит, является описанной около АВС. Теорема доказана.

Замечание 1

Около треугольника можно описать только одну окружность.

Доказательство

Предположим, что около треугольника можно описать две окружности. Тогда центр каждой из них равноудален от его вершин и поэтому совпадает с точкой О пересечения серединных перпендикуляров к сторонам треугольника, а радиус равен расстоянию от точки О до вершин треугольника. Следовательно, эти окружности совпадают, т.е. около треугольника можно описать только одну окружность. Что и требовалось доказать.

Замечание 2

Около четырехугольника не всегда можно описать окружность.

Доказательство

Рассмотрим, например, ромб, не являющийся квадратом. Такой ромб можно “поместить” в окружность так, что две его вершины будут лежать на этой окружности (Рис. 3), но нельзя “поместить” ромб в окружность так, чтобы все его вершины лежали на окружности, т.к. диаметр окружности, равный одной из диагоналей ромба, будет больше (меньше) второй диагонали, т.е. нельзя описать окружность. Что и требовалось доказать.

Если же около четырехугольника можно описать окружность, то его углы обладают следующим замечательным свойством:

В любом вписанном четырехугольнике сумма противоположных углов равна 180 0 .

Доказательство

Рассмотрим четырехугольник АВСD, вписанный в окружность (Рис. 4).

Углы В и D – вписанные, тогда по теореме о вписанном угле: В = АDС, D = АВС, откуда следует В + D = АDС + АВС = (АDС + АВС). Дуги АDС и АВС вместе составляют окружность, градусная мера которой равна 360 0 , т.е. АDС + АВС = 360 0 , тогда В + D = 360 0 = 180 0 . Что и требовалось доказать.

Верно и обратное утверждение:

Если сумма противоположных углов четырехугольника равна 180 0 , то около него можно описать окружность.

Доказательство

Дано: четырехугольник АВСD, BАD + BСD = 180 0 .

Доказать: около АВСD можно описать окружность.

Доказательство:

Проведем окружность через три вершины четырехугольника: А, В и D (Рис. 5), – и докажем, что она проходит также через вершину С, т.е. является описанной около четырехугольника АВСD.

Предположим, что это не так. Тогда вершина С лежит либо внутри круга, либо вне его.

Рассмотрим первый случай, когда точка С лежит внутри круга (Рис. 6).

ВСD – внешний угол СFD, следовательно, BСD = ВFD + FDE. (1)

Углы ВFD и FDE – вписанные. По теореме о вписанном угле ВFD = ВАD и FDE = ЕF, тогда, подставляя данные равенства в (1), получим: BСD = ВАD + ЕF = (ВАD + ЕF), следовательно, ВСDВАD.

BАD – вписанный, тогда по теореме о вписанном угле BАD = ВЕD, тогда BАD + BСD(ВЕD + ВАD).

Дуги ВЕD и ВАD вместе составляют окружность, градусная мера которой равна 360 0 , т.е. ВЕD + ВАD = 360 0 , тогда BАD + BСD360 0 = 180 0 .

Итак, мы получили, что BАD + BСD180 0 . Но это противоречит условию BАD + BСD =180 0 , и, значит, наше предположение ошибочно, т.е. точка С лежит на окружности, значит, около четырехугольника АВСD можно описать окружность.

Рассмотрим второй случай, когда точка С лежит вне круга (Рис. 7).

По теореме о сумме углов треугольника в ВСF: С + В + F = 180 0 , откуда С = 180 0 – ( В + F). (2)

В – вписанный, тогда по теореме о вписанном угле В = ЕF. (3)

F и ВFD – смежные, поэтому F + ВFD = 180 0 , откуда F = 180 0 – ВFD = 180 0 – ВАD. (4)

Подставим (3) и (4) в (2), получим:

С = 180 0 – (ЕF + 180 0 – ВАD) = 180 0 – ЕF – 180 0 + ВАD = (ВАD – ЕF), следовательно, СВАD.

А – вписанный, тогда по теореме о вписанном угле А = ВЕD, тогда А + С(ВЕD + ВАD). Но это противоречит условию А + С =180 0 , и, значит, наше предположение ошибочно, т.е. точка С лежит на окружности, значит, около четырехугольника АВСD можно описать окружность. Что и требовалось доказать.

Примечание:

Окружность всегда можно описать:

Поделись с друзьями в социальных сетях:

[spoiler title=”источники:”]

http://budu5.com/manual/chapter/3523

[/spoiler]

Here are six different approaches I have tried.

1. cv2 based center of mass (get_center_of_mass)
2. shapely based representative point (get_representative_point)
3. cv2 + skimage.skeleton based center of mass of the skeletonized shape (get_skeleton_center_of_mass)
4. scipy based furthest distance to border (get_furthest_point_from_edge)
5. cv2 based version of the previous furthest distance to border -algorithm (get_furthest_point_from_edge_cv2)
6. the “center point of half-area line” algorithm proposed in this thread by @T.Austin (get_center_of_half_area_line)

Let’s begin with imports and some helper functions

import numpy as np
import cv2
from shapely.geometry import Polygon, LineString, MultiLineString, Point, MultiPoint, GeometryCollection
from skimage.morphology import skeletonize, medial_axis
from scipy.optimize import minimize_scalar
from scipy.ndimage.morphology import distance_transform_edt
import matplotlib.pyplot as plt

H, W = 300, 300

def get_random_contour():
    xs = np.random.randint(0, W, 4)
    ys = np.random.randint(0, H, 4)
    cnt = np.array([[x,y] for x,y in zip(xs,ys)])
    mask = draw_contour_on_mask((H,W), cnt)
    cnt, _ = cv2.findContours(mask, 1, 2)
    cnt = cnt[0]
    return cnt

def draw_contour_on_mask(size, cnt, color:int = 255):
    mask = np.zeros(size, dtype='uint8')
    mask = cv2.drawContours(mask, [cnt], -1, color, -1)
    return mask

def get_center_of_mass(cnt):
    M = cv2.moments(cnt)
    cx = int(M['m10']/M['m00'])
    cy = int(M['m01']/M['m00'])
    return cx, cy

def split_mask_by_line(mask, centroid:tuple, theta_degrees:float, eps:float = 1e-4):
    h, w = mask.shape[:2]
    mask = mask[..., None]
    cx, cy = centroid
    # convert theta first to radians and then to line slope(s)
    theta_degrees = np.atleast_1d(theta_degrees)
    theta_degrees = np.clip(theta_degrees, -90+eps, 90-eps)
    theta_rads = np.radians(theta_degrees)
    slopes = np.tan(theta_rads)[:, None]
    # define the line(s)
    x = np.arange(w, dtype="int32")
    y = np.int32(slopes * (x - cx) + cy)
    _y = np.arange(h, dtype="int32")
    # split the input mask into two halves by line(s)
    m = (y[..., None] <= _y).T
    m1 = (m * mask).sum((0,1))
    m2 = ((1 - m) * mask).sum((0,1))
    m2 = m2 + eps if m2==0 else m2
    # calculate the resultant masks ratio
    ratio = m1/m2
    return (x.squeeze(), y.squeeze()), ratio

def get_half_area_line(mask, centroid: tuple, eps: float = 1e-4):
    # find the line that splits the input mask into two equal area halves
    minimize_fun = lambda theta: abs(1. - split_mask_by_line(mask, centroid, theta, eps=eps)[1].item())
    bounds = np.clip((-90, 90), -90 + eps, 90 - eps)
    res = minimize_scalar(minimize_fun, bounds=bounds, method='bounded')
    theta_min = res.x
    line, _ = split_mask_by_line(mask, centroid, theta_min)
    return line

Now let’s define the functions for finding the visual center

def get_representative_point(cnt):
    poly = Polygon(cnt.squeeze())
    cx = poly.representative_point().x
    cy = poly.representative_point().y
    return cx, cy

def get_skeleton_center_of_mass(cnt):
    mask = draw_contour_on_mask((H,W), cnt)
    skel = medial_axis(mask//255).astype(np.uint8) #<- medial_axis wants binary masks with value 0 and 1
    skel_cnt,_ = cv2.findContours(skel,1,2)
    skel_cnt = skel_cnt[0]
    M = cv2.moments(skel_cnt) 
    if(M["m00"]==0): # this is a line
        cx = int(np.mean(skel_cnt[...,0]))
        cy = int(np.mean(skel_cnt[...,1]))
    else:
        cx = int(M['m10']/M['m00'])
        cy = int(M['m01']/M['m00'])
    return cx, cy

def get_furthest_point_from_edge(cnt):
    mask = draw_contour_on_mask((H,W), cnt)
    d = distance_transform_edt(mask)
    cy, cx = np.unravel_index(d.argmax(), d.shape)
    return cx, cy

def get_furthest_point_from_edge_cv2(cnt):
    mask = draw_contour_on_mask((H,W), cnt)
    dist_img = cv2.distanceTransform(mask, distanceType=cv2.DIST_L2, maskSize=5).astype(np.float32)
    cy, cx = np.where(dist_img==dist_img.max())
    cx, cy = cx.mean(), cy.mean()  # there are sometimes cases where there are multiple values returned for the visual center
    return cx, cy

def get_center_of_half_area_line(cnt):
    mask = draw_contour_on_mask((H,W), cnt, color=1)
    # get half-area line that passes through centroid
    cx, cy = get_center_of_mass(mask)
    line = get_half_area_line(mask, centroid=(cx, cy))
    line = LineString(np.array(list(zip(line))).T.reshape(-1, 2))
    # find the visual center
    contours, _ = cv2.findContours(mask, cv2.RETR_EXTERNAL, cv2.CHAIN_APPROX_NONE)
    contours = [c for c in contours if cv2.contourArea(c) > 5]
    polys = [Polygon(c.squeeze(1)) for c in contours if len(c) >= 3]  # `Polygon` must have at least 3 points
    cpoint = Point(cx, cy)
    points = []
    for poly in polys:
        isect = poly.intersection(line)
        if isect.is_empty:
            # skip when intersection is empty: this can happen for masks that consist of multiple disconnected parts
            continue
        if isinstance(isect, (MultiLineString, GeometryCollection)):
            # take the line segment intersecting with `poly` that is closest to the centroid point
            isect = isect.geoms[np.argmin([g.distance(cpoint) for g in isect.geoms])]
        if isinstance(isect, Point):
            # sometimes the intersection can be a singleton point
            points.append(isect)
            continue
        isect = isect.boundary
        if poly.intersects(cpoint):
            points = [isect]
            break
        else:
            points.append(isect)

    if len(points) == 0:
        # multiple reasons for this one:
        # - if len(polys)==0
        # - if len(polys)==1, but for some reason the line does not intersect with polygon
        # - if the above search does not match with any points

        return cx, cy

    points = points[np.argmin([p.distance(cpoint) for p in points])]
    if isinstance(points, Point):
        return np.array(points.xy)
    
    points = [np.array(p.xy).tolist() for p in points.geoms]
    visual_center = np.average(points, (0, 2))
    return visual_center

Here’s my analysis on the topic:

• get_center_of_mass is the fastest but, as mentioned in this thread, the center of mass can be located outside the shape for non-convex shapes.
• get_representative_point is also fast but the identified point, although always guaranteed to stay inside the shape (or with minor edits even multiple disconnected shapes!), does not have much if anything to do with the center of the object
• get_skeleton_center_of_mass returns a perceptually nice center point, but is slow and requires logic for disconnected shapes
• get_furthest_point_from_edge is relatively fast, generalizes easily to disconnected shapes and the center point is visually pleasing
• get_furthest_point_from_edge_cv performs otherwise similarly as get_furthest_point_from_edge but is an order of magnitude faster
• get_center_of_half_area_line performs neatly: the result is usually closest to where I myself would annotate the visual center. Unfortunately, at least my implementation is quite slow.

rows = 4
cols = 4
markers = ['x', '+', "*", "o", '^', "v"]
colors = ['r','b','g','orange', 'purple', 'lime']
functions = [
    get_center_of_mass, 
    get_representative_point, 
    get_skeleton_center_of_mass, 
    get_furthest_point_from_edge,
    get_furthest_point_from_edge_cv2,
    get_center_of_half_area_line
]

plt.figure(figsize=(2*cols, 2*rows, ))
for i in range(rows*cols): 
    cnt = get_random_contour()
    mask = draw_contour_on_mask((H,W), cnt)
    
    plt.subplot(cols,rows, i+1)
    plt.imshow(mask, cmap='gray')
    for c, m, f in zip(colors, markers, functions):
        l = f.__name__
        cx, cy = f(cnt)
        plt.scatter(cx, cy, c=c, s=100, label=l, marker=m, alpha=0.7)

plt.tight_layout()    
plt.legend(loc=3)
plt.show()

Here’s how the algorithms, run on 100 random examples, compare in speed:

N_EXAMPLES = 100
cnts = [get_random_contour() for _ in range(N_EXAMPLES)]

for fn in functions:
    print(fn.__name__+":")
    %time _ = [fn(cnt) for cnt in cnts]
    print("~ "*40)

get_center_of_mass:
CPU times: user 2.35 ms, sys: 777 µs, total: 3.13 ms
Wall time: 1.91 ms
~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ 
get_representative_point:
CPU times: user 15.7 ms, sys: 0 ns, total: 15.7 ms
Wall time: 14.8 ms
~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ 
get_skeleton_center_of_mass:
CPU times: user 6.52 s, sys: 104 ms, total: 6.62 s
Wall time: 6.62 s
~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ 
get_furthest_point_from_edge:
CPU times: user 413 ms, sys: 63 µs, total: 413 ms
Wall time: 413 ms
~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ 
get_furthest_point_from_edge_cv2:
CPU times: user 47.8 ms, sys: 0 ns, total: 47.8 ms
Wall time: 47.8 ms
~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ 
get_center_of_half_area_line:
CPU times: user 1.66 s, sys: 0 ns, total: 1.66 s
Wall time: 1.66 s
~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~