Как найти середину окружности
Планиметрия (прямая и окружность)
Планиметрия изучется в начальном курсе геометрии и зачастую сводится к решению практических задач без изучения теоретической базы.
В данной статье приводятся альтернативные (подсказкам) решения задач из первого раздела (кроме 1.5) приложения Euclidea (геометрические построения с помощью циркуля и линейки).
Решения задач 1.1, 1.2 и 1.3 основаны на том, что с помощью циркуля и линейки можно построить равносторонний треугольник.
1.1 Построить угол 60° с заданой стороной
1.2 Построить серединный перпендикуляр к отрезку
На данной ограниченной прямой построить равносторонний треугольник
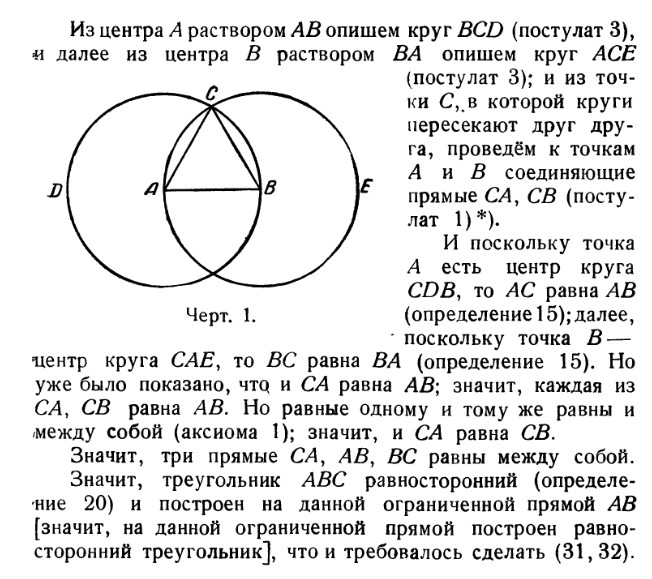
1.3 Середина отрезка
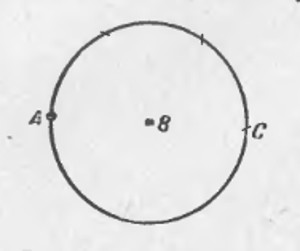
всё, что можно построить с помощью циркуля и линейки, может быть построено с помощью одного циркуля.
Из точки В радиусом АВ описываем окружность.
По этой окружности откладываем от точки А расстояние АВ три раза: получаем точку С, очевидно, диаметрально противоположную А. Расстояние АС представляет собой двойное рассрастояние АВ. Проведя окружность из С радиусом ВС, мы можем таким же образом найти точку,
диаметрально противоположную В и, следовательно, удаленную от А на
тройное расстояние АВ, и т. д.
любое построение, выполнимое на плоскости циркулем и линейкой, можно выполнить одной линейкой, если нарисована хотя бы одна окружность и отмечен её центр.
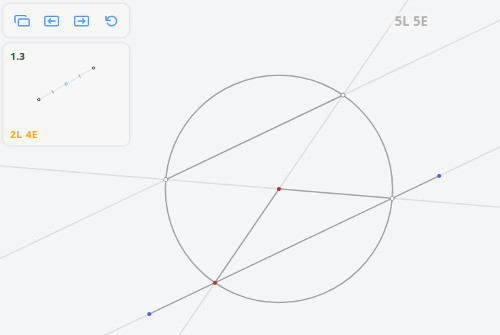
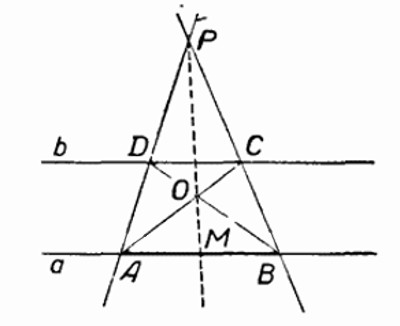
Проведем прямые PA и PB и отметим точки D и C их пересечения прямой b. Пусть О — точка пересечения прямых AC и BD. Тогда, согласно предыдущей лемме, прямая PO пересечёт отрезок AB в его середине M.
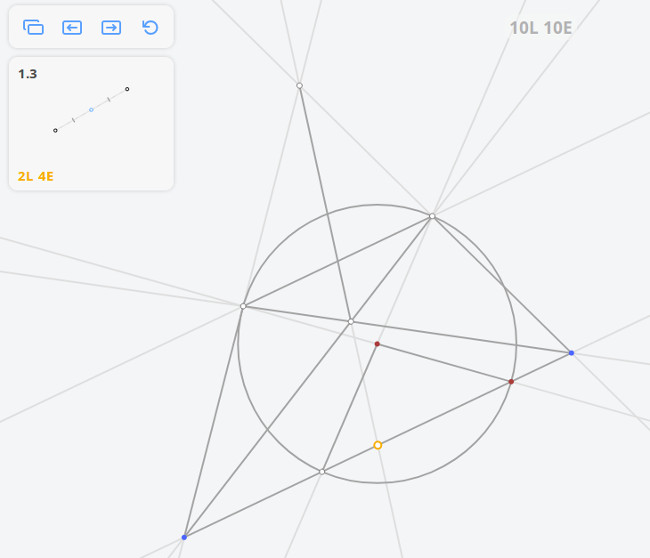
Решением задачи 1.3 по методу Штейнера-Понеселе будет:
1.4 Окружность, вписанная в квадрат
Из точки A, лежащей вне данной полуокружности, опустить на её диаметр перпендикуляр, обходясь при этом без циркуля. Положение центра полуокружности не указано.
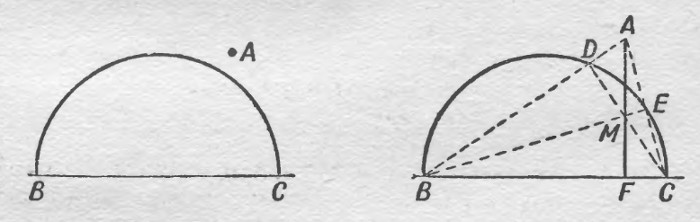
Нам пригодится здесь то свойство треугольника, что все его высоты пересекаются в одной точке. Соединим A с B и C; получим точки D и E. Прямые BE и CD, очевидно, — высоты треугольника ABC. Третья высота — искомый перпендикуляр к BC — должна проходить через пересечение двух других, т.е. через точку M. Проведя по линейке прямую через точки A и M, мы выполним требованиек задачи, не прибегая к услугам циркуля.
И опустив перпендикуляр из точки пересечения диагоналей квадрата на ребро, найдём середину ребра.
Это же построение можно использовать для решения задачи 2.9 Окружность, касающаяся прямой
1.6 Найти центр окружности
Плоский угол, опирающийся на диаметр окружности, — прямой.
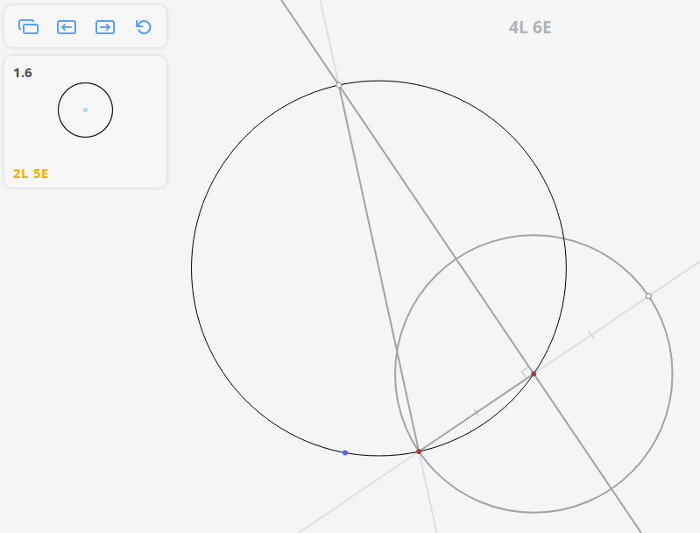
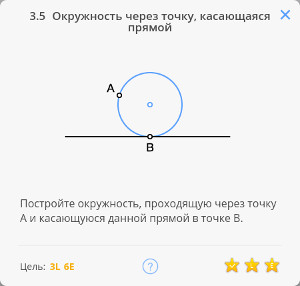
Определение: касательной к окружности называется прямая, имеющая с окружностью одну общую точку. Касательная к окружности перпендикулярна радиусу, проведённому в точку касания.
Рассмотрим задачу 2.8
2.8 Касательная к окружности в точке
Возвращаясь к предыдущей задаче, эту задачу можно решить построив угол, опирающийся на диаметр окружности по теореме Фалеса
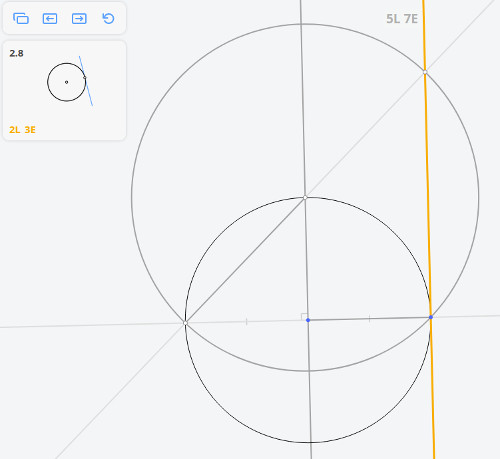
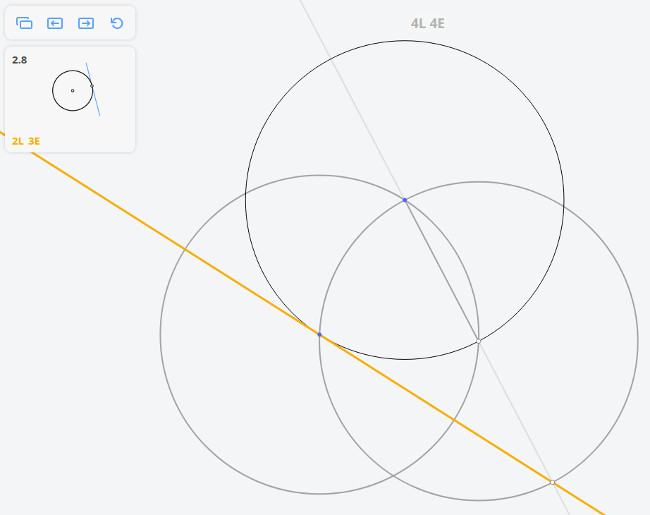
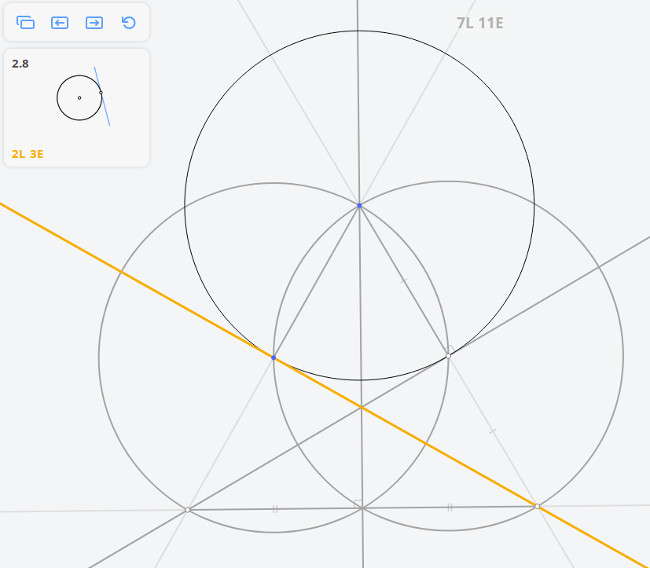
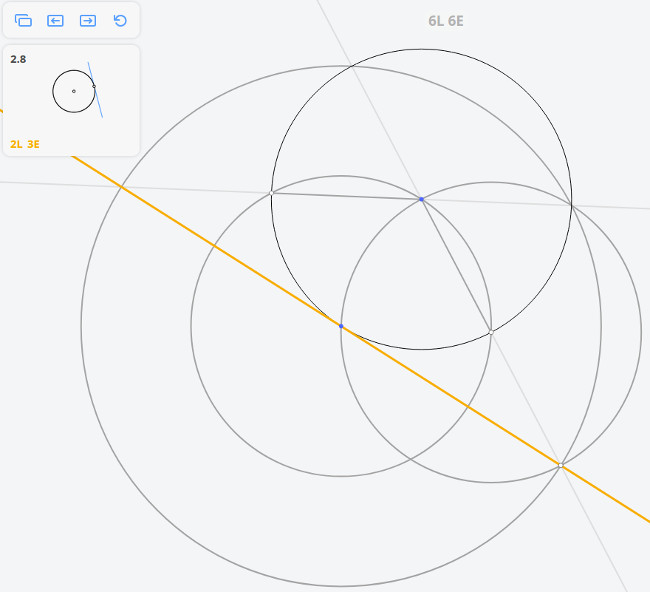
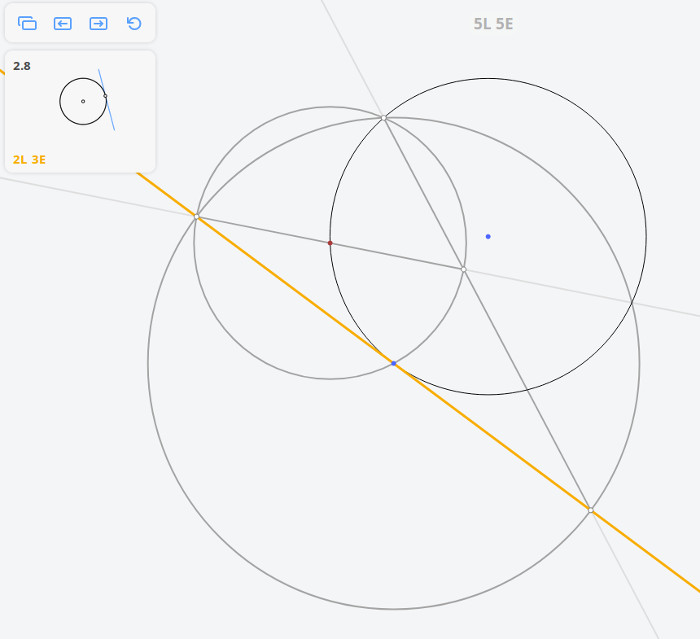
Далее, построив перпендикуляр к касательной, найдём диаметр окружности, и, разделив его пополам, найдём центр окружности.
Ещё об одном способе построения касательной к окружности можно узнать из лекции 1.5 курса «Геометрия и группы» А. Савватеева ссылка
1.7 Квадрат, вписанный в окружность
Задача Наполеона

Решим задачу методом Мора-Маскерони.
Построим три окружности радиусом r и две окружности радиусом
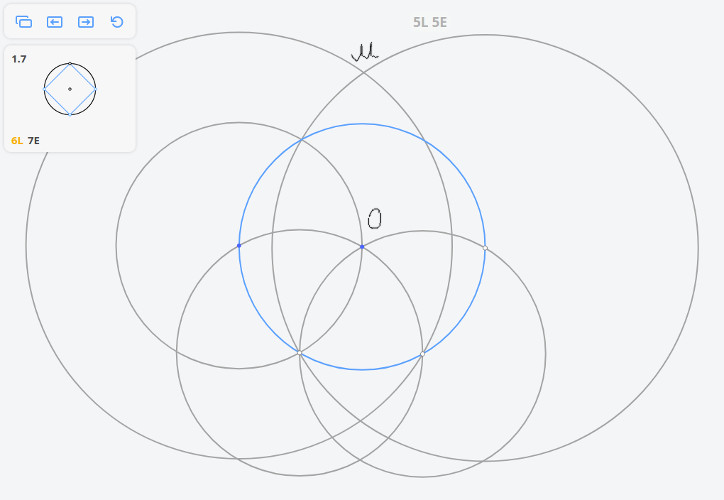
В приложении нет такой операции, как перенос раствора циркуля (равного MO), поэтому необходимо использовать дополнительные построения.
Для того, чтобы построить касательную к исходной окружности, параллельную МО, необходимо произвести построения, которые были приведены выше (построить три окружности радиусом r и две окружности радиусом ), но вместо исходной окружности взять окружность, обозначенную на рисунке синим цветом
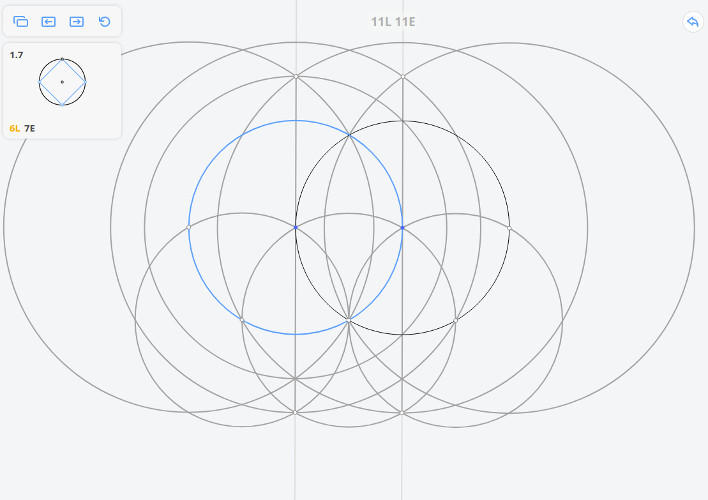
Т.о. мы перенесли раствор циркуля (равный МО) в точку А.
Далее из точки А необходимо провести окружность c радиусом МО 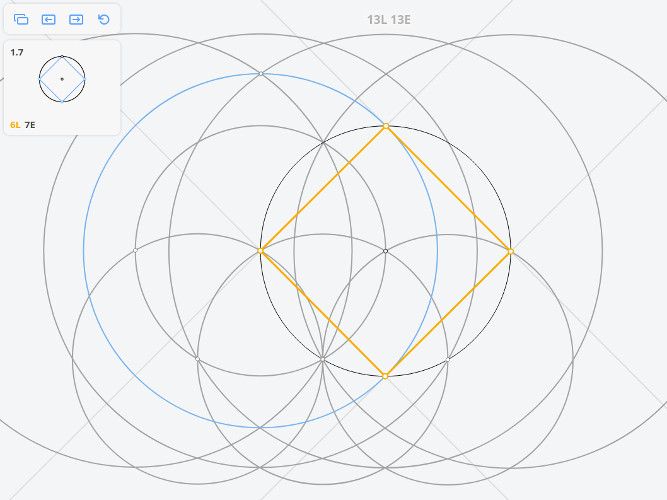
Быстрый способ, как найти центр окружности

В данном обзоре автор поделится с нами довольно простым способом, как быстро найти центр окружности.
Для этого нам потребуется всего два предмета: угольник и карандаш. Первым делом необходимо провести прямую линию в любом месте окружности.

Советуем также прочитать: как изготовить своими руками антенну для усиления 4G сигнала на даче или в частном доме.
После того, как начертили линию, измеряем длину, и делим это расстояние ровно пополам.
В данном случае длина линии составляет 210 мм. Разделив ее пополам, получаем 105 мм — ставим в этом месте отметку.

С помощью угольника проводим вторую линию, которая должна быть перпендикулярна первой (то есть проходить под углом 90 градусов).

Основные этапы работ
На следующем этапе проделываем те же операции с другой стороны окружности (только не параллельно, а немного в стороне).
Чертим линию, измеряем ее длину (в данном случае — 218 мм), делим пополам (109 мм) и откладываем в этом месте точку. После этого проводим перпендикулярную линию, как и в предыдущем случае.

Пересечение двух линий, которые мы чертили под углом 90 градусов, и будет являться центром круга.

Подробно об этом способе можно посмотреть на видео ниже. Статья подготовлена на основе видео с YouTube канала « ПОГРАНЕЦ 13 ».
Как найти Как найти центр окружности?
Как найти центр отверстия?
Через точки пересечения дуг проводят две прямые по направлению к центру до их пересечения в точке О. Точка пересечения этих прямых, и будет искомым центром отверстия.
Как найти центр окружности из уравнения?
Уравнение окружности ω (A; R) имеет вид (x – a) 2 + (y – b) 2 = R 2 , где a и b – координаты центра A окружности ω (A; R) .
Чем размечают отверстия?
Размечать центровые отверстия в деталях диаметром до 40 мм лучше при помощи специального приспособления, называемого колоколом. Оно состоит из корпуса, конического раструба и кернера, перемещаемого в корпусе.
Как найти центр окружности на плоской заготовки?
Есть и совсем простой способ нахождения центра плоской заготовки круглой формы. Всего-то нужно обвести её по периметру, положив на лист бумаги, затем вырезать по начерченной линии круг, согнуть его вчетверо и центр будет найден. Он находится точно на линии пересечения сгибов.
Как правильно разметить отверстия?
Разметка отверстий для сверления.
- Определить расположение отверстия по рабочему чертежу. Аккуратно отмерить расстояние отверстия от обоих краев доски. .
- Наколите центр отверстия шилом. .
- Если должны совпасть отверстия, просверленные в двух досках, зажмите обе доски в тисках.
Окружность. Форма и положение.
Окружность – это замкнутая плоская линия, всякая точки которой равноудалена от одной и той же точки (O), называемой центром.
Прямые (OA, OB, OС. . . ), соединяющие центр с точками окружности – это радиусы.
Бесконечная прямая (MN), прочерченная через какие-нибудь две точки окружности – секущая. а часть ее (EF), заключенная между этими точками, называется хордой.
Всякая хорда (AD), прочерченная через центр – диаметр.
Диаметр представляет наибольшую из хорд..Всякий диаметр делит окружность и круг пополам. Таким образом, всякий диаметр разделит окружность на две полуокружности, а круг на два полукруга.
Какая-нибудь часть окружности (напр. EmF ) называется дугой.
О хорде (EF), соединяющей концы дуги, говорят, что она стягивает эту дугу.
Для определения дуги иногда применяют знак È ; напр., пишут так: ÈEmF.
Часть плоскости, ограниченная окружностью, именуют кругом.
Часть круга (напр., СOB, заштрихованная на чертеже), ограниченная дугой и двумя радиусами, проведенными к концам дуги, обозначают как сектор.
Часть круга, (напр., EmF), ограниченная дугой и стягивающей ее хордой, обозначают как сегмент.
Из этого получаем:
1. Все радиусы одной окружности равны.
2. Два круга с одинаковыми радиусами будут равны.
3. Диаметр равен двум радиусам.
4. Точка, лежащая внутри круга, ближе к центру, а точка, лежащая вне круга, дальше от центра, чем точки окружности.
5. Диаметр, перпендикулярный к хорде, делит эту хорду и обе стягиваемые ею дуги пополам.
6. Дуги, заключенные между параллельными хордами, равны.
При работе с окружностями применяют следующие теоремы:
1. Теорема. Прямая и окружность не могут иметь более двух общих точек.
Из этой теоремы получаем два логично вытекающих следствия:
Никакая часть окружности не может совместиться с прямой, потому что в противном случае окружность с прямой имела бы более двух общих точек.
Линия, никакая часть которой не может совместиться с прямой, называется кривой.
Из предыдущего следует, что окружность есть кривая линия.
2. Теорема. Через всякие три точки, не лежащие на одной прямой, можно провести окружность и только одну.
Как следствие данной теоремы получаем:
Три перпендикуляра к сторонам треугольника вписанного в окружность проведенные через их середины, пересекаются в одной точке, которая является центром окружности.
Решим задачу. Требуется найти центр предложенной окружности.
Отметим на предложенной три любые точки A, B и С , начертим через них две хорды, например, AB и СB, и из середины этих хорд укажем перпендикуляры MN и PQ. Искомый центр, будучи одинаково удален от A, B и С, должен лежать и на MN, и на PQ, следовательно, он находится на пересечении этих перпендикуляров, т.е. в точке O.
Определение центра окружности и центра дуги окружности
Порядок определение центра
Взаимное пересечение перпендикуляров, восставленных в середине каждой хорды, определяет центр окружности (точку О). На фиг. 9,6 показано нахождение центра дуги окружности (построение аналогично предыдущему).
Выпрямление дуги окружности
Определение длины 1 дуги АВ окружности (приближенный способ, фиг. 10).
Через хорду АВ проводят перпендикуляр (фиг. 10,а), пересекающий дугу в точке К. Из точек С и D, как из центров, радиусами г, равными d— диаметру окружности, проводят две дуги до взаимного их пересечения в точке 01.
Расстояние между точками пересечения лучей 01А и O1B с касательной, проведенной к окружности в точке К, определяет приближенное значение спрямленной дуги (отрезок А1В1).
Расстояние между точками С1 и D1 определяет приближенную длину полуокружности. При отсутствии центра окружности
длина дуги АВ (фиг. 10,6) может быть определена следующим путем: хорду А В делят на четыре равные части; одну четвертую часть откладывают от точки В на дуге АВ; полученную точку С соединяют с точкой деления 1. Отрезок 1—С равен половине длины дуги АВ; CD — приближенное значение длины всей дуги АВ.
Определение длины окружности. Длину окружности определяют по формуле l=П*D, где l — длина окружности, П = 3,14159, a D—диаметр окружности. На фиг. 11,а показана длина l окружности диаметра D.
Графически длина окружности приближенно может быть определена путем суммирования длины двух сторон аз равностороннего треугольника и двух сторон а квадрата, вписанных в окружность, как это показано на фиг. 11,6 (2аз + 2а4). Точность определения — 0,01. На фиг. 11,в длина окружности определена следующим способом: из центра О под углом 30° проводят прямую до пересечения ее в точке А с касательной к окружности; от точки А откладывают отрезок АВ, равный трем радиусам R; из точки В, как из центра, радиусом ВМ проводят дугу окружности до пересечения с касательной прямой в точках С и D. Отрезок CD будет равен длине окружности. Точность определения — 0,0001.
Определение приближенной длины очерка эллипса (фиг. 12). Для определения длины очерка эллипса ACBD соединяют точки А и С и из центра О радиусом, равным АС, засекают на осях эллипса точки М и N. Измерив длину отрезка MN, умножают ее на 3,14 и получают приближенную длину очерка эллипса (l = 3,14*MN).
[spoiler title=”источники:”]
http://www.calc.ru/Okruzhnost-Forma-I-Polozheniye.html
http://www.cad-project.ru/opredelenie-czentra-okruzhnosti
[/spoiler]
Download Article
Use the midpoint formula, the distance formula, or a compass to find circumcenter
Download Article
- What is the circumcenter?
- Finding Circumcenter with the Midpoint Formula
- Finding Circumcenter with the Distance Formula
- Drawing the Circumcenter with a Compass
|
|
|
You’ve got a stack of math problems in front of you and they’re all asking the same thing: find the circumcenter of the triangle. You have the triangle and the coordinates of its vertices, but where do you go from here? Well, you’ve come to the right place! In this article, we’ll tell you what formulas you need and how to use them to calculate the circumcenter’s coordinates. To help you visualize the circumcenter of a triangle, we’ll also give you step-by-step instructions on how to draw it with a compass. Read on to learn more!
Things You Should Know
- Circumcenter is where the perpendicular lines at the midpoints of each triangle’s side intersect. Each vertex of the triangle is an equal distance from circumcenter.
- Find circumcenter using a triangle’s vertices and the mid-point and slope-intercept formulas.
- Alternatively, use the distance formula to find circumcenter.
- Draw the circumcenter on a triangle using a compass. Find the perpendicular, bisecting lines on the triangle’s sides and mark where they intersect.
-

Circumcenter is where a triangle’s perpendicular, bisecting lines intersect. If you draw a line at the midpoint of each triangle’s side, you’ll have 3 perpendicular lines bisecting each side. These perpendicular lines all meet together at a point; this is the circumcenter. The circumcenter also forms the triangle’s circumcircle. It is the center of a circle, that when drawn, passes through each vertex of the triangle.[1]
- The main principle behind the circumcenter is that each vertex on the triangle is an equal distance away from the circumcenter.
-
On right triangles, the circumcenter is located at the midpoint of the hypotenuse, or the longest side of the triangle.[2]
- On obtuse triangles, the circumcenter is located outside of the triangle.
- On acute triangles, the circumcenter is located inside the triangle.
Advertisement
-

1
Find the midpoints of the triangle using the vertices’ coordinates. Most math problems give you the (x, y) coordinates of each of the triangle’s vertices. The circumcenter is at the intersection of the perpendicular lines at the midpoint of the triangle’s sides. Because the distance from the circumcenter to each vertex is the same, you only need to find the midpoints of 2 sides.[3]
- A triangle’s verticies are A = (-4, 2), B = (2, 4), and C = (4, -4).
- Use the midpoint formula: [(x1 + x2)/2,( y1 + y2)/2].
- Plug in the coordinates for line AB: [(-4 + 2)/2, (2 + 4)/2].
- Plug in the coordinates for line BC: [(2 + 4)/2, (4 + -4)/2].
- Solve each midpoint: line AB’s midpoint is (-1, 3) and line BC’s is (3, 0).
- A triangle’s verticies are A = (-4, 2), B = (2, 4), and C = (4, -4).
-

2
Calculate the slope of the 2 lines. The perpendicular lines at the triangle’s midpoints intersect to give you the circumcenter. So, calculate the slope of the lines to find out where they intersect. Because these lines are perpendicular, take the opposite reciprocal of the slope to find the perpendicular line’s slope. For example, a slope of 2/1 becomes -½.[4]
- A triangles vertices are A = (-4, 2), B = (2, 4), and C = (4, -4).
- Use the slope formula: m = (y2 – y1) / (x2 – x1).
- Plug in the coordinates for line AB: m = (4 – 2) / (2 – -4).
- Plug in the coordinates for line BC: m = (-4 – 4) / (4 – 2).
- Solve each slope: line AB’s slope is m = ⅓ and line BC’s is m = -4.
- Take the opposite reciprocal of the slope: Flip AB’s slope to 1/(⅓) and change the sign. The perpendicular slope is m = -3. BC’s perpendicular slope is m = ¼.
- A triangles vertices are A = (-4, 2), B = (2, 4), and C = (4, -4).
-

3
Solve each line’s point-slope equation to find the y-intercept. With your slopes identified for the perpendicular lines, use the slope-intercept formula of y – y1 = m(x – x1) to find the entire slope equation.[5]
- Use the point-slope equation: y – y1 = m(x – x1)
- Plug in the midpoint and slope for line AB: y – 3 = -3(x – -1).
- Plug in the midpoint and slope for line BC: y – 0 = ¼(x – 3).
- Solve and simplify each equation: line AB’s is y = -3x. Line BC’s is y = ¼x – ¾ (or 4y = x – 3 if you get rid of the fractions).
- Use the point-slope equation: y – y1 = m(x – x1)
-

4
Set the equations equal to each other to find circumcenter. Use substitution to find where the 2 perpendicular lines intersect. Insert line AB’s y-value into line BC’s point-slope equation. This gives you an x-value. Then, plug the x-value into either point-slope equation to find the y-coordinate. Put the x and y values together to get the circumcenter’s coordinates![6]
- Substitute line AB’s point-slope equation into line BC’s equation: (-3x) = ¼x – ¾.
- Solve for x: x = -3/13.
- Plug x into either equation: y = -3(-3/13) with y = 9/13. So, the circumcenter is located at (-3/13, 9/13).
- Substitute line AB’s point-slope equation into line BC’s equation: (-3x) = ¼x – ¾.
Advertisement
-

1
Use the distance formula to set 2 vertices equal to each other. Each vertex on the triangle is the same distance away from the circumcenter. If the circumcenter is O and the triangle’s vertices are A, B, and C, the distance between A to O is the same as B to O and C to O. So, set AO and BO equal to each other, as well as BO and CO, using the distance formula.[7]
- A triangle’s vertices are A = (−2, 3), B = (2, −1), and C = (4, 0).
- Use a simplified distance formula: (x2 – x1)2 + (y2 – y1)2.
- Set A and B equal to each other: (-2 – x)2 + (3 – y)2 = (2 – x)2 + (-1 – y)2.
- Set B and C equal to each other: (2 – x)2 + (-1 – y)2 = (4 – x)2 + (0 – y)2.
- A triangle’s vertices are A = (−2, 3), B = (2, −1), and C = (4, 0).
-

2
Solve the distance equations. Use the FOIL method (First, Outer, Inner, Last) to multiply the squared expressions together (i.e. (-2-x)2 in the example above). Then, simplify the expression by adding or subtracting the x, y, and numerical values together.[8]
- Use FOIL to solve each equation.
- For AO = BO: x2 + 4x + 4 + y2 − 6y + 9 = x2 − 4x + 4 + y2 + 2y +1
- For BO = CO: x2 − 4x + 4 + y2 + 2y + 1= x2 − 8x + 16 + y2
- Solve and simplify each equation: AO = BO results in y = x + 1. Solving BO = CO results in 4x + 2y = 11.
- Use FOIL to solve each equation.
-

3
Substitute 1 equation into the 2nd to get the circumcenter’s x-value. To find the x-coordinate of the circumcenter, insert the first equation’s y-value in the second equation. Then, solve for x.[9]
- Substitute AO = BO’s equation into BO = CO: 4x + 2(x + 1) = 11.
- Expand the equation: 4x + 2x +2 = 11.
- Solve for x: x = 3/2.
- Substitute AO = BO’s equation into BO = CO: 4x + 2(x + 1) = 11.
-

4
Insert the x-value in one of the equations to find the y-coordinate. Now that you know what the circumcenter’s x-coordinate is, solve for its y-coordinate. Just substitute x into one of the equations and solve. Then, put the x and y-values together to get the circumcenter’s coordinates![10]
- Insert x into one of the equations: y = (3/2) + 1.
- Solve for y: y = 5/2. So, the circumcenter’s coordinates are (3/2, 5/2).
- Insert x into one of the equations: y = (3/2) + 1.
Advertisement
-

1
Use a compass to draw an arc through one of the triangle’s sides. Choose a side of the triangle and place the compass point on one of the line’s vertices; these are the points where 2 lines meet. Open the compass up so it’s a little more than half as long as the line segment. With the point in place, draw one continuous arc spanning below the triangle’s side, through it, and above it.[11]
-

2
Place the compass on the line’s other vertex and draw an arc. Using the same triangle side you chose, move the compass point to the line’s other vertex. Follow the same steps as above to draw an arc above and below this side, too.[12]
-

3
Use a ruler to draw a line through the points where the arcs intersect. With your 2 arcs drawn, you’ll see 2 points where they meet. Just take out a ruler and draw a straight line through these points, taking the line through the triangle’s side. This gives you the midpoint of this triangle line and the perpendicular, bisecting line.[13]
-

4
Follow the same steps for one of the triangle’s other sides. Place the compass point at the vertex of one of the other triangle sides. Adjust the compass so it’s open to about half the size of the line segment. Draw an arc, then move the compass to the side’s other vertex. Make the other arc line, then draw a straight line through the intersecting points.[14]
-

5
Find the circumcenter by marking where the 2 lines intersect. With your 2 perpendicular, bisecting lines drawn, simply mark where they intersect. Depending on the type of triangle you have, the circumcenter might be in the triangle, on one of its sides, or outside of the triangle.[15]
- If you want, find the perpendicular line of the 3rd triangle side, too. You’ll see that its perpendicular, bisecting line also passes through the circumcenter.
-

6
Use the compass to draw the circumcircle around the triangle. Place the compass point at the circumcenter. Then, adjust the compass so the pencil reaches one of the triangle’s vertices. Draw the circle. As you go around the triangle, you’ll notice that the edges of the circle just touch each point of the triangle. This is because the triangle’s vertices are equidistant from the circumcenter.[16]
Advertisement
Ask a Question
200 characters left
Include your email address to get a message when this question is answered.
Submit
Advertisement
References
About This Article
Thanks to all authors for creating a page that has been read 2,229 times.
Did this article help you?
Загрузить PDF
Загрузить PDF
Найдя центр круга или окружности, вы сможете решать различные геометрические задачи, например, на вычисление длины окружности или площади круга. Найти центр круга можно разными способами. Вы можете провести пересекающиеся отрезки; вы можете начертить пересекающиеся окружности; вы можете воспользоваться линейками.
-

1
Начертите окружность. Сделайте это при помощи циркуля. Радиус (диаметр) круга может быть любым. Если окружность вам дана, новую окружность чертить не нужно.
- Циркуль – это инструмент, предназначенный для черчения окружностей и их измерения. Циркуль можно купить в канцелярском магазине или в магазине для школьников.[1]
- Циркуль – это инструмент, предназначенный для черчения окружностей и их измерения. Циркуль можно купить в канцелярском магазине или в магазине для школьников.[1]
-

2
Проведите хорду. Хорда – это отрезок, соединяющий любые две точки, лежащие на окружности, и не проходящий через центр окружности.[2]
Обозначьте эту хорду как АВ.- Проводите прямые и отрезки при помощи карандаша, чтобы иметь возможность стереть их после нахождения центра окружности. Не давите на карандаш, чтобы вам было легче стереть нарисованные линии.
-

3
Проведите вторую хорду. Она должна быть параллельна и равна первой хорде АВ. Обозначьте эту хорду как CD.[3]
-

4
Соедините точки А и С. Эта третья хорда АС должна проходить через центр окружности, но для его нахождения вам понадобится провести четвертую хорду.
-

5
Соедините точки B и D. Это четвертая хорда BD, которая должна пересекаться с третьей хордой AC.
-

6
Найдите центр окружности. Если вы правильно провели все отрезки (хорды), то центр окружности – это точка пересечения хорд AC и BD.[4]
Отметьте центр окружности ручкой или карандашом. Если вам нужно отметить только центр окружности, сотрите четыре хорды, которые вы провели ранее.Реклама
-

1
Между двумя точками окружности проведите хорду. Воспользуйтесь линейкой, чтобы соединить две точки на окружности. Точки можно выбрать произвольно. Обозначьте точки как А и В.
-

2
При помощи циркуля начертите две пересекающиеся окружности. Окружности должны быть одного радиуса. Центром первой окружности сделайте точку А, а второй окружности – точку В. Чертите окружности так, чтобы они пересекались наподобие диаграммы Венна.
- Чертите окружности карандашом, а не ручкой, чтобы иметь возможность стереть их.
-

3
Проведите вертикальную прямую через точки пересечения начерченных окружностей. Окружности будут пересекаться в двух точках, которые расположены одна над другой. Проведите прямую при помощи линейки; убедитесь, что обе точки лежат на этой прямой. Точки, в которых эта прямая пересекает исходную окружность, обозначьте как С и D. Отрезок СD является диаметром исходной окружности.
-

4
Сотрите две начерченные вами окружности. Это необходимо для того, чтобы очистить пространство для последующих действий. Теперь на вашем листе останется исходная окружность и два перпендикулярных друг другу отрезка. Не стирайте центры стертых окружностей (эти центры расположены в точках А и В). Далее вы начертите две новые окружности.
-

5
Начертите две новые окружности. Для этого воспользуйтесь циркулем. Центром первой окружности будет точка С, а второй окружности – точка D. Эти окружности также должны пересекаться наподобие диаграммы Венна. Помните, что точки С и D – это точки пересечения вертикальной прямой с исходной окружностью.
-

6
Проведите прямую через две точки, в которых пересекаются начерченные вами окружности. Эта прямая будет расположена горизонтально. Полученный отрезок представляет собой второй диаметр исходной окружности и должен быть перпендикулярен первому диаметру.
-

7
Найдите центр окружности. Точка пересечения двух диаметров является центром исходной окружности. Отметьте эту точку. Если нужно, сотрите начерченные вами окружности и диаметры.
Реклама
-

1
К данной окружности проведите две касательные. Касательные можно провести к двум произвольным точкам окружности. Но вы облегчите себе работу, если проведете касательные под прямым или острым углом друг к другу.[5]
-

2
Теперь проведите еще две касательные, которые будут параллельны касательным, которые вы провели в предыдущем шаге. Таким образом, проведенные четыре касательные образуют подобие параллелограмма или прямоугольника.
-

3
Проведите диагонали параллелограмма. Точка пересечения этих диагоналей является центром окружности.
-

4
Проверьте правильность нахождения центра окружности при помощи циркуля. Центр окружности расположен строго в точке пересечения диагоналей, только если вы не допустили ошибку при проведении параллельных касательных или диагоналей. Сотрите параллелограмм и его диагонали.
Реклама
Советы
- Вместо чистого листа или листа в линейку работайте на листе в клетку. Так вам будет проще проводить перпендикулярные прямые.
- Центр окружности можно вычислить математически через дополнение до полного квадрата.[6]
Это работает в том случае, если вам дано уравнение окружности, а не сама окружность.
Реклама
Предупреждения
- Поверочная линейка немного отличается от обычной линейки. В отличие от обычной линейки на поверочной линейке нет шкалы. Вы можете превратить поверочную линейку в обычную, если нанесете на нее измерительную шкалу.
- Чтобы найти «истинный» центр окружности, используйте циркуль и поверочную линейку.
Реклама
Что вам понадобится
- Карандаш
- Бумага
- Линейка
- Циркуль
Об этой статье
Эту страницу просматривали 230 390 раз.
Была ли эта статья полезной?
Уверен, у каждого домашнего мастера был случай, когда ему нужно было сделать разметку какой-нибудь круглой заготовки и найти центр ее основания. Казалось бы, это очень просто сделать, но некоторые мастера долго не могут найти выход в данной ситуации. Сегодня я покажу вам два простых решения, с помощью которых можно быстро и точной найти центр любой окружности.
1. Первый способ подойдет для разметки небольших заготовок. В качестве примера я возьму заглушку от пластиковой трубы диаметром 50 мм.
Для того, чтобы найти центр окружности заглушки, не нужны будут какие-то математические вычисления и сложные манипуляции. Нам понадобятся всего лишь строительный угольник и обычная линейка (или второй угольник), которые есть в любой мастерской.
Складываем вместе угольник и линейку, так чтобы образовался угол в 45 градусов.
Затем, придерживая одной рукой угольник и линейку, прикладываем их к круглой заготовке (заглушке) так, чтобы она вплотную соприкасалась с двумя сторонами угольника.
Теперь берем карандаш и чертим на заглушке первую линию, потом немного ее поворачиваем и делаем вторую метку (достаточно провести две линии, но для уверенности можно поставить три метки).
Все задача решена! Точка пересечения этих двух линий и будет центром данной окружности. Данный способ один из самых быстрых и простых.
2. Второй способ подойдет, если окружность имеет большой диаметр или она расположена на плоскости. Для примера я обвел карандашом крышку от кастрюли. В этом случае тоже все очень просто. Для начала выбираем любую точку на окружности.
Потом от этой точки чертим две линии до пересечения с окружностью так, чтобы у нас получился прямой угол (90 градусов). Для построения данных линий проще всего воспользоваться угольником (если окружность очень большая, линии можно продлить с помощью линейки).
А теперь все очень просто, соединяем точки, в которых пересекаются линии с окружностью и измеряем длину получившегося отрезка. Его середина и будет центром окружности. Уверен, многие помнят это из уроков по геометрии. Середина гипотенузы прямого треугольника вписанного в окружность, является центром этой окружности.
![]()
![]()
Очень просто – измеряем диаметр круга, строим вокруг нашей окружности равносторонний квадрат, со сторонами равными диаметру круга. Стороны квадрата пройдут по касательной к окружности. Далее делим этот квадрат по диагонали на четыре треугольника. В точке пересечения линий будет цент круга.

автор вопроса выбрал этот ответ лучшим
![]()
Galina7v7
[120K]
6 лет назад
Когда говорят о нахождении центра круга или окружности, то многие считают, что это просто, мол, проведи два диаметра.и всё.А как провести диаметр, если центра не видно.Но с помощью циркуля и простой линейки это сделать возможно.
Отмечаем на окружности(обрамляющей круг) четыре произвольных точки A,B,C,D,примерно располагающих на одном расстоянии друг от друга(это даже не важно).Из точек А и В произвольным радиусом провести засечки циркулем. Две точки А1 и В1-точки пересечения засечек, соединяем, и она точно лежит на диаметре круга.
Аналогично для точек С и Д получим точки С1 и Д1, соединяем их, и прямая С1Д1 тоже лежит на другом диаметре круга.Пересечение любых двух диаметров окружности даёт её центр, точку О.
И это один из верных способов построения центра круга и окружности.
![]()
Bokatashka
[22.4K]
8 лет назад
Чтобы найти середину круга нужно провести две хорды. У каждой из них найти середины и провести к ним перпендикулярные лучи. Точка пересечения этих лучей и будет центром круга.

Также центр круга можно найти при помощи циркуля. Для этого нужно провести горизонтальную линию от одной точки окружности до другой (отмечаем точки А и В):

При помощи циркуля начертить два одинаковых перекрывающихся круга с центрами в точках А и В.

Далее проводим вертикальную линию через точку, в которой круги пересекаются. Отмечаем на окружности точки C и D:

Для удобства стираем два вспомогательных круга и получаем такой рисунок:

Чертим ещё два одинаковых перекрывающихся круга с центрами в точках С и D:

Проводим горизонтальную линию через точки пересечения этих двух кругов. Отмечаем на окружности точки Е и F:

Стираем вспомогательные круги. Точка пересечения прямых СD и EF (назовём её точкой О) и будет искомой серединой круга.

Чтобы найти центр круга, достаточно провести диаметр и построить к нему перпендикуляр с помощью циркуля и линейки.
сначала проводим через круг линию (можно произвольно, но лично я для удобства провожу горизонтальную) и с помощью циркуля и линейки проводим перпендикулярную линию, которая делит нашу хорду и весь круг ровно пополам. Аналогично проводим перпендикуляр к уже полученному диаметру и находим центр круга. Ко всему прочему – мы еще разделили окружность на четыре ровные части.

Но бывает, что диаметр провести нельзя, так как есть только часть круга, тогда можно применить способ. который подходит практически везде:
в произвольном месте провести две хорды и через их центры провести перпендикуляры – в точке пересечения и будет центр

![]()
Грустный Роджер
[395K]
8 лет назад
Всех делов тут – вспомнить школьную геометрию. Два радиуса и хорда дают равнобедренный треугольник, в котором высота, опущенная на основание, делит его пополам.
Поэтому на окружности надо отметить три произвольные точки, и одну из них соединить с двумя другими. Это даст две хорды. Теперь делим эти хорды пополам и к каждой проводим перпендикуляр к середине – это стандартная школьная задачка на построение циркулем и линейкой. Точка пересечения перпендикуляров и будет центром круга.
![]()
Мне представляется достаточно простой способ нахождения центра окружности путем вписывания в нее прямоугольника. То есть проводим произвольную хорду и принимаем этот отрезок за одну сторону прямоугольника. Достраиваем сперва перпендикулярные стороны из точек пересечения хорды с окружностью, потом достраиваем противоположную параллельную сторону. Вся проблема – в проведении перпендикуляров, но и во всех остальных методах применяется тот же принцип построения. После получения такого прямоугольника проводим в нем диагонали и вуаля, точка их пересечения и будет центром окружности, ну а сами диагонали окажутся диаметрами.

![]()
Ксарфакс
[156K]
6 лет назад
Чтобы найти центр круга, можно отметить 2 любые точки на окружности и провести отрезок.
Затем нужно провести ещё один отрезок, имеющий такую же длину и параллельный первому отрезку.
Соединяем противоположные концы отрезков линиями, которые будут параллельными друг другу.
Таким образом, получится прямоугольник, который будет вписан в круг.
Центр пересечения его диагоналей и будет центром нашего круга.

![]()
Azamatik
[55.3K]
6 лет назад
Для этого берем треугольник (линейку) и проводим диаметр круга. Далее можно с помощью угольника провести такой же диаметр, перпендикулярный первой линии. Пересечение двух этих линий и будет центром (серединой) круга.
![]()
Ярослава Лещинская
[29.9K]
8 лет назад
Найти середину круга очень просто. Надо нарисовать круг и провести диаметр слева направо и сверху вниз, точка соединения линий и будет середина круга. Если круг уже вырезан, сложить его пополам и еще раз пополам, в точке соединений сгибов и будет середина круга.
Водяной
[7.5K]
8 лет назад
Проводим две не параллельные любые хорды. Каждую хорду делим пополам, известным всем способом, как делят отрезки при помощи циркуля и линейки. В точке пересечения разделивших хорды лучей получим центр окружности.
