Определение.
Середина отрезка – это точка, которая лежит на отрезке и находится на равном расстоянии от конечных точек.
В геометрических задачах часто можно столкнуться с необходимостью найти середину отрезка заданного координатами точек его концов, например в задачах поиска медианы, средней линии, …
Каждая координата середины отрезка равна полусумме соответствующих координат концов отрезка.
Формулы вычисления расстояния между двумя точками:
- Формула вычисления координат середины отрезка с концами A(xa, ya) и B(xb, yb) на плоскости:
xc = xa + xb yc = ya + yb 2 2 - Формула вычисления координат середины отрезка с концами A(xa, ya, za) и B(xb, yb, zb) в пространстве:
xc = xa + xb yc = ya + yb zc = za + zb 2 2 2
Примеры задач на вычисление середины отрезка
Примеры вычисления координат середины отрезка на плоскости
Пример 1.
Найти координаты точки С, середины отрезка AB заданного точками A(-1, 3) и B(6, 5).
Решение.
| xc = | xa + xb | = | -1 + 6 | = | 5 | = 2.5 |
| 2 | 2 | 2 |
| yc = | ya + yb | = | 3 + 5 | = | 8 | = 4 |
| 2 | 2 | 2 |
Ответ: С(2.5, 4).
Пример 2.
Найти координаты точки В, если известны координаты точки C(1; 5), середины отрезка AB и точки A(-1, 3).
Решение.
xc =
xa + xb2
=> xb = 2xc – xa = 2·1-(-1)=2+1=3
yc =
ya + yb2
=> yb = 2yc – ya = 2·5-3=10-3=7
Ответ: B(3, 7).
Примеры вычисления координат середины отрезка в пространстве
Пример 3.
Найти координаты точки С середины отрезка AB заданного точками A(-1, 3, 1) и B(6, 5, -3).
Решение.
| xc = | xa + xb | = | -1 + 6 | = | 5 | = 2.5 |
| 2 | 2 | 2 |
| yc = | ya + yb | = | 3 + 5 | = | 8 | = 4 |
| 2 | 2 | 2 |
| zc = | za + zb | = | 1 + (-3) | = | -2 | = -1 |
| 2 | 2 | 2 |
Ответ: С(2.5, 4, -1).
Пример 4.
Найти координаты точки В если известны координаты точки C(1, 5, 2), середины отрезка AB и точки A(-1, 3, 10).
Решение.
xc =
xa + xb2
=> xb = 2xc – xa = 2·1-(-1)=2+1=3
yc =
ya + yb2
=> yb = 2yc – ya = 2·5-3=10-3=7
zc =
za + zb2
=> zb = 2zc – za = 2·2-10=4-10=-6
Ответ: B(3, 7, -6).
Любые нецензурные комментарии будут удалены, а их авторы занесены в черный список!

Средняя точка отрезка с вершинами (x1,
y1) и (
x2,
y2)
Середина отрезка — точка на заданном отрезке, находящаяся на равном расстоянии от обоих концов данного отрезка. Является центром масс как всего отрезка, так и его конечных точек.
Координаты[править | править код]
Средняя точка отрезка в 


.
Таким образом, 

.
Построение[править | править код]

Построение с помощью циркуля и линейки
Если заданы две точки, нахождение середины образованного ими отрезка может быть осуществлено с помощью циркуля и линейки. Для нахождения середины отрезка на плоскости можно сначала построить две дуги равного (и достаточно большого) радиуса с центрами в концах отрезка, а затем через точки пересечения этих дуг провести прямую. Точка, где полученная прямая пересекает отрезок, является его серединой.

Построение с помощью одного циркуля
С использованием теоремы Мора — Маскерони возможно также нахождение середины отрезка с помощью одного только циркуля: на первом шаге для отрезка 







Можно также построить середину отрезка с помощью только линейки при условии, что на плоскости имеется окружность с отмеченным центром[4].
Геометрические свойства[править | править код]
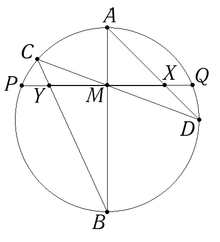
Середина любого диаметра окружности является центром окружности. Перпендикуляр к любой хорде, проходящий через её середину, проходит через центр окружности.
Теорема о бабочке утверждает, что если 










Центр эллипса является серединой отрезка, соединяющего два фокуса эллипса.
Середина отрезка, соединяющего вершины гиперболы, является центром гиперболы.
Перпендикуляры к серединам сторон треугольника пересекаются в одной точке, и эта точка является центром описанной окружности. Центр девяти точек треугольника — середина отрезка, соединяющего центра описанной окружности с ортоцентром данного треугольника. Вершины серединного треугольника данного треугольника лежат в серединах сторон треугольника.
В прямоугольном треугольнике центр описанной окружности является серединой гипотенузы. В равнобедренном треугольнике медиана, высота и биссектриса угла при вершине совпадают с прямой Эйлера и осью симметрии, и эта прямая проходит через середину основания.
Две бимедианы выпуклого четырёхугольника — это отрезки, соединяющие середины противоположных сторон. Две бимедианы и отрезок, соединяющий середины диагоналей, пересекаются в одной точке, которая является серединой этих трёх отрезков[5]. Теорема Брахмагупты утверждает, что если вписанный в окружность четырёхугольник является ортодиагональным (то есть, имеющий перпендикулярные диагонали), то перпендикуляры к сторонам из точки пересечения диагоналей всегда проходят через середину противоположной стороны. Теорема Вариньона утверждает, что середины сторон произвольного четырёхугольника являются вершинами параллелограмма, а если четырёхугольник к тому же является самонепересекающимся, то площадь параллелограмма равна половине площади четырёхугольника. Прямая Ньютона — линия, соединяющая середины двух диагоналей выпуклого четырёхугольника, не являющегося параллелограммом. Отрезки, соединяющие середины противоположных сторон выпуклого четырёхугольника, пересекаются в точке, лежащей на прямой Ньютона.
Правильный многоугольник имеет вписанную окружность, которая касается всех сторон многоугольника в серединах его сторон. В правильном многоугольнике с чётным числом сторон середины диагоналей, соединяющих противоположные центры, являются центром многоугольника. Серединный многоугольник — многоугольник, вершины которого — середины рёбер исходного многоугольника. Растянутый многоугольник серединных точек вписанного многоугольника P является другим вписанным многоугольником, вписанным в ту же окружность, и его вершины являются серединами дуг между вершинами P[6]. Повторение операции создания многоугольника растянутых средних точек приводит к последовательности многоугольников, форма которых сходится к правильному многоугольнику[6][7].
Обобщения[править | править код]
Середина отрезка является аффинным инвариантом, поэтому координатные формулы[⇨] применимы к любой аффинной системе координат.
Середину отрезка невозможно определить в проективной геометрии: любая внутренняя точка отрезка может быть проективно отображена в любую другую точку внутри (того же или любого другого) проективного отрезка. Закрепление одной такой точки в качестве середины определяет аффинную структуру на проективной прямой, содержащей этот отрезок. Четвёртая точка гармонической четвёрки для такой «средней точки» и двух конечных точек является бесконечно удалённой точкой[8].
Понятие середины отрезка можно ввести на геодезических в римановом многообразии, но в отличие от аффинного случая, середина отрезка может быть не единственной.
Примечания[править | править код]
- ↑ Костовский, 1984, с. 20.
- ↑ Курант, Роббинс, 2001, с. 172—179.
- ↑ Wolfram mathworld (29 сентября 2010). Дата обращения: 20 июля 2015. Архивировано из оригинала 25 ноября 2016 года.
- ↑ Адлер, 1940, с. 67—72.
- ↑ Altshiller-Court, 2007.
- ↑ 1 2 Ding, Jiu, Zhang, 2003, с. 255—270.
- ↑ Gomez-Martin, Taslakian, Toussaint, 2008.
- ↑ Coxeter, 1949, с. 119.
Литература[править | править код]
- А. Н. Костовский. Геометрические построения одним циркулем. — М.: «Наука» Главная редакция физико-математической литературы, 1984. — (Популярные лекции по математике).
- Август Адлер. Теория геометрических построений. — Ленинград: Государственное учебно-педагогическое издательство Наркомпроса РСФСР, Ленинградское отделение, 1940.
- Р. Курант, Г. Роббинс. Что такое математика?. — 3-е. — МЦНМО, 2001. — ISBN 5–900916–45–6.
- Jiu Ding, L. Richard Hitt, Xin-Min Zhang. Markov chains and dynamic geometry of polygons // Linear Algebra and its Applications. — 2003. — Т. 367. — doi:10.1016/S0024-3795(02)00634-1.
- Francisco Gomez-Martin, Perouz Taslakian, Godfried T. Toussaint. 18th Fall Workshop on Computational Geometry. — 2008.
- H. S. M. Coxeter. The Real Projective Plane. — New York, Toronto, London: McGraw-Hill, 1949.
- Х. С. М. Коксетер. Действительная проективная плоскость. — М.: Физматлит, 1959.
- Nathan Altshiller-Court. College Geometry. — Mineola, New York: Dover Publ., 2007. — ISBN 0-486-45805-9.
Ссылки[править | править код]
- Animation — showing the characteristics of the midpoint of a line segment
- What is Midpoint Formula
Загрузить PDF
Загрузить PDF
Поиск середины отрезка – легкая задача когда вам известны координаты двух конечных точек. Самый распространенный способ сделать это состоит в использовании формулы для нахождения середины отрезка; но есть еще один способ найти середину отрезка, если линия вертикальная или горизонтальная. Если вы хотите знать, как найти середину отрезка в течение нескольких минут, выполните следующие действия.
-

1
Определение. Середина отрезка – точка, которая находится на равном расстоянии от конечных точек отрезка и лежит на нем. Таким образом, ее координаты – среднее из двух координат х и двух координат у.
-

2
Формула. Формула записывается в виде суммы двух координат х (конечных точек), деленной на два, и суммы двух координат у (конечных точек), деленной на два. Это даст среднее значение х и у координат. Формула:[(x1 + x2)/2,( y1 + y2)/2]
-

3
Найдите координаты конечных точек. Вы не можете использовать формулу, не зная х и у координаты конечных точек. Например, необходимо найти середину (точку О) отрезка, ограниченного точками М (5,4 ) и N (3, -4). Таким образом, (x1, y1) = (5, 4) и (x2, y2) = (3, -4).
- Обратите внимание, что любая пара координат может обозначаться как (x1, y1) или (x2, y2). Так как вы будете просто складывать координаты и делить результат на два, не имеет значения, какую пару координат выбрать в первую очередь.
-

4
Подставьте координаты в формулу. Теперь, когда вам известны координаты конечных точек, подставьте их в формулу. Вот как это делается:
- [(5 + 3)/2, (4 + -4)/2]
-

5
Решите. После того как вы подставили координаты в формулу, проделайте арифметические действия для вычисления середины. Вот как это делается:
- [(5 + 3)/2, (4 + -4)/2] =
- [(8/2), (0/2)] =
- (4, 0)
- Середина отрезка между точками (5,4) и (3, -4) есть точка (4,0).
Реклама
-

1
Рассмотрим вертикальную или горизонтальную линию.
- Линия горизонтальная, если две у- координаты конечных точек равны. Например, отрезок с концами ( -3 , 4) и (5, 4) расположен горизонтально.

- Линия расположена вертикально, если две х -координаты конечных точек равны. Например, отрезок с концами (2, 0 ) и (2 , 3) находится в вертикальном положении.

- Линия горизонтальная, если две у- координаты конечных точек равны. Например, отрезок с концами ( -3 , 4) и (5, 4) расположен горизонтально.
-

2
Найдите длину отрезка. Вот как это сделать:
- Длина горизонтального отрезка с конечными точками (-3 , 4) и ( 5, 4) равна 8. Вы можете найти это сложением абсолютных величин координат х: | -3| + |5| = 8.

- Длина вертикального отрезка с конечными точками (2 ,0) и (2,3) равна 3. Вы можете найти это сложением абсолютных величин координат у: |0| + |3| = 3.

- Длина горизонтального отрезка с конечными точками (-3 , 4) и ( 5, 4) равна 8. Вы можете найти это сложением абсолютных величин координат х: | -3| + |5| = 8.
-

3
Разделите длину отрезка на два. Теперь, когда вы нашли длину отрезка, нужно разделить его на два.
- 8/2 = 4

- 3/2 = 1,5

- 8/2 = 4
-

4
Вычислите координаты середины. Вот как это делается:
- Чтобы найти середину отрезка, ограниченного точками (-3,4) и (5,4), прибавьте или вычтите 4 из х-координаты первой или второй конечной точки соответственно. Для точки (-3 , 4) это будет -3+4=1 и координаты середины: (1, 4) (Вам не нужно менять у- координаты, так как линия горизонтальная и у-координаты постоянны). Итак, середина отрезка (-3,4) и (5,4) есть точка (1,4).

- Чтобы найти середину отрезка, ограниченного точками (2, 0) и (2,3), прибавьте или вычтите 1,5 из у-координаты первой или второй конечной точки соответственно. Для точки (2 ,0) это будет -0+1,5=1,5 и координаты середины: (2,1,5) (Вам не нужно менять х-координаты, так как линия вертикальная и х-координаты постоянны). Итак, середина отрезка (2, 0 ) и (2,3) есть точка (2,1,5).

Реклама
- Чтобы найти середину отрезка, ограниченного точками (-3,4) и (5,4), прибавьте или вычтите 4 из х-координаты первой или второй конечной точки соответственно. Для точки (-3 , 4) это будет -3+4=1 и координаты середины: (1, 4) (Вам не нужно менять у- координаты, так как линия горизонтальная и у-координаты постоянны). Итак, середина отрезка (-3,4) и (5,4) есть точка (1,4).
Что вам понадобится
- Карандаш
- Лист бумаги
- Линейка
Об этой статье
Эту страницу просматривали 31 324 раза.
Была ли эта статья полезной?
В данной публикации мы рассмотрим, что такое середина отрезка, по какой формуле считаются ее координаты (в плоскости и пространстве). Также разберем примеры решения задач по этой теме.
- Расчет координат середины отрезка
- Примеры задач
Расчет координат середины отрезка
Серединой называется точка, лежащая на отрезке и находящаяся на одинаковом расстоянии от его концов.

AC = CB
Если концы отрезка A (xa, ya) и B (xb, yb) расположены в одной плоскости, то координаты его середины (точки C) считаются по формуле:
![]()
Если отрезок с концами A (xa, ya, za) и B (xb, yb, zb) находится в трехмерном пространстве, координаты его середины рассчитываются следующим образом:
![]()
Примеры задач
Задание 1
Вычислим координаты точки C, которая является серединой отрезка AB, образованного точками A (5, -2) и B (11, 10).
Решение:
В данном случае нам подойдут формулы для плоскости:
xc = (5 + 11) / 2 = 8
yc = (-2 + 10) / 2 = 4
Таким образом, точка C имеет координаты (8, 4).
Задание 2
Найдем координаты точки B, являющейся одним из концов отрезка AB. При этом известны координаты точки A (7, 13) и середины отрезка – C (4, -3).
Решение:
Нужные нам формулы можно вывести из выражений для расчета координат середины отрезка:
xb = 2xc – xa = 2 · 4 – 7 = 1
yb = 2yc – ya = 2 · (-3) – 13 = -19
Следовательно, координаты B – (1, -19).
Основное определение отрезка
Определение
Отрезок — это прямая линия, которая соединяет две произвольно расположенные точки, именуемые окончанием отрезка. В качестве конкретного примера можно назвать точки A и B и соответственно отрезок AB.
Прямую АВ можно получить путем удлинения отрезка, который состоит из двух точек. Вследствие чего, можно сказать, что полученный отрезок АВ — это часть прямой, которая ограничена точками А и В. Отрезок объединяет обе точки, которые являются концами прямой, а также множество других точек, лежащих на отрезке.
Например: дана точка К которая расположена между заданными отметками, следовательно, можно сказать, что данная точка лежит на этом отрезке.
Определения
Длина прямой – конкретное отмеренное расстояние, которое задано в масштабе. Чаще всего данный параметр задается как АВ.
Середина отрезка – это некая определенная отметка, которая лежит на прямой и удалена от концов на одинаковом расстоянии друг от друга. Ее можно обозначить как координата С.
Середина отрезка на координатной прямой
Заданы следующие параметры: координатная прямая Ox; точки А и В, которые не совпадают с данной прямой.
Заданным точкам соответствуют действительные числовые значения [x_{A}] и [x_{B}]. Координата С — это середина отрезка А и В. Исходя из этого нужно определить значение координаты [x_{C}] .
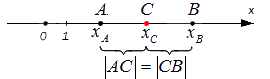
AB = |a — b|, где A и B — это произвольные точки, расстояние между которыми надо найти, то есть, найти длину отрезка AB, a и b — координаты точек.
Выражение |a — b| можно заменить выражением |b — a|, так как a — b и b — a являются противоположными числами и их модули равны.
Следовательно, чтобы найти расстояние между точками координатной прямой надо из координаты одной точки вычесть координату другой точки.
Середина отрезка на плоскости
Зададим следующие параметры: прямоугольная система координат относительно заданной плоскости Oxy; две произвольно расположенные несовпадающие точки, для которых заданы координаты [mathrm{A}left(x_{A} y_{A}right)] и [Bleft(chi_{B} chi_{B}right)]. Точка C — это заданная середина отрезка АВ. Нужно вычислить координаты [x_{C}] и [y_{C}] относительно точки С.
Чтобы правильно проанализировать задачу, возьмем случай, когда точки A и В между собой не совпадают и расположены на одной координатной плоскости.
В свою очередь координатная плоскость является перпендикулярной относительной одной из осей.
Координаты отметок [A_{x} A_{y} B_{x} B_{y} C_{x} C_{y}] — это проекции точек А, В, С.
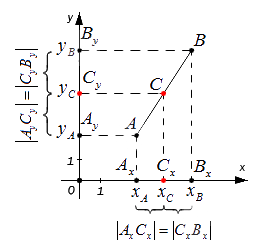
Согласно построению, все прямые можно назвать параллельными; прямые также параллельны между собой. Принимая во внимание данное свойство и теорему Фалеса из равенства А С = С В следуют, что все равенства между собой равны. Также они в свою очередь свидетельствуют о том, что точка [C_{x}] – это середина отрезка [A_{x}] и [B_{x}], [C_{y}] а – середина отрезка [A_{y}] и [B_{y}].
Опираясь на полученное выражение получаем основное уравнение середины отрезка на координатной плоскости.
[x_{c}=frac{x_{A}+x_{B}}{2}text { и } y_{c}=frac{y_{A}+y_{B}}{2}]
Данным набором формул можно использовать, когда точки А и B лежат на одной координатной плоскости или прямой. Которая соответственно перпендикулярна относительной одной из осей.
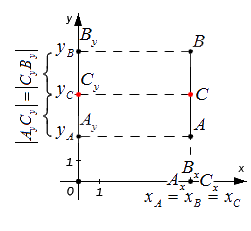
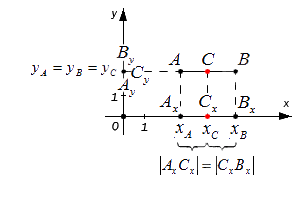
В данном случае координаты отрезка будут определяться по следующей формуле:
[x_{C}=frac{x_{A}+x_{B}}{2} text{ и } y_{c}=frac{y_{A}+y_{B}}{2}]
Параметры середины отрезка в пространстве
Для выведения основной формулы для решения подобного рода задач, нужно рассмотреть конкретный пример.
Дана система координат, две произвольные координатные точки с конкретными координатами [mathrm{A}left(A_{x} A_{y} A_{z}right)] и [mathrm{B}left(B_{chi} B_{y} B_{z}right)]. Нужно определить отметку точки C, которая в свою очередь будет являться серединой отрезка.
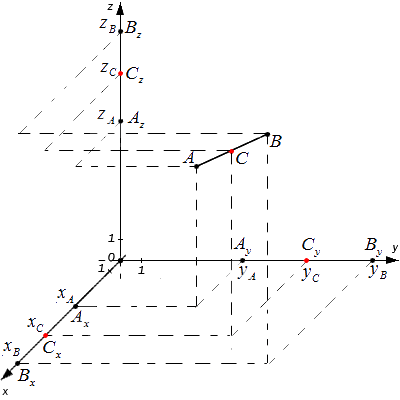
Согласно основной теоремы Фалеса, все равенства между собой являются равными. Следовательно, значение точек С будут являться серединами отрезков, каждой координатной плоскости, коих имеется три.
Можно составить и записать окончательную формулу для определения середины прямой при координатной плоскости, состоящей более чем двух осей.
[x_{c}=frac{x_{A}+x_{B}}{2} text{ и } y_{C}=frac{y_{A}+y_{B}}{2}, z_{c}=frac{z_{A}+z_{B}}{2}]
Данные формулы также можно применять в случаях, когда точки A и B расположены на одной из координатных прямых. Либо на прямой, которая перпендикулярна относительно одной из осей. Есть еще случай, когда точки расположены в одной координатной плоскости, которая перпендикулярна одной из координатных плоскостей.
Нет времени решать самому?
Наши эксперты помогут!
Определение координат середины отрезка через координаты радиус-векторов его концов
Формулу для определения отметок середины отрезка, можно определить применяя алгебраическое правило решения векторных выражений.
Исходные данные: прямоугольная декартова система координат Oxy, точки с конкретно заданными координатами [mathrm{A}left(A_{x} A_{y}right)] и [text { B }left(B_{x} B_{y}right)].
Точка C – это середина отрезка с точками А и В.
Согласно геометрическому правилу и определению, действия над векторами будет выглядеть следующим образом:
[overline{O C}=frac{1}{2} cdot(overline{O A}+overline{O B}).]
Координата С в данной ситуации — это значение, в которой пересекаются диагонали геометрической фигуры параллелограмм. Данная фигура построена на основании следующих векторов [overline{O A}] и [overline{O B}], иными словами — это точка середины диагоналей.
Координатные показатели радиуса — это векторные показатели, которые равны координатам, тогда будут верны и равенства: [overline{O A}left(x_{A} y_{A}right)] и [overline{O B}left(x_{B} y_{B}right)].
Выполним следующие действия над векторными значениями и получим следующие формулы:
[overline{O C}=frac{1}{2} cdot(overline{O A}+overline{O B})=left(frac{x_{A}+y_{B}}{2}, frac{y_{A}+y_{B}}{2}right).]
Следовательно, заданная координата С обладает данными:
[left(frac{x_{A}+y_{B}}{2}, frac{y_{A}+y_{B}}{2}right).]
Аналогичным образом определяется нахождение координат середины заданного отрезка в пространстве.
[Cleft(frac{x_{A}+y_{B}}{2}, frac{y_{A}+y_{B}}{2}, frac{z_{A}+z_{B}}{2}right)]
Примеры решения задачи, при нахождении точки середины отрезка
Примеры
Пример №1:
Заданы координатные данные. Точка А с показателями (-7,3) и В (2,4).
Нужно определить точку с отметками, которая является серединой отрезка А и В.
Решение:
Середину отрезка можно обозначить любой точкой. В данном примере возьмем наименование точки — С.
Координатные значения ее будут вычисляться как половина суммы координат концов заданного отрезка с точками А
и В.
Составим и запишем следующие формулы:
[x_{C}=frac{x_{A}+x_{B}}{2}=frac{-7+2}{2}=-frac{5}{2}\y_{C}=frac{y_{A}+y_{B}}{2}=frac{3+4}{2}=frac{7}{2}]
Ответ: искомые координатные значения середины отрезка будут равны следующим данным:
[mathrm{AB}left(-frac{5}{2}, frac{7}{2}right)]
Пример №2:
Заданы координатные отметки геометрической фигуры треугольника: АВС А(-1,0), В (3,2), С (9,-8). По условию
необходимо вычислить длину медианы АМ.
Решение:
По условию задачи AM – медиана, следовательно, точка M будет являться точкой середины отрезка BC. В первую
очередь необходимо определить координаты середины отрезка BC, а именно: точки M.
[x_{M}=frac{x_{B}+x_{C}}{2}=frac{3+9}{2}=6\y_{M}=frac{y_{B}+y_{C}}{2}=frac{2+(-8)}{2}=-3]
Так как, нам известны координатные значения двух концов медианы, точки А и М. Можно воспользоваться формулой
определения расстояния между заданными значениями, и вычислить окончательное значение медианы.
[AM=sqrt{(6-(-1))^{2}+(-3+0)^{2}}=sqrt{58}]
Ответ: [sqrt{58}].

