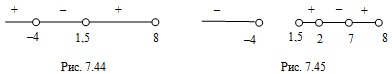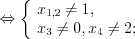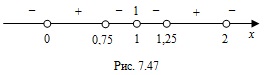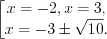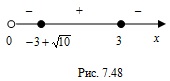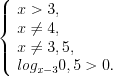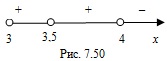Найти середину промежутка,являющийся решением системы нер-ств
Сергей Иванов
Ученик
(11),
закрыт
12 лет назад
Дополнен 12 лет назад
4*x^2-4x-3≤0
x^2≤1
3*x^2-20x-7≤0
Дополнен 12 лет назад
Спс
Лучший ответ
Matricfria
Мыслитель
(5124)
12 лет назад
1) Решите каждое неравенство
2) На координатной прямой отметьте промежутки
3) Найдите пересечение этих промежутков – это будет решение системы
4) От правого конца минусуйте левый и разделите на 2 – это будет середина промежутка.
Остальные ответы
Похожие вопросы
При решении неравенств вы должны свободно владеть понятием числового неравенства, знать, что такое решение неравенства, что значит решить неравенство, помнить свойства неравенств. То же относится и к системам числовых неравенств. Все эти сведения вы можете найти в любом пособии для поступающих в вузы.
Напомним свойства числовых неравенств.
1. Если а > b , то b < а; наоборот, если а < b, то b > а.
2. Если а > b и b > c, то а > c. Точно так же, если а < b и b < c, то а < c.
3. Если а > b, то а + c > b+ c (и а – c > b – c). Если же а < b, то а + c < b+ c (и а – c < b – c). Т. е. к обеим частям неравенства можно прибавлять (или из них вычесть) одну и ту же величину.
4. Если а > b и c > d, то а + c > b + d; точно так же, если а < b и c < d, то а + c < b + d, т. е. два неравенства одинакового смысла можно почленно складывать.
Замечание.
Два неравенства одинакового смысла нельзя почленно вычитать друг из друга, так как результат может быть верным, но может быть и неверным. Например, если из неравенства 11 > 9 почленно вычесть неравенство 3 > 2, то получим верное неравенство 8 > 7. Если из неравенства 11 > 9 почленно вычесть неравенство 7 > 2, то полученное неравенство будет неверным.
5. Если а > b и c < d, то а – c > b – d; если а < b и c > d, то а – c < b – d, т.е. из одного неравенства можно почленно вычесть другое неравенство противоположного смысла, оставляя знак того неравенства, из которого вычиталось другое.
6. Если а > b и m – положительное число, то m а > m b и 
Если же а > b и n – отрицательное число, то n а < n b и 
7. Если а > b и c > d , где а, b, c, d > 0, то а c > b d и если а < b и c < d, где а, b, c, d > 0, то аc < bd, т.е. неравенства одного смысла на множестве положительных чисел можно почленно перемножать.
Следствие. Если а > b, где а, b > 0, то а2 > b2, и если а < b, то а2 < b2, т.е. на множестве положительных чисел обе части неравенства можно возводить в квадрат.
8. Если а > b, где а, b > 0, то 

Виды неравенств и способы их решения
1. Линейные неравенства и системы неравенств
Пример 1. Решить неравенство 
Решение:

Ответ: х < – 2.
Пример 2. Решить систему неравенств 
Решение:

Ответ: (– 2; 0].
Пример 3. Найти наименьшее целое решение системы неравенств
Решение:
Ответ:
2. Квадратные неравенства
Пример 4. Решить неравенство х2 > 4.
Решение:
х2 > 4 (х – 2)∙(х + 2) > 0.
Решаем методом интервалов.
Ответ:
3. Неравенства высших степеней
Пример 5. Решить неравенство (х + 3)∙(х2 – 2х + 1) > 0.
Решение:

Ответ: 
Пример 6. Найти середину отрезка, который является решением неравенства 4х2 – 24х + 24 < 4у2, где 
Решение:
Область определения неравенства: 
С учётом области определения 4х2 – 24х + 24 < 4у2 будет равносильно неравенству
Решаем методом интервалов.
Решение неравенства: 
Середина отрезка: 
Ответ: 
4. Рациональные неравенства
Пример 7. Найти все целые решения, удовлетворяющие неравенству 
Решение:

Методом интервалов:
Решение неравенства: 
Целые числа, принадлежащие полученным полуинтервалам: – 6; – 5; – 4; 1.
Ответ: – 6; – 5; – 4; 1.
5. Иррациональные неравенства
Помните! Начинать решение иррациональных неравенств нужно с нахождения области определения.
Пример 8. Решить неравенство 
Решение:
Область определения: 
Так как арифметический корень не может быть отрицательным числом, то 
Ответ: 
Пример 9. Найти все целые решения неравенства 
Решение:
Область определения 



Целыми числами из этого отрезка будут 2; 3; 4.
Ответ: 2; 3; 4.
Пример 10. Решить неравенство 
Решение:
Область определения: 
Преобразуем неравенство: 


Ответ: 
Пример 11. Решить неравенство 
Решение:
Раскрываем знак модуля.
Объединим решения систем 1) и 2): 
Ответ: 
6. Показательные, логарифмические неравенства и системы неравенств
Пример 12. Решите неравенство 
Решение:

Ответ: 
Пример 13. Решите неравенство 
Решение:

Ответ: 
Пример 14. Решите неравенство 
Решение:
Ответ: 
Пример 15. Решите неравенство 
Решение:
Ответ: 
Задания для самостоятельного решения
Базовый уровень
Целые неравенства и системы неравенств
1) Решите неравенство 2х – 5 ≤ 3 + х.
2) Решите неравенство – 5х > 0,25.
3) Решите неравенство 
4) Решите неравенство 2 – 5х ≥ – 3х.
5) Решите неравенство х + 2 < 5x – 2(x – 3).
6) Решите неравенство
.
7) Решите неравенство (х – 3) (х + 2) > 0.
8) Решить систему неравенств 
9) Найдите целочисленные решения системы неравенств 
10) Решить систему неравенств 
11) Решить систему неравенств 
12) Найти наименьшее целое решение неравенства 
13) Решите неравенство 
14) Решите неравенство 
15) Решите неравенство 
16) Решите неравенство 
17) Найдите решение неравенства 

18) Решить систему неравенств 
19) Найти все целые решения системы 
Рациональные неравенства и системы неравенств
20) Решите неравенство 
21) Решите неравенство 
22) Определите число целых решений неравенства 
23) Определите число целых решений неравенства 
24) Решите неравенство 
25) Решите неравенство 2x<16 .
26) Решите неравенство 
27) Решите неравенство 
28) Решите неравенство 
29) Найдите сумму целых решений неравенства 
30) Решите неравенство 
31) Решите неравенство 
Иррациональные неравенства
32) Решите неравенство 
33) Решите неравенство
34) Решите неравенство 
Показательные, логарифмические неравенства и системы неравенств
35) Решите неравенство 
36) Решите неравенство 
37) Решите неравенство 
38) Решите неравенство 
39) Решите неравенство 
40) Решите неравенство 49∙7х < 73х + 3.
41) Найдите все целые решения неравенства 
42) Решите неравенство 
43) Решите неравенство 
44) Решите неравенство 7x+1-7x<42 .
45) Решите неравенство log3(2x2+x-1)>log32 .
46) Решите неравенство log0,5(2x+3)>0 .
47) Решите неравенство 
48) Решите неравенство 
49) Решите неравенство 
50) Решите неравенство logx+112>logx+12 .
51) Решите неравенство logx9<2.
52) Решите неравенство 
Повышенный уровень
53) Решите неравенство |x-3|>2x.
54) Решите неравенство 2│х + 1| > х + 4.
55) Найдите наибольшее целое решение неравенства 
56) Решить систему неравенств 
57) Решить систему неравенств 
58) Решите неравенство 
59) Решите неравенство 25•2x-10x+5x>25 .
60) Решите неравенство 
Ответы
1) х ≤ 8; 2) х < – 0,05; 3) х ≥ 5; 4) х ≤ 1; 5) х > –2; 6) х < 11; 7) 




20) (0; 2); 21) (0; 1,5); 22) 3; 23) 6; 24) (–1; 1,5); 25) х < 4; 26)
; 29) – 10; 30) (0; + ∞); 31)









.
Логарифмическими называют неравенства, содержащие логарифмическую функцию.
Решение логарифмических неравенств основано на свойствах логарифмической функции.
Логарифмической называют функцию вида 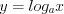


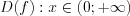
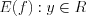
При 

Методы решений неравенств
1. Если неравенство имеет вид
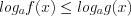



где 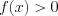
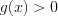
а) при условии, что 
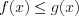
б) при условии, что 
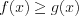
2. Если неравенство имеет вид
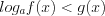
и 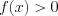
а) при условии, что 
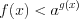
б) при условии, что 
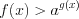
3. Если неравенство имеет вид
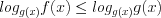
то решают совокупность систем неравенств:
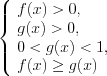

Пример 1. Найдите решение неравенства 
Решение. ОДЗ:
Поскольку решением первого неравенства является промежуток 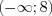
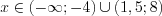
Имеем неравенство вида 7.17, которое на ОДЗ при 
Так как 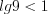
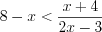
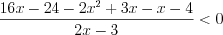

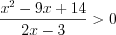
Решим последнее неравенство методом интервалов на ОДЗ исходного неравенства (рис. 7.45) и получим: 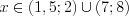
Ответ: 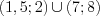
Пример 2. Найдите середину промежутка, на котором выполняется неравенство 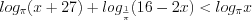
Решение. ОДЗ: 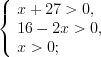
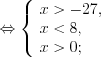
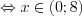
Выполним преобразования: 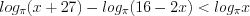
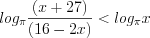
Имеем неравенство вида 7.17, которое на ОДЗ при 
Поскольку основание логарифма 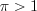
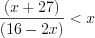
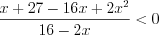
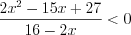

Найдем середину интервала: 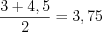
Ответ: 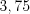
Пример 4. Решите неравенство 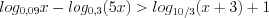
Решение. ОДЗ: 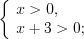
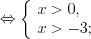
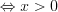
Применяя свойства логарифмов, запишем неравенство в виде:
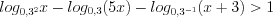
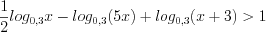
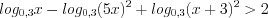
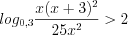
Имеем неравенство вида 7.18, которое на ОДЗ при 
Поскольку основание логарифма 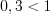
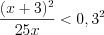
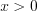
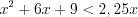
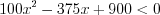
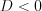
Ответ: 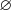
Пример 5. Найдите наименьшее натуральное число, которое не является решением неравенства 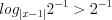
Решение. Имеем неравенство 7.19, которое решим методом интервалов, записав его в виде 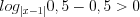
1. Рассмотрим функцию 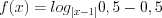
2. 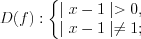
3. Найдем нули функции, решая уравнение 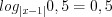
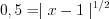
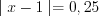
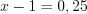
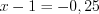
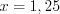
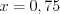
4. Нанесем нули функции на ее область определения и установим знаки значений функции на полученных промежутках (рис. 7.47).
5. Решением неравенства являются промежутки, на которых функция положительна: 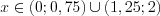
Ответ: 1.
Пример 6. Найдите среднее арифметическое всех целых решений неравенства 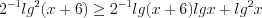
Решение. ОДЗ: 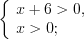
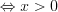
Запишем неравенство в виде 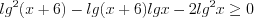
По теореме, обратной теореме Виета, найдем нули функции 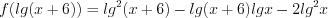
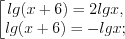
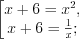

Согласно рисунку 7.48 запишем его решение: 
Запишем целые решения неравенства: 1; 2; 3. Найдем среднее арифметическое этих решений: 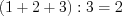
Ответ: 2.
Пример 7. Решите неравенство 
Решение. Запишем неравенство в виде 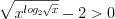
1. Рассмотрим функцию 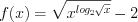
2. 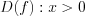
3. Найдем нули функции, решая уравнение 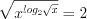
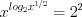
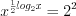
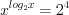

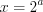

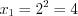

4. Нанесем нули функции на ее область определения и установим знаки ее значений на полученных промежутках (рис. 7.49).
5. Решением неравенства являются промежутки, на которых функция положительна.
Ответ: 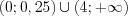
Пример 8. Найдите область определения функции 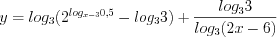
Решение. Найдем область определения функции, решая систему ограничений: 
Рассмотрим решение неравенства 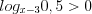
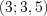
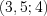
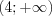
Поскольку функция 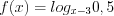
Согласно рисунку 7.50 решением системы неравенств являются промежутки, на которых функция положительна.
Ответ: 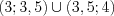
Пример 9. Найдите решение неравенства 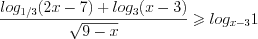
Решение. Запишем данное неравенство в виде 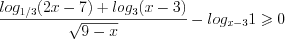
1. Рассмотрим функцию 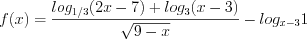
2. 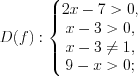
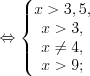
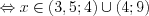
3. На области определения функция примет вид: 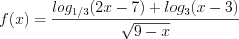
Найдем её нули, решая уравнение: 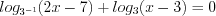
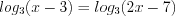
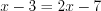
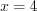
4. Поскольку значение 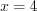
5. Решением неравенства является промежуток, на котором функция не отрицательна.
Ответ: 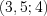
Пример 10. Найдите наименьшее целое решение неравенства 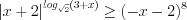
Решение. Поскольку 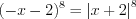
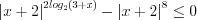
1. Рассмотрим функцию 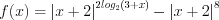
2. 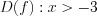
3. Найдем нули функции, решая уравнение 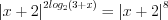
1) 
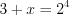
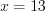
2) 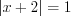
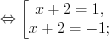
3) 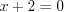
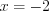
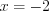
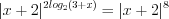
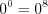
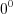
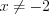
4. Нанесем нули функции на ее область определения и установим знаки ее значений на полученных промежутках (рис.7.52).
5. Решением неравенства является объединение промежутков, на которых функция не отрицательна: ![(-3;-2)cup (-2;-1]cup [13;+ infty) LaTeX formula: (-3;-2)cup (-2;-1]cup [13;+ infty)](https://helpy.quali.me/uploads/formulas/204205492f92e5b607c1c9ae7a0a1c68c176e381.1.1.png)
Число 
Ответ: 
Всякое логарифмическое неравенство можно решить методом интервалов, но наиболее целесообразно этот метод применять в случае решения неравенств 7.19 и комбинированных неравенств.
Как найти середину интервала
При статистической обработке результатов исследований самого разного рода полученные значения часто группируются в последовательность интервалов. Для расчета обобщающих характеристик таких последовательностей иногда приходится вычислять середину интервала – «центральную варианту». Методы ее расчета достаточно просты, но имеют некоторые особенности, вытекающие как из используемой для измерения шкалы, так и из характера группировки (открытые или закрытые интервалы).

Инструкция
Если интервал является участком непрерывной числовой последовательности, то для нахождения ее середины используйте обычные математические методы вычисления среднеарифметического значения. Минимальное значение интервала (его начало) сложите с максимальным (окончанием) и разделите результат пополам – это один из способов вычисления среднеарифметического значения. Например, это правило применимо, когда речь идет о возрастных интервалах. Скажем, серединой возрастного интервала в диапазоне от 21 года до 33 лет будет отметка в 27 лет, так как (21+33)/2=27.
Иногда бывает удобнее использовать другой метод вычисления среднеарифметического значения между верхней и нижней границами интервала. В этом варианте сначала определите ширину диапазона – отнимите от максимального значения минимальное. Затем поделите полученную величину пополам и прибавьте результат к минимальному значению диапазона. Например, если нижняя граница соответствует значению 47,15, а верхняя – 79,13, то ширина диапазона составит 79,13-47,15=31,98. Тогда серединой интервала будет 63,14, так как 47,15+(31,98/2) = 47,15+15,99 = 63,14.
Если интервал не является участком обычной числовой последовательности, то вычисляйте его середину в соответствии с цикличностью и размерностью используемой измерительной шкалы. Например, если речь идет об историческом периоде, то серединой интервала будет являться определенная календарная дата. Так для интервала с 1 января 2012 года по 31 января 2012 серединой будет дата 16 января 2012.
Кроме обычных (закрытых) интервалов статистические методы исследований могут оперировать и «открытыми». У таких диапазонов одна из границ не определена. Например, открытый интервал может быть задан формулировкой «от 50 лет и старше». Середина в этом случае определяется методом аналогий – если все остальные диапазоны рассматриваемой последовательности имеют одинаковую ширину, то предполагается, что и этот открытый интервал имеет такую же размерность. В противном случае вам надо определить динамику изменения ширины интервалов, предшествующих открытому, и вывести его условную ширину, исходя из полученной тенденции изменения.
Источники:
- что такое открытый интервал
Войти на сайт
или
Забыли пароль?
Еще не зарегистрированы?
This site is protected by reCAPTCHA and the Google Privacy Policy and Terms of Service apply.
Все предметы
Биология
География
Физика
Химия
История
Обществознание
Русский язык
Литература
Экономика
Право
Математика
Алгебра
Геометрия
Информатика
Английский язык
Українська мова
Українська література
Другие предметы
Беларуская мова
Қазақ тiлi
Немецкий язык
Окружающий мир
Французский язык
Музыка
МХК
ОБЖ
Психология
Оʻzbek tili
Кыргыз тили
Астрономия
Физкультура и спорт


sechevayana959
+49
Ответ дан
7 лет назад
Алгебра
5 – 9 классы
РЕШИТЕ СРОЧНО!!!!50 БАЛЛОВ!!!!
НАЙДИТЕ СЕРЕДИНУ ПРОМЕЖУТКА, СЛУЖАЩЕГО РЕШЕНИЕМ СИСТЕМЫ НЕРАВЕНСТВ:
А)3Х-13/4 МЕНЬШЕ ИЛИ РАВНЯЕТСЯ Х-1/4-7/8
2 БОЛЬШЕ ИЛИ РАВНЯЕТСЯ Х/4+3-2Х/3
(ЭТО ОДНА СИСТЕМА)
Ответ проверен экспертом
2.5/5
(2 оценки)
3

ВладимирБ
7 лет назад
Светило науки – 11608 ответов – 65744 помощи
решение смотри в приложении

Оцените пользу ответа
Ответ
5/5
(1 оценка)
0

troyan174
7 лет назад
Светило науки – 9 ответов – 0 раз оказано помощи
3х-13/4=х-1/4-7/8…………
Оцените пользу ответа

Мозг
Отвечающий
Остались вопросы?
Задать вопрос