Как найти середину противоположные сторон

Теорема Вариньона

В школьном курсе теорема Вариньона часто фигурирует в качестве обычной задачи, в которой требуется доказать, что середины сторон четырёхугольника являются вершинами параллелограмма.

Её доказательство основано на свойствах средней линии треугольника.

Середины сторон четырёхугольника являются вершинами параллелограмма.

Дано: ABCD — четырёхугольник,

M, N, K, F — середины его сторон.

Доказать : MNKF — параллелограмм.

1) Проведём диагональ AC.

2) Рассмотрим треугольник ABC.

Так как точки M и N — середины сторон AB и BC, отрезок MN — средняя линия треугольника ABC.

3) Аналогично, FK — средняя линия треугольника ADC и

4) По признаку параллельности прямых, две прямые, параллельные третьей прямой, параллельны между собой:

5) В четырёхугольнике MKNF противоположные стороны параллельны и равны. Следовательно, MKNF — параллелограмм (по признаку).

Что и требовалось доказать.

Поскольку в школьном курсе геометрии рассматриваются только выпуклые четырёхугольники, доказательство приведено только для этого случая. Но и для невыпуклых четырёхугольников (в том числе, и для самопересекающихся), теорема также верна (доказывается аналогично).

Параллелограмм, образованный серединами сторон четырёхугольника, называется параллелограммом Вариньона (вариньоновским, вариньоновым).

Периметр параллелограмма Вариньона равен сумме диагоналей исходного параллелограмма:

(так как стороны MNKF равны половине диагонали AC или BD).

Площадь параллелограмма Вариньона равна половине площади исходного параллелограмма:

углы COD и NMF равны (как внутренние накрест лежащие при параллельных прямых AC и MN и секущей BD),

Урок геометрии по теме “Теорема Вариньона. Решение задач”. 8-й класс

Класс: 8

Презентация к уроку

Загрузить презентацию (276 кБ)

Цель: изучить теорему Вариньона и научиться применять ее на практике с наименьшими временными затратами.

Задачи:

1. Изучить теоретический материал: понятия «параллелограмм Вариньона», бимедианы четырехугольника, разобрать доказательство теоремы Вариньона и следствия из нее.
2. Сравнить количество времени, необходимое для решения задач традиционным способом и, используя теорему Вариньона.
3. Показать решение олимпиадных заданий с помощью параллелограмма Вариньона.

Ход урока

Введение

В 21 век, в век информационных технологий, главным ресурсом является время. Тысячи людей желают посещать тренинги, семинары и лекции по тайм-менеджменту, где бы их научили, как рационально, с минимальными потерями и максимальной пользой использовать свое время. Большую часть времени у ученика занимает обучение в школе и приготовление домашнего задания. Одним из самых сложных предметов в школе является геометрия. В частности, задачи на доказательство требуют значительной траты времени, поэтому у многих отсутствует интерес к решению подобных заданий. В теме «Четырехугольники» эту проблему может решить использование теоремы Вариньона.

Пьер Вариньон – французский математик и механик 18 века, который первым доказал, что середины сторон выпуклого четырехугольника являются вершинами параллелограмма. Эта теорема вызвала интерес у отечественных ученых лишь в 20 веке. Подробно ее применение показал украинский геометр – Г.Б.Филипповский и кандидат физико-математических наук, доцент МГУ В.В. Вавилов. В школе теорема Вариньона не входит в курс программы, но считаю изучение её необходимым.

1. Теоретическая часть

Вариньон Пьер [1] (1654–1722)

Пьер Вариньон родился во Франции в 1654 году. Обучался в иезуитском коллеже и университете в Кане, где стал магистром в 1682 году. Вариньон готовился к религиозной деятельности, но, изучая сочинения Эвклида и Декарта, увлекся математикой и механикой. Труды Вариньона посвящены теоретической механике, анализу бесконечно малых, геометрии, гидромеханике и физике. Вариньон был одним из первых ученых, ознакомивших Францию с анализом бесконечно малых. В конце 17 и начале 18 в. Вариньон руководил «Журналом ученых», в котором помещали свои работы по исчислению бесконечно малых братья Бернулли. В геометрии Вариньон изучал различные специальные кривые, в частности ввел термин «логарифмическая спираль». Главные заслуги Вариньона относятся к теоретической механике, а именно к геометрической статике. В 1687 Вариньон представил в Парижскую АН сочинение «Проект новой механики. », в котором сформулировал закон параллелограмма сил. В 1725 в Париже был издан трактат Вариньона «Новая механика или статика», представляющий собой систематическое изложение учения о сложении и разложении сил, о моментах сил и правилах оперирования ими, почти без изменений сохранившееся в учебниках статики до нашего времени. Написал учебник по элементарной геометрии (издан в 1731).

Теорема Вариньона [2]

Четырехугольник, образованный путем последовательного соединения середин сторон выпуклого четырехугольника, является параллелограммом, и его площадь равна половине площади данного четырехугольника.

ABCD – выпуклый четырехугольник

AK=KB; BL=LC; CM=MD; AN=ND

1) KLMN – параллелограмм;

1. Рассмотрим одну из сторон четырехугольника KLMN, например KL. KL– средняя линия треугольника ABC(по определению),следовательно, KL║AC. Аналогично, так как MN– средняя линия треугольника ADC,то MN║AC. Так как KL║AC и MN║AC следовательно, KL║NM и KL=MN=AC/2. Таким образом, KLMN – параллелограмм. Этот параллелограмм называется параллелограммом Вариньона данного четырехугольника.
2. Средняя линия треугольника отсекает от него треугольник, площадь которого в четыре раза меньше площади исходного треугольника,
3. т.е. S_KBL = S_ABC/4, S_MDN=S_ADS/4. Следовательно, S₁+S₃=S_ABCD /4. Аналогично, S₂+S₄=S_ABCD/4. Следовательно, S₁+S₃ + S₂+S₄ = S_ABCD /4 + S_ABCD/4 = S_ABCD/2.

Т.е., SKLMN = S_ABCD/2. Что и требовалось доказать.

Определение. Бимедианы четырехугольниках [3] – это отрезки, соединяющие середины противоположных сторон (диагонали параллелограмма Вариньона)

Следствия из теоремы Вариньона

Параллелограмм Вариньона является ромбом тогда и только тогда, когда в исходном четырехугольнике 1) диагонали равны 2) бимедианы перпендикулярны.

Доказать: KLMN – ромб

Так как AC=BD (диагонали исходного четырехугольника равны по условию), то стороны параллелограмма Вариньона будут равны KL=LM=MN=NK (используя свойство средних линий треугольников, образованных при пересечении диагоналей исходного четырехугольника). Параллелограмм c равными сторонами является ромбом.

KLMN – параллелограмм Вариньона;

KM и LN перпендикулярны

Бимедианы исходного четырехугольника – это диагонали параллелограмма Вариньона. Так как в параллелограмме диагонали перпендикулярны, то этот параллелограмм является ромбом (по признаку ромба).

Что и требовалось доказать.

Параллелограмм Вариньона является прямоугольником тогда и только тогда, когда в исходном четырехугольнике: 1) диагонали перпендикулярны; 2) бимедианы равны

KLMN – параллелограмм Вариньона;

диагонали AC и BD – перпендикулярны

Так как диагонали AC и BD – перпендикулярны, то стороны параллелограмма Вариньона будут перпендикулярны. Следовательно, параллелограмм Вариньона является прямоугольником.

KLMN – параллелограмм Вариньона;

бимедианы KM и LN – равны

Бимедианы исходного четырехугольника – это диагонали параллелограмма Вариньона. Так как в параллелограмме диагонали равны, то этот параллелограмм является прямоугольником (по признаку прямоугольника).

Что и требовалось доказать.

Параллелограмм Вариньона является квадратом тогда и только тогда, когда в исходном четырехугольнике 1) диагонали равны и перпендикулярны; 2) бимедианы равны и перпендикулярны

KLMN – параллелограмм Вариньона;

диагонали AC и BD – перпендикулярны; AC=BD

Так как диагонали исходного четырехугольника AC и BD равны и перпендикулярны, то стороны параллелограмма Вариньона будут равны и перпендикулярны. Следовательно, параллелограмм Вариньона является квадратом.

KLMN – параллелограмм Вариньона;

бимедианы KM и LN – перпендикулярны; KM=LN

Доказать: KLMN – квадрат

Бимедианы исходного четырехугольника – это диагонали параллелограмма Вариньона. Так как в параллелограмме диагонали равны и перпендикулярны, то этот параллелограмм является квадратом (по признаку квадрата).

Что и требовалось доказать.

2. Практическая часть. Решение задач.

Докажите, что а) середины сторон прямоугольника являются вершинами ромба. И наоборот, б) середины сторон ромба являются вершинами прямоугольника.

а) Диагонали прямоугольника равны, поэтому середины сторон прямоугольника являются вершинами ромба (см. следствие 1);

Стороны прямоугольника перпендикулярны, поэтому бимедианы перпендикулярны, тогда середины сторон прямоугольника являются вершинами ромба (см. следствие 1).

б) диагонали ромба перпендикулярны, поэтому середины сторон ромба являются вершинами прямоугольника (см. следствие 2);

Стороны ромба равны, поэтому середины сторон ромба являются вершинами прямоугольника (см. следствие 2).

У четырехугольника диагонали равны aи b. Найдите периметр четырехугольника, вершинами которого являются середины сторон данного четырехугольника.

Периметр параллелограмма Вариньона равен a+b.

Докажите, что середины сторон четырехугольника являются вершинами параллелограмма.

См. теорему Вариньона.

Докажите, что средние линии четырехугольника делятся точкой пересечения пополам.

Т.к. средние линии четырехугольника являются диагоналями параллелограмма Вариньона, то точка пересечения делит их пополам.

Олимпиадные задачи

1. Докажите, что если диагонали четырехугольника равны, то его площадь равна произведению средних линий [5].

Доказать: S_ABCD= KM*LN

Так как диагонали AC = BD, параллелограмм Вариньона является ромбом, площадь ромба равна половине произведения его диагоналей.

Что и требовалось доказать.

2. Докажите, что суммы площадей накрест лежащих четырехугольников, образованных пересечением бимедиан LN и KM выпуклого четырехугольника ABCD равны [6].

Воспользуемся теоремой о средней линии треугольника.

Что и требовалось доказать.

Заключение

«Нет ничего нового под солнцем, но есть кое-что старое, чего мы не знаем», – сказал американский литератор Лоренс Питер.

Пьер Вариньон жил в 18 веке, но теорема Вариньона как нельзя актуальна именно в наши дни, когда чтобы всё успеть, необходимо гораздо больше, чем 24 часа в сутки.

Поэтому была поставлена цель: изучить теорему Вариньона и научиться применять ее на практике с наименьшими временными затратами.

Для этого был разобран весь теоретический материал, решены задачи базового уровня, а также повышенной сложности (олимпиадные). Было подсчитано, что на решение задачи традиционным способом затрачивается 15-20 минут, а зная теорему Вариньона и следствия из нее, доказательство сводится к одному-двум предложениям и занимает 1-2 минуты. При этом экономия времени на доказательство в среднем составляет 15 минут. Таким образом, уже даже решение трех задач добавит дополнительные сорок пять минут (т.е. целый урок) на доказательство других, более сложных.

От этого повышается не только интерес к изучению данного предмета, но и сам процесс работы приносит удовлетворение. Цель работы считаю достигнутой.

Теорема Вариньона.

Теорема. Середины сторон произвольного четырехугольника являются вершинами параллелограмма, стороны которого равны половинам диагоналей данного четырехугольника, а площадь — половине площади данного четырехугольника.

Пример.

Доказательство.

HE — средняя линия треугольника ABD. Следовательно, HE||BD и HE=0,5·BD.

FG — средняя линия треугольника BCD. Следовательно, FG||BD и FG=0,5·BD.

Следовательно, отрезки HE и FG равны и параллельны, следовательно HEFG — параллелограмм.

Докажем, что площадь параллелограмма HEFG равна половине площади четырехугольника.

Пусть BD∩AC=O, тогда

Пусть EH∩AC=K, тогда ∠BOC=∠EKC как соответственные углы при параллельных прямых HE и BD и секущей AC.

∠EKC=∠EHG как соответственные углы при параллельных прямых AC и HG и секущей EH.

[spoiler title=”источники:”]

http://urok.1sept.ru/articles/644122

http://anasta8ia.ru/teorema-varinona/

[/spoiler]

Средние линии треугольников и четырехугольников

107. Мы знаем (п. 102), что геометрическим местом точек, равноотстоящих от двух данных параллельных прямых, служит средняя параллельная. Если таким образом AB и CD (чер. 114) суть две параллельные и MN для них средняя параллельная, то расстояния любой точки E этой средней параллельной от AB и CD равны между собою, т. е., построив EF ⊥ AB и EG ⊥ CD, получим, что EF = EG.

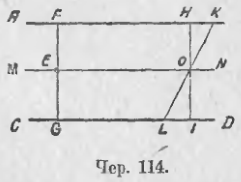
Ясно, что построенные перпендикуляры EF и EG составляют продолжение друг друга и образуют один отрезок FG, перпендикулярный к нашим параллельным AB и CD, причем этот отрезок делится среднею параллельною (в точке E) пополам. Итак, всякий отрезок, перпендикулярный к двум параллельным и заключенный между ними, делится среднею параллельною пополам.

Возникает теперь вопрос: не будет ли также делиться пополам среднею параллельною какой-нибудь отрезок KL, не перпендикулярный к AB и CD. Пусть KL пересекается с MN в точке O. Построим через точку O перпендикулярный к прямым AB и CD отрезок HI. Тогда OH = OI. Так как, кроме того, ∠HOK = ∠IOL, как вертикальные, то прямоугольные треугольники OHK и OIL равны, откуда следует, что OK = OL. Итак, оказывается, что и любой отрезок, заключенный между двумя параллельными, делится среднею параллельною пополам.

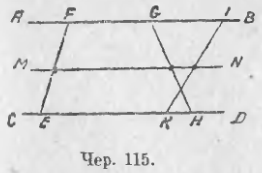
Пусть AB || CD (чер. 115). Построив между ними ряд каких-либо отрезков EF, GH, KI и т. д., мы, согласно предыдущему, найдем, что середины этих отрезков лежат на средней параллельной MN. В общем итоге мы приходим к следующему заключению:

Геометрическим местом середин всевозможных отрезков, заключенных между двумя параллельными, служит средняя параллельная.

Отсюда возникают возможности различных построений средней параллельной для двух данных параллельных прямых: 1) мы можем, построим любой отрезок EF, заключенный между двумя данными параллельными AB и CD, разделить его пополам и через его середину построить прямую MN || AB || CD — это прямая MN и должна служить среднею параллельною, и она должна делить пополам всевозможные отрезки (напр., GH, KI и т. д.), заключенные между AB и CD. 2) Мы можем построить два отрезка, напр., EH и KI, заключенные между AB и CD, разделить каждый из них пополам и через их середины построить прямую MN — она и должна служить среднею параллельною.

108. Применим свойства средней параллельной к знакомым нам фигурам и прежде всего треугольнику.

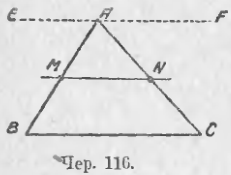
Пусть имеем ∆ABC (чер. 116). Здесь непосредственно мы не имеем двух параллельных, но мы всегда можем их получить, напр., построив через вершину A прямую EF || BC (эту прямую EF можно было бы и не рисовать на чертеже, так как она существенной роли не играет в дальнейшем и так как достаточно лишь знать, что она существует). Тогда мы имеем две параллельных BC и EF и два отрезка AB и AC, заключенных между ними. Разделив их пополам в точках M и N (AM = MB и AN = NC) и построив через M и N прямую MN, мы получим среднюю параллельную MN, т. е. MN || BC (и || EF, но это для нас не существенно). Из этого заключаем:

прямая, соединяющая середины двух сторон треугольника, параллельна его третьей стороне.

Отрезок, соединяющий середины двух сторон треугольника, называют среднею линиею треугольника. Итак, у нас отрезок MN есть средняя лини нашего треугольника.

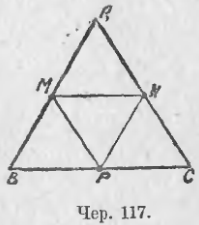
Пусть имеем ∆ABC (чер. 117). Разделим пополам каждую из его сторон: пусть M есть середина AB (сл. AM = MB), N — середина AC (AN = NC) и P — середина BC (BP = PC); соединим точки M, N и P отрезками MN, MP и PN, – каждый из этих отрезков является среднею линиею для нашего треугольника. Таким образом в треугольнике имеется три средних линии.

Согласно предыдущему, будем иметь: MN || BC, MP || AC и NP || AB. Поэтому AMPN, BMNP и PMNC суть параллелограммы. Так как в параллелограмме противоположные стороны равны, то имеем: MN = BP (из параллелограмма BMNP), но BP = BC/2 (ибо точка P есть середина BC); поэтому MN = BC/2. Также из параллелограмма AMPN получим: MP = AN = AC/2 и из параллелограмма AMPN — PN = AM = AB/2. Отсюда заключаем:

каждая средняя линия треугольника, соединяющая середины двух его сторон, параллельна третьей и равна ее половине.

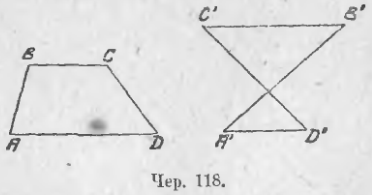
109. Перейдем теперь к четырехугольникам и остановимся сначала на таких четырехугольниках, у которых две стороны параллельны. Принято называть такие четырехугольники трапециями. На чер. 118 изображены два различных вида трапеций: 1) трапеция ABCD, где BC || AD, но AB не параллельна CD, – эта трапеция имеет площадь (см. п. 79) и 2) трапеция A’B’C’D’, где A’D’ || B’C’, – эта трапеция не имеет площади (п. 79).

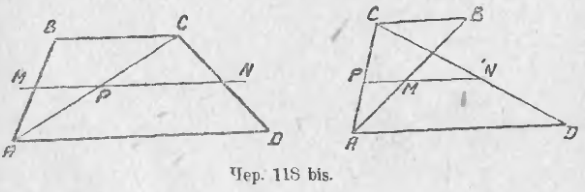
Рассмотрим сначала трапецию ABCD (чер. 118 bis), имеющую площадь. Здесь BD || AD. Поэтому мы имеем две параллельных BC и AD и между ними отрезки AB и CD. Разделив эти отрезки пополам в точках M и N (AM = MB и CN = ND) и соединив их прямою MN, получим среднюю параллельную MN для BC и AD, т. е. MN || BC || AD. Отрезок MN этой прямой называется средней линиею трапеции (следует добавить: «соединяющей середины непараллельных сторон», потому что в трапеции, как и во всяком четырехугольнике, можно рассматривать 6 средних линий, что имеет место в п. 110). Итак, мы получили, что MN || BC || AD. Далее, построив диагональ AC, получим еще третий отрезок AC, заключенный между параллельными BC и AD — его середина должна лежать (п. 107) на средней параллельной, т. е. точка P, где пересекаются MN и AC, есть середина отрезка AC. Поэтому MP есть средняя линия треугольника ABC и PN — средняя линия ∆ACD. На основании предыдущего, имеем: MP = BC/2 и PN = AD/2. Отсюда получаем: MN = MP + PN = BC/2 + AD/2 или MN = (BC + AD)/2. Итак,

средняя линия, соединяющая середины непараллельных сторон трапеции, имеющей площадь, параллельна ее параллельным сторонам и равна их полусумме.

Пусть теперь имеем трапецию ABCD (чер. 118 bis), неимеющую площади. Здесь также BC || AD и поэтому середины M и N сторон AB и CD лежат на средней параллельной, т. е. здесь также имеем: MN || BC || AD. Построив диагональ AC, получим отрезок AC, заключенный между параллельными BC и AD, и его середина, точка P, должна лежать на средней параллельной. Поэтому PM есть средняя линия треугольника ABC и, следовательно PM = BC/2; также PN есть средняя линия ∆ABC и, след., PN = AD/2. Так как MN = PN – PM, то получим MN = PN – PM = AD/2 – BC/2 или MN = (AD – BC) / 2. Итак,

средняя линия, соединяющая середины непараллельных сторон трапеции, неимеющей площади, параллельна ее параллельным сторонам и равна их полуразности.

110. Пусть имеем какой-либо четырехугольник ABCD (имеющий площадь) — (чер. 119). Найдем середины M, N, P и Q его сторон и соединим их попарно. Получим 6 средних линий четырехугольника.

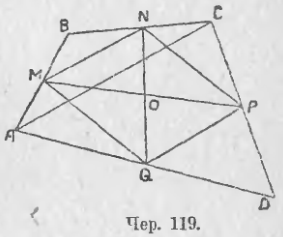
Вот свойства этих средних линий.

1) Средние линии, соединяющие середины последовательных сторон четырехугольника, образуют параллелограмм.

Для выяснения этого свойства построим диагональ AC. Тогда из ∆ABC имеем (п. 108) MN || AC и из ∆ACD на том же основании: PQ || AC, – следов., MN || PQ. Построив другую диагональ BD, найдем при ее помощи, что NP || MQ, следовательно, MNPQ есть параллелограмм.

2) Средние линии четырехугольника, соединяющие середины противоположных сторон, взаимно делятся пополам.

Это свойство теперь очевидно, так как MP и NQ являются диагоналями параллелограмма.
Через точку O пересечения прямых MP и NQ проходят также прямые, соединяющие середины диагоналей AC и BD (на чертеже диагональ BD не дана). Это следует из того, что AC И BD являются сторонами четырехугольника ACBD, не имеющего площади, к которому применимо все, изложенное в начале этого п.

111. Мы умели (пп. 57, 59) делить отрезок пополам и, следов., на 4, на 8 и вообще на 2n равных частей. Теперь мы можем разделить данный отрезок на 3, на 5 и вообще на сколько угодно равных частей.

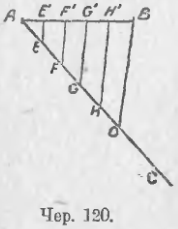
Пусть, напр., требуется отрезок AB (чер. 120) разделить на 5 равных частей. Построим через точку A произвольную прямую AC (образующую с AB угол, отличный от выпрямленного) и отложим на AC пять произвольных, но равных между собою, отрезков AE = EF = FG = GH = HO. Построим прямую OB и через точки E, F, G и Н построим прямые EE’, FF’, GG’, HH’, параллельные OB.

Рассмотрим ∆AFF’, так как AE = EF, то E есть середина стороны AF и EE’ (она || FF’) есть средняя линия этого треугольника, следовательно, AE’ = E’F’.

Рассмотрим затем трапецию EE’G’G. Так как EF = FG, FF’ || EE’, то FF’ есть средняя линия трапеции EE’GG’, – следовательно, E’F’ = F’G’. Также найдем, что GG’ есть средняя линия трапеции FF’H’H и, следов., F’G’ = G’H’ и т. д. Соединяя полученные равенства, найдем AE’ = E’F’ = F’G’ = G’H’ = H’B’, т. е. отрезок AB разделился на 5 равных частей.

Из решения этой задачи можно вывести заключение:

Если на одной стороне угла отложить равные отрезки и чрез их концы построить ряд параллельных прямых, то и на другой стороне угла получим равные между собой отрезки.

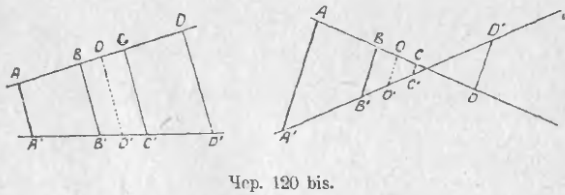
Добавление. Мы откладывали равные отрезки на одной прямой подряд, начиная от точки пересечения двух прямых (AB и AC чертежа 120), но возможно к такому же результату прийти и при ином способе отложения равных отрезков. На чертеже 120 bis дано два варианта такого построения: на прямой AD (см. чер. 120 bis слева или справа) отложим два равных отрезка AB и CD и через их концы построим параллельные AA’ || BB’ || CC’ || DD’. Затем возьмем точку O, середину отрезка BC, и построим OO’ || BB’ || CC’ || AA’ || DD’. Тогда OO’ есть средняя линия трапеции BCC’B’; поэтому B’O’ = O’C (п. 109). Так как AB = CD и BO = OC, то AO также = OD; поэтому OO’ есть также средняя линия трапеции ADD’A’ (на чертеже справа эта трапеция ADD’A’ — не имеющая площади, см. п. 109) — и также A’O’ = O’D’. Отсюда имеем A’O’ – B’O’ = O’D’ – O’C’ (ибо и уменьшаемые и вычитаемые обеих разностей равны), или A’B’ = C’D’. Возможны и иные комбинации (напр., отр. CD правой фигуры отодвинуть так, чтобы точка C оказалась правее точки пересечения прямых AD и A’D’). Общее заключение таково: если построены две прямые, на одной из них отложены как-либо два равных отрезка и через концы их построены параллельные, то эти последние выделят и на другой прямой два равных между собою отрезка.

112. Упражнения.

1. Через вершины данного треугольника построены прямые, параллельные его сторонам. Показать, что новый треугольник имеет стороны вдвое больше, чем стороны данного, и что вершины данного являются серединами сторон нового (сравн. упр. 7 из п. 54).
2. Построить треугольник, если даны середины трех его сторон.
3. Построить параллелограмм, если даны середины трех его сторон.
4. Известно (п. 110), что середины четырех сторон четырехугольника являются вершинами параллелограмма. Когда этот параллелограмм обращается в ромб, когда в прямоугольник, когда в квадрат?
5. Прямая, соединяющая вершину треугольника со срединою противоположной стороны (медиана) и прямая, соединяющая середины двух других сторон треугольника, взаимно делятся пополам.
6. Продолжим одну сторону треугольника на отрезок, равный этой стороне, и соединим конец отрезка со срединою другой стороны. Последняя соединяющая прямая отсекает от третьей стороны треугольника отрезок, равный 1/3 этой стороны. (Построить еще прямую, параллельную последней соединяющей прямой чрез вершину треугольника, противолежащую той его стороне, которая была продолжена).
7. Если на стороне AB параллелограмма ABCD отложить отрезок AM = (1/n)AB (напр., (1/7)AB) и соединить D с M, то DM пересечет диагональ AC в точке N так, что AN = (1/(n+1))AC (во взятом примере (1/8)AC).
   Для выяснения этого надо на продолжении стороны AB отложить BM’ = AM и соединить C с M’; тогда C’M’ || DM, – приметь п. 111.

Что называется медианой треугольника?

Определение.

Медиана треугольника — это отрезок, соединяющий вершину треугольника с серединой противоположной стороны.

Как построить медиану треугольника?

Чтобы построить медиану треугольника, надо:

1) С помощью линейки найти и отметить середину стороны треугольника.

2) Соединить полученную точку с вершиной, лежащей напротив этой стороны.

Рисунок медианы треугольника:

Как построить медиану треугольника с помощью циркуля и линейки без шкалы, мы рассмотрим позже, в теме «Построить треугольник».

Сколько медиан имеет треугольник?

Так как у треугольника три вершины и три стороны, то и отрезков, соединяющих вершину и середину противолежащей стороны, тоже три. Значит, треугольник имеет три медианы.

Все три медианы треугольника пересекаются в одной точке:

Точка пересечения медиан называется центром тяжести треугольника.

В точке пересечения медианы треугольника делятся в отношении два к одному, считая от вершины:

   

Об этом свойстве медиан треугольника, а также о том, как найти длину медианы через длины сторон треугольника, более подробно мы поговорим позже и рассмотрим, как свойства медианы использовать при решении задач.

Кроме того, отдельно будут рассмотрены медиана прямоугольного треугольника, проведенная к гипотенузе и медиана равнобедренного треугольника, проведенная к его основанию, поскольку каждая из них обладает своими свойствами, которые надо знать и уметь применять.