Как найти середину интервала
При статистической обработке результатов исследований самого разного рода полученные значения часто группируются в последовательность интервалов. Для расчета обобщающих характеристик таких последовательностей иногда приходится вычислять середину интервала – «центральную варианту». Методы ее расчета достаточно просты, но имеют некоторые особенности, вытекающие как из используемой для измерения шкалы, так и из характера группировки (открытые или закрытые интервалы).

Инструкция
Если интервал является участком непрерывной числовой последовательности, то для нахождения ее середины используйте обычные математические методы вычисления среднеарифметического значения. Минимальное значение интервала (его начало) сложите с максимальным (окончанием) и разделите результат пополам – это один из способов вычисления среднеарифметического значения. Например, это правило применимо, когда речь идет о возрастных интервалах. Скажем, серединой возрастного интервала в диапазоне от 21 года до 33 лет будет отметка в 27 лет, так как (21+33)/2=27.
Иногда бывает удобнее использовать другой метод вычисления среднеарифметического значения между верхней и нижней границами интервала. В этом варианте сначала определите ширину диапазона – отнимите от максимального значения минимальное. Затем поделите полученную величину пополам и прибавьте результат к минимальному значению диапазона. Например, если нижняя граница соответствует значению 47,15, а верхняя – 79,13, то ширина диапазона составит 79,13-47,15=31,98. Тогда серединой интервала будет 63,14, так как 47,15+(31,98/2) = 47,15+15,99 = 63,14.
Если интервал не является участком обычной числовой последовательности, то вычисляйте его середину в соответствии с цикличностью и размерностью используемой измерительной шкалы. Например, если речь идет об историческом периоде, то серединой интервала будет являться определенная календарная дата. Так для интервала с 1 января 2012 года по 31 января 2012 серединой будет дата 16 января 2012.
Кроме обычных (закрытых) интервалов статистические методы исследований могут оперировать и «открытыми». У таких диапазонов одна из границ не определена. Например, открытый интервал может быть задан формулировкой «от 50 лет и старше». Середина в этом случае определяется методом аналогий – если все остальные диапазоны рассматриваемой последовательности имеют одинаковую ширину, то предполагается, что и этот открытый интервал имеет такую же размерность. В противном случае вам надо определить динамику изменения ширины интервалов, предшествующих открытому, и вывести его условную ширину, исходя из полученной тенденции изменения.
Источники:
- что такое открытый интервал
Войти на сайт
или
Забыли пароль?
Еще не зарегистрированы?
This site is protected by reCAPTCHA and the Google Privacy Policy and Terms of Service apply.
Примеры решений задач по статистике
Решение задач по статистике и выводы к ним
Задача по статистике №1. Найти параметры интервального ряда распределения по данным таблицы, а именно: моду, медиану, среднюю арифметическую величину, среднюю взвешенную величину, коэффициент вариации, среднее квадратическое отклонение.
|
№ группы |
Группы компаний по основным производственным фондам, млн. руб. (х) |
Число компаний (fi) |
Середина интервала (Xi) = (начало интервала+конец интервала)/2 |
|
1 |
10 – 25 |
2 |
17,5 |
|
2 |
25 – 33 |
8 |
29 |
|
3 |
33 – 42 |
14 |
37,5 |
|
4 |
42 – 49 |
9 |
45,5 |
|
5 |
49 – 62 |
3 |
55,5 |
|
Всего: |
36 |
— |
Мы сразу добавили столбец «середина интервала». Для первой группы компаний рассчитали следующим образом: (10+25)/2=17,5 млн. руб. Для 2-5 групп расчеты произведены аналогично.
Теперь рассчитаем среднюю арифметическую величину.
 средняя арифметическая =
средняя арифметическая =  = (17,5+29+37,5+45,5+55,5)/5=37 млн. руб.
= (17,5+29+37,5+45,5+55,5)/5=37 млн. руб.
Далее рассчитаем среднюю взвешенную величину.
 средняя взвешенная =
средняя взвешенная =  = (17,5*2+29*8+37,5*14+45,5*9+55,5*3)/36=38 млн. руб.
= (17,5*2+29*8+37,5*14+45,5*9+55,5*3)/36=38 млн. руб.
Значение средневзвешенной величины можно считать более корректным, чем значение средней арифметической величины, поэтому далее в расчетах будем использовать среднюю взвешенную.
Теперь добавим в таблицу столбцы, данные которых нам понадобятся для расчета дисперсии.
|
Число компаний (f) |
Середина интервала (Xi) = (начало интервала+конец интервала)/2 |
Xi*fi |
|
|
|
|
2 |
17,5 |
35 |
-20,5 |
420,25 |
840,5 |
|
8 |
29 |
232 |
-9 |
81 |
648 |
|
14 |
37,5 |
525 |
-0,5 |
0,25 |
3,5 |
|
9 |
45,5 |
409,5 |
7,5 |
56,25 |
506,25 |
|
3 |
55,5 |
166,5 |
17,5 |
306,25 |
918,75 |
|
Итого: 36 |
— |
1368 |
— |
— |
2917 |
Рассчитаем дисперсию.
 =2917/36=81,03. (дисперсия не имеет размерности)
=2917/36=81,03. (дисперсия не имеет размерности)
Среднеквадратическое отклонение рассчитывается как корень квадратный из дисперсии.
 =9 (млн. руб.).
=9 (млн. руб.).
Рассчитаем коэффициент вариации по формуле:
 =(9/38)*100%=23,68%.
=(9/38)*100%=23,68%.
Рассчитаем моду и медиану.
Найдем моду по формуле. 
Модальный интервал находим по наибольшей частоте. Наибольшая частота, т.е. частота модального интервала fМо=14. Модальный интервал от 33 до 42 млн. руб. Значит величина модального интервала i = 42-33=9.
Нижняя граница модального интервала  равна 33.
равна 33.
Частота предмодального интервала  равна 8.
равна 8.
Частота постмодального интервала  равна 9.
равна 9.
Мода будет равна = 33 + 9*((14-8)/(14-8+14-9))=37,9 млн. руб.
Найдем медиану по формуле. 
Медианный интервал находим по накопленной частоте. Суммируются f частоты, пока не достигается значение, превышающее середину совокупности (36/2=18 млн. руб.).
|
Группы компаний по основным производственным фондам, млн. руб. (х) |
Число компаний (f) |
Накопленная частота S |
|
10 – 25 |
2 |
2 |
|
25 – 33 |
8 |
10 |
|
33 – 42 |
14 |
24 |
|
42 – 49 |
9 |
33 |
|
49 – 62 |
3 |
36 |
Таким образом, медианный интервал от 33 до 42 млн. руб. Значит величина медианного интервала i = 42-33=9.
Частота медианного интервала fМе=14.
Нижняя граница медианного интервала  равна 33.
равна 33.
Накопленная частота предмедианного интервала  равна 10.
равна 10.
Медиана будет равна = 33 + 9*((36/2-10)/(14))=38,14 млн. руб.
Расчеты по теме “индексы”
Пример по выборке.
Задача по группировке.
Решение задачи по расчету средней.
Задача по кореляционному анализу
Контрольные и курсовые работы по общей теории статистики и экономической статистике по этим и другим темам представлены в соответствующем разделе сайта.
По данным выборочного обследования произведена группировка вкладчиков по размеру вклада в Сбербанке города:
| Размер вклада, руб. | До 400 | 400 – 600 | 600 – 800 | 800 – 1000 | Свыше 1000 |
|---|---|---|---|---|---|
| Число вкладчиков | 32 | 56 | 120 | 104 | 88 |
Определите:
1) размах вариации;
2) средний размер вклада;
3) среднее линейное отклонение;
4) дисперсию;
5) среднее квадратическое отклонение;
6) коэффициент вариации вкладов.
Решение:
Данный ряд распределения содержит открытые интервалы. В таких рядах условно принимается величина интервала первой группы равна величине интервала последующей, а величина интервала последней группы равна величине интервала предыдущей.
Величина интервала второй группы равна 200, следовательно, и величина первой группы также равна 200. Величина интервала предпоследней группы равна 200, значит и последний интервал будет иметь величину, равную 200.
| Размер вклада, руб. | 200 – 400 | 400 – 600 | 600 – 800 | 800 – 1000 | 1000 – 1200 |
|---|---|---|---|---|---|
| Число вкладчиков | 32 | 56 | 120 | 104 | 88 |
1) Определим размах вариации как разность между наибольшим и наименьшим значением признака:
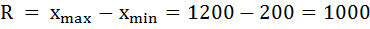
Размах вариации размера вклада равен 1000 рублей.
2) Средний размер вклада определим по формуле средней арифметической взвешенной.
Предварительно определим дискретную величину признака в каждом интервале. Для этого по формуле средней арифметической простой найдём середины интервалов.
Среднее значение первого интервала будет равно:
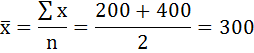
второго – 500 и т. д.
Занесём результаты вычислений в таблицу:
| Размер вклада, руб. | Число вкладчиков, f | Середина интервала, х | xf |
|---|---|---|---|
| 200-400 | 32 | 300 | 9600 |
| 400-600 | 56 | 500 | 28000 |
| 600-800 | 120 | 700 | 84000 |
| 800-1000 | 104 | 900 | 93600 |
| 1000-1200 | 88 | 1100 | 96800 |
| Итого | 400 | – | 312000 |
Средний размер вклада в Сбербанке города будет равен 780 рублей:
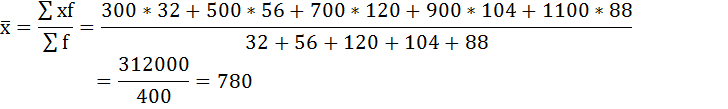
3) Среднее линейное отклонение есть средняя арифметическая из абсолютных отклонений отдельных значений признака от общей средней:
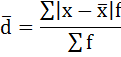
Порядок расчёта среднего линейонго отклонения в интервальном ряду распределения следующий:
1. Вычисляется средняя арифметическая взвешенная, как показано в п. 2).
2. Определяются абсолютные отклонения вариант от средней:
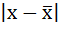
3. Полученные отклонения умножаются на частоты:
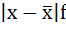
4. Находится сумма взвешенных отклонений без учёта знака:
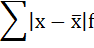
5. Сумма взвешенных отклонений делится на сумму частот:
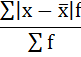
Удобно пользоваться таблицей расчётных данных:
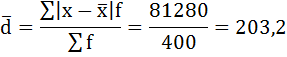
Среднее линейное отклонение размера вклада клиентов Сбербанка составляет 203,2 рубля.
4) Дисперсия – это средняя арифметическая квадратов отклонений каждого значения признака от средней арифметической.
Расчёт дисперсии в интервальных рядах распределения производится по формуле:
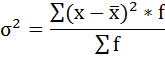
Порядок расчёта дисперсии в этом случае следующий:
1. Определяют среднюю арифметическую взвешенную, как показано в п. 2).
2. Находят отклонения вариант от средней:

3. Возводят в квадрат отклонения каждой варианты от средней:
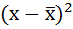
4. Умножают квадраты отклонений на веса (частоты):
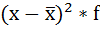
5. Суммируют полученные произведения:
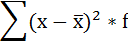
6. Полученная сумма делится на сумму весов (частот):
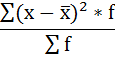
Расчёты оформим в таблицу:
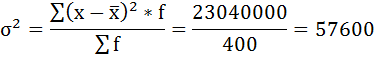
5) Среднее квадратическое отклонение размера вклада определяется как корень квадратный из дисперсии:
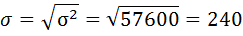
6) Коэффициент вариации – это отношение среднего квадратического отклонения к средней арифметической:
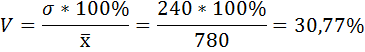
По величине коэффициента вариации можно судить о степени вариации признаков совокупности. Чем больше его величина, тем больше разброс значений признаков вокруг средней, тем менее однородна совокупность по своему составу и тем менее представительна средняя.
Алгоритм построения интервального вариационного ряда с равными интервалами
-
Определяем
число интервалов (групп) вариационного
ряда
Число
групп (интервалов)
приближенно определяется по формуле
Стерджесса:
m
= 1 + 3,322 × lg(n)
где n
– общее число единиц наблюдения (общее
количество элементов в совокупности и
т.д.), lg(n)
– десятичный логарифм от n.
Полученную
по
формуле Стерджесса величину округляют
обычно до целого большего числа,
поскольку количество групп не может
быть дробным числом.
Если
ряд интервальный ряд с таким количеством
групп по каким-то критериям не устраивает,
то можно построить другой интервальный
ряд, округлив m
до
целого меньшего числа и выбрать из двух
рядов более подходящий.
Число
групп не должно быть больше 15.
Также
можно пользоваться следующей таблицей,
если совсем нет возможности вычислить
десятичный логарифм.
|
Объем выборки, |
25-40 |
40-60 |
60-100 |
100-200 |
Больше 200 |
|
Число интервалов, |
5-6 |
6-8 |
7-10 |
8-12 |
10-15 |
-
Определяем
ширину интервала
Ширина
интервала
для интервального вариационного ряда
с равными интервалами определяется по
формуле:
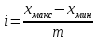
где
Xмакс
– максимальное из значений xi,
Xмин
–
минимальное из значений xi;
m
– число групп (интервалов).
Величину
интервала (i)
обычно округляют до целого числа,
исключение составляют лишь случаи,
когда изучаются малейшие колебания
признака (например, при группировке
деталей по величине размера отклонений
от номинала, измеряемого в долях
миллиметра).
Часто
применяется следующее правило:
|
Количество |
Количество |
Пример |
До |
Пример |
|
0 |
3 |
0,375 |
0,01 |
0,38 |
|
0 |
2 |
0,56 |
0,1 |
0,6 |
|
1 |
3 |
4,658 |
0,01 |
4,66 |
|
1 |
2 |
2,54 |
0,1 |
2,5 |
|
2 |
любое |
12,54 |
1,0 |
13 |
|
3 |
любое |
672,54 |
10,00 |
670 |
|
4 |
любое |
3472,45 |
100,00 |
3500 |
|
и |
-
Определяем
границы интервалов
Нижнюю
границу
первого интервала
принимают равной минимальному значению
признака (чаще всего его предварительно
округляют до целого меньшего числа с
таким же разрядом как ширина интервала).
Например, хмин=
15, i=130,
хн
первого интервала = 10.
хн1
≈ хмин
Верхняя
граница
первого интервала соответствует значению
(Хmin
+ i).
Нижняя
граница второго интервала всегда равно
верхней границе первого интервала. Для
последующих групп границы определяются
аналогично, т е. последовательно
прибавляется величина интервала.
xвi
=
xнi
+ i
xнi
= xвi-1
-
Определяем
частоты интервалов.
Считаем,
сколько значений попало в каждый
интервал. При этом помним, что если
единица обладает значением признака,
равным величине верхней границы
интервала, то ее следует относить к
следующему интервалу.
-
Строим
интервальный ряд в виде таблицы. -
Определяем
середины интервалов.
Для
дальнейшего анализа интервального ряда
понадобится выбрать значение признака
для каждого интервала. Это значение
признака будет общим для всех единиц
наблюдения, попавшим в этот интервал.
Т.е. отдельные элементы «теряют» свои
индивидуальные значения признака и им
присваивается одно общее значение
признака. Таким общим значением является
середина
интервала,
которая обозначается x’i
.
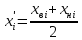
Рассмотрим
на примере с ростом детей, как построить
интервальный ряд с равными интервалами.
Имеются
первоначальные данные.
90,
91, 92, 93, 94, 95, 96, 97, 98, 99,
92,
93, 94, 95, 96, 98,
100,
101, 102, 103, 104, 105, 106, 107, 108, 109,
100,
101, 102, 103, 104, 105, 106, 107, 108, 109,
100,
101, 102, 104,
110,
112, 114, 116, 117, 120, 122, 123, 124, 129,
110,
111, 113, 115, 116, 117, 121, 125, 126, 127,
110,
111, 112, 113, 114, 115, 116, 117, 118, 119, 120, 121, 122, 123, 124,
125, 126, 127, 128, 129,
111,
113, 116, 127,
123, 122, 130,
131, 132, 133, 134, 136, 137, 138, 139, 140, 141, 142, 143, 144, 145,
146, 147, 148, 149, 150,
131,
133, 135, 136, 138, 139, 140, 141, 142, 143, 145, 146, 147, 148
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
17.02.2016629.11 Кб140308126_71740_lekcii_upravlencheskie_resheniya.rtf
- #
- #
- #
- #
- #
- #
- #
- #
Вам понадобится:
- Циркуль
- линейка
- карандаш
#1
Жизнь каждого офисного работника не может обходиться без вычислений и статистики. Каждый офисный работник должен знать про нахождение середины интервала, середины вектора, координат середины вектора, середины окружности и построение середины данного отрезка.
#2
В вопросе какнайти середину интервала, нужно использовать обычные математические методы вычисления. Надо сложить начало интервала с окончанием интервала и полученный ответ разделить пополам. Этот метод используют при вычислении возрастных интервалов. Дальше я расскажу о том, как найти координаты середины вектора.
#3
В вопросе какнайти середину интервала, нужно использовать обычные математические методы вычисления. Надо сложить начало интервала с окончанием интервала и полученный ответ разделить пополам. Этот метод используют при вычислении возрастных интервалов. Дальше я расскажу о том, как найти координаты середины вектора.
#4
Берём отрезок, устанавливаем один конец циркуля в любой из концов отрезка и проводим окружность, при этом радиус должен быть равен длине отрезка. Выполняем тоже самое с другим концом. Обе окружности пересекутся в двух точках. Берём линейку и поводим прямую через точки пересечения окружностей. Где эта прямая пересечётся с отрезком, там и находится середина отрезка. Теперь речь пойдёт о том, как найти середину окружности.
#5
Для нахождения середины окружности, мы используем следующий метод: в окружности проводим две не параллельные хорды, а потом продлеваем их настолько, чтобы они пересеклись. Концы хорд соединяем друг с другом. Далее нужно найти диаметр, но сделать это надо два раза, чтобы получить точку пересечения диаметров, которая поможет найти искомый вами центр. В конце поведаем, как найти середину вектора.
#6
Сначала нужно обозначить точки начала и конца вектора. Для нахождения середины вектора, нужно из конечной координаты вектора вычесть начальные координаты вектора. Длину вектора можно вычислить как корень квадрата из общей суммы квадратов координат. Эту информацию нужно знать не только офисным работникам, но и обычным людям, ведь эти знания могут пригодиться в жизни.



