Как рассчитать коэффициенты сезонности, очищенные от роста?
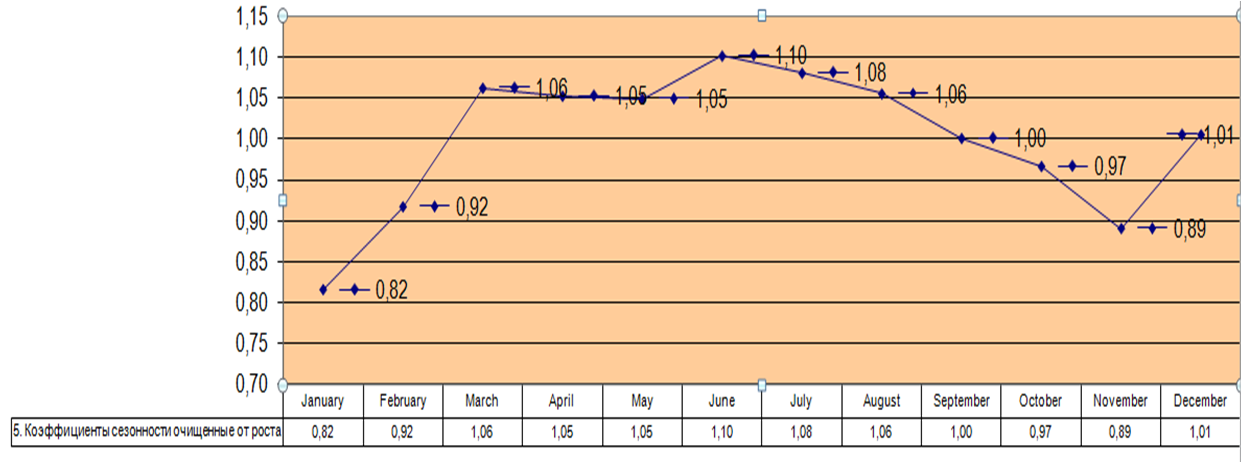
Из данной статьи вы узнаете, как в MS Excel рассчитать коэффициенты сезонности очищенные от роста.
Для чего используют коэффициенты сезонности:
-
Для расчета прогноза;
-
Для планирования деятельности, т.е. для определения приоритетов по месяцам в рамках года;
-
Для выбора лучшего времени проведения мероприятий по стимулированию сбыта для товаров или услуг;
-
Для выбора лучшего времени для рекламирования товаров или услуг;
и т.д.
![]() Из данной статьи вы узнаете, как рассчитать индексы сезонности и пики в Excel. А также, для чего их используют на практике.
Из данной статьи вы узнаете, как рассчитать индексы сезонности и пики в Excel. А также, для чего их используют на практике.
Как рассчитать аддитивную сезонность в Excel
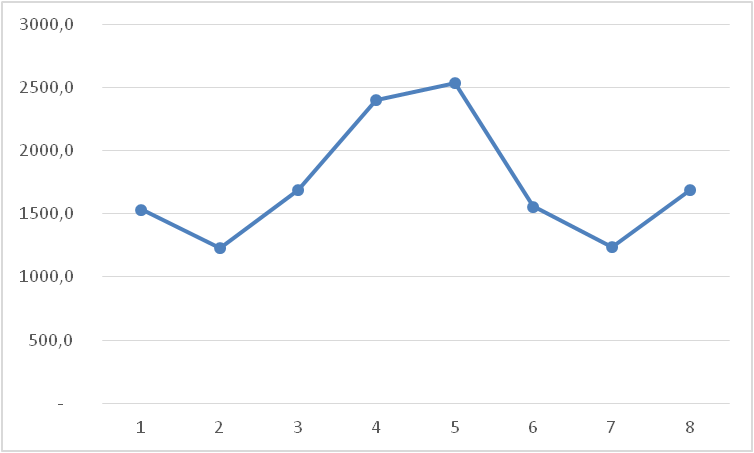 Из данной статьи вы узнаете
Из данной статьи вы узнаете
- Что такое аддитивная сезонность,
- Как рассчитать аддитивную сезонность в Excel,
- Как учесть аддитивную сезонность в прогнозе.
Как сделать эффективный план график продвижения в рамках года?
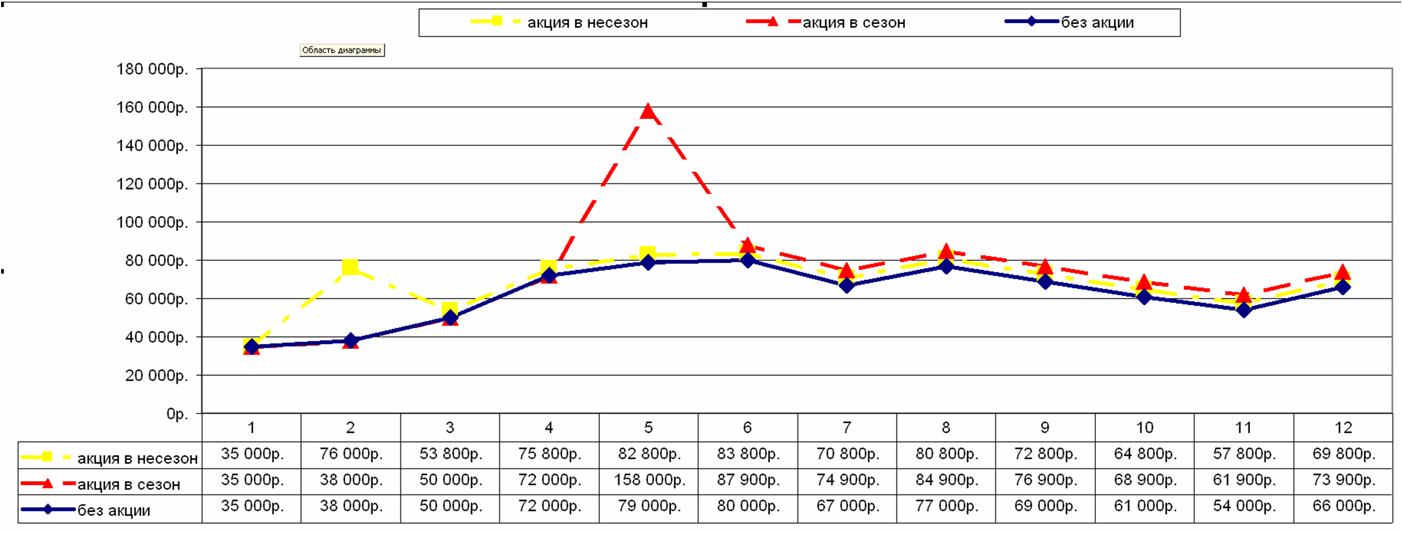
Из данной статьи вы узнаете, как эффективно распределить активность по продвижению товаров из разных товарных групп в рамках года.
Ситуация – у нас более 10 товарных групп с разной сезонностью. Вопрос, в какие месяцы эффективнее всего запланировать и провести мероприятия по стимулированию сбыта, для того, чтобы затраты дали максимальную отдачу?
Видео аддитивная и мультипликативная сезонность
В данной статье вы сможете посмотреть видео о видах сезонности – аддитивной и мультипликативной.
Как оценить сезонность и учитывать ее при прогнозировании, смотрите в видео…
Excel для Microsoft 365 Excel для Microsoft 365 для Mac Excel для Интернета Excel 2021 Excel 2021 для Mac Excel 2019 Excel 2019 для Mac Excel 2016 Excel 2016 для Mac Еще…Меньше
Важно: Функция ПРОГНОЗ. ETS. Сезонность недоступна в Excel для Интернета, iOS или Android.
Возвращает длину повторяющегося фрагмента, обнаруженного программой Excel в заданном временном ряду. ПРОГНОЗ. ETS. СЕЗОННОСТЬ можно использовать после прогноза. ETS для определения того, какая автоматическая сезонность была обнаружена и использована в ФУНКЦИИ ПРОГНОЗ. ETS. Хотя ее можно использовать независимо от ПРЕДСКАЗ.ETS, эти функции связаны между собой: ПРЕДСКАЗ.ETS.СЕЗОННОСТЬ определяет то же значение сезонности, что и ПРЕДСКАЗ.ETS, на основе одинаковых входных параметров, влияющих на порядок заполнения данных.
Синтаксис
ПРЕДСКАЗ.ETS.СЕЗОННОСТЬ(значения;временная_шкала;[заполнение_данных];[агрегирование])
Аргументы функции ПРЕДСКАЗ.ETS.СЕЗОННОСТЬ описаны ниже.
-
Значения — обязательный аргумент. Значения представляют собой ретроспективные данные, на основе которых прогнозируются последующие значения.
-
Временная_шкала — обязательный аргумент. Независимый массив или интервал числовых данных. Даты во временной шкале должны отстоять одна от другой на фиксированный интервал и не должны быть нулевыми. Сортировать временную шкалу не обязательно, так как “ПРОГНОЗ”. ETS. Сезонность будет автоматически отсортировать ее для вычислений. Если на за предоставленной временной шкале не удалось определить константу, спрогнозировали ее. ETS. Сезонность возвращает #NUM! ошибку “#ВЫЧИС!”. Если временная шкала содержит повторяющиеся значения, FORECAST. ETS. Сезонность возвращает #VALUE! ошибку “#ВЫЧИС!”. Если диапазоны временной шкалы и значений не одинаковы, ТО ПРОГНОЗ. ETS. Сезонность возвращает ошибку #N/A.
-
Заполнение_данных — необязательный аргумент. Хотя временная шкала требует постоянного шага между точками данных, FORECAST. ETS. Сезонность поддерживает до 30 % отсутствующих данных и автоматически настраивает их. 0 означает, что алгоритм учитывает отсутствующие точки как нули. Если задано значение 1 (вариант по умолчанию), функция определяет отсутствующие значения как среднее между соседними точками.
-
Агрегирование — необязательный аргумент. Хотя временная шкала требует постоянного шага между точками данных, FORECAST. ETS. Сезонность будет агрегировать несколько точек с одинаковой отметкой времени. Параметр агрегирования — это числовое значение, определяющее способ агрегирования нескольких значений с одинаковой меткой времени. Для значения по умолчанию 0 используется метод СРЗНАЧ; также доступны варианты СУММ, СЧЁТ, СЧЁТЗ, МИН, МАКС и МЕДИАНА.
Скачайте пример книги.
Щелкните эту ссылку, чтобы скачать книгу с Excel FORECAST. Примеры функции ETS
Дополнительные сведения
Вы всегда можете задать вопрос специалисту Excel Tech Community или попросить помощи в сообществе Answers community.
См. также
Функции прогнозирования (справочник)
Нужна дополнительная помощь?
Нужны дополнительные параметры?
Изучите преимущества подписки, просмотрите учебные курсы, узнайте, как защитить свое устройство и т. д.
В сообществах можно задавать вопросы и отвечать на них, отправлять отзывы и консультироваться с экспертами разных профилей.
В прошлой статье мы уже разобрали, что такое временной ряд и функцию тренда. Теперь подробнее разберемся с терминологией и остановимся на одной из моделей временного ряда.
Из чего состоит временной ряд
Уровни временного ряда (Yt) представляют из себя сумму двух компонент:
- Регулярную составляющую
- Случайную составляющую
В свою очередь регулярная составляющая состоит из:
- Тренда
- Сезонности
- Циклической составляющей
Однако, в модели необязательно наличие всех этих компонент сразу.
Случайная компонента отражает влияние случайных возмущений на модель, которые по отдельности имеют незначительное воздействие, но суммарно их влияние ощущается.
То есть, в общем случае временной ряд представляет из себя наличие четырех составляющих:
- Тренд (Tt)
- Сезонность (St)
- Цикличность (Ct)
- Случайные возмущения (Et)
Циклическая компонента, по сравнению с сезонностью, имеет более длительный эффект и меняется от цикла к циклу. Поэтому, ее обычно объединяют с трендом.
Виды моделей временного ряда
Обычно, выделяют две модели временного ряда и третью — смешанную.
- Аддитивная модель
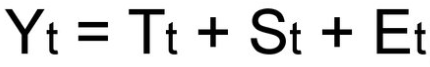
-
Мультипликативная модель
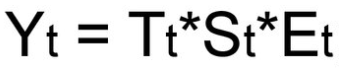
-
Смешанная модель
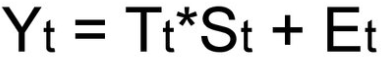
При выборе необходимой модели временного ряда смотрят на амплитуду колебаний сезонной составляющей. Если ее колебания относительно постоянны, то выбирают аддитивную модель. То есть, амплитуда колебаний примерно одинакова:
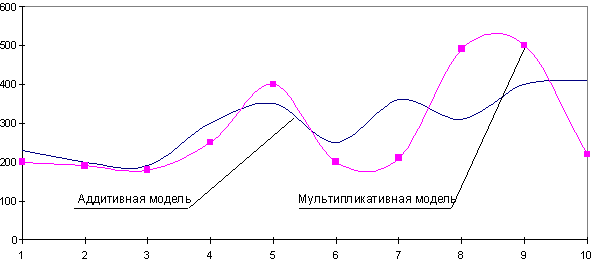
Если амплитуда сезонных колебаний возрастает или уменьшается, строят мультипликативную модель временного ряда, которая ставит уровни ряда в зависимость от значений сезонной компоненты.
Построение этих моделей сводится к расчету тренда (Tt), сезонности (St) и случайных возмущений (Et) для каждого уровня ряда (Yt).
Алгоритм построения модели
- Выравниваем ряд с помощью скользящей средней, то есть сглаживаем ряд и отфильтровываем высокочастотные колебания.
- Рассчитываем значение сезонной компоненты St.
- Рассчитываем значения Tt с использованием полученного уравнения тренда.
- Используя полученные значения St и Tt, находим прогнозные значения уровней временного ряда.
- Оцениваем качество модели.
Реализация на практике
Итак, мы имеем на руках данные о продажах за 2016 и 2017 год и хотим спрогнозировать продажи на 2018 год.
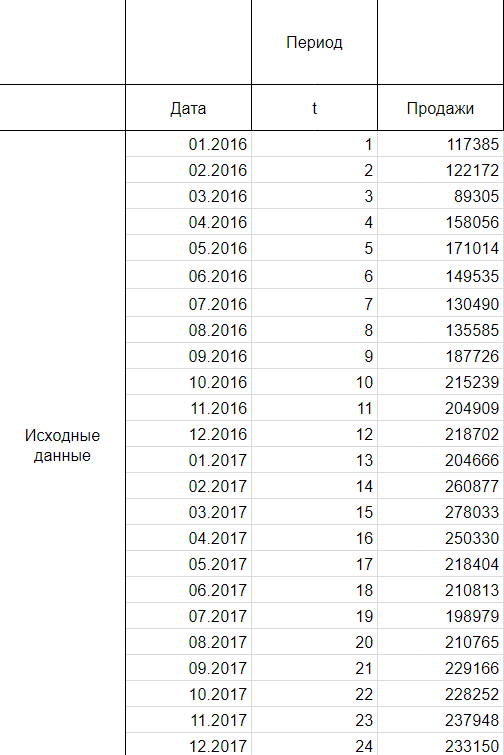
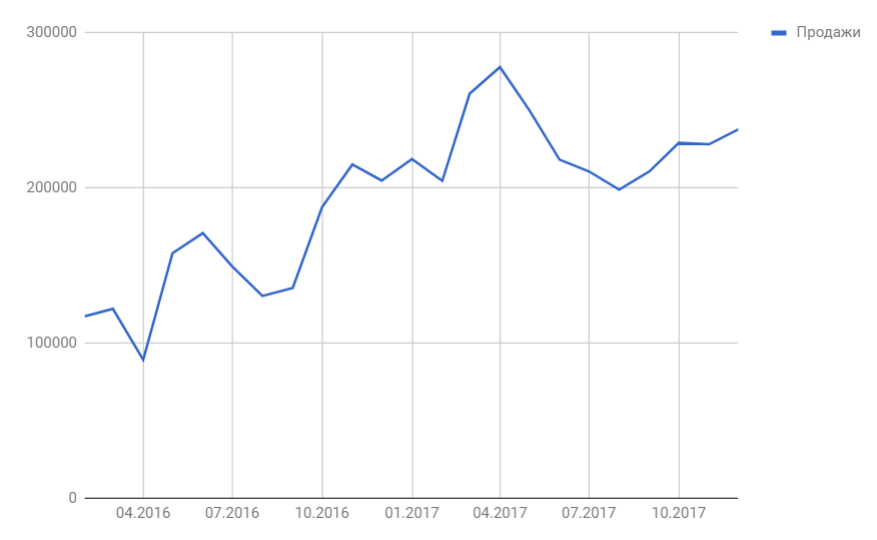
Шаг 1
Следуя нашему алгоритму, мы должны сгладить временной ряд. Воспользуемся методом скользящей средней. Видим, что в каждом году есть большие пики (май-июнь 2016 и апрель 2017), поэтому возьмем период сглаживания пошире, например, месячную динамику, т.е. 12 месяцев.
Удобнее брать период сглаживания в виде нечетного числа, тогда формула для расчета уровней сглаженного ряда:

yi — фактическое значение i-го уровня ряда,
yt — значение скользящей средней в момент времени t,
2p+1 — длина интервала сглаживания.
Но так как мы решили использовать месячную динамику в виде четного числа 12, то данная формула нам не подойдет и мы воспользуемся этой:
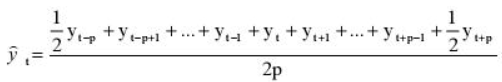
Иными словами, мы учитываем половины от крайних уровней ряда в диапазоне, в остальном формула не претерпела больше никаких изменений. Вот ее точный вид для нашей задачи:
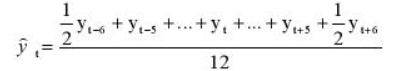
Сглаживаем наши уровни ряда и растягиваем формулу вниз:
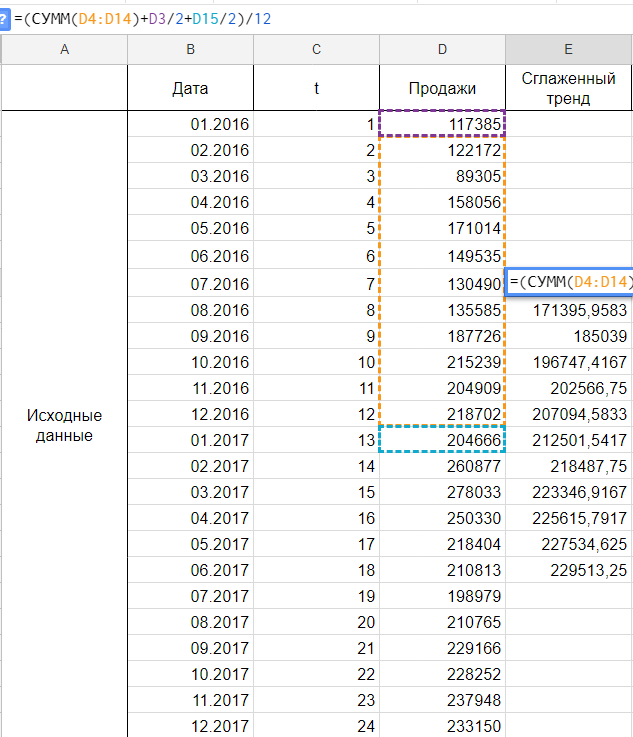
Сразу можем построить график из известных значений уровня продаж и их сглаженной. Выведем ее уравнение и значение коэффициента детерминации R^2:
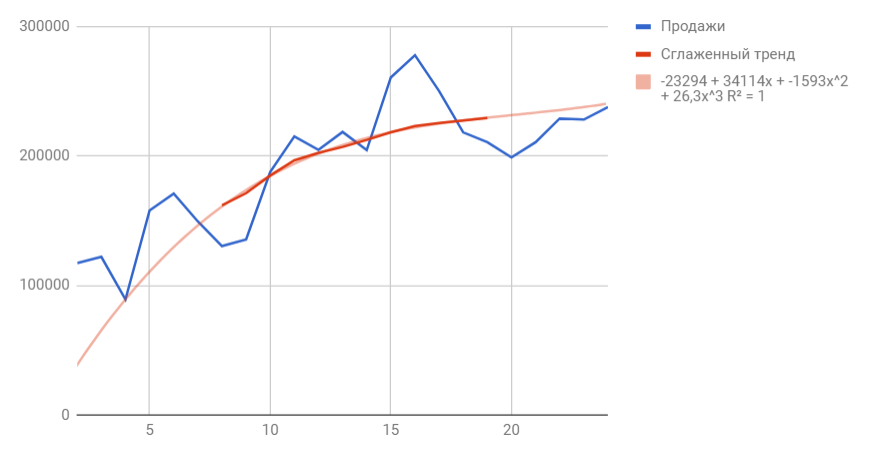
В качестве сглаженной я выбрала полином третьей степени, так как он лучше всего описывал уровни временного ряда и имел наибольший R^2.
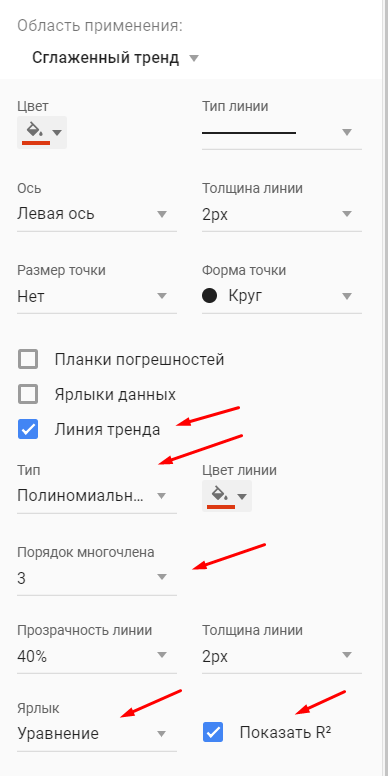
Шаг 2
Так как мы рассматриваем аддитивную модель вида: 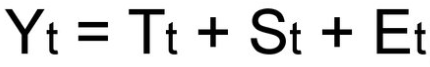
Найдем оценки сезонной компоненты как разность между фактическими уровнями ряда и значениями скользящей средней St+Et = Yt-Tt, так как Yt и Tt мы уже знаем.
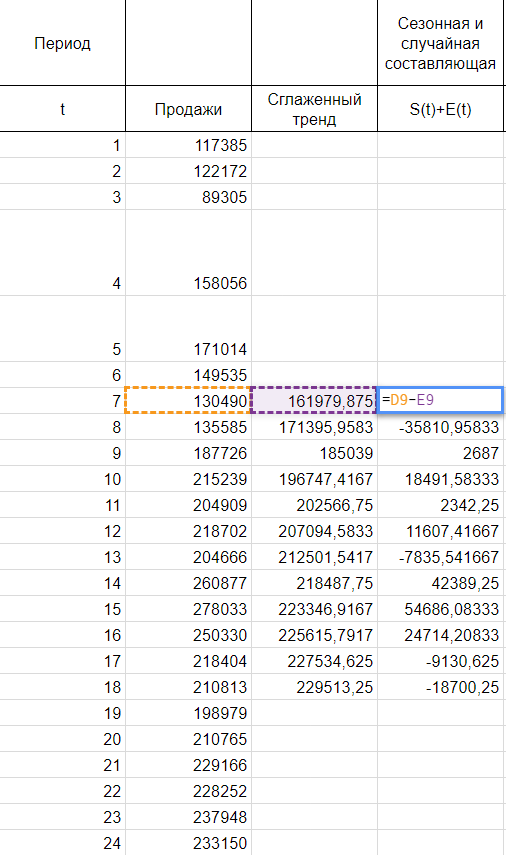
Используем оценки сезонной компоненты (St+Et) для расчета значений сезонной компоненты St. Для этого найдем средние за каждый интервал (по всем годам) оценки сезонной компоненты St.

Средняя оценка сезонной компоненты находится как сумма по столбцу, деленная на количество заполненных строк в этом столбце. В нашем случае оценки сезонной составляющей расположились в строках без пересечений, поэтому сумма по столбцам состоит из одиночных значений, следовательно и среднее будет таким же. Если бы мы располагали периодом побольше, например с 2015, у нас бы добавилась еще одна строка и мы смогли бы полноценно найти среднее, поделив сумму на 2.
В моделях с сезонной компонентой обычно предполагается, что сезонные воздействия за период взаимопогашаются. В аддитивной модели это выражается в том, что сумма значений сезонной компоненты по всем интервалам должна быть равна нулю. Поэтому найдя значение случайной составляющей, поделив сумму средних оценок сезонной составляющей на 12, мы вычитаем ее значение из каждой средней оценки и получаем скорректированную сезонную компоненту, St.
Далее, заполняем нашу таблицу значениями сезонной составляющей дублируя ряд каждые 12 месяцев, то есть три раза:
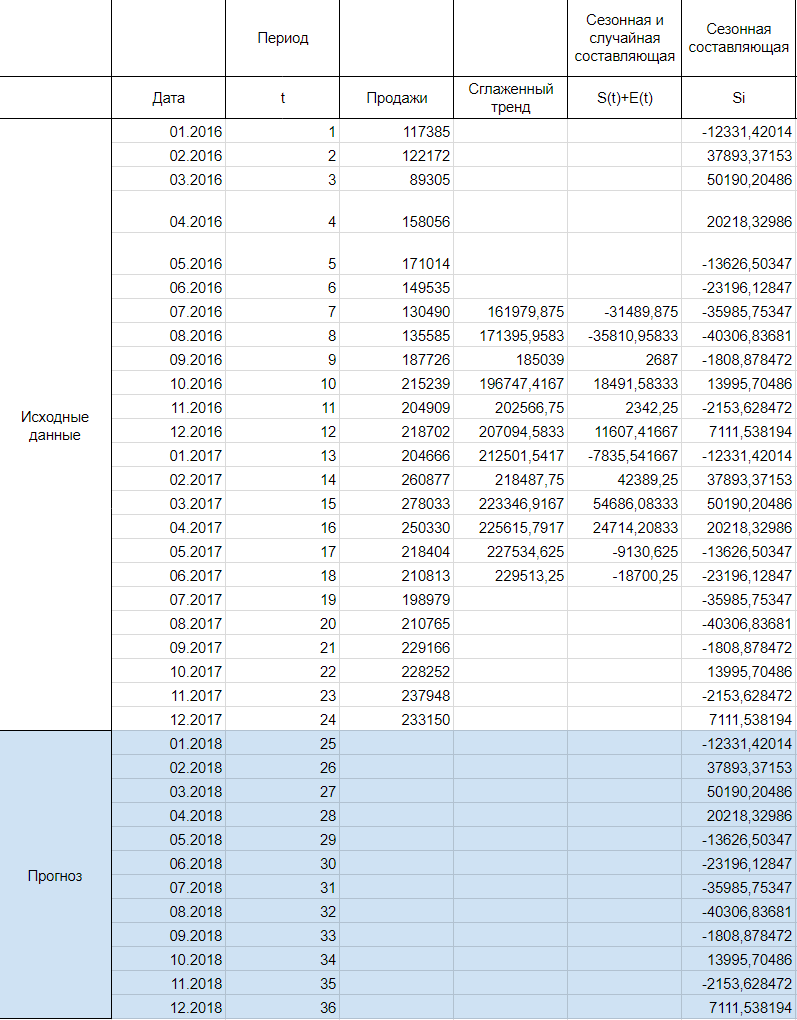
Шаг 3
Теперь рассчитываем значения уровня тренда T(t) по тому уравнению, которое мы получили при построении сглаженного тренда на первом шаге.
T(t) = -23294+34114*t-1593*t^2+26,3*t^3
Вместо t используем значения из столбца Период из соответствующей строки.
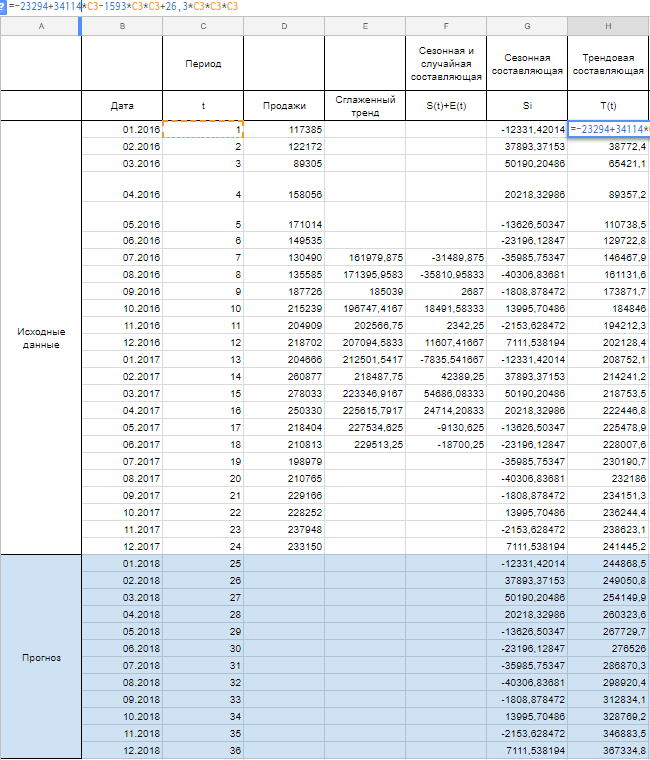
Шаг 4
Имея рассчитанные значения S(t) и T(t) мы можем рассчитать прогнозные значения уровней ряда Y(t). Для этого накладываем уровни сезонности на тренд.
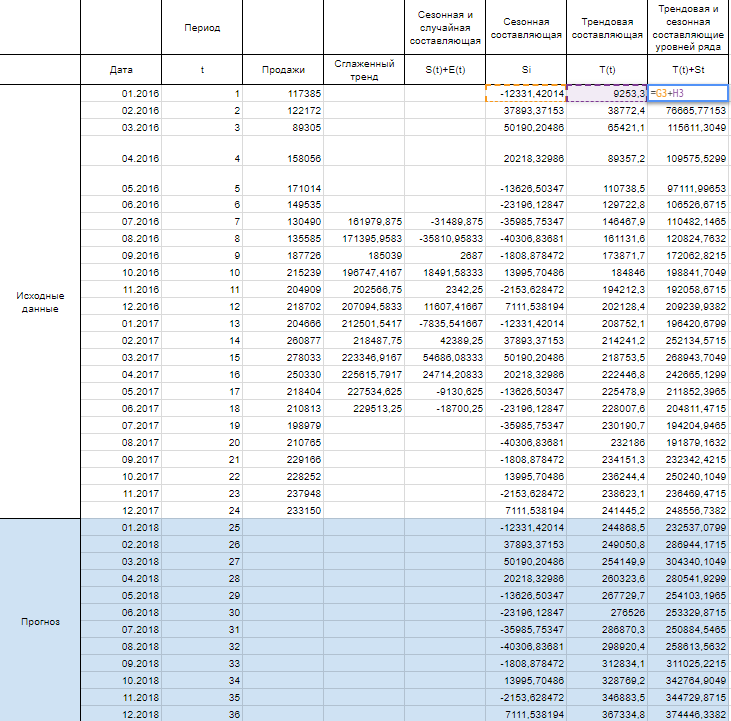
Теперь построим график известных значений Y(t) и спрогнозированных за 2018 год.
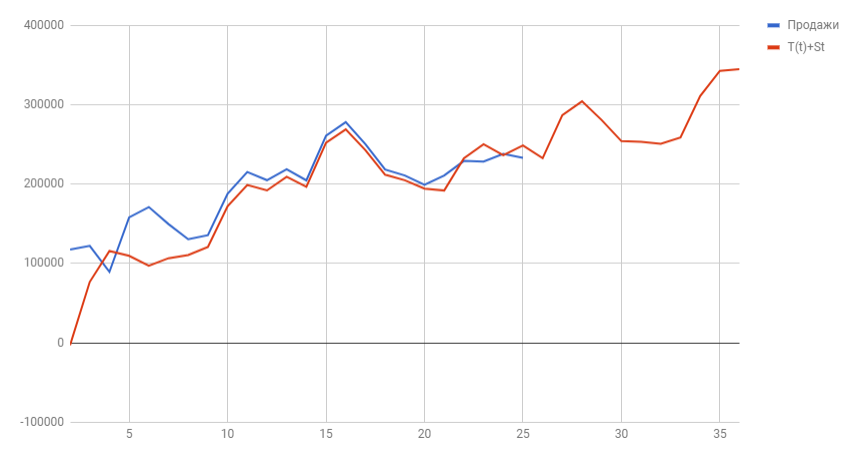
Вот мы и нашли спрогнозированные значения уровней продаж на 2018 год. Значения отражают возрастающую тенденцию и сезонные пики. Конечно, эти данные не дают 100% точности, ведь существует множество внешних воздействий, которые могут изменить направление тренда, поэтому к прогнозным значениям обычно строят доверительный интервал, это такой коридор, внутри которого могут колебаться прогнозные значения с заданной вероятностью (чаще всего выбирают 95%). Но об этом я расскажу в следующей статье.
Шаг 5
Осталось оценить точность модели. Для этого будем использовать среднюю ошибку аппроксимации, которая поможет рассчитать ошибку в относительном выражении. Иными словами, это среднее отклонение расчетных значений от фактических, которое вычисляется по формуле:

yi — спрогнозированные уровни ряда,
yi* — фактические уровни ряда,
n — количество складываемых элементов.
Модель может считаться адекватной, если:

Итак, рассчитываем ошибку аппроксимации для нашего случая. Так как в основе нашего тренда лежит полином третьей степени, прогнозные значения начинают хорошо повторять фактические значения к концу 2016 года, думаю, я думаю, поэтому корректнее было бы рассчитать ошибку аппроксимации для значений 2017 года.
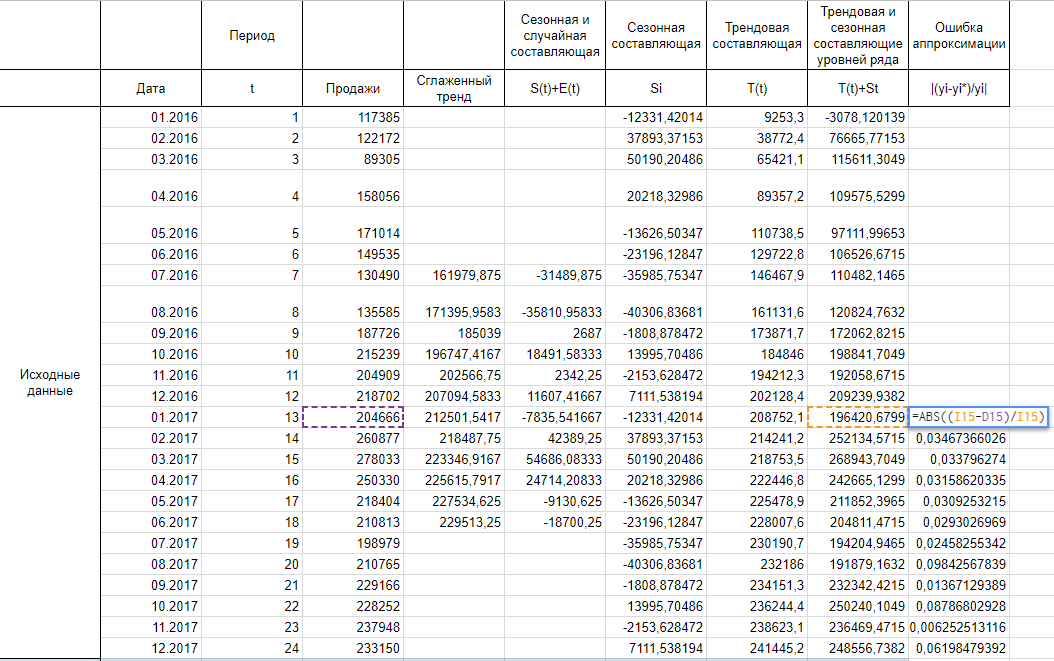
Сложив весь столбец с ошибками аппроксимации и поделив на 12, получаем среднюю ошибку аппроксимации 4,13%. Это значение меньше 15% и можем сделать вывод об адекватности модели.
Не забывайте, что прогнозы не бывают точными на 100%. Любые неожиданные внешние воздействия могут развернуть значения уровней ряда в неизвестном направлении 🙂
Полезные ссылки:
- Ссылка на пример Google Sheets
- Построение функции тренда в Excel. Быстрый прогноз без учета сезонности
- Бывшев В.А. Эконометрика
- Об авторе
- Свежие записи
Прогнозирование продаж в Excel не сложно составить при наличии всех необходимых финансовых показателей.
В данном примере будем использовать линейный тренд для составления прогноза по продажам на бушующие периоды с учетом сезонности.
Линейный тренд хорошо подходит для формирования плана по продажам для развивающегося предприятия.
Excel – это лучший в мире универсальный аналитический инструмент, который позволяет не только обрабатывать статистические данные, но и составлять прогнозы с высокой точностью. Для того чтобы оценить некоторые возможности Excel в области прогнозирования продаж, разберем практический пример.
Пример прогнозирования продаж в Excel
Рассчитаем прогноз по продажам с учетом роста и сезонности. Проанализируем продажи за 12 месяцев предыдущего года и построим прогноз на 3 месяца следующего года с помощью линейного тренда. Каждый месяц это для нашего прогноза 1 период (y).
Уравнение линейного тренда:
y = bx + a
- y — объемы продаж;
- x — номер периода;
- a — точка пересечения с осью y на графике (минимальный порог);
- b — увеличение последующих значений временного ряда.
Допустим у нас имеются следующие статистические данные по продажам за прошлый год.
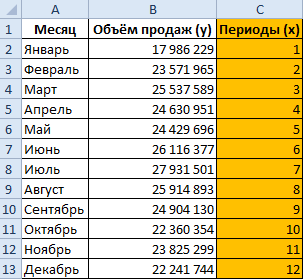
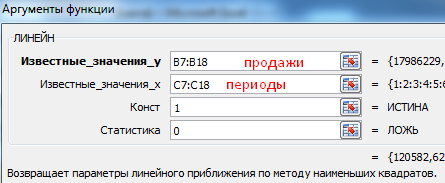
- Рассчитаем значение линейного тренда. Определим коэффициенты уравнения y = bx + a. В ячейке D15 Используем функцию ЛИНЕЙН:
- Выделяем ячейку с формулой D15 и соседнюю, правую, ячейку E15 так чтобы активной оставалась D15. Нажимаем кнопку F2. Затем Ctrl + Shift + Enter (чтобы ввести массив функций для обеих ячеек). Таким образом получаем сразу 2 значения коефициентов для (a) и (b).
- Рассчитаем для каждого периода у-значение линейного тренда. Для этого в известное уравнение подставим рассчитанные коэффициенты (х – номер периода).
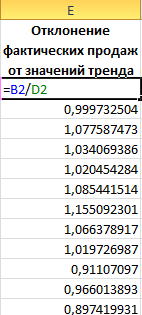
- Чтобы определить коэффициенты сезонности, сначала найдем отклонение фактических данных от значений тренда («продажи за год» / «линейный тренд»).
- Рассчитаем средние продажи за год. С помощью формулы СРЗНАЧ.
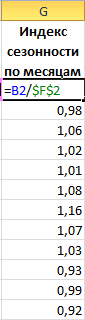
- Определим индекс сезонности для каждого месяца (отношение продаж месяца к средней величине). Фактически нужно каждый объем продаж за месяц разделить на средний объем продаж за год.
- В ячейке H2 найдем общий индекс сезонности через функцию: =СРЗНАЧ(G2:G13).
- Спрогнозируем продажи, учитывая рост объема и сезонность. На 3 месяца вперед. Продлеваем номера периодов временного ряда на 3 значения в столбце I:
- Рассчитаем значения тренда для будущих периодов: изменим в уравнении линейной функции значение х. Для этого можно просто скопировать формулу из D2 в J2, J3, J4.
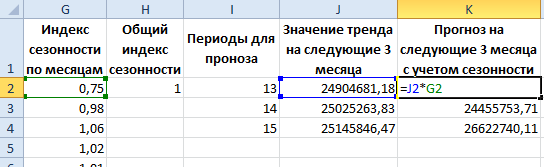
- На основе полученных данных составляем прогноз по продажам на следующие 3 месяца (следующего года) с учетом сезонности:

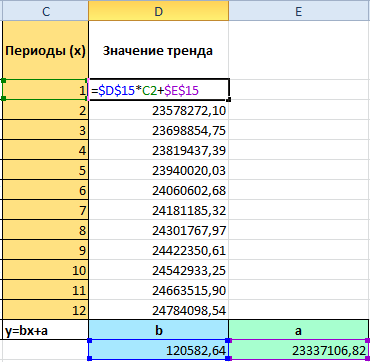


Общая картина составленного прогноза выглядит следующим образом:
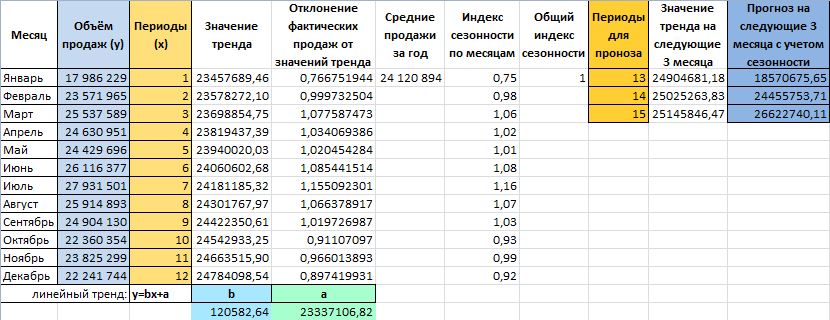
График прогноза продаж:
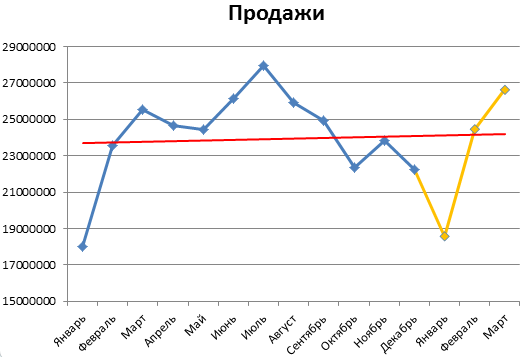
График сезонности:
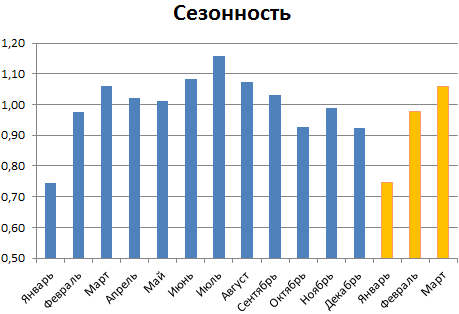
Алгоритм анализа временного ряда и прогнозирования
Алгоритм анализа временного ряда для прогнозирования продаж в Excel можно построить в три шага:
- Выделяем трендовую составляющую, используя функцию регрессии.
- Определяем сезонную составляющую в виде коэффициентов.
- Вычисляем прогнозные значения на определенный период.
Нужно понимать, что точный прогноз возможен только при индивидуализации модели прогнозирования. Ведь разные временные ряды имеют разные характеристики.
- бланк прогноза деятельности предприятия
Чтобы посмотреть общую картину с графиками выше описанного прогноза рекомендуем скачать данный пример:
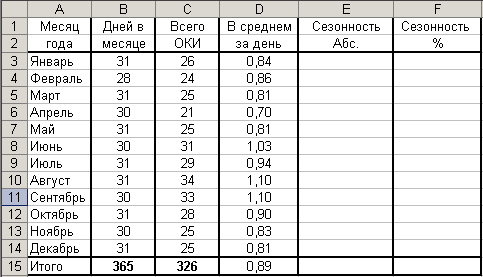
В
качестве примера создадим в Excel
таблицу ” Распределение острых
кишечных инфекций (ОКИ) за год”.
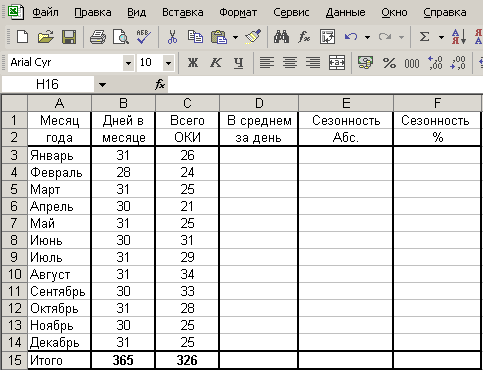
Рисунок
109. Пример формирования в Excel
исходных данных сезонности
-
После
запуска Excel
сформируйте таблицу, содержащую названия
колонок и исходные данные (Рисунок 109) -
Для
изменения ширины столбцов выделите
все столбцы и воспользуйтесь командой
<Столбец/Автоподбор ширины> из меню
<Формат>. Эта команда установит
оптимальную ширину для каждого столбца
в зависимости от размера содержимого
ячеек. -
Для
определения общего числа заболеваний
за год введите в ячейку C15
формулу: =СУММ(C3:C14).
В результате получите число 326. -
Для
определения среднедневного месячного
числа заболеваний введите в ячейку D3
формулу: =C3/В3 -
Заполнение
клеток D4:D15
выполните с помощью процедуры копирования
формул. Для этого:
-
установите
указатель ячейки в ячейку D3,
выберите команду <Копировать> из
меню <Правка>, -
передвиньте
указатель ячейки в ячейку D4
и маркируйте ячейки D4:D15, -
нажмите
клавишу [Enter].
Рисунок
110. Пример расчета в Excel
показателей сезонности
5.
Заполните графу “Показатель сезонности
в абсолютных числах”. Для этого:
-
введите
в ячейку E3
формулу: =D3/$D$15.
Чтобы распространить действие введенной
формулы на весь столбец выполните
копирование формулы по аналогии с пп.4.
6.Для заполнения
графы “Показатель сезонности в
процентах”
-
в
ячейку F3
введите формулу =E3*100; -
Скопируйте
формулу в ячейки F4:F15.
-
Для задания в
столбцах таблицы нового числового
формата:
-
выделите
соответствующий блок ячеек. выполните
команду <Ячейки>
из меню <Формат>, -
в
панели Число
выберите из списка “Числовые форматы”
категорию “Числовой” и установите
необходимое число десятичных знаков, -
активизируйте
кнопку [OK].
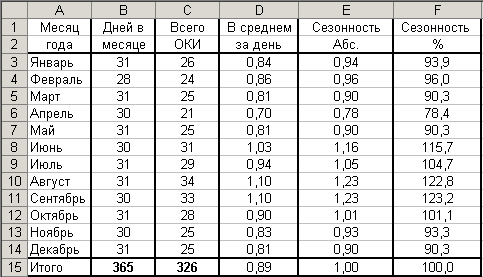
Рисунок
111. Пример итоговых показателей сезонности
-
Повышение наглядности динамических рядов. Прогноз динамики.
Анализ
динамических рядов может строиться на
относительных величинах, получаемых
на этапе сводки и группировки первичного
материала статистического исследования.
Вместе с тем, для углубленного анализа
временных рядов используются более
сложные методики математической
статистики. В первую очередь, применение
таких методик связывается с необходимостью
анализа неясных тенденций и прогнозирования
динамики изучаемого явления.
Если
динамические ряды содержат значительную
случайную ошибку (шум), то можно применить
один из двух наиболее простых приемов
сглаживания
или выравнивания
динамических рядов:
–
укрупнение
интервалов
путем суммирования исходных уровней
по нескольким интервалам. Например:
суммируются числа рождений за 1980,1981 и
1982 годы (84+94+92=270), затем за 1985,1986 и 1987 годы
и т.д. (Таблица 103);
–
вычисление групповых средних,
которые определяются на основе данных
по укрупненным интервалам (270/3=90, 263/3=88
и т.д.);
Таблица
103
Сглаживание динамического ряда укрупнением интервалов и скользящим средним
|
Учетный год |
Число |
Суммы |
Средние |
Скользящие |
|
1982 1983 1984 |
84 94 92 |
270 |
90,0 |
– 90,0 89,7 |
|
1985 1986 1987 |
83 91 88 |
262 |
87,3 |
88,7 87,3 87,0 |
|
1988 1989 1990 |
82 90 77 |
249 |
83,0 |
86,7 83,0 82,3 |
|
1991 1992 1993 |
80 90 78 |
248 |
82,7 |
82,3 82,7 – |
Укрупнение
интервалов
или расчет группового среднего внутри
этих интервалов позволяет относительно
легко повысить наглядность ряда, особенно
если большинство «шумовых» составляющих
находятся именно внутри этих интервалов.
Но в случае если шум не согласуется с
этой периодичностью, распределение
уровней показателей становится грубым,
что ограничивает возможности детального
анализа изменения явления во времени.
Более точные характеристики получаются,
когда используются – скользящие
средние.
Этот метод – один из самых широко
применяемых методов сглаживания
показателей временного ряда.
Он
основан на переходе от начальных значений
ряда к значениям, усредненным в
определенном интервале времени. В этом
случае интервал времени при вычислении
каждого последующего показателя как
бы скользит по временному ряду.
Применение
скользящего среднего особенно полезно
при неясных тенденциях динамического
ряда или в ситуациях, когда на показатели
сильно воздействуют циклически
повторяющиеся выбросы (резко выделяющиеся
данные, так называемые интервенции).
Таблица
104
Вычисление
скользящего среднего
|
Годы |
Травм |
Арифметические |
|
1982 |
84 |
– |
|
1983 |
94 |
(84+94+92)/3= |
|
1984 |
92 |
(94+92+83)/3= |
|
1985 |
83 |
(92+83+91)/3= |
|
1986 |
91 |
(83+91+88)/3= |
|
1987 |
88 |
(91+88+82)/3= |
|
1988 |
82 |
(88+82+90)/3= |
|
1989 |
90 |
(82+90+77)/3= |
|
1990 |
77 |
(90+77+80)/3= |
|
1991 |
80 |
(77+80+90)/3= |
|
1992 |
90 |
(80+90+78)/3= |
|
1993 |
78 |
– |
Рисунок
112. Результаты сглаживания методом
скользящего среднего
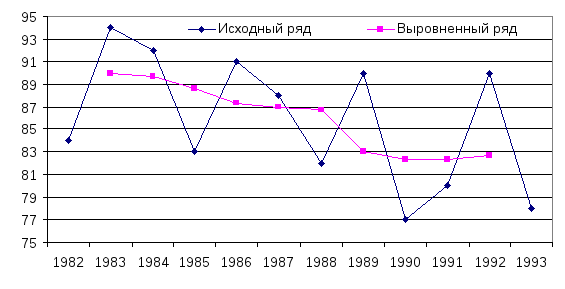
В
приведенном примере временной интервал
для вычисления скользящего среднего
принят равным 3 годам. В результате
проведенного сглаживания основная
тенденция динамического ряда стала
более наглядной. В частности, при оценке
динамики травматизма можно утверждать,
что наиболее интенсивно показатели
травматизма снижались в период с 1984 по
1986 гг. и с 1988 по 1990 гг. Периоды с 1986 по
1988 гг. и с 1990 по 1993 гг. отличались
относительной стабильностью, несмотря
на размахи колебаний годовых показателей.
В
целом, чем больше интервал сглаживания,
тем более плавный вид имеет диаграмма
скользящих средних. При выборе величины
интервала сглаживания необходимо
исходить из величины динамического
ряда (числа отдельных временных точек)
и содержательного смысла отражаемой
динамики. Большая величина динамического
ряда с большим числом точек наблюдения
позволяет использовать более крупные
временные интервалы сглаживания (5,7,10
и т.д.). Если процедура скользящего
среднего используется для сглаживания
не сезонного ряда, то чаще всего величину
интервала сглаживания принимают равной
3.
Весьма
результативным методом, хотя, в своей
основе, и более сложным, является
сглаживание (выравнивание) рядов динамики
с помощью
различных математических функций
аппроксимации.
При
помощи этих функций формируется плавный
уровень общей тенденции и основная ось
динамики, около которой на протяжении
определенного периода времени происходят
колебания вверх и вниз.
Одним
из самых эффективных методов сглаживания
с помощью математических функций
является простое
экспоненциальное сглаживание.
Не вдаваясь в детальное математическое
описание этого метода, следует отметить,
что в отличие от скользящего среднего
или группового среднего, методикой
простого экспоненциального сглаживания
учитываются все предшествующие наблюдения
ряда, а не те, что попали в определенное
интервальное окно. Точная формула
простого экспоненциального сглаживания
имеет следующий вид:
![]()
где:![]() – каждое новое сглаженное значение в
– каждое новое сглаженное значение в
момент времениt;![]() – сглаженное значение в предыдущий
– сглаженное значение в предыдущий
момент времени
t-1;![]() – фактическое значение ряда в момент
– фактическое значение ряда в момент
времениt;
![]() – параметр сглаживания. Если
– параметр сглаживания. Если![]() равно 1, то предыдущие наблюдения
равно 1, то предыдущие наблюдения
полностью игнорируются. Если![]() равно0, то
равно0, то
игнорируются текущие наблюдения.
Значения
![]() между0, 1
между0, 1
дают промежуточные результаты. Изменяя
значения этого параметра можно подобрать
наиболее приемлемый вариант выравнивания.
Выбор наиболее оптимального значения
![]() осуществляется путем анализа полученных
осуществляется путем анализа полученных
графических изображений исходной и
выровненной кривых, либо на основе учета
суммы квадратов ошибок (погрешностей)
вычисленных точек. Более полно практическое
использование этого метода представлено
далее, в разделе «Обработка динамических рядов и прогноз динамики в MS Excel.».
Одним
из самых эффективных считается
выравнивание по способу наименьших
квадратов. Согласно ему из бесконечного
числа линий, которые могли бы быть
теоретически проведены между точками,
изображающими исходный ряд, выбирается
только одна прямая, которая имела бы
наименьшую сумму квадратов отклонений
исходных (эмпирических) точек от этой
теоретической прямой. Практически
выравнивание производят либо по уравнению
прямой
![]() ,
,
либо по уравнению параболы. Уравнение
параболы второго порядка выглядит
следующим образом![]() .
.
В основе выбора параболы для выравнивания
лежит предположение о том, что не скорость
динамики, а ускорение является постоянной
величиной. Гдеа.b
иc– постоянные
величины,t – .порядковый
номер какого-либо периода или момента
времени (года и т.п.). С помощью этого
уравнения вычисляются необходимые для
построения соответствующие данные
Показателем
правильности выбора того или иного
уравнения аппроксимации служит
коэффициент R2
. Чем больше
его значение приближается к единице,
том большее соответствие фактического
и выровненного распределений. Максимальное
значение, которое R2
может принимать в предельном случае,
равно 1.
Следует
отметить, что при решении проблемы
выбора типа прямой или кривой, нельзя
исходить из формальных соображений: та
линия лучше, которая дает меньшую сумму
отклонений эмпирического ряда от
теоретического распределения. Выбор
кривой может быть обоснованным только
на основе глубокого знания сути
исследуемого явления.
Современные
программы статистической обработки
данных позволяют получать различные
теоретические кривые в автоматическом
режиме, без каких-либо усилий со стороны
исследователя. Имея эти результаты
можно проводить математическую
экстраполяцию,
то есть давать прогноз показателей в
продолжение проанализированного
периода, или проводить интерполяцию
рядов, то есть определять утраченные
или отсутствующие показатели в любой
точке середины интервала анализируемого
временного ряда.
Говорить
о достоверности статистических прогнозов
динамики каких-либо явлений можно лишь
при сохранении общих тенденций, то есть
при наличии определенной степени
инерционности явлений. Здесь имеется
в виду инерционность статистических
взаимосвязей, которая обеспечивает
сохранение в общих чертах механизма
формирования явления, и инерционность
характера динамики процесса (темп,
направление, устойчивость) на протяжении
достаточно длительных отрезков времени.
При этом существует закономерность:
чем на больший период времени вперед
(или назад) производится экстраполяция
данных, том ниже точность прогноза.
Особенно резко снижается точность
прогноза при значениях R2
0,6.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
