Как найти сферические координаты по декартовым - Сайт, где вы сможете решить свои вопросы

Сферические координаты (сферическая система координат)

Для введения сферической системы координат в пространстве выбирается плоскость (основная плоскость) и на ней задается полярная система координат с полюсом (начало сферической системы координат) и полярной осью . Через точку перпендикулярно основной плоскости проведем ось (ось аппликат) и выберем ее направление так, чтобы возрастание полярного угла со стороны положительного направления оси происходило против часовой стрелки (рис.2.36,а).

В сферической системе координат положение точки , не лежащей на оси аппликат, характеризуется расстоянием rho=|overrightarrow{OM}| до начала координат, полярным углом varphi точки M_0 – ортогональной проекции точки на основную плоскость, и углом theta между вектором и положительным направлением оси аппликат. Таким образом, сферические координаты точки – это упорядоченная тройка чисел rho,varphi,theta – радиус (rhogeqslant0) , долгота (-pi<varphileqslantpi) и широта (0leqslantthetaleqslantpi) . У точек, принадлежащих оси аппликат, не определена долгота, их положение задается радиусом rho и широтой theta=0 для положительной части оси и theta=pi для отрицательной ее части. Начало координат задается нулевым значением радиуса rho . Иногда вместо угла theta широтой называют угол $psi=frac{pi}{2}-theta$ , принимающий значения $-frac{pi}{2}leqslantpsileqslantfrac{pi}{2}$ .

Сферическая система координат и её связь с прямоугольными координатами

Со сферической системой координат Orhovarphitheta можно связать прямоугольную систему координат Ovec{i}vec{j}vec{k} (рис.2.36,б), у которой начало и базисные векторы vec{i},vec{k} совпадают с началом сферической системы координат и единичными векторами на полярной оси и оси аппликат соответственно, а базисный вектор vec{j} выбирается так, чтобы тройка vec{i},vec{j},vec{k} была правой (при этом базис оказывается стандартным).

Наоборот, если в пространстве задана правая прямоугольная система координат, то, приняв положительную полуось абсцисс за полярную ось, получим сферическую систему координат (связанную с данной прямоугольной).

Переход от сферических координат к декартовым (прямоугольным)

Получим формулы, связывающие между собой прямоугольные координаты x,y,z точки и её сферические координаты rho,varphi,theta . По рис.2.36,б получаем

$begin{cases}x=rhocdotcosvarphicdotsintheta,\y=rhocdotsinvarphicdotsintheta,\z=rhocdotcostheta.end{cases}$

(2.21)

Эти формулы перехода позволяют найти прямоугольные координаты по известным сферическим координатам. Обратный переход выполняется по формулам

$left{!begin{aligned} rho&=sqrt{x^2+y^2+z^2},\ cosvarphi&=frac{x}{sqrt{x^2+y^2}},\ sinvarphi&=frac{y}{sqrt{x^2+y^2}},\ theta&=arccosfrac{z}{rho}=arccosfrac{z}{sqrt{x^2+y^2+z^2}}. end{aligned}right.$

(2.22)

Формулы (2.22) определяют долготу varphi с точностью до слагаемых 2pi n , где ninmathbb{Z} . При xne0 из них следует, что $operatorname{tg}varphi=frac{y}{x}$ . Главное значение долготы varphi~(-pi<varphileqslantpi) находится по формулам (см. рис.2.29).

Пример 2.13. В сферической системе координат Orhovarphitheta :

а) построить координатные поверхности rho=R,~varphi=varphi_0,~z=z_0 ;

б) найти сферические координаты rho,varphi,theta точки , если известны её прямоугольные координаты A(4,-3,12) ;

в) найти прямоугольные координаты x,y,z точки , если известны её сферические координаты: $rho=4,~varphi=frac{2pi}{3},~theta=frac{3pi}{4}$ .

Построение поверхностей в сферической системе координат

Решение. а) Координатной поверхностью rho=R , т.е. геометрическим местом точек M(R,varphi,theta) при фиксированном значении радиуса rho=R , является сфера с центром в начале координат (рис.2.37). Этим объясняется название сферической системы координат. Координатной поверхностью varphi=varphi_0 , т.е. геометрическим местом точек M(rho,varphi_0,theta) при фиксированном значении долготы , является полуплоскость, ограниченная осью аппликат (на рис.2.37 изображена полуплоскость varphi=0 ). Координатной поверхностью theta=theta_0 , т.е. геометрическим местом точек M(rho,varphi,theta_0) при фиксированном значении широты $theta=thetanefrac{pi}{2}$ , является конус, ось которого совпадает с осью аппликат, а вершина – с началом координат. При $theta=frac{pi}{2}$ получаем основную плоскость. На рис.2.37 изображены конус $theta=thetanefrac{pi}{2}$ и основная плоскость $theta=frac{pi}{2}$ .

б) Найдем сферические координаты точки A(4,-3,12) . По формулам (2.22), учитывая рис.2.29 (см. пример 2.12), получаем

$rho=sqrt{4^2+(-3)^2+12^2}=13;quad varphi=-operatorname{arctg}frac{3}{4};quad theta=arccosfrac{12}{13}.$

в) По формулам (2.21) получаем

$begin{gathered} x=rhocdotcosvarphicdotsintheta=4cdot!left(-frac{1}{2}right)!cdot!left(frac{sqrt{2}}{2}right)=-sqrt{2};\[2pt] y=rhocdotsinvarphicdotsintheta=4cdot!left(frac{sqrt{3}}{2}right)!cdot!left(frac{sqrt{2}}{2}right)=sqrt{6};\[2pt] z=rhocdotcostheta=4cdot!left(-frac{sqrt{2}}{2}right)=-2sqrt{2}. end{gathered}$

Математический форум (помощь с решением задач, обсуждение вопросов по математике).

Кнопка "Поделиться"

Если заметили ошибку, опечатку или есть предложения, напишите в комментариях.

Источник

Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 25 декабря 2020 года; проверки требуют 4 правки.

Сферическая система координат — трёхмерная система координат, в которой каждая точка пространства определяется тремя числами , где — расстояние до начала координат (радиальное расстояние), а theta и varphi — зенитный и азимутальный углы соответственно.

Понятия зенит и азимут широко используются в астрономии. Зенит — направление вертикального подъёма над произвольно выбранной точкой (точкой наблюдения), принадлежащей фундаментальной плоскости. В качестве фундаментальной плоскости в астрономии может быть выбрана плоскость, в которой лежит экватор, или плоскость, в которой лежит горизонт, или плоскость эклиптики и т. д., что порождает разные системы небесных координат. Азимут — угол между произвольно выбранным лучом фундаментальной плоскости с началом в точке наблюдения и другим лучом этой плоскости, имеющим общее начало с первым.

Рис. 1.Точка имеет три декартовых и три сферических координаты

Если рассматривать сферическую систему координат относительно декартовой системы Oxyz , фундаментальной плоскостью будет плоскость , зенитным углом точки, заданной радиус-вектором , будет угол между и осью , а азимутом — угол между проекцией на плоскость и осью . Это объясняет названия углов и то, что сферическая система координат может служить обобщением множества видов систем небесных координат.

Определения[править | править код]

Положение точки в сферической системе координат определяется тройкой , где

Угол theta называется зенитным, или полярным, также он может называться наклонением, или коширотой, а угол varphi — азимутальным. Углы theta и varphi не определены при r=0 , также не определён угол varphi при (то есть при или $theta =180^{circ }$ ).

Такое соглашение установлено в стандарте (ISO 31-11). Кроме того может использоваться соглашение, когда вместо зенитного угла theta , используется угол между радиус-вектором точки и плоскостью , равный ${displaystyle 90^{circ }-theta }$ . Он называется широтой и может быть обозначен той же буквой theta . Широта может изменяться в пределах $-90^{circ }leqslant theta leqslant 90^{circ }$ . При этом соглашении углы theta и varphi не имеют значения при r=0 , так же как и в первом случае, а varphi не имеет значения при (то есть при $theta =-90^{circ }$ или $theta =90^{circ }$ ).

Переход к другим системам координат[править | править код]

Декартова система координат[править | править код]

Если заданы сферические координаты точки , то переход к декартовым осуществляется по формулам:

${begin{cases}x=rsin theta cos varphi ,\y=rsin theta sin varphi ,\z=rcos theta .end{cases}}$

Обратно, от декартовых к сферическим:

${displaystyle {begin{cases}r={sqrt {x^{2}+y^{2}+z^{2}}},\theta =arccos {dfrac {z}{sqrt {x^{2}+y^{2}+z^{2}}}}=mathrm {arctg} {dfrac {sqrt {x^{2}+y^{2}}}{z}},\varphi =mathrm {arctg} {dfrac {y}{x}}.end{cases}}}$

Якобиан преобразования к сферическим координатам равен

${displaystyle {begin{alignedat}{2}J&={frac {partial (x,y,z)}{partial (r,theta ,varphi )}}={begin{vmatrix}sin theta cos varphi &rcos theta cos varphi &-rsin theta sin varphi \sin theta sin varphi &rcos theta sin varphi &rsin theta cos varphi \cos theta &-rsin theta &0end{vmatrix}}=\&=cos theta (r^{2}cos varphi ^{2}cos theta sin theta +r^{2}sin ^{2}varphi cos theta sin theta )+rsin theta (rsin ^{2}theta cos ^{2}varphi +rsin ^{2}theta sin ^{2}varphi )=\&=r^{2}cos ^{2}theta sin theta +r^{2}sin ^{2}theta sin theta =\&=r^{2}sin theta .end{alignedat}}}$

Таким образом, элемент объёма при переходе от декартовых к сферическим координатам будет выглядеть следующим образом:

${displaystyle mathrm {d} V=mathrm {d} x,mathrm {d} y,mathrm {d} z=J(r,theta ,varphi ),mathrm {d} r,mathrm {d} theta ,mathrm {d} varphi =r^{2}sin theta ,,mathrm {d} r,mathrm {d} theta ,mathrm {d} varphi }$

Цилиндрическая система координат[править | править код]

Если заданы сферические координаты точки, то переход к цилиндрическим осуществляется по формулам:

${begin{cases}rho =rsin theta ,\varphi =varphi ,\z=rcos theta .end{cases}}$

Обратно от цилиндрических к сферическим:

${displaystyle {begin{cases}r={sqrt {rho ^{2}+z^{2}}},\theta =mathrm {arctg} {dfrac {rho }{z}},\varphi =varphi .end{cases}}}$

Якобиан преобразования от сферических к цилиндрическим .

Дифференциальные характеристики[править | править код]

Вектор , проведённый из точки в точку , равен

mathrm {d} mathbf {r} =mathrm {d} r,{boldsymbol {hat {r}}}+r,mathrm {d} theta ,{boldsymbol {hat {theta }}}+rsin {theta },mathrm {d} varphi ,mathbf {boldsymbol {hat {varphi }}} ,

где

{displaystyle {boldsymbol {hat {r}}}=sin theta cos varphi {boldsymbol {hat {imath }}}+sin theta sin varphi {boldsymbol {hat {jmath }}}+cos theta {boldsymbol {hat {k}}}}

{displaystyle {boldsymbol {hat {theta }}}=cos theta cos varphi {boldsymbol {hat {imath }}}+cos theta sin varphi {boldsymbol {hat {jmath }}}-sin theta {boldsymbol {hat {k}}}}

{displaystyle {boldsymbol {hat {varphi }}}=-sin varphi {boldsymbol {hat {imath }}}+cos varphi {boldsymbol {hat {jmath }}}}

ортогональные единичные векторы сферических координат в направлении увеличения , соответственно, а — единичные векторы декартовых координат. Сферические координаты являются ортогональными, поэтому метрический тензор имеет в них диагональный вид:

$g_{ij}={begin{pmatrix}1&0&0\0&r^{2}&0\0&0&r^{2}sin ^{2}theta end{pmatrix}},quad g^{ij}={begin{pmatrix}1&0&0\0&{dfrac {1}{r^{2}}}&0\0&0&{dfrac {1}{r^{2}sin ^{2}theta }}end{pmatrix}}$

$det(g_{ij})=r^{4}sin ^{2}theta .$
Квадрат дифференциала длины дуги:

$ds^{2}=dr^{2}+r^{2},dtheta ^{2}+r^{2}sin ^{2}theta ,dvarphi ^{2}.$

Коэффициенты Ламе:

$H_{r}=1,quad H_{theta }=r,quad H_{varphi }=rsin theta .$

Символы Кристоффеля :

$Gamma _{22}^{1}=-r,quad Gamma _{33}^{1}=-rsin ^{2}theta ,$

$Gamma _{21}^{2}=Gamma _{12}^{2}=Gamma _{13}^{3}=Gamma _{31}^{3}={frac {1}{r}},$

$Gamma _{33}^{2}=-cos theta sin theta ,quad Gamma _{23}^{3}=Gamma _{32}^{3}=mathrm {ctg} ,theta .$

Остальные равны нулю.

Математическое моделирование Земли[править | править код]

Сферическая географическая система координат[править | править код]

Сферическая географическая система координат строится следующим образом^[1]:

Вектор магнитной индукции магнитного поля Земли имеет компоненты

${displaystyle B_{r}=-Bsin I,;B_{theta }=-Bcos Icos D,;B_{varphi }=Bcos Isin D,}$

где — магнитное наклонение; — магнитное склонение.

Компоненты вектора ускорения свободного падения равны

${displaystyle g_{r}=-g,;g_{theta }=g_{varphi }=0.}$

Наконец, компоненты вектора угловой скорости вращения Земли такие:

${displaystyle Omega _{r}=Omega cos theta ,;Omega _{theta }=-Omega sin theta ,;Omega _{varphi }=0.}$

В сферических географических координатах оптимально решать уравнения, описывающие поведение нейтральных частиц околоземного пространства^[1].

Сферическая геомагнитная система координат[править | править код]

Сферическая геомагнитная система координат строится следующим образом^[1]:

Географические координаты северного магнитного полюса равны

${displaystyle theta _{0}=4,6^{circ },;varphi _{0}=43,0^{circ };(2012).}$

В сферической геомагнитной системе координат склонение D=0 и

${displaystyle B_{r}=-Bsin I,;B_{Theta }=-Bcos I,;B_{Lambda }=0,}$

${displaystyle g_{r}=-g,;g_{Theta }=g_{Lambda }=0.}$

${displaystyle Omega _{r}=Omega (cos theta _{0}cos Theta -sin theta _{0}sin Theta cos Lambda ),}$

${displaystyle Omega _{Theta }=-Omega (cos theta _{0}sin Theta +sin theta _{0}cos Theta cos Lambda ),}$

${displaystyle Omega _{Lambda }=Omega sin theta _{0}sin Lambda .}$

Формулы, связывающие географические и геомагнитные сферические координаты^[1]:

${displaystyle cos Theta =cos theta _{0}cos theta +sin theta _{0}sin theta cos(varphi -varphi _{0}),}$

${displaystyle cos Lambda ={frac {-sin theta _{0}cos theta +cos theta _{0}sin theta cos(varphi -varphi _{0})}{sin Theta }},}$

${displaystyle cos theta =cos theta _{0}cos Theta -sin theta _{0}sin Theta cos Lambda ,}$

${displaystyle cos(varphi -varphi _{0})={frac {sin theta _{0}cos Theta +cos theta _{0}sin Theta cos Lambda }{sin theta }}.}$

В сферических геомагнитных координатах проще, чем в сферических географических координатах, описывать влияние геомагнитного поля на заряженные частицы околоземного пространства^[1].

См. также[править | править код]

Углы Эйлера
Гиперсферические координаты

Примечания[править | править код]

↑ ¹ ² ³ ⁴ ⁵ Брюнелли Б. Е., Намгаладзе А. А. Физика ионосферы. М.: Наука, 1988. § 3.5, С. 172—173. ISBN 5-02-000716-1

Ссылки[править | править код]

Weisstein, Eric W. Сферические координаты (англ.) на сайте Wolfram MathWorld.

Источник

Рассмотрим
в пространстве координатную плоскость
Р, на которой задана полярная система
координат. ПустьOz –координатная
ось, перпендикулярная плоскостиРи пересекающая ее в полюсеО.
Координатная осьOz направлена так,
чтобы из конца положительного направления
осиOz направление отсчета положительных
значений полярного углаφот полярной
осиОхбыло видно против часовой
стрелки. Совокупность этих элементов
называетсяполярной системой
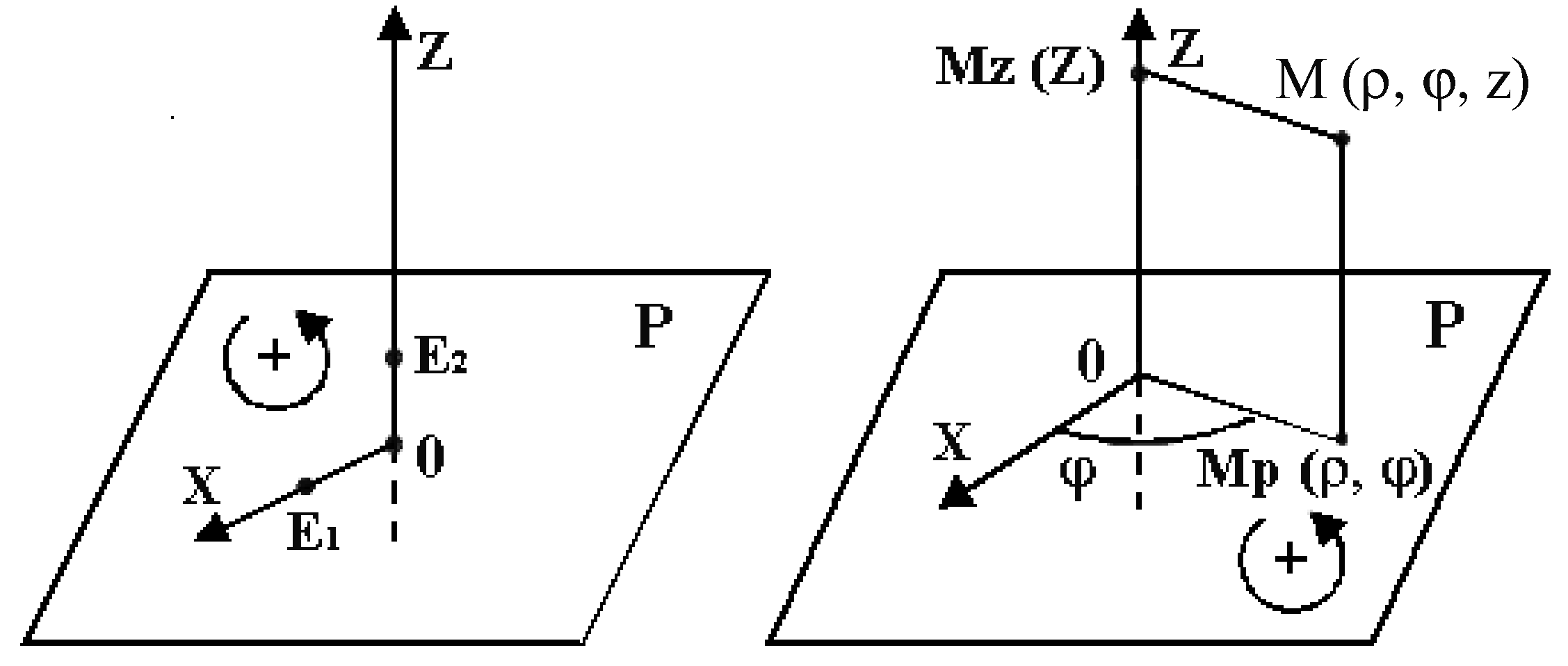
координат в пространстве(рис.3.2).

Координатная
плоскость Рназываетсяэкваториальной,
а координатная осьOz–зенитной.
Для удобства будем полагать, что
масштабные отрезки одинаковы (ОЕ₁=ОЕ₂) и точка отсчетаОкоординатной осиOzсовпадает с
полюсомО.

Цилиндрическими
координатами точкиМ, не лежащими
на зенитной оси, называется упорядоченная
тройка чиселρ, φ, z, гдеρиφ– полярные координаты ортогональной
проекцииМ_р точкиМна экваториальную плоскость, аz–
координата на зенитной осиOzпроекцииМ_zточкиМна зенитную
ось (рис. 3.3). Для точек зенитной оси
считаютρ = 0,φ– любое число, аzопределяется так, как указано выше.
Тот факт, чтоρ, φ иzесть
цилиндрические координаты точкиМ в
пространстве, записывают так:М(ρ,φ,z).

Заметим,
что при помощи цилиндрических координат
не устанавливается взаимно однозначного
соответствия между множеством всех
точек геометрического пространства и
множеством упорядоченных троек
действительных чисел.

Рис. 3.2
Рис. 3.3

Сферическими
координатами точкиМ, не лежащей
на зенитной оси, называется упорядоченная
тройка чиселr, φ, Θ, гдеr– длина отрезкаОМ,φ– угол от
полярной осиОхдо лучаОМ_р(М_р– проекция точкиМна экваториальную плоскость), аΘ–
угол между лучамиОМ_риОМ, который принимает значения в
интервале,
причем считается, чтоΘ= 0, если точкаМлежит в экваториальной плоскости,Θ> 0, если лучОМобразует острый
угол с зенитной осью, иΘ< 0, если
лучОМобразует тупой угол с зенитной
осью (рис.3.4).

Рис. 3.4

Если
точка М лежит на зенитной оси и не
совпадает с полюсомО, то считают,
чтоφ– любое число, аилив зависимости от того, совпадает ли
направление лучаОМ с направлением
зенитной оси или противоположно ему.
Для полюса считаютr= 0,φиΘ– любые числа. При помощи сферических
координат не устанавливается взаимно
однозначного соответствия между
множеством всех точек пространства и
множеством упорядоченных троек
действительных чисел.

Найдем
зависимости между прямоугольными
декартовыми координатами точки М(х,
у, z) и ее цилиндрическими координатамиМ(ρ, φ, z) и сферическими
координатамиМ(r, φ, θ).
Введем декартову прямоугольную систему
координат, принимая за положительную
полуосьОхполярную ось, за осьОу– ось, полученную из осиОхповоротом
ее вокруг полюса в экваториальной
плоскости на уголи зенитную ось за осьОz
(рис.3.4.).

Из
рис.3.4, учитывая формулы (1.7) и рис.3.3.
находим

,,z= z(1.12)

Cдругой стороны,,
а,
значит,

(1.13)

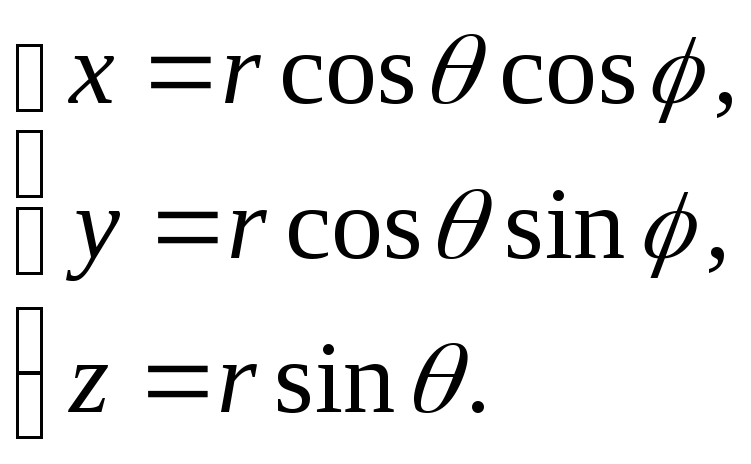
Формулы
(1.12) и (1.13) верны и для того случая, когда
точка Млежит на зенитной оси и когда
она совпадает с полюсом (при дополнительных
соглашениях о величинахρ иφв
этом случае).

По
формулам (1.12) вычисляются декартовы
прямоугольные координаты точки Мв случае, если известны ее цилиндрические
координаты, а по формулам (1.13) – если
известны ее сферические координаты.

Из
формул (1.13) следует, что

откуда

значит,

(1.14)

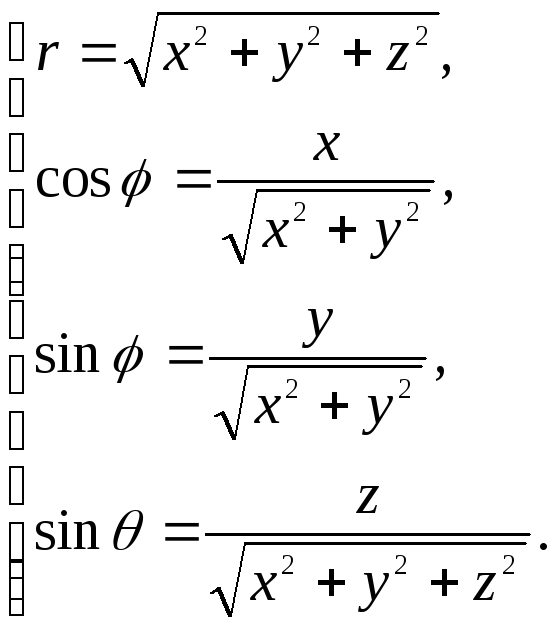
По этим
формулам вычисляются сферические
координаты r,φ, ΘточкиМ,
не лежащей на зенитной оси по ее декартовым
прямоугольным координатамx,y,z
(при указанном взаимном расположении
этих двух систем координат).

Цилиндрические
координаты ρ, φ, zточкиМ
вычисляются по ее декартовым
прямоугольным координатамx, y,
zиз формул (1.12) с учетом формул (1.8) и
(1.9) или (1.10).

Аналогично
декартовым координатам определяется
уравнение поверхности в сферических
координатах:

и в цилиндрических
координатах
.

Замечание.Вторую сферическую координатуφчасто называютдолготой, третьюΘ – широтой. Иногда вместо
широтыΘрассматривают уголψ
между положительным направлением
зенитной оси и лучомОМ, идущим из
полюсаО в данную точкуМ; величинаψизменяется в пределах от 0 доπ.
Величинаψназываетсязенитным
расстоянием.

Так
как
,
то в формулах (1.13) и (1.14) (в случае, если
за третью сферическую координату
принимается зенитное расстояние)иследует заменить соответственно наи
.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

Источник

Этот калькулятор предназначен для преобразования координат в пространстве, заданных в трех системах:

Прямоугольной (декартовой)
Цилиндрической
Сферической
Прямоугольная, цилиндрическая и сферическая системы координат

Прямоугольная система координат

Определяет точку в пространстве при помощи трех чисел : x, y, z. Каждое число соответствует длине кратчайшего отрезка, проложенного параллельно одноименной оси координат до плоскости, образованной другими осями координат. Длина берется со знаком минус, если точка находится со стороны отрицательных значений шкалы координат.

Цилндрическая система координат

Определяет точку в пространстве при помощи радиуса r, угла азимута φ, и высоты z. Высота z соответствует координате z в прямоугольной системе координат. Радиус r – всегда неотрицательное число, задающее минимальное расстояние от точки в пространстве до оси z. Азимутальный угол φ – значение в диапазоне 0 ..360 градусов – определяет угол, между положительной полуосью x и радиусом, проложенным через проекцию точки на плоскость, образованную осями x и y.

Сферическая система координат

Определяет точку в пространстве при помощи радиуса ρ, азимута φ, и полярного угла θ. Азимут φ совпадает со значением азимута в цилиндрических координатах. Радиус ρ – расстояние от центра координат, до точки. Полярный угол образован положительной полуосью z и радиусом из центра координат до точки в пространстве.

Прямоугольные координаты в пространстве

Точность вычисления

Знаков после запятой: 2

Цилиндрические координаты

Сферические координаты

Полярный угол (θ), градусы

Формулы преобразования декартовых координат

Цилиндрические координаты

Точность вычисления

Знаков после запятой: 2

Прямоугольные координаты

Сферические координаты

Полярный угол (θ), градусы

Формулы преобразования цилиндрических координат

Декартовы координаты:
,

Радиус в сферической системе:
$rho = sqrt{r^2+z^2}$
Полярный угол:
, см Арктангенс с двумя аргументами

Сферические координаты

Полярный угол (θ), градусы

Точность вычисления

Знаков после запятой: 2

Прямоугольные координаты

Цилиндрические координаты

Формулы преобразования сферических координат

Декартовы координаты:
,
,

Радиус в цилиндрической системе:

Источник

Сферическими координатами называют систему координат для отображения геометрических свойств фигуры в трёх измерениях посредством задания трёх координат , где — кратчайшее расстояние до начала координат (радиальное расстояние), а theta и varphi — зенитный и азимутальный углы соответственно.

Понятия зенит и азимут широко используются в астрономии. Вообще зенит — это направление вертикального подъёма над произвольно выбранной точкой (точкой наблюдения), принадлежащей так называемой фундаментальной плоскости. В качестве фундаментальной плоскости в астрономии может быть выбрана плоскость, в которой лежит экватор, или плоскость, в которой лежит горизонт, или плоскость эклиптики и т. д., что порождает разные системы небесных координат. Азимут — угол между произвольно выбранным лучом фундаментальной плоскости с началом в точке наблюдения и другим лучом этой плоскости, имеющим общее начало с первым.

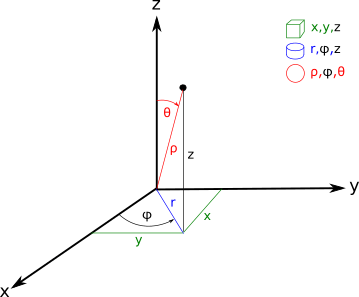
Рис.1.Точка имеет три декартовых и три сферических координаты

Применительно к нашему рисунку сферической системы координат, фундаментальная плоскость — это плоскость xy. Зенит — некая удалённая точка, лежащая на оси Z и видимая из начала координат. Азимут отсчитывается от оси X до проекции радиус-вектора r на плоскость xy. Это объясняет названия углов, как и то, что сферическая система координат может служить обобщением (пусть хотя бы и приближённым) множества видов систем небесных координат.

Содержание

1 Определения
2 Переход к другим системам координат
- 2.1 Декартова система координат
- 2.2 Цилиндрическая система координат
3 Дифференциальные характеристики
4 См. также
5 Ссылки

Определения

Три координаты точки вводятся с помощью декартовой системы координат. Криволинейные координатные линии, проходящие через точку , образуются при изменении одной координаты при фиксированных остальных. За направление координатной линии в точке принимается направление возрастания соответствующей координаты. Векторы базиса ${displaystyle ({mathsf {r}}_{r},{mathsf {r}}_{theta },{mathsf {r}}_{varphi })}$ в точке являются частными производными радиус – вектора по переменным и составляют правую тройку.

Угол theta называется зенитным, или полярным, или нормальным, а также он может быть назван английским словом colatitude, а угол varphi — азимутальным. Углы theta и varphi не имеют значения при r=0 , а varphi не имеет значения при (то есть при или $theta =180^{circ }$ ).

Такое соглашение установлено в стандарте (ISO 31-11^ru_en). Кроме того может использоваться соглашение, когда вместо зенитного угла theta , используется угол между радиус-вектором точки r и плоскостью xy, равный $90^{circ }$ — theta . Он называется широтой и может быть обозначен той же буквой theta . Широта может изменяться в пределах $-90^{circ }leqslant theta leqslant 90^{circ }$ . При этом соглашении углы theta и varphi не имеют значения при r=0 , так же как и в первом случае, а varphi не имеет значения при (то есть при $theta =-90^{circ }$ или $theta =90^{circ }$ ).

Часто, по аналогии с цилиндрической системой координат , которая является правой, используют сферическую систему координат , где изменен порядок следования координат в отличие от определенного выше. Такая система координат является левой, так как векторы базиса ${displaystyle ({mathsf {r}}_{r},{mathsf {r}}_{varphi },{mathsf {r}}_{theta })}$ при определении области изменения угла $0leqslant theta leqslant 180^{circ }$ составляют левую тройку векторов (луч из точки , направленный в указанной последовательности на концы векторов, двигается против часовой стрелки), в то время как исходная системе координат (x,y,z) является правой. Для векторных операций при переходе от одной системы координат к другой существенно, чтобы правая система переходила в правую. Сферическая система координат будет правой, если определить угол theta ' следующим образом: ${displaystyle theta '=180^{circ }-theta ,0leqslant theta leqslant 180^{circ }}$ .

Переход к другим системам координат

Декартова система координат

Если заданы сферические координаты точки , то переход к декартовым осуществляется по формулам:

${begin{cases}x=rsin theta cos varphi ,\y=rsin theta sin varphi ,\z=rcos theta .end{cases}}$

Обратно, от декартовых к сферическим:

${begin{cases}r={sqrt {x^{2}+y^{2}+z^{2}}},\theta =arccos left({dfrac {z}{sqrt {x^{2}+y^{2}+z^{2}}}}right)=mathrm {arctg} left({dfrac {sqrt {x^{2}+y^{2}}}{z}}right),\varphi =mathrm {arctg} left({dfrac {y}{x}}right).end{cases}}$

(здесь, конечно, требуется определенное естественное уточнение для значений varphi вне первого октанта; то же для всех формул с арктангенсом здесь и ниже; впрочем, замена на соответствующую формулу с арккосинусом снимает этот вопрос в отношении координаты theta ).

Якобиан преобразования к сферическим координатам имеет вид:

$J=r^{2}sin theta .$

Вывод

Переход от декартовых координат (x, y, z) к сферическим координатам (r, θ, φ):

Матрица перехода имеет следующий вид

${hat {I}}(r,theta ,phi )={begin{bmatrix}{dfrac {partial x}{partial r}}&{dfrac {partial x}{partial theta }}&{dfrac {partial x}{partial phi }}\[3pt]{dfrac {partial y}{partial r}}&{dfrac {partial y}{partial theta }}&{dfrac {partial y}{partial phi }}\[3pt]{dfrac {partial z}{partial r}}&{dfrac {partial z}{partial theta }}&{dfrac {partial z}{partial phi }}\end{bmatrix}}={begin{bmatrix}sin theta ,cos phi &r,cos theta ,cos phi &-r,sin theta ,sin phi \sin theta ,sin phi &r,cos theta ,sin phi &r,sin theta ,cos phi \cos theta &-r,sin theta &0end{bmatrix}}.$

Столбцы матрицы перехода от декартовых координат к сферическим представляют собой декартовы координаты векторов базиса ${displaystyle {displaystyle ({mathsf {r}}_{r},{mathsf {r}}_{theta },{mathsf {r}}_{varphi })}}$ , а якобиан — есть определитель матрицы перехода: $J(r,theta ,phi )=det {hat {I}}(r,theta ,phi )=det {begin{bmatrix}sin theta ,cos phi &r,cos theta ,cos phi &-r,sin theta ,sin phi \sin theta ,sin phi &r,cos theta ,sin phi &r,sin theta ,cos phi \cos theta &-r,sin theta &0end{bmatrix}}=r^{2}sin theta .$

Цилиндрическая система координат

Если заданы сферические координаты точки, то переход к цилиндрическим осуществляется по формулам:

${begin{cases}rho =rsin theta ,\varphi =varphi ,\z=rcos theta .end{cases}}$

Обратно от цилиндрических к сферическим:

${begin{cases}r={sqrt {rho ^{2}+z^{2}}},\theta =mathrm {arctg} left({dfrac {rho }{z}}right),\varphi =varphi .end{cases}}$

Якобиан преобразования от сферических к цилиндрическим:

Дифференциальные характеристики

Вектор , проведённый из точки в точку , равен

где

ортогональные единичные векторы сферических координат в направлении увеличения , соответственно,
а — единичные векторы декартовых координат.
Сферические координаты являются ортогональными, поэтому метрический тензор имеет в них диагональный вид:

$g_{ij}={begin{pmatrix}1&0&0\0&r^{2}&0\0&0&r^{2}sin ^{2}theta end{pmatrix}},quad g^{ij}={begin{pmatrix}1&0&0\0&{dfrac {1}{r^{2}}}&0\0&0&{dfrac {1}{r^{2}sin ^{2}theta }}end{pmatrix}}$

$det(g_{ij})=r^{4}sin ^{2}theta .$
Квадрат дифференциала длины дуги:

$ds^{2}=dr^{2}+r^{2},dtheta ^{2}+r^{2}sin ^{2}theta ,dvarphi ^{2}.$

Коэффициенты Ламе:

$H_{r}=1,quad H_{theta }=r,quad H_{varphi }=rsin theta .$

Символы Кристоффеля :

$Gamma _{22}^{1}=-r,quad Gamma _{33}^{1}=-rsin ^{2}theta ,$

$Gamma _{21}^{2}=Gamma _{12}^{2}=Gamma _{13}^{3}=Gamma _{31}^{3}={frac {1}{r}},$

$Gamma _{33}^{2}=-cos theta sin theta ,quad Gamma _{23}^{3}=Gamma _{32}^{3}=mathrm {ctg} ,theta .$

Остальные равны нулю.

См. также

Углы Эйлера
Гиперсфера § Гиперсферические координаты

Ссылки

Weisstein, Eric W. Сферические координаты (англ.) на сайте Wolfram MathWorld.

Источник

Сферические координаты (сферическая система координат)

Переход от сферических координат к декартовым (прямоугольным)

Определения[править | править код]

Переход к другим системам координат[править | править код]

Декартова система координат[править | править код]

Цилиндрическая система координат[править | править код]

Дифференциальные характеристики[править | править код]

Математическое моделирование Земли[править | править код]

Сферическая географическая система координат[править | править код]

Сферическая геомагнитная система координат[править | править код]

См. также[править | править код]

Примечания[править | править код]

Ссылки[править | править код]

Прямоугольная система координат

Цилндрическая система координат

Сферическая система координат

Прямоугольные координаты в пространстве

Цилиндрические координаты

Сферические координаты

Формулы преобразования декартовых координат

Цилиндрические координаты

Прямоугольные координаты

Сферические координаты

Формулы преобразования цилиндрических координат

Сферические координаты

Прямоугольные координаты

Цилиндрические координаты

Формулы преобразования сферических координат

Содержание

Определения

Переход к другим системам координат

Декартова система координат

Цилиндрическая система координат

Дифференциальные характеристики

См. также

Ссылки

Вам также может понравиться

Как найти частоту случайной величины

Как найти свой бронированный авиабилет

Как исправить диск с расширением raw

Добавить комментарий Отменить ответ