Для того, чтобы понять, что такое область определения функции, необходимо знать области определения основных элементарных функций. Для этого нужно разбираться в определенных понятиях и находить весомые аргументы и методы решения, что и предложено данной статьей. Будут рассмотрены различные сложнейшие комбинации функций вида y=x+x-2 или y=5·x2+1·x3, y=xx-5 или y=x-15-3. Рассмотрим теорию и решим несколько примеров с подобными заданиями, чтобы вам больше не нужно было определять все это онлайн.
Что значит найти область определения
После того как функция задается, указывается ее область определения. Иначе говоря, без области определения функция не рассматривается. При задании функции вида y=f(x) область определения не указывается, так как ее ОДЗ для переменной x будет любым. Таким образом, функция определена на всей области определения.
Область определения и область значения можно найти и для кубического корня (куб. √), к примеру, для x+2.
Ограничение области определения
Область определения функции или ООФ рассматривается еще в школьном курсе алгебры. У действительных чисел она может быть (0, +∞) или такой [−3, 1)∪[5, 7). Еще по виду функции можно визуально узнавать ее ОДЗ. Рассмотрим, на что может указывать наличие области определения:
- при имеющемся знаменателе необходимо производить деление такого типа функции как y=x+2·xx4-1;
- при наличии переменной под знаком корня необходимо обращать внимание на сложение корня четной степени типа y=x+1 или y=23·x+3x;
- при наличии переменной в основании степени с отрицательным или нецелым показателем такого типа, как y=5·(x+1)-3, y=-1+x113, y=(x3-x+1)2, которые определены не для всех чисел;
- при наличии переменной под знаком логарифма или в основании вида y=lnx2+x4 или y=1+logx-1(x+1) причем основание является числом положительным, как и число под знаком логарифма;
- при наличии переменной, находящейся под знаком тангенса и котангенса вида y=x3+tg2·x+5 или y=ctg(3·x3-1), так как они существуют не для любого числа;
- при наличии переменной, расположенной под знаком арксинуса или арккосинуса вида y=arcsin(x+2)+2·x2, y=arccosx-1+x, область определения которых определяется ни интервале от -1 до 1.
При отсутствии хотя бы одного признака, область определения приходится искать другим образом (и это не с калькулятором). Рассмотрим пример функции вида y=x4+2·x2-x+12+223·x. Видно, что никаких ограничений она не имеет, так как в знаменателе нет переменной.
Правила нахождения области определения
Для примера рассмотрим функцию типа y=2·x+1. Для вычисления ее значения можем определить x. Из выражения 2·x+1 видно, что функция определена на множестве всех действительных чисел. Рассмотрим еще один пример для подробного определения.
Если задана функция типа y=3x-1, а необходимо найти область определения, тогда понятно, что следует обратить внимание на знаменатель. Известно, что на ноль делить нельзя. Отсюда получаем, что 3x-1знаменатель равняется нулю при х=1, поэтому искомая область определения данной функции примет вид (−∞, 1)∪(1, +∞) и считается числовым множеством.
На рассмотрении примера y=x2-5·x+6 видно, что имеется подкоренное выражение, которое всегда больше или равно нулю. Значит запись примет вид x2−5·x+6≥0. После решения неравенства получим, что имеются две точки, которые делят область определения на отрезки, которые записываются как (−∞, 2]∪[3, +∞).
При подготовке ЕГЭ и ОГЭ можно встретить множество комбинированных заданий для функций, где необходимо в первую очередь обращать внимание на ОДЗ. Только после его определения можно приступать к дальнейшему решению.
Область определения суммы, разности и произведения функций
Перед началом решения необходимо научиться правильно определять область определения суммы функций. Для этого нужно иметь следующее утверждение:
Когда функция ff считается суммой n функций f1, f2, …, fn, иначе говоря, эта функция задается при помощи формулы y=f1(x)+f2(x)+…+fn(x), тогда ее область определения считается пересечением областей определения функций f1, f2, …, fn. Данное утверждение можно записать как:
D(f)=D(f1)D(f2)…D(fn)
Поэтому при решении рекомендуется использование фигурной скобки при записи условий, так как это является удобным способом, чтобы понимать понимания перечисления числовых множеств.
Найти область определения функции вида y=x7+x+5+tgx.
Решение
Заданная функция представляется как сумма четырех: степенной с показателем 7,степенной с показателем 1, постоянной, функции тангенса.
По таблице определения видим, что D(f1)=(−∞, +∞), D(f2)=(−∞, +∞), D(f3)=(−∞, +∞), причем область определения тангенса включает в себя все действительные числа, кроме π2+π·k, k∈Z.
Областью определения заданной функции f является пересечение областей определения f1, f2, f3 и f4. То есть для функции существует такое количество действительных чисел, куда не входит π2+π·k, k∈Z.
Ответ: все действительные числа кроме π2+π·k, k∈Z.
Чтобы найти область определения произведения функций необходимо применять правило:
Когда функция f считается произведением n функций f1, f2, f3 и fn, тогда существует такая функция f, которую можно задать при помощи формулы y=f1(x)·f2(x)·…·fn(x), тогда ее область определения считается областью определения для всех функций.
Запишется D(f)=D(f1)D(f2)…D(fn)
Найти область определения функции y=3·arctg x·ln x.
Решение
Правая часть формулы рассматривается как f1(x)·f2(x)·f3(x), где за f1 является постоянной функцией, f2 является арктангенсом, f3 – логарифмической функцией с основанием e. По условию имеем, что D(f1)=(−∞, +∞), D(f2)=(−∞, +∞) и D(f3)=(0, +∞). Мы получаем, что
D(f)=D(f1)D(f2)D(fn)=(-∞, +∞)(-∞, +∞)D(0, +∞)=(0, +∞)
Ответ: область определения y=3·arctg x·ln x – множество всех действительных чисел.
Необходимо остановиться на нахождении области определения y=C·f(x), где С является действительным числом. Отсюда видно, что ее областью определения и областью определения f совпадающими.
Функция y=C·f(x) – произведение постоянной функции и f. Область определения – это все действительные числа области определения D(f). Отсюда видим, что область определения функции y=C·f(x) является -∞, +∞D(f)=D(f).
Естестввенным образом получили, что область определения y=f(x) и y=C·f(x), где C является некоторое действительное число, совпадают. Это видно на примере определения корня y=x считается [0, +∞), потому как область определения функции y=-5·x – [0, +∞).
Области определения y=f(x) и y=−f(x) совпадают , что говорит о том, что его область определения разности функции такая же, как и область определения их суммы.
Найти область определения функции y=log3x−3·2x.
Решение
Необходимо рассмотреть как разность двух функций f1 и f2.
f1(x)=log3x и f2(x)=3·2x. Тогда получим, что D(f)=D(f1)D(f2).
Область определения записывается как D(f1)=(0, +∞). Приступим к области определения f2. В данном случае она совпадает с областью определения показательной, тогда получаем, что D(f2)=(−∞, +∞).
Для нахождения области определения функции y=log3x−3·2x получим, что
D(f)=D(f1)D(f2)=(0, +∞)-∞, +∞
Ответ: (0, +∞).
Необходимо озвучить утверждение о том, что областью определения y=anxn+an-1xn-1+…+a1x+a0 является множество действительных чисел.
Рассмотрим y=anxn+an-1xn-1+…+a1x+a0, где в правой части имеется многочлен с одной переменной стандартного вида в виде степени n с действительными коэффициентами. Допускается рассматривать ее в качестве суммы (n+1)-ой функции. Область определения для каждой из таких функций включается множество действительных чисел, которое называется R.
Найти область определения f1(x)=x5+7×3-2×2+12.
Решение
Примем обозначение f за разность двух функций, тогда получим, что f1(x)=x5+7×3-2×2+12 и f2(x)=3·x-ln 5. Выше было показано, что D(f1)=R. Область определения для f2 является совпадающей со степенной при показателе –ln5, иначе говоря, что D(f2)=(0, +∞).
Получаем, что D(f)=D(f1)D(f2)=-∞, +∞(0, +∞)=(0, +∞).
Ответ: (0, +∞).
Область определения сложной функции
Для решения данного вопроса необходимо рассмотреть сложную функцию вида y=f1(f2(x)). Известно, что D(f) является множеством всех x из определения функции f2, где область определения f2(x) принадлежит области определения f1.
Видно, что область определения сложной функции вида y=f1(f2(x)) находится на пересечении двух множеств таких, где x∈D(f2) и f2(x)∈D(f1). В стандартном обозначении это примет вид
x∈D(f2)f2(x)∈D(f1)
Рассмотрим решение нескольких примеров.
Найти область определения y=ln x2.
Решение
Алгоритм решения этого уравнения или функции следующий.
Данную функцию представляем в виде y=f1(f2(x)), где имеем, что f1 является логарифмом с основанием e, а f2 – степенная функция с показателем 2.
Для решения необходимо использовать известные области определения D(f1)=(0, +∞) и D(f2)=(−∞, +∞).
Тогда получим систему неравенств вида
x∈D(f2)f2(x)∈D(f1)⇔x∈-∞, +∞x2∈(0, +∞)⇔⇔x∈(-∞, +∞)x2>0⇔x∈(-∞, +∞)x∈(-∞, 0)∪(0, +∞)⇔⇔x∈(-∞, 0)∪(0, +∞)
Искомая область определения найдена. Вся ось действительных чисел кроме нуля является областью определения.
Ответ: (−∞, 0)∪(0, +∞).
Найти область определения функции y=(arcsin x)-12.
Решение
График решения следующий.
Так как дана сложная функция, необходимо рассматривать ее как y=f1(f2(x)), где f1 является степенной функцией с показателем -12, а f2 функция арксинуса, теперь необходимо искать ее область определения. Необходимо рассмотреть D(f1)=(0, +∞) и D(f2)=[−1, 1]. Теперь найдем все множества значений x, где x∈D(f2) и f2(x)∈D(f1). Получаем систему неравенств вида
x∈D(f2)f2(x)∈D(f1)⇔x∈-1, 1arcsin x∈(0, +∞)⇔⇔x∈-1, 1arcsin x>0
Для решения arcsin x>0 необходимо прибегнуть к свойствам функции арксинуса. Его возрастание происходит на области определения [−1, 1], причем обращается в ноль при х=0, значит, что arcsin x>0 из определения x принадлежит промежутку (0, 1].
Преобразуем систему вида
x∈-1, 1arcsin x>0⇔x∈-1, 1x∈(0, 1]⇔x∈(0, 1]
Область определения искомой функции имеет интервал равный (0, 1].
Ответ: (0, 1].
Постепенно подошли к тому, что будем работать со сложными функциями общего вида y=f1(f2(…fn(x)))). Область определения такой функции ищется из x∈D(fn)fn(x)∈D(fn-1)fn-1(fn(x))∈D(fn-2)…f2(f3(…(fn(x)))∈D(f1).
Найти область определения y=sin(lg x4).
Решение
Заданная функция может быть расписана, как y=f1(f2(f3(x))), где имеем f1 – функция синуса, f2 – функция с корнем 4 степени, f3 – логарифмическая функция.
Имеем, что по условию D(f1)=(−∞, +∞), D(f2)=[0, +∞), D(f3)=(0, +∞). Тогда областью определения функции – это пересечение множеств таких значений, где x∈D(f3), f3(x)∈D(f2), f2(f3(x))∈D(f1). Получаем, что
x∈D(f3)f3(x)∈D(f2)f2(f3(x))∈D(f1)⇔x∈(0, +∞)lg x∈[0, +∞)lg x4∈-∞, +∞
Условие lg x4∈-∞, +∞ аналогично условию lg x∈[0, +∞), значит
x∈(0, +∞)lg x∈[0, +∞)lg x4∈-∞, +∞⇔x∈(0, +∞)lg x∈[0, +∞)lg x∈[0, +∞)⇔⇔x∈(0, +∞)lg x∈[0, +∞)⇔x∈(0, +∞)lg x≥0⇔⇔x∈(0, +∞)lg x≥lg 1⇔x∈(0, +∞)x≥1⇔⇔x∈[1, +∞)
Ответ: [1, +∞).
При решении примеров были взяты функции, которые были составлены при помощи элементарных функций, чтобы детально рассмотреть область определения.
Область определения дроби
Рассмотрим функцию вида f1(x)f2(x). Стоит обратить внимание на то, что данная дробь определяется из множества обеих функций, причем f2(х) не должна обращаться в ноль. Тогда получаем, что область определения f для всех x записывается в виде x∈D(f1)x∈D(f2)f2(x)≠0.
Запишем функцию y=f1(x)f2(x) в виде y=f1(x)·(f2(x))-1. Тогда получим произведение функций вида y=f1(x) с y=(f2(x))-1. Областью определения функции y=f1(x) является множество D(f1), а для сложной y=(f2(x))-1 определим из системы вида x∈D(f2)f2(x)∈(-∞, 0)∪(0, +∞)⇔x∈D(f2)f2(x)≠0.
Значит, x∈D(f1)x∈D(f2)f2(x)∈(-∞, 0)∪(0, +∞)⇔x∈D(f1)x∈D(f2)f2(x)≠0.
Найти область определения y=tg(2·x+1)x2-x-6.
Решение
Заданная функция дробная, поэтому f1 – сложная функция, где y=tg(2·x+1) и f2 – целая рациональная функция, где y=x2−x−6, а область определения считается множеством всех чисел. Можно записать это в виде
x∈D(f1)x∈D(f2)f2(x)≠0
Представление сложной функции y=f3(f4(x)), где f3 –это функция тангенс, где в область определения включены все числа, кроме π2+π·k, k∈Z, а f4 – это целая рациональная функция y=2·x+1 с областью определения D(f4)=(−∞, +∞). После чего приступаем к нахождению области определения f1:
x∈D(f4)2·x+1∈D(f3)⇔x∈(-∞, +∞)2x+1≠π2+π·k, k∈Z⇔x≠π4-12+π2·k, k∈Z
Еще необходимо рассмотреть нижнюю область определения y=tg(2·x+1)x2-x-6. Тогда получаем, что
x∈D(f1)x∈D(f2)f2(x)≠0⇔x≠π4-12+π2·k, k∈Zx∈-∞, +∞x2-x-6≠0⇔⇔x≠π4-12+π2·k, k∈Zx≠-2x≠3
Ответ: множество действительных чисел, кроме -2, 3 и π4-12+π2·k, k∈Z.
Действия с корнями
Корни в математике, в частности, функцию с корнем можно определить следующим образом:
y=n√x. N здесь — натуральное число, большее за единицу.
Область определения корня зависит от того, каков показатель: четный или нечетный.
Если n является четным числом (n=2m). Это значит, что область определения представляет собой множество всех неотрицательных действительных чисел.
Если показатель корня — нечетное число, большее за единицу (n=2m+1 и m принадлежит к n), то областью определения корня будет множество всех действительных чисел.
Также важным является вопрос, как складывать корни.
Сложение и вычитание корней возможно при условии наличия одинакового подкоренного выражения. К примеру, сложение и вычитание корней возможно 2√3 и 4√3. Можно ли складывать корни или вычитать в случае 2√3 и 2√5? Ответ — нет.
Как решать корни во втором случае? Вы можете упростить подкоренное выражение и привести их корни к одинаковому подкоренному выражению. После этого вы сможете как считать корни, так и вычитать корни.
К основным действиям с корнями относят:
- умножение корней;
- деление корней;
- корень минус корень или плюс.
Область определения логарифма с переменной в основании
Определение логарифма существует для положительных оснований не равных 1. Отсюда видно, что функция y=logf2(x)f1(x) имеет область определения, которая выглядит так:
x∈D(f1)f1(x)>0x∈D(f2)f2(x)>0f2(x)≠1
К аналогичному заключению можно прийти, когда функцию можно изобразить в таком виде:
y=logaf1(x)logaf2(x), a>0, a≠1. После чего можно приступать к области определения дробной функции.
Область определения логарифмической функции – это множество действительных положительных чисел, тогда области определения сложных функций типа y=logaf1(x) и y=logaf2(x) можно определить из получившейся системы вида x∈D(f1)f1(x)>0 и x∈D(f2)f2(x)>0. Иначе эту область можно записать в виде y=logaf1(x)logaf2(x), a>0, a≠1, что означает нахождение y=logf2(x)f1(x) из самой системы вида
x∈D(f1)f1(x)>0x∈D(f2)f2(x)>0logaf2(x)≠0=x∈D(f1)f1(x)>0x∈D(f2)f2(x)>0f2(x)≠1
Обозначить область определения функции y=log2·x(x2-6x+5).
Решение
Следует принять обозначения f1(x)=x2−6·x+5 и f2(x)=2·x, отсюда D(f1)=(−∞, +∞) и D(f2)=(−∞, +∞). Необходимо приступить к поиску множества x, где выполняется условие x∈D(f1), f1(x)>0, x∈D(f2), f2(x)>0, f2(x)≠1. Тогда получаем систему вида
x∈(-∞, +∞)x2-6x+5>0x∈(-∞, +∞)2·x>02·x≠1⇔x∈(-∞, +∞)x∈(-∞, 1)∪(5, +∞)x∈(-∞, +∞)x>0x≠12⇔⇔x∈0, 12∪12, 1∪(5, +∞)
Отсюда видим, что искомой областью функции y=log2·x(x2-6x+5) считается множнство, удовлетворяющее условию 0, 12∪12, 1∪(5, +∞).
Ответ: 0, 12∪12, 1∪(5, +∞).
Область определения показательно-степенной функции
Показательно-степенная функция задается формулой вида y=(f1(x))f2(x). Ее область определения включает в себя такие значения x, которые удовлетворяют системе x∈D(f1)x∈D(f2)f1(x)>0.
Эта область позволяет переходить от показательно-степенной к сложной вида y=aloga(f1(x))f2(x)=af2(x)·logaf1(x), где где a>0, a≠1.
Найти область определения показательно-степенной функции y=(x2-1)x3-9·x.
Решение
Примем за обозначение f1(x)=x2−1 и f2(x)=x3-9·x.
Функция f1 определена на множестве действительных чисел, тогда получаем область определения вида D(f1)=(−∞, +∞). Функция f2 является сложной, поэтому ее представление примет вид y=f3(f4(x)), а f3 – квадратным корнем с областью определения D(f3)=[0, +∞), а функция f4 – целой рациональной,D(f4)=(−∞, +∞). Получаем систему вида
x∈D(f4)f4(x)∈D(f3)⇔x∈(-∞, +∞)x3-9·x≥0⇔⇔x∈(-∞, +∞)x∈-3, 0∪[3, +∞)⇔x∈-3, 0∪[3, +∞)
Значит, область определения для функции f2 имеет вид D(f2)=[−3, 0]∪[3, +∞). После чего необходимо найти область определения показательно-степенной функции по условию x∈D(f1)x∈D(f2)f1(x)>0.
Получаем систему вида x∈-∞, +∞x∈-3, 0∪[3, +∞)x2-1>0⇔x∈-∞, +∞x∈-3, 0∪[3, +∞)x∈(-∞, -1)∪(1, +∞)⇔⇔x∈-3, -1∪[3, +∞)
Ответ: [−3, −1)∪[3, +∞)
В общем случае
Для решения обязательным образом необходимо искать область определения, которая может быть представлена в виде суммы или разности функций, их произведений. Области определения сложных и дробных функций нередко вызывают сложность. Благодаря выше указанным правилам можно правильно определять ОДЗ и быстро решать задание на области определения.
Таблицы основных результатов
Весь изученный материал поместим для удобства в таблицу для удобного расположения и быстрого запоминания.
| Функция | Ее область определения |
|
Сумма, разность, произведение функций f1, f2,…, fn |
Пересечение множеств D(f1), D(f2), …, D(fn) |
|
Сложная функция y=f1(f2(f3(…fn(x)))) В частности, y=f1(f2(x)) |
Множество всех x, одновременно удовлетворяющих условиям x∈D(fn),fn(x)∈D(fn-1),fn-1(fn(x))∈D(fn-2),… ,f2(f3(…fn(x)))∈D(f1) x∈D(f2),f2(x)∈D(f1) |
Расположим функции и их области определения.
| Функция | Ее область определения |
|
Прямая пропорциональность y=k·x |
R |
| Линейная y=k·x+b | R |
|
Обратная пропорциональность y=kx |
-∞, 0∪0, +∞ |
| Квадратичная y=a·x2+b·x+c | R |
| y=anxn+an-1xn-1+…+a1x+a0 | R |
| Целая рациональная | R |
| y=C·f(x), где C – число | D(f) |
|
Дробная y=f1(x)f2(x) В частности, если f1(x), f2(x) – многочлены |
Множество всех x, которые одновременно удовлетворяют условиям f2(x)≠0 |
| y=f(x)n, где n – четное | x∈D(f1), f(x)≥0 |
|
y=logf2(x)f1(x) В частности, y=logaf1(x) В частности, y=logf2(x)a |
x∈D(f1), f1(x)>0,x∈D(f2), f2(x)>0, f2(x)≠1 x∈D(f1), f1(x)>0 x∈D(f2), f2>0, f2(x)≠1 |
| Показательно-степенная y=(f1(x))f2(x) | x∈D(f1), x∈D(f2), f1(x)>0 |
Отметим, что преобразования можно выполнять, начиная с правой части выражения. Отсюда видно, что допускаются тождественные преобразования, которые на область определения не влияют. Например, y=x2-4x-2 и y=x+2 являются разными функциями, так как первая определяется на (−∞, 2)∪(2, +∞), а вторая из множества действительных чисел. Из преобразования y=x2-4x-2=x-2x+2x-2=x+2 видно, что функция имеет смысл при x≠2.
Вспомним кратко основные определения функции в математике.
Функция — это зависимость переменной « y » от
независимой переменной « x ».
Функцию можно задать через формулу (аналитически). Например:
у = 2x
- « x » называют независимым аргументом функции;
- « y » зависимой переменной или значением функции.
Вместо « x » (аргумента функции) в формулу «у = 2x» подставляем произвольные числовые значения
и по заданной формуле вычисляем
значение « y ».
Подставим несколько числовых значений вместо « x » в формулу «у = 2x» и запишем результаты в таблицу.
| x | y = 2x | ||||||
|---|---|---|---|---|---|---|---|
| x = −2 | у = 2 · (−2) = −4 | ||||||
| x = 0 | y = 2 · 0 = 0 | ||||||
x =
|
y = 2 ·
= 1 |
||||||
| x = 3 | y = 2 · 3 = 6 |
Запомните!
![]()
Область определения функции — это множество числовых значений, которые можно подставить вместо « x » (аргумента функции).
Обозначают область определения функции как:
D(y)
Вернемся к нашей функции «у = 2x» и найдем её область определения.
Посмотрим ещё раз на таблицу функции «y = 2x», где
мы подставляли произвольные числа вместо « x », чтобы найти « y ».
| x | y = 2x | ||
|---|---|---|---|
| −2 | −4 | ||
| 0 | 0 | ||
|
1 | ||
| 3 | 6 |
Так как у нас не было никаких ограничений на числа, которые можно подставить вместо « x », можно утверждать,
что вместо « x » мы могли подставлять любое действительное число.
Другими словами, вместо « x » можно подставить любые числа, например:
- −2
- 0
- 10
- 30,5
- 1 000 000
- и так далее…
Запомните!
![]()
Областью определения функции называют множество чисел,
которые можно подставить вместо « x ».
В нашей функции «у = 2x» вместо « x »
можно подставить любое число, поэтому область определения функции «у = 2x» — это любые действительные числа.
Запишем область определения функции «у = 2x» через математические обозначения.
у = 2x
D(y): x — любое действительное число
Ответ выше написан словами без использования специального математического языка. Заменим лишние слова на
математические символы.
Для этого вспомним понятие числовой оси.
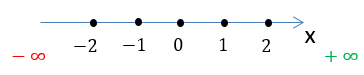
Заштрихуем область на числовой оси, откуда можно брать значения для « x » в функции «у = 2x».
Так как в функции
«у = 2x» нет ограничений для « x »,
заштрихуем всю числовую ось от минус бесконечности «−∞» до плюс бесконечности
«+∞».
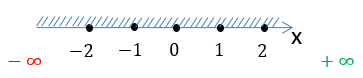
Запишем результат по правилам записи неравенств.

D(y): x ∈ (−∞ ; +∞)
Запись выше читается как: « x » принадлежит промежутку от минус бесконечности
до плюс бесконечности.
Запишем окончательный ответ для области определения функции.
Ответ:
D(y): x ∈ (−∞ ; +∞)
По-другому промежуток
« x ∈ (−∞ ; +∞) » можно записать
как
«x ∈ R».
Читается «x ∈ R» как: « x » принадлежит всем действительным числам».
Записи « x ∈ (−∞ ; +∞) » и
«x ∈ R» одинаковы по своей сути.
Область определения функции с дробью
Разберем пример сложнее, когда в задании на поиск области определения функции есть дробь с « x » в знаменателе.
Разбор примера
Найдите область определения функции:
Задание «Найдите область определения функции» означает, что нам нужно определить все числовые значения, которые может принимать « x »
в функции
« f(x) = ».
По законам математики из школьного курса мы помним, что на ноль делить нельзя.
Иначе говоря,
знаменатель (нижняя часть дроби) не может быть равен нулю.
Переменная « x » находится в знаменателе функции «f(x) = ».
Так как на ноль делить нельзя, запишем, что знаменатель не равен нулю.
x + 5 ≠ 0
Решим полученное линейное уравнение.
Получается, что « x » может принимать любые числовые значения кроме «−5».
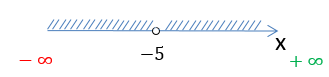
На числовой оси заштрихуем все доступные значения для « x ».
Число «−5» отмечено
«пустой»
точкой на числовой оси, так как не входит в область допустимых значений.
Запишем заштрихованную область на числовой оси через знаки неравенства.
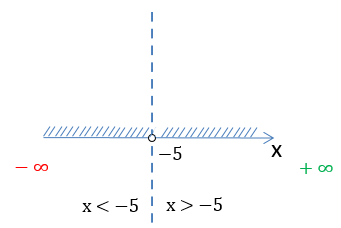
Запишем промежутки через математические символы. Так как число «−5» не входит
в область определения функции, при записи ответа рядом с ним будет стоять
круглая скобка.
Вспомнить запись ответа через математические символы можно в уроке
«Как записать ответ неравенства».

x ∈ (−∞ ; −5) ∪ (−5 ; +∞)
Запишем окончательный ответ для области определения функции
«f(x) = ».
Ответ:
D(y): x ∈ (−∞ ; −5) ∪ (−5 ; +∞)
Область определения функции с корнем
Рассмотрим другой пример. Требуется определить область определения функции, в которой содержится квадратный корень.
Разбор примера
Найти область определения функции:
y = √6 − x
Из урока «Квадратный корень» мы помним,
что подкоренное выражение корня чётной степени должно быть больше или равно нулю.
Найдём, какие значения может принимать « x » в функции
«у = √6 − x».
Подкоренное выражение
«6 − x» должно быть больше или равно нулю.
6 − x ≥ 0
Решим линейное неравенство по правилам урока «Решение линейных неравенств».
6 − x ≥ 0
−x ≥ −6 | ·(−1)
x ≤ 6
Запишем полученный ответ, используя числовую ось и математические символы. Число «6» отмечено
«заполненной»
точкой на числовой оси, так как входит в область допустимых значений.
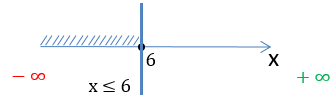
x ∈ (−∞ ; 6]
Запишем окончательный ответ для области определения функции
«y = √6 − x» .
Так как число «6» входит
в область определения функции, при записи ответа рядом с ним будет стоять
квадратная скобка.
Ответ:
D(y): x ∈ (−∞ ; 6]
Правило для определения области определения функции
Запомните!
![]()
Чтобы найти область определения функции нужно проверить формулу функции по двум законам школьного курса математики:
- на ноль делить нельзя (другими словами, знаменатели дробей с « x » не должны быть равны нулю);
- подкоренные выражения корней чётной степени должны быть больше или равны нулю.
При нахождении области определения функции необходимо всегда задавать себе два вопроса:
- есть ли в функции дроби со знаменателем, в котором есть « x »?
- есть ли корни четной
степени с « x »?
Если на оба вопроса вы получаете отрицательный ответ, то область определения функции — это все действительные числа.
Рассмотрим пример поиска области определения функции с корнем и дробью.
Разбор примера
Найдите область определения функции:
Идем по алгоритму. Задаём себе первый вопрос, есть ли в функции дробь с « x » в знаменателе. Ответ: да, есть.
В функции «
f(x) = √x + 3 +
»
есть дробь «
»,
где « x » расположен в знаменателе. Запишем условие, что знаменатель
« x 2 − 9 »
не может быть равен нулю.
Решаем квадратное уравнение через
формулу квадратного уравнения.
x1;2 =
x2 − 9 ≠ 0
x1;2 =
| −0 ± √02 − 4 · 1 · (−9) |
| 2 · 1 |
x1;2 ≠
x1;2 ≠
x1;2 ≠
x1;2 ≠ ±3
Запомним полученный результат. Задаем себе
второй
вопрос.
Проверяем, есть ли в формуле функции
«
f(x) = √x + 3 +
»
корень четной степени.
В формуле есть квадратный корень «
√x + 3
».
Подкоренное выражение «x + 3»
должно быть больше или равно нулю.
x + 3 ≥ 0
Решим линейное неравенство.
x + 3 ≥ 0
x ≥ −3
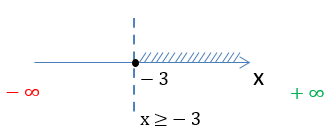
Объединим полученные ответы по обоим вопросам:
- знаменатель дроби
«
» не равен нулю ; - подкоренное выражение «
√x + 3
» должно быть больше или равно нулю.
Объединим все полученные результаты на числовых осях.
Сравнивая полученные множества, выберем только те промежутки, которые удовлетворяют обоим условиям.
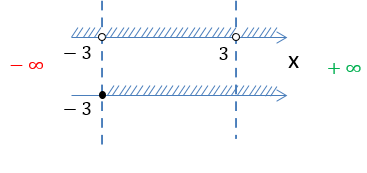
Выделим красным заштрихованные промежутки, которые совпадают на обеих числовых осях.
Обратим внимание, что числа «−3» и «3» отмечены «пустыми» точками и не входят в итоговое решение.
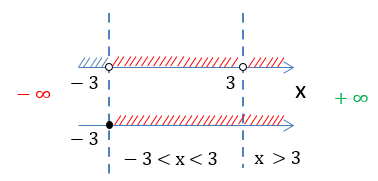
Получаем два числовых
промежутка «−3 < x < 3» и «x > 3», которые являются областью определения функции
«f(x) = √x + 3 + ».
Запишем окончательный ответ.
Ответ:
D(y): x ∈ (−3 ; 3) ∪ (3 ; +∞)
Примеры определения области определения функции
Разбор примера
Найти область определения функции:
y = 6√x +
5√1 + x
Для поиска области определения функций задаем себе
первый вопрос.
Есть ли знаменатель, в котором содержится « x »?
Ответ: в формуле функции
«y = 6√x +
5√1 + x»
нет дробей.
Задаем
второй вопрос.
Есть ли в функции корни четной степени?
Ответ: в функции есть корень шестой степени:
«6√x».
Степень корня — число «6». Число «6» — чётное,
поэтому подкоренное выражение корня «6√x»
должно быть больше или равно нулю.
x ≥ 0
В формуле функции «y = 6√x +
5√1 + x»
также есть корень пятой степени
«5√1 + x
».
Степень корня «5» — нечётное число, значит, никаких ограничений на подкоренное выражение
«1 + x»
не накладывается.
Получается, что единственное ограничение области определения функции
«y = 6√x +
5√1 + x»
— это ограничение подкоренного выражения
«6√x».
x ≥ 0
Нарисуем область определения функции на числовой оси и запишем ответ.
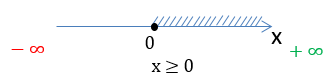
Ответ:
D(y): x ∈ [0 ; +∞)
Разбор примера
Найдите область определения функции:
Есть ли в функции знаменатель, в котором содержится « x »? В заданной функции подобных знаменателей два.
Выделим знаменатели с « x » красным цветом.
Запишем условие, что каждый из знаменателей не должен быть равен нулю.
| √x + 2 ≠ 0 | |
| x2 − 7x + 6 ≠ 0 |
Обозначим их номерами «1» и
«2» и решим каждое уравнение отдельно.
| √x + 2 ≠ 0 (1) | |
| x2 − 7x + 6 ≠ 0 (2) |
Решаем первое уравнение.
√x + 2 ≠ 0 (1)
Если значение квадратного корня
«√x + 2 ≠ 0» не должно быть равно нулю,
значит, подкоренное выражение
«x + 2 ≠ 0»
также не должно быть равно нулю.
√x + 2 ≠ 0 (1)
x + 2 ≠ 0
x ≠ −2
Теперь решим уравнение под номером «2», используя
формулу квадратного уравнения.
x1;2 =
x2 − 7x + 6 ≠ 0 (2)
x1;2 =
| −(−7) ± √(−7)2 − 4 · 1 · 6 |
| 2 · 1 |
x1;2 =
x1;2 =
x1;2 =
Запишем все полученные ответы в порядке возрастания вместе под знаком системы, чтобы их не забыть.
Знаменатели с « x »
мы проверили. Настала очередь
проверить
формулу функции
на
наличие корней четной степени .
В формуле функции
«f(x) =
+
»
есть два корня
«√x − 4» и
«√x + 2». Их подкоренные
выражения должны быть больше или равны нулю.
Решим полученную
систему неравенств.
Нарисуем полученные решения на числовой оси. Выберем заштрихованный промежуток, который есть на обеих числовых осях.
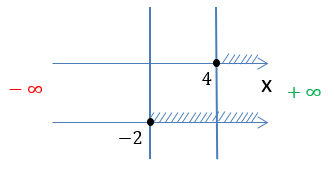
Выпишем результат решения системы неравенств.
x ≥ 4
Объединим в таблицу ниже полученные ответы по обеим
проверкам:
- проверка, что знаменатели
дробей
с « x »
не равны нулю; - проверка, что
подкоренные выражения корней четной степени должно быть больше или равны нулю.
| Условие проверки | Результат |
|
Результат проверки, что знаменатели дробей с « x » не равны нулю |
|
|
Результат проверки, что подкоренные выражения должно быть больше или равны нулю |
x ≥ 4 |
Нарисуем полученные результаты проверок на числовых осях, чтобы определить, какая заштрихованная область удовлетворяет
всем полученным условиям.
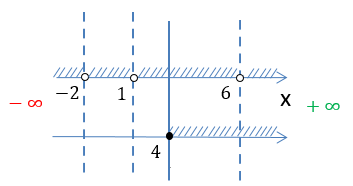
Запишем окончательный ответ для области определения функции
«f(x) =
+
»
с использованием математических символов.
Ответ:
D(y): x ∈ [4 ; 6) ∪ (6; +∞)
Ваши комментарии
Важно!

Чтобы оставить комментарий, вам нужно войти на наш сайт при помощи
«ВКонтакте».

Оставить комментарий:
17 декабря 2016 в 18:02
Татьяна Цыганова

Профиль
Благодарили: 0
Сообщений: 1

Татьяна Цыганова
Профиль
Благодарили: 0
Сообщений: 1
Найти ОДЗ функции у=?(р1+р2х+x2)
Я не могу понять за какое число воспринимать p1, p2
0
Спасибо
Ответить
17 декабря 2016 в 19:10
Ответ для Татьяна Цыганова
Евгений Фёдоров

Профиль
Благодарили: 0
Сообщений: 60

Евгений Фёдоров
Профиль
Благодарили: 0
Сообщений: 60
x2 + p2x + p1 ? 0.
0
Спасибо
Ответить
24 февраля 2016 в 20:29
Влад Алексеев

Профиль
Благодарили: 0
Сообщений: 1

Влад Алексеев
Профиль
Благодарили: 0
Сообщений: 1
Постройте график функции y=-
. Укажите область определения функции
0
Спасибо
Ответить
25 февраля 2016 в 8:10
Ответ для Влад Алексеев
Евгений Колосов

Профиль
Благодарили: 12
Сообщений: 197

Евгений Колосов
Профиль
Благодарили: 12
Сообщений: 197
Область определения функции: знаменатель не равен 0.
x+1?0
x?-1
Графиком является гипербола, смещеная влево относительно оси Y.
0
Спасибо
Ответить
5 февраля 2018 в 14:30
Ответ для Влад Алексеев
Кирилл Косован

Профиль
Благодарили: 0
Сообщений: 1

Кирилл Косован
Профиль
Благодарили: 0
Сообщений: 1
0
Спасибо
Ответить
11 февраля 2018 в 15:44
Ответ для Влад Алексеев
Татьяна Мирная

Профиль
Благодарили: 0
Сообщений: 1

Татьяна Мирная
Профиль
Благодарили: 0
Сообщений: 1
у=-
0
Спасибо
Ответить
7 октября 2015 в 21:21
Катерина Яроцкая

Профиль
Благодарили: 0
Сообщений: 1

Катерина Яроцкая
Профиль
Благодарили: 0
Сообщений: 1
Помогите найти область определения функции

0
Спасибо
Ответить
12 сентября 2016 в 15:59
Ответ для Катерина Яроцкая
Евгений Колосов

Профиль
Благодарили: 12
Сообщений: 197

Евгений Колосов
Профиль
Благодарили: 12
Сообщений: 197
К сожалению, картинка не отражается.
0
Спасибо
Ответить
Содержание
- сфера применения
- Смотреть что такое «сфера применения» в других словарях:
- Какой бывает сфера применения:
- Делаем Карту слов лучше вместе
- Ассоциации к слову «сфера»
- Ассоциации к слову «применение»
- Синонимы к словосочетанию «сфера применения»
- Предложения со словосочетанием «сфера применения»
- Значение слова «сфера»
- Значение слова «применение»
- Афоризмы русских писателей со словом «сфера»
- Отправить комментарий
- Дополнительно
- Значение слова «сфера»
- Значение слова «применение»
- Предложения со словосочетанием «сфера применения»
- сфера использования
- Смотреть что такое «сфера использования» в других словарях:
- Сферы общественной жизни
- Подсистемы общества
- Экономическая сфера общественной жизни
- Политическая сфера общественной жизни
- Социальная сфера общественной жизни
- Духовная сфера общественной жизни
- Таблица с примерами сфер общественной жизни
- Сфера Деятельности
- Смотреть что такое «Сфера Деятельности» в других словарях:
сфера применения
Русско-китайский финансово-экономическому словарь. — «Восток – Запад» . 2007 .
Смотреть что такое «сфера применения» в других словарях:
сфера применения роботов — robotų taikymo sritis statusas T sritis automatika atitikmenys: angl. application field of robots vok. Anwendungsbereich der Roboter, m rus. область применения роботов, f; сфера применения роботов, f pranc. domaine d emploi des robots, m … Automatikos terminų žodynas
область или сфера применения — — [А.С.Гольдберг. Англо русский энергетический словарь. 2006 г.] Тематики энергетика в целом EN application niche … Справочник технического переводчика
Ртуть: свойства, сфера применения, опасности для здоровья и экологии — Ртуть (Hg) – химический элемент II группы периодической системы Менделеева, атомный номер 80, атомная масса 200,59; серебристо белый тяжелый металл, жидкий при комнатной температуре. Ртуть – один из семи металлов, известных с… … Энциклопедия ньюсмейкеров
Сфера культуры — область применения культурной деятельности. Источник: РАСПОРЯЖЕНИЕ Минкультуры МО от 17.08.2007 N 447 Р ОБ УТВЕРЖДЕНИИ МЕТОДИЧЕСКИХ РЕКОМЕНДАЦИЙ ПО ФОРМИРОВАНИЮ ЦЕН НА ПЛАТНЫЕ УСЛУГИ, ОКАЗЫВАЕМЫЕ ГОСУДАРСТВЕННЫМИ И МУНИЦИПАЛЬНЫМИ УЧРЕЖДЕНИЯМИ… … Официальная терминология
Сфера обеспечения безопасности — область применения комплекса различных мер, сил и средств по выявлению и предупреждению угроз и создания системы защиты от них. Источник: Распоряжение Правительства Москвы от 16.04.2010 N 707 РП Об утверждении Концепции комплексной безопасности … Официальная терминология
сфера — сущ., ж., употр. сравн. часто Морфология: (нет) чего? сферы, чему? сфере, (вижу) что? сферу, чем? сферой, о чём? о сфере; мн. что? сферы, (нет) чего? сфер, чему? сферам, (вижу) что? сферы, чем? сферами, о чём? о сферах 1. Сферой называется шар… … Толковый словарь Дмитриева
Сфера — по [12] 1) шар; поверхность шара; геометрическое место точек, одинаково удаленных от одной определенной точки центра сферы; сфера небесная воображаемая шаровая поверхность произвольного радиуса, служащая для представления взаимного расположения и … Теоретические аспекты и основы экологической проблемы: толкователь слов и идеоматических выражений
сфера (чего) — ▲ совокупность ↑ связанный (с), что л. объект сфера чего совокупность связанных чем л. объектов; область принадлежности чему л. (# услуг). | в области чего (крупный специалист в этой области). область (# применения. # техники. относиться к… … Идеографический словарь русского языка
Области применения систем спутниковой навигации — Развитие рынка перевозок, в первую очередь, дорогих и опасных грузов объективно диктует необходимость в системах позиционирования, использующих спутниковую навигацию, радиосвязь и электронные карты. Первые системы такого рода были чрезвычайно… … Википедия
область применения роботов — robotų taikymo sritis statusas T sritis automatika atitikmenys: angl. application field of robots vok. Anwendungsbereich der Roboter, m rus. область применения роботов, f; сфера применения роботов, f pranc. domaine d emploi des robots, m … Automatikos terminų žodynas
Информационная сфера — представляет собой ЧЛЕН информации, информационной инфраструктуры, субъектов, осуществляющих сбор, формирование, распространение и использование информации, а также системы регулирования возникающих при этом общественных отношений.[1]… … Википедия
Источник
Какой бывает сфера применения:

Делаем Карту слов лучше вместе
 Привет! Меня зовут Лампобот, я компьютерная программа, которая помогает делать Карту слов. Я отлично умею считать, но пока плохо понимаю, как устроен ваш мир. Помоги мне разобраться!
Привет! Меня зовут Лампобот, я компьютерная программа, которая помогает делать Карту слов. Я отлично умею считать, но пока плохо понимаю, как устроен ваш мир. Помоги мне разобраться!
Спасибо! Я стал чуточку лучше понимать мир эмоций.
Вопрос: осрамиться — это что-то нейтральное, положительное или отрицательное?
Ассоциации к слову «сфера»
Ассоциации к слову «применение»
Синонимы к словосочетанию «сфера применения»
Предложения со словосочетанием «сфера применения»
- В современных условиях многие страны идут по пути расширения сферы применения унифицированных материально-правовых норм, но унификация не может охватывать все вопросы.
Значение слова «сфера»
СФЕ́РА , -ы, ж. 1. Шар или его внутренняя поверхность (о земном шаре, небесном своде). Земная сфера. (Малый академический словарь, МАС)
Значение слова «применение»
ПРИМЕНЕ́НИЕ , -я, ср. Действие по знач. глаг. применить—применять и примениться—применяться. Применение минеральных удобрений. (Малый академический словарь, МАС)
Афоризмы русских писателей со словом «сфера»
- Вся разница между умным и глупым в одном: первый всегда подумает и редко скажет, второй всегда скажет и никогда не подумает. У первого язык всегда в сфере мысли; у второго мысль вне сферы языка. У первого язык — секретарь мысли, у второго — ее сплетник и доносчик.
Отправить комментарий
Дополнительно
Значение слова «сфера»
СФЕ́РА , -ы, ж. 1. Шар или его внутренняя поверхность (о земном шаре, небесном своде). Земная сфера.
Значение слова «применение»
ПРИМЕНЕ́НИЕ , -я, ср. Действие по знач. глаг. применить—применять и примениться—применяться. Применение минеральных удобрений.
Предложения со словосочетанием «сфера применения»
В современных условиях многие страны идут по пути расширения сферы применения унифицированных материально-правовых норм, но унификация не может охватывать все вопросы.
Нам предстоит рассмотреть, как биткоин-технология и её различные ответвления могут реорганизовать общественные институты и найти новые сферы применения.
Но данная книга – не об отдельных странах, а о совокупности принципов, имеющих более широкую сферу применения.
Источник
сфера использования
Универсальный русско-немецкий словарь . Академик.ру . 2011 .
Смотреть что такое «сфера использования» в других словарях:
Сфера (космический аппарат) — Сфера (индекс ГУКОС 11Ф621) серия первых советских геодезических спутников, запускавшихся в период с 1968 по 1978 год. Предназначались для создания единой системы координат всей поверхности земного шара, установления геодезических… … Википедия
Сфера правового регулирования (правовое пространство) — отношения, которые уже урегулированы правом либо могут и должны быть им урегулированы. Близким и во многом сходным с понятием сферы правового регулирования в политической и публицистической лексике используется термин «правовое поле». Правовое… … Элементарные начала общей теории права
Сфера услуг — Сфера услуг часть экономики, которая включает в себя все виды коммерческих и некоммерческих услуг; сводная обобщающая категория, включающая воспроизводство разнообразных видов услуг, оказываемых предприятиями, организациями, а также… … Википедия
Сфера Вернона — Сфера Вернона шаровой термометр представляет собой полую, тонкостенную, металлическую (из латуни или алюминия) сферу диаметром 0,1 0,15 м. Наружная поверхность сферы зачернена так, что она поглощает ε ≈ 95 % теплового… … Википедия
СФЕРА УСЛУГ — сфера экономики, где производятся блага, полезный эффект которых проявляется в самом процессе их создания. Производство экономических (ограниченных) благ делится на две сферы сферу материального производства и С.у. В первой сфере потребление… … Юридическая энциклопедия
Сфера деятельности и функции Росприроднадзора — Официальное прошение об отставке замглавы Росприроднадзора Олега Митволя в Минприроды не поступало. Ранее стало известно, что прошение об отставке подал глава Росприроднадзора Сергей Сай, место которого может занять бывший первый вице губернатор… … Энциклопедия ньюсмейкеров
Сфера Дайсона — Оболочка Дайсона (англ. Dyson shell), вариант сферы Дайсона, с радиусом в 1 астрономическую единицу Сфера Дайсона … Википедия
сфера — сущ., ж., употр. сравн. часто Морфология: (нет) чего? сферы, чему? сфере, (вижу) что? сферу, чем? сферой, о чём? о сфере; мн. что? сферы, (нет) чего? сфер, чему? сферам, (вижу) что? сферы, чем? сферами, о чём? о сферах 1. Сферой называется шар… … Толковый словарь Дмитриева
Сферы использования контрольных таблиц (списков) — Основная статья: Контрольные таблицы (списки) … Википедия
Финансовая сфера — это область общественных отношений, складывающихся в процессе аккумуляции, распределения и использования государством денежных средств … Административно-процессуальное право: словарь терминов и понятий
Рынок труда — (Labor market) Рынок труда это сфера формирования спроса и предложения на рабочую силу Определение рынка труда, определение рабочей силы, структура рынка труда, субъекты рынка труда, конъюнктура рынка труда, сущность открытого и скрытого рынка… … Энциклопедия инвестора
Источник
Сферы общественной жизни

О чем эта статья:
6 класс, 8 класс, 10 класс
Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат (в правом нижнем углу экрана).
Подсистемы общества
Человеческое общество — это сложная система, в которой происходит огромное количество разнообразных процессов.
Для анализа сложноорганизованных систем есть специальное понятие «подсистема».
Подсистемы — это промежуточные комплексы, которые сложнее элементов, при этом менее сложные, чем сама система. Они образуют определенные группы общественных отношений.
По сути термины «сферы общественной жизни» и «подсистемы общества» равнозначны, их можно использовать для обозначения одного и того же.
Сферы жизни общества — это независимые, но в то же время взаимосвязанные области человеческой деятельности.
Выделяют четыре основные подсистемы или сферы общественной жизни: экономическая, политическая, социальная и духовная. Рассмотрим каждую из них.

Экономическая сфера общественной жизни
Экономическая сфера — это хозяйственная деятельность страны, общества, семьи и т. д.
Основные элементы экономической сферы:
- производство — создание материальных благ;
- распределение — разделение созданных благ между производителями, рынками, потребителями;
- обмен — торговля, бартер;
- потребление — использование произведенных продуктов.
Эта сфера дает возможность получить средства для организации всех остальных сфер общественной жизни, так как производство материальных благ — это один из основных факторов жизнедеятельности человека.
В экономическую сферу жизни общества входят: сельское хозяйство, промышленность, производство, рыночная и банковская системы и т. п.
Политическая сфера общественной жизни
Политическая сфера — это сфера деятельности людей, которая связана с проблемами реализации властных полномочий, безопасности общества, государственного устройства, судебной системы.
Основные части этой сферы: государство, политические партии и организации, законодательство.
Политическая сфера жизни общества обеспечивает мирную жизнь людей, регулирует их совместную деятельность, определяет направление развития.
Социальная сфера общественной жизни
Социальная сфера — это люди, социальные общности и группы, народы, классы и сословия.
У социальной сферы есть две формы:
- общество в целом, которое включает в себя территорию, национальности, демографические особенности, менталитет.
- совокупность организаций и учреждений, которые отвечают за благосостояние населения.
Духовная сфера общественной жизни
Духовная сфера — это сфера, которая отражает духовно-нравственную жизнь общества. Ее элементы: культура, наука, религия, мораль, идеология, искусство.
Основная функция духовной сферы — производство и передача новых знаний и ценностей. Благодаря определению ценностей можно понять уровень развития общественного сознания.
При этом общественное сознание — это совокупность действующих факторов и процессов, которые определяют мировоззрение определенной части населения страны, города, социальной группы.
Поэтому общественное сознание — это основной элемент духовной сферы жизни общества. Общественное сознание можно назвать продуктом культуры. Оно включает в себя философскую, политическую, экономическую, нравственную, эстетическую, правовую, религиозную формы сознания, в каждой из которых есть элементы как идеологии, так и психологии.
Таблица с примерами сфер общественной жизни
Отношения, в которые вступают люди в рамках этой сферы
Отношения в процессе производства, обмена и потребления.
Отношения по поводу права собственности.
Отношения в процессе предпринимательской деятельности.
Взаимосвязь государства и экономики.
Заводы, фирмы, банки, биржи и др.
Отношения по поводу власти и управления обществом.
Отношения человека и государства.
Отношения между большими группами населения по вопросам управления, национальных отношений и пр.
формы государственной власти;
Парламент, правительство, партии, общественные организации и др.
Взаимоотношения социальных групп между собой (классов, страт, профессиональных и социально-демографических групп, национальных общностей). Порядок и принципы этих взаимоотношений.
социальная мобильность и социальные лифты;
национальные отношения; семья.
Системы здравоохранения, социального обеспечения, коммунальные службы и др.
Отношения людей, в основе которых лежат духовные ценности (культура, религия, образование, наука, мировоззрение и пр.).
Отношения в процессе создания, распространения и усвоения этих ценностей.
Источник
Сфера Деятельности
Словарь бизнес-терминов. Академик.ру . 2001 .
Смотреть что такое «Сфера Деятельности» в других словарях:
СФЕРА ДЕЯТЕЛЬНОСТИ — вид работ и услуг, предусмотренных уставом организации, предприятия. Перечень видов выполняемых работ и услуг может включать в себя различные направления деятельности, не запрещенные законодательством … Большой бухгалтерский словарь
сфера деятельности — круг деятельности … Справочный коммерческий словарь
СФЕРА ДЕЯТЕЛЬНОСТИ — вид работ и услуг, предусмотренных уставом организации, предприятия. Перечень видов выполняемых работ и услуг может включать в себя различные направления деятельности, не запрещенные законодательством … Большой экономический словарь
СФЕРА ДЕЯТЕЛЬНОСТИ — область действия, пределы распространения профессиональной деятельности … Словарь по профориентации и психологической поддержке
Сфера деятельности и функции Росприроднадзора — Официальное прошение об отставке замглавы Росприроднадзора Олега Митволя в Минприроды не поступало. Ранее стало известно, что прошение об отставке подал глава Росприроднадзора Сергей Сай, место которого может занять бывший первый вице губернатор… … Энциклопедия ньюсмейкеров
Сфера деятельности/SCOPE — в частности, определенные области деятельности, для которых разрабатывается план восстановления … Толковый словарь по информационному обществу и новой экономике
НАУКА (сфера деятельности) — НАУКА, сфера человеческой деятельности, функция которой выработка и теоретическая систематизация объективных знаний о действительности; одна из форм общественного сознания; включает как деятельность по получению нового знания, так и ее результат… … Энциклопедический словарь
pегламентированная сфера деятельности — reglamentuojama veiklos sritis statusas Aprobuotas sritis Atitikties vertinimas ir akreditacija apibrėžtis Teisės aktų nustatytas privalomas produktų, procesų, paslaugų, atitikties įvertinimo įstaigų ar fizinių asmenų kvalifikacijos atlikti tam… … Lithuanian dictionary (lietuvių žodynas)
нерегламентированная сфера деятельности — nereglamentuojama veiklos sritis statusas Aprobuotas sritis Atitikties vertinimas ir akreditacija apibrėžtis Teisės aktais nenustatytas privalomas ir tiekėjo iniciatyva atliekamas produktų, procesų, paslaugų, vadybos sistemų, atitikties… … Lithuanian dictionary (lietuvių žodynas)
Андрей Козлов и сфера деятельности — К материалам об убийстве первого зампреда Центробанка Андрея Козлова Родился 6 января 1965 г. в г. Москве. В 1983 1985 гг. прошел срочную воинскую службу в ВС СССР. В 1989 г. окончил факультет международных экономических отношений Московского… … Энциклопедия ньюсмейкеров
Источник
Область определения функции
Данный калькулятор позволит найти область определения функции онлайн.
Область определения функции y=f(x) – это множество всех значений аргумента x, на котором задана функция. Другими словами, это все x, для которых могут существовать значения y. На графике областью определения функции является промежуток, на котором есть график функции.
Область определения функции f(x), как правило, обозначается как D(f). Принадлежность к определенному множеству обозначается символом ∈, а X – область определения функции. Таким образом, формула x∈X означает, что множество всех значений x принадлежит к области определения функции f(x).
Приведем примеры определения основных элементарных функций. Областью определения постоянной функции y=f(x)=C является множество всех действительных чисел. Когда речь идет о степенной функции y=f(x)=xa, область определения зависит от показателя степени данной функции. При нахождении области определения функции y=f(x)= √(n&x) (корень n-ой степени) следует обращать внимание на четность или нечетность n.
Областью определения логарифмической функции являются все положительные действительные числа, и она не зависит от основания логарифма. Областью определения показательной функции, также как и у постоянной функции, является множество всех действительных чисел.
Областью определения сложных функций y=f1(f2(x)) является пересечение двух множеств: x∈D(f2) и множества всех x, для которых f2(x) ∈ D(f1). Следовательно, для того чтобы найти область определения сложной функции, необходимо решить систему неравенства.
Преимуществом онлайн калькулятора является то, что Вам нет необходимости знать и понимать, как находить область определения функции. Чтобы получить ответ, укажите функцию, для которой Вы хотите найти область определения. Основные примеры ввода функций и переменных для данного калькулятора указаны ниже.
Примеры функций: sqrt(16-ln(x^2))/sin(x)) или (5x^7+4x^6-3)/((3+2x-x^2)x^4)
×
Пожалуйста напишите с чем связна такая низкая оценка:
×
Для установки калькулятора на iPhone – просто добавьте страницу
«На главный экран»

Для установки калькулятора на Android – просто добавьте страницу
«На главный экран»

План внедрения научной организации труда включает мероприятия, обеспечивающие как повышение использования трудовых и материальных ресурсов, так и создание наиболее благоприятных условий труда. Сюда относятся совершенствование форм разделения и кооперации труда работников, расширение зон обслуживания по основным и вспомогательным операциям, расширение сферы применения коллективных форм организации труда, более широкое совмещение профессий и др. совершенствование организации рабочих мест, участков, цехов на основе разработки и внедрения типовых проектов организации труда, комплексная организация труда рабочих, ИТР и служащих расширение сферы и совершенствование нормирования труда рабочих, ИТР, служащих на базе внедрения прогрессивных отраслевых и межотраслевых норм, повышения качества норм изучение и широкое распространение передовых методов труда улучшение условий труда и отдыха работников и их санитарно-бытового обслуживания. [c.130]
В целях расширения сферы применения натуральных (Показателей иногда используют условно-натуральные показатели объема продукции, в частности, в отраслях топливной промышленности, где выпускают продукцию одного назначения (обеспечить потребности народного хозяйства в различных видах топлива), но при различных технологических процессах и имеющих различную народнохозяйственную ценность. Различные виды топлива пересчитывают в условные тонны по их теплотворной способности, при этом за единицу перерасчета принято топливо с теплотворной способностью 22,3 кДж/кг. Стоимостные показатели. Для соизмерения результатов деятельности по выпуску продукции двух или нескольких отраслей или производства продукции нескольких видов используют стоимостной показатель объема промышленной продукции, имеющий следующие разновидности. [c.46]
В настоящее время для оценки основных фондов в промышленности применяют натуральные и стоимостные показатели. Натуральная форма оценки определяется в значительной мере особенностями технологического процесса и составом основных фондов каждой отрасли промышленности. В натуральных показателях, как правило, учитываются только наиболее важные виды оборудования. В нефтегазодобыче, например, это эксплуатационный фонд скважин, парк буровых установок, т. е. те виды оборудования, которые предназначены непосредственно для выпуска целевой продукции и определяют производственную мощность предприятия. Поэтому натуральные показатели имеют ограниченную сферу применения, ибо в них можно оценивать основные фонды одного вида. [c.158]
В зависимости от сферы применения различают отраслевые и межотраслевые нормативы, а но территориально-административному признаку -…..общесоюзные, республиканские, районные и местные. [c.144]
Следует добавить, что бурное развитие электроники дало такой толчок распространению информации, в том числе и в международном общении, что любые данные мгновенно становятся достоянием всего мира. Поэтому во всех странах фирмы действуют одинаково они ищут новинки, которые могут дать какие-либо преимущества, пусть в очень узкой сфере применения, разрабатывают их и запускают в производство. Это дополнительно обостряет конкуренцию. [c.207]
Без сомнения, для обоих путей развития технологий необходим творческий подход. Но сферы применения технологий могут расти по-разному в первом случае вширь, во втором — вглубь. Оба пути, при всех различиях, предполагают оригинальность мышления. Оба пути нехожены, рискованны в коммерческом отношении и требуют смелости. Они тесно связаны друг с другом технологии будущего , возникающие в общем русле технического прогресса и раздвигающие его рубежи, создают широкую материальную базу для технологий культуры будущего. [c.250]
Научно-техническая революция нашего времени отличается от всех прежних технических переворотов необычно широкой сферой применения нововведений. Особое значение для модернизации производственных и управленческих процессов имеют успехи в микроэлектронике. Благодаря большим усилиям японского бизнеса, направленным на внедрение достижений микроэлектроники в управление, японская экономика оказалась подготовленной к созданию на всей территории страны компьютеризированной коммуникационной сети, включающей в себя различные технологии по приему, передаче и воспроизведению речевой и изобразительной информации, позволяющей наладить принципиально новую систему управления. Реализация программы по развертыванию указанной сети началась в 1984 г. [c.105]
Из нефтепродуктов наиболее широкую сферу применения имеют газойль и дизельное топливо. В потреблении моторного горючего автомобилями на их долю приходится 31%, сельскохозяйственными тракторами — 77 %. Полностью на дизельном топливе работают локомотивы и самоходные речные баржи. Уровень использования автомобильного газойля в отдельных западноевропейских странах обусловлен разницей в размере налогов. На долю автомобильного газойля в общем потреблении автомобильного горючего приходится в ФРГ — 34, в Италии — 38, в Португалии — 50, в Англии и Норвегии — по 28, во Франции и в Швеции — по 25%. [c.180]
Таким образом, в комплексной автоматизированной системе нормативов можно выделить следующие основные блоки норм расхода сырья и материалов норм расхода топливно-энергетических ресурсов нормативов использования оборудования и определения потребности в нем нормативов продолжительности освоения производственных мощностей нормативов капитального строительства норм затрат труда и заработной платы нормативов финансовых ресурсов нормативов непроизводственной сферы нормативов качества. Каждый блок формируется из отдельных групп норм с более дробной классификацией их по характеру использования и сфере применения. [c.389]
В зависимости от сферы применения различают два вида краткосрочного кредита один участвует в организации движения оборотных средств, другой используется в воспроизводстве основных фондов. Последний предназначен для кредитования основных фондов, на внедрение новой техники, на расширение производства товаров народного потребления. [c.169]
При расчете эффекта следует также учитывать, что его величина зависит от времени и сферы применения. Так, по мере освоения выпуска снижаются затраты на изготовление нового электротехнического изделия и в то же время происходит насыщение потребителей данным изделием, что снижает потребность в нем и соответственно величину эффекта. Чем больше времени работает электротехническое изделие у потребителя, тем большими оказываются затраты на поддержание его в работоспособном состоянии, материальный ущерб от выхода электроизделий из строя. В этой связи формула расчета эффекта должна представляться в виде тройной суммы по годам выпуска электроизделий, годам службы у потребителя, областям их применения. [c.246]
Создание изделий электротехники можно определить как сложный многогранный процесс, сочетающий творческий поиск, теоретический анализ, эксперимент, организацию и управление. На этот процесс оказывают влияние такие факторы, как степень новизны электротехнической системы, существующая организация разработки, широта сферы применения, квалификация разработчиков, характер взаимосвязей разработчиков с производственниками, потребителями и заказчиками и др. [c.254]
К концу 1940 г. общее число нефтебаз в стране составило 1688. В 1940 г. общая поставка нефтепродуктов, отражающая внутреннее потребление, увеличилась по сравнению с 1937 г. в 1,25 раза, с 1928 г. — более чем в 3 раза, а с 1913 г. – в 4,29 раза. При снижении потребления нефтяного топлива с 76% в 1913 г. до 45% в 1940 г. удельный вес светлого горючего повысился до 45,1% против достигнутых 19% в 1927 г. и 29,7% в 1932 г. потребление горючего в 1940 г. в абсолютном значении в сравнении с 1913 г. увеличилось в 9,6 раза. Расширение сферы применения нефтепродуктов привело к увеличению их перевозок по железной дороге. Развивался и совершенствовался трубопроводный транспорт, а также нефтеналивной речной и морской флот. Стали применять речные нефтеналивные баржи грузоподъемностью 10—12 тыс. т. [c.26]
В работе дан анализ применения графических методов при планировании и управлении в нефтяной промышленности. Показаны преимущества и недостатки линейных графиков и сферы применения сетевых моделей. Изложена краткая история развития методов и систем СПУ. Обобщен опыт применения СПУ па предприятиях нефтяной промышленности и даны методические рекомендации по расширению его применения, учитывающие специфические условия и характер работ. [c.2]
Каждый из методов и их разновидностей имеет преимущественную сферу применения, где он наиболее эффективен и широко распространен. Так измерительные и физические методы наиболее широко распространены в машиностроении и металлообработке, деревообработке, строительстве, промышленности строительных материалов, легкой промышленности. [c.35]
Стандарты классифицируются по степени их значимости, сфере применения, по объекту стандартизации, по содержанию и назначению. [c.190]
Принимая (с определенным допущением) цену буровой установки за величину приведенных затрат (себестоимость изготовления плюс нормативная прибыль) на основе формулы (7) для рассматриваемой (t -й) сферы применения новой техники годовой эффект можно определить [c.77]
Поэтому натуральные показатели имеют ограниченную сферу применения, ибо в них можно оценивать основные фонды одного вида. [c.175]
Естественно, что натуральные показатели имеют ограниченную сферу применения, ибо в них можно оценивать производственные возможности основных фондов одного вида, одного назначения. При необходимости оценить всю совокупность основных фондов, имеющихся в распоряжении одного предприятия или промышленности IB целом, проследить их динамику, прибегают к стоимостной оценке. [c.173]
Наличие нормативно-исследовательских станций в каждом нефтедобывающем районе, соответствующей отраслевой нормативной базы и т. д. создает предпосылки для организации такой работы в целом по отрасли. Поэтому дальнейшее расширение сферы применения нормативов по труду должно стать одним из главных направлений улучшения методики и практики планирования производительности труда. [c.135]
I Для расширения сферы применения данного метода плани-/ рования производительности труда следует организовать на всех / предприятиях точный учет влияния каждого фактора. [c.139]
Показатели снижения капитальных Вложений и себестоимости Сравнительная В сфере применения новой техники [c.109]
Косвенный метод — это экономическое стимулирование производственно-хозяйственной деятельности, установление системы экономических нормативов, эффективного использования системы материального стимулирования, кредитования и финансирования, разработка экономически обоснованных цен. Главный принцип хозяйственного расчета — соизмерение затрат с результатами производства, т. е. возмещение производственных расходов собственными доходами и обеспечение рентабельности производства. Сфера применения хозрасчета постоянно расширяется. Он не только внедряется в верхнее и среднее звенья управления, но и углубляется внутри производственного объединения и предприятия, в частности, на хозрасчет переходят основные, вспомогательные производства и цехи, сквозные бригады. [c.153]
На рис. В.1 представлена функциональная схема системы подготовки производства новых видов продукции в машиностроении. Как видно из схемы, подготовка производства в современных условиях предполагает необходимость проведения значительного объема работ научного характера по конструированию изделий, технологическому и организационному проектированию, перестройке производственного процесса на выпуск новой продукции, освоению новой техники в сфере применения. Поэтому подготовка производства должна рассматриваться не только как техническая, но и как комплексная. [c.11]
Успешно решить задачу создания новой техники можно лишь на основе комплексного подхода к осуществлению намеченной цели. Работы по созданию новых типов машин должны быть организованы по единому плану, охватывающему весь комплекс процессов от исследований до основания нового изделия в производстве и в сфере применения. Необходимо учитывать на каждом этапе разнородные требования, состояние и уровень производства, возможность получения новых результатов. Принцип комплексности требует также [c.20]
Что же касается полного эффекта от внедрения АСПР, то он, помимо сказанного, выражается также в значительном повышении точности и оперативности плановых расчетов, расширении сферы применения нормативных методов при определении потребности в материальных, трудовых и финансовых ресурсах, повышении качества разрабатываемых балансов и комплексности плановых решений. [c.217]
В нефтегазодобывающей промышленности и бурении скважин косвенная С. ф. з. п. имеет относительно широкую сферу применения. Например, по косвенной С. ф. з. п. может оплачиваться труд слесаря по ремонту бурового оборудования, входящего в состав буровой бригады, работа которой оплачивается по прямой С. ф. з. п. [c.57]
Современная жизнедеятельность людей теснейшим образом связана с потреблением материальных ресурсов. В зависимости от сферы применения их можно разделить на три группы. [c.39]
В ПБУ 10/99 также не говорится о соотношении понятий расходы-затраты , что, безусловно, является существенным недостатком стандарта и не позволяет разграничить сферу применения данных категорий. Из текста ПБУ 10/99 следует, что термины затраты и расходы идентичны. Однако мы не можем согласиться с такой позицией. Согласно МСФО расходы могут быть признаны в отчете о прибылях и убытках на основании непосредственной связи с полученными доходами (принцип соответствия доходов и расходов). В результате такого подхода доходы у организации возникают только после перехода права собственности, а следовательно, лишь в этом случае произведенные затраты, отраженные ранее на счетах 20 Основное производство , 43 Готовая продукция , 45 Товары отгруженные , признаются расходами. В соответствии с методологией учета произведенные за отчетный период затраты сначала накапливаются на счетах учета затрат в разрезе экономических элементов и калькуляционных статей, затем часть из них остается на счете 20 в виде незавершенного производства, другая списывается на счет 43 в качестве фактической себестоимости готовой продукции, а третья аккумулируется на счете 45 в том случае, если договором предусмотрен особый порядок перехода права собственности. При отсутствии реализации продукции произведенные затраты расходами не являются, а представляют собой активы, которые отражаются в соответствующих строках баланса. Понятие расходы и затраты будут тождественны лишь в случае, если организация применяет метод директ-костинг, классифицирует общехозяйственные расходы как периодические и ежемесячно списывает их на уменьшение выручки от обычных видов деятельности (дебет 90 Продажи кредит 26 Общехозяйственные расходы ). В данном случае при отсутствии кредитовых оборотов по счету 90 затраты, отраженные на счете 26. [c.175]
Для оценки эффективности новых методов необходимо выяснить возможные сферы применения каждого из них на различных стадиях разработки. Вероятно, что даже из числа наиболее полно изученных методов имеются такие, которые эффективны в узком диапазоне природных геологических условий. [c.7]
Разработка современной электронной аппаратуры на высоком научно-техническом уровне, выбор из ряда возможных конструкций оптимального варианта, обеспечивающего получение максимального эффекта при минимальных затратах, а также дальнейшее расширение сферы применения изделий электронной техники т повышение эффективности их использования в значительной степени зависят от качества организационно-экономической подготовки инженеров. [c.3]
В случае применения новой блочной продукции в различных сферах определяется несколько уровней лимитной цены, отражающих эффективность новых БКУ для конкретных сфер применения. [c.163]
Удостоверение, свидетельство на право пользования, владения чем-либо или совершение каких-либо операций. В соответствии со сферами применения различают следующие виды С. В страховом деле под С. понимается документ, содержащий условия договора страхования (страховой С.). Такой С. заменяет обычно страховой полис. С. называют также документ, удостоверяющий качество товара. Документ о качестве товара выдается государственными инспекциями или другими уполномоченными на то организациями. Аудиторский С. удостоверяет правильность опубликованного баланса фирмы и выдается по результатам работы аудита. На Западе имеется С., удостоверяющий долю владельца фирмы в ее активах или доходах. Такой С. может испол, зоваться, например, при передаче капитала в доверительное управление (управляющему и др). Расчетный С. используется обычно в периоды финансовых кризисов и представляет собой свидетельство задолженности одного члена клиринговой палаты перед другим. Закладной С. представляет собой разновидность облигации, которая обеспечивается закладными. С. участия – обязательство банка или правительственных агентств о предоставлении возобновляемого кредита акционерный С. удостоверяет права его владельца на часть капитала компании транзитный С. представляет собой заявку на вывоз товара с промежуточной станции с оплатой перевозки по сквозному тарифу акционерный доверительный С. используется при передаче акций в доверительное управление. [c.331]
Оба способа имеют свои достоинства и недостатки, свою сферу применения. В целом они не исключают, а дополняют друг друга. В работах первого направления оценивают конечный результат воздействия системы управления на итоговые показатели системы производства, частью которой является управление. В связи с этим эффективность управления и методы ее оценки здесь предопределяются методами оценки эффективности производства. Будучи направляющим, организующим и побудительным фактором развития производства, управление реализует общехозяйственный принцип соизмерения затрат и результатов, достижения в интересах общества наибольших результатов при наименьших штратах. [c.365]
Поскольку устанавливаемые отраслям плановые задания могут включаться в план только при наличии соответствующего ресурсного обеспечения, выполняется проверка их обеспечения на основе балансовых методов. Это достигается с помощью построения системы материальных, трудовых и финансовых балансов отрасли. Поэтому балансовый метод используется в планировании как способ увеличения обоснованности плановых заданий. Они разрабатываются Госпланом СССР, Госснабом СССР, отраслевыми министерствами, в том числе Минэлектротехпромом. По охвату материальных ресурсов балансы подразделяются на однопродук-товые и многопродуктовые, по сферам применения — на отраслевые и многоотраслевые, по времени — на годовые и пятилетние. [c.72]
Таким образом, в настоящее время, учитывая большую разносор-тность нефтей и разнообразие климатических условий в местах добычи нефти, в соответствии с современным уровнем насосостроения можно говорить о сфере применения центробежных и винтовых негерметичных насосов. [c.62]
Возникающие сегодня новые стандарты оборудования, программного обеспечения и средств связи должны заново сформировать модели поведения пользователя на работе и в быту. Не пройдет и десяти лет, как для большинства людей ПК станет незаменимым атрибутом домашней и рабочей обстановки, а электронная почта и связь через Интернет — обычным делом, они будут носить с собой цифровые устройства, хранящие их личную и деловую информацию. Появятся новые потребительские устройства, которые будут обрабатывать практически любой вид информации — текст, числа, голос, фотографии, видеозаписи — в цифровом формате. Когда я говорю веб-стиль жизни и веб-стиль работы , я имею в виду именно поведение людей, пользующихся возможностями Сети в офисе и дома. Сегодня схема доступа к информации выглядит так человек сидит за своим письменным столом, а связь с Интернетом осуществляется посредством материального кабеля. Но через некоторое время переносные цифровые устройства будут сопровождать нас везде, обеспечивая нам постоянный контакт с другими цифровыми устройствами и с другими людьми. Счетчики электроэнергии и расхода воды, системы сигнализации, автомобили и прочие материальные предметы нашего повседневного быта будут готовы в любой момент отчитаться о своем состоянии через Интернет. Все упомянутые сферы применения электронной информации подходят сегодня к точке перегиба — моменту, когда перемены в характере их использования потребителями станут стремительными и массовыми. В совокупности все эти изменения приведут к радикальному преобразованию как мира бизнеса, так и нашей повседневной жизли. [c.15]
Как только в 1946 году была построена первая в мире универсальная ЭВМ ЕМ1АС, компьютеры быстро доказали свое превосходство над людьми в скорости и точности вычислений во множестве сфер применения, справляясь как с управлением записями о клиентах крупнейших учреждений, так и с автоматизацией практически любых технических процессов, которые могут быть разложены на дискретные, многократно повторяющиеся шаги. Однако высшие сферы были компьютерам недоступны. Они помогали людям, но эту помощь трудно было назвать интеллектуальной. Для того чтобы понять физику процессов и разработать подробные программы вычисления траекторий артиллерийских снарядов или баллистических ракет, требуется человеческий мозг — и лишь затем для мгновенного выполнения этих вычислений в дело вступает гениальный тупица — компьютер. [c.33]
Большинство этих показателей, кроме трудоемкости добычи нефти, широко применяют для проведения различных технико-экономических расчетов. Несмотря на то что понятие трудоемкость добычи нефти широко используют в нефтяной промышленности, содержание, методика измерения и сфера применения его не определены. Этот показатель, широко применяемый в промышленности США, ГДР, Венгрии, Польши и ряде отраслей промышленности СССР (машиностроение, промышленность стройматериалов, угольная, мебельная, рыбная промышленность, геология, добыча торфа, сланца и т. д.), наиболее полно отвечает всем требованиям к показателям производительности труда. При определении трудоемкости обеспечивается полная соизмеримость затрат и результатов труда, сопоставимость между НГДУ, исключается влияние материалоемкости и рентабельности продукции, создаются условия для учета влияния природных факторов, определения участия отдельных групп работников в общих затратах труда, выявления резервов снижения затрат труда по отдельным технологическим операциям, цехам, НГДУ. [c.116]
Внеш ние (общеобъектные) функции отражают функциональные отношения между объектом (или его составляющими) и сферой применения. Среди них различают главные и второстепенные функции. [c.85]
