Как найти шаг если есть дисперсия - Сайт, где вы сможете решить свои вопросы

Интервальный вариационный ряд и его характеристики

Построение интервального вариационного ряда по данным эксперимента
Гистограмма и полигон относительных частот, кумулята и эмпирическая функция распределения
Выборочная средняя, мода и медиана. Симметрия ряда
Выборочная дисперсия и СКО
Исправленная выборочная дисперсия, стандартное отклонение выборки и коэффициент вариации
Алгоритм исследования интервального вариационного ряда
Примеры

п.1. Построение интервального вариационного ряда по данным эксперимента

Интервальный вариационный ряд – это ряд распределения, в котором однородные группы составлены по признаку, меняющемуся непрерывно или принимающему слишком много значений.

Общий вид интервального вариационного ряда

Интервалы, (left.left[a_{i-1},a_iright.right))	(left.left[a_{0},a_1right.right))	(left.left[a_{1},a_2right.right))	…	(left.left[a_{k-1},a_kright.right))
Частоты, (f_i)	(f_1)	(f_2)	…	(f_k)

Здесь k – число интервалов, на которые разбивается ряд.

Размах вариации – это длина интервала, в пределах которой изменяется исследуемый признак: $$ F=x_{max}-x_{min} $$

Правило Стерджеса
Эмпирическое правило определения оптимального количества интервалов k, на которые следует разбить ряд из N чисел: $$ k=1+lfloorlog_2 Nrfloor $$ или, через десятичный логарифм: $$ k=1+lfloor 3,322cdotlg Nrfloor $$

Скобка (lfloor rfloor) означает целую часть (округление вниз до целого числа).

Шаг интервального ряда – это отношение размаха вариации к количеству интервалов, округленное вверх до определенной точности: $$ h=leftlceilfrac Rkrightrceil $$

Скобка (lceil rceil) означает округление вверх, в данном случае не обязательно до целого числа.

Алгоритм построения интервального ряда
На входе: все значения признака (left{x_jright}, j=overline{1,N})
Шаг 1. Найти размах вариации (R=x_{max}-x_{min})
Шаг 2. Найти оптимальное количество интервалов (k=1+lfloorlog_2 Nrfloor)
Шаг 3. Найти шаг интервального ряда (h=leftlceilfrac{R}{k}rightrceil)
Шаг 4. Найти узлы ряда: $$ a_0=x_{min}, a_i=1_0+ih, i=overline{1,k} $$ Шаг 5. Найти частоты (f_i) – число попаданий значений признака в каждый из интервалов (left.left[a_{i-1},a_iright.right)).
На выходе: интервальный ряд с интервалами (left.left[a_{i-1},a_iright.right)) и частотами (f_i, i=overline{1,k})

Заметим, что поскольку шаг h находится с округлением вверх, последний узел (a_kgeq x_{max}).

Например:
Проведено 100 измерений роста учеников старших классов.
Минимальный рост составляет 142 см, максимальный – 197 см.
Найдем узлы для построения соответствующего интервального ряда.
По условию: (N=100, x_{min}=142 см, x_{max}=197 см).
Размах вариации: (R=197-142=55) (см)
Оптимальное число интервалов: (k=1+lfloor 3,322cdotlg ⁡100rfloor=1+lfloor 6,644rfloor=1+6=7)
Шаг интервального ряда: (h=lceilfrac{55}{5}rceil=lceil 7,85rceil=8) (см)
Получаем узлы ряда: $$ a_0=x_{min}=142, a_i=142+icdot 8, i=overline{1,7} $$

(left.left[a_{i-1},a_iright.right)) cм

(left.left[142;150right.right))

(left.left[150;158right.right))

(left.left[158;166right.right))

(left.left[166;174right.right))

(left.left[174;182right.right))

(left.left[182;190right.right))

(left[190;198right])

п.2. Гистограмма и полигон относительных частот, кумулята и эмпирическая функция распределения

Относительная частота интервала (left.left[a_{i-1},a_iright.right)) – это отношение частоты (f_i) к общему количеству исходов: $$ w_i=frac{f_i}{N}, i=overline{1,k} $$

Гистограмма относительных частот интервального ряда – это фигура, состоящая из прямоугольников, ширина которых равна шагу ряда, а высота – относительным частотам каждого из интервалов.
Площадь гистограммы равна 1 (с точностью до округлений), и она является эмпирическим законом распределения исследуемого признака.

Полигон относительных частот интервального ряда – это ломаная, соединяющая точки ((x_i,w_i)), где (x_i) – середины интервалов: (x_i=frac{a_{i-1}+a_i}{2}, i=overline{1,k}).

Накопленные относительные частоты – это суммы: $$ S_1=w_1, S_i=S_{i-1}+w_i, i=overline{2,k} $$ Ступенчатая кривая (F(x)), состоящая из прямоугольников, ширина которых равна шагу ряда, а высота – накопленным относительным частотам, является эмпирической функцией распределения исследуемого признака.
Кумулята – это ломаная, которая соединяет точки ((x_i,S_i)), где (x_i) – середины интервалов.

Например:
Продолжим анализ распределения учеников по росту.
Выше мы уже нашли узлы интервалов. Пусть, после распределения всех 100 измерений по этим интервалам, мы получили следующий интервальный ряд:

i	1	2	3	4	5	6	7
(left.left[a_{i-1},a_iright.right)) cм	(left.left[142;150right.right))	(left.left[150;158right.right))	(left.left[158;166right.right))	(left.left[166;174right.right))	(left.left[174;182right.right))	(left.left[182;190right.right))	(left[190;198right])
(f_i)	4	7	11	34	33	8	3

Найдем середины интервалов, относительные частоты и накопленные относительные частоты:

(x_i)	146	154	162	170	178	186	194
(w_i)	0,04	0,07	0,11	0,34	0,33	0,08	0,03
(S_i)	0,04	0,11	0,22	0,56	0,89	0,97	1

Построим гистограмму и полигон:

Построим кумуляту и эмпирическую функцию распределения:

Эмпирическая функция распределения (относительно середин интервалов): $$ F(x)= begin{cases} 0, xleq 146\ 0,04, 146lt xleq 154\ 0,11, 154lt xleq 162\ 0,22, 162lt xleq 170\ 0,56, 170lt xleq 178\ 0,89, 178lt xleq 186\ 0,97, 186lt xleq 194\ 1, xgt 194 end{cases} $$

п.3. Выборочная средняя, мода и медиана. Симметрия ряда

Выборочная средняя интервального вариационного ряда определяется как средняя взвешенная по частотам: $$ X_{cp}=frac{x_1f_1+x_2f_2+…+x_kf_k}{N}=frac1Nsum_{i=1}^k x_if_i $$ где (x_i) – середины интервалов: (x_i=frac{a_{i-1}+a_i}{2}, i=overline{1,k}).
Или, через относительные частоты: $$ X_{cp}=sum_{i=1}^k x_iw_i $$

Модальным интервалом называют интервал с максимальной частотой: $$ f_m=max f_i $$ Мода интервального вариационного ряда определяется по формуле: $$ M_o=x_o+frac{f_m-f_{m-1}}{(f_m-f_{m-1})+(f_m+f_{m+1})}h $$ где
(h) – шаг интервального ряда;
(x_o) – нижняя граница модального интервала;
(f_m,f_{m-1},f_{m+1}) – соответственно, частоты модального интервала, интервала слева от модального и интервала справа.

Медианным интервалом называют первый интервал слева, на котором кумулята превысила значение 0,5. Медиана интервального вариационного ряда определяется по формуле: $$ M_e=x_o+frac{0,5-S_{me-1}}{w_{me}}h $$ где
(h) – шаг интервального ряда;
(x_o) – нижняя граница медианного интервала;
(S_{me-1}) накопленная относительная частота для интервала слева от медианного;
(w_{me}) относительная частота медианного интервала.

Расположение выборочной средней, моды и медианы в зависимости от симметрии ряда аналогично их расположению в дискретном ряду (см. §65 данного справочника).

Например:
Для распределения учеников по росту получаем:

(x_i)	146	154	162	170	178	186	194	∑
(w_i)	0,04	0,07	0,11	0,34	0,33	0,08	0,03	1
(x_iw_i)	5,84	10,78	17,82	57,80	58,74	14,88	5,82	171,68

$$ X_{cp}=sum_{i=1}^k x_iw_i=171,68approx 171,7 text{(см)} $$ На гистограмме (или полигоне) относительных частот максимальная частота приходится на 4й интервал [166;174). Это модальный интервал.
Данные для расчета моды: begin{gather*} x_o=166, f_m=34, f_{m-1}=11, f_{m+1}=33, h=8\ M_o=x_o+frac{f_m-f_{m-1}}{(f_m-f_{m-1})+(f_m+f_{m+1})}h=\ =166+frac{34-11}{(34-11)+(34-33)}cdot 8approx 173,7 text{(см)} end{gather*} На кумуляте значение 0,5 пересекается на 4м интервале. Это – медианный интервал.
Данные для расчета медианы: begin{gather*} x_o=166, w_m=0,34, S_{me-1}=0,22, h=8\ \ M_e=x_o+frac{0,5-S_{me-1}}{w_me}h=166+frac{0,5-0,22}{0,34}cdot 8approx 172,6 text{(см)} end{gather*} begin{gather*} \ X_{cp}=171,7; M_o=173,7; M_e=172,6\ X_{cp}lt M_elt M_o end{gather*} Ряд асимметричный с левосторонней асимметрией.
При этом (frac{|M_o-X_{cp}|}{|M_e-X_{cp}|}=frac{2,0}{0,9}approx 2,2lt 3), т.е. распределение умеренно асимметрично.

п.4. Выборочная дисперсия и СКО

Выборочная дисперсия интервального вариационного ряда определяется как средняя взвешенная для квадрата отклонения от средней: begin{gather*} D=frac1Nsum_{i=1}^k(x_i-X_{cp})^2 f_i=frac1Nsum_{i=1}^k x_i^2 f_i-X_{cp}^2 end{gather*} где (x_i) – середины интервалов: (x_i=frac{a_{i-1}+a_i}{2}, i=overline{1,k}).
Или, через относительные частоты: $$ D=sum_{i=1}^k(x_i-X_{cp})^2 w_i=sum_{i=1}^k x_i^2 w_i-X_{cp}^2 $$

Выборочное среднее квадратичное отклонение (СКО) определяется как корень квадратный из выборочной дисперсии: $$ sigma=sqrt{D} $$

Например:
Для распределения учеников по росту получаем:

$x_i$	146	154	162	170	178	186	194	∑
(w_i)	0,04	0,07	0,11	0,34	0,33	0,08	0,03	1
(x_iw_i)	5,84	10,78	17,82	57,80	58,74	14,88	5,82	171,68
(x_i^2w_i) – результат	852,64	1660,12	2886,84	9826	10455,72	2767,68	1129,08	29578,08

$$ D=sum_{i=1}^k x_i^2 w_i-X_{cp}^2=29578,08-171,7^2approx 104,1 $$ $$ sigma=sqrt{D}approx 10,2 $$

п.5. Исправленная выборочная дисперсия, стандартное отклонение выборки и коэффициент вариации

Исправленная выборочная дисперсия интервального вариационного ряда определяется как: begin{gather*} S^2=frac{N}{N-1}D end{gather*}

Стандартное отклонение выборки определяется как корень квадратный из исправленной выборочной дисперсии: $$ s=sqrt{S^2} $$

Коэффициент вариации это отношение стандартного отклонения выборки к выборочной средней, выраженное в процентах: $$ V=frac{s}{X_{cp}}cdot 100text{%} $$

Подробней о том, почему и когда нужно «исправлять» дисперсию, и для чего использовать коэффициент вариации – см. §65 данного справочника.

Например:
Для распределения учеников по росту получаем: begin{gather*} S^2=frac{100}{99}cdot 104,1approx 105,1\ sapprox 10,3 end{gather*} Коэффициент вариации: $$ V=frac{10,3}{171,7}cdot 100text{%}approx 6,0text{%}lt 33text{%} $$ Выборка однородна. Найденное значение среднего роста (X_{cp})=171,7 см можно распространить на всю генеральную совокупность (старшеклассников из других школ).

п.6. Алгоритм исследования интервального вариационного ряда

На входе: все значения признака (left{x_jright}, j=overline{1,N})
Шаг 1. Построить интервальный ряд с интервалами (left.right[a_{i-1}, a_ileft.right)) и частотами (f_i, i=overline{1,k}) (см. алгоритм выше).
Шаг 2. Составить расчетную таблицу. Найти (x_i,w_i,S_i,x_iw_i,x_i^2w_i)
Шаг 3. Построить гистограмму (и/или полигон) относительных частот, эмпирическую функцию распределения (и/или кумуляту). Записать эмпирическую функцию распределения.
Шаг 4. Найти выборочную среднюю, моду и медиану. Проанализировать симметрию распределения.
Шаг 5. Найти выборочную дисперсию и СКО.
Шаг 6. Найти исправленную выборочную дисперсию, стандартное отклонение и коэффициент вариации. Сделать вывод об однородности выборки.

п.7. Примеры

Пример 1. При изучении возраста пользователей коворкинга выбрали 30 человек.
Получили следующий набор данных:
18,38,28,29,26,38,34,22,28,30,22,23,35,33,27,24,30,32,28,25,29,26,31,24,29,27,32,24,29,29
Постройте интервальный ряд и исследуйте его.

1) Построим интервальный ряд. В наборе данных: $$ x_{min}=18, x_{max}=38, N=30 $$ Размах вариации: (R=38-18=20)
Оптимальное число интервалов: (k=1+lfloorlog_2⁡ 30rfloor=1+4=5)
Шаг интервального ряда: (h=lceilfrac{20}{5}rceil=4)
Получаем узлы ряда: $$ a_0=x_{min}=18, a_i=18+icdot 4, i=overline{1,5} $$

(left.left[a_{i-1},a_iright.right)) лет

(left.left[18;22right.right))

(left.left[22;26right.right))

(left.left[26;30right.right))

(left.left[30;34right.right))

(left.left[34;38right.right))

Считаем частоты для каждого интервала. Получаем интервальный ряд:

(left.left[a_{i-1},a_iright.right)) лет	(left.left[18;22right.right))	(left.left[22;26right.right))	(left.left[26;30right.right))	(left.left[30;34right.right))	(left.left[34;38right.right))
(f_i)	1	7	12	6	4

2) Составляем расчетную таблицу:

(x_i)	20	24	28	32	36	∑
(f_i)	1	7	12	6	4	30
(w_i)	0,033	0,233	0,4	0,2	0,133	1
(S_i)	0,033	0,267	0,667	0,867	1	–
(x_iw_i)	0,667	5,6	11,2	6,4	4,8	28,67
(x_i^2w_i)	13,333	134,4	313,6	204,8	172,8	838,93

3) Строим полигон и кумуляту

Эмпирическая функция распределения: $$ F(x)= begin{cases} 0, xleq 20\ 0,033, 20lt xleq 24\ 0,267, 24lt xleq 28\ 0,667, 28lt xleq 32\ 0,867, 32lt xleq 36\ 1, xgt 36 end{cases} $$ 4) Находим выборочную среднюю, моду и медиану $$ X_{cp}=sum_{i=1}^k x_iw_iapprox 28,7 text{(лет)} $$ На полигоне модальным является 3й интервал (самая высокая точка).
Данные для расчета моды: begin{gather*} x_0=26, f_m=12, f_{m-1}=7, f_{m+1}=6, h=4\ M_o=x_o+frac{f_m-f_{m-1}}{(f_m-f_{m-1})+(f_m+f_{m+1})}h=\ =26+frac{12-7}{(12-7)+(12-6)}cdot 4approx 27,8 text{(лет)} end{gather*}
На кумуляте медианным является 3й интервал (преодолевает уровень 0,5).
Данные для расчета медианы: begin{gather*} x_0=26, w_m=0,4, S_{me-1}=0,267, h=4\ M_e=x_o+frac{0,5-S_{me-1}}{w_{me}}h=26+frac{0,5-0,4}{0,267}cdot 4approx 28,3 text{(лет)} end{gather*} Получаем: begin{gather*} X_{cp}=28,7; M_o=27,8; M_e=28,6\ X_{cp}gt M_egt M_0 end{gather*} Ряд асимметричный с правосторонней асимметрией.
При этом (frac{|M_o-X_{cp}|}{|M_e-X_{cp}|} =frac{0,9}{0,1}=9gt 3), т.е. распределение сильно асимметрично.

5) Находим выборочную дисперсию и СКО: begin{gather*} D=sum_{i=1}^k x_i^2w_i-X_{cp}^2=838,93-28,7^2approx 17,2\ sigma=sqrt{D}approx 4,1 end{gather*}
6) Исправленная выборочная дисперсия: $$ S^2=frac{N}{N-1}D=frac{30}{29}cdot 17,2approx 17,7 $$ Стандартное отклонение (s=sqrt{S^2}approx 4,2)
Коэффициент вариации: (V=frac{4,2}{28,7}cdot 100text{%}approx 14,7text{%}lt 33text{%})
Выборка однородна. Найденное значение среднего возраста (X_{cp}=28,7) лет можно распространить на всю генеральную совокупность (пользователей коворкинга).

Источник

Все курсы > Оптимизация > Занятие 3

Как мы уже говорили, исследуя изменения случайных величин, мы зачастую обнаруживаем, что между этими изменениями существует взаимосвязь (bivariate relationship, association).

Откроем ноутбук к этому занятию⧉

Возьмем вот такой простой набор данных.

toy_df = pd.DataFrame({

‘a’:[1, 4, 5, 6, 9],

‘b’:[2, 3, 5, 6, 8],

‘c’:[6, 5, 4, 3, 2],

‘d’:[7, 4, 3, 4, 6]

})

toy_df

Посмотрим на распределения величин с помощью boxplot.

plt.figure(figsize = (8, 6))

sns.boxplot(data = toy_df)

plt.show()

Очевидно, распределения отличаются друг от друга, однако пока что мы мало можем сказать об этих распределениях или их взаимосвязи.

Начнем с расчета дисперсии.

Дисперсия

Дисперсия (variance) показывает изменение переменной относительно среднего значения. Приведем формулу для расчета дисперсии генеральной совокупности.

$$ sigma^2 = frac{sum (x_i-mu)^2}{N} $$

где $mu$ — среднее генеральной совокупности из $ x_i $ элементов, а $N$ — ее размер. Дисперсию выборки мы рассчитываем немного иначе.

$$ s^2 = frac{sum (x_i-bar{x})^2}{n-1} $$

В данном случае деление на $n-1$, а не на $n$ называется поправкой Бесселя (Bessel’s correction). Зачем нужна такая поправка? Оказывается, можно показать, что сумма квадратов расстояний, то есть числитель формулы, до среднего генсовокупности (population mean) будет всегда больше, чем сумма квадратов расстояний до выборочного среднего (sample mean).

Как следствие, если при расчете выборочной дисперсии делить на $n$, то мы будем постоянно недооценивать дисперсию генсовокупности. Поправка с делением на $ n-1 $ увеличит дисперсию выборки и сделает ее несмещенной оценкой (unbiased estimation) дисперсии генеральной совокупности.

Приведем основные выводы для показателя дисперсии.

Большая дисперсия показывает, что значения далеки от среднего и далеки друг от друга
Дисперсия не может быть отрицательной
Нулевая дисперсия означает, что все элементы выборки или генеральной совокупности идентичны

Замечу, что далее мы в большинстве случаев будем приводить формулы и вычислять именно выборочные показатели.

Найдем дисперсию для переменной a.

# применим формулу дисперсии к первому столбцу

(np.square(toy_df[‘a’] – toy_df[‘a’].mean())).sum() / (toy_df.shape[0] – 1)

Дисперсию для каждой переменной можно измерить с помощью функции np.var() библиотеки Numpy.

# рассчитаем дисперсию по столбцам с делением на n – 1

np.var(toy_df, ddof = 1)

a 8.5

b 5.7

c 2.5

d 2.7

dtype: float64

Точно такой же результат можно получить с помощью метода .var() библиотеки Pandas.

# ddof = 1 можно не указывать, это параметр по умолчанию

toy_df.var()

a 8.5

b 5.7

c 2.5

d 2.7

dtype: float64

Параметр ddof означает Delta Degrees of Freedom (дельта степеней свободы) и указывает на размер поправки при расчете дисперсии выборки. Соответственно ddof = 1 как раз использует деление на $n-ddof = n-1$. Как мы видим, дисперсия переменной a существенно больше, чем, например, переменной d.

Показатель дисперсии представляет собой квадрат измеряемых нами величин. Для понимания величины отклонения это не очень удобно. В этом смысле лучше подойдет среднее квадратическое отклонение.

Среднее квадратическое отклонение

Среднее квадратическое отклонение (СКО, standard deviation) как раз вычисляется как корень из дисперсии.

$$ sigma = sqrt{sigma^2} $$

$$ s = sqrt{s^2} $$

Рассчитаем СКО для первого столбца.

np.sqrt((np.square(toy_df[‘a’] – toy_df[‘a’].mean())).sum() / (toy_df.shape[0] – 1))

Мы также можем использовать функцию np.std() библиотеки Numpy и метод .std() библиотеки Pandas.

# для расчета СКО будем также делить на n – 1

np.std(toy_df, ddof = 1)

a 2.915476

b 2.387467

c 1.581139

d 1.643168

dtype: float64

# опять же, этот параметр установлен по умолчанию, и его можно не указывать

toy_df.std()

a 2.915476

b 2.387467

c 1.581139

d 1.643168

dtype: float64

Теперь перейдем к изучению взаимосвязи между переменными. Одним из способов измерения взаимосвязи является ковариация.

Ковариация

Ковариация (covariance) измеряет направление изменения двух переменных. Другими словами она позволяет понять как изменится одна из двух переменных при изменении второй.

Построим три точечные диаграммы (scatter plots) для переменных a и b, b и c, и c и d соответственно.

# создадим сетку 1 х 3 с подграфиками для каждой из пар переменных

f, (pair1, pair2, pair3) = plt.subplots(nrows = 1,

ncols = 3,

figsize = (12, 4),

constrained_layout = True)

# в первый подграфик поместим точечную диаграмму переменных a и b

pair1.scatter(toy_df[‘a’], toy_df[‘b’])

pair1.set_title(‘a vs. b’, fontsize = 14)

pair1.set(xlabel = ‘a’)

pair1.set(ylabel = ‘b’)

# во второй – b и c

pair2.scatter(toy_df[‘b’], toy_df[‘c’])

pair2.set_title(‘b vs. c’, fontsize = 14)

pair2.set(xlabel = ‘b’)

pair2.set(ylabel = ‘c’)

# в третий – c и d

pair3.scatter(toy_df[‘c’], toy_df[‘d’])

pair3.set_title(‘c vs. d’, fontsize = 14)

pair3.set(xlabel = ‘c’)

pair3.set(ylabel = ‘d’)

plt.show()

На первом и втором графике мы видим линейную взаимосвязь. Приведем формулу для ее измерения.

$$ Cov_{x, y} = frac{sum (x_i-bar{x})(y_i-bar{y})}{n-1} $$

Как вы видите, ковариация представляет собой сумму произведений отклонений переменных от своего среднего значения, усредненную на количество наблюдений ($n-1$).

Рассчитаем ковариацию a и b с помощью Питона.

((toy_df[‘a’] – toy_df[‘a’].mean()) * (toy_df[‘b’] – toy_df[‘b’].mean())).sum() / (toy_df.shape[0] – 1)

Если использовать функцию np.cov() библиотеки Numpy или метод .cov() библиотеки Pandas, то мы получим так называемую ковариационную матрицу (covariance matrix).

# для расчета по столбцам нужно использовать параметр rowvar = False

np.cov(toy_df, ddof = 1, rowvar = False)

array([[ 8.5 , 6.75, -4.5 , -1. ],

[ 6.75, 5.7 , -3.75, -0.55],

[-4.5 , -3.75, 2.5 , 0.5 ],

[-1. , -0.55, 0.5 , 2.7 ]])

По диагонали указана дисперсия, вне диагонали — ковариация любых двух переменных.

Переменные a и b имеют положительную ковариацию, с увеличением a увеличивается и b. Переменные b и c — отрицательную, переменные c и d демонстрируют нулевую или близкую к нулевой ковариацию.

Интересно, что если переменные независимы (между ними нет взаимосвязи) — ковариация будет равна нулю, при этом обратное не обязательно верно. Если ковариация равна нулю, взаимосвязь может быть, просто она нелинейна (возможно именно такая взаимосвязь существует между c и d).

Недостатком ковариации является то, что она измеряет только направление, но не силу взаимосвязи. Если мы умножим значения обеих переменных, например, на три, то ковариация, исходя из формулы выше, увеличится в девять раз (поскольку как x, так и y каждой пары переменных умножаются на три), при этом очевидно сила взаимосвязи никак не изменится.

# умножим данные на три, рассчитаем ковариацию

# и разделим на ковариационную матрицу исходного датасета,

# чтобы посмотреть масштаб изменения

(toy_df * 3).cov() / toy_df.cov()

Этот недостаток исправляет коэффициент корреляции.

Корреляция

Корреляция (correlation) между двумя переменными (случайными величинами) измеряет не только направление, но и силу взаимосвязи.

Параметрические и непараметрические тесты

Прежде чем перейти к различным коэффициентам корреляции несколько слов про разделение статистических тестов или методов на параметрические и непараметрические.

Параметрические методы (parametric methods) основываются на допущении (assumption) или предпосылке о том, как распределена генеральная совокупность, из которой взята изучаемая выборка. Например, статистический тест может предполагать, что данные имеют нормальное распределение.

Непараметрические методы (non-parametric) таких допущений соответственно не предполагают.

На практике это означает, что если допущения параметрического теста не выполняются, его результат нельзя считать достоверным. Для непараметрического теста такое ограничение отсутствует.

Коэффициент корреляции Пирсона

Коэффициент корреляции Пирсона (Pearson correlation coefficient) — это параметрический тест, который строится на основе расчета ковариации двух переменных, разделенного на произведение СКО каждой из них.

$$ r_{pearson} = frac{Cov_{x, y}}{s_x s_y} $$

Деление на произведение СКО $(s_x s_y)$ выражает любой коэффициент ковариации в единицах этого произведения (нормализует его). Как следствие, мы получаем возможность сравнения коэффициентов корреляции, а значит измерения не только направления, но и силы взаимосвязи.

Коэффициент корреляции всегда находится в диапазоне от $-1$ до $1$.

Значения, приближающиеся к 1 указывают на сильную положительную линейную корреляцию. Близкие к −1 — на сильную отрицательную линейную корреляцию. Околонулевые значения означают отсутствие линейной корреляции.

Посмотрим на график возможных вариантов корреляции данных, приведенный на занятии вводного курса.

Библиотека Numpy предлагает нам функцию np.corrcoef() для создания корреляционной матрицы (correlation matrix) коэффициента Пирсона.

# для расчета корреляции по столбцам используем параметр rowvar = False

np.corrcoef(toy_df, rowvar = False).round(2)

array([[ 1. , 0.97, -0.98, -0.21],

[ 0.97, 1. , -0.99, -0.14],

[-0.98, -0.99, 1. , 0.19],

[-0.21, -0.14, 0.19, 1. ]])

В Pandas мы можем воспользоваться методом .corr().

# параметр method = ‘pearson’ используется по умолчанию,

# его можно не указывать

toy_df.corr(method = ‘pearson’).round(2)

Корреляция переменной с самой собой равна единице, что и отражают значения на главной диагонали матрицы. Кроме того, очевидно, что величина X также коррелирует с Y, как Y c X.

Продемонстрируем также, что изменение масштаба данных не отразится на коэффициенте корреляции.

# умножим значения датасета на два и снова рассчитаем коэффициент Пирсона

(toy_df * 2).corr().round(2)

Особенности коэффициента Пирсона

Несколько важных замечаний.

Замечание 1. Ни ковариация, ни корреляция не устанавливают причинно-следственной связи (correlation does not imply causation). Например, мы можем наблюдать существенную корреляцию между потреблением мороженого и продажами кондиционеров, при этом изменения в обеих переменных могут быть вызваны третьей, на рассматриваемой нами переменной, в частности, температурой воздуха.

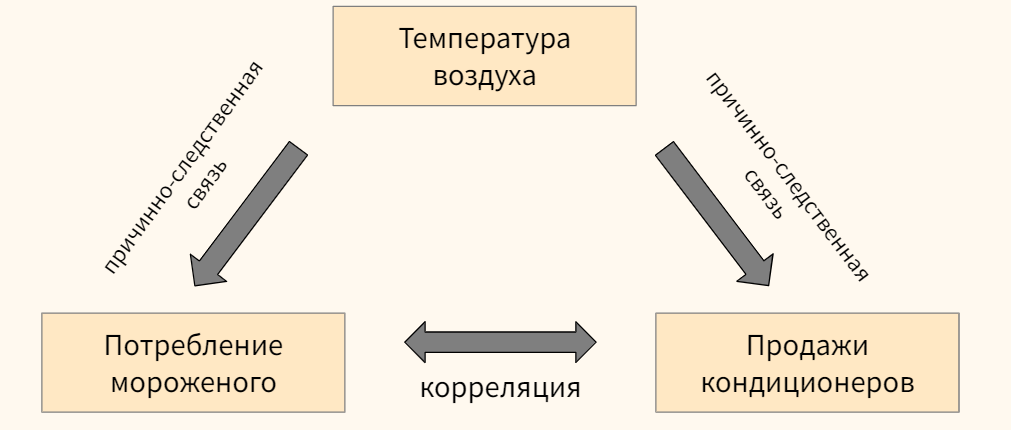
корреляция не устанавливает причинно-следственной связи: потребление мороженого и продажи кондиционеров

Кроме того в некоторых случаях корреляция может быть чистой случайностью.

Замечание 2. Коэффициент корреляции Пирсона измеряет взаимосвязь (1) количественных переменных и (2) предполагает, что обе переменные имеют нормальное распределение (это и есть упомянутое выше допущение (assumption) параметрического теста).

Замечание 3. Как и в случае с ковариацией, отсутствие линейной корреляции не означает отсутствие взаимосвязи. Возможно взаимосвязь есть, но она нелинейна.

Замечание 4. Более того, на коэффициент корреляции существенное влияние оказывают выбросы (outliers).

Последние два замечения хорошо иллюстрируются квартетом Энскомба (Anscombe’s quartet), набором небольших датасетов (кстати, встроенных в сессионное хранилище Google Colab) с совершенно разными распределениями x и y, но одинаковым средним арифметическим и СКО переменной y, а также одинаковым коэффициентом корреляции Пирсона.

Вначале получим необходимые данные.

# загрузим данные в формате json из сессионного хранилища,

# преобразуем в датафрейм и посмотрим на первые три строки

anscombe = pd.read_json(‘/content/sample_data/anscombe.json’)

anscombe.head(3)

# разобьем данные на четыре части по столбцу Series

series_by_group = [x for _, x in anscombe.groupby(‘Series’)]

# отдельно получим названия каждой из четырех частей

labels = anscombe.Series.unique()

labels

array([‘I’, ‘II’, ‘III’, ‘IV’], dtype=object)

# создадим пустой словарь

datasets = {}

# в цикле пройдемся по названиям и значениям переменных x и y каждой из частей

for label, series in zip(labels, series_by_group):

# каждое название части станет ключом словаря, а переменные x и y – значениями

datasets[label] = (list(series.X.round(2)), list(series.Y.round(2)))

# выведем содержимое словаря с помощью функции pprint()

from pprint import pprint

pprint(datasets)

{‘I’: ([10, 8, 13, 9, 11, 14, 6, 4, 12, 7, 5],

[8.04, 6.95, 7.58, 8.81, 8.33, 9.96, 7.24, 4.26, 10.84, 4.81, 5.68]),

‘II’: ([10, 8, 13, 9, 11, 14, 6, 4, 12, 7, 5],

[9.14, 8.14, 8.74, 8.77, 9.26, 8.1, 6.13, 3.1, 9.13, 7.26, 4.74]),

‘III’: ([10, 8, 13, 9, 11, 14, 6, 4, 12, 7, 5],

[7.46, 6.77, 12.74, 7.11, 7.81, 8.84, 6.08, 5.39, 8.15, 6.42, 5.73]),

‘IV’: ([8, 8, 8, 8, 8, 8, 8, 19, 8, 8, 8],

[6.58, 5.76, 7.71, 8.84, 8.47, 7.04, 5.25, 12.5, 5.56, 7.91, 6.89])}

Теперь выведем каждый из четырех датасетов на графиках.

# создадим сетку подграфиков 2 х 2

fig, axs = plt.subplots(2, 2,

sharex = True,

sharey = True,

figsize = (10, 10),

gridspec_kw = {‘wspace’: 0.08, ‘hspace’: 0.08})

# определим границы осей и отметки на осях x и y

axs[0, 0].set(xlim = (0, 20), ylim = (2, 14))

axs[0, 0].set(xticks = (0, 10, 20), yticks = (4, 8, 12))

# пройдемся по подграфикам, а также ключам и значениям словаря datasets

for ax, (label, (x, y)) in zip(axs.flat, datasets.items()):

# выведем название (номер) группы

ax.text(0.1, 0.9, label, fontsize = 20, transform = ax.transAxes, va = ‘top’)

ax.tick_params(direction = ‘in’, top = True, right = True)

# построим точечные диаграммы

ax.scatter(x, y)

# обучим модель линейной регрессии

slope, intercept = np.polyfit(x, y, deg = 1)

# выведем график линейной регрессии

x_vals = np.linspace(0, 20, num = 1000)

y_vals = intercept + slope * x_vals

ax.plot(x_vals, y_vals, ‘r’)

# рассчитаем среднее арифметическое, СКО и корреляцию Пирсона

stats = (f‘$\mu$ = {np.mean(y):.2f}n’

f‘$\sigma$ = {np.std(y):.2f}n’

f‘$r$ = {np.corrcoef(x, y)[0][1]:.2f}’)

# создадим отформатированное пространство на графике

bbox = dict(boxstyle = ‘square’, pad = 0.5,

fc = ‘#c5d4e6’,

ec = ‘#89a8cc’,

alpha = 0.5)

# и выведем в нем рассчитанные выше статистические показатели

ax.text(0.95, 0.07, stats, fontsize = 15,

bbox = bbox, transform = ax.transAxes,

horizontalalignment = ‘right’)

plt.show()

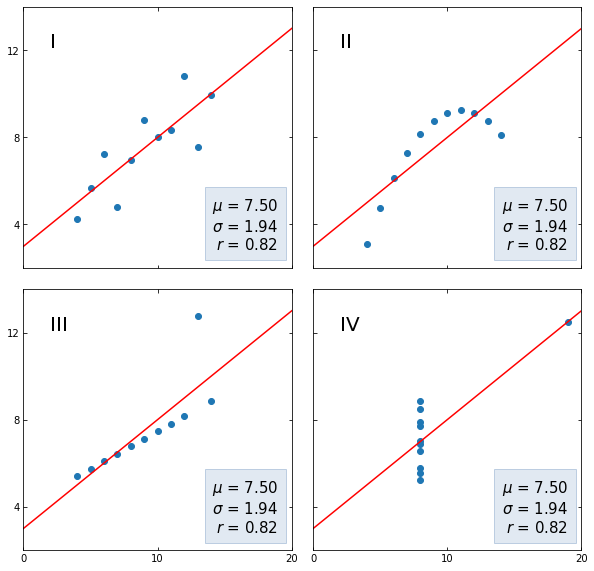
Как мы видим, на первом графике прослеживается линейная корреляция без каких-либо сюрпризов;
Во втором наборе данных у нас нелинейная зависимость, силу которой мы не смогли отразить с помощью коэффициента Пирсона;
В третьем наборе коэффициент корреляции находится под сильным влиянием выброса;
В четвертом, корреляция по сути отсутствует и тем не менее одного наблюдения оказывается достаточно для появления достаточно сильной корреляции.

Помимо ограничений коэффициента корреляции, эти наборы данных демонстрируют в целом важность визуальной оценки данных.

Коэффициент Пирсона как скалярное произведение векторов

Распишем формулу корреляции более подробно (см. формулы ковариации, дисперсии и СКО).

$$ r_{pearson} = frac{ frac{sum (x_i-bar{x})(y_i-bar{y})}{n-1} }{ sqrt {frac{sum (x_i-bar{x})^2}{n-1} frac{sum (y_i-bar{y})^2}{n-1} } } $$

Упростим выражение.

$$ r_{pearson} = frac{ sum (x_i-bar{x})(y_i-bar{y}) } { sqrt {sum (x_i-bar{x})^2} sqrt{ sum (y_i-bar{y})^2 } } $$

Теперь давайте представим случайные величины X и Y в форме векторов

$$ textbf{x} = [x_1, x_2, x_3,…, x_n] $$

$$ textbf{y} = [y_1, y_2, y_3,…, y_n] $$

со средними значениями $ bar{x} $ и $ bar{y} $. Затем определим новые векторы $ textbf{x}^c $ и $ textbf{y}^c $, в которых из значений $x_i$ и $y_i$ вычтем соответствующие средние значения.

$$ textbf{x}^c = [x_1-bar{x}, x_2-bar{x}, x_3-bar{x},…, x_n-bar{x}] $$

$$ textbf{y}^c = [y_1-bar{x}, y_2-bar{x}, y_3-bar{y},…, y_n-bar{y}] $$

Обратим внимание, что (1) числитель (1) в формуле коэффициента корреляции представляет собой покомпонентное умножение векторов с последующим сложением произведений (то есть скалярное произведение).

Знаменатель (2) же представляет собой покомпонентное умножение и сложение произведений векторов самих на себя. Как мы узнаем на курсе линейной алгебры, корень из скалярного произведение вектора на самого себя есть длина этого вектора. Приведем пример для вектора $ textbf{x} $

$$ sqrt { textbf{x}^2 } = sqrt { textbf{x} cdot textbf{x} } = || textbf{x} || $$

Исходя из этих двух соображений, перепишем формулу расчета коэффициента Пирсона.

$$ r_{pearson} = frac { textbf{x}^c cdot textbf{y}^c }{|| textbf{x}^c || cdot || textbf{y}^c || } $$

Это формула косинусного сходства двух векторов. Другими словами, коэффициент корреляции равен косинусу угла между двумя векторами данных. Рассчитаем корреляцию через косинусное сходство с помощью Питона.

# возьмем данные первой группы квартета Энскомба

x = np.array([10, 8, 13, 9, 11, 14, 6, 4, 12, 7, 5])

y = np.array([8.04, 6.95, 7.58, 8.81, 8.33, 9.96, 7.24, 4.26, 10.84, 4.81, 5.68])

# вычтем из каждого значения x и y соответствующее среднее арифметическое

xc = x – np.mean(x)

yc = y – np.mean(y)

# используем формулу косинусного сходства и округлим результат

np.round(np.dot(xc, yc)/(np.linalg.norm(xc) * np.linalg.norm(yc)), 2)

Как уже было сказано, у коэффициента Пирсона есть ряд ограничений, в частности, он выявляет только линейную взаимосвязь количественных переменных. В этой связи рассмотрим коэффициент Спирмена.

Коэффициент ранговой корреляции Спирмена

Коэффициент ранговой корреляции Спирмена (Spearman’s Rank Correlation Coefficient) хорошо измеряет постоянно возрастающую или постоянно убывающую (монотонную) зависимость двух переменных, а также подходит для работы с категориальными порядковыми данными.

Это непараметрический тест, который не предполагает каких-либо допущений о распределении генеральной совокупности.

Монотонная зависимость

Напомню, что функция или зависимость называется монотонной (monotonic), если на заданном интервале ее производная (градиент) не меняет знака (то есть всегда имеет неотрицательное или неположительное значение). Приведем пример.

монотонно возрастающая, монотонно убывающая и немонотонная функции

Рассмотрим взаимосвязь площади (area) и цены (price) квартиры.

# поместим данные площади и цены квартиры в датафрейм

flats = pd.DataFrame({

‘area’ :[78, 90, 74, 69, 63, 57, 72, 67, 83],

‘price’ :[9.1, 9.0, 8.9, 8.2, 6.0, 5.8, 8.7, 7.5, 9.2]

})

flats

Выведем эти данные с помощью точечной диаграммы (scatter plot).

plt.figure(figsize = (8, 6))

plt.scatter(flats.area, flats.price)

plt.xlabel(‘Площадь, кв. м.’, fontsize = 15)

plt.ylabel(‘Цена, млн. руб.’, fontsize = 15)

plt.grid()

plt.show()

Рассчитаем коэффициент корреляции Пирсона.

# применим метод .corr() с параметром method = ‘pearson’

# выведем одно из значений корреляционной матрицы с помощью .iloc[0, 1] и округлим результат

flats.corr(method = ‘pearson’).iloc[0, 1].round(2)

Достаточно высокий уровень корреляции. При этом, как мы видим, зависимость нелинейна и возможно коэффициент Пирсона не до конца уловил силу взаимосвязи. Как нам преодолеть ограничение линейности?

Обратите внимание, прежде чем построить график, Питон упорядочил значения площади (ось x). Упорядочил, то есть присвоил им ранг (порядковый номер) от первого до, в данном примере, девятого. В каком случае значения цены (ось y) будут также возрастать? Только в случае если их ранги мало отличаются от рангов значений площади квартиры.

Коэффициент корреляции Спирмена как раз считает степень отличия рангов двух переменных.

Приведем формулу.

$$ r_{spearman} = frac{6 sum d_i^2 }{n(n^{2}-1)} $$

Вычислим коэффициент Спирмена с помощью Питона. Вначале присвоим каждому значению в обоих столбцах ранг (порядковый номер), предварительно упорядочив значения по убыванию.

# для этого используем метод .rank() с параметром ascending = False

flats[‘area_rank’] = flats.area.rank(ascending = False)

flats[‘price_rank’] = flats.price.rank(ascending = False)

flats

Таким образом площади дома в 90 квадратных метров и цене в 9,2 миллона рублей будет присвоен ранг 1. Теперь мы можем вычислить разницу рангов для каждого из наблюдений и возвести ее в квадрат.

# вычтем из рангов площади ранги цены

flats[‘diff’] = flats[‘area_rank’] – flats[‘price_rank’]

# возведем разницу в квадрат

flats[‘diff_sq’] = np.square(flats[‘diff’])

flats

Выполним оставшиеся вычисления в соответствии с приведенной выше формулой.

# поместим количество наблюдений в переменную n

n = flats.shape[0]

# применим формулу для расчета коэффициента Спирмена

1 – ((6 * flats[‘diff_sq’].sum()) / (n * (n**2 – 1)))

Рассчитаем корреляцию Спирмена с помощью метода .corr() библиотеки Pandas с параметром method = ‘spearman’.

flats[[‘area’, ‘price’]].corr(method = ‘spearman’).iloc[0, 1].round(2)

Как мы видим, этот коэффициент гораздо лучше уловил монотонную нелинейную зависимость двух переменных.

Также замечу, что коэффициент корреляции Спирмена менее чувствителен к выбросам, находящимся на «краях» обеих выборок, потому что опять же учитывает не само значение, а присвоенный ему ранг.

Категориальные порядковые данные

Как уже было сказано, помимо количественных значений коэффициент Спирмена способен измерить направление и силу взаимосвязи категориальных порядковых значений (categorical ordinal data).

Это могут быть оценки уровня удовлетворености клиента (очень понравилось, понравилось, не понравилось), размеры, выраженные категорией (S, M, L, …) и так далее.

В качестве примера рассмотрим оценку собственного самочувствия по шкале от 1 до 10, которую пациенты поставили себе до и после нового метода лечения.

# создадим датафрейм с данными о самочувствии

treatment = pd.DataFrame(

[

[3, 2],

[4, 3],

[2, 1],

[1, 5],

[6, 7],

[7, 6],

[5, 4]

columns = [‘Before’, ‘After’])

treatment

# выведем данные на графике

plt.figure(figsize = (8, 6))

plt.scatter(treatment.Before, treatment.After)

plt.xlabel(‘Before’, fontsize = 15)

plt.ylabel(‘After’, fontsize = 15)

plt.grid()

plt.show()

По всей видимости корреляция должна быть меньше, чем в предыдущем примере. Приступим к измерениям. Сделать это на самом деле очень просто, потому что порядковые значения уже сами по себе представляют собой ранги. Остается только найти квадрат их разности и применить формулу коэффициента корреляции.

# найдем квардрат разницы рангов

treatment[‘diff’] = treatment[‘Before’] – treatment[‘After’]

treatment[‘diff_sq’] = np.square(treatment[‘diff’])

treatment

# применим формулу коэффициента корреляции Спирмена

n = treatment.shape[0]

round(1 – ((6 * treatment[‘diff_sq’].sum()) / (n * (n**2 – 1))), 2)

Остается сравнить с методом .corr() библиотеки Pandas.

treatment[[‘Before’, ‘After’]].corr(method = ‘spearman’).iloc[0, 1].round(2)

Обратите внимание, ни в количественных данных, ни в порядковых у нас не было повторяющихся или совпадающих наблюдений. В случае совпадающих наблюдений (tied ranks), то есть когда значения x или y повторяются, расчет коэффициента корреляции Спирмена также возможен, но немного усложняется.

Коэффициент ранговой корреляции Кендалла

Коэффициент ранговой корреляции Кендалла (еще говорят тау Кендалла или тау-коэффициент, Kendall’s $tau$ rank correlation coefficient), как и метод Спирмена, может применяться для измерения силы взаимосвязи количественных и порядковых категориальных переменных и подходит для анализа нелинейных зависимостей. Это также непараметрический тест.

Смысл и методику расчета коэффициента Кендалла легко понять на примере. Вновь возьмем данные о самочувствии до и после лечения.

# вернем датафрейм к исходному виду

treatment = treatment[[‘Before’, ‘After’]]

treatment

Теперь рассмотрим две пары наблюдений, например, под индексом 0 и 1.

Мы видим, что в столбце Before значения наблюдения 0 меньше, чем значение наблюдения 1 (потому что 3 < 4). То же самое можно наблюдать в столбце After (2 < 3). Такая пара наблюдений называется конкордантной (concordant). Конкордантной будет и пара наблюдений, где оба значения в первом наблюдении больше обоих значений во втором. К ним относятся, например, пары 1 и 2 (где 4 > 2, а 3 > 1).

Если же описанные выше условия не выполняются, то такая пара наблюдений будет называться дискордантной (discordant). К таким наблюдениям относятся, например, наблюдения 4 и 5 (6 > 7, но 7 < 6).

Отнесем каждую из пар нашего датасета к одному из этих классов.

# 0

# 1 C

# 2 C C

# 3 D D D

# 4 C C C C

# 5 C C C C D

# 6 C C C D C C

# 0 1 2 3 4 5 6

Получилось 16 конкордантных (C) и 5 дискордантных (D) пар. Их общее количество очевидно равно 21. Это значение удобно посчитать по формуле сочетаний.

$$ C(n, r) = frac{n!}{(n-r)! r!} rightarrow C(7, 2) = frac{7!}{(7-2)! 2!} = 21 $$

где n — количество наблюдений, а r равно двум, потому что мы ищем сочетания пар элементов. Можно воспользоваться и упрощенной формулой.

$$ C(r) = frac{(n cdot (n-1))}{2} rightarrow C(7) = frac{7 cdot (7-1)}{2} = 21 $$

# найдем количество парных сочетаний с помощью Питона

n = 7

pairs = (7 * (7 – 1)) // 2

pairs

Так вот, коэффициент корреляции Кендалла показывает соотношение конкордантных и дискордантных пар по следующей формуле.

$$ tau = frac{text{concordant pairs}-text{discordant pairs}}{text{total pairs}}$$

Применим ее к нашему датасету.

concordant = 16

discordant = pairs – concordant

np.round((concordant – discordant) / pairs, 2)

Точно такого же результата можно добиться с помощью метода .corr() библиотеки Pandas.

treatment.corr(method = ‘kendall’).iloc[0, 1].round(2)

Смысл этого коэффициента в следующем.

Чем больше доля конкордантных пар, тем больше схожих рангов, а значит сильнее взаимосвязь между переменными.

Коэффициент неопределенности

Определение и понятие симметричности теста

Коэффициент неопределенности (uncertainty coefficient) или U Тиля (Theil’s U) позволяет оценить взаимосвязь между двумя категориальными признаками, например, X и Y. Формально он определяется как значение X при условии данного Y.

$$U(x|y)$$

Более того, в отличие от некоторых других тестов, он несимметричен (asymmetric), что позволяет узнать зависит ли Y от X, так же как X от Y.

$$U(y|x) neq U(x|y)$$

Понятие симметричности теста легко представить на следующем простом примере.

Очевидно, что мы легко можем предсказать Y зная X, а вот зная Y мы можем меньше сказать про X (обратите внимание, что категории в X не совпадают для двух категорий в Y).

Используем этот несложный датасет для дальнейших расчетов.

# возьмем две категориальные переменные со следующими значениями

x = np.array([‘q’, ‘t’, ‘q’, ‘n’, ‘n’, ‘c’])

y = np.array([‘A’, ‘A’, ‘A’, ‘B’, ‘B’, ‘B’])

Как рассчитывается

Условная энтропия

U Тиля основывается на понятии условной энтропии (condition entropy), которая позволяет измерить объем информации, необходимый для описания значений переменной X с помощью переменной Y.

$$ S(X|Y) = -sum p(x,y) logfrac{p(x,y)}{p(y)} $$

Теоретическое обоснование формул условной энтропии и энтропии выходит за рамки сегодняшнего занятия. Мы сосредоточимся на расчете и практическом применении каждой из них.

Рассчитаем условную энтропию с помощью Питона. Вначале нам необходимо рассчитать частоту классов категориальных переменных. Для этого прекрасно подойдет класс Counter модуля collections.

# импортируем класс Counter модуля collections

from collections import Counter

Посмотрим, сколько раз встречаются классы переменной Y.

# найдем частоту классов переменной y

y_counts = Counter(y)

y_counts

Counter({‘A’: 3, ‘B’: 3})

Далее возьмем каждую пару значений X и Y и рассчитаем, сколько раз встречается каждая из них.

# возьмем каждую пару значений X и Y с помощью функций zip() и list()

list(zip(x, y))

[(‘q’, ‘A’), (‘t’, ‘A’), (‘q’, ‘A’), (‘n’, ‘B’), (‘n’, ‘B’), (‘c’, ‘B’)]

# рассчитаем их частоту

xy_counts = Counter(list(zip(x, y)))

xy_counts

Counter({(‘A’, ‘q’): 2, (‘A’, ‘t’): 1, (‘B’, ‘n’): 2, (‘B’, ‘c’): 1})

Теперь найдем общее количество значений.

total_counts = len(x)

total_counts

В соответствии с формулой выше нам нужно найти вероятность Y ($p(y)$) и вероятность X при условии Y ($p(x,y)$). Для расчета $p(y)$ мы пройдемся по ключам словаря xy_counts и посмотрим в словаре y_counts сколько раз встречается второй элемент каждого ключа.

# пройдемся по ключам xy_counts

for xy in xy_counts.keys():

# (выведем ключ для наглядности)

print(xy)

# и посмотрим в y_counts сколько раз встречается второй элемент каждого кортежа

print(y_counts[xy[1]])

(‘q’, ‘A’)

(‘t’, ‘A’)

(‘n’, ‘B’)

(‘c’, ‘B’)

Мы видим, что категория A и категория B в нашем случае встречаются по три раза. Остается разделить частоту каждой категории на общее количество элементов.

# найдем p(y) разделив каждую частоту на общее количество элементов

for xy in xy_counts.keys():

print(y_counts[xy[1]] / total_counts)

Выполним похожее упражнение для того, чтобы найти $p(x,y)$.

# снова пройдемся по парам значений

for xy in xy_counts.keys():

# (выведем эти пары для наглядности)

print(xy)

# выведем частоту каждой пары (на этот раз именно пары, а нее ее второго элемента)

print(xy_counts[xy])

# и рассчитаем вероятность

print(xy_counts[xy] / total_counts)

(‘q’, ‘A’)

0.3333333333333333

(‘t’, ‘A’)

0.16666666666666666

(‘n’, ‘B’)

0.3333333333333333

(‘c’, ‘B’)

0.16666666666666666

# для дальнейшей работы нам понадобится модуль math

import math

Теперь остается подставить $p(y)$ и $p(x,y)$ в формулу.

# объявим переменную для условной энтропии

cond_entropy = 0.0

# в цикле снова пройдемся по парам значений

for xy in xy_counts.keys():

# найдем p(y)

p_y = y_counts[xy[1]] / total_counts

# и p(x,y)

p_xy = xy_counts[xy] / total_counts

# подставим их в формулу и просуммируем результат

# (мы использовали логарифм с основанием два, но можно использовать, например, и натуральный логарифм)

cond_entropy += p_xy * math.log(p_y / p_xy, 2)

cond_entropy

Поместим этот код в функцию.

# поместим код в функцию

def conditional_entropy(x, y, log_base: float = 2):

y_counts = Counter(y)

xy_counts = Counter(list(zip(x, y)))

total_counts = len(x)

cond_entropy = 0.0

for xy in xy_counts.keys():

p_xy = xy_counts[xy] / total_counts

p_y = y_counts[xy[1]] / total_counts

cond_entropy += p_xy * math.log(p_y / p_xy, log_base)

return cond_entropy

# вновь рассчитаем условную энтропию

conditional_entropy(x, y)

Убедимся в несимметричности объема информации, содержащегося в X относительно Y и в Y относительно X, поменяв переменные местами.

conditional_entropy(y, x)

Здесь становится очевидным важный факт.

Если условная энтропия равна нулю, это значит, что с помощью переменной Y мы можем полностью описать переменную X (в нашем примере наоборот). При этом, чем выше условная энтропия, тем меньше информации об X содержится в переменной Y.

Теперь рассмотрим второй компонент формулы коэффициента неопределенности.

Энтропия

Энтропия (entropy) случайной величины рассчитывается по следующей формуле.

$$ S(X) = -sum p(x)log{p(x)} $$

Это значение тем выше, чем менее вероятным является каждый из исходов испытания. Например, энтропия бросания игральной кости будет выше, чем подбрасывания монеты. В первом случае вероятность каждого исхода равна 1/6, во втором 1/2.

Убедимся в этом с помощью функции entropy() модуля stats библиотеки scipy.

# импортируем модуль stats библиотеки scipy

import scipy.stats as st

# рассчитаем энтропию бросания кости и подбрасывания монеты

st.entropy([1/6, 1/6, 1/6, 1/6, 1/6, 1/6], base = 2), st.entropy([1/2, 1/2], base = 2)

Выполним расчет вручную. Вначале найдем вероятность каждого из значений случайной величины $p(x)$.

# найдем частоту каждого элемента в X

x_counts = Counter(x)

# их общее количество

total_counts = len(x)

# разделим каждую частоту на общее количество элементов

p_x = list(map(lambda n: n / total_counts, x_counts.values()))

# выведем результат

print(p_x)

[0.3333333333333333, 0.16666666666666666, 0.3333333333333333, 0.16666666666666666]

Теперь подставим это значение в формулу и найдем энтропию.

# объявим переменную для условной энтропии

entropy = 0.0

# подставим каждую вероятность в формулу и просуммируем

for p in p_x:

entropy += –p * math.log(p, 2)

# выведем результат

entropy

Проверим правильность результата с помощью функции библиотеки scipy().

st.entropy(p_x, base = 2)

Также объявим соответствующую функцию.

# объявим функцию

def entropy(x, log_base: float = 2):

x_counts = Counter(x)

total_counts = len(x)

p_x = list(map(lambda n: n / total_counts, x_counts.values()))

entropy = 0.0

for p in p_x:

entropy += –p * math.log(p, 2)

return entropy

# проверим результат

entropy(x)

Замечу, что условная энтропия S(X|Y) равна энтропии случайной величины S(X), если величины X и Y независимы.

$$ S(X|Y) = S (X) iff X ⫫ Y $$

Из этого следует, что самое большее условная энтропия может быть равна энтропии этой переменной (в случае, если Y никак не объясняет X).

$$ S(X) leq S(X|Y) $$

Все это важно для расчета коэффициента неопределенности.

U Тиля

Приведем и обсудим формулу.

$$ U(X|Y) = frac{S(X)-S(X|Y)}{S(X)} $$

Зачем рассчитывать не только условную энтропию, но и энтропию случайной величины? Дело в том, что так мы можем не просто измерять «объяснимость» переменной X с помощью Y, но и сравнивать между собой условную энтропию любых категориальных переменных.

Арифметически, чем ниже условная энтропия, тем ближе значение показателя к единице. Чем она выше, тем коэффициент неопределенности ближе к нулю.

Таким образом, U Тиля всегда находится в диапазоне от 0 до 1. При этом, ноль означает, что переменная Y не несет никакой информации относительно переменной X, единица — что переменная Y содержит всю необходимую информацию.

Рассчитаем U Тиля с помощью Питона.

# сразу объявим функцию

def ucoef(x, y, log_base = 2):

# найдем условную энтропию S(X,Y)

s_xy = conditional_entropy(x, y, log_base)

# энтропию S(X)

s_x = entropy(x, log_base)

# подставим эти значения в формулу

u = (s_x – s_xy) / s_x

# выведем результат

return u

Найдем коэффициент неопределенности для X и Y.

Кроме того, убедимся, что X полностью объясняет Y.

Обратите внимание, что коэффициент не может принимать отрицательных значений. Это логично, потому что строго говоря в случае категориальных переменных мы измеряем не корреляцию (направление и силу взаимного изменения, correlation), а степень взаимосвязи (association) между двумя переменными, которая либо есть (и может доходить до единицы), либо ее нет (равна нулю).

Точечно-бисериальная корреляция

Точечно-бисериальная корреляция (point-biserial correlation) позволяет оценить взаимосвязь между количественной переменной и дихотомической (выраженной двумя значениями) качественной переменной. Например, нам может быть важно оценить связь возраста (X) и выживаемости пассажиров «Титаника» (Y, классы 0 и 1). Приведем формулу.

Формула

$$ r_{pb} = frac{M_1-M_0}{s_n} sqrt{frac{n_1 n_0}{n^2}} $$

В данном случае мы делим наблюдения на две группы, в первую группу попадут наблюдения, относящиеся к классу 0, во вторую — к классу 1. Для каждой группы мы считаем средние значения ($M_0$ и $M_1$) и делим их разность на среднее квадратическое отклонение всех значений в переменной X ($s_n$).

Под корнем находится произведение относительного размера двух групп ($n_0$ и $n_1$ — это размеры групп, $n$ — общее число наблюдений).

Коэффициент точечно-бисериальной корреляции находится в диапазоне от $-1$ до $1$ и интерпретируется так же, как и коэффициент корреляции Пирсона.

Выше приведена формула для генеральной совокупности. Если нам доступна лишь выборка, формула выглядит следующим образом.

$$ r_{pb} = frac{M_1-M_0}{s_{n-1}} sqrt{frac{n_1 n_0}{n(n-1)}} $$

СКО ($s_{n-1}$) в этом случае также рассчитывается по формуле для выборки. Приведем пример.

Пример расчета на Питоне

Подгрузим датасет о вине из библиотеки sklearn. На основе свойств вин нам предлагается спрогнозировать один из трех классов вина (классы 0, 1 и 2). Так как нам нужна дихотомическая переменная, удалим наблюдения, относящиеся к классу 2.

# из модуля datasets библиотеки sklearn импортируем датасет о вине

from sklearn import datasets

data = datasets.load_wine()

# превратим его в датафрейм

wine = pd.DataFrame(data.data, columns = data.feature_names)

# добавим целевую переменную

wine[‘target’] = data.target

# оставим только классы 0 и 1

wine = wine[wine.target != 2]

# убедимся, что в целевой переменной осталось только два класса

np.unique(wine.target)

Найдем корреляцию между целевой переменной и содержанием пролина (proline).

# оставим только интересующие нас столбцы

wine = wine[[‘proline’, ‘target’]]

wine.head(3)

Теперь напишем функцию для расчета точечно-бисериальной корреляции (будем использовать формулу для выборки).

# объявим функцию для расчета точечно-бисериальной корреляции

# функция будет принимать два параметра: количественную и качественную переменные

def pbc(continuous, binary):

# преобразуем количественную переменную в массив Numpy

continuous_values = np.array(continuous)

# классы качественной переменной превратим в нули и единицы

binary_values = np.unique(binary, return_inverse = True)[1]

# создадим две подгруппы количественных наблюдений

# в зависимости от класса дихотомической переменной

group0 = continuous_values[np.argwhere(binary_values == 0).flatten()]

group1 = continuous_values[np.argwhere(binary_values == 1).flatten()]

# найдем средние групп,

mean0, mean1 = np.mean(group0), np.mean(group1)

# а также длины групп и всего датасета

n0, n1, n = len(group0), len(group1), len(continuous_values)

# рассчитаем СКО количественной переменной

std = continuous_values.std()

# подставим значения в формулу

return (mean1 – mean0) / std * np.sqrt( (n1 * n0) / (n * (n–1)) )

Применим эту функцию для нахождения корреляции между пролином и классом вина.

pbc(wine[‘proline’], wine[‘target’])

Для расчета корреляции мы также можем воспользоваться функцией из библиотеки Scipy.

# импортируем модуль stats из библиотеки scipy

from scipy import stats

# передадим данные в функцию и выведем первый результат[0]

stats.pointbiserialr(wine[‘proline’], wine[‘target’])[0]

Небольшие различия связаны с тем, что функция библиотеки Scipy использует формулу для генеральной совокупности.

Что интересно, математически коэффициент точечно-бисериальной корреляции дает тот же результат, что и коэффициент корреляции Пирсона.

# сравним в корреляцией Пирсона

wine.corr().iloc[0,1]

Пояснения к коду

Сделаем пояснения к приведенному коду. Упростим пример и предположим, что нам нужно рассчитать, есть ли зависимость между количеством сна и результатом экзамена.

# количество сна в часах поместим в массив Numpy

sleep = np.array([6, 8, 9, 7])

# результат будет записан с помощью двух категорий pass и fail

exam = [‘pass’, ‘fail’, ‘pass’, ‘fail’]

Для расчета точечно-бисериальной корреляции нам нужно разделить данные о сне в зависимости от результата экзамена на две группы. В первую очередь, преобразуем строковые значения переменной exam в числа. Для этого, в частности, мы можем использовать функцию np.unique() с параметром return_inverse = True.

exam_encoded = np.unique(exam, return_inverse = True)

exam_encoded

(array([‘fail’, ‘pass’], dtype='<U4′), array([1, 0, 1, 0]))

Вторым результатом [1] будут числовые значения категорий. Теперь используем функцию np.argwhere(), чтобы найти индексы тех, кто сдал экзамены и тех, кто не сдал.

# функция выводит индексы элементов, соответствующих заданному условию

fail_index = np.argwhere(exam_encoded[1] == 0)

pass_index = np.argwhere(exam_encoded[1] == 1)

# студенты, провалившие тест, должны быть на втором и четвертом местах

fail_index

# сдавшие – на первом и третьем

pass_index

Остается убрать второе измерение массивов.

fail_index, pass_index = fail_index.flatten(), pass_index.flatten()

(array([1, 3]), array([0, 2]))

Теперь используем индексы для группировки часов сна в зависимости от результатов экзамена.

sleep[fail_index], sleep[pass_index]

(array([8, 7]), array([6, 9]))

Теперь мы можем легко посчитать нужные метрики и подставить их в формулу точечно-бисериальной корреляции.

Корреляционное отношение

Корреляционное отношение (correlation ratio) выявляет взаимосвязь между количественной переменной и категориальной переменной с любым количеством категорий. Смысл этой метрики лучше всего понять на простом примере из Википедии⧉.

Простой пример

Предположим, что у нас есть результаты экзаменов по трем предметам (алгебре, геометрии и статистике), и нам нужно понять, есть ли взаимосвязь между предметом и поставленными оценками. Взглянем на данные:

алгебра: 45, 70, 29, 15, 21 (5 оценок)
геометрия: 40, 20, 30, 42 (4 оценки)
статистика: 65, 95, 80, 70, 85, 73 (6 оценок)

Шаг 1. Найдем средние значения внутри каждой группы и общее среднее всех наблюдений.

алгебра: 36
геометрия: 33
статистика: 78
общее среднее: 52

Шаг 2. Теперь найдем, насколько наблюдения в каждой из групп отличаются от группового среднего. Возведем результаты в квадрат для того, чтобы положительные и отрицательные значения не взаимоудалялись, и сложим их. Например, для алгебры сумма квадратов отклонений от среднего будет равна

$$ (36-45)^2+(36-70)^2+(36-29)^2+(36-15)^2+(36-21)^2 = 1959 $$

Для геометрии — 308, для статистики — 600. Сложим внутригрупповые отклонения от среднего и получим $1959+308+600=2860$

Сумма квадратов отклонений всех наблюдений от общего среднего составит 9640.

Шаг 3. Теперь выясним, какую долю в общей дисперсии составляет внутригрупповая дисперсия. Для этого разделим 2860 на 9640.

$$ frac{2860}{9640} approx 0,29668 $$

Соответственно доля не объясненных внутригрупповой дисперсией отклонений (ее принято обозначать греческой буквой $eta$, «эта») составляет

$$ eta^2 = 1-frac{2860}{9640} approx 0,70332 $$

Логично предположить, что чем выше доля не объясненных внутригрупповыми отклонениями дисперсии (чем выше $eta^2$), тем большую важность имеет дисперсия между группами. Другими словами, тем важнее отклонения между предметами, а не между оценками внутри каждого предмета.

Значит, чем выше $eta^2$, тем теснее связь между категориями и количественными оценками.

Шаг 4. Извлечем корень из получившегося значения для того, чтобы вернуться к исходным единицам измерения.

$$ eta = sqrt{0,70332} approx 0,83864 $$

Подведем итог. Корреляционное отношение изменяется от 0 до 1. Если показатель равен нулю, общая дисперсия объясняется исключительно внутригрупповыми отклонениями и связи между качественной и количественной переменными нет. Если показатель равен единице, общая дисперсия полностью объясняется только дисперсией между группами и связь между переменными велика.

Можно также сказать, что если $eta$ равна нулю, то внутригрупповые средние одинаковы, если $eta$ равна единице, все значения в каждой из категорий должны быть одинаковы (например, все студенты по алгебре должны получить одинаковую оценку и т.д.).

Еще один способ расчета

Для расчета корреляционного отношения можно также найти взвешенные по количеству элементов квадраты отклонений общего среднего от внутригрупповых средних. Для примера выше арифметика выглядит следующим образом

$$ 5(36-52)^2+4(33-52)^2+6(78-52)^2 = 6780 $$

Обратите внимание, это то же самое, что и $9640-2860=6780$, то есть сумма отклонений, не объясняемых внутригрупповой дисперсией. Таким образом,

$$ eta^2 = frac{6780}{9640} approx 0,70332 $$

$$ eta = sqrt{0,70332} approx 0,83864 $$

Остается написать функцию для расчета корреляционного отношения на Питоне.

Код на Питоне

Используем те же данные, что и в примере выше.

# создадим датафрейм с результатами экзаменов по трем предметам

test = pd.DataFrame({

# используем список с названиями предметов

‘subject’ : [‘algebra’] * 5 + [‘geometry’] * 4 + [‘stats’] * 6,

# и соответствующими оценками

‘score’ : [45, 70, 29, 15, 21, 40, 20, 30, 42, 65, 95, 80, 70, 85, 73 ]

})

Вначале возьмем значения оценок, рассчитаем сумму квадратов отклонений от среднего значения, а также закодируем категориальные переменные числами. Для этого как и ранее в случае точечно-бисериальной корреляцией используем функцию np.unique() с параметров return_inverse = True.

# возьмем значения оценок

values = np.array(test.score)

# и рассчитаем сумму квадратов отклонений от среднего значения

ss_total = np.sum((values.mean() – values) ** 2)

# закодируем категории предметов числами

cats = np.unique(test.subject, return_inverse = True)[1]

cats

array([0, 0, 0, 0, 0, 1, 1, 1, 1, 2, 2, 2, 2, 2, 2])

Теперь применим первый вариант расчета корреляционного отношения.

# объявим переменную для внутригрупповой дисперсии

ss_ingroups = 0

# в цикле, состоящем из количества категорий

for c in np.unique(cats):

# вычленим группу оценок по каждому предмету

group = values[np.argwhere(cats == c).flatten()]

# найдем суммы квадратов отклонений значений от групповых средних

# и сложим эти результаты для каждой группы

ss_ingroups += np.sum((group.mean() – group) ** 2)

# найдем долю внутригрупповой дисперсии и вычтем ее из единицы

eta_squared = 1 – ss_ingroups/ss_total

# найдем корень из предыщущего значения

eta = np.sqrt(eta_squared)

# это и будет корреляционное отношение

eta

Напомню, что использование функции np.argwhere() мы уже рассмотрели ранее на этом занятии. Рассчитаем по второму варианту.

# объявим переменную для межгрупповой дисперсии

ss_betweengroups = 0

# в цикле, состоящем из количества категорий,

for c in np.unique(cats):

# вычленим группу оценок по каждому предмету

group = values[np.argwhere(cats == c).flatten()]

# для каждой группы

# найдем взвешенный по количеству элементов в группе

# квадрат отклонения группового среднего от общего среднего

# и сложим результаты

ss_betweengroups += len(group) * (group.mean() – values.mean()) ** 2

# найдем долю межгрупповой дисперсии

eta_squared = ss_betweengroups/ss_total

# найдем корень из предыщущего значения

eta = np.sqrt(eta_squared)

# это и будет корреляционное отношение

eta

Мы готовы написать функции.

# вариант 1

def correlation_ratio1(numerical, categorical):

values = np.array(numerical)

ss_total = np.sum((values.mean() – values) ** 2)

cats = np.unique(categorical, return_inverse = True)[1]

ss_ingroups = 0

for c in np.unique(cats):

group = values[np.argwhere(cats == c).flatten()]

ss_ingroups += np.sum((group.mean() – group) ** 2)

return np.sqrt(1 – ss_ingroups/ss_total)

# проверим результат

correlation_ratio1(test.score, test.subject)

# вариант 2

def correlation_ratio2(numerical, categorical):

values = np.array(numerical)

ss_total = np.sum((values.mean() – values) ** 2)

cats = np.unique(categorical, return_inverse = True)[1]

ss_betweengroups = 0

for c in np.unique(cats):

group = values[np.argwhere(cats == c).flatten()]

ss_betweengroups += len(group) * (group.mean() – values.mean()) ** 2

return np.sqrt(ss_betweengroups/ss_total)

# проверим результат

correlation_ratio2(test.score, test.subject)

Подведем итог

Для удобства, давайте обобщим, какие методы и когда можно использовать.

Если речь идет о двух количественных переменных мы можем использовать:
- коэффициент Пирсона, если речь идет о выявлении линейной зависимости
- коэффициенты Спирмена и Кендалла, если требуется оценить нелинейную взаимосвязь
В случае двух категориальных переменных, подойдут:
- уже упомянутые коэффициенты Спирмена и Кендалла для порядковых категорий, а также
- коэффициент неопределенности Тиля
Когда перед нами одна количественная и одна категориальная переменные, мы можем рассчитать:
- точечно-бисериальный коэффициент корреляции, в случае, если категориальная переменная имеет дихотомическую шкалу; или
- корреляционное отношение в случае множества категорий

Вопросы для закрепления

Вопрос. Чем параметрические тесты отличаются от непараметрических?

Посмотреть правильный ответ

Ответ: параметрический тест показывает корректный результат, если данные, на которых он основывается соответствуют определенным критериям или допущениям, для непараметрического теста такие критерии отсутствуют.

При этом обратите внимание, отсутствие допущений не отменяет ограничения на применение тестов только к определенным типам данных. Например, метод Спирмена, как уже было сказано, не подойдет для выявления немонотонной зависимости.

Вопрос. При расчете коэффициента корреляции Пирсона, что дает деление ковариации на произведение СКО двух переменных $s_x s_y$?

Посмотреть правильный ответ

Ответ: таким образом мы выражаем любую ковариацию как долю от произведения двух СКО и, как следствие, можем измерять силу взаимосвязи двух переменных и сравнивать коэффициенты корреляции между собой.

Вопрос. Что такое симметричность и несимметричность корреляционного метода?

Посмотреть правильный ответ

Ответ: симметричный метод покажет одинаковую силу взаимосвязи переменной X с переменной Y, и переменной Y с переменной X даже если в действительности взаимосвязь не одинаковая; несимметричный метод покажет разную корреляцию X с Y и Y с X, если такое различие действительно существует.

Полезные ссылки

Библиотека dython⧉. Прямые ссылки на документацию⧉ и исходный код⧉ функций.

Корреляция показывает степень совместного изменения двух признаков. При этом, как уже было сказано, в корреляционном анализе нет зависимых и независимых переменных. Они эквивалентны.

Количественным предсказанием одной переменной (зависимой) на основании другой (независимой) занимается регрессионный анализ.

Источник

Стохастический Градиентный Спуск (SGD) имеет достаточно простую запись:

$$
x_{k+1} = x_k – alpha_k g_k.
$$

Здесь $g_k$ — это некоторая аппроксимация градиента целевой функции $nabla f(x_k)$ в точке $x_k$, называемая стохастическим градиентом (или просто стох. градиентом), $alpha_k > 0$ — это размер шага (stepsize, learning rate) на итерации $k$. Для простоты мы будем считать, что $alpha_k = alpha > 0$ для всех $k geq 0$. Обычно предполагается, что стох. градиент является несмещённой оценкой $nabla f(x_k)$ при фиксированном $x_k$: $mathbb{E}left(g_k mid x_kright) = nabla f(x_k)$.

Доказательство сходимости

Зададимся следующим вопросом: с какой скоростью и в каком смысле SGD сходится к решению и сходится ли? Во-первых, как и во многих работах по стохастической оптимизации, нас будет интересовать сходимость метода в среднем, т.е. оценки на $mathbb{E}left(vphantom{frac14}vertvert x_k – x_astvertvert^2right)$ или $mathbb{E}left(f(x_k) – f(x_ast)right)$, где $x_ast$ — решение задачи (для простоты будем считать, что оно единственное).

Во-вторых, чтобы SGD сходился в указанном смысле, необходимо ввести дополнительные предположения. Действительно, например, если дисперсия стох. градиента не ограничена $mathbb{E}left(vphantom{frac14}vertvert g_k – nabla f(x_k)vertvert^2 mid x_kright) = infty$, то $mathbb{E}left(vphantom{frac14}vertvert x_k – x_astvertvert^2right) = infty$ и никаких разумных гарантий доказать не удаётся. Поэтому дополнительно к несмещённости часто предполагается, что дисперсия равномерно ограничена: предположим, что существует такое число $sigma ge 0$, что для всех $k ge 0$ выполнено

$$
mathbb{E}left(left.vphantom{frac14}vertvert g_k – nabla f(x_k)vertvert^2right| x_kright) leq sigma^2.
$$

Данное предположение выполнено, например, для задачи логистической регрессии (поскольку в данной задаче норма градиентов слагаемых ограничена), но в то же время является весьма обременительным. Его можно заменить на более реалистичные предположения, что мы немного затронем далее. Однако при данном предположении анализ SGD является очень простым и полезным для дальнейших обобщений и рассуждений.

Для простоты везде далее мы будем считать, что функция $f$ является $L$-гладкой и $mu$-сильно выпуклой, т.е. для всех $x, y in mathbb{R}^d$ выполнены неравенства

$$
vertvertnabla f(x) – nabla f(y)vertvert leq Lvertvert x-yvertvert,
$$

$$
f(y) geq f(x) + langlenabla f(x), y- x rangle + frac{mu}{2}vertvert y – xvertvert^2.
$$

Теорема. Предположим, что $f$ является $L$-гладкой и $mu$-сильно выпуклой, стох. градиент $g_k$ имеет ограниченную дисперсию, и размер шага удовлетворяет $0 < alpha leq 1/L$. Тогда для всех $k geq 0$ выполняется неравенство

$$
mathbb{E}left(vphantom{frac14}vertvert x_k – x_{ast}vertvert^2right) leq (1 – alphamu)^kvertvert x_0 – x_{ast}vertvert^2 + frac{alphasigma^2}{mu}.
$$

Доказательство. Используя выражение для $x_{k+1}$, мы выводим

$$
vertvert x_{k+1} – x_ast vertvert^2 = vertvert x_k – x_{ast} – alpha g_kvertvert^2
= vertvert x_k – x_{ast}vertvert^2 – 2alpha langle x_k – x_{ast}, g_k rangle + alpha^2 vertvert g_kvertvert^2
$$

Далее мы берём условное матожидание $mathbb{E}left(cdotmid x_kright)$ от левой и правой частей и получаем:

$$
mathbb{E}left(left.vphantom{frac14}vertvert x_{k+1} – x_astvertvert^2right| x_kright) = vertvert x_k – x_{ast}vertvert^2 – 2alphamathbb{E}left( langle x_k – x_{ast}, g_k rangle mid x_kright) + alpha^2 mathbb{E}left(left.vphantom{frac14}vertvert g_kvertvert^2right| x_kright)
= vertvert x_k – x_{ast}vertvert^2 – 2alphaleftlangle x_k – x_{ast}, mathbb{E}left(g_k mid x_kright) rightrangle + alpha^2 mathbb{E}left(left.vphantom{frac14}vertvert g_kvertvert^2right| x_kright)
= vertvert x_k – x_{ast}vertvert^2 – 2alphalangle x_k – x_{ast}, nabla f(x_k)rangle + alpha^2 mathbb{E}left(left.vphantom{frac14}vertvert g_kvertvert^2right| x_kright).
$$

Следующий шаг в доказательстве состоит в оценке второго момента $mathbb{E}left(vphantom{frac14}vertvert g_kvertvert^2 mid x_kright)$. Используя предположение об ограниченности дисперсии стох. градиента, мы выводим:

$$
mathbb{E}left(left.vphantom{frac14}vertvert g_kvertvert^2right| x_kright) = mathbb{E}left(left.vphantom{frac14}vertvertnabla f(x_k) + g_k – nabla f(x_k)vertvert^2right| x_kright)
= vertvertnabla f(x_k)vertvert^2 + mathbb{E}left(langle nabla f(x_k), g_k – nabla f(x_k) rangle mid x_kright) + mathbb{E}left(left.vphantom{frac14}vertvert g_k – nabla f(x_k)vertvert^2 right| x_kright)
= vertvertnabla f(x_k)vertvert^2 + leftlangle nabla f(x_k), mathbb{E}left(g_k – nabla f(x_k) mid x_kright)rightrangle + mathbb{E}left(left.vphantom{frac14}vertvert g_k – nabla f(x_k)vertvert^2 right| x_kright)
= vertvertnabla f(x_k)vertvert^2 + mathbb{E}left(left.vphantom{frac14}vertvert g_k – nabla f(x_k)vertvert^2 right| x_kright)
leq vertvertnabla f(x_k)vertvert^2 + sigma^2
$$

Чтобы оценить сверху $vertvertnabla f(x_k)vertvert^2$, мы используем следующий факт, справедливый для любой выпуклой $L$-гладкой функции $f$ (см. книгу Ю. Е. Нестерова “Методы выпуклой оптимизации”, 2010):

$$
vertvertnabla f(x) – nabla f(y)vertvert^2 leq 2Lleft(f(x) – f(y) – langle nabla f(y), x- y rangleright).
$$

Беря в этом неравенстве $x = x_k$, $y = x_ast$ и используя $nabla f(x_ast) = 0$, получаем

$$
mathbb{E}left(left.vphantom{frac14}vertvert g_kvertvert^2right| x_kright) leq 2Lleft(f(x_k) – f(x_ast)right) + sigma^2.
$$

Далее мы подставляем эту оценку в выражение для $mathbb{E}left(vertvert x_{k+1} – x_astvertvert^2 mid x_kright)$:

$$
mathbb{E}left(left.vphantom{frac14}vertvert x_{k+1} – x_astvertvert^2right| x_kright) leq vertvert x_k – x_{ast}vertvert^2 – 2alphalangle x_k – x_{ast}, nabla f(x_k)rangle + 2alpha^2Lleft(f(x_k) – f(x_ast)right) + alpha^2sigma^2.
$$

Остаётся оценить скалярное произведение в правой части неравенства. Это можно сделать, воспользовавшись сильной выпуклостью функции $f$: из

$$
f(x_ast) geq f(x_k) + langlenabla f(x_k), x_ast – x_k rangle + frac{mu}{2}vertvert x_ast – x_kvertvert^2
$$

следует

$$
langlenabla f(x_k), x_k – x_ast rangle geq f(x_k) – f(x_ast) + frac{mu}{2}vertvert x_k – x_astvertvert^2.
$$

Используя это неравенство в выведенной ранее верхней оценке на $mathbb{E}left(vertvert x_{k+1} – x_astvertvert^2mid x_kright)$, мы приходим к следующему неравенству:

$$
mathbb{E}left(left.vphantom{frac14}vertvert x_{k+1} – x_astvertvert^2right| x_kright) leq (1-alphamu)vertvert x_k – x_{ast}vertvert^2 -2alpha(1 – alpha L)left(f(x_k) – f(x_ast)right) + alpha^2sigma^2
leq (1-alphamu)vertvert x_k – x_{ast}vertvert^2 + alpha^2sigma^2,
$$

где в последнем неравенстве мы воспользовались неотрицательностью $2alpha(1 – alpha L)left(f(x_k) – f(x_ast)right)$, что следует из $0 < alpha leq 1/L$ и $f(x_k) geq f(x_ast)$. Чтобы получить результат, заявленный в теореме, нужно взять полное мат. ожидание от левой и правой частей полученного неравенства (воспользовавшись при этом крайне полезным свойством условного мат. ожидания — tower property: $mathbb{E}left(mathbb{E}left(cdotmid x^kright)right) = mathbb{E}left(cdotright)$)

$$
mathbb{E}left(vphantom{frac14}vertvert x_{k+1} – x_astvertvert^2right) leq (1-alphamu)mathbb{E}left(vphantom{frac14}vertvert x_k – x_{ast}vertvert^2right) + alpha^2sigma^2,
$$

а затем, применяя это неравенство для $mathbb{E}left(vphantom{frac14}vertvert x_k – x_{ast}vertvert^2right)$, $mathbb{E}left(vphantom{frac14}vertvert x_{k-1} – x_{ast}vertvert^2right)$, $ldots$ , $mathbb{E}left(vphantom{frac14}vertvert x_1 – x_{ast}vertvert^2right)$, получим

$$
mathbb{E}left(vphantom{frac14}vertvert x_{k+1} – x_astvertvert^2right) leq (1-alphamu)^{k+1}vertvert x_0 – x_{ast}vertvert^2 + alpha^2sigma^2sumlimits_{t=0}^k (1-alphamu)^t
leq (1-alphamu)^{k+1}vertvert x_0 – x_{ast}vertvert^2 + alpha^2sigma^2sumlimits_{t=0}^infty (1-alphamu)^t
= (1 – alphamu)^{k+1}vertvert x_0 – x_{ast}vertvert^2 + frac{alphasigma^2}{mu},
$$

что и требовалось доказать.

Данный результат утверждает, что SGD с потоянным шагом сходится линейно к окрестности решения, радиус которой пропорционален $tfrac{sqrt{alpha} sigma}{sqrt{mu}}$. Отметим, что чем больше размер шага $alpha$, тем быстрее SGD достигает некоторой окрестности решения, в которой продолжает осциллировать. Однако чем больше размер шага, тем больше эта окрестность. Соответственно, чтобы найти более точное решение, необходимо уменьшать размер шага в SGD. Этот феномен хорошо проиллюстрирован здесь.

Теорема выше доказана при достаточно обременительных предположениях: мы предположили, что функция является сильно выпуклой, $L$-гладкой и стох. градиент имеет равномерно ограниченную дисперсию. В практически интересных задачах данные условия (в данном виде) выполняются крайне редко. Тем не менее, выводы, которые мы сделали из доказанной теоремы, справедливы для многих задач, не удовлетворяющих введённым предположениям (во многом потому, что указанные свойства важны лишь на некотором компакте вокруг решения задачи, что в свою очередь не так и обременительно).

Более того, если мы сделаем немного другое предположение о стохастических градиентах, то сможем покрыть некоторые случаи, когда дисперсия не является равномерно ограниченной на всём пространстве. Предположим теперь, что $g_k = nabla f_{xi_k}(x_k)$, где $xi_k$ просэмплировано из некоторого распределения $cal D$ независимо от предыдущих итераций, $f(x) = mathbb{E}_{xisim cal D}left(f_{xi}(x)right)$ и $f_{xi}(x)$ является выпуклой и $L_{xi}$-гладкой для всех $xi$ (данное предположение тоже можно ослабить, но для простоты изложения остановимся именно на такой формулировке). Будем называть данные условия предположением о выпуклых гладких стохастчиеских реализациях. Они выполнены, например, для задач линейно регрессии и логистической регрессии.

В таком случае, для точек, сгенерированных SGD, справедливо, что SGD с потоянным шагом сходится линейно к окрестности решения, радиус которой пропорционален $tfrac{sqrt{alpha} sigma}{sqrt{mu}}$. Отметим, что чем больше размер шага $alpha$, тем быстрее SGD достигает некоторой окрестности решения, в которой продолжает осциллировать. Однако чем больше размер шага, тем больше эта окрестность. Соответственно, чтобы найти более точное решение, необходимо уменьшать размер шага в SGD. Этот феномен хорошо проиллюстрирован здесь.

В таком случае, для точек, сгенерированных SGD, справедлив следующий результат.

Теорема. Предположим, что $f$ является $L$-гладкой и $mu$-сильно выпуклой, стохастчиеские реализации являются выпуклыми и гладкими, и размер шага удовлетворяет $0 < alpha leq 1/2L_{max}$, где $L_{max} = max_{xisim cal D} L_{xi}$. Тогда для всех $k geq 0$ выполняется неравенство

$$
mathbb{E}left(vphantom{frac14}vertvert x_k – x_{ast}vertvert^2right) leq (1 – alphamu)^kvertvert x_0 – x_{ast}vertvert^2 + frac{2alphasigma_ast^2}{mu},
$$

где $sigma_ast^2 = mathbb{E}_{xisim cal D}vertvertnabla f_{xi}(x_ast)vertvert^2$.

Доказательство. Аналогично предыдущей доказательству предыдущей теоремы, получаем

$$
mathbb{E}left(left.vphantom{frac14}vertvert x_{k+1} – x_astvertvert^2right| x_kright) = vertvert x_k – x_{ast}vertvert^2 – 2alphalangle x_k – x_{ast}, nabla f(x_k)rangle + alpha^2 mathbb{E}left(left.vphantom{frac14}vertvert g_kvertvert^2right| x_kright).
$$

Поскольку $f_{xi}(x)$ является выпуклой и $L_xi$-гладкой, имеем (см. книгу Ю. Е. Нестерова “Методы выпуклой оптимизации”, 2010):

$$
vertvertnabla f_{xi}(x) – nabla f_{xi}(y)vertvert^2 leq 2L_{xi}left(f_{xi}(x) – f_{xi}(y) – langle nabla f_{xi}(y), x – y rangleright).
$$

Применяя это неравенство для $x = x_k$, $y = x_{ast}$, получаем

$$
mathbb{E}left(left.vphantom{frac14}vertvert g_kvertvert^2right| x_kright) = mathbb{E}_{xi_k sim mathcal{D}}left(vertvertnabla f_{xi_k}(x_k) – nabla f_{xi_k}(x_ast) + nabla f_{xi_k}(x_ast)vertvert^2right)\
leq 2mathbb{E}_{xi_k sim mathcal{D}}left(vertvertnabla f_{xi_k}(x_k) – nabla f_{xi_k}(x_ast)vertvert^2right) + 2mathbb{E}_{xi_k sim mathcal{D}}left(vertvertnabla f_{xi_k}(x_ast)vertvert^2right)\
leq mathbb{E}_{xi_k sim mathcal{D}}left(4L_{xi_k}left(f_{xi_k}(x_k) – f_{xi_k}(x_ast) – langle nabla f_{xi_k}(x_ast), x_k – x_ast rangleright)right) + 2mathbb{E}_{xi sim mathcal{D}}left(vertvertnabla f_{xi_k}(x_ast)vertvert^2right)\
leq 4L_{max} left(f(x_k) – f(x_ast) – langle nabla f(x_ast), x_k – x_astrangleright) + 2sigma_{ast}^2 \
= 4L_{max} left(f(x_k) – f(x_ast)right) + 2sigma_{ast}^2,
$$

где во втором переходе мы воспользовались стандартным фактом: $vertvert a+bvertvert^2 leq vertvert avertvert^2 + vertvert bvertvert^2$ для любых $a, b in mathbb{R}^n$. Подставим полученное неравенство в выражение для $mathbb{E}left(vertvert x_{k+1} – x_astvertvert^2 mid x_kright)$, доказанное ранее:

$$
mathbb{E}left(left.vphantom{frac14}vertvert x_{k+1} – x_astvertvert^2right| x_kright) = vertvert x_k – x_{ast}vertvert^2 – 2alphalangle x_k – x_{ast}, nabla f(x_k)rangle + 4L_{max}alpha^2 left(f(x_k) – f(x_ast)right) + 2alpha^2sigma_{ast}^2.
$$

$$
f(x_ast) geq f(x_k) + langlenabla f(x_k), x_ast – x_k rangle + frac{mu}{2}vertvert x_ast – x_kvertvert^2
$$

следует

$$
langlenabla f(x_k), x_k – x_ast rangle geq f(x_k) – f(x_ast) + frac{mu}{2}vertvert x_k – x_astvertvert^2.
$$

Используя это неравенство в выведенной ранее верхней оценке на $mathbb{E}left(vertvert x_{k+1} – x_astvertvert^2 mid x_kright)$, мы приходим к следующему неравенству:

$$
mathbb{E}left(left.vphantom{frac14}vertvert x_{k+1} – x_astvertvert^2right| x_kright) leq (1-alphamu)vertvert x_k – x_{ast}vertvert^2 -2alpha(1 – 2alpha L_{max})left(f(x_k) – f(x_ast)right) + 2alpha^2sigma^2
leq (1-alphamu)vertvert x_k – x_{ast}vertvert^2 + 2alpha^2sigma_{ast}^2,
$$

где в последнем неравенстве мы воспользовались неотрицательностью $2alpha(1 – 2alpha L_{max})left(f(x_k) – f(x_ast)right)$, что следует из $0 < alpha leq 1/2L_{max}$ и $f(x_k) geq f(x_ast)$. Действуя по аналогии с доказательством предыдущей теоремы, получаем требуемый результат.

Выводы, которые можно сделать из данной теоремы, очень похожи на те, что мы уже сделали из прошлой теоремы. Главные отличия заключаются в том, что $L_{max}$ может быть гораздо больше $L$, т.е. максимальный допустимый размер шага $alpha$ в данной теореме может быть гораздо меньше, чем в предыдущей. Однако размер окрестности теперь зависит от дисперсии стох. градиента в решении $sigma_ast^2$, что может быть значительно меньше $sigma^2$.

Рассмотрим важный частный случай — задачи минимизации суммы функций:

$$
minlimits_{x in mathbb{R}^d}left{f(x) = frac{1}{n}sumlimits_{i=1}^n f_i(x)right}.
$$

Обычно $f_i(x)$ имеет смысл функции потерь на $i$-м объекте датасета. Предположим, что $f_i(x)$ — выпуклая и $L_i$-гладкая функция. Тогда выполняется предположение о выпуклых гладких стохастчиеских реализациях: действительно, достаточно задать $xi$ как случайное число из ${1,2,ldots,n}$, имеющее равномерное распределение. Тогда справедлив результат предыдущей теоремы с $L_{max} = max_{iin 1,ldots,n)}L_i$ и $sigma_ast^2 = tfrac{1}{n}sum_{i=1}^n vertvertnabla f_i(x_ast)vertvert^2$.

Для любого $K ge 0$ можно выбрать шаг в SGD следующим образом:

$$
text{если } K leq frac{2L_{max}}{mu}, gamma_k = frac{1}{2L_{max}},
text{если } K > frac{2L_{max}}{mu} text{ и } k < k_0, gamma_k = frac{1}{2L_{max}},
text{если } K > frac{2L_{max}}{mu} text{ и } k geq k_0, gamma_k = frac{1}{4L_{max} + mu(k-k_0)},
$$

где $k_0 = lceil K/2 rceil$. Тогда из доказанного выше результата следует (см. Лемму 3 из статьи С. Стиха), что после $K$ итераций

$$
mathbb{E}left(vphantom{frac14}vertvert x_K – x_astvertvert^2right) = cal Oleft(frac{L_{max} vertvert x_0 – x_astvertvert^2}{mu}expleft(-frac{mu}{L_{max}}Kright) + frac{sigma_{ast}^2}{mu^2 K}right).
$$

Таким образом, чтобы гарантировать $mathbb{E}left(vphantom{frac14}vertvert x_K – x_astvertvert^2right) leq varepsilon$, SGD требуется

$$
cal Oleft(frac{L_{max} }{mu}logleft(frac{L_{max} vertvert x_0 – x_astvertvert^2}{muvarepsilon}right) + frac{sigma_{ast}^2}{mu^2 varepsilon}right)
$$

итераций/подсчётов градиентов слагаемых. Чтобы гарантировать то же самое, градиентному спуску (GD) необходимо сделать

$$
cal Oleft(nfrac{L}{mu}logleft(frac{vertvert x_0 – x_astvertvert^2}{varepsilon}right)right)
$$

подсчётов градиентов слагаемых, поскольку каждая итерация GD требует $n$ подсчётов градиентов слагаемых (нужно вычислять полный градиент $nabla f(x) = tfrac{1}{n}sum_{i=1}^n nabla f_i(x)$). Можно показать, что $L leq L_{max} leq nL$, поэтому в худшем случае полученная оценка для SGD заведомо хуже, чем для GD. Однако в случае, когда $L_{max} = cal O(L)$, однозначного вывода сделать нельзя: при большом $varepsilon$ может доминировать первое слагаемое в оценке сложности SGD, поэтому в таком случае SGD будет доказуемо быстрее, чем GD (если пренебречь логарифмическими множителями).

Иными словами, чтобы достичь не очень большой точности решения, выгоднее использовать SGD, чем GD. В ряде ситуаций небольшой точности вполне достаточно, но так происходит не всегда. Поэтому возникает ествественный вопрос: можно ли так модифицировать SGD, чтобы полученный метод сходился линейно асимптотически к точному решению (а не к окрестности как SGD), но при этом стоимость его итераций была сопоставима со стоимостью итераций SGD? Оказывается, что да и соответствующие методы называются методами редукции дисперсии.

Методы редукции дисперсии

Перед тем, как мы начнём говорить о методах редукции дисперсии, хотелось бы раскрыть подробнее причину того, что SGD не сходится линейно асимптотически к точному решению. Мы рассмотрели анализ SGD в двух предположениях, и в обоих случаях нам требовалось вывести некоторую верхнюю оценку на второй момент стох. градиента, т.е. на $mathbb{E}left(vertvert g_kvertvert^2 mid x_kright)$. В обоих случаях эта оценка содержала некоторый константный член ($sigma^2$ или $2sigma_ast^2$ — зависит от рассматриваемого предположения), который потом возникал и в финальной оценке на $mathbb{E}left(vphantom{frac14}vertvert x_k – x_astvertvert^2right)$, препятствуя тем самым линейно сходимости метода. Конечно, это рассуждение существенно опирается на конкретный способ анализа метода, а потому не является строгим объяснением, почему SGD не сходится линейно.

Однако важно отметить, что оценка на $mathbb{E}left(vertvert g_kvertvert^2 mid x_kright)$ достаточно точно отражает поведение метода вблизи решения: даше если точка $x_k$ оказалась по какой-то причине близка к решению $x_ast$ (или даже просто совпала с решением), то $mathbb{E}left(vertvert g_kvertvert^2 mid x_kright)$ и, в частности, $mathbb{E}left(vertvert g_k – nabla f(x_k)vertvert^2 mid x_kright)$ будут порядка $sigma^2$ или $sigma_{ast}^2$. Следовательно, при следующем шаге метод с большой вероятностью отдалится от/выйдет из решения, поскольку $mathbb{E}left(vphantom{frac14}vertvert x_{k+1} – x_kvertvert^2right) = alpha^2mathbb{E}left(vphantom{frac14}vertvert g_kvertvert^2right) sim alpha^2sigma^2$ или $alpha^2sigma_{ast}^2$.

Из приведённых выше рассуждений видно, что дисперсия стох. градиента мешает методу сходится линейно к точному решению. Поэтому хотелось бы как-то поменять правило вычисления стох. градиента, чтобы выполнялись 3 важных свойства: (1) новый стох. градиент должен быть не сильно дороже в плане вычислений, чем подсчёт стох. градиента в SGD (градиента слагаемого), (2) новый стох. градиент должен быть несмещённой оценкой полного градиента $nabla f(x_k)$, и (3) дисперсия нового стох. градиента должна уменьшаться в процессе работы метода. Например, можно рассмотреть следующий стох. градиент:

$$
g_k = nabla f_{j_k}(x_k) + s_k,
$$

где $j_k$ выбирается случайно равновероятно из множества ${1, 2, ldots, n}$ и $mathbb{E}left(s_kmid x_kright) = 0$. В таком случае, будет выполнено свойство (2) из списка выше. Чтобы достичь желаемой цели, необходимо как-то специфицировать выбор случайного вектора $s_k$. Исторически одним из первых способов выбора $s_k$ был $s_k = -nabla f_{j_k}(w_k) + nabla f(w_k)$, где точка $w_k$ обновляется раз в $m sim n$ итераций:

$$
w_{k+1} = begin{cases} w_k, & text{if } k+1 mod m neq 0, x_{k+1}, & text{if } k+1 mod m = 0. end{cases}
$$

Данный метод называется Stochastic Variance Reduced Gradient (SVRG). Данный методы был предложен и проанализирован в NeurIPS статье Джонсона и Жанга в 2013 году. Теперь же убедимся, что метод удовлетворяет всем трём отмеченным свойствам. Начнём с несмещённости:

$$
g_k = nabla f_{j_k}(x_k) – nabla f_{j_k}(w_k) + nabla f(w_k),
$$

$$
mathbb{E}left(g_kmid x_kright) = frac{1}{n}sumlimits_{i=1}^n left(nabla f_{i}(x_k) – nabla f_{i}(w_k) + nabla f(w_k)right) = nabla f(x_k).
$$

Далее, вычисление $g_k$ подразумевает 2 подсчёта градентов слагаемых при $k mod m neq 0$ и $n+2$ подсчёта градентов слагаемых при $k mod m neq 0$. Таким образом, за $m$ последователльных итераций SVRG происходит вычисление $2(m-1) + n + 2 = 2m + n$ градиентов слагаемых, в то время как SGD требуется $m$ подсчётов градиентов слагаемых. Если $m = n$ (стандартный выбор параметра $m$), то $n$ итераций SVRG лишь в 3 раза дороже, чем $n$ итераций SGD. Иными словами, в среднем итерация SVRG не сильно дороже итерации SGD.

Наконец, если мы предположим, что метод сходится $mathbb{E}left(vphantom{frac14}vertvert x_k – x_astvertvert^2right) to 0$ (а он действительно сходится, см., например, доказательство вот тут), то получим, что $mathbb{E}left(vphantom{frac14}vertvert w_k – x_astvertvert^2right) to 0$, а значит $mathbb{E}left(vphantom{frac14}vertvert x_k – w_kvertvert^2right) to 0$ и $mathbb{E}left(vphantom{frac14}vertvertnabla f(w_k)vertvert^2right) to 0$. Но тогда в силу Липшицевости градиентов $f_i$ для всех $i=1,ldots,n$ имеем:

$$
mathbb{E}left(vphantom{frac14}vertvert g_kvertvert^2right) = mathbb{E}left(vphantom{frac14}vertvertnabla f_{j_k}(x_k) – nabla f_{j_k}(w_k) + nabla f(w_k)vertvert^2right)
leq 2mathbb{E}left(vphantom{frac14}vertvertnabla f_{j_k}(x_k) – nabla f_{j_k}(w_k)vertvert^2right) + 2mathbb{E}left(vphantom{frac14}vertvertnabla f(w_k)vertvert^2right)
leq 2L_{max} mathbb{E}left(vphantom{frac14}vertvert x_k – w_kvertvert^2right) + 2mathbb{E}left(vphantom{frac14}vertvertnabla f(w_k)vertvert^2right) to 0,
$$

а значит, дисперсия $g_k$ стремится к нулю.

Приведённые выше рассуждения не являются формальным доказательством сходимости метода, но частично объясняют, почему метод сходится и, самое главное, объясняют интуицию позади формул, задающих метод. Строгое доказательство можно прочитать вот тут. Мы же здесь приведём результат о сходимости немного другого метода — Loopless Stochastic Variance Reduced Gradient (L-SVRG), который был предложен в 2015 году и переоткрыт в 2019 году. Основное отличие от SVRG состоит в том, что точка $w_k$ теперь обновляется на каждой итерации с некоторой маленькой вероятностью $p sim 1/n$:

$$
w_{k+1} = begin{cases} w_k, & text{с вероятностью } 1-p, x_{k}, & text{с вероятностью } p. end{cases}
$$

Иными словами, L-SVRG имеет случайную длину цикла, в котором $w_k$ не обновляется. Вся интуиция и все наблюдения приведённые для SVRG выше, справедливы и для L-SVRG.

Можно доказать следующий результат.

Теорема. Предположим, что $f$ является $L$-гладкой, $mu$-сильно выпуклой и имеет вид суммы, функции $f_i$ являются выпуклыми и $L_i$-гладкими для всех $i=1,ldots, n$, и размер шага удовлетворяет $0 < alpha leq 1/6L_{max}$, где $L_{max} = max_{iin 1,ldots,n} L_{i}$. Тогда для всех $k geq 0$ для итераций L-SVRG выполняется неравенство

$$
mathbb{E}left(vphantom{frac14}vertvert x_k – x_{ast}vertvert^2right) leq left(1 – minleft{alphamu, frac{p}{2}right}right)^kV_0,
$$

где $V_0 = vertvert x_0 – x_astvertvert^2 + tfrac{4alpha^2}{p}sigma_0^2$, $sigma_0^2 = tfrac{1}{n}sum_{i=1}^n vertvertnabla f_i(x_0) – nabla f_i(x_ast)vertvert$.

Замечание. В частности, если $alpha = 1/6L_{max}$ и $p = 1/n$, то

$$
mathbb{E}left(vphantom{frac14}vertvert x_k – x_{ast}vertvert^2right) leq left(1 – minleft{frac{mu}{6L_{max}}, frac{1}{2n}right}right)^kV_0.
$$

Следовательно, чтобы гарантировать $mathbb{E}left(vphantom{frac14}vertvert x_k – x_astvertvert^2right) leq varepsilon$, L-SVRG требуется

$$
cal Oleft(left(n + frac{L_{max} }{mu}right)logleft(frac{V_0}{varepsilon}right)right)
$$

итераций/подсчётов градиентов слагаемых (в среднем). Напомним, что чтобы гарантировать то же самое, градиентному спуску (GD) необходимо сделать

$$
cal Oleft(nfrac{L}{mu}logleft(frac{L vertvert x_0 – x_astvertvert^2}{muvarepsilon}right)right)
$$

подсчётов градиентов слагаемых, поскольку каждая итерация GD требует $n$ подсчётов градиентов слагаемых (нужно вычислять полный градиент $nabla f(x) = tfrac{1}{n}sum_{i=1}^n nabla f_i(x)$). Можно показать, что $L leq L_{max} leq nL$, поэтому в худшем случае полученная оценка для L-SVRG не лучше, чем для GD. Однако в случае, когда $L_{max} = cal O(L)$, L-SVRG имеет сложность значительно лучше, чем GD (если пренебречь логарифмическими множителями).

В заключение этого раздела, хотелось бы отметить, что существуют и другие методы редукции дисперсии. Одним из самых популярных среди них является SAGA. В отличие от SVRG/L-SVRG, в методе SAGA хранится набор градиентов $nabla f_1(w_k^1), nabla f_2(w_k^2), ldots, nabla f_n(w_k^n)$. Здесь точка $w_k^i$ обозначает точку, в которой в последний раз был подсчитан градиент функции $i$ до итерации $k$. Формально это можно записать следующим образом:

$$
w_0^1 = w_0^2 = ldots = w_0^n,
$$

$$
g_k = nabla f_{j_k}(x_k) – nabla f_{j_k}(w_k^{j_k}) + frac{1}{n}sumlimits_{i=1}^n nabla f_{i}(w_k^{i}),
$$

$$
w_{k+1}^{j_k} = x_k, quad w_{k+1}^i = w_k^i text{ для всех } i neq j_k,
$$

$$
x_{k+1} = x_k – alpha g_k.
$$ Основное преимущество SAGA состоит в том, что не требуется вычислять полный градиент всей суммы по ходу работы метода, однако в начале требуется посчитать градиенты всех слагаемых (отмечаем здесь, что эта операция может быть гораздо дороже по времени, чем вычисление полного градиента) и, более того, требуется хранить $n$ векторов, что может быть недопустимо для больших датасетов. В плане теоретических гарантий SAGA и L-SVRG не отличимы.

Ниже приведён график с траекториями SGD (с постоянным шагом), L-SVRG и SAGA при решении задачи логистической регрессии. Как можно видеть из графика, SGD достаточно быстро достигает не очень высокой точности и начинает осциллировать вокруг решения. В то же время, L-SVRG и SAGA достигают той же точности медленнее, но зато не осциллируют вокруг решения, а продолжают сходится (причём линейно).

Сравнение работы SGD, L-SVRG и SAGA при решении задачи логистической регрессии на датасете gisette из библиотеки LIBVSM.

Источник

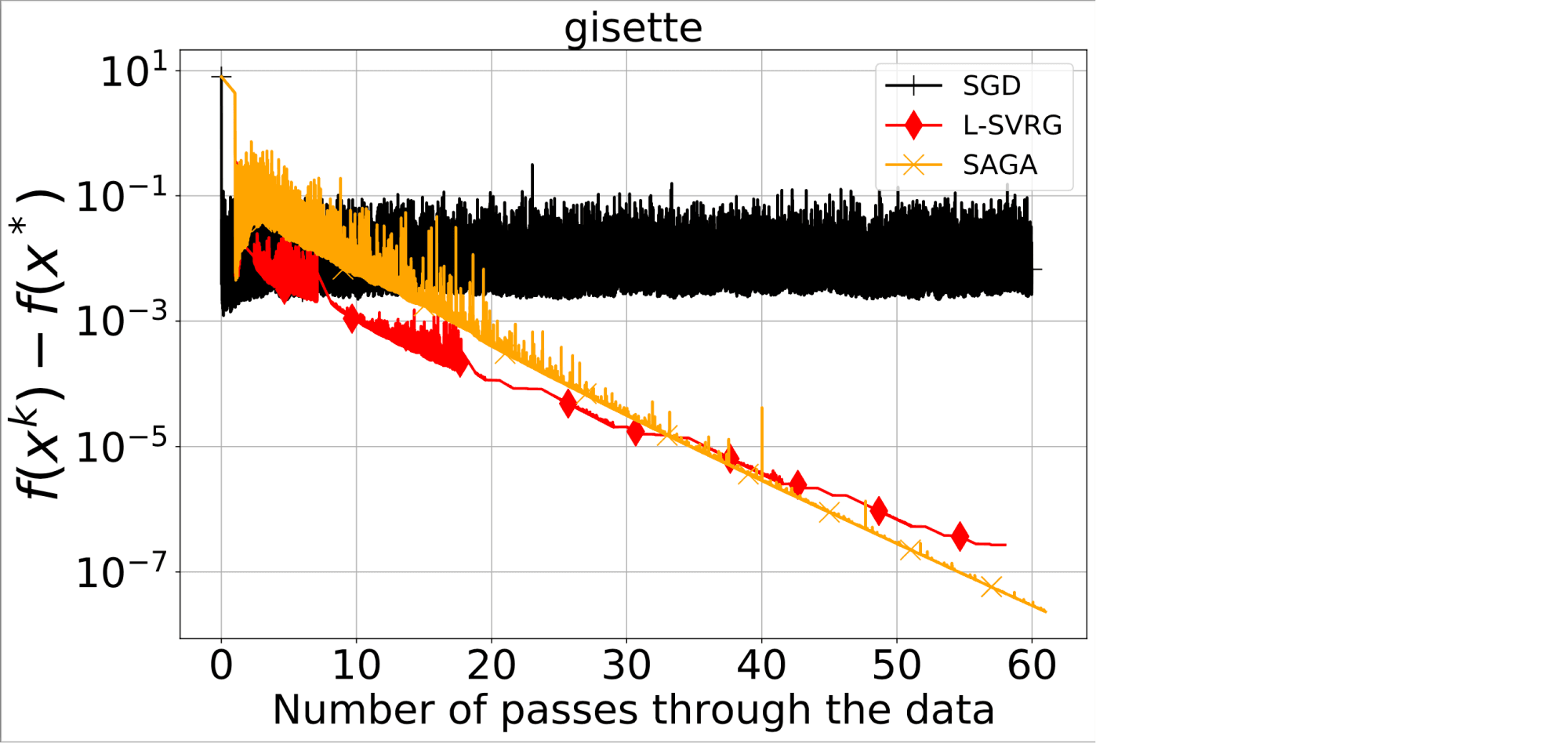
Знание математики — залог плюсовой игры. Можно не работать с покерными калькуляторами, ничего не понимать в диапазонах рук, но отрицать основы покерной математики глупо. Дисперсия — одно из фундаментальных понятий в теории игры. Что это такое, как рассчитать дисперсию, кто сумел обмануть дисперсию, а у кого это не вышло, советы по уменьшению влиянии дисперсии — обо всём этом расскажем прямо сейчас.

Что такое дисперсия?

В покере, как и в жизни, восприятие решает. Одни игроки верят в удачу, и всячески пытаются привлечь её. Другие верят в математику и продолжают бесконечный гринд. По сути, и любители, и профессионалы говорят на разных языках об одном и том же — о дисперсии.

Дисперсия — это отклонение между реальными результатами и математическим ожиданием на дистанции.

Например, вам выпали карманные Тузы. С этой стартовой комбинацией вы будете выигрывать в выставлениях против случайной руки в 4 случаях из 5. Соответственно, ваше математическое ожидание от розыгрыша этой руки в 5 случаях будет равняться +4бай-инам. Но вдруг что-то пошло не так, и вы проиграли все 5 олл-инов. В этом случае, ваш реальный выигрыш оказался -5 бай-инов. Такое отклонение реального результата от математического и есть дисперсия.

Иными словами, дисперсия — удача или неудача с точки зрения математики. Рассчитав дисперсию, можно реально увидеть влияние удачи в конкретной дисциплине. Если в 15% случаев вам не суждено выиграть в выставлении с АА, то вы обязаны попасть в эту выборку. Таковы правила игры.

Как рассчитать дисперсию?

Для расчета дисперсии в покере используются специальные калькуляторы. Калькулятор дисперсии не требует установки и его можно найти по запросу «Variance Calculator». К примеру, для расчета влияния дисперсии в турнирах нужно ввести количество игроков, количество призовых мест, бай-ин, рейк, ROI и количество турниров. После чего калькулятор выдаст такой график:

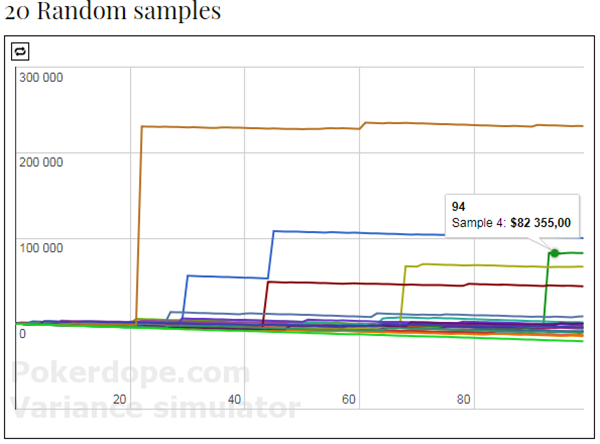
Мы рассчитали дисперсию для 100 турниров Sunday Million для игрока, показывающего на дистанции ROI 15%. Выиграть Sunday Million — мечта любого онлайн-игрока. Глядя на приз в $200.000 за первое место, самоуверенные любители регистрируются в главном событии воскресенья с верой, что в этот раз точно повезёт.

Но помимо 7.500-10.000 участников турнира против вас играет также дисперсия. За дистанцию мы взяли 100 турниров, график выдал 20 случайных вариантов развития событий, если вы отыграете 100 турниров. В единственном лучшем варианте на дистанцию в 100 турниров ваш профит составит $231.000. Но это единственный вариант на 1000 примеров.

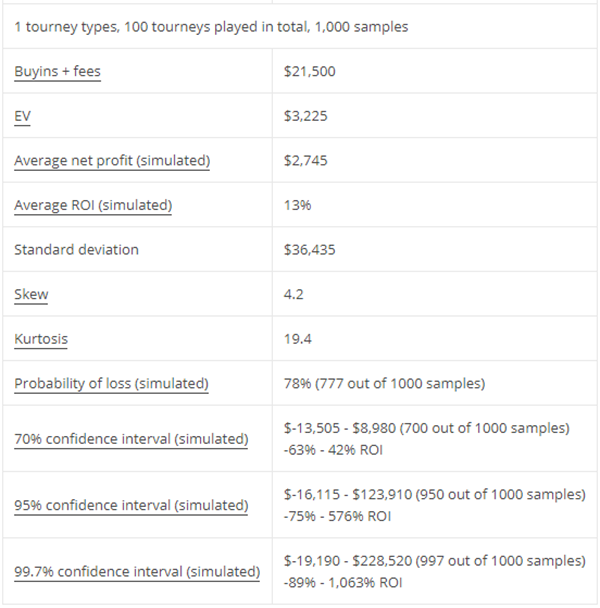
В этой таблице собрана статистическая информация. Стандартное отклонение дисперсии на 100 турниров Sunday Million = $36.435 или 170 бай-инов. В 78% случаев вы будете проигрывать всё.

Аналогично рассчитывается дисперсия для кэш-игр, только указываются другие вводные: винрейт / 100 рук, наблюдаемый винрейт / 100 рук, стандартное отклонение в бб/100 и количество рук.

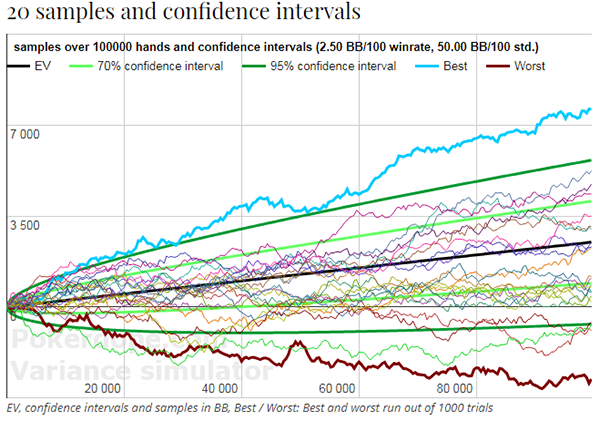
Они обманули дисперсию

Как в любом правиле, в дисперсии есть свои исключения. Истории известны случаи, когда игроки пренебрегали законами дисперсии, а, скорее, довольствовались правилом: «Пришёл. Увидел. Победил». Больше всего удивительных историй с обманом дисперсии ежегодно дарит WSOP.

В 2017 году одним из главных героев покерных новостных лет стал Джеймс Мур. Ему удалось то, что не под силу многим профессиональным игрокам. Джеймс Мур второй год подряд одержал победу в одном и том же турнире — $1,000 Super Seniors Event. Причём в 2016 году в этом турнире участвовало 1476 человек, а в 2017 — 1720. Калькулятор дисперсии показывает, что в 81% случаев Джеймс Мур должен был проиграть всё.

Джеймс Мур

В том же году случилась ещё одна удивительная история. Шейн Бакволл после 24 часов, проведённых в самолёте зарегистрировался за компанию со своим другом в первом для себя турнире WSOP по Лимитному Холдему, обыграл 615 игроков и получил золотой браслет и $178.000 призовых. После победы Шейн поделился в интервью, что не планирует больше играть в покер и мечтает свою жизнь посвятить готовке. Вот такой вот хит-энд-ран Мировой Серии и покера.

Шейн Бакволл

Это два случая, когда игроки сумели обмануть дисперсию. Но зачастую судьба распоряжается иначе, и даже профессиональные игроки из года в год штурмуют WSOP без попадания за финальный стол.

Кто не сумел обмануть дисперсию

Анатолий Филатов

Сложно представить, что Анатолий Филатов попал в список невезучих игроков. В онлайне карьера «NL_Profit» складывается очень удачно: общая сумма призовых во всех румах приближается к $3.000.000. Но на Мировой серии дела складываются не так удачно. С 2012 года Анатолий Филатов не пропустил ни одной серии WSOP. Причём играет очень плотную загрузку по нескольку десятков турниров. Но лучший кэш Анатолия — $28.389 (в турнире за $10.000). А ближе всего к браслету Анатолий оказался в 2015 году — 30-е место (в турнире на 1244 участника). Дисперсия в Вегасе не на стороне Анатолия.

Как уменьшить влияние дисперсии в покере?

Дисперсия в покере — это не хорошо и не плохо. Это нормально. Это то обстоятельство, с которым всем игрокам приходится смириться. Но чтобы дисперсия не съела ваш банкролл и чтобы она не била сильнее других, игроки придумали несколько правил, как нивелировать влияние дисперсии.

1. Соблюдайте банкролл-менеджмент

Первое правило успешного покериста — соблюдать банкролл-менеджмент. Суть простая: хороший игрок верит в свои силы и свой скилл, принимает во внимание фактор дисперсии и продолжает играть в покер, несмотря на её влияние. Отыгрывая огромную дистанцию, игроки стараются выйти на математическое ожидание от своей игры, естественно все уверены, что оно у них плюсовое. Именно поэтому многие профессиональные игроки, осознавая своё преимущество над полем, продолжают штурмовать WSOP в надежде, что дисперсия станет на их сторону.

2. Объединяйтесь в пулы

Этот способ борьбы особенно актуален для игроков Spin&Go, где дисперсия особенно велика. Суть его заключается в том, что игроки объединяются в команду, играют общим банкроллом и распределяют свой доход от игры по чипЕВ (chipEV). Цель у пула — отыграть максимально длинную дисциплину в надежде выйти на своё математическое ожидание от игры.

3. Игра в менее дисперсионные дисциплины

Не сможешь справиться с дисперсией — избегай её. Обратите внимание на другие дисциплины. Играйте кэш или Sit&Go на 9 человек или DoNы. В этих турнирах влияние дисперсии минимально.

Дисперсия не враг

Не нужно рассматривать дисперсию как врага, как обстоятельство, из-за которого вы никак не можете выиграть Sunday Million. Дисперсия — это то, что распределяет ваше преимущество на дистанции. Именно благодаря дисперсии в трансляциях финальных столов WSOP, EPT и других серий можно встретить домохозяйку, садовника или повара пиццерии. Дисперсия делает покер увлекательной и зрелищной игрой.

Живой покер в Минске

Живой покер в Харькове

Живой покер в Киеве

Живой покер в Тбилиси

Живой покер в Ереване

Живой покер в Сочи

Турниры по покеру в Сочи

Еще больше интересных и полезных статей из мира покера вы можете прочесть в нашем блоге. Также ищите покерные клубы по стране и городу, узнавайте о предстоящих покерных турнирах или кэш-играх на портале PokerDiscover.com.

Если вам понравилась статья, не забудьте поделиться ей с друзьями в социальных сетях.

Источник

Онлайн-калькулятор дисперсии поможет вам определить дисперсию, сумму квадратов и коэффициент дисперсии для определенного набора данных. Кроме того, этот калькулятор также отображает среднее значение и стандартное отклонение путем пошагового расчет дисперсии онлайн. Прочтите, чтобы узнать, как найти дисперсию онлайн и стандартное отклонение, используя формулу выборочной дисперсии.

Что такое дисперсия?

Дисперсия группы или набора чисел – это число, которое представляет «разброс» набора. Формально это квадрат отклонения набора от среднего и квадрат стандартного отклонения.

Другими словами, небольшая дисперсия означает, что точки данных имеют тенденцию быть близкими к среднему и очень близко друг к другу. Высокая дисперсия указывает на то, что точки данных далеки от среднего значения и друг от друга. Дисперсия – это среднее значение квадрата расстояния от каждой точки до среднего.

Типы дисперсии:

Вариация выборки: дисперсия выборки не охватывает всю возможную выборку (случайная выборка людей).

Дисперсия населения: дисперсия, которая измеряется для всего населения (например, всех людей).

Однако онлайн-калькулятор стандартного отклонения позволяет определить стандартное отклонение (σ) и другие статистические измерения данного набора данных.

Формулы отклонения:

Формула дисперсии совокупности

дисперсия формула (совокупности):

Дисперсия (обозначается как σ2) выражается как среднеквадратическое отклонение от среднего для всех точек данных. Мы пишем:

$$ σ2 = ∑ (xi – μ) ^ 2 / N $$

где,

σ2 – дисперсия;
μ – среднеквадратическое значение; а также
xᵢ представляет i-ю точку данных среди N общих точек данных.

Вы можете рассчитать его с помощью калькулятора дисперсии генеральной совокупности, в противном случае есть три шага для оценки дисперсии:

Чтобы найти разницу между средним значением точки, используйте формулу: xi – μ
Теперь возьмите в квадрат разницу между средним значением каждой точки: (xi – μ) ^ 2
Затем найдите среднее квадратическое отклонение от среднего: ∑ (xi – μ) ^ 2 / N.

Это дисперсия формула совокупности.

Пример формулы отклонения

Уравнение выборки дисперсии имеет следующий вид:

s2 = ∑ (xi – x̄) 2 / (N – 1)

где,

s2 – оценка дисперсии;

x – выборочное среднее; а также

xi – i-я точка данных среди N общих точек данных.

Как рассчитать дисперсию?

Чтобы найти среднее значение данного набора данных. Подставьте все значения и разделите на размер выборки n.

ni = 1x дюйм x = ∑ i = 1 nx дюйм

Теперь найдите среднюю разницу значений данных, вам нужно вычесть среднее значение данных и возвести результат в квадрат.

(хи – х) ^ 2 (хи – х) ^ 2

Затем вычислите квадратичные разности и сумму квадратов всех квадратичных разностей.

S = ∑ I = 1n (xi – x) ^ 2

Итак, найдите дисперсию, дисперсия формула генеральной совокупности:

Дисперсия = σ ^ 2 = Σ (xi – μ) ^ 2

Уравнение дисперсии набора данных выборки:

Дисперсия = s ^ 2 = Σ (xi – x) ^ {2n − 1}

Эти формулы запоминать не нужно. Чтобы вам было удобно, наш примерный калькулятор дисперсии выполняет все расчет дисперсии онлайн, связанные с дисперсией, автоматически, используя их.

Тем не менее, Калькулятор диапазона среднего среднего значения режима поможет вам рассчитать средний средний режим и диапазон для введенного набора данных.

Пример расчета

Давайте посчитаем дисперсию оценок пяти студентов на экзамене: 50, 75, 89, 93, 93. Выполните следующие действия:

Найдите среднее

Чтобы найти среднее значение (x), разделите сумму всех этих значений на количество точек данных:

х = (50 + 75 + 89 + 93 + 93) / 5

х̄ = 80

Вычислите разницу между средним значением и квадратом отличий от среднего. Следовательно, среднее значение равно 80, мы используем формулу для вычисления разницы от среднего:

xi – x̄

Первая точка – 50, поэтому разница от среднего составляет 50 – 80 = -30.

Квадрат отклонения от среднего – это квадрат предыдущего шага:

(xi – x̄) 2

Итак, квадрат отклонения равен:

(50 – 80) 2 = (-30) 2 = 900

В приведенной ниже таблице квадрат отклонения рассчитан на основе среднего значения всех результатов испытаний. Столбец «Среднее отклонение» – это результат минус 30, а столбец «Стандартное отклонение» – это столбец перед квадратом.

Счет	Отклонение от среднего	Квадратное отклонение
50	-30	900
75	-5	25
89	9	81
93	13	169
93	13	169

Рассчитайте стандартное отклонение и дисперсию

Затем используйте квадраты отклонений от среднего:

σ2 = ∑ (xi – x̄) 2 / N

σ2 = (900 + 25 + 81 + 169 + 169) / 5

σ2 = 268,5

дисперсия случайной величины онлайн результатов экзамена составила 268,8.

Как работает калькулятор дисперсии?

Онлайн-калькулятор дисперсии совокупности вычисляет дисперсию для заданных наборов данных. Вы можете просмотреть работу, проделанную для расчет дисперсии онлайн из набора данных, следуя этим инструкциям:

Вход:

Сначала введите значения набора данных через запятую.
Затем выберите дисперсию для выборки или совокупности.
Нажмите кнопку «Рассчитать», чтобы получить результаты.

Выход:

Калькулятор дисперсии выборки отображает дисперсию, стандартное отклонение, количество, сумму, среднее значение, коэффициент дисперсии и сумму квадратов.
Этот калькулятор также обеспечивает пошаговые вычисления дисперсии, коэффициента дисперсии и стандартного отклонения.

ЧАСТО ЗАДАВАЕМЫЕ ВОПРОСЫ:

В чем разница между стандартным отклонением и дисперсией?

Дисперсия – это квадрат отклонения от среднего, а стандартное отклонение – это квадратный корень из числа. Оба показателя отражают изменчивость распределения, но их единицы разные: стандартное отклонение определяется в той же единице, что и исходное значение (например, минуты или метры).

Значение высокой дисперсии – это плохо или хорошо?

Низкая дисперсия связана с меньшим риском и более низкой доходностью. Акции с высокой дисперсией обычно выгодны для агрессивных инвесторов с меньшим неприятием риска, в то время как акции с низкой дисперсией обычно выгодны для консервативных инвесторов с более низкой толерантностью к риску.

Каков диапазон отклонений?

Диапазон – это разница между высоким и низким значением. Поскольку используются только крайние значения, потому что эти значения будут сильно на него влиять. Чтобы найти диапазон отклонения, возьмите максимальное значение и вычтите минимальное значение.

Заключение:

Воспользуйтесь этим онлайн-калькулятором дисперсии, который работает как с выборкой, так и с наборами данных о генеральной совокупности, используя формулу генеральной и выборочной дисперсии. Это лучший образовательный калькулятор, который расскажет вам, как рассчитать дисперсию заданных наборов данных за доли секунды.

Other Languages: Variance Calculator, Varyans Hesaplama, Calculadora De Variancia, Kalkulator Varians, Kalkulator Wariancji, Výpočet Rozptylu, 分散計算.

Источник

Интервальный вариационный ряд и его характеристики

п.1. Построение интервального вариационного ряда по данным эксперимента

п.2. Гистограмма и полигон относительных частот, кумулята и эмпирическая функция распределения

п.3. Выборочная средняя, мода и медиана. Симметрия ряда

п.4. Выборочная дисперсия и СКО

п.5. Исправленная выборочная дисперсия, стандартное отклонение выборки и коэффициент вариации

п.6. Алгоритм исследования интервального вариационного ряда

п.7. Примеры

Дисперсия

Среднее квадратическое отклонение

Ковариация

Корреляция

Параметрические и непараметрические тесты

Коэффициент корреляции Пирсона

Особенности коэффициента Пирсона

Коэффициент Пирсона как скалярное произведение векторов

Коэффициент ранговой корреляции Спирмена

Монотонная зависимость

Категориальные порядковые данные

Коэффициент ранговой корреляции Кендалла

Коэффициент неопределенности

Определение и понятие симметричности теста

Как рассчитывается

Условная энтропия

Энтропия

U Тиля

Точечно-бисериальная корреляция

Формула

Пример расчета на Питоне

Пояснения к коду

Корреляционное отношение

Простой пример

Еще один способ расчета

Код на Питоне

Подведем итог

Вопросы для закрепления

Полезные ссылки

Доказательство сходимости

Методы редукции дисперсии

Что такое дисперсия?

Как рассчитать дисперсию?

Они обманули дисперсию

Кто не сумел обмануть дисперсию

Как уменьшить влияние дисперсии в покере?

1. Соблюдайте банкролл-менеджмент

2. Объединяйтесь в пулы

3. Игра в менее дисперсионные дисциплины

Дисперсия не враг

Что такое дисперсия?

Типы дисперсии:

Формулы отклонения:

Формула дисперсии совокупности

Пример формулы отклонения

Как рассчитать дисперсию?

Как работает калькулятор дисперсии?

Вход:

Выход:

ЧАСТО ЗАДАВАЕМЫЕ ВОПРОСЫ:

В чем разница между стандартным отклонением и дисперсией?

Значение высокой дисперсии – это плохо или хорошо?

Каков диапазон отклонений?

Заключение:

Вам также может понравиться

Как найти теплоемкость ложки

Как найти длину площадь грани а1а2а3

Как найти товар в интернете от производителя

Добавить комментарий Отменить ответ