Что такое шаг арифметической прогрессии?
Если для некой последовательности величина разности между соседними членами будет величиной постоянной, то такую последовательность называют арифметической.
Рассмотрим последовательность: a1, a2, a3, a4, a5.
Где d у нас некая постоянная величина, которую обычно называют шагом арифметической прогрессии.
Примеры арифметических прогрессий:
5, 10, 15, 20, 25. Здесь мы имеем арифметическую прогрессию с шагом 5 (10-5=5).
Каковы 6 шага к решению уравнения?
Точно так же, каковы 4 шага к решению уравнения? У нас есть 4 способа решения одношаговых уравнений: Сложение, вычитание, умножение и деление. Если мы прибавим одно и то же число к обеим частям уравнения, обе стороны останутся равными. Если мы вычтем одно и то же число из обеих частей уравнения, обе части останутся равными.
Какие 3 шагов для решения уравнения?
Похожие страницы:Блог
Какие есть 3 вида налогов?
Как найти среднюю точку между двумя точками?
Как вы делаете кадровые прогнозы?
Как найти начальную скорость, зная только время?
Каковы шаги решения стандартного уравнения или неравенства? Шаг 1: Распределите 2 на (x + 2), умножив на 2. Шаг 2: Объедините одинаковые термины, вычтя 9 из 15 (15 – 9 = 6). Шаг 3: Переместите все переменные в одну часть уравнения, вычитая 2x из обеих сторон. Шаг 4: Вычтите 6 с обеих сторон.
Во-вторых, каково золотое правило решения уравнений? Делайте с одной частью уравнения то, что вы делаете с другой!
Если мы что-то надеваем или снимаем с одной стороны, шкала (или уравнение) становится несбалансированной. При решении математических уравнений мы должны всегда сохраняйте баланс «шкалы» (или уравнения), чтобы обе стороны ВСЕГДА были равны.
Каков первый шаг алгебры?
Самое первое, что вам нужно освоить в алгебре, это понятие переменной. Переменные — это буквы, которые служат заполнителями для чисел, значение которых вам неизвестно. Так, например, в уравнении 1 + 2 = x, x является заполнителем для 3, который должен занимать другую сторону уравнения.
тогда Как вы решаете простые уравнения?
Что такое одношаговое уравнение? Одношаговое уравнение уравнение, для решения которого требуется один шаг. Решать, используйте обратную операцию, чтобы изолировать переменную саму по себе. Помните, что вы делаете с одной стороной, вы должны делать и с другой. Чтобы проверить решение, просто подставьте значение в переменную, чтобы увидеть, верно ли уравнение.
Что такое пятишаговый метод математики?
Как сделать многошаговый?
Что такое решения в математике?
Научные определения решения
Математика Значение или значения, которые при замене переменной в уравнении делают уравнение верным. Например, решения уравнения x2 = 4 равны 2 и -2.
Что такое пример уравнения? Уравнение — это математическое предложение, в котором две равные стороны разделены знаком равенства. 4 + 6 = 10 это пример уравнения. Мы можем видеть слева от знака равенства 4 + 6 и справа от знака равенства 10.… Например, 12 — это коэффициент в уравнении 12n = 24.
Что является правильным первым шагом в решении неравенства?
Ответ: Первым шагом в решении данного неравенства является использовать распределительное свойство и открыть скобки, то есть -8x + 4 > 5 — 3x.
Можешь объяснить мне алгебру?
Алгебра помогает в представлении проблем или ситуаций в виде математических выражений. Он включает в себя переменные, такие как x, y, z, и математические операции, такие как сложение, вычитание, умножение и деление, для формирования осмысленного математического выражения. … Простой пример выражения в алгебре: 2x + 4 = 8.
Что на первом месте в математических уравнениях? Порядок операций можно запомнить по аббревиатуре PEMDAS, которая означает: круглые скобки, показатели степени, умножение и деление слева направо, сложение и вычитание слева направо. Первый, упрости скобки. Затем сделайте показатели. Далее умножайте.
Что обозначают буквы в алгебре? В алгебраических выражениях буквы представляют переменные. Эти буквы на самом деле являются замаскированными числами. В этом выражении переменные x и y. Мы называем эти буквы «переменными», потому что числа, которые они представляют, могут быть разными, то есть мы можем заменить буквы в выражении одним или несколькими числами.
Как начать преподавать алгебру?
8 нестандартных идей для преподавания алгебры и геометрии
- Используйте интересные видео. …
- Добавьте художественный компонент в подход STEAM. …
- Свяжите своих учеников с личным тренером по математике. …
- Сделайте это игрой! …
- Войдите в мир реалити-шоу. …
- Используйте примеры из реальной жизни. …
- Рассмешите их. …
- Используйте стены слов.
Что такое базовая алгебра? Основная алгебра область математики, которая на шаг абстрактнее арифметики. … Алгебра вводит переменную, которая обозначает неизвестное число или может быть заменена целой группой чисел.
Могу ли я сам выучить алгебру?
Вы можете сами выучить алгебру, так как их много. образовательные ресурсы доступны для тех, кто может бороться с этой темой. Вы можете получить доступ к множеству книг и курсов, которые позволят вам изучать алгебру в свободное время, если вы уделяете время практике.
Как легко выучить алгебру? Вот 7 советов, которые ваш ребенок может использовать при изучении алгебры.
Что такое шаг в алгебре
Шаг [step] — в многошаговом расчете (например, при решении задач нелинейного программирования) этап, дающий промежуточный результат, позволяющий обычно судить о приближении или, наоборот, удалении расчета от цели. Одной из разновидностей шага является итерация в машинном расчете, которая отличается от других его этапов лишь значениями переменных величин, а не составом процедур обработки информации. Пример см. в статье Алгоритм.
Экономико-математический словарь: Словарь современной экономической науки. — М.: Дело . Л. И. Лопатников . 2003 .
Смотреть что такое «Шаг» в других словарях:
шаг — шаг/ … Морфемно-орфографический словарь
ШАГ — шага (шагу) и (с колич. числит.) шага, предл. п. о шаге и на (в) шагу, мн. шаги, м. 1. Движение ногой при ходьбе. Сделать шаг вперед. Два шага. Крупные шаги. Мелкие шаги. Размеренные шаги. «Услышав его шаги, она вздрогнула.» Тургенев. «Она… … Толковый словарь Ушакова
шаг — сущ., м., употр. часто Морфология: (нет) чего? шага и шагу, чему? шагу, (вижу) что? шаг, чем? шагом, о чём? о шаге и в шагу; мн. что? шаги, (нет) чего? шагов, чему? шагам, (вижу) что? шаги, чем? шагами, о чём? о шагах о движении человека 1.… … Толковый словарь Дмитриева
Шаг — Шаг: В Викисловаре есть статья «шаг» Шаг движение ногой при ходьбе. Шаг способ передвижения военнослужащего (строевой и походный шаг) Шаг расстояние между основными поперечными несущими конструкциями (колоннами, стенами). Шаг … … Википедия
шаг — Выступка, поступь, ход, походка, па. Шаг бодрый, вольный, сдержанный, тихий, форсированный, черепаший. Выделывать па.. Ср. . См. аллюр, действие, походка бодрым шагом, ленивым шагом, ловкий шаг, ложный шаг, первый шаг, прибавить шагу, сделать шаг … Словарь синонимов
шаг — а ( у); (с числительными: два, три, четыре шага); предл. в шаге и в шагу; мн. шаги; м. 1. Движение ноги, перемещающее человека, животное с одного места на другое (при ходьбе, беге). Идти медленным, быстрым шагом. Сделать ш. в сторону. Шагу нельзя … Энциклопедический словарь
ШАГ — (1) расстояние между одноимёнными профилями, точками или осями изделия; напр. шаг резьбы, шаг заклёпок, шаг зубьев, шаг зацепления и др.; (2) Ш. алгоритма ступень (этап) исполнения (см.), состоящая в выполнении одной или нескольких простых команд … Большая политехническая энциклопедия
ШАГ — ШАГ, а ( у) и а, о шаге, на (в) шагу, мн. и, ов, муж. 1. Движение ногой при ходьбе, беге, а также расстояние от ноги до ноги при таком движении. Сделать ш. Отмерить шагами. Услышать чьи н. шаги (звуки, возникающие при ходьбе). В нескольких или… … Толковый словарь Ожегова
шаг — шаг, а и у и (с колич. числит. 2, 3, 4) а, предл. п. в ш аге и в шаг у, мн. ч. и, ов … Русский орфографический словарь
шаг — бодрый (П.Я.); журавлиный (Давыдов); легкий (Цензор); медлительный (Жуковский); увесистый (Златовратский); унылый (П.Я.); хлюпающий (Гусев Оренбургский); черепаший (Гончаров, Мельников Печерский, Писемский, Салтыков Щедрин) Эпитеты литературной… … Словарь эпитетов
шаг — [шаг] шага/, м. (на) шагу/, мн. шаги/, шаг і/y (моне/та) … Орфоепічний словник української мови
Данный калькулятор предназначен для нахождения шага или разности арифметической прогрессии онлайн.
Арифметическая прогрессия – это числовая последовательность, каждый член которой равен сумме предыдущего числа и определенного фиксированного числа. Это неизменное число называется разностью арифметической прогрессии. Другими словами, разность (шаг) арифметической прогрессии – разность между последующим и предыдущим членом.
Если разность арифметической прогрессии положительная, то такую прогрессию называют возрастающей, если же разность отрицательная, то имеет место убывающая арифметическая прогрессия.
Разность арифметической прогрессии можно вычислить по следующим формулам
где ai и aj элементы прогрессии
где Sn сумма n первых элементов прогрессии, a1 – первый элемент прогрессии.
Заполните ячейки калькулятора соответствующими значениями, чтобы найти разность арифметической прогрессии онлайн.
Арифметическая прогрессия — это последовательность чисел, в которой разница между двумя соседними числами — постоянна.
Пример:
Последовательность 1, 2, 3, 4,… является арифметической прогрессией с шагом(разностью) прогрессии 1.
Пример:
Последовательность 3, 5, 7, 9, 11,… является арифметической прогрессией с разностью 2.
Пример:
Последовательность 20, 10, 0, -10, -20, -30,… является арифметической прогрессией с разностью -10.
Последовательности
Будем выписывать в порядке возрастания положительные четные числа. Первое такое число равно 2, второе 4, третье 6, четвертое 8 и т. д. Получим последовательность
2; 4; 6; 8; … .
Очевидно, что на пятом месте в этой последовательности будет число 10, на десятом — число 20, на сотом — число 200. Вообще для любого натурального числа п можно указать соответствующее ему положительное четное число; оно равно 2n.
Рассмотрим еще одну последовательность. Будем выписывать в порядке убывания правильные дроби с числителем, равным 1:
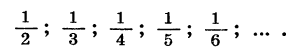
Для любого натурального числа n мы можем указать соответствующую ему дробь; она равна 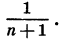
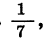
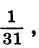
Числа, образующие последовательность, называют соответственно первым, вторым, третьим, четвертым и т. д. членами последовательности. Члены последовательности обычно обозначают буквами с индексами, указывающими порядковый номер члена. Например, 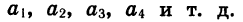
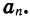
Заметим, что последовательность может содержать конечное число членов. В таком случае ее называют конечной. Например, конечной является последовательность двузначных чисел:
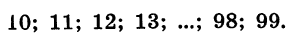
Чтобы задать последовательность, нужно указать способ, позволяющий найти член последовательности с любым номером.
Часто последовательность задают с помощью формулы n-го члена последовательности. Например, последовательность положительных четных чисел можно задать формулой 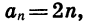
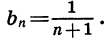
Пример:
Пусть последовательность задана формулой 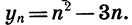
Рассматриваемая последовательность начинается так:
Пример:
Пусть последовательность задана формулой 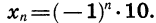
Получаем последовательность
Пример:
Формулой 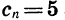
Рассмотрим еще один способ задания последовательности.
Пример:
Пусть первый член последовательности 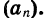
С помощью формулы 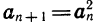
Формулу, выражающую любой член последовательности, начиная с некоторого, через предыдущие (один или несколько), называют рекуррентной (от латинского слова recurro — возвращаться).
Определение арифметической прогрессии
Формула n-го члена арифметической прогрессии:
Рассмотрим последовательность натуральных чисел, которые при делении на 4 дают в остатке 1:
Каждый ее член, начиная со второго, получается прибавлением к предыдущему члену числа 4. Эта последовательность является примером арифметической, прогрессии.
Определение:
Арифметической прогрессией называется последовательность, каждый член которой, начиная со второго, равен предыдущему члену, сложенному с одним и тем же числом.
Иначе говоря, последовательность
где d — некоторое число.
Из определения арифметической прогрессии следует, что разность между любым ее членом, начиная со второго, и предыдущим членом равна d, т. е. при любом натуральном n верно равенство
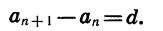
Число d называют разностью арифметической прогрессии.
Чтобы задать арифметическую прогрессию, достаточно указать ее первый член и разность. Приведем примеры.
Если 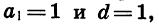
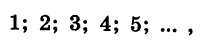
члены которой — последовательные натуральные числа.
Если 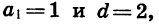
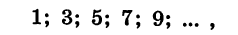
которая является последовательностью положительных нечетных чисел.
Если 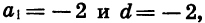
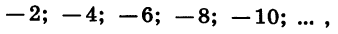
которая является последовательностью отрицательных четных чисел.
Если 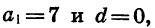
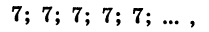
все члены которой равны между собой.
Зная первый член и разность арифметической прогрессии, можно найти любой ее член, вычисляя последовательно второй, третий, четвертый и т. д. члены. Однако для нахождения члена прогрессии с большим номером такой способ неудобен. Постараемся отыскать способ, требующий меньшей вычислительной работы.
По определению арифметической прогрессии
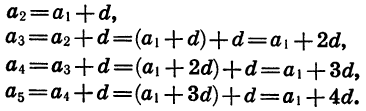
Точно так же находим, что 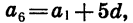
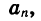
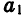
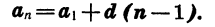
Мы получили формулу n-го члена арифметической прогрессии.
Приведем примеры решения задач с использованием этой формулы.
Пример:
Последовательность 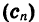
Имеем:
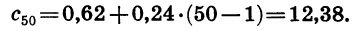
Пример:
Выясним, является ли число —122 членом арифметической прогрессии
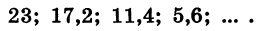
В данной арифметической прогрессии 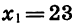
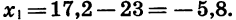
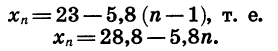
Число —122 является членом арифметической прогрессии 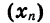
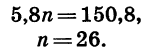
Значит, число —122 является 26-м членом данной арифметической прогрессии.
Формулу n-го члена арифметической прогрессии 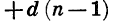
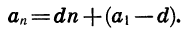
Отсюда ясно, что любая арифметическая прогрессия может быть задана формулой вида
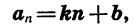
где k и b — некоторые числа.
Верно и обратное: последовательность 
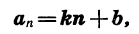
где k и b — некоторые числа, является арифметической прогрессией.
Действительно, найдем разность (n + 1)-го и n-го членов последовательности 
Значит, при любом n справедливо равенство 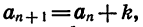

Формула суммы n первых членов арифметической прогрессии
Пусть требуется найти сумму первых ста натуральных чисел. Покажем, как можно решить эту задачу, не выполняя непосредственного сложения чисел.
Обозначим искомую сумму через S и запишем ее дважды, расположив в первом случае слагаемые в порядке возрастания, а во втором — в порядке убывания:
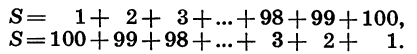
Каждая пара чисел, расположенных друг под другом, дает в сумме 101. Число таких пар равно 100. Поэтому, сложив равенства почленно, получим:
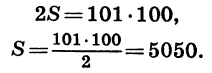
Итак,
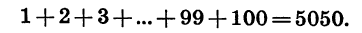
С помощью аналогичных рассуждений можно найти сумму первых членов любой арифметической прогрессии.
Обозначим сумму n первых членов арифметической прогрессии 
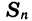
Сумма каждой пары членов прогрессии, расположенных друг под другом, равна 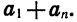
и т. д.
Число таких пар равно n. Поэтому, сложиd почленно равенства (1) и (2), получим:
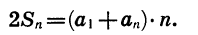
Разделив обе части последнего равенства на 2, получим формулу суммы п первых членов арифметической прогрессии:

Приведем примеры на вычисление суммы членов арифметической прогрессии.
Пример:
Найдем сумму первых тридцати членов арифметической прогрессии 4; 5,5; … .
В данной арифметической прогрессии 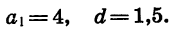
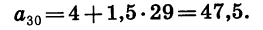
Теперь вычислим сумму первых тридцати членов:
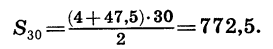
Заметим, что если заданы первый член и разность арифметической прогрессии, то удобно пользоваться формулой суммы, представленной в другом виде. Подставим в формулу (I) вместо 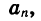
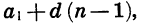
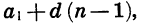
Если для решения рассмотренной задачи воспользоваться формулой (II), то вычисления будут выглядеть так:
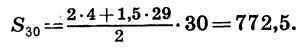
Пример:
Найдем сумму первых сорока членов последовательности 
Последовательность 
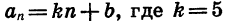
Найдем первый и сороковой члены этой арифметической прогрессии: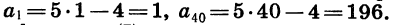
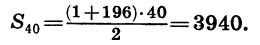
Пример:
Найдем сумму 1 + 2 + 3 + … + n, слагаемыми в которой являются все натуральные числа от 1 до n.
Применив формулу 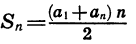
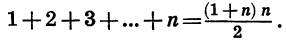
Пример:
Найдем сумму всех натуральных чисел, кратных шести и не превосходящих 250.
Натуральные числа, кратные шести, образуют арифметическую прогрессию, которую можно задать формулой 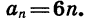
Значит, число членов прогрессии, сумму которых надо найти, равно 41. Имеем:
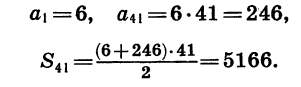
Решение заданий и задач по предметам:
- Математика
- Высшая математика
- Математический анализ
- Линейная алгебра
Дополнительные лекции по высшей математике:
- Тождественные преобразования алгебраических выражений
- Функции и графики
- Преобразования графиков функций
- Квадратная функция и её графики
- Алгебраические неравенства
- Неравенства
- Неравенства с переменными
- Прогрессии в математике
- Геометрическая прогрессия
- Показатели в математике
- Логарифмы в математике
- Исследование уравнений
- Уравнения высших степеней
- Уравнения высших степеней с одним неизвестным
- Комплексные числа
- Непрерывная дробь (цепная дробь)
- Алгебраические уравнения
- Неопределенные уравнения
- Соединения
- Бином Ньютона
- Число е
- Непрерывные дроби
- Функция
- Исследование функций
- Предел
- Интеграл
- Двойной интеграл
- Тройной интеграл
- Интегрирование
- Неопределённый интеграл
- Определенный интеграл
- Криволинейные интегралы
- Поверхностные интегралы
- Несобственные интегралы
- Кратные интегралы
- Интегралы, зависящие от параметра
- Квадратный трехчлен
- Производная
- Применение производной к исследованию функций
- Приложения производной
- Дифференциал функции
- Дифференцирование в математике
- Формулы и правила дифференцирования
- Дифференциальное исчисление
- Дифференциальные уравнения
- Дифференциальные уравнения первого порядка
- Дифференциальные уравнения высших порядков
- Дифференциальные уравнения в частных производных
- Тригонометрические функции
- Тригонометрические уравнения и неравенства
- Показательная функция
- Показательные уравнения
- Обобщенная степень
- Взаимно обратные функции
- Логарифмическая функция
- Уравнения и неравенства
- Положительные и отрицательные числа
- Алгебраические выражения
- Иррациональные алгебраические выражения
- Преобразование алгебраических выражений
- Преобразование дробных алгебраических выражений
- Разложение многочленов на множители
- Многочлены от одного переменного
- Алгебраические дроби
- Пропорции
- Уравнения
- Системы уравнений
- Системы уравнений высших степеней
- Системы алгебраических уравнений
- Системы линейных уравнений
- Системы дифференциальных уравнений
- Арифметический квадратный корень
- Квадратные и кубические корни
- Извлечение квадратного корня
- Рациональные числа
- Иррациональные числа
- Арифметический корень
- Квадратные уравнения
- Иррациональные уравнения
- Последовательность
- Ряды сходящиеся и расходящиеся
- Тригонометрические функции произвольного угла
- Тригонометрические формулы
- Обратные тригонометрические функции
- Теорема Безу
- Математическая индукция
- Показатель степени
- Показательные функции и логарифмы
- Множество
- Множество действительных чисел
- Числовые множества
- Преобразование рациональных выражений
- Преобразование иррациональных выражений
- Геометрия
- Действительные числа
- Степени и корни
- Степень с рациональным показателем
- Тригонометрические функции угла
- Тригонометрические функции числового аргумента
- Тригонометрические выражения и их преобразования
- Преобразование тригонометрических выражений
- Комбинаторика
- Вычислительная математика
- Прямая линия на плоскости и ее уравнения
- Прямая и плоскость
- Линии и уравнения
- Прямая линия
- Уравнения прямой и плоскости в пространстве
- Кривые второго порядка
- Кривые и поверхности второго порядка
- Числовые ряды
- Степенные ряды
- Ряды Фурье
- Преобразование Фурье
- Функциональные ряды
- Функции многих переменных
- Метод координат
- Гармонический анализ
- Вещественные числа
- Предел последовательности
- Аналитическая геометрия
- Аналитическая геометрия на плоскости
- Аналитическая геометрия в пространстве
- Функции одной переменной
- Высшая алгебра
- Векторная алгебра
- Векторный анализ
- Векторы
- Скалярное произведение векторов
- Векторное произведение векторов
- Смешанное произведение векторов
- Операции над векторами
- Непрерывность функций
- Предел и непрерывность функций нескольких переменных
- Предел и непрерывность функции одной переменной
- Производные и дифференциалы функции одной переменной
- Частные производные и дифференцируемость функций нескольких переменных
- Дифференциальное исчисление функции одной переменной
- Матрицы
- Линейные и евклидовы пространства
- Линейные отображения
- Дифференциальные теоремы о среднем
- Теория устойчивости дифференциальных уравнений
- Функции комплексного переменного
- Преобразование Лапласа
- Теории поля
- Операционное исчисление
- Системы координат
- Рациональная функция
- Интегральное исчисление
- Интегральное исчисление функций одной переменной
- Дифференциальное исчисление функций нескольких переменных
- Отношение в математике
- Математическая логика
- Графы в математике
- Линейные пространства
- Первообразная и неопределенный интеграл
- Линейная функция
- Выпуклые множества точек
- Система координат
У этого термина существуют и другие значения, см. Прогрессия.
Арифмети́ческая прогре́ссия — числовая последовательность вида
то есть последовательность чисел (членов прогрессии), в которой каждое число, начиная со второго, получается из предыдущего добавлением к нему постоянного числа 

Любой член арифметической прогрессии равен первому её члену, сложенному с произведением разности прогрессии на число членов, предшествующих определяемому, т. е. он выражается формулой[2]:
Арифметическая прогрессия является монотонной последовательностью. При 



Свойства[править | править код]
Общий член арифметической прогрессии[править | править код]
Член арифметической прогрессии с номером 
- где
— первый член прогрессии,
— её разность,
— член арифметической прогрессии с номером
.
Доказательство формулы общего члена арифметической прогрессии
Пользуясь соотношением 




Заметив закономерность, делаем предположение, что 

База индукции 

Переход индукции:
Пусть наше утверждение верно при 



Итак, утверждение верно и при 


Отметим, что в формулах общего члена 
Доказательство
Необходимость. Пусть 








Достаточность. Пусть 





Рассмотрим 
Отсюда следует, что 



Суммы членов арифметической прогрессии с равными суммами номеров равны, т. е.
.
Характеристическое свойство арифметической прогрессии[править | править код]
Последовательность 

Доказательство характеристического свойства арифметической прогрессии
Необходимость.
Поскольку 



Сложив эти равенства и разделив обе части на 2, получим 
Достаточность.
Имеем, что для каждого элемента последовательности, начиная со второго, выполняется 



База индукции 

Переход индукции:
Пусть наше утверждение верно при 



Но по предположению индукции следует, что 

Итак, утверждение верно и при 

Обозначим эти разности через 





Тождество арифметической прогрессии[править | править код]
Доказательство тождества арифметической прогрессии
С помощью формулы общего члена выразим 


Вычитая почленно из первого равенства второе, а из второго третьего, получим:
Выражая из этих равенств 
По основному свойству пропорции:
Откуда следует доказываемое тождество:
■
Следствие 1. Всякий член арифметической прогрессии вырази́м[5] через любую пару других членов.
Доказательство
Преобразовав тождество арифметической прогрессии
к виду
можно заметить, что 


■
Следствие 2. Для того, чтобы число 


Формулировка ещё одного признака арифметической прогрессии.
Следствие 3 [критерий]. Числовая последовательность является арифметической прогрессией в том и только в том случае, если выполняется тождество арифметической прогрессии для всех членов данной последовательности. Другими словами, чтобы каждый член был вырази́м через любую пару остальных членов последовательности.
Доказательство
Необходимость. Утверждение

очевидно (см. доказательство тождества арифметической прогрессии).
Достаточность. Докажем, что
Равенство
можно преобразовать к виду
Если все три номера различны, тогда
Обозначим выражение, например, в левой части равенства за 
Откуда можно прийти к следующему предложению:
Наконец, методом математической индукции, например, по 
Действительно, при 
Предположим истинность утверждения (для 


По предположению индукции (


Методом тождественных преобразований имеем равносильное предложение
А это, в свою очередь, рекуррентное соотношение для арифметической прогрессии.
Значит, по принципу математической индукции можно утвердать, что для всякого 

Аналогичные рассуждения проводятся для формулы 
Данное следствие целиком и полностью считается доказанным.■
Сумма первых n членов арифметической прогрессии[править | править код]
Сумма первых 

, где
— первый член прогрессии,
— член с номером
,
— количество суммируемых членов.
— где
— первый член прогрессии,
— второй член прогрессии
— член с номером
.
, где
— первый член прогрессии,
— разность прогрессии,
— количество суммируемых членов.
, если
— нечётное натуральное число.
| Доказательство |
|---|
| Запишем сумму двумя способами:
Теперь сложим оба равенства, последовательно складывая в правой части слагаемые, которые стоят на одной вертикали:
Покажем, что все слагаемые (все скобки) полученной суммы равны между собой. В общем виде каждое слагаемое можно подать в виде
Получили, что каждое слагаемое не зависит от
Третья формула для суммы получается подстановкой Замечание: Вместо |
Формулировка ещё одного факта: для всякой арифметической прогрессии при любом 
Примечание: 

| Доказательство |
|---|
|
1. Очевидно, что Прибавим к обеим частям 2. Покажем, что Это так, поскольку можно написать верное равенство:
3. Теперь докажем, что Но гораздо лучше представить это равенство в виде 4. А следовательно, 5. Тем самым, |
Предыдущее свойство имеет обобщение.
Для любых натуральных 


Ещё один признак арифметической прогрессии.
Сумма членов арифметической прогрессии от n-го до m-го[править | править код]
Сумма членов арифметической прогрессии с номерами от 


, где
— член с номером
,
— член с номером
,
— количество суммируемых членов.
где 



Произведение членов арифметической прогрессии[править | править код]
Произведением первых 





Свойство произведения:
Число множителей-скобок ![{displaystyle {left(a_{frac {n+1}{2}}^{2}-{left[idright]}^{2}right)}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a1f5e0446601c4de55f4794545d3b48010c7c6bb)

![{displaystyle a_{frac {n+1}{2}}cdot prod limits _{i=1}^{frac {n-1}{2}}{left(a_{frac {n+1}{2}}^{2}-{left[idright]}^{2}right)}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e795e5a3e7f8d913c426ffdedbc3839227684faf)

Сходимость арифметической прогрессии[править | править код]
Арифметическая прогрессия 


| Доказательство |
|---|
Записав выражение для общего члена и исследуя предел  , получаем искомый результат. , получаем искомый результат.
|
Связь между арифметической и геометрической прогрессиями[править | править код]
Пусть 




| Доказательство |
|---|
| Проверим характеристическое свойство для образованной геометрической прогрессии:
Воспользуемся выражением для общего члена арифметической прогрессии: Итак, поскольку характеристическое свойство выполняется, то |
Следствие: если последовательность положительных чисел образует геометрическую прогрессию, то последовательность их логарифмов образует арифметическую прогрессию.
Арифметические прогрессии высших порядков[править | править код]
Арифметической прогрессией второго порядка называется такая последовательность чисел, что последовательность их разностей сама образует простую арифметическую прогрессию. Примером может служить последовательность квадратов натуральных чисел:
- 1, 4, 9, 16, 25, 36, …
разности которых образуют простую арифметическую прогрессию с разностью 2:
- 3, 5, 7, 9, 11, …
Треугольные числа 

Тетраэдральные числа 
Аналогично определяются и прогрессии более высоких порядков. В частности, последовательность n-ных степеней образует арифметическую прогрессию n-го порядка.
Если ![left[a_{{i}}right]_{{1}}^{{n}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d20714616bd224035f33bf8f7d3d80d5a18e82d9)




Примеры[править | править код]
Формула для разности[править | править код]
Если известны два члена арифметической прогрессии, а также их номера в ней, то можно найти разность как
.
Сумма чисел от 1 до 100[править | править код]
Согласно легенде, школьный учитель математики юного Гаусса, чтобы занять детей на долгое время, предложил им сосчитать сумму чисел от 1 до 100. Гаусс заметил, что попарные суммы с противоположных концов одинаковы: 1+100=101, 2+99=101 и т. д., и мгновенно получил результат: 5050.
Действительно, легко видеть, что решение сводится к формуле
то есть к формуле суммы первых 
См. также[править | править код]
- Геометрическая прогрессия
- Арифметико-геометрическая прогрессия
Примечания[править | править код]
- ↑ Такое соотношение называют рекуррентным соотношением первого порядка. Поэтому арифметическая прогрессия есть множество последовательностей, задающихся именно таким образом.
- ↑ Фильчаков П. Ф. Глава II. Алгебра и элементарные функции. Функции натурального аргумента (§ 75. Арифметическая прогрессия) // Справочник по элементарной математике: для поступающих в вузы : книга / под ред. чл.-кор. АН УССР П. Ф. Фильчакова. — Киев : «Наукова думка», 1972. — С. 303. — 528 с. — 400 000 экз. — УДК 51 (08)(G).
- ↑ Шахмейстер А. Х. Прогрессии. Арифметическая прогрессия // Множества. Функции. Последовательности. Прогрессии : книга / А. Х. Шахмейстер, под общ. ред. Б. Г. Зива. — 2-е изд., испр. и доп. — СПб. : «Петроглиф» : «Виктория плюс» ; М. : Издательство МЦНМО, 2008. — С. 135. — 296 с. : илл. — (Математика. Элективные курсы). — 3000 экз. — ББК 22.141я71.6. — УДК 373.167.1:512(G). — ISBN 978-5-94057-423-1. — ISBN 978-5-98712-027-9. — ISBN 978-5-91673-006-7.
- ↑ Соотношение между любыми тремя членами арифметической прогрессии и их номерами (Мусинов В. А.) // Материалы студенческой научной сессии Института математики и информатики МПГУ. 2021–2022 учебный год : сборник статей / под общ. ред. Е. С. Крупицына. — М.: МПГУ, 2022. — С. 91—93. — 156 с. — ISBN 978-5-4263-1109-1, ББК 22.1я431+32.81я431+22.1р30я431+74.262.21я431+74.263.2я431.
- ↑ Это означает, что выражаемый член есть комбинация любых двух других членов данной последовательности, причём эта комбинация составлена с помощью арифметических операций и конечного набора символов. Для арифметической последовательности такая комбинация будет линейной.
- ↑ Шахмейстер А. Х. Прогрессии. Арифметическая прогрессия // Множества. Функции. Последовательности. Прогрессии : книга / А. Х. Шахмейстер, под общ. ред. Б. Г. Зива. — 2-е изд., испр. и доп. — СПб. : «Петроглиф» : «Виктория плюс» ; М. : Издательство МЦНМО, 2008. — С. 141. — 296 с. : илл. — (Математика. Элективные курсы). — 3000 экз. — ББК 22.141я71.6. — УДК 373.167.1:512(G). — ISBN 978-5-94057-423-1. — ISBN 978-5-98712-027-9. — ISBN 978-5-91673-006-7.
- ↑ Из доказательства необходимости следует, что
, поэтому, если
, то необходимо сделать проверку. Например, если
— сумма первых
членов последовательности, то такая последовательность НЕ является арифметической прогрессией. А последовательность, заданная суммой
первых
членов, будет арифметической прогрессией.
- ↑ При
произведение
равно
, что безусловно верно.
- ↑ Эту формулу удобно использовать для выполнения итераций в программном коде, так как результат зависит от значения только двух величин: постоянного числа — разности, и члена, стоящего ровно по середине между первым и
-м членом.
- ↑
Пример применения формулы.
Пусть, где
.
По формуленайдём произведение пяти первых членов. Количество сомножителей должно равняться
. Причём первым сомножителем будет
.
Далее.
Наконец,.
- ↑ Бронштейн, 1986, с. 139.
Литература[править | править код]
- Бронштейн И. Н., Семендяев К. А. Справочник по математике для инженеров и учащихся втузов. — М.: Наука, 1986. — 544 с.
Ссылки[править | править код]
- Арифметическая прогрессия // Энциклопедический словарь Брокгауза и Ефрона : в 86 т. (82 т. и 4 доп.). — СПб., 1890. — Т. II. — С. 98.
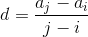
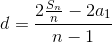

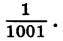
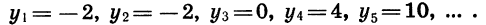
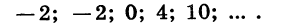
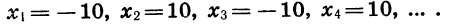
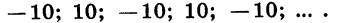
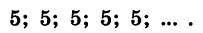
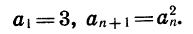
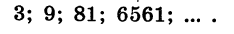
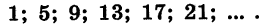
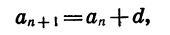
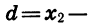
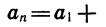
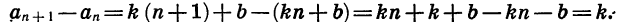
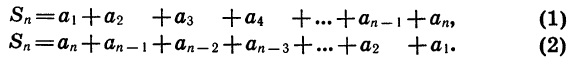
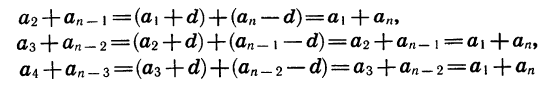
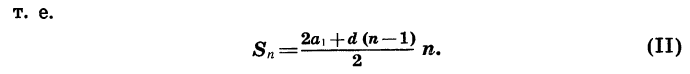
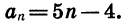
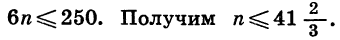






































































![{displaystyle P_{n}=a_{frac {n+1}{2}}cdot prod limits _{i=1}^{frac {n-1}{2}}{left(a_{frac {n+1}{2}}^{2}-{left[idright]}^{2}right)}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f4a28f4de39d0d48768e2ef5936a8ad00b7d4a3d)


![{displaystyle prod limits _{i=1}^{frac {5-1}{2}}{left(a_{frac {5+1}{2}}^{2}-{left[idright]}^{2}right)}=prod limits _{i=1}^{2}{left(a_{3}^{2}-{left[idright]}^{2}right)}=}](https://wikimedia.org/api/rest_v1/media/math/render/svg/18b06ac0706c6f74ed1b55aa11ccf2ee7f10f8d6)
![{displaystyle ={left(a_{3}^{2}-{left[dright]}^{2}right)}cdot {left(a_{3}^{2}-{left[2dright]}^{2}right)}={left(169-49right)}cdot {left(169-4cdot 49right)}=}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ce576d86396ed744fa2a8265a340514ae927eee4)


