Как найти шаг спирали

Данный калькулятор позволяет рассчитать неизвестные параметры спирали по известным параметрам.

Архимедова спираль

Есть пять параметров спирали: внешний диаметр – D, внутренний диаметр – d, толщина (шаг спирали) – t, длина спирали – L, число витков – n. Есть уравнения, устанавливающие связь между этими параметрами (формулы приведены под калькулятором). По этим уравнениям, зная какие-либо три параметра, можно вычислить два оставшихся неизвестных параметра.

Где мы встречаемся со спиралью? Чаще всего при покупке каких-либо материалов в рулонах, будь то рулоны обоев или рулоны туалетной бумаги. Используя калькулятор ниже, можно рассчитать, например, количество погонных метров в рулоне т.е. длину спирали, зная или измерив толщину материала или посчитав количество витков, и измерив внутренний и внешний диаметры рулона. Калькулятор также может решать и обратные задачи , например, по длине спирали и её диаметрам найти толщину и количество витков спирали. Теория и формулы, как обычно, приведены под калькулятором.

При вводе известных параметров проверяйте правильно ли указана размерность для введенных значений. 20 метров это не тоже самое что 20 миллиметров…

Расчет спирали

Точность вычисления

Знаков после запятой: 4

Архимедова спираль

Под Архимедовой спиралью понимают плоскую кривую (спираль), которая отображает траекторию точки М, равномерно движущейся вдоль луча ОА, в то время как сам луч равномерно вращается вокруг точки О.

Архимедова спираль

Если обозначить расстояние от О до М как ρ, а угол поворота луча как φ, то в полярных координатах зависимость расстояния вдоль луча от угла поворота луча можно записать как

где k это параметр спирали, соответствующий величине смещения точки вдоль луча при повороте на один радиан. Повороту на 2π будет соответствовать смещение на 2πk.

Так как 2π это полный оборот, число a, также называемое шагом спирали, будет соответствовать расстоянию между двумя соседними витками спирали и начальное уравнение можно переписать в виде.

$rho = frac{a}{2 pi} phi$

Так как шаг спирали постоянный, то чем дальше от центра, тем больше витки спирали по форме напоминают окружность. К слову, если движение точки описывается другим уравнением, то это какая-то другая спираль.

Для того, чтобы вывести формулу вычисления длины спирали, рассмотрим бесконечно малое приращение длины.

Длина спирали

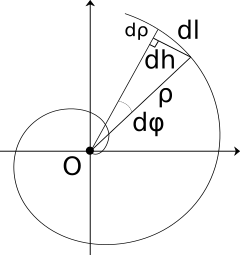
Бесконечно малый отрезок дуги dl можно представить как гипотенузу прямоугольного треугольника с катетами dρ и dh. По теореме Пифагора гипотенуза равна

$dl = sqrt{drho^2+dh^2}$

Бесконечно малый отрезок dh можно заменить на бесконечно малую часть дуги окружности с радиусом ρ, длина которой ρdφ.

$dl = sqrt{drho^2+rho^2dphi^2}$

Из уравнения спирали заменяем ρ на kφ, и dρ на kdφ

$dl = sqrt{k^2dphi^2+k^2phi^2dphi^2}=kdphisqrt{1+phi^2}=frac{a}{2pi}sqrt{1+phi^2}dphi$

Таким образом мы получили зависимость dl от dφ. Чтобы найти длину L достаточно взять интеграл от начального угла поворота луча до конечного угла поворота луча.

$L=int limits _{phi_0}^{phi_1}frac{a}{2pi}{sqrt {1+phi ^{2}}}dphi$

Интеграл я выводить не буду, его уже вывели до меня. Конечный результат

$L=frac{a}{2pi}left( frac{phi_1}{2}sqrt{phi_1^2+1}+frac{1}{2}ln(phi_1+sqrt{phi_1^2+1}) - frac{phi_0}{2}sqrt{phi_0^2+1}-frac{1}{2}ln(phi_0+sqrt{phi_0^2+1}) right)$

В случае если спираль выходит из точки О, то есть начальный угол поворота луча равен 0, формула упрощается

$L=frac{a}{2pi}left( frac{phi_1}{2}sqrt{phi_1^2+1}+frac{1}{2}ln(phi_1+sqrt{phi_1^2+1}) right)$

Если мы говорим о рулоне, то там скорее всего начальный угол все же не равен нулю, то есть есть ненулевой внутренний диаметр (например, там есть втулка). Как же перейти от углов к диаметрам, и найти число витков спирали?

Число витков спирали связано с углами следующим очевидным соотношением:

$n = frac{phi_1-phi_0}{2pi}$

Диаметры можно связать с углом непосредственно по уравнению спирали (если вспомнить что диаметр это два радиуса)

$D = frac{a}{pi}phi_1 \ d = frac{a}{pi}phi_0$

Эти соотношения и используются для нахождения неизвестных параметров спирали по известным. Осталось только заметить, что уравнение длины является трансцендентным, и решение обратной задачи – по известной длине найти что-то неизвестное, невозможно найти аналитически. Для получения решения приходится прибегать к численным методам, в частности, в калькуляторе выше используется метод секущих.

Источник

Спираль Архимеда

Первый ученый который открыл и изучил свойства этой линии, был великий математик и философ из древней Греции, Архимед. Его именем она и была названа.

Спираль Архимеда

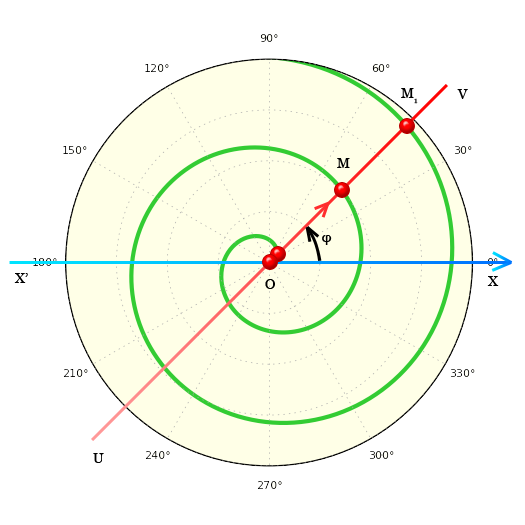
Построение спирали Архимеда

Некоторая прямая UV изначально совпадает с прямой XX`. Прямая UV равномерно вращается относительно точки O. По прямой UV равномерно перемещается точка M отдаляясь от точки O. В результате точка M, перемещаясь по вышеуказанным правилам, описывает линию — спираль Архимеда.

Шаг спирали Архимеда

При повороте прямой UV из любого положения на некоторый угол Δφ точка M смещается на расстояние Δρ. Смещение MM₁ происходит за один оборот прямой UV, и всегда равно одному и тому же числу. Это число называется шагом спирали Архимеда

[ a = MM_1 ]

Полярное уравнение спирали Архимеда

[ frac{ρ}{a} = frac{φ}{2π} ]

В этом уравнении можно перейти от шага спирали Архимеда a к параметру спирали Архимеда k

[ k = frac{a}{2π} ]

Тогда уравнение спирали примет вид

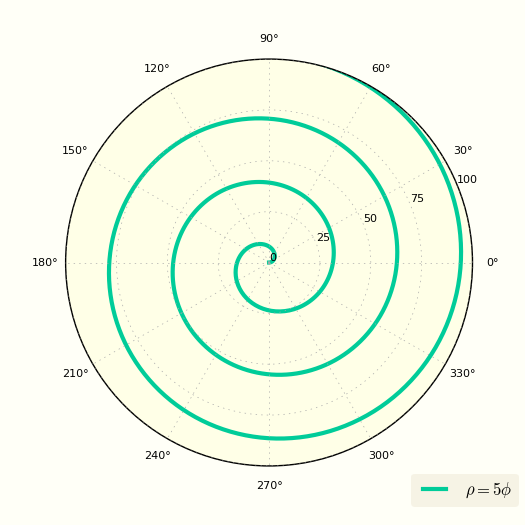
[ ρ = kφ ]

Построить спираль Архимеда

Спираль Архимеда	стр. 123

Источник

Как определить шаг спирали, по которой движется частица в магнитном поле?

Наталья Шершнёва

Ученик

(141),
на голосовании

13 лет назад

Голосование за лучший ответ

D.mas

Мастер

(2313)

13 лет назад

Шаг спирали определяется продольной скоростью движения частицы и периодом вращения по спирали.. . А период вращения тесно связан с силой Лоренца, а именно mV^2 / R = Fл, период T = 2pi*R / V. V – скорость частицы.
А так, смотря что дано в задаче, от того и плясать))

Источник

From Wikipedia, the free encyclopedia

The right-handed helix (cos t, sin t, t) from t = 0 to 4π with arrowheads showing direction of increasing t

A helix () is a shape like a corkscrew or spiral staircase. It is a type of smooth space curve with tangent lines at a constant angle to a fixed axis. Helices are important in biology, as the DNA molecule is formed as two intertwined helices, and many proteins have helical substructures, known as alpha helices. The word helix comes from the Greek word ἕλιξ, “twisted, curved”.^[1]
A “filled-in” helix – for example, a “spiral” (helical) ramp – is a surface called helicoid.^[2]

Properties and types[edit]

The pitch of a helix is the height of one complete helix turn, measured parallel to the axis of the helix.

A double helix consists of two (typically congruent) helices with the same axis, differing by a translation along the axis.^[3]

A circular helix (i.e. one with constant radius) has constant band curvature and constant torsion.

A conic helix, also known as a conic spiral, may be defined as a spiral on a conic surface, with the distance to the apex an exponential function of the angle indicating direction from the axis.

A curve is called a general helix or cylindrical helix^[4] if its tangent makes a constant angle with a fixed line in space. A curve is a general helix if and only if the ratio of curvature to torsion is constant.^[5]

A curve is called a slant helix if its principal normal makes a constant angle with a fixed line in space.^[6] It can be constructed by applying a transformation to the moving frame of a general helix.^[7]

For more general helix-like space curves can be found, see space spiral; e.g., spherical spiral.

Handedness[edit]

Helices can be either right-handed or left-handed. With the line of sight along the helix’s axis, if a clockwise screwing motion moves the helix away from the observer, then it is called a right-handed helix; if towards the observer, then it is a left-handed helix. Handedness (or chirality) is a property of the helix, not of the perspective: a right-handed helix cannot be turned to look like a left-handed one unless it is viewed in a mirror, and vice versa.

Two types of helix shown in comparison. This shows the two chiralities of helices. One is left-handed and the other is right-handed. Each row compares the two helices from a different perspective. The chirality is a property of the object, not of the perspective (view-angle)

Mathematical description[edit]

A helix composed of sinusoidal x and y components

In mathematics, a helix is a curve in 3-dimensional space. The following parametrisation in Cartesian coordinates defines a particular helix;^[8] perhaps the simplest equations for one is

As the parameter t increases, the point (x(t),y(t),z(t)) traces a right-handed helix of pitch 2π (or slope 1) and radius 1 about the z-axis, in a right-handed coordinate system.

In cylindrical coordinates (r, θ, h), the same helix is parametrised by:

A circular helix of radius a and slope a/b (or pitch 2πb) is described by the following parametrisation:

Another way of mathematically constructing a helix is to plot the complex-valued function e^xi as a function of the real number x (see Euler’s formula).
The value of x and the real and imaginary parts of the function value give this plot three real dimensions.

Except for rotations, translations, and changes of scale, all right-handed helices are equivalent to the helix defined above. The equivalent left-handed helix can be constructed in a number of ways, the simplest being to negate any one of the x, y or z components.

Arc length, curvature and torsion[edit]

The arc length of a circular helix of radius a and slope a/b (or pitch = 2πb) expressed in Cartesian coordinates as

equals $Tcdot sqrt{a^2+b^2}$ , its curvature is $frac{|a|}{a^2+b^2}$
and its torsion is $frac{b}{a^2+b^2}.$
A helix has constant non-zero curvature and torsion.

A helix is the vector-valued function

${displaystyle |mathbf {v} |={sqrt {(-asin t)^{2}+(acos t)^{2}+b^{2}}}={sqrt {a^{2}+b^{2}}}}$

${displaystyle |mathbf {a} |={sqrt {(-asin t)^{2}+(acos t)^{2}}}=a}$

${displaystyle s(t)=int _{0}^{t}{sqrt {a^{2}+b^{2}}}dtau ={sqrt {a^{2}+b^{2}}}t}$

So a helix can be reparameterized as a function of , which must be unit-speed:

${displaystyle mathbf {r} (s)=acos {frac {s}{sqrt {a^{2}+b^{2}}}}mathbf {i} +asin {frac {s}{sqrt {a^{2}+b^{2}}}}mathbf {j} +{frac {bs}{sqrt {a^{2}+b^{2}}}}mathbf {k} }$

The unit tangent vector is

${displaystyle {frac {dmathbf {r} }{ds}}=mathbf {T} ={frac {-a}{sqrt {a^{2}+b^{2}}}}sin {frac {s}{sqrt {a^{2}+b^{2}}}}mathbf {i} +{frac {a}{sqrt {a^{2}+b^{2}}}}cos {frac {s}{sqrt {a^{2}+b^{2}}}}mathbf {j} +{frac {b}{sqrt {a^{2}+b^{2}}}}mathbf {k} }$

The normal vector is

${displaystyle {frac {dmathbf {T} }{ds}}=kappa mathbf {N} ={frac {-a}{a^{2}+b^{2}}}cos {frac {s}{sqrt {a^{2}+b^{2}}}}mathbf {i} +{frac {-a}{a^{2}+b^{2}}}sin {frac {s}{sqrt {a^{2}+b^{2}}}}mathbf {j} +0mathbf {k} }$

Its curvature is ${displaystyle left|{frac {dmathbf {T} }{ds}}right|=kappa ={frac {|a|}{a^{2}+b^{2}}}}$ .

The unit normal vector is

${displaystyle mathbf {N} =-cos {frac {s}{sqrt {a^{2}+b^{2}}}}mathbf {i} -sin {frac {s}{sqrt {a^{2}+b^{2}}}}mathbf {j} +0mathbf {k} }$

The binormal vector is

${displaystyle mathbf {B} =mathbf {T} times mathbf {N} ={frac {1}{sqrt {a^{2}+b^{2}}}}left[bsin {frac {s}{sqrt {a^{2}+b^{2}}}}mathbf {i} -bcos {frac {s}{sqrt {a^{2}+b^{2}}}}mathbf {j} +amathbf {k} right]}$

${displaystyle {frac {dmathbf {B} }{ds}}={frac {1}{a^{2}+b^{2}}}left[bcos {frac {s}{sqrt {a^{2}+b^{2}}}}mathbf {i} +bsin {frac {s}{sqrt {a^{2}+b^{2}}}}mathbf {j} +0mathbf {k} right]}$

Its torsion is ${displaystyle tau =left|{frac {dmathbf {B} }{ds}}right|={frac {b}{a^{2}+b^{2}}}}$ .

Examples[edit]

An example of double helix in molecular biology is the nucleic acid double helix.

An example of conic helix is the Corkscrew roller coaster at Cedar Point amusement park.

Some curves found in nature consist of multiple helices of different handedness joined together by transitions known as tendril perversions.

Most hardware screw threads are right-handed helices. The alpha helix in biology as well as the A and B forms of DNA are also right-handed helices. The Z form of DNA is left-handed.

In music, pitch space is often modeled with helices or double helices, most often extending out of a circle such as the circle of fifths, so as to represent octave equivalency.

In aviation, geometric pitch is the distance an element of an airplane propeller would advance in one revolution if it were moving along a helix having an angle equal to that between the chord of the element and a plane perpendicular to the propeller axis; see also: pitch angle (aviation).

A natural left-handed helix, made by a climber plant
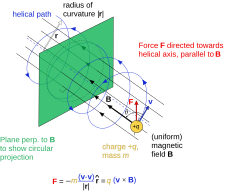
A charged particle in a uniform magnetic field following a helical path

References[edit]

^ ἕλιξ Archived 2012-10-16 at the Wayback Machine, Henry George Liddell, Robert Scott, A Greek-English Lexicon, on Perseus
^ Weisstein, Eric W. “Helicoid”. MathWorld.
^ “Double Helix Archived 2008-04-30 at the Wayback Machine” by Sándor Kabai, Wolfram Demonstrations Project.
^ O’Neill, B. Elementary Differential Geometry, 1961 pg 72
^ O’Neill, B. Elementary Differential Geometry, 1961 pg 74
^ Izumiya, S. and Takeuchi, N. (2004) New special curves and developable surfaces. Turk J Math Archived 2016-03-04 at the Wayback Machine, 28:153–163.
^ Menninger, T. (2013), An Explicit Parametrization of the Frenet Apparatus of the Slant Helix. arXiv:1302.3175 Archived 2018-02-05 at the Wayback Machine.
^ Weisstein, Eric W. “Helix”. MathWorld.

Источник

Шаг винта с учетом угла наклона спирали Калькулятор

Search
Дом	физика ↺
физика	Дизайн машины ↺
Дизайн машины	Проектирование элементов машин ↺
Проектирование элементов машин	Силовые винты ↺

✖Угол винтовой линии винта определяется как угол между этой развернутой окружной линией и шагом винтовой линии.ⓘ Угол подъема винта [α]

+10%

-10%

✖Средний диаметр силового винта — это средний диаметр опорной поверхности, или, точнее, удвоенное среднее расстояние от центральной линии резьбы до опорной поверхности.ⓘ Средний диаметр силового винта [d_m]

+10%

-10%

✖Ход силового винта — это линейное перемещение гайки за один оборот винта, и именно так обычно указываются силовые винты.ⓘ Шаг винта с учетом угла наклона спирали [L]

⎘ копия

Шаг винта с учетом угла наклона спирали Решение

ШАГ 0: Сводка предварительного расчета

ШАГ 1. Преобразование входов в базовый блок

Угол подъема винта: 4.5 степень –> 0.0785398163397301 Радиан (Проверьте преобразование здесь)
Средний диаметр силового винта: 46 Миллиметр –> 0.046 метр (Проверьте преобразование здесь)

ШАГ 2: Оцените формулу

ШАГ 3: Преобразуйте результат в единицу вывода

0.011373440383317 метр –>11.373440383317 Миллиметр (Проверьте преобразование здесь)

16 Силовые винты Калькуляторы

Шаг винта с учетом угла наклона спирали формула

Ход силового винта = tan(Угол подъема винта)*pi*Средний диаметр силового винта

L = tan(α)*pi*d_m

Определить шаг винта?

Шаг – это осевое перемещение спирали или винта за один полный оборот (360 °). Шаг винтовой резьбы – это осевое перемещение за один оборот. Шаг определяется как осевое расстояние между соседними резьбами на спирали или винте.

Источник

Расчет спирали

Архимедова спираль

Спираль Архимеда

Построение спирали Архимеда

Шаг спирали Архимеда

Полярное уравнение спирали Архимеда

Построить спираль Архимеда

Спираль Архимеда

Как определить шаг спирали, по которой движется частица в магнитном поле?

Properties and types[edit]

Handedness[edit]

Mathematical description[edit]

Arc length, curvature and torsion[edit]

Examples[edit]

See also[edit]

References[edit]

Шаг винта с учетом угла наклона спирали Калькулятор

Шаг винта с учетом угла наклона спирали Решение

16 Силовые винты Калькуляторы

Шаг винта с учетом угла наклона спирали формула

Определить шаг винта?

Добавить комментарий Отменить ответ

Расчет спирали

Архимедова спираль

Спираль Архимеда

Построение спирали Архимеда

Шаг спирали Архимеда

Полярное уравнение спирали Архимеда

Построить спираль Архимеда

Спираль Архимеда

Как определить шаг спирали, по которой движется частица в магнитном поле?

Properties and types[edit]

Handedness[edit]

Mathematical description[edit]

Arc length, curvature and torsion[edit]

Examples[edit]

See also[edit]

References[edit]

Шаг винта с учетом угла наклона спирали Калькулятор

Шаг винта с учетом угла наклона спирали Решение

16 Силовые винты Калькуляторы

Шаг винта с учетом угла наклона спирали формула

Определить шаг винта?

Вам также может понравиться

Как найти елену александровну

Как найти созданную папку в outlook

Как найти силу которую необходимо приложить

Добавить комментарий Отменить ответ