Как найти шаг выборки

1. Вероятностные способы формирования выборочной совокупности

Строгое обоснование
выборки как модели генеральной
совокупности и степени ее репрезентативности
— все это в “полной мере осуществимо
только для
вероятностных
(случайных) выборок.

Понятие случайного
способа формирования выборочной
сово­купности нельзя понимать в
обыденном значении этого слова, ибо
случайная выборка предполагает
определенные процедуры ее организации
и предъявляет социологу определенные
тре­бования.

Существует ряд
приемов формирования выборочных
совокуп­ностей, которые строятся по
подобию вероятностных, но для которых
нельзя строго обосновать, что выборочные
характеристики выступают оценками
соответствующих характеристик
генераль­ной совокупности. Такие
выборки можно назвать эмпирическими,
так как они не имеют теоретического
вероятностного обоснования.

Основная цель
выборочного исследования — сформировать
репрезентативную выборку. Для этого
необходимо обеспечить всем элементам
генеральной сово­купности равные
возможности- попасть в выборку. При этих
условиях элементы генеральной совокупности
оказываются пред­ставленными в выборке
с вероятностями, которые приближаются
к их распределению в генеральной
совокупности. Объекты, которые чаще
встречаются в генеральной совокупности,
чаще будут преоб­ладать и в выборке.
Такой результат является проявлением
дей­ствия закона больших чисел. Именно
подобные типы выборок, воспроизводящие
закон распределения генеральной
совокупно­сти, получили название
вероятностных.

Различают следующие
виды
вероятностной выборки:
простую, систематическую и серийную
(«гнездовую»).

1. Простая вероятностная выборка.

Собственно случайная
выборка лежит в основе всех остальных
типов выборки, которые будут рассмотрены
далее.

Выборка называется
собственно
случайной,
если при извлечении выборки объема n
все возможные комбинации из n
элементов, которые могут быть получены
из генеральной совокупности объема N,
имеют равную вероятность быть извлеченными.

По определению,
при собственно случайной выборке
выполняется принцип случайности.

Отбор производится
с помощью жеребьевки, таблицы (либо
генератора) случайных чисел. Главный
принцип –
случайность,
т.е. все единицы генеральной совокупности
имеют равную вероятность попасть в
выборочную совокупность. Другие
принципы:

1. Принцип жеребьевки.
   Каждый элемент генеральной совокупности
   заносится на бумажку (это могут быть
   фамилии, адреса, просто номера (в этом
   случае выпавшие номера ставят в
   соответствие с людьми в списках) и
   т.д.), затем бумажки помещаются в барабан,
   перемешиваются и не глядя вытаскиваются.

2. Принцип таблицы
   случайных
   чисел.
   Начиная с любого места таблицы, берем
   четыре следующих друг за другом числа.
   Эти числа и будут номерами людей в
   списке, которых следует отобрать в
   выборку (числа, превышающие численность
   генеральной совокупности, опускаются).

3. Принцип генератора
   случайных чисел.
   Это то же самое, что и таблицы случайных
   чисел, только числа вырабатываются
   компьютером (для этого существует
   специальная программа).

Процедура
построения
простой
случайной выборки
включает
в себя следую­щие шаги.

1. Во-первых,
   нужно получить полный список членов
   генеральной совокупности и пронумеровать
   этот список. Такой список, напомним,
   называется основой
   выборки.

2. Во-вторых,
   следует определить предполагаемый
   объем
   выборки, т.
   е. ожидае­мое число опрошенных.

3. В-третьих,
   нужно
   извлечь из таблицы
   случайных чисел (либо с помощью генератора
   случайных чисел)
   столько чисел, сколько нам требуется
   выборочных единиц. Если в выборке должно
   ока­заться 100 человек, из таблицы
   берут 100 случайных чисел.

4. В-четвертых,
   нужно
   выбрать из списка-основы те наблюдения,
   но­мера которых соответствуют
   выписанным случайным числам¹.

Различают повторную
и бесповторную
выборку.

Простая повторная
выборка.
На карточки наносятся номе­ра
респондентов. Карточки перемешиваются.
Вслепую вынимается карточка, записывается
ее помер, затем карточка возвра­щается
в колоду, и карточки снова перемешиваются.
Эта операция называется повторным
отбором. Сама процедура повторной
выборки почти не используется для
социологических исследований, и возможное
дублирование единиц отбора для многих
программ социологического исследова­ния
равносильно сокращению намеченного
объема выборки. При повторном отборе
каждый выбранный элемент возвращается
в ГС.

Простая
бесповторная выборка.
При бесповторном отборе выбранный
элемент не возвращается в ГС².
Респонденты отбираются как и при простой
повторной выборке, но отобранные карточки
не возвращаются в колоду, а откладываются
в сторону.

Плюсом простого
случайного отбора является полное
соблюдения принципа случайности и, как
следствие – избежание систематических
ошибок.

Случайная выборка
обладает рядом недостатков, которые
затрудняют ее применение на практике.
Эти недостатки можно представить в трех
пунктах:

1. Необходимость
   наличия списка элементов генеральной
   совокупности. Обычно
   элементами генеральной совокупности
   являются люди; в этом случае
   в качестве
   списка могут выступать адреса, телефоны
   и т.д. Трудность здесь заключается в
   том, что получить такой список далеко
   не всегда представляется возможным.
   Следовательно, в тех случаях, когда
   невозможно получить список элементов
   генеральной совокупности, невозможно
   проводить и случайный отбор.

2. Сложность
   проведения опроса.
   Процедура опроса при случайном отборе
   является очень громоздкой и требующей
   много времени. Ведь в результате
   случайного отбора исследователь
   получает на выходе список фамилий
   респондентов (телефонов, адресов и
   т.д.), которых необходимо опросить. Иными
   словами, интервьюерам приходится
   «бегать» за каждым респондентом и
   добиваться от него согласия ответить
   на «парочку вопросов».

Осложняет дело и
то, что респондентов порой бывает не
так просто достать; в случае отсутствия
респондента его приходится посещать
по нескольку раз (по крайней мере не
менее трех раз).

Все вышеперечисленное
ведет к повышенным временным затратам
на проведение опроса. Временные затраты
можно уменьшить только благодаря
привлечению дополнительных интервьюеров,
т.е. только за счет дополнительных
денежных расходов. Помимо этого возникает
еще так называемая проблема
неответивших.

1. Сравнительно
   большой объем выборки.
   Для получения результатов со сравнительно
   высокой степенью точности собственно
   случайный отбор требует достаточно
   большого объема выборки по сравнению
   с другими видами отбора. Другими словами,
   случайный отбор обладает меньшей
   степенью точности, что, в конечном
   счете, является причиной его меньшей
   эффективности¹.

Довольно
часто исследователь сталкивается с
ситуацией, когда временные и финансовые
затраты на осуществление простой
случайной выборки становятся неприемлемо
высокими. Наиболее ра­зумным выходом
здесь является использование других,
«компромиссных», про­цедур случайного
отбора.
Часто используются различные методы
моделирования случайности.

Использование
различных типов случайного отбора
позволяет несколько сгладить некоторые
из вышеупомянутых трудностей, возникающих
при проведении собственно случайного
отбора. Например, некоторые типы
случайного отбора позволяют упростить
организацию опроса, но главное – это
то, что они увеличивают эффективность
выборки.

Так при случайном
отборе ошибка выборки контролируется
только за счет изменения объема выборки.
В рассматриваемых же нами типах случайного
отбора эффективность выборки можно
повысить за счет моделирования выборки
без увеличения ее объема.

Под моделированием
выборки понимается проведение случайного
опроса с учетом информации о генеральной
совокупности. Это означает, что по
некоторым параметрам составляется
модель генеральной совокупности для
того, чтобы уже на стадии, предшествующей
стадии случайного отбора, повысить
соответствие этих параметров в выборке
и генеральной совокупности².

Однако модификации
случайного отбора не могут преодолеть
всех трудностей, связанных со случайной
выборкой. Это связано с тем, что все они
являются разновидностями
именно случайного отбора
и в них используется принцип случайности.

Из этого следует,
что проводить любой случайный отбор
невозможно без списка элементов
генеральной совокупности. Более того,
большинство типов случайного отбора
приводят к тем же трудностям при
организации опроса, что и при собственно
случайной выборке. Главное, чего достигают
эти модификации случайного отбора, так
это увеличения точности выборки.

Однако при формальном
сходстве с собственно случайной выборкой,
любая ее вариация есть все же некоторое
отклонение от принципа случайности.
Эти отклонения могут приводить к
систематическим ошибкам, которые
невозможны при собственно случайной
выборке. Теперь непосредственно перейдем
к рассмотрению типов случайного отбора.

2. Механическая
(или систематическая вероятностная)
выборка
— это
упрощенный вариант вероятностного
отбора. Систематическая
выборка
по качеству часто приближается к простой
случай­ной. Систематическая выборка,
как и простая случайная, требует полного
списка или заданного упорядочения
совокупности (различные
алфавитные списки, картотеки учреждений,
книги жильцов в до­моуправлении).
Техника
осуществления систематического отбора
элементарна: сначала случайным образом
отбирается первая единица, затем отбору
подлежит каждый k-й
элемент.
Число k
в
данном случае называют шагом
выборки.
Можно,
например, отбирать каждый 25-й или каждый
200-й элемент. Чтобы определить шаг отбора,
нужно поделить изве­стный объем
генеральной совокупности (N)
на
предполагаемый объем вы­борки (n).

(k)

.

Начало отбора
выбирается случайным образом в пределах
шага выборки. Например, если шаг выборки
равен 20, то начинать отбор надо с любого
числа от 1 до 20.

Не существует
никаких априорных статистических или
социо­логических правил для определения
объема имеющейся информа­ции.
Единственное общее
правило
заключается в том, что чем
более статистически однородна генеральная
совокупность, тем объем выборки может
быть меньше; чем меньше информации о
ха­рактере генеральной совокупности,
тем больше должен быть объем выборки.

Пусть, например,
нужно отобрать 200 человек из 20000 владельцев
телефонов:

1)
определим шаг отбора: N/n
= 20000
: 200 = 100;

2) с помощью таблицы
случайных чисел найдем первую выборочную
еди­ницу. Если, скажем, выпал номер
«053», то из списка владельцев телефонов
выпишем того, кто значится под этим
номером;

3) с установленным
шагом отбираем номера: 153, 253, 353, 453 и т.
д. до исчерпания списка.

Выбор величины k
зависит от характера поставленной
пробле­мы. Предположим, что основой
выборки является пронумерован­ный
список школ данного города от 1 до 100.
Если исследователя интересует соотношение
мальчиков и девочек в выпускных клас­сах,
то достаточно взять k
=20 (п
= 5), а если исследуется профессиональная
ориентация школьников, то может оказаться
слишком большим и k
= 10 (га == 10).
Это объясняется тем, что во втором случае
поднимается более сложная задача, ее
изучение зависит от большого числа
воздействующих факторов, а значит —
больше вариаций.

Допустим, что часть
школ расположена в типичном заводском
районе. Тогда профессиональная ориентация
школьников, воз­можно, окажется в нем
отличной от профессиональной ориентации
в школах, расположенных в центре города.
В большинстве иссле­дований k
берется равным 10, хотя определение
интервала чаще всего зависит от размера
генеральной совокупности и намеченного
размера выборки.

Иногда
генеральная совокупность (и соответственно
основа выборки) слиш­ком велика либо
исследователю известен не полный список,
а лишь правило
упорядочения элементов в
генеральной совокупности. Предположим,
что мы хотим составить представление
о весе и формате книг, содержащихся в
некой библиотеке, при том, что мы не
располагаем полным каталогом, а лишь
видим, как книги расставлены на стеллажах.
При условии, что объем библиотечного
собрания нам приблизительно известен,
мы можем воспользоваться процеду­рой
систематического отбора и отобрать,
скажем, каждую 55-ю книгу. Очень важно
отобрать «стартовую» единицу сугубо
случайным образом.
Именно в этом пункте кроется основная
слабость
систематического отбора.
Если в способе упорядочения единиц
совокупности имеет место некая
цикличность, т. е. неиз­вестная
нам «система» (систематический
паттерн), а случайность в выборе «старта»
должным образом не обеспечена, то
полученная выборка может так­же
оказаться смещенной
(если
о систематическом паттерне мы знаем
заранее, то он не представляет собой
угрозы валидности и может быть учтен в
ходе отбора). Если воспользоваться
примером с отбором книг в библиотеке,
то легко представить себе такую
гипотетическую ситуацию: исследователь
выбирает в качестве стартовой первую
книгу
на нижней полке ближайшего стеллажа и
далее двигается с шагом 250 единиц. Если
на каждом стеллаже размещается около
500 книг, то приблизительно половина его
выборки будет взята с нижних полок.
Однако известно, что на нижних полках
многих библиотек нередко раз­мещают
книги больших форматов — художественные
альбомы, атласы и т. п. Если в нашем
примере это правило упорядочения будет
соблюдено хотя бы в половине случаев
(т. е. половина нижних полок будет отведена
под «неформат­ные» издания, под так
называемые фолио), любые выборочные
оценки «направ­ленности» библиотечного
собрания или формата представленных в
нем книг окажутся невалидными.

Аналогией
примеру с библиотечными книгами мо­жет
служить случай
систематической выборки городских
квартир. Если
в ре­зультате осуществляемого
непосредственно «в поле» интервьюерами
система­тического отбора в выборке
будут сверхпредставлены квартиры,
расположен­ные на первых и последних
этажах, возникнет систематическая
выборочная ошибка. На первых и последних
этажах в российских городах часто живут
люди из групп, имеющих более низкий
социально-экономический статус и
соответственно ограниченные финансовые
ресурсы: квартиры, расположенные на
«крайних» этажах и соприкасающиеся с
системами коммунального водо- и
теп­лоснабжения, обычно стоят дешевле,
так как названные системы в России
тра­диционно являются источником
неприятностей и дисфункций в структуре
жиз­необеспечения.

Систематическая
выборка является экономным и удобным
спо­собом формирования выборочной
совокупности, хотя следует учи­тывать
возможность систематического распределения
в списках единиц различного типа,
повторяемости в их распределении,
ко­торая может совпадать с величиной
интервала отбора, равной k.

Проиллюстрируем
это положение. При составлении основы
выборки для опроса рабочих в одном из
цехов завода выбранный интервал k
может совпасть с числом рабочих в
бригаде, в списке которой первым окажется
бригадир. Поэтому при выборе интер­вала
отбора, который совпадает со скрытой
периодичностью в ге­неральной реальной
совокупности, выборка может оказаться
полностью смещенной. Опасность в данном
случае состоит в том, что можно отобрать
только одних бригадиров.

Таким образом,
если при систематическом отборе в
генераль­ной совокупности существует
какой-либо определенный порядок
размещения ее единиц (расположение их
по возрастанию или убы­ванию изучаемого
признака), возникает опасность
систематической ошибки.

Выборка может
оказаться смещенной в том случае, если,
напри­мер, ее основой является платежная
ведомость, в которой лица расположены
в порядке возрастания размера заработной
платы. В этом случае выборка из начала
списка приводит к занижению средней
величины заработной платы и к преуменьшению
величины средней ошибки выборки. Отбор
из конца списка приводит к
их завышению.

Возможности и
ограничения систематической выборки.
Си­стематическая выборка часто
применяется при проведении кон­кретных
социологических исследований. Этот
способ выборки лучше всего использовать
при более или менее однородной гене­ральной
совокупности. В связи с этим систематическая
выборка часто используется в качестве
последней, завершающей ступени отбора
в сложных выборках.

1. Стратифицированная
   (районированная) выборки.
   Вероятностная выборка с любой техникой
   отбора (простая вероятностная,
   систематическая, серийная и даже
   многоступенчатая) становится
   районированной, если процедурам отбора
   единиц наблюдения предшествует
   раз­деление генеральной совокупности
   на однородные части.

В статистическом
смысле районирование соответствует
выде­лению такого числа и таких
статистически однородных групп, чтобы
колебаемость изучаемых признаков внутри
их была меньше, чем между ними. Это и
свидетельствует (с формальной стороны)
о качественном районировании.

Эта дифференциация
внутри генеральной совокупности на
качественно более однородные группы
содержательно связана с предметом
исследования.

Необходимость
районирования вызвана сложной структурой
социальных объектов.

Районирование
совокупности оказывается необходимым
во всех случаях, когда она является
неоднородной с точки зрения социальных,
экономических и других характеристик,
формирую­щих ее социальных объектов.

Например, чтобы
избежать совпадений цикличности, которая
могла встретиться в уже приведенных
примерах (отбор бригадиров или по
ведомостям заработной платы), можно
всех бригадиров данного цеха или лиц,
получающих одинаковую заработную
пла­ту, выделить в отдельные группы
и в каждой из этих групп про­изводить
случайный отбор. Такая выборка,
предусматривающая предварительное
разделение генеральной совокупности
на содержательные сходные группы
(страты), и
является примером районированной
выборки.

Так, исследуя
профессиональную ориентацию школьников
в пределах одного города, можно в одну
группу отнести 16 школ, расположенных в
заводском районе, во вторую — 20 школ,
рас­положенных в центральной части
города, в третью — 64 школы, расположенные
в остальных его частях, где население
в основном занято малоквалифицированным
трудом. Для опроса можно отоборать
выпускников из двух школ первой группы,
двух школ из второй группы и двух — из
третьей. Если такая группировка школ
действительно отражает различия районов
по их расположению, которые существенно
учитывать в исследовании, например
раз­личие социально-профессиональной
структуры населения, то колеблемость
изучаемых признаков внутри каждой
группы школ должна быть меньше, чем
между группами. Тогда несмотря на
от­носительное уменьшение доли
представительства третьей группы
репрезентативность выборки не уменьшается.

Применительно
к стратифицированному отбору часто
высказывают все те не­верные и
предрассудочные мнения, которые в начале
XX
века высказывались относительно квотной
выборки (см. ниже) и ее воображаемых
преимуществ перед случайным отбором.
В действительности стратифицированный
отбор име­ет определенные практические
преимущества до тех пор, пока сохраняется
его вероятностный, случайный характер.
Как только стратифицированная выборка
превращается в более или менее специально
отобранную квотную выборку, воспроизводящую
некоторые известные пропорции генеральной
совокупности (например, 51% женщин, 30%
горожан и т. п.), любые статистические,
т. е. стро­гие, оценки параметров
генеральной совокупности становятся
невозможными.

Стратификацией,
строго говоря, называют процедуру, при
которой отбор осу­ществляют как бы
из нескольких
«параллельных» подсовокупностей,
заданных
на
одной
и той же генеральной совокупности. Это
абстрактное определение можно прояснить
с помощью примера. Пусть у нас есть
генеральная совокуп­ность взрослых
горожан, относительно которой мы
располагаем какой-то су­щественной
с точки зрения исследовательских гипотез
информацией. Наличие такой предварительной
информации — необходимое
условие стратифициро­ванного отбора.
Предположим, мы знаем, что в генеральной
совокупности 60% рабочих и 40% служащих.
Это соотношение может оказаться весьма
суще­ственным с точки зрения наших
исследовательских гипотез, если оно
задает одну из независимых
переменных, как,
например, при изучении влияния рода
занятий на частоту посещения футбольных
матчей. Даже при отсутствии зна­чительной
систематической погрешности небольшие
смещения в реализации случайной
выборочной процедуры могут привести к
ситуации, когда в нашей конкретной
выборке соотношение рабочих и служащих
будет существенно (на 5—7%) отклоняться
от ожидаемой «правильной» пропорции,
имеющей место в генеральной совокупности
(см. обсуждение нормальной кривой и
индук­тивного статистического вывода
в гл. 8). Соответственно под угрозой
окажется точность наших оценок взаимосвязи
между главной независимой переменной
(профессиональным статусом) и интересом
к футболу. Такого рода неточность может
быть устранена при использовании еще
одной случайной выборки из генеральной
совокупности, но здесь вступают в силу
экономические соображе­ния, так как
исследовательский бюджет обычно
ограничен. В описанной ситу­ации
желательно заранее обеспечить
представленность обеих интересующих
нас групп, т. е. страт,
сохранив
вероятностный характер отбора. Этого
можно добиться, если осуществить некую
независимую процедуру случайного отбора
для каждой социальной группы в отдельности
(в нашем примере для рабочих и служащих)
и затем объединить полученные случайные
подвыборки в одну (за­метьте, что для
нашего примера объем подвыборки рабочих,
в согласии с зара­нее известной
пропорцией, будет в 1,5 раза больше объема
подвыборки служа­щих). Полученная в
результате выборка будет и стратифицированной
(по
про­фессиональному статусу), и
вероятностной.

На
практике две случайные процедуры отбора
в подвыборки-страты можно тех­нически
объединить в одну, если мы располагаем
априорной информацией о принадлежности
каждой выборочной единицы к той или
иной страте. Для это­го достаточно
вести параллельный отбор из списка-основы
в несколько подвыборок (по числу страт).
Собственно выборочная процедура может
быть и про­стой
случайной, и
систематической
(соответственно
мы получим либо про­стую, либо
систематическую стратифицированную
выборку).

Рассмотрим
эту процедуру на примере составления
систематической выборки населения,
стратифицированной по этнической
принадлежности. Пусть мы осуществляем
выборку взрослых жителей небольшого
промышленного центра, при этом полученная
выборка должна отражать существу­ющую
этнодемографическую ситуацию: 80% русских,
10% украинцев и 10% представителей других
национальностей. Основываясь на
информа­ции, хранящейся в паспортных
столах милиции (или на избирательных
списках), мы в идеальном случае можем
составить полный список-осно­ву,
включающий 100000 известных административным
органам постоян­ных жителей. Если
предварительно мы предполагаем включить
в нашу выборку около 1000 человек, нам
нужно отобрать из картотек паспортных
столов (или избирательных списков)
каждого сотого. То есть доля генеральной
совокупности f,
включенная в выборку, составит ¹/₁₀₀:

f
=
объем выборки (и) / объем целевой
совокупности (N).

Выборка
объемом в 1000 человек будет включать в
себя 800 русских, 100 украинцев и 100
представителей других национальностей.
Причем шаг систематического отбора (К)
для
всех трех подсовокупностей будет равен
100.

Таким
образом, мы будем выписывать из реальных
картотек
(списков) каж­дого сотого русского,
каждого сотого украинца и т.п. (естественно,
украинцы и представители других
национальностей будут встречаться в
спис­ках в среднем в 10 раз реже
русских)¹.

Вес
каждой единицы (респон­дента) в k-й
страте
равен отношению числа таких элементов
в генеральной со­вокупности к объему
выборки для k-й
страты²,
т.е.:

Выборка
в описанном нами примере является
пропорциональной,
так
как она представляет все страты в той
пропорции, в которой они содержатся в
гене­ральной совокупности.

Другой,
более дешевый, метод заключается в
непропорциональной
стратификации, т.
е. в непропорциональном отборе из
различных подсовокупностей. Нередко
возникает необходимость сделать
«распространенные» и «редкие» страты
равно представленными
в
выборке. Если вернуться к обсуждавшемуся
выше примеру исследования городского
населения, можно, в частности, представит_;
ситуацию,
когда необходимо сравнить кулинарные
предпочтения русских и ук­раинцев.
Очевидно, не вполне корректно сравнивать
800 русских и 100 украин­цев. В этом случае
можно прибегнуть к непропорциональному
систематичес­кому отбору из названных
страт: если отбирать каждого 200-го
русского и каж­дого 25-го украинца, мы
получим две вполне сопоставимые, равные
по объему, — 400 и 400 человек — подвыборки
(однако эти равные подвыборки будут
непропорционально
репрезентировать
доли соответствующих подсовокупностей,
в чем можно убедиться, самостоятельно
произведя подсчеты по описанным выше
формулам).

Выбор между
пропорциональной и непропорциональной
стратификацией ис­следователь
осуществляет, исходя из содержательных
и экономических сооб­ражений.

Типические
группы. В
качестве типических группировок
районирования могут быть использованы
как естественные обра­зования, так и
специально формируемые для определенного
ис­следования. Например, при большом
географическом разбросе выборки такими
группировками могут выступать
экономико-геогра­фические регионы
или области страны. Другим примером
такого районирования может быть
классификация городов по их
админи­стративному статусу и по
численности населения.

Группами районирования
могут выступать и идеальные обра­зования.
Примером такого районирования является
выделение в генеральной совокупности
при исследовании отношения моло­дежи
к труду шести групп по содержанию труда.

Признак
районирования или расслоения.
Признак, на основа­нии которого
производится расслоение генеральной
совокупно­сти, называется признаком
расслоения или районирования. Районирование
может проводиться по одному или по
нескольким признакам.

Организация
районированной выборки и ее типы.
С точки зрения процедур отбора генеральная
совокупность районирован­ной выборки
выступает как сумма типических групп.
Районирован­ный отбор иногда называют
типическим.

Организация
районированной выборки требует
представления о характере распределения
во всей совокупности тех признаков,
которые должны быть положены в основу
образования типических групп или
выделения районов.

Неправильный выбор
признака для группировки элементов
генеральной совокупности может привести
не к повышению репрезентативности
выборочных данных, а, напротив, к ее
по­нижению.

Организация
районированной репрезентативной выборки
свя­зана на практике с известными
трудностями, особенно если типи­ческие
группы неравночисленны. Математическая
статистика ре­комендует в этих случаях,
чтобы размеры различных типических
групп в выборке были бы пропорциональны
средним квадрати-ческим отклонениям
соответствующих групп генеральной
сово­купности. Но дисперсии, как
правило, неизвестны. Поэтому при
организации репрезентативной
районированной выборки отбор из
типических групп генеральной совокупности
производится пропорционально их размеру
(доле) в общей численности совокуп­ности.

Комбинированная
выборка.
Прием районирования превращает любую
вероятностную выборку в комбинированную.

На основе
предварительного районирования
генеральной сово­купности можно
организовать любую вероятностную
выборку из числа уже описанных: простую
случайную, систематическую (механическую)
или серийную (гнездовая, кластерная).

Из районированной
генеральной совокупности выборочная
со­вокупность может формироваться
при помощи или только одной процедуры
отбора (простой случайной серийной или
систе­матической) — это одноступенчатая
районированная выборка, или несколькими
последовательными процедурами — это
районирован­ная многоступенчатая
выборка. В зависимости от задач
исследо­вания и характера информации
на этих ступенях могут последова­тельно
комбинироваться уже описанные способы
формирования вероятностных выборок
(см. настоящую главу, 5).

Районированные
выборки не обязательно имеют строго
вероят­ностный характер.

Квотная выборка.
Уже описанная квотная выборка чаще
всего организуется как ступень сбора
информации на основе райони­рованной
генеральной совокупности. Группами
расслоения обычно выступают типы
населенных пунктов. Такие выборки
попользо­вались при опросе читательских
аудиторий центральных газет ¹².

Районированные
выборки с отбором типичных объектов.
Дру­гим примером могут быть районированные
выборки, в которых из каждой группы
районирования производится не случайный
отбор (по схеме простой выборки,
систематической или серийной), а
выбирается один типичный объект.

В современных
социологических исследованиях
формирование выборки из типичных
объектов па основе предварительного
райо­нирования генеральной совокупности
используется при выборе регионов,
городов, населенных пунктов, которые в
том или ином отношении являются
«типичными» для более обширной
терри­тории. Типичными называют
объекты, которые по большинству своих
изучаемых в исследовании характеристик
приближаются к сродним показателям. В
рамках выборочного метода этот способ
выборки почти не разработан. Это касается
прежде всего расчета характеристик
выборки.

Существует трудность
определения типичного объекта с
увеличением числа интересующих
исследователя признаков: средние по
одним показателям, они не будут средними
по другим.

Таким образом,
райони­рованная выборка при прочих
равных условиях дает более точные
результаты.

1.Гнездовая
(серийная, кластерная) выборка.
«Кластеры»
(дословно с англ. cluster
— гроздь, группа) — это естествен­ные
группировки единиц наблюдения. Здесь
отбираются не люди, а группы. Группы
отбираются случайным образом, а внутри
них проводится сплошной опрос. Например,
в ВУЗе с большим количеством студенческих
групп отбор можно проводить путем
случайного отбора этих групп и дальнейшего
сплошного опроса в этих группах.

Сначала изучаемая
совокупность делится на взаимоисключающие
и взаимодополняющие подгруппы, называемые
кластерами. Затем с помощью вероятностного
метода выборки, такого как простая
случайная выборка, отбираются кластеры.
В выборку включаются либо все элементы
отобранного кластера, либо проводится
их отбор вероятностным методом.

Корректное
применение кластерной процедуры основано
на неукоснительном соблюдении четырех
необходимых условий:

1)
кластеры должны быть однозначно и явно
заданы: каждый член гене­ральной
совокупности должен принадлежать к
одному
(и
только одному) кластеру;

2) число членов
генеральной совокупности, входящих в
каждый кластер, должно быть известно
или поддаваться оценке с приемлемой
степенью точности;

3) кластеры должны
быть не слишком велики и географически
компактны, иначе кластерная выборка
теряет всякий финансовый смысл;

4) выбор кластеров
должен быть осуществлен таким способом,
который минимизирует рост выборочной
ошибки (последний процесс, в свою
оче­редь, является неизбежным следствием
кластеризации).

Серийная выборка
может организовываться по схемам простой
случайной и систематической выборок.
Наконец, она может формироваться после
предварительного районирования
генеральной совокупности.

В первых двух
случаях к информации о генеральной
совокуп­ности — основе выборки —
предъявляются те же требования, что и
для всех вероятностных выборок: размещение
элементов генеральной совокупности
(серий) не должно быть каким-либо образом
систематизировано. Серийная выборка
может быть ис­пользована, например,
для изучения семьи, выпускных классов
школ в репрезентативных локальных
исследованиях или в каче­стве последней
ступени комбинированной выборки в
географиче­ских точках, включенных
в выборку.

Основное различие
между кластерной и стратифицированной
выборкой
состоит в том, что в первом случае
используются только отобранные подгруппы
(кластеры), в то время как в стратифицированной
выборке все подгруппы (слои) используются
для дальнейшего отбора. Эти методы
преследуют разные цели. Цель кластерной
выборки — увеличить эффективность
выборки, уменьшив затраты на ее проведение.
Цель стратифицированной выборки —
увеличение точности. По однородности
и неоднородности критерии формирования
кластеров прямо противоположны критериям
формирования слоев. Элементы кластера
должны быть максимально разнородны, а
сами кластеры — как можно более
однородными. В идеале каждый кластер
должен представлять собой небольшую
модель генеральной совокупности. При
кластерной выборке основа выборочного
наблюдения необходима только для
кластеров, которые вошли в выборку.

Главное достоинство
этого типа отбора в том, что он гораздо
проще в организационном плане.
Действительно, гораздо проще выбрать
несколько групп и опросить их целиком,
чем бегать за каждым респондентом. Это
дает нам выигрыш в средствах и во времени.

Но при этом
необходимо следить, чтобы количество
групп в генеральной совокупности было
достаточно большим, иначе ни о каком
принципе случайности не может быть и
речи. Более того, возможны перекосы
из-за того, что на момент опроса не
удается застать всех членов группы. К
тому же объем выборки при гнездовом
отборе обычно больше, чем при случайном
отборе.

В
принципе можно показать, что рост
выборочной ошибки для кластер­ной
выборки (в сравнении с простой случайной)
является функцией двух
нере­шенных проблем
— величины кластеров
и гомогенности
(гетерогенности) исследуемого
признака внутри каждого кластера

Распространенная
форма кластерной выборки — территориальная
выборка
(area sampling), в
которой кластеры состоят из географических
территорий, таких как округа, жилые
районы или кварталы. Если отбор основных
элементов проводится в один этап
(например, исследователь выбирает
некоторые кварталы, а затем все семьи,
живущие в этих кварталах, включаются в
выборку), такой выборочный метод
называется одноступенчатой территориальной
выборкой. Если отбор основных элементов
проводится в два (или больше) этапа
(исследователь выбирает кварталы, а
затем в каждом таком квартале отбирает
семьи, которые будут включены в выборку),
такой метод называется двухступенчатой
(или многоступенчатой) территориальной
выборкой. Отличительная черта
одноступенчатой территориальной выборки
заключается в том, что все семьи из
выбранных кварталов (или географических
регионов) включаются в выборку.

Метод маршрутного
опроса (как вариация территориальной
выборки).
Этот метод социологи часто ис­пользуют,
когда единицей наблюдения выступает
семья.

В выборочную
совокупность, например, намечено включить
определенное число случайно отобранных
семей уили
квартир.
На карте города или населенного пункта
нумеруются все улицы. С помощью таблицы
случайных чисел отбираются большие
числа, которые позволят идентифицировать
семьи или квартиры, попав­шие в выборку.
Каждое большое число рассматривается
как со­стоящее из трех компонентов:
первые две или три цифры в нем указывают
на номер улицы, следующая цифра — номер
дома, последняя цифра — номер квартиры
в выбранном доме.

Например, число
42—25—3 указывает на квартиру № 3 (можно
этой же цифре приписать все десятки в
пределах сотни: или 13, или 23 и т. д.) дома
№
25 (возможно также 125, если улицы очень
длинны) на 42-й улице.

Организация
серийной выборки методом маршрутного
опроса наиболее приспособлена к городам,
где преобладают отдельные квартиры,
или к населенным пунктам, где еще
сохраняется част­ное домовладение
(в последнем случае отпадает необходимость
выбирать номер квартиры).

Случайная (вероятностная) выборка — это выборка, для которой каждый элемент генеральной совокупности имеет определенную, заранее заданную вероятность быть отобранным. Это позволяет исследователю рассчитать, насколько правильно выборка отражает генеральную совокупность, из которой она выделена (спроектирована). Такую выборку иногда называют еще случайной.

Вероятностные методы включают:

• простой случайный отбор,
• систематический отбор,
• кластерный отбор,
• стратифицированный отбор.

Реализовать случайную выборку можно двумя приемами: лотерейным методом и с помощью таблицы случайных чисел. С помощью случайной выборки строится подавляющее большинство телефонных опросов и опросов на основе избирательных списков. Для построения такой выборки необходимо иметь полный список всех элементов генеральной совокупности.

Простой случайный отбор

Простой случайный отбор предполагает, что вероятность быть включенным в выборку известна и является одинаковой для всех единиц совокупности. Он реализуется двумя методами:

• отбор вслепую (другое название — метод лотереи или жребия),
• отбор не вслепую (происходит с помощью таблицы случайных чисел).

Итак, в одном случае вы осуществляете свой выбор не глядя, в другом — все осознавая, но для того, чтобы самому не вмешаться и ничего не испортить, обращаетесь к специальным таблицам.

Кроме того, простой случайный отбор подразделяется на две разновидности уже по другому критерию, а именно — возвращению или невозвращению лотерейного шара (вместо него может быть фамилия респондента) обратно в корзину. В этом случае выделяют:

• случайный повторный (с возвращением) отбор,
• случайный бесповторный (без возвращения) отбор.

В чем сходство и различие двух классификаций? В первом случае — вслепую/не вслепую — ученый мог смотреть на то, как осуществляется отбор, хотя никак не мог ему помешать (если отбор проводился вслепую), или выбор осуществляли не его руки, вынимающие из корзины шар, а таблица случайных чисел. Во втором случае — повторный/бесповторный — дело заключается не в исследователе (если отбор проводился не вслепую), а в лотерейном шаре: его либо возвращают для нового выбора, либо не возвращают и продолжают процесс без него.

Соединив оба членения простого случайного метода в декартову систему координат, получим четыре модальности.

Сразу оговоримся, что получившаяся схема не является в строгом смысле изображением логического квадрата, с помощью которого принято показывать отношения совместимости, эквивалентности, противоположности (контрарности), частичной совместимости (субконтрарности), подчинения и противоречивости суждений. В нашей схеме лишь некоторые квадраты дают новый тип случайного отбора или свидетельствуют о том, что данная комбинация действий осуществима. При использовании метода выборки вслепую единицы генеральной совокупности (фамилии, названия или просто номера из списка) можно вносить в карточки, а карточки в перемешанном виде поместить в какую-то непрозрачную емкость (ящик, коробку). Из этой емкости кто-то случайным образом вытягивает число карточек, определяемое объемом выборки. После каждого вытягивания и регистрации карточки ее можно возвращать, а можно не возвращать назад. В первом случае говорят о повторном, во втором — о бесповторном отборе. Их комбинация дает два квадрата, имеющих реальное содержание: можно вслепую выбирать из корзины шары и возвращать их для нового выбора, а можно их откладывать в сторону. Однако выборка не вслепую предполагает использование таблицы случайных чисел. Возвращать в нее выбранный номер невозможно, стало быть, образуемые вдоль этой оси квадраты не являются реальными.

Предлагаемая схема выполняет скорее мнемоническую функцию, помогая лучше запомнить материал. Можно также считать, что она имеет демонстративный смысл, но никак не логический. Она придумана для того, чтобы внести какую-то ясность в типологию разновидностей простого случайного отбора.

Вероятностную выборку целесообразно применять только при наличии соответствующих условий. Первое условие осуществления вероятностной выборки — наличие полного списка всех элементов генеральной совокупности (отсутствие или недоступность которого чаще всего и препятствует ее реализации) от 1 до N, где N — общее число всех элементов. Если же он имеется, то производится нумерация, после чего можно использовать вышеописанные методики. При использовании лотерейного метода (или метода жребия) жетоны с номерами всех элементов помещают в урну, тщательно перемешивают и извлекают последовательно п жетонов, где n — число элементов выборочной совокупности. Элементы генеральной совокупности, имеющие номера, оказавшиеся на извлеченных жетонах, будут составлять выборочную совокупность. Это довольно трудоемкая и продолжительная (при больших размерах выборки) операция, к тому же достаточно трудоемкая, поскольку «для обеспечения равного шанса выбора требуется тщательное перемешивание жетонов» после каждой выемки очередного номера.

Второе условие вероятностной выборки — хорошая перемешанность элементов генеральной совокупности. Если выборка элементов производится из ящика, то его содержимое следует тщательно перемешать и уже после этого брать карточки случайным образом. Только при таких условиях все они имеют одинаковую вероятность попасть в выборку. Часто для образования случайной выборки элементы генеральной совокупности предварительно нумеруются, а каждый номер записывается на отдельной карточке. В результате получается пачка карточек, число которых совпадает с объемом генеральной совокупности. После тщательного перемешивания из этой пачки берут по одной карточке. Объект (респондент), имеющий одинаковый номер с карточкой, считается попавшим в выборку. При этом возможны два принципиально различных способа образования выборочной совокупности.

Первый — вынутая карточка после фиксации ее номера возвращается в пачку, после чего карточки снова тщательно перемешиваются. Повторяя такие выборки по одной карточке, можно образовать выборочную совокупность любого объема. Выборочная совокупность, образованная по такой схеме, получила название случайной возвратной выборки.

Второй— каждая вынутая карточка после ее записи обратно не возвращается. Повторяя по такой схеме выборки по одной карточке, можно получить выборочную совокупность любого заданного объема. Выборочную совокупность, образованную по данной схеме называют случайной безвозвратной выборкой. Она возможна лишь в том случае, если из тщательно перемешанной пачки сразу берут нужное число карточек.

Заметим, что различие между случайными выборками с возвратом и без возврата стирается, если они составляют незначительную часть большой генеральной совокупности.

Однако при большом объеме генеральной совокупности этот метод оказывается очень трудоемким, и поэтому гораздо удобнее пользоваться таблицей случайных чисел. Она доказала свою эффективность при формировании равновероятностной выборки из больших совокупностей.
 

Систематический отбор

Систематический отбор является вторым по научной значимости, но первым по популярности употребления видом простого случайного отбора. Его называют еще механическим отбором и считают упрощенным вариантом простого случайного отбора.

Примером служат разного рода квартирные выборки: выбираются улицы, на которых интервьюер проводит квартирный опрос. Квартиры выбираются по определенной схеме (крайняя квартира справа от лестницы на последнем этаже первого подъезда и т.д.).

Если под рукой таблицы случайных чисел нет, а генсовокупность относительно невелика14, то можно воспользоваться алфавитным списком, например, персонала предприятия (картотека всегда есть в отделе кадров) или избирательного участка (при опросе по месту жительства). Процедура систематического отбора проста: количество единиц генеральной совокупности, предположим 2000 работников предприятия, делится на количество анкет, скажем 200, и определяется шаг выборки. Он предполагает, что, начиная с любого номера из списка, опрашивается каждый десятый (2000:200 = 10). В формализованном виде данная процедура выглядит так. Из пронумерованного списка через равные интервалы £ отбирается заданное число респондентов. При этом шаг выборки к рассчитывается по простой формуле:

K = N / n

где N — численность генеральной совокупности, n — численность выборочной совокупности.

Таким образом, шаг выборки, а его еще называют «интервалом скачка» или просто «интервалом», — это математический показатель, рассчитанный как отношение объема генеральной совокупности к объему выборки. Он показывает, сколько номеров в списке фамилий людей, вошедших в генеральную совокупность, надо пропустить (через сколько перешагнуть), чтобы в итоге получить список выборочной совокупности. Буквально шаг выборки озная чает расстояние между соседними фамилиями респондентов, из меренное количеством отбракованных фамилий из списка генеральной совокупности.

Другой пример. Предположим, что нам нужно спроектировать выборку численностью 100 из списка 5000 студентов какого-то вуза. Если мы намерены использовать систематическую выборку, то должны вначале рассчитать интервал выборки делением числа элементов в списке на размер выборки. В данном случае, разделив 5000 имен на требуемый размер выборки 100 ед., мы получим интервал (шаг) выборки 50. Так что мы будем систематически двигаться по списку и отбирать каждого пятидесятого студента (отобрав таким образом 100 имен). Определение того места в списке, с которого мы начнем, проводится случайным образом, по таблице случайных чисел (это называется случайным стартом). Таким образом, если случайно выбрана точка старта под номером 31, то в выборку будут включены студенты, стоящие под номерами 31, 81, 131, 181 и т.д.

Итак, в основу систематической выборки положены не вероятностные процедуры, а алфавитные списки, картотеки, схемы, которые обеспечивают равновероятное попадание в выборку всех единиц генеральной совокупности.

Несмотря на свои преимущества, систематическая выборка может иногда иметь своим результатом предубежденную выборку. Такая ситуация возникает, например, когда элементы размещены в списке, ранжированном по каким-то характеристикам. В этой ситуации определение места начала случайного отбора будет влиять на средние характеристики всей выборки. Например, если студенты расставлены в списке в соответствии со средним оценочным баллом от высшего к низшему, систематическая выборка, включающая студентов, стоящих в списке под номерами 1,51,101, будет иметь более низкий средний балл, чем выборка, включающая студентов под номерами 50, 100 и 150. Каждая новая выборка будет давать другой средний балл, который представляет собой предубежденную картину студенческой популяции.

Районированная и стратифицированная выборки

Если генеральная совокупность велика, а такое в эмпирическом исследовании случается очень часто, то приходится разделять обследуемую совокупность на более или менее однородные части, а затем осуществлять отбор единиц внутри этих частей. Такую раздробленную на части выборку правильнее всего было бы называть расслоенной. Однако в русском языке подобный термин не утвердился, видимо, как не соответствующий нормам правильного произношения.

Поскольку в отечественной социологии очень много иностранных слов — и это правильно с точки зрения унификации научной терминологии, приведения ее к международным стандартам, — то слову «расслоенная» попытались найти эквивалент. В числе претендентов оказались две наилучшие кандидатуры, а именно термины «районированная» и «стратифицированная».

В русском языке первое слово явно тяготеет к географическому языковому ареалу и обозначает территориальную зону. Поскольку генеральную совокупность, особенно очень большую, например население всей страны, можно разбивать в том числе и по региональному признаку, в отечественной литературе утвердился термин «районированная выборка». Но наряду с тем генеральную совокупность можно расслаивать и по стратам (полу, возрасту, доходам и т.д.), получая в качестве критерия уже не географический район, а социальную группу.

В итоге сложилась практика различения двух разновидностей расслоенной выборки. Если деление происходит по стратам (социальным группам), то выборку именуют стратифицированной, если по экономико-географическим районам, то районированной.

В литературе (да и в маркетинговой практике) два термина — районированная и стратифицированная выборки — нередко считаются эквивалентными. Происходит это потому, что в основе той и другой лежит одна и та же процедура расслоения, а расслаивать в социологии можно двояко: либо по социальным группам (тогда речь идет о социальной структуре и стратификации как ее частном виде), либо по географическим районам. Когда объединяют оба понятия в одно, как правило, дают обобщающее определение подобной выборки, например, такое:
Районированная выборка — вид выборки, при котором отбору предшествует процедура районирования (расслоения, стратификации), т.е. разделения исходной совокупности на статистически или качественно однородные подсовокупности, называемые слоями, стратами или типичными группами. Отбор единиц, который может носить как случайный, так и направленный характер, производится независимо из каждого слоя, поэтому районированная выборка равносильна ряду выборок, извлеченных из меньших совокупностей-страт.

В этом определении исходное понятие «районированная выборка» без ущерба для дела можно заменить на «стратифицированную выборку». Таким образом, одинаково правильно будет как разделять одну выборку на две самостоятельные разновидности, районированную и стратифицированную, так и подавать их как единое целое. За единство двух приемов выступает практика социологических исследований. Оказывается, в крупномасштабных проектах социологи начинают с районированной выборки, а затем переходят на стратифицированную. Так, например, в обследованиях Центра «Социо-Экспресс» Института социологии РАН в основе построения районированной выборки лежат десять экономико-географических зон, в каждой из которых выделяются крупные города (численностью свыше 500 тыс. населения), средние города (50-500 тыс.), малые города (до 50 тыс.) или поселки городского типа, а также сельские населенные пункты. Внутри отобранных городов респондентов отбирают случайным методом. Репрезентативность контролируется по региональным пропорциям численности населения, пропорциям между городским и сельским населением, пропорциям между населением указанных типов населенных пунктов.

В международной практике не используется русское слово «район» как географическая зона (ареал, регион, часть территории), поэтому здесь не встретишь и термина «районированная выборка». Вместо него употребляют термин «стратифицированная выборка», подразумевая, что, разбивая единое целое на части, не обязательно точно указывать, что они собой представляют — группы или районы.

В таком случае стратифицированная выборка (stratified sampling) — вероятностная выборка, обеспечивающая равномерное представительство в выборочной совокупности различных частей, типов, групп и слоев населения.

В английском языке слово «стратификация» мало чем отличается от слов «расслоение», «разделение», «разбиение». Это социологи придали стратификации социальный смысл, а в геологии, откуда мы позаимствовали термин, стратификация означает вертикальное расслоение земли на однородные пласты. Ни классов, ни доходов, ни социальных групп здесь нет.

Надо учитывать и другой нюанс. Дело в том, что в зарубежных словарях, прежде всего американских и главным образом ведущих, все, что связано с территориальным признаком, в том числе и расслоение по районам, относится к квотной выборке. К примеру, в знаменитом Оксфордском словаре социологии на термин «stratified sampling» стоит отсылка: см. sampling. Открываем с. 576—577 и читаем о том, что в случае стратифицированной вероятностной {random) выборки речь идет о разбиении совокупности на подгруппы, т.е. страты, например мужчин и женщин, а о районированной выборке в нашем понимании не говорится ни слова. Близкий к районам термин «local areas» употребляется Гордоном Маршаллом (а он считается знатоком в этом деле) только в связи: 1) с первой стадией многоступенчатого отбора, 2) с квотной выборкой.

Возвращаясь от лингвистических тонкостей к методическим, подчеркнем вот еще что: отбор единиц, который может носить как случайный, так и направленный характер, производится независимо из каждого слоя или района, поэтому районированно-стратифицированная выборка (если можно так выразиться) равносильна ряду выборок, извлеченных из меньших совокупностей-страт (районов).

Стратифицированная случайная выборка (в узком значении) основана на выборке по каждой страте отдельно. Это повышает точность результатов либо уменьшает время, силы и стоимость исследования, допуская меньшие размеры выборки при заданном уровне точности. Например, известно, что бедность наиболее часто встречается среди пожилых, безработных и в монородительских семьях. Исследуя проблемы бедности, можно с равным успехом выбрать в качестве объекта любую из трех страт. В отобранных районах или стратах выбор единиц обследования проводится по вероятностному методу.

Основная цель всякого расслоения — повышение точности выборочных оценок. Слои выделяются таким образом, чтобы дисперсия изучаемых переменных внутри слоев была значительно меньше, чем между ними. При расслоении вариация между слоями не входит в среднюю ошибку выборки, а компенсируется самой процедурой выделения слоев. Поэтому расслоение позволяет добиться более высокой степени точности оценок по сравнению с простым случайным отбором. Если каждый слой представляет собой статистически однородную группу, то для любого из них даже выборка малого объема позволит получить достаточно точные оценки, которые, будучи объединены, дадут хорошую оценку для всей совокупности.

Различают стратификацию одномерную и многомерную в зависимости от того, один или несколько признаков положены в основу разделения совокупности. Эти признаки должны иметь тесную связь с изучаемыми переменными, от их выбора в высокой степени зависит эффективность расслоения.

Гнездовая выборка

Противоположность районированной и стратифицированной выборке составляет гнездовая выборка.

Гнездовая выборка — вид выборки, при котором отбираемые объекты представляют собой группы или гнезда (кластеры) более мелких единиц. Гнездом называют единицу отбора высшей ступени, состоящую из более мелких единиц низшей ступени. В выборку могут быть включены как все единицы низшего уровня, так и их часть. Число единиц, образующих гнездо, называют его размером.

В качестве гнезд выступают населенные пункты, районы, дома, подъезды, предприятия, цехи, бригады.

Гнездовой отбор обладает большими организационными преимуществами — проще осуществлять отбор и обследование нескольких компактных групп, чем десятков или сотен отдельных единиц. Технические преимущества гнездового отбора особенно ощутимы при построении территориальной выборки. Отбор небольшого числа территориальных сегментов (населенных пунктов, районов, жилых кварталов и т.п.), затем выборочный или сплошной опрос проживающего в них населения существенно уменьшают стоимость исследования и сроки проведения.

Процедурно такой метод применить легче, чем вероятностный либо районированный. Проблемы, которые возникают здесь, связаны с определением величины гнезда, количеством гнезд, которые надо обследовать, их размещением в генеральной совокупности.

Основные рекомендации при выборе гнезд сводятся к тому, чтобы различия между гнездами были бы по возможности более неоднородными. Это правило прямо противоположно основному принципу расслоения, в соответствии с которым выигрыш в точности тем больше, чем более однородными будут выделенные слои. Другая рекомендация касается выбора размера гнезд: большое число малых гнезд предпочтительнее малого числа крупных.

Группировка наблюдений

Группировка наблюдений

При большом числе наблюдений, $n>80$, статистический материал, помещённый в таблицу, трудно обозрим. Поэтому составляется группировка. Это делается так: Находится

1. размах выборки,
2. шаг выборки,
3. интервалы { разбиение на интервалы } ,
4. центры интервалов,
5. абсолютные частоты,
6. относительные частоты.

1. Чтобы найти размах выборки надо найти максимальные и минимальные значения вариант. Разность между ними называется размахом выборки $x_ { max } -x_ { min } =Delta $.
2. Определим шаг выборки. Для этого надо разделить $Delta $ на $k$ – частей, где $k$ должно быть не более $20div 25$ и не менее $6div 10$. Обычно $6div 10leqslant kleqslant 20div 25$. Иногда $k$ считают по формуле $log _2 n+1approx k$, где $n$ – объём выборки. Шаг выборки вычисляется по формуле $h=frac { Delta } { k } $.
3. Разбить на интервалы шириной $h$ по формуле $[x_i ,,,x_i +h)$.
4. Найти центры интервалов по формуле $x_i =frac { x_i +x_ { i+1 } } { 2 } $.
5. Найти абсолютные частоты. Для этого нужно подсчитать число выборочных значений $n_i $ величины $X$, попадающей в каждый интервал. Существует контроль $sum { n_i =n } $.
6. Подсчитать относительные частоты по формуле $W_i =frac { n_i } { n } $.
7. Выписать полученные интервалы или центры интервалов, выборочные значения и относительные частоты в таблицу.
8. Представить выборку графически. Графическим представлением является полигон и гистограмма.

Полигон и гистограмма

Определение Полигоном абсолютных частот называют ломаную линию, отрезки которой соединяют точки $( { x_1 ,n_1 } ),( { x_2 ,n_2 } ),( { x_3 ,n_3 } )ldots ( { x_k ,n_k } )$.

На оси абсцисс откладывают варианты $x_i $, на оси ординат – соответствующие им частоты $n_i $.

Определение Полигоном относительных частот называют ломаную линию, отрезки которой соединяют точки $( { x_1 ,w_1 } ),( { x_2 ,w_2 } ),( { x_3 ,w_3 } )ldots ( { x_k ,w_k } )$. Для построения полигона относительных частот на оси $OX$ откладывают варианты $x_i $, а на оси ординат соответствующие им относительные частоты $w_i $. Точки $( { x_i ,w_i } )$ соединяют прямыми и получают полигон относительных частот.

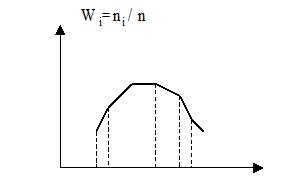
Определение Гистограммой частот называют ступенчатую фигуру, состоящую из прямоугольников, основаниями служат интервалы длиной $h$, а высотами являются плотности частоты $frac { n_i } { h } $. Площадь гистограммы частот равна сумме всех частот, т. е. объёму выборки.

Определение Гистограммой относительных частот называют ступенчатую фигуру, состоящую из прямоугольников с основаниями длиной $h$ и высотами $frac { W_i } { h } $ { плотность относительных частот } . Площадь гистограммы равна сумме всех относительных частот, т. е. 1

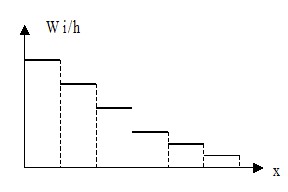
Замечание Полигон и гистограмма строятся для того, чтобы получить представление о форме функции плотности распределения.

Пример группировки

Составить группировку и представить её графически, разбив на шесть интервалов

$mathbf { 16,,,, } mathbf { 17,,,, } mathbf { 9,,,, } mathbf { 13,,,, } mathbf { 21,,,, } mathbf { 11,,,, } mathbf { 7,,,, } mathbf { 19,,,, } mathbf { 5,,,, } mathbf { 20 } $

$mathbf { 17,,,, } mathbf { 5,,,,7,,,, } mathbf { 18,,,, } mathbf { 11,,,, } mathbf { 4,,,,6,,,, } mathbf { 22,,,,21,,,, } mathbf { -1 } $

$mathbf { 15,,,, } mathbf { 22,,,, } mathbf { 19,,,, } mathbf { 23,,,, } mathbf { 15 } $

Объём выборки $n=25$

1) $x_ { max } =23,x_ { min } =-1,Delta =x_ { max } -x_ { min } =23+1=24$.

2) Разделим $Delta $ на шесть частей $h=frac { 24 } { 6 } =4$.

Вывод Будем иметь шесть интервалов, ширина интервала $h=4$.

3) Найдём выборочные значения $n_i $ в каждом интервале. Контроль $sum { n_i =n } $

4) Подсчитаем относительные частоты $ W_i =frac { n_i } { n } $

5) Подсчитаем плотность относительных частот $ f( x )=frac { W_i } { h } . $

6) Строим полигон и гистограмму.

Занесем полученные значения в таблицу.

begin{array} { |l|l|l|l|l|l|l| } hline №& Интервал& Выборочные~частоты~ n_i & x_i -центр~интервала& W_i =frac { n_i } { n } & f( x )=frac { W_i } { h } & frac { n_i } { h } \ hline 1& [ -1,3 ]& 1& 1& 0,04& 0,01& 0,25 \ hline 2& ( 3,7 ]& 6& 5& 0,24& 0,06& 1,5 \ hline 3& ( 7,11 ]& 3& 9& 0,12& 0,03& 0,75 \ hline 4& ( 11,15 ]& 3& 13& 0,12& 0,03& 0,75 \ hline 5& ( 15,19 ]& 6& 17& 0,24& 0,06& 1,5 \ hline 6& ( 19,23 ]& 6& 21& 0,24& 0,06& 1,5 \ hline sum & & sum { n_i =n } =25& & sum { W_i =1 } & &\ hline end{array}

Гистограмма частот n$_ { i } $

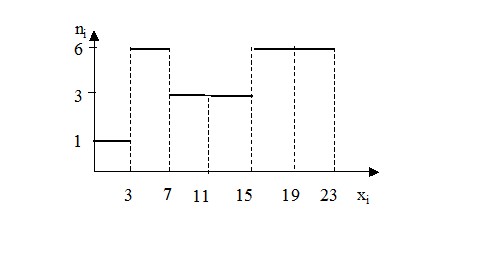полигон частот $n_i $ для средины интервалов

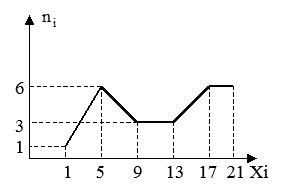
Гистограмма плотности частот $frac { n_i } { h } $

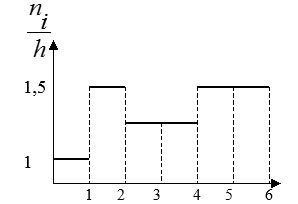
Гистограмма плотности относительных частот $frac { W_i } { h } $

Эта величина носит вероятностный характер.

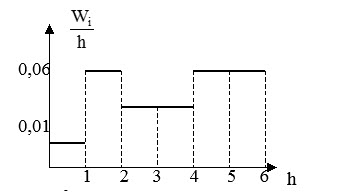
По полученной гистограмме выдвигается гипотеза о равномерном распределении.

Авторы статьи — А.М. Степанов, социолог отдела аналитических и социологических исследований, М.В. Иванов, начальник отдела аналитических и социологических исследований МАУ «ИРСИ».

Параметры расчета выборочной совокупности

Вне
зависимости от метода расчета выборки нужно помнить о ключевых параметрах,
влияющих на объем выборочной совокупности. Таких параметров мы выделим три –
это общий объём, однородность и абсолютная
ошибка.

Общий
объем генеральной совокупности. Чем больше изучаемая генеральная
совокупность, тем больший объем выборки нам может понадобиться для
репрезентативного исследования. Однако это утверждение касается лишь определенного
числового диапазона! Увеличение выборки идет не пропорционально увеличению
генеральной совокупности. Ведь если речь пойдет о генеральной совокупности как о
малочисленной величине, исчисляемой десятками и сотнями единиц, то
целесообразно предположить, что чем больше будет объем выборки, тем точнее
данные. В идеале можно и нужно стремиться, чтобы в таком случае выборка
составляла не менее 50%, а то и 2/3 изучаемой генеральной совокупности. Если же
(а чаще всего это так и есть) мы имеем дело с генеральными совокупностями,
исчисляемыми десятками, сотнями тысяч и миллионами (например, население
крупного города, региона, страны), то, конечно же, мы не будем опрашивать ни
50%, ни 25%, ни 10%. Нам понадобится значительно меньшее число участников
опроса (респондентов). Стоит отметить, что при сравнении выборки при объеме
генеральной совокупности в 100 тысяч и 1 миллион человек, разница в объеме
выборки может составить всего несколько десятков респондентов (см. таблицу).

+ В этих случаях достаточным
будет более 50% от объема выборки.

Источник: Мангейм
Дж.Б., Рич Р.К. Политология:
Методы исследования. – М., 1997. С.517.

Однородность генеральной совокупности.
В данном случае речь идёт об однородности признаков у единиц генеральной
совокупности. То есть чем более схожи между собой единицы генеральной
совокупности, тем меньше потребуется объем выборки для представления
репрезентативных результатов исследования. Причем под однородностью
рассматриваемых признаков мы можем понимать и социально-демографические
характеристики (пол, возраст, уровень образования, район проживания, социальное
положение), ценностные и социально-политические ориентации, культурно-языковые
различия, материальный достаток и т.д.

Размер ошибки (погрешности) выборки. Задачи
и характер исследования определяют допустимый размер погрешности полученных
данных. Самым оптимальным и часто используемым вариантом при расчете выборки
является ошибка в 5%, она позволяет получить данные с высокой степенью
репрезентативности и при этом не затратить много ресурсов на опрос излишнего
числа респондентов. Для прикладного
исследования нормальной будет выборка с ошибкой 4–5%. Ошибка выборки,
рассчитываемой ВЦИОМ, ФОМ (для федеральных исследований),
находится на уровне не ниже 2,5%. Стандартные
выборки МАУ ИРСИ по г. Ярославлю
обеспечивает ошибку выборки в диапазоне от 3,6
до 4,8%. Если говорить простым языком о том, что собой представляет ошибка
выборки в 5%, то можно представить, что в случае проведения 100 одинаковых
исследований по одной и той же теме и с одинаковым объемом выборки в 95 случаях
из 100 результаты исследования будут совпадать с мнением всей генеральной
совокупности. Однако в определенных случаях требуется снижение ошибки выборки,
которое чаще всего производится посредством наращивания объема выборочной
совокупности.

В
зависимости от имеющихся ресурсов и задач исследования для формирования выборки
существует несколько способов. В первую очередь нужно понимать, что отбор единиц
в выборочную совокупность может происходить как случайным образом, так и
неслучайным. Случайной или вероятностной выборкой можно назвать
только ту выборочную совокупность, в которой соблюдается принцип равной
вероятности для каждой единицы генеральной совокупности попасть в выборку.
Такой способ формирования выборки наиболее актуален для небольшого объема
генеральной совокупности, поскольку при изучении больших групп принцип равной
вероятности для всех элементов генеральной совокупности соблюсти крайне
затруднительно или нецелесообразно, с точки зрения высоких затрат ресурсов.
Для  соблюдения принципа равной
вероятности случайной выборки зачастую используют механический отбор, такой
отбор возможен только при наличии полного списка единиц генеральной
совокупности, которые можно упорядочить по определенному признаку. В рамках
механического отбора из списка выбирается случайным образом первый элемент,
который служит отправной точкой, и каждый последующий выбирается через
определенный шаг. Размер шага определяется частным размера генеральной
совокупности и размера предполагаемой выборки K(шаг) = N(генеральная совокупность)/n(выборочная совокупность).

Другим
способом для соблюдения принципа случайности в выборке может быть стратифицированный (районированный) отбор.
Данный метод полезен в случае неоднородной генеральной совокупности и
подразумевает разделение единиц генеральной совокупности, на более мелкие
группы по определенным признакам. Внутри каждой выделенной группы производится
отбор единиц в выборочную совокупность случайным образом или при помощи
механического отбора. Наиболее корректно использовать этот метод в том случае,
когда в результате разделения на группы по выбранным признакам внутри каждой
группы образуется небольшое количество единиц, или когда существует полный
список единиц каждой выделенной группы, что позволяет в дальнейшем отборе соблюсти
принцип равной возможности для каждой единицы попасть в выборку.

Кластерный (гнездовой) отбор
является еще одним методом при формировании случайной выборки, в рамках данного
метода производиться случайным образом отбор целых групп (кластеров) из генеральной
совокупности. Впоследствии производится отбор единиц из кластеров в выборочную
совокупность, в зависимости от объема кластера это могут быть как и все единицы
кластера, так и часть из них, отобранная случайным образом. Например, в случае
отбора по территориальному признаку кластером могут служить населенные пункты,
отобранные в случайном порядке. В зависимости от количества населения
производится опрос всех жителей или только жителей, отобранных случайным
образом. При наличии полного списка единиц в каждом кластере возможен отбор
единиц с применением механического отбора. 

В
исследованиях, где в качестве генеральной совокупности выступают тысячи или
даже миллионы людей, наиболее удобно использовать выборки с неслучайным
отбором, где отбор производится по заранее заготовленной схеме или стихийным
образом. Стихийная выборка подразумевает опрос по принципу «всех подряд» из
наиболее доступных респондентов. Здесь, как правило, производится опрос
наиболее удобных для интервьюера респондентов. Зачастую стихийная выборка
страдает слабой репрезентативностью по причине несоответствия некоторых
признаков выборочной совокупности признакам генеральной. Происходит это
вследствие упущения в ходе исследования некоторых значимых категорий
респондентов, которые являются труднодоступными для интервьюера. Поэтому данный
способ формирования выборки может использоваться в условиях ограниченности
ресурсов.

Наиболее
предпочтительным выглядит вариант с использованием квотной выборки. Суть данного метода сводится к тому, чтобы
выделить несколько интересующих социальных групп по признакам, обусловленным
задачами исследования. Далее необходимо рассчитать объем респондентов для
опроса в каждой группе, то есть объем квоты для каждой группы, руководствуясь
сохранением пропорций признаков  генеральной
совокупности в выборке. На примере гендерной характеристики можем представить,
что если в генеральной совокупности соотношение женщин и мужчин 55% на 45%, то именно
такое же соотношение женщин и мужчин должно быть в рамках выборочной
совокупности.

Аналогичным
образом  составляются квоты и по другим
признакам. Целью данного подхода является максимальное повторение в рамках
выборки свойств и особенностей генеральной совокупности. Иногда для упрощения
поиска респондентов, подходящих под критерии отбора, может использоваться метод
«снежного кома». Особенность
«снежного кома» во многом объясняется названием метода и подразумевает поиск
контактов подходящих для опроса людей у респондентов, уже участвовавших в
опросе. Как правило, это выглядит следующим образом: по завершении опроса
интервьюер интересуется у респондента, нет ли среди его друзей и знакомых,
подходящих под параметры исследования, и просит дать контакты подходящих людей.
Данная процедура повторяется до тех пор, пока не будет опрошено необходимое
количество респондентов. Основной минус данного метода отбора респондентов заключается
в предъявлении высоких требований к коммуникативным навыкам интервьюеров,
поскольку контакты родственников и друзей являются персональными данными, и многие
респонденты отказываются их давать, особенно если интервьюеру не удается
расположить собеседника к себе.

Еще
одним методом отбора для построения неслучайной выборки является метод основного массива, который
подразумевает отбор единиц, имеющих наибольшую удельную значимость, по мнению
исследователя; и если существует возможность, то отбирается абсолютное
большинство единиц из генеральной совокупности. Данный метод может быть
полезен, когда объектом для изучения являются узкая категория людей, специалисты
той или иной отрасли. В случае необходимости проведения опроса, например среди
медработников в регионе, отбирается несколько наиболее крупных медицинских
учреждений как имеющих наибольший вес, и проводится опрос медработников данных
учреждений. Но если количество медучреждений не столь велико, и возможен охват
абсолютного большинства медработников, то проводится опрос более 50%
медицинских работников региона.

Существует
еще несколько вариантов составления выборочной совокупности, некоторые методы являются
комбинированием уже перечисленных, но хотелось бы рассмотреть применение
наиболее оптимальных методов построения выборки на примере населения г.
Ярославля. Золотым стандартом, на наш взгляд, при проведении исследования, где
в качестве генеральной совокупности выступают все жители Ярославля, является
применение квотной выборки.  Мы используем при расчете квот трехмерное распределение,
а именно распределение по половому признаку, возрасту и району проживания, что
позволяет в рамках выборочной совокупности повторить пропорции генеральной
совокупности по указанным признакам. Такой подход позволяет учесть мнение всех
категорий жителей Ярославля: мужчин и женщин, молодежи, работающего населения,
пенсионеров, жителей всех районов города. При этом сохраняется удельная
значимость каждой из указанных категорий так же, как в генеральной
совокупности.  Как это выглядит? Например,
если в Ярославле в Дзержинском районе проживает гораздо больше жителей города,
чем в Кировском районе города, то мнение жителей Дзержинского района имеют
гораздо большее влияние на формирование мнения всего населения города, чем мнение
жителей Кировского района. Наша задача состоит в том, чтобы сохранить подобную пропорциональность
генеральной совокупности в рамках выборки. Если говорить о конкретных цифрах,
то для репрезентативных результатов мнения жителей города с населением более
чем 600 тыс. при использовании квотной выборки и соблюдением ошибки не более 5%
достаточно опросить 400 человек. В случае, когда проблема исследования носит
более дифференцированный характер, и предполагается, что данная проблема может
затрагивать различные категории жителей по-разному, целесообразно расширить объем
выборки до 500-600 человек.

В
случае, когда проблема исследования носит общий или даже глобальный характер, и
предполагается, что дифференциация по полу и возрасту, району проживания вряд
ли может серьезно оказывать влияние на мнение респондента, может использоваться
метод стихийной выборки. Метод
стихийного отбора позволяет существенно сократить время и ресурсы на проведение
исследования, однако в таком случае рекомендуется расширить объем выборки до
600, а в некоторых случаях до 750 или даже 1000 человек, чтобы минимизировать вероятность
потери какой-либо категории респондентов в процессе проведения опроса.

Использование
случайных методов формирования выборки для проведения опроса среди населения
достаточно крупного города выглядит нерационально и порой даже нереалистично. Ведь
жители Ярославля в качестве генеральной совокупности есть  величина непостоянная, поскольку ежедневно
жители города как приезжают, так и покидают город, и в таких условия обеспечить
принцип равного шанса попадания в выборку для всех жителей Ярославля
проблематично. Использование механического отбора требует полного списка всех
жителей Ярославля с контактными данными, получение которого не представляется
возможным в силу федерального закона «О персональных данных», а также выглядит
нецелесообразным ввиду высокой трудоемкости процесса и больших временных затрат
на построение выборки.

Подводя
итог, хочется сказать о том, что грамотно составленная выборка на сегодняшний
день — это ключ к оперативному получению достоверной и актуальной информации,
которая поможет в принятии правильных управленческих решений. Главное достоинство
использования выборки — это, конечно же, экономия времени и трудовых ресурсов.
Получаемая информация с течением времени 
и в зависимости от происходящих процессов в обществе может быстро терять
актуальность и уже не отражать полной картины социальной реальности, что в свою
очередь может повлечь принятие ошибочных решений. Отсюда можно сделать вывод о
том, что исследование, задачей которого является получение объективной
информации о текущем положении дел, проведенное в кротчайшие сроки с
использованием грамотно составленной выборки, даст более актуальную информацию
и объективную картину, чем исследование с большим охватом опроса в 6,  10, 15 и более тысяч человек. Исследование с
бОльшим охватом респондентов требует бОльшего времени для проведения опроса, за
этот период положение дел может значительно измениться, и ответы, полученные в
начале исследования, могут к его окончанию стать устаревшими и неактуальными; как
итог — будет потерян весь смысл такого исследования.

Желаете получить достоверную,
актуальную и надежную информацию по вашей проблеме в результате проведения
социологического исследования? Специалисты МАУ ИРСИ помогут вам в этом!