Как найти шестиугольник в треугольнике

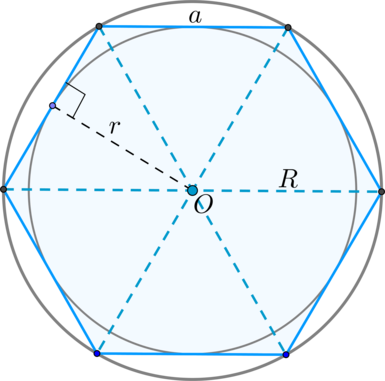
Гексагон

Гексагон — правильный выпуклый многоугольник с шестью сторонами или шестиугольник.

Шестиугольник – это многоугольник, имеющий шесть сторон и шесть углов. В правильном шестиугольнике все стороны равны, а углы образуют шесть равносторонних треугольников.

Выпуклый шестиугольник – это многоугольник, с общим количеством вершин, равным шести, при этом все точки такого шестиугольника лежат по одну сторону от прямой, которая проведена между двумя любыми соседними его вершинами.

Правильный шестиугольник – это шестиугольник, все стороны которого равны между собой.

Сумма углов выпуклого шестиугольника определяется по общей формуле 180°(n-2) и равна 180 ( 6 – 2 ) = 720 градусов.

При решении задач для нахождения площади произвольного (неправильного) шестиугольника используют метод трапеций, который заключается в разбиении фигуры на отдельные трапеции, площадь каждой из которых можно найти по известным всем формулам.

Свойства правильного шестиугольника

• все внутренние углы равны между собой
• каждый внутренний угол правильного шестиугольника равен 120 градусам
• все стороны равны между собой
• сторона правильного шестиугольника равна радиусу описанной окружности
• большая диагональ правильного шестиугольника является диаметром описанной вокруг него окружности и равна двум его сторонам
• меньшая диагональ правильного шестиугольника в ( sqrt <3>) раз больше его стороны.
• vеньшая диагональ правильного шестиугольника перпендикулярна его стороне
• правильный шестиугольник заполняет плоскость без пробелов и наложений
• диагонали пересекаются в одной точке и делят его на 6 равносторонних треугольников, у которых высота равна радиусу вписанной в правильный шестиугольник окружности. 6.
• инвариантен относительно поворота плоскости на угол, кратный относительно центра описанной окружности (слово “инвариантный” означает, что при таких поворотах правильный шестиугольник перейдёт в себя, то есть такие повороты являются его симметриями)
• nреугольник, образованный стороной шестиугольника, его большей и меньшей диагоналями, прямоугольный, а его острые углы равны 30° и 60° .

Внутренние углы Внутренние углы в правильном шестиугольнике равны (120^circ) :

Апофема Апофема правильного шестиугольника (перпендикуляр, проведенный из центра к любой стороне)

Апофема Апофема правильного шестиугольника (перпендикуляр, проведенный из центра к любой стороне)

Радиус вписанной окружности правильного шестиугольника равен апофеме:

(r = m = alargefrac<<sqrt 3 >><2>normalsize)

Радиус описанной окружности равен стороне правильного шестиугольника:

Периметр правильного шестиугольника

Площадь правильного шестиугольника Формула площади правильного шестиугольника через длину стороны

(S = pr = largefrac<<3sqrt 3 >><2>normalsize),
где (p) − полупериметр шестиугольника.

Площадь правильного шестиугольника Формула площади правильного шестиугольника через радиус вписанной окружности

Площадь правильного шестиугольника Формула площади правильного шестиугольника через радиус описанной окружности

Если материал понравился Вам и оказался для Вас полезным, поделитесь им со своими друзьями!

Правильный шестиугольник и его свойства

Определение

Выпуклый многоугольник называется правильным, если все его стороны равны и все его углы равны.

Замечание

Т.к. сумма всех углов (n) –угольника равна (180^circ(n-2)) , то каждый угол правильного (n) –угольника равен [alpha_n=dfracn cdot 180^circ]

Пример

Каждый угол правильного четырехугольника (т.е. квадрата) равен (dfrac <4-2>4cdot 180^circ=90^circ) ;

каждый угол правильного шестиугольника равен (dfrac<6-2>6cdot 180^circ=120^circ) .

Теоремы

1. Около любого правильного многоугольника можно описать окружность, и притом только одну.

2. В любой правильный многоугольник можно вписать окружность, и притом только одну.

Следствия

1. Окружность, вписанная в правильный многоугольник, касается всех его сторон в серединах.

2. Центры вписанной и описанной окружности у правильного многоугольника совпадают.

Теорема

Если (a) – сторона правильного (n) –угольника, (R) и (r) – радиусы описанной и вписанной окружностей соответственно, то верны следующие формулы: [begin S&=dfrac n2ar\ a&=2Rcdot sindfrac<180^circ>n\ r&=Rcdot cosdfrac<180^circ>n end]

Свойства правильного шестиугольника

1. Сторона равна радиусу описанной окружности: (a=R) .

2. Радиус описанной окружности является биссектрисой угла правильного шестиугольника.

3. Все углы правильного шестиугольника равны (120^circ) .

4. Площадь правильного шестиугольника со стороной (a) равна (dfrac<3sqrt<3>><2>a^2) .

5. Диагонали пересекаются в одной точке и делят его на 6 равносторонних треугольников, у которых высота равна радиусу (r) вписанной в правильный шестиугольник окружности.

6. Инвариантен относительно поворота плоскости на угол, кратный (60^circ) относительно центра описанной окружности (слово “инвариантный” означает, что при таких поворотах правильный шестиугольник перейдёт в себя, то есть такие повороты являются его симметриями).

Замечание

В общем случае правильный (n) -угольник инвариантен относительно поворота на угол (dfrac<360^circ>) .

Техническое черчение

Popular

Основы черчения

Строительное

Машиностроительное

Построение вписанного в окружность правильного шестиуголь­ника. Построение шестиугольника основано на том, что сторона его равна радиусу описанной окружности. Поэтому для построения доста­точно разделить окружность на шесть равных частей и соединить най­денные точки между собой (фиг. 60, а).

Правильный шестиугольник можно построить, пользуясь рейсшиной и угольником 30X60°. Для выполнения этого построения принимаем горизонтальный диаметр окружности за биссектрису углов 1 и 4 (фиг. 60, б), строим стороны 1 —6, 4—3, 4—5 и 7—2, после чего прово­дим стороны 5—6 и 3—2.

Построение вписанного в окружность равностороннего треуголь­ника. Вершины такого треугольника можно построить с помощью циркуля и угольника с углами в 30 и 60° или только одного цир­куля.

Рассмотрим два способа построения вписанного в окружность рав­ностороннего треугольника.

Первый способ (фиг. 61,a) основан на том, что все три угла треугольника 7, 2, 3 содержат по 60°, а вертикальная прямая, прове­дённая через точку 7, является одновременно высотой и биссектрисой угла 1. Так как угол 0—1—2 равен 30°, то для нахождения стороны

1—2 достаточно построить по точке 1 и стороне 0—1 угол в 30°. Для этого устанавливаем рейсшину и угольник так, как это показано на фигуре, проводим линию 1—2, которая будет одной из сторон искомого треугольника. Чтобы построить сторону 2—3, устанавливаем рейсшину в положение, показанное штриховыми линиями, и через точку 2 прово­дим прямую, которая определит третью вершину треугольника.

Второй способ основан на том, что,если построить правильный шестиугольник, вписанный в окружность, и затем соединить его вер­шины через одну, то получится равносторонний треугольник.

Для построения треугольника (фиг. 61, б) намечаем на диаметре вершину—точку 1 и проводим диаметральную линию 1—4. Далее из точки 4 радиусом, равным D/2, описываем дугу до пересечения с окруж­ностью в точках 3 и 2. Полученные точки будут двумя другими вер­шинами искомого треугольника.

Построение квадрата, вписанного в окружность. Это построение можно выполнить при помощи угольника и циркуля.

Первый способ основан на том, что диагонали квадрата пере­секаются в центре описанного круга и наклонены к его осям под углом 45°. Исходя из этого, устанавливаем рейсшину и угольник с углами 45° так, как это показано на фиг. 62, а, и отмечаем точки 1 и 3. Далее через эти точки проводим при помощи рейсшины горизонтальные сто­роны квадрата 4—1 и 3—2. Затем с помощью рейсшины по катету угольника проводим вертикальные стороны квадрата 1—2 и 4—3.

Второй способ основан на том, что вершины квадрата делят пополам дуги окружности, заключённые между концами диаметра (фиг. 62, б). Намечаем на концах двух взаимно перпендикулярных диа­метров точки А, В и С и из них радиусом у описываем дуги до вза­имного их пересечения.

Далее через точки пересечения дуг проводим вспомогательные пря­мые, отмеченные на фигуре сплошными линиями. Точки их пересече­ния с окружностью определят вершины 1 и 3; 4 и 2. Полученные таким образом вершины искомого квадрата соединяем последовательно между собою.

Построение вписанного в окружность правильного пятиугольника.

Чтобы вписать в окружность правильный пятиугольник (фиг. 63), про­изводим следующие построения.

Намечаем на окружности точку 1 и принимаем её за одну из вер­шин пятиугольника. Делим отрезок АО пополам. Для этого радиусом АО из точки А описываем дугу до пересечения с окружностью в точ­ках M и В. Соединив эти точки прямой, получим точку К, которую соединяем затем с точкой 1. Радиусом, равным отрезку A7, описываем из точки К дугу до пересечения с диаметральной линией АО в точке H. Соединив точку 1 с точкой H, получим сторону пятиугольника. Затем раствором циркуля, равным отрезку 1H, описав дугу из вершины 1 до пересечения с окружностью, найдём вершины 2 и 5. Сделав тем же раствором циркуля засечки из вершин 2 и 5, получим остальные вер­шины 3 и 4. Найденные точки последовательно соединяем между собой.

Построение правильного пятиугольника по данной его стороне.

Для построения правильного пятиугольника по данной его стороне (фиг. 64) делим отрезок AB на шесть равных частей. Из точек А и В радиусом AB описываем дуги, пересечение которых даст точку К. Через эту точку и деление 3 на прямой AB проводим вертикальную прямую.

Далее от точки К на этой прямой откладываем отрезок, равный 4/6 AB.

Получим точку 1—вершину пятиугольника. Затем радиусом, равным АВ, из точки 1 описываем дугу до пересечения с дугами, ранее проведён­ными из точек А и В. Точки пересечения дуг определяют вершины пятиугольника 2 и 5. Найденные вершины соединяем последовательно между собой.

Построение вписанного в окружность правильного семиугольника.

Пусть дана окружность диаметра D; нужно вписать в неё правильный семиугольник (фиг. 65). Делим вертикальный диаметр окружности на семь равных частей. Из точки 7 радиу­сом, равным диаметру окружности D, описываем дугу до пересечения с про­должением горизонтального диаметра в точке F. Точку F назовём полюсом многоугольника. Приняв точку VII за одну из вершин семиугольника, прово­дим из полюса F через чётные деления вертикального диаметра лучи, пересече­ние которых с окружностью определят вершины VI, V и IV семиугольника. Для получения вершин / — // — /// из точек IV, V и VI проводим до пересечения с окружностью горизонтальные прямые. Найденные вершины соединяем после­довательно между собой. Семиугольник может быть построен путём проведе­ния лучей из полюса F и через нечётные деления вертикального диаметра.

Приведённый способ годен для построения правильных многоуголь­ников с любым числом сторон.

Деление окружности на любое число равных частей можно произ­водить также, пользуясь данными табл. 2, в которой приведены коэф­фициенты, дающие возможность определять размеры сторон правильных вписанных многоугольников.

В первой колонке этой таблицы указаны числа сторон правильного вписанного многоугольника, а во второй—коэффициенты.

Длина стороны заданного многоугольника получится от умножения радиуса данной окружности на коэффициент, соответствующий числу сторон этого многоугольника.

[spoiler title=”источники:”]

http://shkolkovo.net/theory/77

http://www.nacherchy.ru/postroenie_pravilnich_mnogougolnikov.html

[/spoiler]

Если постепенно уменьшать длину отрезков деления, продолжая вписывать соответствующие правильные треугольники, то через некоторое время начнут проглядываться кривые (рис. 2, слева). Продолжая этот процесс до бесконечности, в итоге получим три кривые, которыми ограничивается желтая фигура (рис. 2, справа), — это огибающие семейств сторон вписанных треугольников.

Чтобы выяснить вид этих кривых, рассмотрим прямоугольную систему координат (Oxy). Треугольник расположим так, чтобы одна из вершин совпадала с началом координат (O), а противоположная ей сторона (AB) была параллельна оси (Ox) (рис. 3).

Пусть (MN) — это сторона одного из вписанных треугольников, касающихся кривой (AKB); пусть (D) и (E) — проекции точек (M) и (N) на ось абсцисс. Примем сторону исходного треугольника (AOB) за (2a). Пусть (OD=t), тогда (OM=2t), (AM=2a-2t=ON), поэтому (OE=a-t). Получаем, что абсциссы точек (M) и (N) равны соответственно (t) и (a-t). Ординату точки (M) найдем из треугольника (OMD) — она равна (tsqrt3); аналогично, ордината точки (N) равна ((a-t)sqrt3).

По координатам точек (M(t,,tsqrt3)) и (N(a-t,,(a-t)sqrt3)) найдем уравнение прямой (MN): (frac{x-t}{(a-t)-t}=frac{y-tsqrt3}{(a-t)sqrt3-tsqrt3}). После упрощения получим (ay-2atsqrt3=2xtsqrt3-axsqrt3-2t^2sqrt3) — это параметрическое уравнение всех касательных к кривой (AKB). Можно это уравнение привести к стандартному уравнению прямой, но в этом нет необходимости, потому что в таком виде его легче дифференцировать.

Продифференцируем это уравнение по параметру (t): (-2asqrt3=2xsqrt3-4tsqrt3). Отсюда можно выразить параметр (t) через (x) и (a): (t=frac{x+a}{2}). Подставим полученное выражение в параметрическое уравнение касательных:

[ay-2asqrt3cdotfrac{x+a}{2}=2xsqrt3cdotfrac{x+a}{2}-axsqrt3-2sqrt3cdotleft(frac{x+a}{2}right)^2.]

После упрощения получим формулу кривой, частью которой является дуга (AKB):

[y=frac{sqrt3}{2a}x^2+frac{asqrt3}{2}.]

Понятно, что линия — парабола.

Заметим, что вершина параболы проходит через середину высоты треугольника. Это легко обосновать, если в формулу этой параболы подставить (x=0): получим ординату (frac{asqrt3}{2}) точки пересечения, а это как раз половина высоты исходного равностороннего треугольника.

Из соображений симметрии можно утверждать, что две другие дуги тоже являются параболами. Пересекаясь, эти три параболы ограничивают криволинейный треугольник (TLP) (рис. 4). Чтобы найти координаты точек пересечения, нужно знать формулы этих парабол. Нами найдено уравнение только одной параболы. Вывод уравнений других парабол можно осуществить, опираясь на общую теорию кривых второго порядка, но на этом пути нас ждут громоздкие вычисления.

Поступим иначе. Заметим, что точка (P) — не просто точка пересечения двух парабол: через нее также проходит одна из высот исходного треугольника. Обозначим ее (BH) (рис. 5). Уравнение параболы уже найдено, а уравнение высоты (BH) можно найти по координатам точек (B(-a,,asqrt3)) и (Hleft(frac a2,,frac{asqrt3}{2}right)). Уравнение прямой (BH) записывается так: (frac{x+a}{a/2+a}=frac{y-asqrt3}{asqrt3/2-asqrt3}). После упрощения его можно переписать в стандартном виде: (y=-frac{sqrt3}{3}x+frac{2asqrt{3}}{3}).

Теперь координаты точки (P) можно найти из системы уравнений, описывающих параболу (APB) и высоту (BH):

[left{begin{array}{l}y=frac{sqrt3}{2a}x^2+frac{asqrt3}{2},\ y=-frac{sqrt3}{3}x+frac{2asqrt{3}}{3}.end{array}right.]

Приравнивая правые части уравнений системы, получим уравнение (frac{sqrt3}{2a}x^2+frac{asqrt3}{2}=-frac{sqrt3}{3}x+frac{2asqrt{3}}{3}), сводящееся к квадратному. Его корнями являются числа (x_1=frac a3) и (x_2=-a). Уточним, что (x_2) — это абсцисса точки (B), нас же интересует (x_1) — абсцисса точки (P). Нетрудно найти и ординату (y_1=frac{5asqrt3}{9}) точки (P).

Теперь можно приступить к вычислению площади центральной фигуры (TLP), представляющей собой объединение равностороннего треугольника (TLP) и трех равных сегментов параболы: (S=S_{TLP}+3S_{text{сегмента}}) (рис. 6).

Сторона (TP) равностороннего треугольника (TLP) равна (frac{2a}{3}), поэтому его площадь равна (S_{TLP}=frac{a^2sqrt3}{9}). Площадь сегмента (TPF) вычислим с помощью определенного интеграла:

[S_{text{сегмента}}=2intlimits_{0}^{frac a3}left(frac{5asqrt5}{9}-left(frac{sqrt3}{2a}x^2+frac{asqrt3}{2}right)right)mathrm{d}x=left.left(frac{asqrt3}{9}x-frac{sqrt3}{3a}x^3right)right|_{0}^{frac a3}=frac{2a^2sqrt3}{81}.]

Поэтому площадь центральной фигуры равна

[S=frac{a^2sqrt3}{9}+3cdotfrac{2a^2sqrt3}{81}=frac{5a^2sqrt3}{27}.]

Площадь исходного треугольника со стороной (2a) равна (S_{AOB}=frac{(2a)^2sqrt3}{4}=a^2sqrt{3}).

Теперь можно найти отношение площади центральной фигуры к площади исходного треугольника. Оно равно (frac{5}{27}).

Определение

Выпуклый многоугольник называется правильным, если все его стороны равны и все его углы равны.

Замечание

Т.к. сумма всех углов (n)–угольника равна (180^circ(n-2)), то каждый угол правильного (n)–угольника равен [alpha_n=dfrac{n-2}n cdot 180^circ]

Пример

Каждый угол правильного четырехугольника (т.е. квадрата) равен (dfrac {4-2}4cdot 180^circ=90^circ);

каждый угол правильного шестиугольника равен (dfrac{6-2}6cdot
180^circ=120^circ).

Теоремы

1. Около любого правильного многоугольника можно описать окружность, и притом только одну.

2. В любой правильный многоугольник можно вписать окружность, и притом только одну.

Следствия

1. Окружность, вписанная в правильный многоугольник, касается всех его сторон в серединах.

2. Центры вписанной и описанной окружности у правильного многоугольника совпадают.

Теорема

Свойства правильного шестиугольника

1. Сторона равна радиусу описанной окружности: (a=R).

2. Радиус описанной окружности является биссектрисой угла правильного шестиугольника.

3. Все углы правильного шестиугольника равны (120^circ).

4. Площадь правильного шестиугольника со стороной (a) равна (dfrac{3sqrt{3}}{2}a^2).

5. Диагонали пересекаются в одной точке и делят его на 6 равносторонних треугольников, у которых высота равна радиусу (r) вписанной в правильный шестиугольник окружности.

6. Инвариантен относительно поворота плоскости на угол, кратный (60^circ) относительно центра описанной окружности (слово “инвариантный” означает, что при таких поворотах правильный шестиугольник перейдёт в себя, то есть такие повороты являются его симметриями).

Замечание

В общем случае правильный (n)-угольник инвариантен относительно поворота на угол (dfrac{360^circ}{n}).

Шестиугольник, виды, свойства и формулы.

Шестиугольник – это многоугольник, общее количество углов (вершин) которого равно шести.

Шестиугольник, выпуклый и невыпуклый шестиугольник

Правильный шестиугольник (понятие и определение)

Свойства правильного шестиугольника

Формулы правильного шестиугольника

Правильный шестиугольник в природе, технике и культуре

Звездчатый шестиугольник

Восьмиугольник

Шестиугольник, выпуклый и невыпуклый шестиугольник:

Шестиугольник – это многоугольник с шестью углами.

Шестиугольник – это многоугольник, общее количество углов (вершин) которого равно шести.

Шестиугольник может быть выпуклым и невыпуклым.

Выпуклым многоугольником называется многоугольник, все точки которого лежат по одну сторону от любой прямой, проходящей через две его соседние вершины. Невыпуклыми являются все остальные многоугольники.

Соответственно выпуклый шестиугольник – это шестиугольник, у которого все его точки лежат по одну сторону от любой прямой, проходящей через две его соседние вершины.

Рис. 1. Выпуклый шестиугольник

  Рис. 2. Невыпуклый шестиугольник

Сумма внутренних углов любого выпуклого шестиугольника равна 720°.

.

Правильный шестиугольник (понятие и определение):

Правильный шестиугольник (гексагон) – это правильный многоугольник с шестью сторонами.

В свою очередь правильный многоугольник – это многоугольник, у которого все стороны и углы одинаковые.

Правильный шестиугольник – это шестиугольник, у которого все стороны равны, а все внутренние углы равны 120°.

Рис. 3. Правильный шестиугольник

Правильный шестиугольник имеет 6  сторон, 6 углов и 6 вершин.

Углы правильного шестиугольника образуют шесть равносторонних треугольников.

Правильный шестиугольник можно построить с помощью циркуля и линейки.

Свойства правильного шестиугольника:

1. Все стороны правильного шестиугольника равны между собой.

a₁ = a₂ = a₃ = a₄= a₅ = a₆. 

2. Все углы равны между собой и составляют 120°.

α₁ = α₂ = α₃ = α₄ = α₅ = α₆ = 120°.

Рис. 4. Правильный шестиугольник

3. Сумма внутренних углов любого правильного шестиугольника равна 720°.

4. Все биссектрисы углов между сторонами равны и проходят через центр правильного шестиугольника O.

Рис. 5. Правильный шестиугольник

5. Количество диагоналей правильного шестиугольника равно 9.

Рис. 6. Правильный шестиугольник

6. Центр вписанной окружности O₁ совпадает с центром описанной окружности O₂, что и образуют центр многоугольника O.

Рис. 7. Правильный шестиугольник

7. Правильные шестиугольники замощают плоскость (то есть могут заполнять плоскость без пробелов и наложений).

8. Радиус описанной окружности правильного шестиугольника и его сторона равны.

Рис. 8. Правильный шестиугольник

R = a

Правильный шестиугольник в природе, технике и культуре:

Пчелиные соты имеют форму правильного шестиугольника.

Графит, графен имеют гексагональную кристаллическую решетку.

Гигантский гексагон – атмосферное явление на Сатурне – имеет форму правильного шестиугольника.

Рис. 9. Гигантский гексагон на Сатурне

Сечение гайки и многих карандашей имеет вид правильного шестиугольника.

Игровое поле гексагональных шахмат составляют шестиугольники, в отличие от квадратов традиционной шахматной доски.

Панцирь черепахи состоит из шестиугольников.

Гексагоном иногда называют материковую часть Франции, потому что её географические очертания напоминают данную геометрическую фигуру.

Рис. 10. Материковая часть Франции

Формулы правильного шестиугольника:

Пусть a – сторона шестиугольника, r – радиус окружности, вписанной в шестиугольник, R – радиус описанной окружности шестиугольника, P – периметр шестиугольника, S – площадь шестиугольника.

Формулы периметра правильного шестиугольника:

Формулы площади правильного шестиугольника:

Формула радиуса окружности, вписанной в правильный шестиугольник:

 

Формула радиуса окружности, описанной вокруг правильного шестиугольника:

R = a

Звездчатый шестиугольник:

Звездчатый шестиугольник (гексаграмма) – это многоугольник, у которого все стороны и углы равны, а вершины совпадают с вершинами правильного многоугольника.

Гексаграмма (др.-греч. ἕξ – «шесть» и γραμμή – «черта, линия») – это звезда с шестью углами, которая образуется из двух наложенных друг на друга равносторонних треугольников.

Прямоугольник

Прямоугольный треугольник

Равнобедренный треугольник

Равносторонний треугольник

Шестиугольник

Примечание: © Фото https://www.pexels.com, https://pixabay.com

Коэффициент востребованности
7 445

На этой странице сайта, в категории Математика размещен ответ на вопрос
Как начертить два треугольника чтобы их пересечением был шестиугольник?. По уровню сложности вопрос рассчитан на учащихся
10 – 11 классов. Чтобы получить дополнительную информацию по
интересующей теме, воспользуйтесь автоматическим поиском в этой же категории,
чтобы ознакомиться с ответами на похожие вопросы. В верхней части страницы
расположена кнопка, с помощью которой можно сформулировать новый вопрос,
который наиболее полно отвечает критериям поиска. Удобный интерфейс
позволяет обсудить интересующую тему с посетителями в комментариях.