Как найти ширину диаграммы направленности

Аннотация

Перед тем как перейти к рассмотрению конструкции и работы разного типа антенн, рассмотрим одну из важнейших характеристик антенны – диаграмму направленности и те параметры, которые из нее напрямую вытекают.
Рекомендую, также, ознакомиться с предыдущей статьёй – Ликбез: основы теории по антеннам.

Введение

Антенна, вне зависимости от конструкции, обладает свойством обратимости (может работать как на прием, так и на излучение). Часто в радиорелейных трактах одна и та же антенна может быть подключена одновременно к приемнику и передатчику. Это позволяет излучать и принимать сигнал в одном направлении на разных частотах.

Почти все параметры приемной антенны соответствуют параметрам передающей антенны, но иногда имеют несколько другой физический смысл.

Несмотря на то, что приемная и передающая антенны обладают принципом двойственности, в конструктивном отношении они могут существенно отличаться. Связано это с тем, что передающая антенна должна пропускать через себя значительные мощности для передачи электромагнитного сигнала на большие (максимально возможные) расстояния. Если же антенна работает на прием, то она взаимодействует с полями очень малой напряженности. Вид токопередающей конструкции антенны часто определяет ее конечные габариты.

Пожалуй, основная характеристика любой антенны это диаграмма направленности. Из нее вытекает множество вспомогательных параметров и такие важные энергетические характеристики как коэффициент усиления и коэффициент направленного действия.

Диаграмма направленности

Диаграмма направленности (ДН) – это зависимость напряженности поля, создаваемого антенной на достаточно большом расстоянии, от углов наблюдения в пространстве. В объеме диаграмма направленной антенны может выглядеть так, как показано на рисунке 1.

Рисунок 1

То, что изображено на рисунке выше также еще называют пространственной диаграммной направленностью, которая является поверхностью объема и может иметь несколько максимумов. Главный максимум, выделенный на рисунке красным цветом, называется главным лепестком диаграммы и соответствует направлению главного излучения (или приема). Соответственно первые минимальные или (реже) нулевые значения напряженности поля вокруг главного лепестка определяют его границу. Все остальные максимальные значения поля называются боковыми лепестками.

На практике встречаются различные антенны, которые могут иметь несколько направлений максимального излучения, или не иметь боковых лепестков вовсе.

Для удобства изображения (и технического применения) ДН их принято рассматривать в двух перпендикулярных плоскостях. Как правило, это плоскости электрического вектора E и магнитного вектора H (которые друг другу в большинстве сред перпендикулярны), рисунок 2.

Рисунок 2

В некоторых случаях ДН рассматривают в вертикальной и горизонтальной плоскостях по отношению к плоскости Земли. Плоские диаграммы изображают полярной или декартовой (прямоугольной) системами координат. В полярных координатах диаграмма более наглядна, и при наложении ее на карту можно получить представление о зоне действия антенны радиостанции, рисунок 3.

Рисунок 3

Представление диаграммы направленности в прямоугольной системе координат более удобно для инженерных расчетов, такое построение чаще применяется для исследования самой структуры диаграммы. Для этого диаграммы строят нормированными, с главным максимумом, приведенным к единице. На рисунке ниже приводится типичная нормированная диаграмма направленности зеркальной антенны.

Рисунок 4

В том случае, когда интенсивность бокового излучения довольно небольшая и в линейном масштабе измерение бокового излучения затруднительно, применяют логарифмический масштаб. Как известно децибелы маленькие значения делают большими, а большие – маленькими, поэтому та же самая диаграмма в логарифмическом масштабе выглядит так, как показано ниже:

Рисунок 5

Из одной только диаграммы направленности можно вытащить довольно большое количество важных для практики характеристик. Исследуем подробнее диаграмму, изображенную выше.

Один из наиболее важных параметров – это ширина главного лепестка по нулевому излучению θ₀ и ширина главного лепестка по уровню половинной мощности θ_0,5. Половина мощности соответствует уровню 3 дБ, или уровню 0,707 по напряженности поля.

Рисунок 6

Из рисунка 6 видно, что ширина главного лепестка по нулевому излучению составляет θ₀ = 5,18 град, а ширина по уровню половины мощности θ_0,5 = 2,15 град.

Также диаграммы оценивают по интенсивности бокового и обратного излучения (мощности боковых и задних лепестков), отсюда вытекает еще два важных параметры антенны – это коэффициент защитного действия, и уровень боковых лепестков.

Коэффициент защитного действия – это отношение напряженности поля, излученного антенной в главном направлении к напряженности поля, излученного в противоположном направлении.  Если рассматривают ориентацию главного лепестка диаграммы в направлении на 180 градусов, то обратного – на 0 градусов. Возможны и любые другие направления излучения. Найдем коэффициент защитного действия рассматриваемой диаграммы. Для наглядности изобразим ее в полярной системе координат (рисунок 7):

Рисунок 7

На диаграмме маркерами m1,m2 изображены уровни излучения в обратном и прямом направлениях соответственно. Коэффициент защитного действия определяется как:

 

– в относительных единицах. То же самое значение в дБ: 

. 

Уровень боковых лепестков (УБЛ) принято указывать в дБ, показывая тем самым, насколько уровень бокового излучения слаб по сравнению с уровнем главного лепестка, рисунок 8.

Рисунок 8

УБЛ в районе -18 дБ считается довольно хорошим показателем для высоконаправленной антенны. На рисунке изображены уровни первых боковых лепестков. Аналогично можно указывать также уровни всех последующих, но практической ценности их значение имеет мало, а представляет скорее академический интерес. Дело в том, что первые боковые лепестки находятся как правило “ближе всех остальных” к максимуму диаграммы направленности и могут оказывать помехи. Например, если сопровождение объекта происходит на уровне главного лепестка диаграммы -3дБ, а уровень первого бокового лепестка близок к этому значению (например -5:7 дБ), то велика вероятность начать цеплять объект боковым излучением со всеми вытекающими отсюда последствиями (неправильное позиционирование, потеря объекта и др.). Низкий УБЛ необходим не только для радиолокации, но и для области связи, ведь наличие паразитного излучения это всегда дополнительные помехи.

Коэффициент направленного действия и коэффициент усиления

Это два немаловажных параметра любой антенной системы, которые напрямую вытекают из определения диаграммы направленности. КНД и КУ часто путают между собой. Перейдем к их рассмотрению.

Коэффициент направленного действия

Коэффициент направленного действия (КНД) – это отношение квадрата напряженности поля, созданного в главном направлении (Е₀²), к среднему значению квадрата напряженности поля по всем направлениям (Е_ср²). Как понятно из определения, КНД характеризует направленные свойства антенны. КНД не учитывает потери, так как определяется по излучаемой мощности. Из сказанного выше можно указать формулу для расчета КНД:

D=E₀²/E_ср²

Если антенна работает на прием, то КНД показывает, во сколько раз улучшится отношение сигнал/шум по мощности, при замене направленной антенны ненаправленной, если помехи приходят равномерно со всех направлений.

Для передающей антенны КНД показывает, во сколько раз нужно уменьшить мощность излучения, если ненаправленную антенну заменить направленной, при сохранении одинаковых напряженностей поля в главном направлении.

КНД абсолютно ненаправленной антенны, очевидно, равно единице. Физически пространственная диаграмма направленности такой антенны выглядит в виде идеальной сферы:

Рисунок 9

Такая антенна одинаково хорошо излучает во всех направлениях, но на практике нереализуема. Поэтому это своего рода математическая абстракция.

Коэффициент усиления

Как уже было сказано выше, КНД не учитывает потери в антенне. Параметр, который характеризует направленные свойства антенны и учитывает потери в ней, называется коэффициентом усиления.

Коэффициент усиления (КУ) G – это отношение квадрата напряженности поля, созданного антенной в главном направлении (Е₀²), к среднему значению квадрата напряженности поля (Е_оэ²), созданного эталонной антенной, при равенстве подводимых к антеннам мощностей. Также отметим, что при определении КУ учитываются КПД эталонной и измеряемой антенны.

Понятие эталонной антенны очень важно в понимании коэффициента усиления, и в разных частотных диапазонах используют разные типы эталонных антенн. В диапазоне длинных/средних волн за эталон принят вертикальный несимметричный вибратор длиной четверть волны (рисунок 10).    

Рисунок 10

Для такого эталонного вибратора D_э=3,28, поэтому коэффициент усиления длинноволновой/средневолновой антенны определяется через КНД так: G=D*ŋ/3,28,  где ŋ – КПД антенны.

В диапазоне коротких волн в качестве эталонной антенны принимают симметричный полуволновый вибратор, для которого Dэ=1,64, тогда КУ:

G=D*ŋ/1,64

В диапазоне СВЧ (а это почти все современные Wi-Fi, LTE и др. антенны) за эталонный излучатель принят изотропный излучатель, дающий D_э=1, и имеющий пространственную диаграмму, изображенную на рисунке 9.

Коэффициент усиления является определяющим параметром передающих антенн, так как показывает, во сколько раз необходимо уменьшить мощность, подводимую к направленной антенне, по сравнению с эталонной, чтобы напряженность поля в главном направлении осталась неизменной.

КНД и КУ в основном выражают в децибелах: 10lgD, 10lgG.

Заключение

Таким образом, мы рассмотрели некоторые полевые характеристики антенны, вытекающие из диаграммы направленности и энергетические характеристики (КНД и КУ). Коэффициент усиления антенны всегда меньше коэффициента направленного действия, так как КУ учитывает потери в антенне. Потери могут возникать из-за отражения мощности обратно в линию питания облучателя, затекания токов за стенки (например, рупора), затенение диаграммы конструктивными частями антенны и др. В реальных антенных системах разница между КНД и КУ может составлять 1.5-2 дБ.    

1. Характеристики направленности антенны

Если антенна
направленная, то плотность потока
мощности излучения такой антенны в
разных направлениях различная. Абсолютно
ненаправленным является только точечный
изотропный излучатель, а всякая реальная
антенна хотя бы в какой-то мере направлена.
О направленных свойствах антенны судят
по ее характеристике направленности и
параметрам — ширине диаграммы
направленности, коэффициентам
направленного действия и усиления
антенны.

Характеристикой
направленности антенны называется
зависимость напряженности поля излучения
от направления при условии измерения
этого поля на одинаковом расстоянии от
антенны.

Напряженность
поля в полной мере характеризуется
амплитудой, фазой и поляризацией. В
связи с этим можно говорить об амплитудной,
фазовой и поляризационной характеристиках
направленности. Чаще всего пользуются
амплитудной характеристикой направленности;
в ее названии обычно опускают слово
«амплитудная». Функция, выражающая эту
характеристику, называется функцией
направленности. Графически представленная
функция направленности называется
диаграммой направленности.

Шириной диаграммы
направленности называется угловой
сектор, охватывающий часть главного
лепестка диаграммы, в пределах которого
напряженность поля изменяется до

= 0,707 от напряженности поля в направлении
максимального излучения. Это, очевидно,
соответствует изменению по мощности
до (

= 0,5 (3 дб). Иногда ширина диаграммы
направленности антенны отсчитывается
на нулевом уровне (обозначается

)
или на уровне 0,1 (обозначается

)
от максимума.

Коэффициентом
направленного действия (КНД) D называется
отношение плотности потока мощности,
излучаемой данной антенной в определенном
направлении, к плотности потока мощности,
которая излучалась бы абсолютно
ненаправленной антенной в любом
направлении, при равенстве полной
мощности излучения обеих антенн и при
условии, что измерения производятся на
одинаковом удалении от них. Наибольший
интерес представляет КНД в направлении
максимального излучения антенны:

(72)

Этот коэффициент
впервые введен А. А. Пистолькорсом в
1929 г.

Обозначим действующие
значения напряженности поля на расстоянии
r
от
данной антенны в направлении ее
максимального излучения через

и на том же расстоянии от фиктивного
ненаправленного (изотропного) излучателя
через

.
Так как

,
a

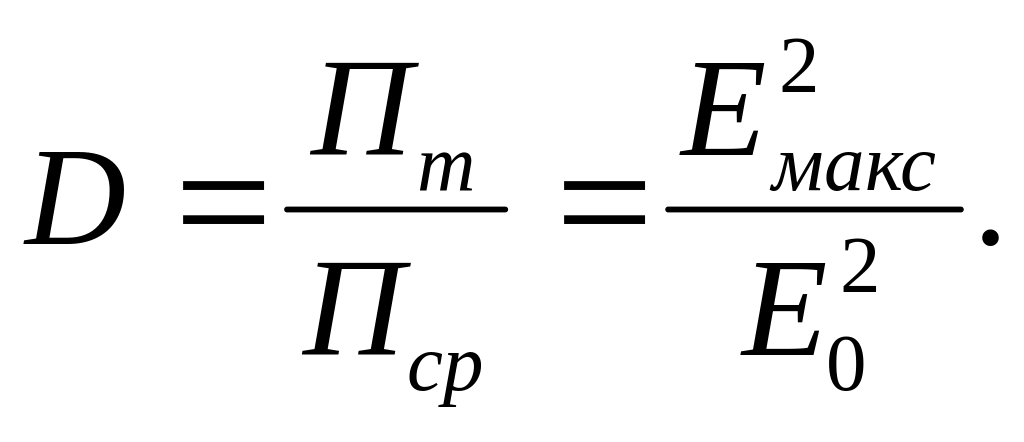
(73)

Теперь выведем
зависимость коэффициента D от параметров
вибратора с равномерным распределением
тока. По определению, мощность излучения
этого вибратора

должна
быть равна мощности излучения изотропного
излучателя. Поэтому, разделив

на поверхность сферы радиуса г, т. е. на

,
получим плотность потока мощности
изотропного излучателя

.
Вместе с тем

где

.

Отсюда находим:

. (74)

Это соотношение
позволяет записать:

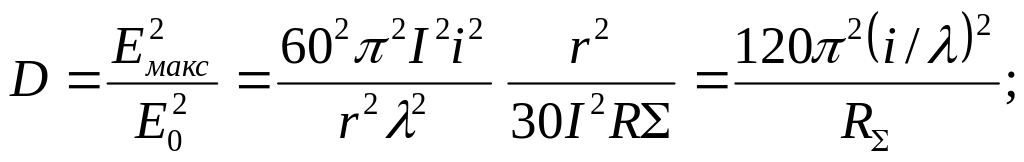
(75)

Для диполя
Герца сопротивление излучения:

(76)

и, следовательно,
его коэффициент направленного действия
равен:

Коэффициентом
усиления антенны (КУ) G называется
произведение коэффициента направленного
действия на к. п. д. антенны, т. е.

(77)

КУ более полно
характеризует антенну, чем КНД, так как
множитель D учитывает только концентрацию
энергии в определенном направлении, а
другой множитель г)А — еще и уменьшение
излучения вследствие потерь мощности
в антенне.

Коэффициенты
направленного действия и усиления
антенны могут быть измерены в неперах
и децибелах.

Допустим, что
мощность излучения антенны равномерно
распределена по всем направлениям,
тогда в направлении, где плотность
потока мощности максимальна

,
она уменьшится до

.
Пусть, кроме того, такая ненаправленная
антенна станет идеальной, т. е. в ней не
будет потерь (к. п. д.

); тогда плотность потока мощности
излучения уменьшится менее значительно
до величины.

В антенне, не
имеющей потерь, мощность излучения
равна подводимой. Следовательно, для
реальной антенны плотность

соответствует подводимой мощности и
ее к. п. д.

равен:

;
(78)

а коэффициент
усиления:

; (79)

Иначе говоря,
коэффициент направленного действия
определяется на основе сравнения данной
антенны с ненаправленной, имеющей такие
же потери, как данная направленная
антенна, т. е. отношением

,
а коэффициент усиления на основе
сравнения с ненаправленной и не имеющей
потерь антенной, т. е. отношением
.

Так как абсолютно
ненаправленных излучателей нет, то
коэффициент усиления антенны часто
определяют, сравнивая ее с симметричным
вибратором длиной

.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #

  30.04.2022646.66 Кб640.doc

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

При проектировании и сооружении антенн, как правило, необходимо знать направленности поля, создаваемые антеннами различного типа. Будем использовать приближенные формулы, справедливые для очень тонких цилиндрических проводов, размещенных в изотропной и лишенной потерь среде.

Рассмотрим наиболее часто встречающиеся на практике методы расчета направленных свойств. На рис. 2.66 приведена пространственная диаграмма направленности элементарного диполя, а также даны сечения этой диаграммы в двух плоскостях: в E-плоскости и в H-плоскости. Диаграмма направленности диполя в H-плоскости представляет собой окружность. Поэтому будем в дальнейшем изучать направленные свойства таких антенн только в E-плоскости.

Вибратор может иметь различную физическую длину (т. е. характеризоваться различным отношением l/λ), а также различные способы питания: симметричный и несимметричный. Оба отмеченных фактора оказывают существенное влияние на диаграмму направленности вибратора. Если вдоль вибратора укладывается целое число полуволн, то такой вибратор называют гармоническим. Длина гармонического вибратора $$begin{equation}l=nfrac{lambda}{2}end{equation}tag{2.160}$$ где n — целое число.

На рис. 2.67а приведена схема вибраторной антенны длиной l, оба плеча которой возбуждены симметрично. Точка наблюдения О находится на расстоянии r от фазового центра N, расположенного в центре вибраторной антенны. Направление r составляет угол ϴ с осью вибратора. Из рассмотрения данного рисунка следует, что расстояния r₁ и r₂от двух симметрично расположенных точек на вибраторе до точки наблюдения О различны. Поэтому приходящие в точку О две волны имеют разные фазы. Мгновенное значение напряженности поля в точке О, находящейся на расстоянии r от вибратора и расположенной на линии, составляющей угол θ с его осью: $$begin{equation}e_theta=left(frac{60I_m}{r}right)sinleft(omega{t}+krright)fleft(thetaright)end{equation}tag{2.161а}$$

Из анализа этого выражения следует, что е_θ, во-первых, прямо пропорционально амплитуде тока I_m в вибраторе и обратно пропорционально расстоянию r от вибратора до точки наблюдения; во-вторых, распространяющаяся волна имеет зависимость от расстояния типа kr, а также изменяется во времени с частотой ω. И, наконец, направленные свойства антенны определяются функцией f(θ), называемой диаграммой направленности.

Для дальнейшего анализа достаточно ограничиться рассмотрением только изменения амплитуды напряженности поля $$begin{equation}E_m=left(frac{60I_m}{r}right)fleft(thetaright)end{equation}tag{2.161б}$$

Вид диаграммы направленности различен для разных типов антенны. Для симметричного вибратора диаграмма направленности может быть описана выражением $$begin{equation}fleft(thetaright)=frac{cosleft(dfrac{pi{l}}{lambda}costhetaright)}{sintheta}end{equation}tag{2.162}$$

Отношение πl/λ можно представить в виде πl/λ = kl/2, где k — волновое число.

Для элементарного диполя (диполя Герца) $$begin{equation}fleft(thetaright)=sinthetaend{equation}tag{2.163а}$$

На рис. 2.68а приведена диаграмма направленности элементарного диполя. Она представляет собой две соприкасающихся окружности. Ширина диаграммы направленности (по уровню половинной мощности) θ_0,5 = 90°.

Для полуволнового диполя, для которого l=λ/2, n=1, выражение для диаграммы направленности может быть представлено в виде $$begin{equation}fleft(thetaright)=frac{cosleft(dfrac{pi}{2}costhetaright)}{sintheta}end{equation}tag{2.163б}$$

Диаграмма направленности полуволнового диполя дана сплошной линией на рис. 2.68б. Здесь же для сравнения пунктирной линией дана диаграмма направленности диполя Герца. Ширина диаграммы направленности полуволнового диполя θ_0,5=78°. Сравнение обеих диаграмм на этом рисунке показывает, что они достаточно похожи друг на друга. Поэтому на практике для анализа направленных свойств полуволнового диполя вместо формулы (2.163б) можно пользоваться формулой (2.163а).

Для волнового симметричного вибратора (l=λ, n=2) выражение для диаграммы направленности имеет вид $$begin{equation}fleft(thetaright)=frac{1+cosleft(picosthetaright)}{sintheta}end{equation}tag{2.164}$$

На рис. 2.68в приведена диаграмма направленности волнового вибратора. Максимальное излучение вибратора приходится на угол θ=90, причем для θ=90° f(90°)=2. Ширина диаграммы направленности θ_0,5=47°.

Из анализа диаграмм направленности полуволнового и волнового вибраторов следует, что в направлении максимального излучения уровни их излучения различны: для полуволнового вибратора f_max(θ)= l, и для волнового — f_max(θ)=2.

Для удобства сравнения диаграмм направленности различных антенн вводится понятие нормированной диаграммы направленности, которая определяется отношением $$begin{equation}F_{theta}=frac{fleft(thetaright)}{f_{max}left(thetaright)}end{equation}tag{2.165}$$

Для полуволнового диполя F(θ)=f(θ), а для волнового — F(θ)=0,5f(θ).

На рис. 2.68д изображен вибратор длиной l=1,5λ. В той части вибратора, длина которой равна 0,25λ, фаза тока отличается на π от фазы тока в остальной части вибратора. В этом случае напряженность поля в пределах главного лепестка диаграммы убывает быстрее, чем на диаграмме волнового диполя, и уже для θ=θ” f(θ”)=0, при дальнейшем увеличении угла наблюдения θ появляется боковой лепесток, имеющий максимум при θ=θ’. Отметим, что фаза излучения в направлениях, соответствующих боковому лепестку, отличается на π от фазы излучения в пределах основного лепестка. Если будем и далее увеличивать длину вибратора, то уровень боковых лепестков будет расти, а уровень основного лепестка (θ=90°) — уменьшаться. При l=2λ боковые лепестки, ориентированные под углом θ=54°, достигают своего максимума, а в направлении θ=90° f(θ)=0 (рис. 2.68е).

Изменение формы диаграммы направленности с дальнейшим ростом длины вибратора показано на рис. 2.68ж,з,и. Анализ приведенных диаграмм показывает, что направление максимального излучении вибраторов соответствует углам, которые уменьшаются с ростом длины вибратора, т. е. с ростом длины вибратор все более интенсивно излучает под небольшими углами к своей оси. Однако надо иметь в виду, что для всех рассматриваемых антенн в направлении θ=0° (или θ=180°) E=0.

Одновременно с увеличением длины вибратора растет число боковых лепестков в диаграмме направленности. Полезно запомнить следующую зависимость между числом лепестков и длиной вибратора. В пределах одной половины диаграммы направленности (0°<θ<180°) число боковых лепестков равно числу волн, укладывающихся по длине вибратора.

Так, для вибратора длиной l=3λ (см. рис. 2.68ж) общее число лепестков диаграммы направленности N=2·3=6, для вибратора с l=4λ (см. рис 2.68з) N=2·4=8, а для вибратора с l=5λ (см. рис. 2.68и) N=2·5=10.

Полезно также запомнить следующую информацию для вибраторов, длина которых равна четному числу волн, в направлении θ=90° (или θ=270°) f(θ)=0.

До сих пор анализировались диаграммы направленности вибраторов, имеющих симметричное питание. Обратимся теперь к рассмотрению диаграмм направленности вибраторов, имеющих несимметричное питание На рис. 2.68г приведена диаграмма направленности вибратора с несимметричным питанием длиной l=λ. Эта диаграмма идентична диаграмме направленности вибратора с симметричным питанием длиной l=2λ (см. рис. 2.68е). Такая закономерность сохраняется и для более длинных вибраторов, т. е. диаграмма направленности вибратора с несимметричным питанием длиной l=λ, 3λ, 5λ, 7λ,… идентична диаграмме направленности вибратора с симметричным питанием длиной l=2λ, 6λ, 10λ, 14λ,…

При расположении источника сигнала в дальнем поле большой радиус сферического волнового фронта приводит к тому, что линии распространения волн сигнала на подступах к антенной решетке оказываются параллельны. Как следствие, углы отклонения луча будут равны, и каждый соседний элемент будет иметь длину пути, которую необходимо преодолеть фронту сигнала на dsinθ больше, чем у его соседа. Данный вывод значительно упрощает расчеты и означает, что выведенные ранее уравнения (1) и (2) могут быть применены для расчета линейных решеток с несколькими тысячами элементов при условии, что они имеют одинаковый шаг.
Но как вычислить, где начинается дальнее поле? Начало дальнего поля можно условно принять за величину, определяемую по формуле:
Дальнее поле >2D²/λ, (3)

где D — диаметр антенны ((N-1) х d для эквидистантной линейной решетки).
Для линейных решеток с небольшим количеством компонентов (небольшое значение D) или при работе с низкочастотными сигналами (большая λ) расстояние до дальнего поля имеет небольшую величину, однако если количество элементов в решетке составляет несколько тысяч, а сама система работает исключительно на высоких частотах, расстояние до начала дальнего поля может измеряться десятками, а то и сотнями километров. Столь большое расстояние значительно затрудняет тестирование и калибровку системы. В таких случаях рекомендуется выполнить более подробный расчет и построение модели при расположении источника сигнала в ближнем поле, а затем скорректировать их при построении решения для использования в реальных условиях, в том числе с расположением источника в дальнем поле.

Усиление, направленность и апертура антенны
Прежде чем мы перейдем к расчету и построению диаграмм, не лишним будет определить усиление, направленность и апертуру антенны. Начнем с небольшого пояснения относительно усиления и направленности антенны, поскольку их часто меняют местами из-за сходных формул расчета. Данные величины определяются путем сравнения с показателями изотропной антенны — идеальной антенны, которая излучает равномерно во всех направлениях. Направленность антенны — это сравнение максимальной измеренной мощности Pmax в определенном направлении со средней мощностью, излучаемой во всех направлениях, Pav. Когда направление не определено, направленность вычисляется по формуле:
D = Pmax/Pav. (4)

Направленность — это важная характеристика, используемая при сравнении антенн, поскольку именно она определяет способность фокусировать энергию в одном направлении.
Усиление рассчитывается по той же формуле, однако помимо максимальной измеренной мощности Pmax и мощности, излучаемой во всех направлениях, Pav в нее также добавляется коэффициент потерь:
G = kD, (5)

где k = Prad/Pin, Prad — это общая излучаемая мощность, Pin — входная мощность антенны, k — коэффициент потерь.
Перенесем диаграмму направленности антенны в трехмерную плоскость и рассмотрим направленность антенны как функцию ширины луча (рис. 8).

Адаптивные антенные решётки: как это работает? (Основы)

Доброго времени суток.

Последние несколько лет я посвятил исследованию и созданию различных алгоритмов пространственной обработки сигналов в адаптивных антенных решётках, и продолжаю заниматься этим в рамках своей работы в настоящее время. Здесь я хотел бы поделиться теми знаниями и фишками, которые открыл для себя. Надеюсь, что это будет полезно для людей начинающих изучать эту область обработки сигналов или же просто интересующихся.

Что такое адаптивная антенная решётка?

Антенная решётка – это набор антенных элементов, некоторым образом размещённых в пространстве. Упрощённо структуру адаптивной антенной решётки, которую мы будем рассматривать, можно представить в следующем виде:

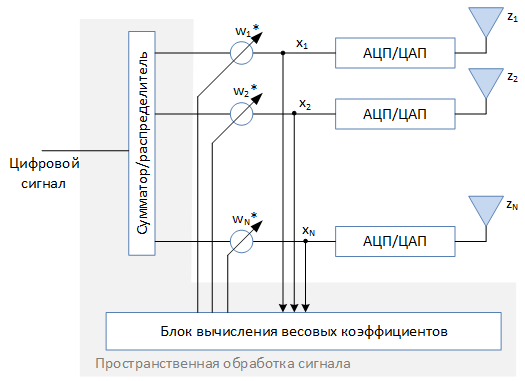
Адаптивные антенные решётки не редко называют «умными» антеннами (Smart antenna). «Умной» антенную решётку делает блок пространственной обработки сигнала и алгоритмы, реализованные в нём. Эти алгоритмы анализируют принимаемый сигнал и формируют набор весовых коэффициентов

, которые определяют амплитуду и начальную фазу сигнала для каждого из элементов. Заданное амплитудно-фазовое распределение определяет диаграмму направленности всей решётки в целом. Возможность синтезировать диаграмму направленности необходимой формы и изменять её в процессе обработки сигнала — одна из главных особенностей адаптивных антенных решёток, позволяющая решать широкий спектр задач. Но обо всём по порядку.

Как формируется диаграмма направленности?

Диаграмма направленности характеризует мощность сигнала, излучаемую в некотором направлении. Для простоты положим элементы решётки изотропными, т.е. для каждого из них мощность излучаемого сигнала не зависит от направления. Усиление или ослабление мощности, излучаемой решёткой в некотором направлении, получается вследствие интерференции ЭМВ, излученных различными элементами антенной решётки. Устойчивая интерференционная картина для ЭМВ возможна только при условии их когерентности, т.е. разность фаз сигналов не должна меняться со временем. В идеальном случае каждый из элементов антенной решётки должен излучать гармонический сигнал на одной и той же несущей частоте

. Однако на практике приходится работать с узкополосными сигналами, имеющими спектр конечной ширины

.
Пусть все элементы АР излучают один и тот же сигнал с комплексной амплитудой

. Тогда на удаленном приёмнике принятый от n-ного элемента сигнал можно представить в аналитическом виде:

где

– задержка в распространении сигнала от антенного элемента до точки приёма.
Такой сигнал является «квазигармоническим», и для выполнения условия когерентности необходимо, чтобы максимальная задержка в распространении ЭМВ между любыми двумя элементами была много меньше характерного времени изменения огибающей сигнала

, т.е.

. Таким образом, условие на когерентность узкополосного сигнала можно записать следующим образом:

где

— максимальное расстояние между элементами АР, а

— скорость света.

При приёме сигнала когерентное суммирование производится в цифровом виде в блоке пространственной обработки. В этом случае комплексное значение цифрового сигнала на выходе этого блока определяется выражением:

Последнее выражение удобнее представить в виде скалярного произведения N-мерных комплексных векторов в матричной форме:

где w и x — векторы-столбцы, а

— операция эрмитового сопряжения.

Векторное представление сигналов является одним из базовых при работе с антенными решётками, т.к. часто позволяет избежать громоздких математических выкладок. Кроме того, отождествление принятого в некоторый момент времени сигнала с вектором часто позволяет абстрагироваться от реальной физической системы и понять, что же именно происходит с точки зрения геометрии.

Чтобы рассчитать диаграмму направленности антенной решётки необходимо мысленно и последовательно «запустить» на неё набор плоских волн со всех возможных направлений. В этом случае значения элементов вектора x можно представить в следующем виде:

где k – волновой вектор,

и

– азимутальный угол и угол места, характеризующие направление прихода плоской волны,

– координата антенного элемента,

– элемент фазирующего вектора s плоской волны с волновым вектором k (в англоязычной литературе фазирующий вектор называют steerage vector). Зависимость квадрата амплитуды величины y от

и

определяет диаграмму направленности антенной решётки на приём при заданном векторе весовых коэффициентов w.

Особенности диаграммы направленности антенной решётки

Исследовать общие свойства диаграммы направленности антенных решёток удобно на линейной эквидистантной антенной решётке в горизонтально плоскости (т.е. ДН зависит только от азимутального угла

). Удобно с двух точек зрения: аналитических выкладок и визуального представления.

Рассчитаем ДН для единичного весового вектора (

), следуя описанному выше подходу.

В итоге получим:

Периодичность диаграммы направленности

Полученная диаграмма направленности антенной решётки – периодическая функция от синуса угла. Это значит, что при определённых значениях соотношения d/λ она имеет дифракционные (дополнительные) максимумы.

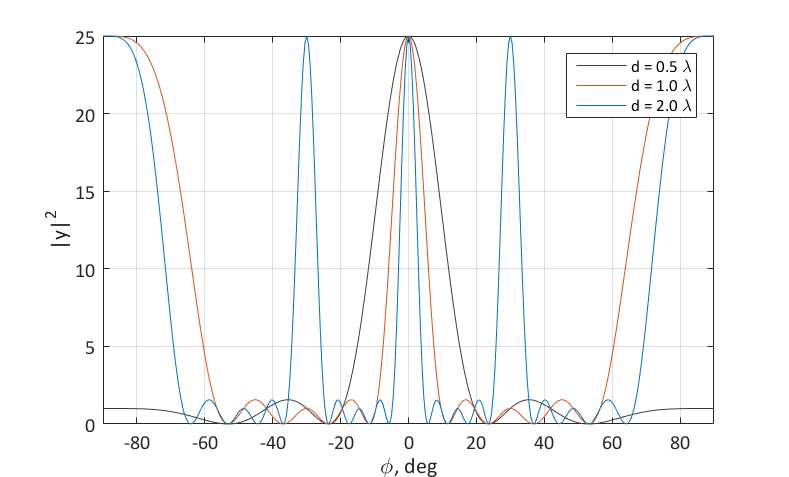
Ненормированная диаграмма направленности антенной решётки для N = 5

Нормированная диаграмма направленности антенной решётки для N = 5 в полярной системе координат

Положение «дифракционников» можно посмотреть напрямую из формулы для ДН. Однако мы попробуем понять, откуда они берутся физически и геометрически (в N-мерном пространстве).

Элементы фазирующего вектора s представляют собой комплексные экспоненты

, значения которых определяются величиной обобщённого угла

. Если существуют два обобщённых угла, соответствующих различным направлениям прихода плоской волны, для которых выполняется

, то это значит две вещи:

• Физически: плоские волновые фронты, приходящие с этих направлений, индуцируют на элементах антенной решётки идентичные амплитудно-фазовые распределения электромагнитных колебаний.
• Геометрически: фазирующие вектора для этих двух направлений совпадают.

Связанные подобным образом направления прихода волны являются с точки зрения антенной решётки эквивалентными и не различимы между собой.

Как определить область углов, в которой всегда лежит только один главный максимум ДН? Сделаем это в окрестностях нулевого азимута из следующих соображений: величина набега фаз между двумя соседними элементами должна лежать в интервале от

до

.

Разрешая данное неравенство получим условие на область однозначности в окрестности нуля:

Видно, что размер области однозначности по углу зависит от соотношения d/λ. Если d = 0.5λ, то каждое направление прихода сигнала «индивидуально», а область однозначности охватывает полный диапазон углов. Если же d = 2.0λ, то направления 0, ±30, ±90 – эквивалентны. На диаграмме направленности появляются дифракционные лепестки.

Обычно, дифракционные лепестки стремятся подавить с помощью направленных антенных элементов. В этом случае полная диаграмма направленности антенной решётки является произведением ДН одного элемента и решётки изотропных элементов. Параметры ДН одного элемента обычно выбирают исходя из условия на область однозначности антенной решётки.

Ширина главного лепестка

Широко известна инженерная формула для оценки ширины главного лепестка антенной системы:

, где D – характерный размер антенны. Формула используется для различного вида антенн, в том числе зеркальных. Покажем, что она справедлива и для антенных решёток.

Определим ширину главного лепестка первыми нулями ДН в окрестности главного максимума. Числитель выражения для

обращается в ноль при

. Первые нули соответствуют m = ±1. Полагая

получаем

.

Обычно ширину ДН направленности АР определяют по уровню половинной мощности (-3 дБ). В этом случае используют выражение:

Шириной главного лепестка можно управлять, задавая различные значения амплитуд для весовых коэффициентов антенной решётки. Рассмотрим три распределения:

На рисунке показаны получившиеся нормированные диаграммы направленности в логарифмическом масштабе:

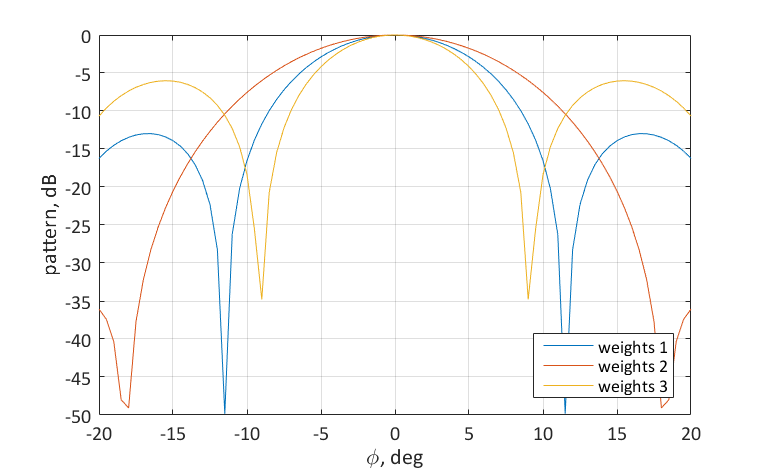
Из рисунка можно проследить следующие тенденции: спадающее к краям решётки распределение амплитуд весовых коэффициентов приводит к уширению главного лепестка ДН, но уменьшению уровня боковых лепестков. Увеличивающиеся к краям антенной решётки значения амплитуд, напротив, приводят к сужению главного лепестка и увеличению уровня боковиков. Здесь удобно рассмотреть предельные случаи:

1. Амплитуды весовых коэффициентов всех элементов, кроме крайних, равны нулю. Веса для крайних элементов равны единице. В этом случае решётка становится эквивалентна двухэлементной АР с периодом D = (N-1)d. Не трудно прикинуть по представленной выше формуле ширину главного лепестка. При этом боковики превратятся в дифракционные максимумы и выровнятся по уровню с главным максимумом.
2. Вес центрального элемента равен единице, а всех остальных – нулю. В этом случае мы получили по сути одну антенну с изотропной диаграммой направленности.

Направление главного максимума

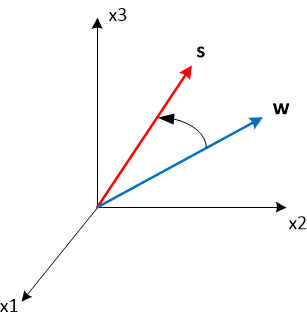
Итак, мы посмотрели, как можно регулировать ширину главного лепестка ДН АР. Теперь посмотрим, как порулить направлением. Вспомним векторное выражение для принятного сигнала. Пусть мы хотим, что бы максимум диаграммы направленности смотрел в некотором направлении

. Это значит, что с этого направления должна приниматься максимальная мощность. Данному направлению соответствует фазирующий вектор

в N-мерном векторном пространстве, а принимаемая мощность определяется как квадрат скалярного произведения этого фазирующего вектора на вектор весовых коэффициентов w. Скалярное произведение двух векторов максимально, когда они коллинеарны, т.е.

, где β – некоторый нормирующий множитель. Таким образом, если мы выберем весовой вектор равным фазирующему для требуемого направления, то повернём максимум диаграммы направленности.

Рассмотрим в качестве примера следующие весовые коэффициенты:

В итоге получим диаграмму направленности с главным максимумом в направлении 10°.

Теперь применим те же самые весовые коэффициенты, но не для приёма сигнала, а для передачи. Здесь стоит учесть, что при передаче сигнала направление волнового вектора меняется на противоположное. Это значит, что элементы фазирующего вектора для приёма и передачи отличаются знаком в показателе экспоненты, т.е. связаны между собой комплексным сопряжением. В итоге получим максимум диаграммы направленности на передачу в направлении -10°, что не совпадает с максимумом ДН на приём при тех же весовых коэффициентах.Что бы исправить ситуацию, необходимо применить комплексное сопряжение также и к весовым коэффициентам.

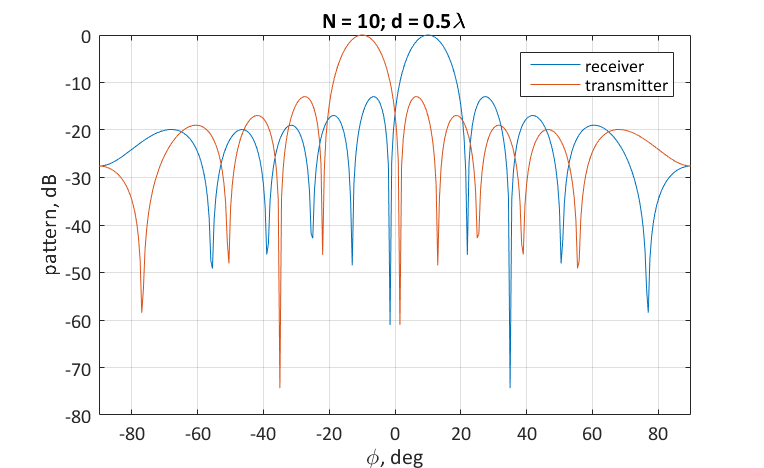
Описанную особенность формирования ДН на приём и передачу следует всегда иметь в виду при работе с антенными решётками.

Поиграем с диаграммой направленности

Несколько максимумов

Поставим задачку сформировать два главных максимума диаграммы направленности в направлении: -5° и 10°. Для этого выберем в качестве весового вектора взвешенную сумму фазирующих векторов для соответствующих направлений.

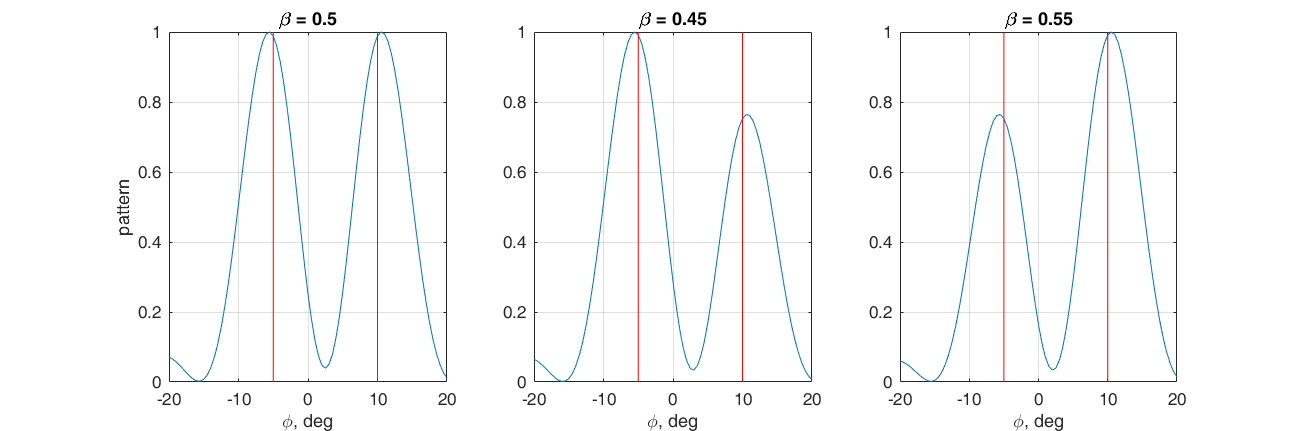Регулируя коэффициент β можно регулировать соотношение между главными лепестками. Здесь опять удобно посмотреть на происходящее в векторном пространстве. Если β больше 0.5, то вектор весовых коэффициентов лежит ближе к s(10°), иначе к s(-5°). Чем ближе весовой вектор к одному из фазоров, тем больше соответствующее скалярное произведение, а следовательно и величина соответствующего максимума ДН.

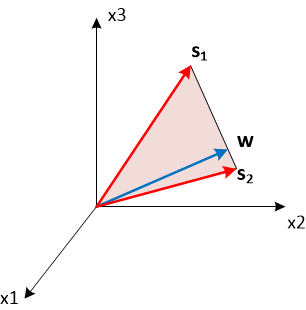
Однако стоит учесть, что оба главных лепестка имеют конечную ширину, и если мы захотим настроиться на два близких направления, то эти лепестки сольются в один, ориентированный на некоторое среднее направление.

Один максимум и ноль

Теперь попробуем настроить максимум диаграммы направленности на направление

и одновременно подавить сигнал, приходящей с направления

. Для этого необходимо выставить ноль ДН для соответствующего угла. Сделать это можно следующим образом:

где

, а

.

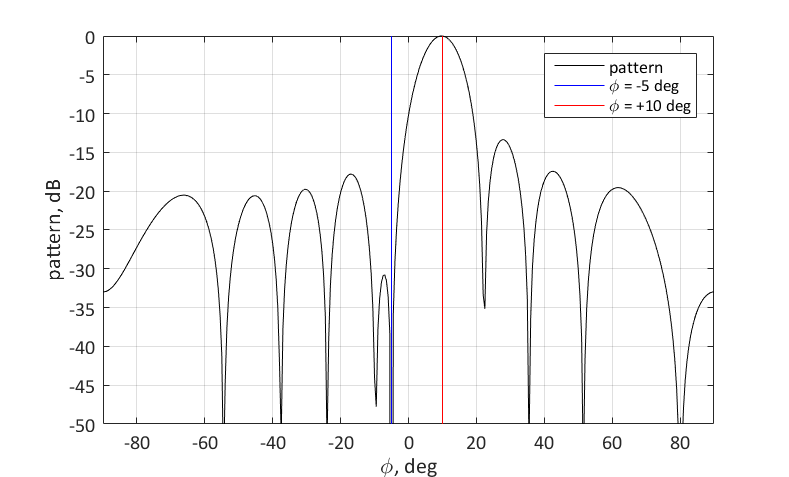
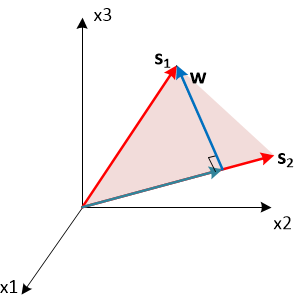
Геометрический смысл выбора весового вектора следующий. Мы хотим, что бы этот вектор w имел максимальную проекцию на

и при этом был ортогонален вектору

. Вектор

можно представить в виде двух слагаемых: вектора коллинеарного

и вектор ортогонального

. Чтобы удовлетворить постановке задачи, необходимо выбрать вторую компоненту в качестве вектора весовых коэффициентов w. Рассчитать коллинеарную компоненту можно спроектировав вектор

на нормированный вектор

с помощью скалярного произведения.

Соответственно, вычитая из исходного фазирующего вектора

его коллинеарную компоненту, получим искомый весовой вектор.

Некоторые дополнительные замечания

1. Везде выше я опустил вопрос нормировки весового вектора, т.е. его длины. Так вот, нормировка весового вектора не влияет на характеристики диаграммы направленности антенной решётки: направление главного максима, ширину главного лепестка и т.п. Можно также показать, что эта нормировка не влияет и на ОСШ на выходе блока пространственной обработки. В связи с этим при рассмотрении алгоритмов пространственной обработки сигнала обычно принимаю единичную нормировку весового вектора, т.е.
2. Возможности по формированию ДН антенной решётки определяются количеством элементов N. Чем больше элементов, тем шире возможности. Тем больше степеней свободы при осуществлении пространственной весовой обработки, больше вариантов как «покрутить» весовым вектором в N-мерном пространстве.
3. При осуществлении приёма ДН антенной решётки физически не существует, а все это существует лишь в «воображении» вычислительного блока, осуществляющего обработку сигнала. Это значит, что в один и тот же момент времени можно синтезировать несколько ДН и вести независимо обработку сигналов приходящих с различных направлений. В случае с передачей все несколько сложнее, однако также существует возможность синтезировать несколько ДН для передачи различных потоков данных. Такая технология в системах связи получила название MIMO.
4. С помощью представленного matlab кода можно самостоятельно поиграться с ДН

   Код

   % antenna array settings
   N = 10;             % number of elements
   d = 0.5;            % period of antenna array
   wLength = 1;        % wavelength
   mode = 'receiver';  % receiver or transmitter
   
   % weights of antenna array
   w = ones(N,1);    
   % w = 0.5 + 0.3*cos(2*pi*((0:N-1)-0.5*(N-1))/N).';
   % w = 0.5 - 0.3*cos(2*pi*((0:N-1)-0.5*(N-1))/N).';
   % w = exp(2i*pi*d/wLength*sin(10/180*pi)*(0:N-1)).';
   % b = 0.5; w = b*exp(2i*pi*d/wLength*sin(+10/180*pi)*(0:N-1)).' + (1-b)*exp(2i*pi*d/wLength*sin(-5/180*pi)*(0:N-1)).';
   % b = 0.5; w = b*exp(2i*pi*d/wLength*sin(+3/180*pi)*(0:N-1)).' + (1-b)*exp(2i*pi*d/wLength*sin(-3/180*pi)*(0:N-1)).';
   
   % s1 = exp(2i*pi*d/wLength*sin(10/180*pi)*(0:N-1)).';
   % s2 = exp(2i*pi*d/wLength*sin(-5/180*pi)*(0:N-1)).';
   % w = s1 - (1/N)*s2*s2'*s1;
   % w = s1;
   
   % normalize weights
   w = w./sqrt(sum(abs(w).^2));
   
   % set of angle values to calculate pattern
   angGrid_deg = (-90:0.5:90);
   
   % convert degree to radian
   angGrid = angGrid_deg * pi / 180;
   % calculate set of steerage vectors for angle grid
   switch (mode)
       case 'receiver'
           s = exp(2i*pi*d/wLength*bsxfun(@times,(0:N-1)',sin(angGrid)));
       case 'transmitter'
           s = exp(-2i*pi*d/wLength*bsxfun(@times,(0:N-1)',sin(angGrid)));
   end
   
   % calculate pattern
   y = (abs(w'*s)).^2;
   
   %linear scale
   plot(angGrid_deg,y/max(y));
   grid on;
   xlim([-90 90]);
   
   % log scale
   % plot(angGrid_deg,10*log10(y/max(y)));
   % grid on;
   % xlim([-90 90]);

Какие задачи можно решать с помощью адаптивной антенной решётки?

Спасибо за внимание