Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 26 апреля 2021 года; проверки требуют 6 правок.
У этого термина существуют и другие значения, см. BFS.

Поиск в ширину (англ. breadth-first search, BFS) — один из методов обхода графа. Пусть задан граф 





Поиск в ширину имеет такое название потому, что в процессе обхода мы идём вширь, то есть перед тем как приступить к поиску вершин на расстоянии 

Поиск в ширину является одним из неинформированных алгоритмов поиска[2].
Работа алгоритма[править | править код]

Белый — вершина, которая ещё не обнаружена. Серый — вершина, уже обнаруженная и добавленная в очередь. Чёрный — вершина, извлечённая из очереди[3].
Поиск в ширину работает путём последовательного просмотра отдельных уровней графа, начиная с узла-источника 
Рассмотрим все рёбра 





Неформальное описание[править | править код]
- Поместить узел, с которого начинается поиск, в изначально пустую очередь.
- Извлечь из начала очереди узел
и пометить его как развёрнутый.
- Если узел
является целевым узлом, то завершить поиск с результатом «успех».
- В противном случае, в конец очереди добавляются все преемники узла
, которые ещё не развёрнуты и не находятся в очереди.
- Если узел
- Если очередь пуста, то все узлы связного графа были просмотрены, следовательно, целевой узел недостижим из начального; завершить поиск с результатом «неудача».
- Вернуться к п. 2.
Примечание: деление вершин на развёрнутые и не развёрнутые необходимо для произвольного графа (так как в нём могут быть циклы). Для дерева эта операция не нужна, так как каждая вершина будет выбрана один-единственный раз.
Формальное описание[править | править код]
Ниже приведён псевдокод алгоритма для случая, когда необходимо лишь найти целевой узел. В зависимости от конкретного применения алгоритма, может потребоваться дополнительный код, обеспечивающий сохранение нужной информации (расстояние от начального узла, узел-родитель и т. п.)
Рекурсивная формулировка:
BFS(start_node, goal_node) {
return BFS'({start_node}, ∅, goal_node);
}
BFS'(fringe, visited, goal_node) {
if(fringe == ∅) {
// Целевой узел не найден
return false;
}
if (goal_node ∈ fringe) {
return true;
}
return BFS'({child | x ∈ fringe, child ∈ expand(x)} visited, visited ∪ fringe, goal_node);
}
Итеративная формулировка:
BFS(start_node, goal_node) {
for(all nodes i) visited[i] = false; // изначально список посещённых узлов пуст
queue.push(start_node); // начиная с узла-источника
while(! queue.empty() ) { // пока очередь не пуста
node = queue.pop(); // извлечь первый элемент в очереди
if(node == goal_node) {
return true; // проверить, не является ли текущий узел целевым
}
visited[node] = true; // пометить текущую ноду посещенной
foreach(child in expand(node)) { // все преемники текущего узла, ...
if(visited[child] == false) { // ... которые ещё не были посещены ...
queue.push(child); // ... добавить в конец очереди...
visited[child] = true; // ... и пометить как посещённые
}
}
}
return false; // Целевой узел недостижим
}
Реализация на Pascal:
function BFS(v : Node) : Boolean; begin enqueue(v); while queue is not empty do begin curr := dequeue(); if is_goal(curr) then begin BFS := true; exit; end; mark(curr); for next in successors(curr) do if not marked(next) then begin enqueue(next); end; end; BFS := false; end;
Свойства[править | править код]
Обозначим число вершин и рёбер в графе как 

Пространственная сложность[править | править код]
Так как в памяти хранятся все развёрнутые узлы, пространственная сложность алгоритма составляет 
Алгоритм поиска с итеративным углублением похож на поиск в ширину тем, что при каждой итерации перед переходом на следующий уровень исследуется полный уровень новых узлов, но требует значительно меньше памяти.
Временная сложность[править | править код]
Так как в худшем случае алгоритм посещает все узлы графа, при хранении графа в виде списков смежности, временная сложность алгоритма составляет 
Полнота[править | править код]
Если у каждого узла имеется конечное число преемников, алгоритм является полным: если решение существует, алгоритм поиска в ширину его находит, независимо от того, является ли граф конечным. Однако если решения не существует, на бесконечном графе поиск не завершается.
Оптимальность[править | править код]
Если длины рёбер графа равны между собой, поиск в ширину является оптимальным, то есть всегда находит кратчайший путь. В случае взвешенного графа поиск в ширину находит путь, содержащий минимальное количество рёбер, но не обязательно кратчайший.
Поиск по критерию стоимости является обобщением поиска в ширину и оптимален на взвешенном графе с неотрицательными весами рёбер. Алгоритм посещает узлы графа в порядке возрастания стоимости пути из начального узла и обычно использует очередь с приоритетами.
История и применения[править | править код]
Поиск в ширину был формально предложен Э. Ф. Муром в контексте поиска пути в лабиринте[4]. Ли независимо открыл тот же алгоритм в контексте разводки проводников на печатных платах[5][6][7].
Поиск в ширину может применяться для решения задач, связанных с теорией графов:
См. также[править | править код]
- Поиск с ограничением глубины
- Поиск в глубину
- Алгоритм Дейкстры
Примечания[править | править код]
- ↑ Томас Х. Кормен, Чарльз И. Лейзерсон, Рональд Л. Ривест, Клиффорд Штайн. Алгоритмы: построение и анализ. — 3-е изд. — Издательский дом “Вильямс”, 2013. — С. 630. — 1328 с. — ISBN 978-5-8459-1794-2 (рус.). — ISBN 978-0-2620-3384-8 (англ.).
- ↑ 1 2 3 4 5 6 MAXimal :: algo :: Поиск в ширину в графе и его приложения Архивная копия от 16 сентября 2013 на Wayback Machine
- ↑ 1 2 НГТУ Структуры и алгоритмы обработки данных Обход графа в ширину Архивная копия от 30 декабря 2012 на Wayback Machine
- ↑ 1 2 Moore E. F. The shortest path through a maze (англ.) // Proceedings of an International Symposium on the Theory of Switching (Cambridge, Massachusetts, 2–5 April 1957) — Harvard University Press, 1959. — Vol. 2. — P. 285—292. — 345 p. — (Annals of the Computation Laboratory of Harvard University; Vol. 30) — ISSN 0073-0750
- ↑ 1 2 C. Y. Lee (1961), An algorithm for path connection and its applications. IRE Transactions on Electronic Computers, EC-10(3), pp. 346–365
- ↑ Cormen et al, Introduction to Algorithms, 3rd edition, p. 623
- ↑ Mathematics Stack Exchange Origin of the Breadth-First Search algorithm
Литература[править | править код]
- T. H. Cormen, C. E. Leiserson, R. L. Rivest, C. Stein. Introduction to Algorithms. — 3rd edition. — The MIT Press, 2009. — ISBN 978-0-262-03384-8.. Перевод 2-го издания: Томас Х. Кормен, Чарльз И. Лейзерсон, Рональд Л. Ривест, Клиффорд Штайн. Алгоритмы: построение и анализ = Introduction to Algorithms. — 2-е изд. — М.: «Вильямс», 2006. — С. 1296. — ISBN 0-07-013151-1.
- Левитин А. В. Глава 5. Метод уменьшения размера задачи: Поиск в ширину // Алгоритмы. Введение в разработку и анализ — М.: Вильямс, 2006. — 576 с. — ISBN 978-5-8459-0987-9
Ссылки[править | править код]
- Steven M. Rubin Computer Aids for VLSI Design. Chapter 4: Synthesis Tools
- Волновой алгоритм поиска пути
- Поиск в ширину на Pascal и C++
Время на прочтение
5 мин
Количество просмотров 155K
Доброго времени суток.
Представляю вашему вниманию перевод статьи «Algorithms on Graphs: Let’s talk Depth-First Search (DFS) and Breadth-First Search (BFS)» автора Try Khov.
Что такое обход графа?
Простыми словами, обход графа — это переход от одной его вершины к другой в поисках свойств связей этих вершин. Связи (линии, соединяющие вершины) называются направлениями, путями, гранями или ребрами графа. Вершины графа также именуются узлами.
Двумя основными алгоритмами обхода графа являются поиск в глубину (Depth-First Search, DFS) и поиск в ширину (Breadth-First Search, BFS).
Несмотря на то, что оба алгоритма используются для обхода графа, они имеют некоторые отличия. Начнем с DFS.
Поиск в глубину
DFS следует концепции «погружайся глубже, головой вперед» («go deep, head first»). Идея заключается в том, что мы двигаемся от начальной вершины (точки, места) в определенном направлении (по определенному пути) до тех пор, пока не достигнем конца пути или пункта назначения (искомой вершины). Если мы достигли конца пути, но он не является пунктом назначения, то мы возвращаемся назад (к точке разветвления или расхождения путей) и идем по другому маршруту.
Давайте рассмотрим пример. Предположим, что у нас есть ориентированный граф, который выглядит так:

Мы находимся в точке «s» и нам нужно найти вершину «t». Применяя DFS, мы исследуем один из возможных путей, двигаемся по нему до конца и, если не обнаружили t, возвращаемся и исследуем другой путь. Вот как выглядит процесс:

Здесь мы двигаемся по пути (p1) к ближайшей вершине и видим, что это не конец пути. Поэтому мы переходим к следующей вершине.

Мы достигли конца p1, но не нашли t, поэтому возвращаемся в s и двигаемся по второму пути.

Достигнув ближайшей к точке «s» вершины пути «p2» мы видим три возможных направления для дальнейшего движения. Поскольку вершину, венчающую первое направление, мы уже посещали, то двигаемся по второму.

Мы вновь достигли конца пути, но не нашли t, поэтому возвращаемся назад. Следуем по третьему пути и, наконец, достигаем искомой вершины «t».

Так работает DFS. Двигаемся по определенному пути до конца. Если конец пути — это искомая вершина, мы закончили. Если нет, возвращаемся назад и двигаемся по другому пути до тех пор, пока не исследуем все варианты.
Мы следуем этому алгоритму применительно к каждой посещенной вершине.
Необходимость многократного повторения процедуры указывает на необходимость использования рекурсии для реализации алгоритма.
Вот JavaScript-код:
// при условии, что мы имеем дело со смежным списком
// например, таким: adj = {A: [B,C], B:[D,F], ... }
function dfs(adj, v, t) {
// adj - смежный список
// v - посещенный узел (вершина)
// t - пункт назначения
// это общие случаи
// либо достигли пункта назначения, либо уже посещали узел
if(v === t) return true
if(v.visited) return false
// помечаем узел как посещенный
v.visited = true
// исследуем всех соседей (ближайшие соседние вершины) v
for(let neighbor of adj[v]) {
// если сосед не посещался
if(!neighbor.visited) {
// двигаемся по пути и проверяем, не достигли ли мы пункта назначения
let reached = dfs(adj, neighbor, t)
// возвращаем true, если достигли
if(reached) return true
}
}
// если от v до t добраться невозможно
return false
}
Заметка: этот специальный DFS-алгоритм позволяет проверить, возможно ли добраться из одного места в другое. DFS может использоваться в разных целях. От этих целей зависит то, как будет выглядеть сам алгоритм. Тем не менее, общая концепция выглядит именно так.
Анализ DFS
Давайте проанализируем этот алгоритм. Поскольку мы обходим каждого «соседа» каждого узла, игнорируя тех, которых посещали ранее, мы имеем время выполнения, равное O(V + E).
Краткое объяснение того, что означает V+E:
V — общее количество вершин. E — общее количество граней (ребер).
Может показаться, что правильнее использовать V*E, однако давайте подумаем, что означает V*E.
V*E означает, что применительно к каждой вершине, мы должны исследовать все грани графа безотносительно принадлежности этих граней конкретной вершине.
С другой стороны, V+E означает, что для каждой вершины мы оцениваем лишь примыкающие к ней грани. Возвращаясь к примеру, каждая вершина имеет определенное количество граней и, в худшем случае, мы обойдем все вершины (O(V)) и исследуем все грани (O(E)). Мы имеем V вершин и E граней, поэтому получаем V+E.
Далее, поскольку мы используем рекурсию для обхода каждой вершины, это означает, что используется стек (бесконечная рекурсия приводит к ошибке переполнения стека). Поэтому пространственная сложность составляет O(V).
Теперь рассмотрим BFS.
Поиск в ширину
BFS следует концепции «расширяйся, поднимаясь на высоту птичьего полета» («go wide, bird’s eye-view»). Вместо того, чтобы двигаться по определенному пути до конца, BFS предполагает движение вперед по одному соседу за раз. Это означает следующее:

Вместо следования по пути, BFS подразумевает посещение ближайших к s соседей за одно действие (шаг), затем посещение соседей соседей и так до тех пор, пока не будет обнаружено t.
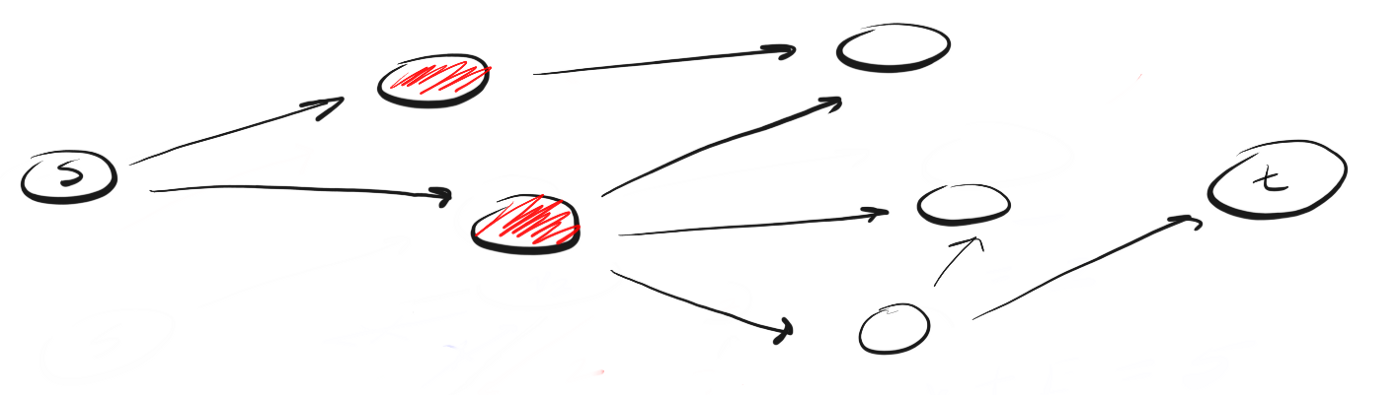

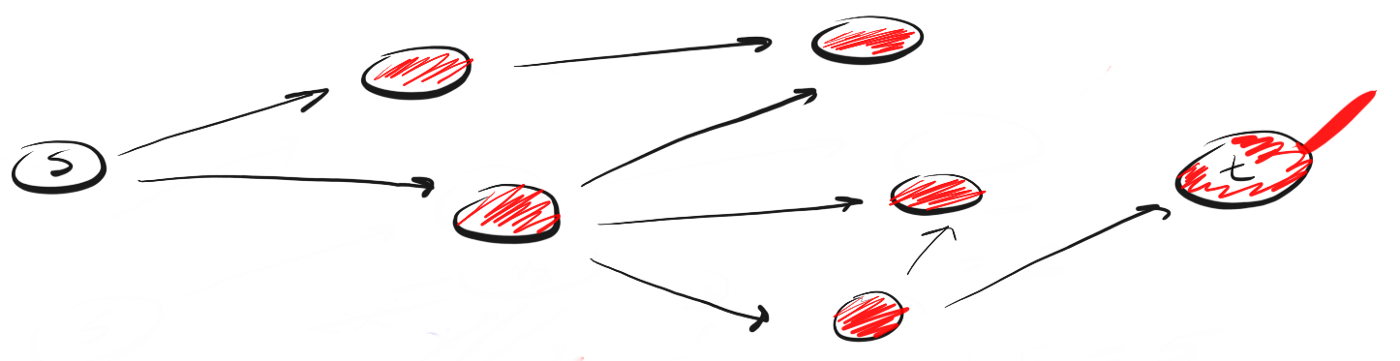
Чем DFS отличается от BFS? Мне нравится думать, что DFS идет напролом, а BFS не торопится, а изучает все в пределах одного шага.
Далее возникает вопрос: как узнать, каких соседей следует посетить первыми?
Для этого мы можем воспользоваться концепцией «первым вошел, первым вышел» (first-in-first-out, FIFO) из очереди (queue). Мы помещаем в очередь сначала ближайшую к нам вершину, затем ее непосещенных соседей, и продолжаем этот процесс, пока очередь не опустеет или пока мы не найдем искомую вершину.
Вот код:
// при условии, что мы имеем дело со смежным списком
// например, таким: adj = {A:[B,C,D], B:[E,F], ... }
function bfs(adj, s, t) {
// adj - смежный список
// s - начальная вершина
// t - пункт назначения
// инициализируем очередь
let queue = []
// добавляем s в очередь
queue.push(s)
// помечаем s как посещенную вершину во избежание повторного добавления в очередь
s.visited = true
while(queue.length > 0) {
// удаляем первый (верхний) элемент из очереди
let v = queue.shift()
// abj[v] - соседи v
for(let neighbor of adj[v]) {
// если сосед не посещался
if(!neighbor.visited) {
// добавляем его в очередь
queue.push(neighbor)
// помечаем вершину как посещенную
neighbor.visited = true
// если сосед является пунктом назначения, мы победили
if(neighbor === t) return true
}
}
}
// если t не обнаружено, значит пункта назначения достичь невозможно
return false
}
Анализ BFS
Может показаться, что BFS работает медленнее. Однако если внимательно присмотреться к визуализациям, можно увидеть, что они имеют одинаковое время выполнения.
Очередь предполагает обработку каждой вершины перед достижением пункта назначения. Это означает, что, в худшем случае, BFS исследует все вершины и грани.
Несмотря на то, что BFS может казаться медленнее, на самом деле он быстрее, поскольку при работе с большими графами обнаруживается, что DFS тратит много времени на следование по путям, которые в конечном счете оказываются ложными. BFS часто используется для нахождения кратчайшего пути между двумя вершинами.
Таким образом, время выполнения BFS также составляет O(V + E), а поскольку мы используем очередь, вмещающую все вершины, его пространственная сложность составляет O(V).
Аналогии из реальной жизни
Если приводить аналогии из реальной жизни, то вот как я представляю себе работу DFS и BFS.
Когда я думаю о DFS, то представляю себе мышь в лабиринте в поисках еды. Для того, чтобы попасть к цели мышь вынуждена много раз упираться в тупик, возвращаться и двигаться по другому пути, и так до тех пор, пока она не найдет выход из лабиринта или еду.

Упрощенная версия выглядит так:

В свою очередь, когда я думаю о BFS, то представляю себе круги на воде. Падение камня в воду приводит к распространению возмущения (кругов) во всех направлениях от центра.

Упрощенная версия выглядит так:

Выводы
- Поиск в глубину и поиск в ширину используются для обхода графа.
- DFS двигается по граням туда и обратно, а BFS распространяется по соседям в поисках цели.
- DFS использует стек, а BFS — очередь.
- Время выполнения обоих составляет O(V + E), а пространственная сложность — O(V).
- Данные алгоритмы имеют разную философию, но одинаково важны для работы с графами.
Прим. пер.: я не специалист по алгоритмам и структурам данных, поэтому при обнаружении ошибок, неточностей или некорректности формулировок, прошу написать в личку для исправления и уточнения. Буду признателен.
Благодарю за внимание.
Поиск в ширину (англ. breadth-first search) — один из основных алгоритмов на графах, позволяющий находить все кратчайшие пути от заданной вершины и решать многие другие задачи.
Поиск в ширину также называют обходом — так же, как поиск в глубину и все другие обходы, он посещает все вершины графа по одному разу, только в другом порядке: по увеличению расстояния до начальной вершины.
#Описание алгоритма
На вход алгоритма подаётся невзвешенный граф и номер стартовой вершины $s$. Граф может быть как ориентированным, так и неориентированным — для алгоритма это не важно.
Основную идею алгоритма можно понимать как процесс «поджигания» графа: на нулевом шаге мы поджигаем вершину $s$, а на каждом следующем шаге огонь с каждой уже горящей вершины перекидывается на всех её соседей, в конечном счете поджигая весь граф.
Если моделировать этот процесс, то за каждую итерацию алгоритма будет происходить расширение «кольца огня» в ширину на единицу. Номер шага, на котором вершина $v$ начинает гореть, в точности равен длине её минимального пути из вершины $s$.
Моделировать это можно следующим образом. Создадим очередь, в которую будут помещаться горящие вершины, а также заведём булевый массив, в котором для каждой вершины будем отмечать, горит она или нет — или иными словами, была ли она уже посещена. Изначально в очередь помещается только вершина $s$, которая сразу помечается горящей.
Затем алгоритм представляет собой такой цикл: пока очередь не пуста, достать из её головы одну вершину $v$, просмотреть все рёбра, исходящие из этой вершины, и если какие-то из смежных вершин $u$ ещё не горят, поджечь их и поместить в конец очереди.
В итоге, когда очередь опустеет, мы по одному разу обойдём все достижимые из $s$ вершины, причём до каждой дойдём кратчайшим путём. Длины кратчайших путей можно посчитать, если завести для них отдельный массив $d$ и при добавлении в очередь пересчитывать по правилу $d_u = d_v + 1$. Также можно компактно сохранить дополнительную информацию для восстановления самих путей, заведя массив «предков», в котором для каждой вершины хранится номер вершины из которой мы в неё попали.
#Реализация
Если мы всё равно поддерживаем массив расстояний, то отдельный булевый массив с метками горящих вершин можно не создавать, а вместо этого просто присвоить изначальное расстояние всех вершин некоторым некоторым специальным значением (например, -1), которое будет сигнализировать а том, что эту вершину мы ещё не просмотрели.
vector<int> g[maxn];
void bfs(int s) {
queue<int> q;
q.push(s);
vector<int> d(n, -1), p(n);
d[s] = 0;
while (!q.empty()) {
int v = q.front();
q.pop();
for (int u : g[v]) {
if (d[u] == -1) {
q.push(u);
d[u] = d[v] + 1;
p[u] = v;
}
}
}
}
Теперь, чтобы восстановить кратчайший путь до какой-то вершины $v$, это можно сделать через массив p:
while (v != s) {
cout << v << endl;
v = p[v];
}
Обратим внимание, что путь выведется в обратном порядке.
#В неявных графах
Поиск в ширину часто применяется для поиска кратчайшего пути в неявно заданных графах.
В качестве конкретного примера, пусть у нас есть булева матрица размера $n times n$, в которой помечено, свободна ли клетка с координатами $(x, y)$, и требуется найти кратчайший путь от $(x_s, y_t)$ до $(x_y, y_t)$ при условии, что за один шаг можно перемещаться в свободную соседнюю по вертикали или горизонтали клетку.

Можно сконвертировать граф в явный формат: как-нибудь пронумеровать все ячейки (например по формуле $x cdot n + y$) и для каждой посмотреть на всех её соседей, добавляя ребро в $(x pm 1, y pm 1)$, если соответствующая клетка свободна.
Такой подход будет работать за оптимальное линейное время, однако с точки зрения реализации проще адаптировать не входные данные, а сам алгоритм обхода в глубину:
bool a[N][N]; // свободна ли клетка (x, y)
int d[N][N]; // кратчайшее расстояние до (x, y)
// чтобы немного упростить код
struct cell {
int x, y;
};
void bfs(cell s, cell t) {
queue<cell> q;
q.push(s);
memset(d, -1, sizeof d);
d[s.x][x.y] = 0;
while (!q.empty()) {
auto [x, y] = q.front();
q.pop();
// просматриваем всех соседей
for (auto [dx, dy] : {{-1, 0}, {+1, 0}, {0, -1}, {0, +1}}) {
// считаем координаты соседа
int _x = x + dx, _y = y + dy;
// и проверяем, что он свободен и не был посещен ранее
if (a[_x][_y] && d[_x][_y] == -1) {
d[_x][_y] = d[x][y] + 1;
q.push_back({_x, _y});
}
}
}
}
Перед запуском bfs следует убедиться, что не произойдет выход за пределы границ. Вместо того, чтобы добавлять проверки на _x < 0 || x >= n и т. п. при просмотре возможных соседей, удобно сделать следующий трюк: изначально создать матрицу a с размерностями на 2 больше, чем нужно, и на этапе чтения данных заполнять её в индексации не с нуля, а с единицы. Тогда границы матрицы всегда будут заполнены нулями (то есть помечены непроходимыми) и алгоритм никогда в них не зайдет.
#Применения и обобщения
Помимо нахождения расстояний в невзвешенном графе, обход в ширину можно использовать для многих задач, в которых работает обход в глубину, например для поиска компонент связности или проверки на двудольность.
Множественный BFS. Добавив в очередь изначально не одну, а несколько вершин, мы найдем для каждой вершины кратчайшее расстояние до одной из них.
Это полезно для задач, в которых нужно моделировать пожар, наводнение, извержение вулкана или подобные явления, в которых источник «волны» не один. Также так можно чуть быстрее находить кратчайший путь для конкретной пары вершин, запустив параллельно два обхода от каждой и остановив в тот момент, когда они встретятся.
Игры. С помощью BFS можно найти решение какой-либо задачи / игры за наименьшее число ходов, если каждое состояние системы можно представить вершиной графа, а переходы из одного состояния в другое — рёбрами графа.
В качестве (нетривиального) примера: собрать кубик Рубика за наименьшее число ходов.
Кратчайшие циклы. Чтобы найти кратчайший цикл в ориентированном невзвешенном графе, можно произвести поиск в ширину из каждой вершины. Как только в процессе обхода мы пытаемся пойти из текущей вершины по какому-то ребру в уже посещённую вершину, то это означает, что мы нашли кратчайший цикл для данной вершины, и останавливаем обход. Среди всех таких найденных циклов (по одному от каждого запуска обхода) выбираем кратчайший.
Такой алгоритм будет работать за $O(n^2)$: худшим случаем будет один большой цикл, в котором мы для каждой вершины пройдемся по всем остальным.
Ребра на кратчайшем пути. Мы можем за линейное время найти все рёбра, лежащие на каком-либо кратчайшем пути между заданной парой вершин $a$ и $b$. Для этого нужно запустить два поиска в ширину: из $a$ и из $b$.
Обозначим через $d_a$ и $d_b$ массивы кратчайших расстояний, получившиеся в результате этих обходов. Тогда каждое ребро $(u,v)$ можно проверить критерием
$$
d_a[u] + d_b[v] + 1 = d_a[b]
$$
Альтернативно, можно запустить один обход из $a$, и когда он дойдет до $b$, начать рекурсивно проходиться по всем обратным ребрам, ведущим в более близкие к $a$ вершины (то есть те, для которых $d[u] = d[v] – 1$), отдельно помечая их.
Аналогично можно найти все вершины на каком-либо кратчайшем пути.
0-1 BFS. Если веса некоторых ребер могут быть нулевыми, то кратчайшие пути искать не сильно сложнее.
Ключевое наблюдение: если от вершины $a$ до вершины $b$ можно дойти по пути, состоящему из нулевых рёбер, то кратчайшие расстояния от вершины $s$ до этих вершин совпадают.
Если в нашем графе оставить только $0$-рёбра, то он распадётся на компоненты связности, в каждой из которых ответ одинаковый. Если теперь вернуть единичные рёбра и сказать, что эти рёбра соединяют не вершины, а компоненты связности, то мы сведём задачу к обычному BFS.
Получается, запустив обход, мы можем при обработке вершины $v$, у которой есть нулевые ребра в непосещенные вершины, сразу пройтись по ним и добавить все вершины нулевой компоненты, проставив им такое же расстояние, как и у $v$.
Это можно сделать и напрямую, запустив BFS внутри BFS, однако можно заметить, что достаточно при посещении вершины просто добавлять всех её непосещенных соседей по нулевым ребрам в голову очереди, чтобы обработать их раньше, чем те, которые там уже есть. Это легко сделать, если очередь заменить деком:
vector<int> d(n, -1);
d[s] = 0;
deque<int> q;
q.push_back(s);
while (!q.empty()) {
int v = q.front();
q.pop_front();
for (auto [u, w] : g[v]) {
if (d[u] == -1) {
d[u] = d[v] + w;
if (w == 0)
q.push_front(u);
else
q.push_back(u);
}
}
}
Также вместо дека можно завести две очереди: одну для нулевых ребер, а другую для единичных, в внутри цикла while сначала просматривать первую, а только потом, когда она станет пустой, вторую. Этот подход уже можно обобщить.
1-k BFS. Теперь веса рёбер принимают значения от $1$ до некоторого небольшого $k$, и всё так же требуется найти кратчайшие расстояния от вершины $s$, но уже в плане суммарного веса.
Наблюдение: максимальное кратчайшее расстояние в графе равно $(n – 1) cdot k$.
Заведём для каждого расстояния $d$ очередь $q_d$, в которой будут храниться вершины, находящиеся на расстоянии $d$ от $s$ — плюс, возможно, некоторые вершины, до которых мы уже нашли путь длины $d$ от $s$, но для которых возможно существует более короткий путь. Нам потребуется $O((n – 1) cdot k)$ очередей.
Положим изначально вершину $s$ в $q_0$, а дальше будем брать вершину из наименьшего непустого списка и класть всех её непосещенных соседей в очередь с номером $d_v + w$ и релаксировать $d_u$, не забывая при этом, что кратчайшее расстояние до неё на самом деле может быть и меньше.
int d[maxn];
d[s] = 0;
queue<int> q[maxd];
q[0].push_back(s);
for (int dist = 0; dist < maxd; dist++) {
while (!q[dist].empty()) {
int v = q[dist].front();
q[dist].pop();
// если расстояние меньше и мы уже рассмотрели эту вершину,
// но она всё ещё лежит в более верхней очереди
if (d[v] > dist)
continue;
for (auto [u, w] : g[v]) {
if (d[u] < d[v] + w) {
d[u] = d[v] + w;
q[d[u]].push(u);
}
}
}
}
Сложность такого алгоритма будет $O(k n + m)$, поскольку каждую вершину мы можем прорелаксировать и добавить в другую очередь не более $k$ раз, а просматривать рёбра, исходящие из вершины мы будем только когда обработаем эту вершину в самый первый раз.
На самом деле, нам так много списков не нужно. Если каждое ребро имеет вес не более $k$, то в любой момент времени не более $k$ очередей будут непустыми. Мы можем завести только $k$ списков, и вместо добавления в $(d_v + w)$-ый список использовать $(d_v+w) bmod k$.
Заметим, что алгоритм также работает когда есть общее ограничение на длину пути, а не только на вес каждого ребра. Для более общего случая, когда веса ребер могут быть любыми неотрицательными, есть алгоритм Дейкстры, который мы разберем в следующей статье.
Обход в ширину (Поиск в ширину, англ. BFS, Breadth-first search) — один из простейших алгоритмов обхода графа, являющийся основой для многих важных алгоритмов для работы с графами.
Содержание
- 1 Описание алгоритма
- 2 Анализ времени работы
- 3 Корректность
- 4 Дерево обхода в ширину
- 5 Реализация
- 6 Вариации алгоритма
- 6.1 0-1 BFS
- 6.2 1-k BFS
- 7 См. также
- 8 Источники информации
Описание алгоритма
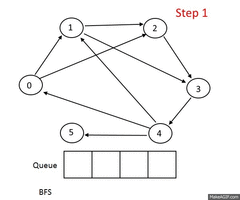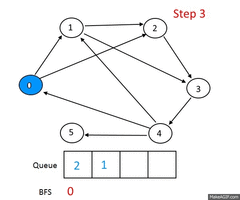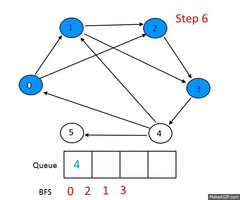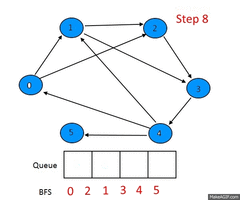
Алгоритм BFS
посещенные вершины
Пусть задан невзвешенный ориентированный граф , в котором выделена исходная вершина . Требуется найти длину кратчайшего пути (если таковой имеется) от одной заданной вершины до другой. Частным случаем указанного графа является невзвешенный неориентированный граф, т.е. граф, в котором для каждого ребра найдется обратное, соединяющее те же вершины в другом направлении.
Для алгоритма нам потребуются очередь и множество посещенных вершин , которые изначально содержат одну вершину . На каждом шагу алгоритм берет из начала очереди вершину и добавляет все непосещенные смежные с вершины в и в конец очереди. Если очередь пуста, то алгоритм завершает работу.
Анализ времени работы
Оценим время работы для входного графа , где множество ребер представлено списком смежности. В очередь добавляются только непосещенные вершины, поэтому каждая вершина посещается не более одного раза. Операции внесения в очередь и удаления из нее требуют времени, так что общее время работы с очередью составляет операций. Для каждой вершины рассматривается не более ребер, инцидентных ей. Так как , то время, используемое на работу с ребрами, составляет . Поэтому общее время работы алгоритма поиска в ширину — .
Корректность
| Утверждение: |
|
В очереди поиска в ширину расстояние вершин до монотонно неубывает. |
|
Докажем это утверждение индукцией по числу выполненных алгоритмом шагов. Введем дополнительный инвариант: у любых двух вершин из очереди, расстояние до отличается не более чем на . База: изначально очередь содержит только одну вершину . Переход: пусть после итерации в очереди вершин с расстоянием и вершин с расстоянием . Рассмотрим итерацию. Из очереди достаем вершину , с расстоянием . Пусть у есть непосещенных смежных вершин. Тогда, после их добавления, в очереди находится вершин с расстоянием и, после них, вершин с расстоянием . Оба инварианта сохранились, после любого шага алгоритма элементы в очереди неубывают. |
| Теорема: |
|
Алгоритм поиска в ширину в невзвешенном графе находит длины кратчайших путей до всех достижимых вершин. |
| Доказательство: |
|
Допустим, что это не так. Выберем из вершин, для которых кратчайшие пути от найдены некорректно, ту, настоящее расстояние до которой минимально. Пусть это вершина , и она имеет своим предком в дереве обхода в ширину , а предок в кратчайшем пути до — вершина . Так как — предок в кратчайшем пути, то , и расстояние до найдено верно, . Значит, . Так как — предок в дереве обхода в ширину, то . Расстояние до найдено некорректно, поэтому . Подставляя сюда два последних равенства, получаем , то есть, . Из ранее доказанной леммы следует, что в этом случае вершина попала в очередь и была обработана раньше, чем . Но она соединена с , значит, не может быть предком в дереве обхода в ширину, мы пришли к противоречию, следовательно, найденные расстояния до всех вершин являются кратчайшими. |
Дерево обхода в ширину
Поиск в ширину также может построить дерево поиска в ширину. Изначально оно состоит из одного корня . Когда мы добавляем непосещенную вершину в очередь, то добавляем ее и ребро, по которому мы до нее дошли, в дерево. Поскольку каждая вершина может быть посещена не более одного раза, она имеет не более одного родителя. После окончания работы алгоритма для каждой достижимой из вершины путь в дереве поиска в ширину соответствует кратчайшему пути от до в .
Реализация
Предложенная ниже функция возвращает кратчайшее расстояние между двумя вершинами.
- — исходная вершина
- — конечная вершина
- — граф, состоящий из списка вершин и списка смежности . Вершины нумеруются целыми числами.
- — очередь.
- В поле хранится расстояние от до .
int BFS(G: (V, E), source: int, destination: int):
d = int[|V|]
fill(d, )
d[source] = 0
Q =
Q.push(source)
while Q
u = Q.pop()
for v: (u, v) in E
if d[v] ==
d[v] = d[u] + 1
Q.push(v)
return d[destination]
Если требуется найти расстояние лишь между двумя вершинами, из функции можно выйти, как только будет установлено значение .
Еще одна оптимизация может быть проведена при помощи метода meet-in-the-middle.
Вариации алгоритма
0-1 BFS
Пусть в графе разрешены ребра веса и , необходимо найти кратчайший путь между двумя вершинами. Для решения данной задачи модифицируем приведенный выше алгоритм следующим образом:
Вместо очереди будем использовать дек (или можно даже steque). Если рассматриваемое ее ребро имеет вес , то будем добавлять вершину в начало, а иначе в конец. После этого добавления, дополнительный введенный инвариант в доказательстве расположения элементов в деке в порядке неубывания продолжает выполняться, поэтому порядок в деке сохраняется. И, соответственно, релаксируем расстояние до всех смежных вершин и, при успешной релаксации, добавляем их в дек.
Таким образом, в начале дека всегда будет вершина, расстояние до которой меньше либо равно расстоянию до остальных вершин дека, и инвариант расположения элементов в деке в порядке неубывания сохраняется. Значит, алгоритм корректен на том же основании, что и обычный BFS. Очевидно, что каждая вершина войдет в дек не более двух раз, значит, асимптотика у данного алгоритма та же, что и у обычного BFS.
1-k BFS
Пусть в графе разрешены ребра целочисленного веса из отрезка , необходимо найти кратчайший путь между двумя вершинами. Представим ребро веса как последовательность ребер (где — новые вершины). Применим данную операцию ко всем ребрам графа . Получим граф, состоящий (в худшем случае) из ребер и вершин. Для нахождения кратчайшего пути следует запустить BFS на новом графе. Данный алгоритм будет иметь асимптотику .
См. также
- Обход в глубину, цвета вершин
- Алгоритм Дейкстры
- Теория графов
Источники информации
- Томас Х. Кормен, Чарльз И. Лейзерсон, Рональд Л. Ривест, Клиффорд Штайн Алгоритмы: построение и анализ — 2-е изд. — М.: «Вильямс», 2007. — с. 459. — ISBN 5-8489-0857-4
- MAXimal :: algo :: Поиск в ширину
- Wikipedia — Breadth-first search
- Wikipedia — Поиск в ширину
- Визуализатор алгоритма
Лекция 8. Алгоритмы на графах
Нерекурсивный обход дерева сверху-вниз
В лекции 7 был рассмотрен рекурсивный обход корневого дерева с порядком обработки вершин “сверху-вниз”. Вот как может выглядеть нерекурсивный алгоритм обхода дерева с тем же порядком обоаботки верщин:
ConnectList{T} = AbstractVector{<:AbstractVector{T}}
function treetrace(rootindex::T, tree::ConnectList{T}) where T
stack = [rootindex]
while !isempty(stack)
v = pop!(stack)
println(v) # "обработка" вершины
for u in tree[v]
push!(stack,u)
end
end
end
В этом алгоритме используется стек, определяющий порядок обработки вершин.
Стек – это способ организации последовательной памяти, для которого реализуется принцип “последним пришёл – первым ушёл” (Last Iinput – First Output, LIFO).
В программе стек реализован на базе динамического массива (stack).
Обход дерева начинается с того, что сначала в стек помещается стартовая вершина, потом при входе в цикл она извлекается из него, “обрабатывается” и после этого в стек помещаются все ее дочерние вершины, последняя из которых будет обработана на последующей итерации, и т.д.
В конце концов, когда новые вершины перестанут добавляться в стек, оставшиеся в стеке вершины будут только последовательно из него извлекаться и обрабатываться, до тех пор пока стек не станет пустым. На этом обход дерева завершается.
Обход графа – поиск в глубину
Если теперь у нас имеется не дерево, а граф (заданный, например, списком смежностей). Тогда обход этого графа можно начать с какой-либо его вершиы, действуя подобно тому, как мы только что обходили корневое дерево (начиная с его корня). Отличие графа общего вида от дерева состоит, во-первых, в том, что в графе могут быть циклы, и, чтобы не было бесконечного “хождения” по циклам, потребуется принять соответствующие меры. Во-вторых, из выбранной вершины не все остальные верширы могут быть доступнны, но с этим уже ничего не поделаешь.
Для того, чтобы исключить зацикливания, ранее посещённые вершины нужно как-то помечать, чтобы их не помещать повторно в стек. Для этого можно завести специальный массив, который будет выполнять роль индикатора множесва уже посещенных вершин.
Соответствующий код может иметь следующий вид.
function dfsearch(start_ver::T, graph::ConnectList{T}) where T mark = zeros(Bool, length(graph)) stack = [start_ver] # стек вершин, откуда они затем извлекаются на "обработки" mark[start_ver] = 1 # - вершина statver "помечена", как помещавшаяся в стек while !isempty(stack) v = pop!(stack) # - очередная вершина взята со стека println(v) # "обработка" вершины for u in graph[v] # - перебор смежных с v вершин if mark[u] == 0 push!(stack,u) # - все смежные с v вершины последовательно помещаются на стек mark[u] = 1 # - вершина u "помечена", как помещавшаяся в стек end end end end
Такая процедура обхода графа называется поиском в глубину (Depth-first search, DFS). Это название обусловленно тем, что порядок посещения вершин определяется использованием стека, в который каждый раз помещается сначала стартовая вершина, а на последующих шагах алгоритма все смежные с последней обработанной вершиной. При этом очередная обрабатываемая вершины снимается с вершины этого стека, т.е. процесс обхода все время удаляется от стартовой вершины, до тех пор пока в какой-то момент либо продвижение “в глубь” окажется невозможным по причине отсутствия более удаленных вершин от стартовой вершины, либо – цикл не замкнётся на стартовой вершине (но такое замыкание допущено не будет).
Замечание. Как и обход дерева, поиск в глубину может быть также реализован рекурсивно. При этом, однако, не понадобится реализовывать стек с помощью специального массива. В случае рекурсии для той же цели будет неявно использован так называемый аппаратный стек, именно благодаря которому и возможна организация рекурсивных вызовов. При вызове любой функции в аппаратный стек помещаются все её локальные переменные и адрес возврата, а после завершения функции все её локальные переменные автоматически снимаются с этого стека.
Следующий код даёт рекурсивную реализацию поиска в глубину.
function dfs(start_ver::T, graph::ConnectList{T}) where T function dfs!(v) # эта функция изменяет внешний массив mark println(v) # Условно можно считать, что v - помещена на вершину аппаратного стека mark[v]=true # - помечен факт "входа" в вершину for u in graph[v] if !mark[u] # в случае если mark[u] == 1 ребро (v,u) будет проигнорировано dfs!(u) end end # имеет место факт "выхода" из вершины end n=length(graph) mark=zeros(Bool, n) dfs!(start_ver) end
Обход графа – поиск в ширину
Если в рассмотренном выше алгоритме обхода графа стек заменить на очередь, то получится алгоритм обхода, называемый поиском в шириу (breadth-first search, BFS).
Очередь – это способ организации последовательной памяти, для которого реализуется принцип “первым пришёл – первым ушёл” (First Input – First Output, FIFO).
function bfsearch(startver::T, graph::ConnectList{T}) where T mark = zeros(Bool, length(graph)) queue = [startver] # - в очередь помещена стартовая вершина mark[startver] = 1 # - вершина statver "помечена", как помещавшаяся в очередь while !isempty(queue) v = popfirst!(queue) # - очередная вершина взята из очереди println(v) # - "обработка" вершины for u in graph[v] # - перебор смежных с v вершин if mark[u] == 0 push!(queue, u) # - все смежные с v вершины последовательно помещаются в очередь mark[u] = 1 # - вершина u "помечена", как помещавшаяся в очередь end end end end
В соответствии с этим при поиске в ширину вершины обрабатываются в порядке их удаленности от стартовой вершины: сначала будут обработаны все вершины, смежные со стартовой, затем все вершины, удаленные от стартовой на 2 ребра, за тем все удаленные на 3 ребра, и т.д., до тех пор, пока не начнут замыкаться циклы (замыкания которых не допускаются).
Связность графа
Неориетированный граф (неорграф) называется связным, если любая его вершина достижима из любой другой.
Ориентированный граф (орграф) называется сильно связным, если любая его вершина достижима из любой другой.
Орграф называется слабосвязным (или односвязным), если связным является соответсвующий неорграф, получаемый из исходного орграфа заменой ориентированных ребер неориентированными.
Задача. Орграф задан списком смежностей. Требуется написать функцию, возвращающую значение true, если он является сильно связным, и значение false – в противном случае.
Решение. Идея решения заключена в следующем. Если из некоторой произвольно выбранной вершины попытаться обойти все остальные вершины графа (используя поиск в глубину или поиск в ширину), и если при этом некоторые вершины окажутся недостижимыми (в результате индикатор множества посещенных вершин будет иметь нулевые элементы), то данный орграф не является сильно связным. В противном случае дать определенный овет нельзя, требуется оcуществить ту же процедуру обхода, стартуя по очереди из всех остальных вершин. И только в случае, если в результате каждого такого старта не обнаружатся недостижимые вершины, то данный орграф является сильносвязным.
Соответствующий программный код может иметь следующий вид.
function strongly_connected(graph::ConnectList) for s in 1:length(graph) if all_achievable(s, graph) == false return false end end return true end function all_achievable(started_ver::Integer, graph::ConnectList) mark = zeros(Bool,length(graph)) attempt_achievable!(started_ver, graph, mark) return count(m->m==0, mark) == 0 #all(mark .== 1) end
Здесь использована встроенная функция высшего порядка, возвращающая число элементов массива, удовлетворяющих заданному условию.
Также используется следующая вспомогательная функция, осуществляющая процедуру обхода графа на основе алгоритма поиска в глубину, начиная с заданной стартовой вершины, но для которой массив mark (индикатор множества посещённых вершин) является внешним, и данная функция его модифицирует (это единственное, что она делает).
function attempt_achievable!(start_ver::T, graph::ConnectList{T}, mark::AbstractVector{<:Integer}) where T stack = [start_ver] mark[start_ver] = 1 while !isempty(stack) v = pop!(stack) for u in graph[v] if mark[u] == 0 push!(stack,u) mark[u] = 1 end end end end
Целесообразность отдельного определения функции attempt_achievable! (achievable – достижимый), помечающая во внешнем массиве все посещенные при поиске в глубину, определена тем, что данная процедура является основой для решения и некоторых других задач.
Замечание. В функции all_achievable в последняя стрчка выглядела так:
return count(m->m==0, mark) == 0 #all(mark .== 1)
Однако вместо функции высшего порядка count можно было бы воскользовать функцией all, возвращающей значение true тогда и только тогда, кода все элеметы её аргумента (вектора) имеют значение true:
Формально результат будет тот же самый, но второе решение хуже, так оно влечет размещение в памяти промежуточного массива, являющегося результатом выполнения операции mark .== 1.
Задача: проверить, является ли орграф слабосязным
Идея решения.
- превратить заданный (списком смежностей) орграф в неорграф
- проверить, является ли получившийся неорграф сязным
Чтобы превратить заданный орграф в неорграф, необходимо только в его список смежностей добавить отсутствующие “встречные” ребра (если таковые имеются).
Это можно сделать, например, так:
- по заданному списку смежностей
orgraphпострить матрицу смежностей; - из получившейся матрицы смежностей получить соответствующую симметричную матрицу смежностей;
- построить список смежностей
neorgraph, соответствующий полученной симметричной матрице смежностей;
Теперь, проверка того, является ли полученный неорграф (neorgraph) связным, сводится к вызову функции:
all_achievable(1, neorgraph)
Замечание. На самом деле, чтобы по заданному списку смежностей orgraph построить ссоответствующий ему список смежностей neorgraph, нет необходимости в качестве промежуточного этапа использовать матрицу смежностей. Это легко сделать и непоспредственно при обходе графа orgraph, только на базе алгоритма поиска в глубину (или в ширину).
Компоненты связности неорграфа
Пусть имеется граф $G=(V, varepsilon)$ (см. лекцию 7).
Рассмотрим подграф $G_1=(V_1, varepsilon_1)$, где
- $V’ subset V$
- отображение $varepsilon_1: V_1 times V_1 to {0,1,2…}$ – есть сужение отображения $varepsilon: V times V to {0,1,2…}$ на $V_1 times V_1$
Определение. Подграф $G_1$ называется компонентой связности неорграфа $G$, если
- он является связным;
- невозможно добавить к нему никакую вершину из $V setminus V_1$ с какими-либо инцидентными ей ребрами так, чтобы получившийся подграф оставался связным.
Задача. Посчитать число компонент связности в неорграфе, представленного списком смежностей graph.
Идея решения:
- заведем массив, который будет представлять собой индикатор посещенных вершин;
- будем перебирать подряд все еще не посещенные вершины графа, и выполнять обход графа с помощью функции
attempt_achievable!, начиная с очередной выбранной вершины, до тех пор пока в индикаторе множества посещенных вершин, не останется ни одного нуля (массив, представляющий индикатор, является внешним по отношению к функцииattempt_achievable!); - при этом нужно завести счетчик числа компонет связности и при каждом новом старте увеличивать его на 1.
Задача. Найти все компоненты связности в неорграфе, представленного списком смежностей graph, т.е. написать функцию, возвращающую вектор, длина которого равна числу компонент связности, и каждый i-ый элемент содержит индекс какой-либо вершины соответсвующей компоненты связности.
Идея решения: в отличие от предыдущей задачи, вместо того, чтобы заводить счетчик числа компонент связности, надо будет завести динамический массив, в который помещать индекс каждой новой стартовой вершины.
Двудольный граф
Определение. Граф называется двудольным графом, если множество его вершин $V$ можно разбить на два не пересекающихся не пустых подможества $V=V_1+V_2$ так, чтобы в подграфах c вершинами $V_1$ и $V_2$ не было ни одного ребра.
Утверждение. Любое дерево (не обязательно корневое) является двудольным графом.
В самом деле:
- превратим дерево в неорграф (если только оно таковым не было изначально), примем любую его вершину за корень (и тем самым определим новую ориетацию его ребер), и отнесем его к $V_1$;
- смежные с корнем вершины, отнесем к $V_2$, затем все вершины из следущего яруса отнесем снова к $V_1$, и т.д.
В результате, все вершины одного яруса дерева обязательно будут отнесены к одному и тому же множеству вершин: или все к $V_1$ или все к $V_2$. И, поскольку никакие две вершины одного яруса не могут быть смежными, то утверждение доказано.
Задача. Проверить, является ли граф двудольным, т.е. написать функцию, получающую список смежностей некоторого графа, и возвращающую true, если граф двудольный, и false – в противном случае.
Идея решения:
- превратим исходный граф в неорграф (если только он изначально не был таковым).
- начнем обход полученного неорграфа, например, в ширину, начиная с 1-ой вершины, такому обходу соответствует некоторое корневое дерево;
- при этом обходе (в ширину) вершины соседних ярусов этого дерева должны относиться к разным множествам, например, вершины ярусов с четными номерами (начиная с 0) будем относить к $V_1$, а с нечетными номерами – к $V_2$;
- для этого заведём внешний массив
mark(внешний – по отношению к функции, выполняющей обход), в котором на позициях с индексами ещё непосещенных вершин будут находиться нули, на позициях с индексами уже посещенных вершин и отнесенных к $V_1$, должны быть записаны единицы, а на позициях с индексами уже посещенных вершин и отнесеннных к $V_2$ – двойки; - массив
markтакже будет служить для того, чтобы с его помощью предотвращать зацикливания при обходе графа, при этом, если на некотором шаге обхода графа концы какого-либо ребра, замыкающего цикл, окажутся отнесенными к одному и тому же множеству: либо к $V_1$, либо к $V_2$, то это будет означать, что граф не является двудольным.
Реализовать это можно с помощью следующей вспомогательной функции:
function attempt_devide!(start_ver::T, graph::ConnectList{T}, mark::AbstractVector{<:Integer}) where T queue = [startver] # queue - очередь mark[startver] = 1 while !isempty(queue) v = popfirst!(queue) for u in graph[v] next_num = (mark[v] % 2) + 1 if mark[u] == 0 push!(queue, u) mark[u] = next_num elseif mark[u] == next_num return false end end end return true end
Замечание. На самом деле, в этом алгоритме процедуру обхода в ширину можно заменить на обход в глубину – результат от этого не изменится.
Поиск кратчайшего пути между двумя заданными вершинами не взвешенного графа
Задача. Заданы две вершины некоторого орграфа. Требуется найти кратчайший путь, ведущий из первой вершины во вторую (длина пути исчисляется числом ребер графа, сосотавляющих путь).
Эту задачу можно было бы решить, воспользовавшись, например, алгоритмом Дейкстры, положив весовую матрцу графа равной матрице смежностей, в которой нули заменены бесконечностями (можно также сказать, что требуемая весовая матрица получается путем инвертирования каждого элемента матрицы смежностей).
Однако мы рассотрим другой алгоритм, основанный на поиске в ширину.
Идея алгоритма. Начнем обход графа в ширину, стартуя из первой вершины, и этот обход будет продолжаться, пока не встретится вторая вершина. Тогда искомое кратчайшее расстояние будет равно номеру яруса в дереве посещенных вершин в котром находится вторая вершина (т.к. при поиске в шириу сначала пребираются вершина из 1-го яруса, затем из 2-го и т.д.).
Соответственно, алгоритм поиска кратчайшего пути может выглядеть так
function shortest_dist(start_ver::T, finish_ver::T, graph::ConnectList{T}) where T n = length(graph) dists = zeros(Int, n) queue = [start_ver] # - в очередь помещена стартовая вершина dist[start_ver] = 1 # - вершина stat_ver "помечена", как помещавшаяся в очередь (значением на 1 большем расстояния до start_ver) while !isempty(queue) v = popfirst!(queue) # - очередная вершина взята из очереди if v == finish_ver return dist[v]-1 end for u in graph[v] # - перебор смежных с v вершин if dist[u] == 0 push!(queue, u) # - все смежные с v вершины последовательно помещаются в очередь dist[u] = dist[v] + 1 # - вершина u "помечена", как помещавшаяся в очередь (значением на 1 большем расстояния от u до start_ver) end end end end
Вопрос: что вернёт функция shortest_path, если окажется, что вторяя вершина не достижима из первой?
(почему правильный ответ – значение nothing?).
Теперь зададимся вопросом, как надо модернизировать функцию shortest_dist, чтобы вместо значения кратчайшего расстояния она возращала бы сам оптимальный путь, или, может быть, – информацию, из которой его было бы легко востановить.
Проблема в том, что процесс поиска происходит в дереве, и до тех пор, пока не будет обнаружена финишная вершина, не известно какая именно ветвь дерева поиска будет составлять искомый путь. Поэтому придется хранить всё дерево поиска, а потом взять из него только нужную ветвь.
Это дерево удобно будет представить с помощью так называемого вектора предков. Длина этого вектора равна числу вершин графа, и в процессе поиска в него записываются индесы вершин графа по следующему принципу: в каждую его i-ую позицию записывает индекс родительской вершины в дереве поика. При этом, поскольку стартовая вершина является корнем этого дерева, то у нее не долно быть родительской вершины, и поэтому на позицию с индексом start_ver должно быть записано значение, которое заведомо не может быть индексом вершины, например, можно положить его равным -1 (можно было бы взять также и значение 0, но, как мы увидим в дальнейшем, значение -1 удобнее).
С учетом сказанного модифицируем наш код следующим образом, введя в него вектор parent для хранения дерева поиска.
function shortest_path(start_ver::T, finish_ver::T, graph::ConnectList{T}) where T n = length(graph) dist = zeros(Int, n) queue = [start_ver] # - в очередь помещена стартовая вершина dist[start_ver] = 1 # - вершина stat_ver "помечена", как помещавшаяся в очередь parent = fill(-1, n) while !isempty(queue) v = popfirst!(queue) # - очередная вершина взята из очереди if v == finish_ver return parent end for u in graph[v] # - перебор смежных с v вершин if dist[u] == 0 # можно заменить на parent[u] == 0 push!(queue, u) # - все смежные с v вершины последовательно помещаются в очередь dist[u] = dist[v]+1 # - вершина u "помечена", как помещавшаяся в очередь parent[u] = v end end end end
Теперь по завершению данной процедуры поиска (в случае, если финишная вершина оказаласть достижимой) в векторе parent находится все дерево поиска, в том числе и искомый путь:
parent[finish_ver], parent[parent[finish_ver]],..., start_ver
Для извлечения этого пути из вектора предков можно предложить следующую функцию
function get_shortest_path(parent::AbstractVector{T}, finish_ver::T) where T path=T[] i = finish_ver while parent[i] != -1 push!(path, i) i = parent[i] end return reverse(path) end
Замечание. Можно заметить, что в функции shorted_path можно было бы легко обойтись без массива dists, возложив его фунуцию на массив parent. Для этого потребуются только незначительные изменения в написанном коде, а также то, что ранее мы решили использовать значение -1 для обозначения отсутствия предка у стартовой вершины, вместо значения 0. Теперь значение 0 можно будет продожать использовать для обозначения того, что какя-либо вершина ещё не была посещена, но теперь это 0 бутем аписывать в массив parent.
function shortest_path(start_ver::T, finish_ver::T, graph::ConnectList{T}) where T n = length(graph) parent = zeros(Int,n) parent[start_ver] = -1 queue = [start_ver] # - в очередь помещена стартовая вершина while !isempty(queue) v = popfirst!(queue) # - очередная вершина взята из очереди if v == finish_ver return parent end for u in graph[v] # - перебор смежных с v вершин if dist[u] == 0 # можно заменить на parent[u] == 0 push!(queue, u) # - все смежные с v вершины последовательно помещаются в очередь parent[u] = v end end end end
Топологическая сортировка вершин графа
Пусть имеется орграф, и пусть этот граф не имеет циклов.
Отметим, что такой орграф не обязательно является корневым деревом, в отличии от дерева его вершины могут иметь валентности по выходу и большие 1.
Такой граф легко себе представить, если расмотреть какое-либо корневое дерево, в нём некоторые вершины, находящиеся в одном и том же ярусе, “слить” в одну.
На самом деле граф может сосотоять из нескольких таких несвязных или слабосвязных частей.
Отличительной особенностью такого орграфа является то, что его можно нарисовать так, чтобы все его ребра (они предполагаются ориетированными) были бы направлены в одну и туже сторону.
Задача топологической сортировки как раз и состоит в том, чтобы так перенумеровать индексы вершин орграфа (не содержащего циклов), чтобы если вершины орграфа расположить слева направо (или сверху вниз) в порядке возрастания их новой нумерации, то все ребра были бы направлены в одну сторону, например, с лева направо (сверху вниз).
В результате самая левая вершина будет иметь нулевую валентность по входу (таких вершин может быть несколько и все они могут следовать в любом порядке), а самая правая – нулевую по выходу (таких вершин тоже может быть несколько и они могут следовать в любом порядке).
Соответствующую картинку можно посмотреть, например, здесь
Практический смысл этой задачи можно пояснить следующим примером. Пусть вершинам графа соответствут некоторые бюрократические инстанции, у которых требуется получить разрешение на какую-либо деятельность, причем в некотре инстунции необходимо обращаться только после того как получено разрешение от других инстанций. Ориетированные ребра как раз и соответствуют таким обращениям.
Ясно, если такой граф будет содержать циклы, то никакого разрешения получить будет невозможно.
Т.о. после выпонения топологической сортировки станет понятна очередность посещения всех инстанций.
Идея алгоритма топологической сортировки.
- Сначала надо какую-либо вершину с нулевой валентностью по выходу (таких вершин в графе может быть несколько). Найденная вершина должна будет занять последнюю позицию в отсортированной последовательности вершин.
- Затем удалить из графа все рёбра, ведущие в эту вершины, и проделать предыдущую процедуру с оставшейся частью графа. Очередная найденная вершина должна будет занять позицию в отсортированной последовательности, предшествующую всем прежде найденными.
- Повторять данные действия следует до тех пор, пока в формируемой последовательности вершин не окажутся все вершины графа.
В действительности удалять указанные ребра из графа необходимости нет, достаточно лишь их специальным образом помечать, чтобы алгоритм сортировки в дальнейшем мог их игнорировать.
Эта идея может быть реализована на базе поиска в глубину следующим образом.
function topological_sort(graph) function dfs!(v) # функция dfs! изменяет внешний массив mark mark[v]=true # - помечен факт "входа" в вершину for u in graph[v] if !mark[u] # в случае если mark[u] == 1 ребро (v,u) будет проигнорировано dfs!(u) end end # имеет место факт "выхода" из вершины push!(series_ver, v) end n = length(graph) mark = zeros(Bool,n) series_ver = [] for s in 1:n if !mark[s] dfs!(s) end end return reverse(series_ver) end
Здесь вложеннная функция dfs! реализует поиск в глубину рекурсивно, начиная с заданной вершины v. При этом при выходе из этой вершины, т.е. после завершения соответствующей цепочки рекурсивных вызовов, эта вершина помещается в в конец внешнего массива series_ver. Таким образом, после завершения вызова функции dfs!(1) в массиве series_ver будет находится последовательность вершин, из той части графа, которая доступна из вершины 1, причем в порядке, обратном к требуемому. Поэтому, чтобы добавить в эту последовательность индексы всех остальных вершин, которые при этом также будут помещаться в самый конец вектора series_ver, в цикле for s in 1:n функция dfs! вызывается повторно, если только после предыдущих её вызовов остаются не посещенные вершины графа.
В результате, чтобы получить последовательность вершин графа в порядке его топологической сортировки, остаётся только к вектору series_ver применить встроенную функцию reverse, которая перевернет его в требуемом обратном порядке.
Замечание. Рассмотренный алгоритм предполагает, что граф является ациклическим (не содержит циклов). Но если в реальности всё же циклы в графе будут, то алгоритм этого не заметит и выдаст не правильный ответ. Правильный ответ состоял бы в том, что в этом случае топологическая сортировка не возможна. В таком случае, например, функция может “бросать исключение” с помощью throw.
Чтобы обеспечить такой контроль, можно предусмотреть возможность для трех (а не двух) значений элементов массива mark: 0,1,2, так, чтобы при “входе” в вершину v присваивать mark[v]=1, а при выходе из неё – уже mark[v]=2. Тогда, если при поиске в глубину вдруг окажется, что mark[v] == 1, то это будет означать, что обнаружился цикл.
function topological_sort(graph) function dfs!(v) # функция dfs! изменяет внешний массив mark mark[v]=1 # - помечен факт "входа" в вершину for u in graph[v] if mark[u] == 0 dfs!(u) elseif mark[u]==1 throw("Граф содержит цикл") end end # имеет место факт "выхода" из вершины mark[v]=2 push!(series_ver, v) end n = length(graph) mark = zeros(Int,n) series_ver = [] for s in 1:n if mark[s]==0 dfs!(s) end end return reverse(series_ver) end

