Основание правильной пирамиды является правильный многоугольник – равносторонний треугольник, квадрат. Основанием пирамиды называют ту фигуру, над которой расположена вершина пирамиды.То есть это та грань пирамиды, которая не включает в себя ее вершину. Площадь основания пирамиды – это площадь этой плоской фигуры.
Площадь основания правильной пирамиды
Правильная пирамида может быть трех видов:
- треугольная,
- четырехугольная,
- шестиугольная.
Соответственно у правильной треугольной пирамида основание – равносторонний треугольник. У правильной четырехугольной пирамиды основание – квадрат. В основании шестиугольной правильной пирамиды в основании лежит шестиугольник. Приведем формулы для нахождения площади основания пирамиды:
Площадь основания правильной треугольной пирамиды
В основании равносторонний треугольник – находим его площадь:
, где
– сторона треугольника.
, где 
Площадь основания правильной четырехугольной пирамиды
В основании правильной четырехугольной пирамиды лежит квадрат, площадь квадрата:
, где
– сторона квадрата.
Площадь основания правильной шестиугольной пирамиды
Это площадь правильного шестиугольника. Если известна сторона шестиугольника, то площадь правильного шестиугольника находится по формуле:
Площадь основания любой пирамиды
Площадь основания любой пирамиды – это площадь ее основания.
Если в основании пирамиды треугольник, то формулы для нахождения площади любого треугольника вы можете посмотреть в статье “Площадь треугольника”.
В основании пирамиды может лежать любой прямоугольник, любой многоугольник. Обычно в школьных задачах, в основании пирамиды часто лежит треугольник, редко прямоугольник. Задачи, в которых в основании пирамиды лежит пятиугольник, семиугольник или произвольных многоугольник, практически не встречаются. Хотя их можно увидеть в олимпиадных задачах.
Теперь давайте решим несколько задач для нахождения площади основания пирамиды
Примеры решения задач
Задача 1
Дана правильная треугольная пирамида. Сторона основания пирамиды равна 2. Найдите площадь основания пирамиды.
Решение: пирамида правильная и треугольная, значит, в основании равносторонний треугольник. Тогда площадь основания пирамиды находится по формуле: . Нам дана сторона
, тогда
Ответ:
Задача 2
Строитель решил построить здание в форме правильной шестиугольной пирамиды, для основания пирамиды у него есть доски, каждая площадью 0,5 м2. Сколько досок ему понадобится, если сторона основания пирамиды равна 6 м?
Решение:
Рассчитаем площадь основания правильной шестиугольной пирамиды. Для этого воспользуемся формулой: . Подставим в нее значение стороны
. Получим:
м2.
Теперь подсчитаем, сколько нам понадобится досок: 
.
Ответ: 108 досок.
Задача 3
Основанием пирамиды является прямоугольный равнобедренный треугольник, с катетом, равным 4. Найдите площадь основания пирамиды.
Решение: иными словами – нас просят определить площадь прямоугольного равнобедренного треугольника. Так как треугольник прямоугольный и равнобедренный, то один из катетов будет основанием треугольника, а другой – высотой. Определяем площадь по формуле:
.
Ответ: 8
Когда человек слышит слово “пирамида”, то сразу вспоминает величественные египетские сооружения. Тем не менее древние каменные гиганты являются лишь одним из представителей класса пирамид. В данной статье рассмотрим с геометрической точки зрения свойства правильной четырехугольной пирамиды .
Что такое пирамида в общем случае?
В геометрии под ней понимают объемную фигуру, получить которую можно, если соединить все вершины плоского многоугольника с одной единственной точкой, лежащей в другой плоскости, чем этот многоугольник. Рисунок ниже показывает 4 фигуры, которые удовлетворяют данному определению.
Вам будет интересно:Литовские статуты: даты и история изданий, регламент, хронология принятия статутов
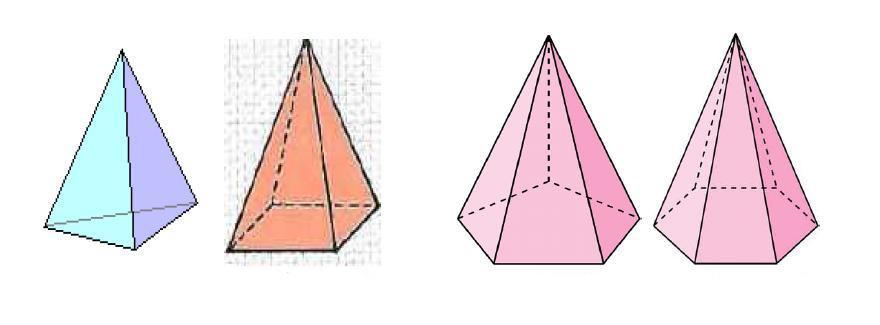
Мы видим что первая фигура имеет треугольное основание, вторая – четырехугольное. Две последние представлены пяти- и шестиугольным основанием. Однако боковая поверхность всех пирамид образована треугольниками. Их число точно равно количеству сторон или вершин многоугольника в основании.
Особым типом пирамид, которые от остальных представительниц класса отличаются идеальной симметрией, являются правильные пирамиды. Чтобы фигура была правильной, должны выполняться следующие два обязательных условия:
- в основании должен находиться правильный многоугольник;
- боковая поверхность фигуры должна состоять из равных равнобедренных треугольников.
Отметим, что второе обязательное условие можно заменить иным: перпендикуляр, проведенный к основанию из вершины пирамиды (точка пересечения боковых треугольников), должен пересекать это основание в его геометрическом центре.
Правильная четырехугольная пирамида
Теперь перейдем к теме статьи и рассмотрим, какие свойства правильной четырехугольной пирамиды характеризуют ее. Сначала покажем на рисунке, как выглядит эта фигура.
Ее основание является квадратом. Боковые стороны представляют 4 одинаковых равнобедренных треугольника (они также могут быть равносторонними при определенном соотношении длины стороны квадрата и высоты фигуры). Опущенная из вершины пирамиды высота пересечет квадрат в его центре (точка пересечения диагоналей).
Эта пирамида имеет 5 граней (квадрат и четыре треугольника), 5 вершин (четыре из них принадлежат основанию) и 8 ребер. Ось симметрии четвертого порядка, проходящая через высоту пирамиды, переводит ее в саму себя путем поворота на 90o.
Египетские пирамиды в Гизе являются правильными четырехугольными.
Далее приведем формулы, позволяющие определить все характеристики этой фигуры.
Четыре основных линейных параметра
Начнем рассмотрение математических свойств правильной четырехугольной пирамиды с формул высоты, длины стороны основания, бокового ребра и апофемы. Сразу скажем, что все эти величины связаны друг с другом, поэтому достаточно знать только две из них, чтобы однозначно вычислить оставшиеся две.
Предположим, что известна высота h пирамиды и длина a стороны квадратного основания, тогда боковое ребро b будет равно:
b = √(a2 / 2 + h2)
Теперь приведем формулу для длины ab апофемы (высота треугольника, опущенная на сторону основания):
ab = √(a2 / 4 + h2)
Очевидно, что боковое ребро b всегда больше апофемы ab.
Оба выражения можно применять для определения всех четырех линейных характеристик, если известны другие два параметра, например ab и h.
Площадь и объем фигуры
Это еще два важных свойства правильной четырехугольной пирамиды . Основание фигуры имеет следующую площадь:
So = a2
Эту формулу знает каждый школьник. Площадь боковой поверхности, которая образована четырьмя одинаковыми треугольниками, можно определить через апофему ab пирамиды так:
Sb = 2 × a × ab
Если ab является неизвестной, то можно ее определить по формулам из предыдущего пункта через высоту h или ребро b.
Общая площадь поверхности рассматриваемой фигуры складывается из площадей So и Sb:
S = So + Sb = a2 + 2 × a × ab = a (a + 2 × ab)
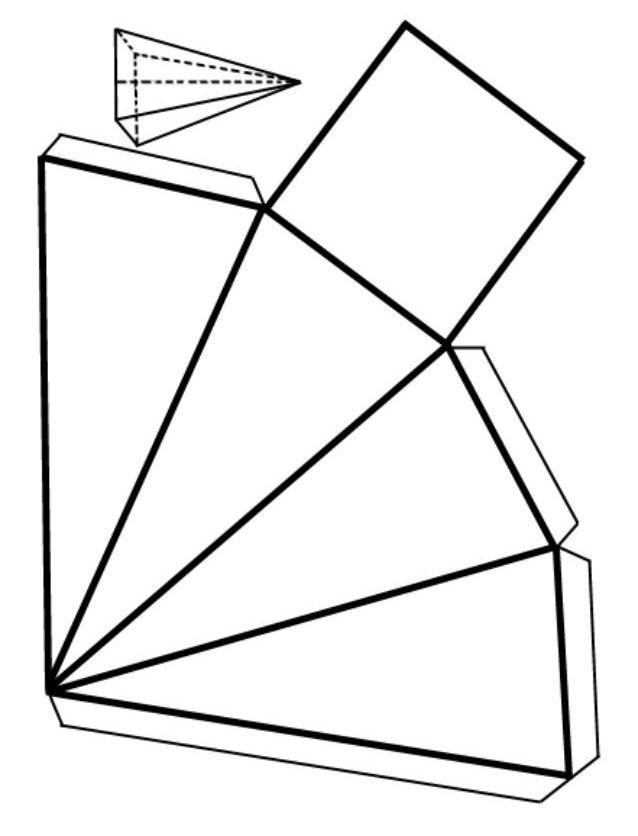
Рассчитанная площадь всех граней пирамиды показана на рисунке ниже в виде ее развертки.
Описание свойств правильной четырехугольной пирамиды не будет полным, если не рассмотреть формулу для определения ее объема. Эта величина для рассматриваемой пирамиды вычисляется следующим образом:
V = 1/3 × h × a2
То есть V равен третьей части произведения высоты фигуры на площадь ее основания.
Свойства правильной усеченной четырехугольной пирамиды
Получить эту фигуру можно из исходной пирамиды. Для этого необходимо срезать верхнюю часть пирамиды плоскостью. Оставшаяся под плоскостью среза фигура будет называться пирамидой усеченной.
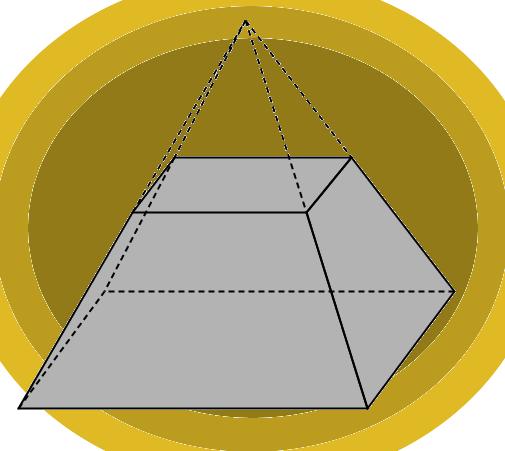
Удобнее всего изучать характеристики усеченной пирамиды, если ее основания параллельны друг другу. В этом случае нижнее и верхнее основания будут подобными многоугольниками. Поскольку в четырехугольной правильной пирамиде основание – это квадрат, то образованное при срезе сечение тоже будет представлять квадрат, но уже меньшего размера.
Боковая поверхность усеченной фигуры образована не треугольниками, а равнобедренными трапециями.
Одним из важных свойств этой пирамиды является ее объем, который рассчитывается по формуле:
V = 1/3 × h × (So1 + So2 + √(So1 × So2))
Здесь h – расстояние между основаниями фигуры, So1, So2 – площади нижнего и верхнего оснований.
Объем правильной треугольной пирамиды
Пусть сторона основания равна ( displaystyle a), а боковое ребро равно ( displaystyle b). Нужно найти ( displaystyle {{S}_{осн}}) и ( displaystyle H).
( displaystyle {{S}_{осн}}) – это площадь правильного треугольника ( displaystyle ABC).
Вспомним, как искать эту площадь.
Используем формулу площади:
( displaystyle S=frac{1}{2}abcdot sin gamma )
У нас «( displaystyle a)» – это ( displaystyle a), а «( displaystyle b)» — это тоже ( displaystyle a), а ( displaystyle sin gamma =sin 60{}^circ =frac{sqrt{3}}{2})
Значит, ( displaystyle {{S}_{ABC}}=frac{1}{2}{{a}^{2}}frac{sqrt{3}}{2}=frac{{{a}^{2}}sqrt{3}}{4}).
Теперь найдем ( displaystyle H).
По теореме Пифагора для ( displaystyle Delta SOC)
( displaystyle {{H}^{2}}={{b}^{2}}-O{{C}^{2}})
Чему же равно ( displaystyle OC)?
Это радиус описанной окружности в ( displaystyle Delta ABC), потому что пирамида правильная и, значит, ( displaystyle O) — центр ( displaystyle Delta ABC)
Найдем ( displaystyle OC) (Подробнее смотри в теме «Правильный треугольник»).
( displaystyle OC=frac{2}{3}CK), так как ( displaystyle O) — точка пересечения и медиан тоже.
( displaystyle C{{K}^{2}}=A{{C}^{2}}-A{{K}^{2}}) (теорема Пифагора для ( displaystyle Delta ACK))
( displaystyle C{{K}^{2}}-{{a}^{2}}-frac{{{a}^{2}}}{4}=frac{3{{a}^{2}}}{4}); ( displaystyle CK=frac{asqrt{3}}{2})
Значит, ( displaystyle OC=frac{2}{3}cdot frac{asqrt{3}}{2}=frac{asqrt{3}}{3})
Подставим ( displaystyle OC) в формулу для ( displaystyle H).
( displaystyle {{H}^{2}}={{b}^{2}}-O{{C}^{2}}={{b}^{2}}-{{left( frac{asqrt{3}}{3} right)}^{2}}={{b}^{2}}-frac{{{a}^{2}}}{3})
И подставим все в формулу объема:
( displaystyle V=frac{1}{3}{{S}_{ABC}}cdot H=frac{1}{3}cdot frac{{{a}^{2}}sqrt{3}}{4}cdot sqrt{{{b}^{2}}-frac{{{a}^{2}}}{3}})
( displaystyle V=frac{{{a}^{2}}sqrt{3}}{12}sqrt{{{b}^{2}}-frac{{{a}^{2}}}{3}}).
Внимание: если у тебя правильный тетраэдр (т.е. ( displaystyle b=a)), то формула получается такой:
( displaystyle V=frac{{{a}^{3}}}{6sqrt{2}}).
Вы уже знакомы с пирамидой, т. е. многогранником, одна грань которого является многоугольником, а остальные грани-треугольники имеют общую вершину.
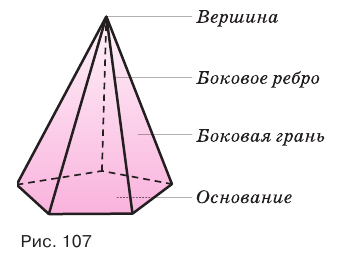
Треугольные грани пирамиды, имеющие общую вершину, называют боковыми гранями, а эту общую вершину — вершиной пирамиды. Ребра боковых граней, сходящиеся в вершине пирамиды, называют боковыми ребрами пирамиды. Многоугольник, которому не принадлежит вершина пирамиды, называют основанием пирамиды (рис. 107).
Пирамиды разделяют на треугольные, четырехугольные, пятиугольные и т. д. в зависимости от количества сторон их оснований. Пирамида, изображенная на рисунке 107, — пятиугольная, а на рисунке 108, — восьмиугольная. Треугольную пирамиду называют еще тетраэдром. У тетраэдра все грани являются треугольниками (рис. 109).
Перпендикуляр, проведенный из вершины пирамиды к плоскости ее основания, называется высотой пирамиды. На рисунке 108 показана высота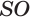 
Плоскость, проходящая через два боковых ребра пирамиды, не принадлежащие одной грани, называется диагональной плоскостью, а сечение пирамиды диагональной плоскостью — диагональным сечением. На рисунке 111 показано диагональное сечение шестиугольной пирамиды.
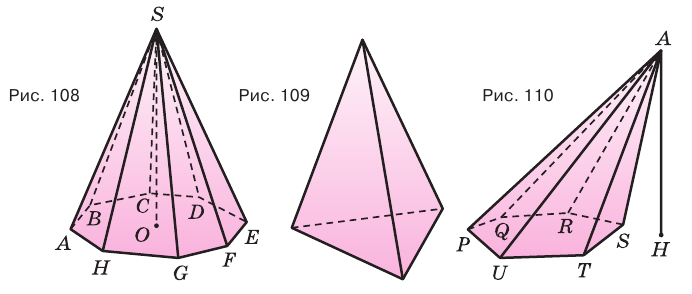
Пирамида, основанием которой является правильный многоугольник, а основание ее высоты совпадает с центром этого многоугольника, называется правильной пирамидой (рис. 112).
Высота боковой грани правильной пирамиды, проведенная из ее вершины, называется апофемой пирамиды.
Отметим, что в правильной пирамиде:
- боковые ребра равны;
- боковые грани равны;
- апофемы, равны;
- двугранные углы при основании равны;
- двугранные углы при боковых ребрах равны;
- каждая точка высоты равноудалена от вершин основания;
- каждая точка высоты равноудалена от ребер основания;
- каждая точка высоты равноудалена от боковых граней.
Отметим, что если в пирамиде равны все:
- боковые ребра, то около ее основания можно описать окружность, и центр этой окружности совпадает с основанием высоты пирамиды (рис. 113);
- двугранные углы при основании, то в это основание можно вписать окружность, и центр этой окружности совпадает с основанием высоты пирамиды (рис. 114).
Боковые грани составляют боковую поверхность пирамиды, а боковые грани вместе с основанием — полную поверхность пирамиды.
Вы знаете, что боковая поверхность правильной пирамиды равна произведению полупериметра ее основания и апофемы.
Теорема 1.
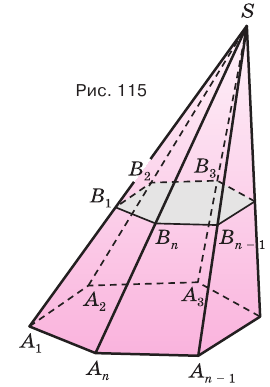
Если пирамиду пересечь плоскостью, параллельной основанию, то:
- а) боковые ребра и высота разделяются на пропорциональные части;
- б) в сечении получается многоугольник, подобный основанию;
- в) площади сечения и основания относятся как квадраты их расстояний от вершины пирамиды.
Используя рисунок 115, докажите эту теорему самостоятельно.
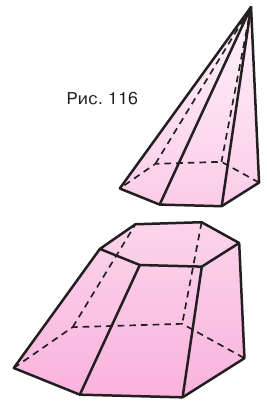
Секущая плоскость, параллельная основанию пирамиды, разделяет ее на две части (рис. 116). Одна из этих частей также является пирамидой, а другая — многогранником, который называется усеченной пирамидой.
Параллельные грани усеченной пирамиды называются ее основаниями (рис. 117). Основания усеченной пирамиды — подобные многоугольники, стороны которых попарно параллельны, поэтому ее боковые грани являются трапециями.
Высотой усеченной пирамиды называется перпендикуляр, проведенный из какой-либо точки одного основания пирамиды к плоскости другого основания.
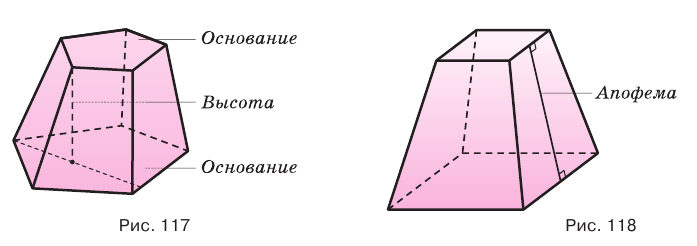
Усеченная пирамида называется правильной, если она является частью правильной пирамиды. Высота боковой грани правильной усеченной пирамиды называется апофемой усеченной пирамиды. На рисунке 118 показана четырехугольная правильная усеченная пирамида и одна из ее апофем.
Теорема 2.
Боковая поверхность правильной усеченной пирамиды равна произведению полусуммы периметров ее оснований и апофемы:
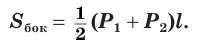
Доказательство:
Пусть есть правильная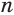 
-угольная усеченная пирамида (рис. 119). Пусть 
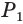и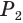 
— соответственно периметры нижнего и верхнего оснований и 
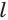— апофема пирамиды.
Боковая поверхность данной пирамиды состоит из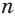 
равных трапеций. Пусть 
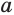и 
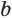— основания одной из этих трапеций, тогда ее площадь равна 
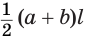. Учитывая, что боковая поверхность пирамиды состоит из 
таких трапеций, получим, что
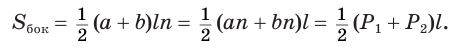
Теперь установим формулу для вычисления объема пирамиды.
Тела, имеющие равные объемы, называются равновеликими.
Теорема 3.
Треугольные пирамиды с равновеликими основаниями и равными высотами равновелики.
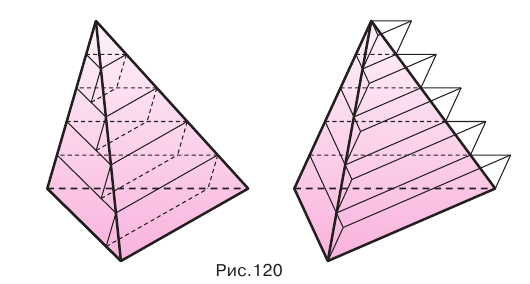
Доказательство:
Пусть есть две треугольные пирамиды с равновеликими основаниями и равными высотами (рис. 120). Разделим высоты одной и другой пирамид на 
долей и через точки деления проведем плоскости, параллельные основаниям. Этим самым пирамиды разделяются на 
частей. Для каждой части первой пирамиды построим наибольшие по объему призмы, целиком содержащиеся в пирамиде, а для каждой части другой пирамиды — наименьшие по объему призмы, целиком содержащие эту часть.
Пусть 
и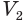 
— объемы первой и второй пирамид, a 
и 
— суммарные объемы призм, построенных для этих пирамид. При счете от оснований пирамид призма в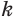 
-й части первой пирамиды равновелика призме для 
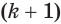-й части второй пирамиды, так как у этих призм равновелики основания и равные высоты. Поэтому объем больше объема на объем первой призмы, у которой основанием является основание второй пирамиды, а высота равна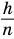 
, где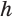 
— высота пирамиды (см. рис. 120), т.е. 
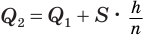, или 
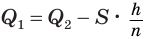, где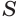 
— площадь основания пирамиды. Теперь учтем, что 
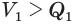, a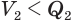 
. Поэтому 
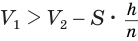, или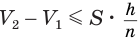 
. При увеличении значения переменной 
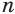значение выражения 
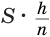стремится к нулю, а это означает, что 
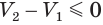, или
Такие же рассуждения можно провести, если первую и вторую пирамиды поменять ролями. В результате получим неравенство
Из неравенств (1) и (2) следует, что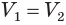 
.
Теорема 4.
Объем пирамиды равен третьей доле произведения площади ее основания и высоты:
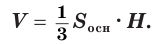
Доказательство:
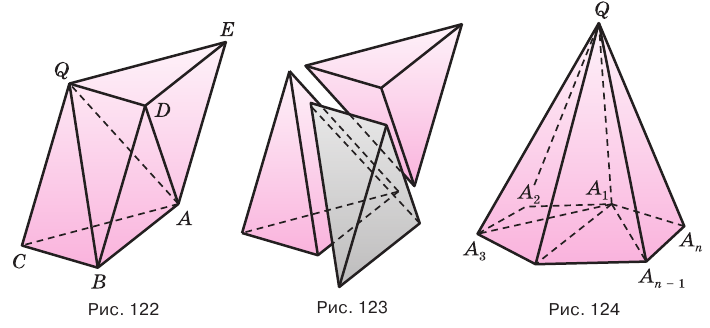
Пусть есть треугольная пирамида 
(рис. 121). Достроим ее до призмы 
с основанием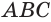 
(рис. 122). Отделим от призмы данную пирамиду, получится четырехугольная пирамида 
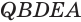(рис. 122 и 123). Диагональная плоскость 
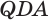разделяет ее на две пирамиды 
и 
, у которых одна и та же высота, проведенная из вершины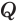 
, и равные основания 
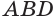и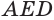 
. Поэтому, в соответствии с теоремой 3, пирамиды и равновелики. Сравним пирамиду с данной пирамидой . У них равные основания 
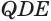и 
и высоты, проведенные из вершин 
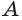и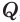 
, поэтому эти пирамиды также равновелики. Получается, что все три пирамиды , и равновелики. Поскольку объем призмы равен произведению 
площади 
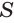основания и высоты призмы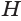 
, которая равна высоте пирамиды , то объем пирамиды , т. е. третьей части призмы , равен третьей доле этого объема, т. е.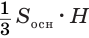 
.
Пусть теперь есть произвольная пирамида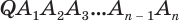 
(рис. 124). Через диагонали 
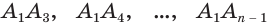основания 
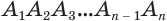, выходящие из одной вершины 
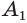, проведем диагональные сечения, они разделят данную пирамиду на треугольные пирамиды 
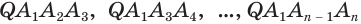. Поскольку все они имеют общую высоту 
, то
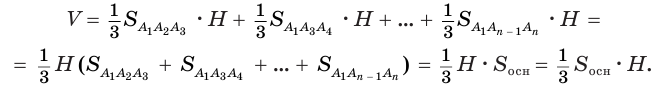
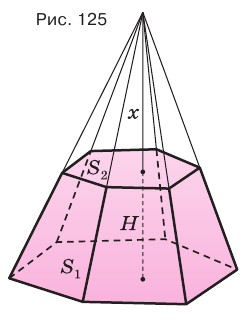
Пример:
Найдем объем усеченной пирамиды, нижнее и верхнее основания которой имеют площад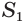и 
и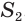 
, а высота равна (рис. 125).
Для этого достроим данную усеченную пирамиду до полной. Пусть высота дополнительной пирамиды равна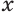 
. Искомый объем 
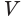можно найти как разность объемов полной и дополнительной пирамид:
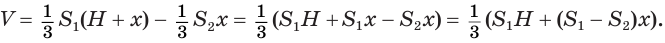
Чтобы найти высоту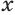 
, используем установленное в теореме 1 утверждение о том, что площади сечений пирамиды относятся как квадраты их расстояний от вершины:
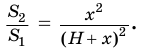
Решим это уравнение, учитывая, что 
и 
— положительные числа:
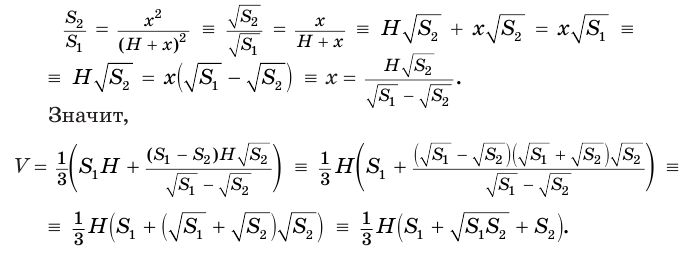
Таким образом, объем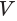 
усеченной пирамиды равен третьей доле произведения высоты 
пирамиды и суммы площадей и оснований пирамиды и их среднего геометрического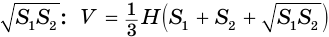 
.
- Конус в геометрии
- Сфера в геометрии
- Шар в геометрии
- Правильные многогранники в геометрии
- Возникновение геометрии
- Призма в геометрии
- Цилиндр в геометрии
- Стереометрия – формулы, определение и вычисление
В данной публикации мы рассмотрим, как можно вычислить площадь поверхности различных видов правильных пирамид: треугольной, четырехугольной и шестиугольной.
Правильная пирамида – это пирамида, вершина которой проецируется в центр основания, являющегося правильным многоугольником.
-
Формула площади правильной пирамиды
- 1. Общая формула
- 2. Площадь правильной треугольной пирамиды
- 3. Площадь правильной четырехугольной пирамиды
-
4. Площадь правильной шестиугольной пирамиды
Формула площади правильной пирамиды
1. Общая формула
Площадь (S) полной поверхности пирамиды равняется сумме площади ее боковой поверхности и основания.
Sполн. = Sбок. + Sосн.
Боковой гранью правильной пирамиды является равнобедренный треугольник.
Площадь треугольника вычисляется по формулам:
1. Через длину основания (a) и высоту (h):
2. Через основание (a) и боковую сторону (b):
Формула площади основания правильной пирамиды зависит от вида многогранника. Далее мы рассмотрим самые популярные варианты.
2. Площадь правильной треугольной пирамиды
Основание: равносторонний треугольник.
L (апофема) – перпендикулярная линия, опущенная из вершины пирамиды на ребро основания. Т.е. апофема пирамиды является высотой (h) ее боковой грани.
3. Площадь правильной четырехугольной пирамиды
Основание: квадрат.
| Площадь | Формула |
| основание | Sосн. = a2 |
| боковая поверхность | Sбок. = 2aL |
 |
|
| полная | Sполн. = a2 + 2aL |
 |
microexcel.ru
4. Площадь правильной шестиугольной пирамиды
Основание: правильный шестиугольник
