Задача о теплице, входит в первые пять заданий огэ по математике, и является практико-ориентированной задачей. Сложность данной задачи заключается в том, что в 5 задании требуется найти приближенное значение арифметического квадратного корня, и попасть в интервал ответов.
Вот текст задачи:
По этому тексту, нужно ответить на 5 вопросов.
1) Какое наименьшее количество дуг, нужно нужно заказать, чтобы расстояние между соседними дугами было не более 70 см.
Из первого предложения текста задачи, мы узнаем, что длина теплицы составляет 6 метров. Поэтому, первым делом находим количество интервалов, между дугами.
Теперь найдем, сколько будет дуг. Количество дуг = количество интервалов +1 = 9+1 = 10 дуг. Ответ 10
2) Сколько упаковок плитки необходимо купить для дорожек между грядками, она продается в упаковках по 14 штук?
Для этого вопроса, информация в тексте задачи дана в последнем предложении “Между грядками будут дорожки шириной 50 см, для которых необходимо купить тротуарную плитку размером 25х25”
Поскольку у нас ширина дорожки 50 см, а ширина плитки 25 см, то в ширину дорожки можно уложить 2 плитки. Длина у нас 6 метров, что составляет 600 см, поэтому в длину уместится 24 плитки. Тогда во всей дорожке будет 48 плитки. а в двух дорожках 96 штук.
Расчет количества упаковок приведен ниже.
3) Найдите ширину теплицы. Ответ дайте в метрах до сотых.
Ширина теплицы – это отрезок АD. Поскольку теплица состоит из дуг, то АD- это диаметр окружности.
Диаметр окружности связан с длиной окружности следующей формулой:
В этой формуле, L-длина окружности, D- диаметр окружности, “пи”=3,14
Длину окружности, найдем из следующей информации: “….металлические дуги в форме полуокружности длиной 5,53 метра….”
Поскольку известна длина полуокружности – 5,53 м, то длина окружности равна:
Из этих расчетов получаем, что ширина теплицы (с округлением до сотых) равна 3,52
4) Найти ширину центральной грядки, если она в два раза больше ширины узкой грядки. Ответ дайте до десятков, с точностью до десятков.
Для ответе на этот вопрос, сделаем схематический чертеж:
В этой задаче, за Х взяли ширину узкой грядки. Тогда широкая грядка будет 2Х. В задаче у нас две дорожки, что показано на схеме, которые составляю по 50 см.
По схеме составим уравнение:
Поскольку в задаче написано условие, что результат нужно округлить до десятков, поэтому получаем ответ 130.
5)Найти высоту входа в теплицу. Ответ дайте в сантиметрах.
Для расчета высоты теплицы, нам необходимо сделать дополнительные построения. Проводим ОС1. Получаем прямоугольный треугольник, ОС1С. Дальше по теореме Пифагора, выразим СС1. Для этой задачи, покажу три разных варианта завершения задачи.
Первый вариант:
При таком решении, получаем неизвлекаемый корень из 3. На экзамене, хорошо, что хоть кто нибудь вспомнит, что примерно он равен 1,7. Но такого значения не достаточно, поскольку мы получаем, что высота входа равна 149,6. Но такой ответ нас не устраивает, поскольку верный ответ находится в интервале от 150-160 см
Поэтому в этой задаче, чем точнее ответ, тем больше вероятность, что ответ будет не верный, не попадете в интервал правильного ответа.
Второй вариант:
В этом варианте, мы не будем раскладывать числа до последнего множителя, а будем раскладывать число на множители таким образом, что бы получилось приближенное число из таблицы квадратов. В этом случае, 23232 можно поделить на 16 (признак делимости на 4, если последние два числа делятся на 4)
Как видите, оба ответа, 152 и 156 подходят под наш интервал решения.
Третий вариант: воспользуемся канадской формулой вычисления приближенного значения квадратного корян.
Как видим, эту формулу. так же можно использовать для решения этой задачи.
Вы меня очень поддержите, если поставите лайк и подпишитесь на мой блог.
Найдите примерную ширину MN теплицы в метрах. Число π возьмите равным 3,14. Результат округлите до десятых.
Требуется: найти примерную ширину MN теплицы в метрах
Дано: теплица, её длина = 4.5 метров.
Ширина: диаметр полукруга металлической дуги = 5.2 метров.
Число π = 3,14. Результат округлить до 1 числа после запятой.
Виртуальная окружность или две дуги = 5.2 х 2 = 10.4
Диаметр или ширина теплицы равна 10.4/π = 10.4/3.14 = 3.31
Округляем до десятой получается, что MN теплицы в метрах = 3.3 метра.
Можно и площадь вычислить, но это в следующем вопросе.
автор вопроса выбрал этот ответ лучшим
Tanyetta
[298K]
11 месяцев назад
Данная задача, является достаточно актуальной, ведь сейчас начинается дачный период и каждый дачник, что-то докупает для своего садового участка. Нам предстоит решить математическую задачку, чтобы определить ширину MN теплицы в метрах. Из условия задачи нам известно, что Алексей Юрьевич решил приобрести на свою любимую дачу теплицу длиной 4,5 метра и для этого, он уже сделал прямоугольный фундамент. Далее Алексей Юрьевич заказывает металлические дуги в форме полуокружностей, длина которых составляет 5,2 метра каждая и пленку для обтягивания теплицы.
- 5,2 * 2 = 10,4 (метров) – составляет окружность двух дуг.
- L = 2пR = пD, L = 10,4/3,4=3,31 (метр) – ширина теплицы.
Ответ: 3,3 метра составляет ширина теплицы.
Пашенька
[189K]
более года назад
Планируя строить теплицу, Алексей Юрьевич решил, что она должна быть полукруглой. Мне кажется, что это не самый лучший вариант, но не мне судить хозяина теплицу. По условию нам дана длина теплицу, а также нам известна длина дуги – 5.2 м.
- Зная длину дуги, можно подсчитать длину окружности:
5.2х2=10.4 – м – длина окружности.
- Теперь мы знаем длину окружности, поэтому из формулы L=2пR мы можем вывести значение значение диаметра
- L = пД, Д = L/п, Д = 10.4/3,4=3,31=3,3 – метра.
Ответ: 3.3
Niki M
[390K]
более года назад
Чем больше теплица в пересчете на квадратный метр, тем дешевле она получается.
В зависимости от местоположения и использования существуют разные типы теплиц: теплицы, односкатные теплицы и политоннели.
Классический вариант – отдельно стоящая теплица.
Что мы имеем по задаче:
4.5 – длина.
5.2 – ширина дуги – у нас их две.
5.2х2=10.4
Далее решаем по формуле:
Росинка Роса
[474K]
более года назад
Примерная ширина теплицы вычисляется по формуле длины окружности.
Для решения задачи у нас есть необходимые и избыточные данные.
Избыточными являются сведение о длине теплицы, а также о ее фундаменте.
Необходимое сведение – длина дугового пролета в форме полуокружности.
Если длина полуокружности известна, умножим ее на 2 и получим длину окружности, в которой диаметр и будет шириной нашей теплицы.
Производим вычисления:
5,2 Х 2 = 10,4
Это число нам надо разделить на число ПИ (3.14) и получим искомый диаметр, он же – ширина теплицы, которую героически самостоятельно возводит на своем дачном участке Алексей Юрьевич.
10,4 : 3,14 = 3,31
Округляем до десятых долей
3,3 метра.
Знаете ответ?
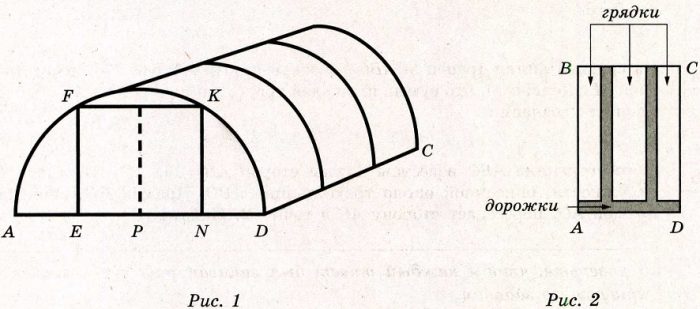
Глеб Сергеевич начал строить на дачном участке теплицу длинной 5 метров (DC на рис. 1). Для этого он сделал прямоугольный фундамент (рис. 2). Для каркаса теплицы нужно заказать металлические дуги в форме полуокружностей длиной 6 м каждая и покрытие для обтяжки теплицы. Отдельно требуется купить плёнку для передней и задней стенок теплицы. В передней стенке планируется вход, показанный на рис. 1 прямоугольником ЕFКN, где точки Е, Р и N делят отрезок АD на равные части. Внутри теплицы Глеб Сергеевич планирует сделать три грядки, как показано на рис. 2. Между грядками и при входе в теплицу будут дорожки шириной 40 см, для которых надо купить тротуарную плитку размером 20×20 см.
Источник: ОГЭ Ященко 2023 (36 вар)
Задание 1
Какое наименьшее количество дуг нужно заказать, чтобы расстояние между соседними дугами было не более 70 см?
Решение:
Длинна теплицы 5 метров = 500 см. Наименьшее количество дуг по 70 см:
500/70 ≈ 7,1..
Значит минимум 8 дуг, и плюс ещё одна дуга в самом начале теплицы от которой отступали по 70 см. Всего дуг:
8 + 1 = 9
Ответ: 9.
Задание 2
Найдите ширину теплицы в метрах с точностью до десятых.
Решение:
Знаем, что длина дуги полуокружности равна 6 м, шириной теплицы является диаметр AD:
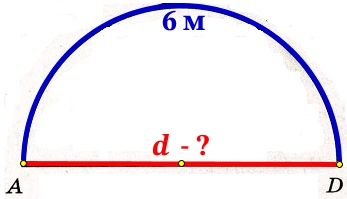
Длина всей окружности равна:
6·2 = 12 метров
Формула длины окружности из справочного материала:
l = 2πR
Радиус равен половине диаметра:
R=frac{d}{2}
Подставим в формулу:
l=2pifrac{d}{2}=pi d
Найдём диаметр и округлим до десятых:
12 = 3,14·d
d = 12/3,14 ≈ 3,82.. ≈ 3,8 м
Ответ: 3,8.
Задание 3
Сколько нужно купить упаковок плитки для дорожек, если в каждой упаковке 8 штук?
Решение:*
По условию ширина дорожек равна 40 см. Длина нижней дорожки, равна ширине теплицы AD = 3,8 м = 380 см. Длины двух других дорожек равны длине теплицы DC = 5 м = 500 см:
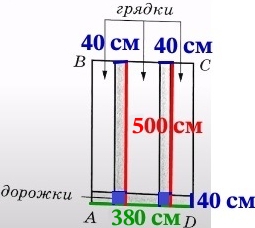
Найдём общую площадь всех трёх дорожек:
40·380 + 40·500 + 40·500 = 40·(380 + 500 + 500) = 40·1380 = 55200 см2
Дорожки пересекаются, площадь двух квадратов посчитали дважды, вычтем их:
55200 – 40·40 – 40·40 = 52000 см2
Площадь одной тротуарной плитки равна 20х20 см:
20·20 = 400 см2
Найдём сколько нужно купить:
52000/400 = 130 плиток
В одной упаковке 8 плиток, значит надо купить:
130/8 = 16,25
Такое количество упаковок нам не продадут, значит надо брать минимум 17 упаковок.
Ответ: 17.
Задание 4
Найдите площадь участка внутри теплицы, отведённого под грядки, в квадратных метрах. Результат округлите до десятых.
Решение:*
Теплица имеет длину 5 метров и ширину 3,8 метров, найдём её площадь:
S▭ = 5·3,8 = 19 м2
Площадь отведённая в теплице под дорожки равна 52000 см2 (задание 3), переведём в м2 (1 м2 = 1м·1м = 100см·100см = 10000см2):
52000/10000 = 5,2 м2
Вся остальная площадь теплицы будет занята грядками, найдём её:
19 – 5,2 = 13,8 м2
Ответ: 13,8.
Задание 5
Найдите высоту ЕF входа в теплицу в сантиметрах с точностью до целого.
Решение:
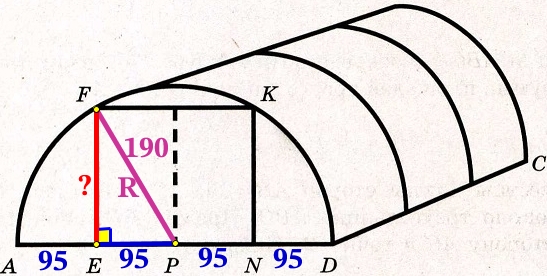
По условию отрезок AD поделен на 4 равные части, AD = ширина = 3,8 м = 380 см. Каждый отрезок тогда равен:
380/4 = 95 см
PF – это радиус, найдём его длину:
R=PF=frac{d}{2}=frac{380}{2}=190
Высотой входа в теплицу является EF, по теореме Пифагора, найдём:
EP2 + EF2 = PF2
952 + EF2 = 1902
EF2 = 1902 – 952 = 36100 – 9025 = 27075
EF = √27075
Корень не извлекается. Приходится подбирать, сколько примерно это сантиметров.
1652 = 27225
1642 = 26896
К нашему числу 27075, наиболее близко расположено 165 см, его я и запишу в ответ.
По ответам сборника, будет верный любой ответ в диапазоне 161 – 168 см.
Ответ: 165.
Есть три секунды времени? Для меня важно твоё мнение!
Насколько понятно решение?
Средняя оценка: 4.7 / 5. Количество оценок: 214
Оценок пока нет. Поставь оценку первым.
Новости о решённых вариантах ЕГЭ и ОГЭ на сайте ↙️
Вступай в группу vk.com 😉
Расскажи, что не так? Я исправлю в ближайшее время!
В отзыве оставь любой контакт для связи, если хочешь, что бы я тебе ответил.
Рассмотрим первые пять задач Варианта 16 из ОГЭ. Математика: типовые экзаменационные варианты:36 вариантов /под ред . И.В. Ященко на нахождение неизвестных величин теплицы.
Сергей Петрович решил построить на дачном участке теплицу длиной 6 м. Для этого он сделал прямоугольный фундамент. Для каркаса теплицы Сергей Петрович заказал металлические дуги в форме полуокружностей длиной 5 м каждая и покрытие для обтяжки.
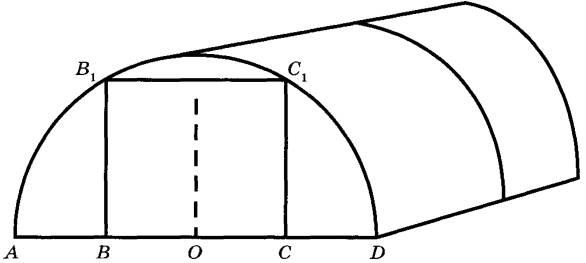
Отдельно требуется купить плёнку для передней и задней стенок теплицы. В передней стенке планируется вход, показанный на рисунке прямоугольником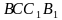 
, где точки B, O и C делят отрезок AD на четыре равные части. Внутри теплицы Сергей Петрович планирует сделать три грядки по длине теплицы — одну центральную широкую грядку и две узкие грядки по краям. Между грядками будут дорожки шириной 50 см, для которых необходимо купить тротуарную плитку размером 25 см х 25 см.
Задание 1. Какое наименьшее количество дуг нужно заказать, чтобы расстояние между соседними дугами было не более 80 см?
Решение.
Длина теплицы 6 м = 600 см. Разделим эту длину на 80 см и округлим результат до ближайшего наибольшего целого, получим:
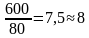
то есть, нужно заказать 8 дуг + 1 первая дуга = 9 дуг.
Ответ: 9.
Задание 2. Сколько упаковок плитки необходимо купить для дорожек между грядками, если она продаётся в упаковках по 10 штук?
Решение.
В теплице 3 грядки, между которыми будут две дорожки. Длина каждой дорожки равна длине теплицы – 600 см, а ширина – 50 см.
Площадь одной дорожки 600∙50 = 30 000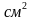 
,
тогда площадь двух дорожек 2∙30 000 = 60 000 .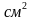
Тротуарная плитка имеет размеры 25х25 см площадь одной плитки 625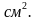
Найдем сколько плиток необходимо для дорожек
площадь двух дорожек : площадь одной плитки
60 000:625 = 96 плиток
Так как плитки продаются в упаковках по 10 штук, то необходимо купить
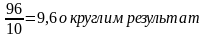
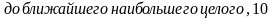упаковок
Ответ: 10.
Задание 3. Найдите ширину теплицы. Ответ дайте в метрах с точностью до десятых.
Решение.
Ширина теплицы определяется диаметром полуокружности длиной 5 метров. Для вычисления радиуса такой полуокружности можно воспользоваться формулой длины окружности L=2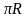
. Нам дана длина полуокружности =5м, следовательно
полная длина окружности будет 10м. Подставим
2*3,14R=10
R=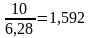
ширина теплицы равна диаметру , поэтому 2*1,592=3,184.
Ответ дать в метрах с точностью до десятых 3,2 м.
Ответ: 3,2.
Задание 4. Найдите ширину узкой грядки, если ширина центральной грядки относится к ширине узкой грядки как 5:3. Ответ дайте в сантиметрах с точностью до десятков.
Решение.
Условно представим теплицу с грядками: две по краям с шириной 3x см и одна центральная с шириной в 5х см. Между ними дорожки шириной 50 см.
|
3х |
50 |
5х |
50 |
3х |
Учитывая, что вся ширина теплицы примерно 3,2 м = 320 см, получаем уравнение:
3х+50+5х+50+3х=320,
11х=320-50-50,
Х=220/11
Х=20. Найдите ширину узкой грядки 3х=3*20=60 см.
Ответ: 60.
Задание 5. Сколько квадратных метров пленки необходимо купить дл передней и задней стенок, если с учетом крепежа ее нужно брать с запасом 15% ? Ответ округлите до десятых.
Решение. Ширина теплицы 3,2 м , а радиус 1,6 м
Так как передние и задние части стенок теплицы являются полуокружностями ,то вместе они образуют круг. Площадь круга S=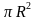
= 3,14*
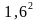= 8,0384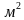 
С учетом крепежа ее нужно брать с запасом 15%
8,0384+0,15*8,0384=9,24416 Ответ округлите до десятых 9,2
Ответ: 9,2
ОГЭ 2020 ЗАДАНИЯ 1 – 5 (ТЕПЛИЦА)
Прочитайте внимательно текст и выполните залдания 1 — 5.
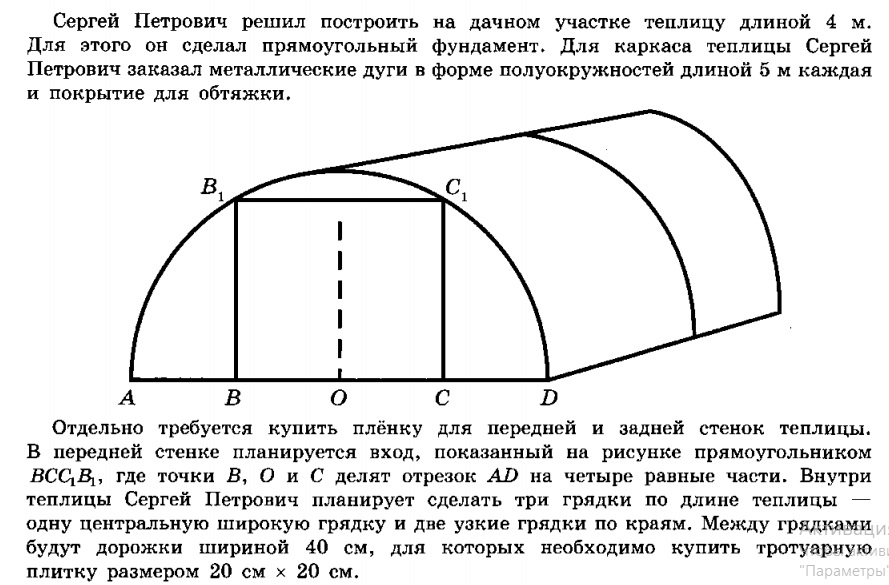
Задание 1 (ОГЭ 2020)
Какое наименьшее количество дуг нужно заказать, чтобы расстояние между соседними дугами было не более 60 см?
Решение: Длина теплицы составляет 4 м = 400 см. Рассчитаем количество дуг для теплицы, соблюдая условие: расстояние между соседними дугами меньше или равно 60 см. Разделим 400 на 60. Получится 6 дуг и в остатке 40 см. Учитывая две крайние дуги, получается:6 + 2 = 8 (дуг).
Ответ: 8.
Задание 2 (ОГЭ 2020)
Сколько упаковок плитки необходимо купить для дорожек между грядками, если она продается в упаковках по 6 штук?
Решение: Из условия задачи имеем, что грядок в теплице планируется 3. Дорожек будет 2. Длина дорожки совпадает с длиной теплицы, то есть 4 м = 400 см. Ширина дорожки – 40 см. Найдем площадь двух дорожек. 2 * 40 * 400 = 32000 (кв. см).
Площадь одной плитки: 20 * 20 = 400 (кв. см).
32000 : 400 = 80 (штук) плиток нужно купить для двух дорожек.
80 : 6 = 13 (остаток 2).
Понадобится 13 + 1 = 14 упаковок плитки.
Ответ: 14.
Задание 3 (ОГЭ 2020)
Найдите ширину теплицы. Ответ дайте в метрах с точностью до десятых.
Решение:
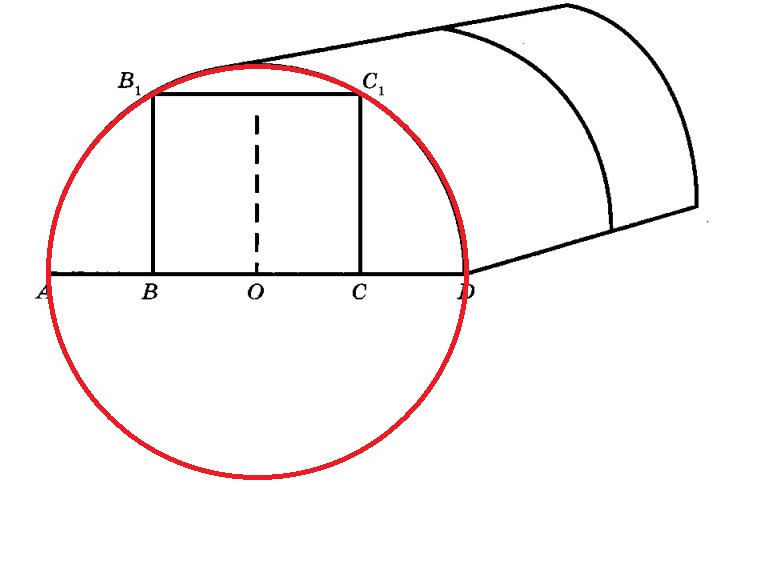
Дуги для теплицы имеют форму полуокружности. Чтобы найти ширину теплицы, нужно достроить окружность и найти радиус окружности OD.
Ширина теплицы AD является диаметром окружности. AD = 2 * OD.
Длина дуги теплицы равна 5 м и вычисляется по формуле П * OD (это длина полуокружности).
OD = 5 : 3,14 = 1,6 (м).
AD = 2 * OD = 2 * 1,6 = 3,2 (м).
Ответ: 3,2.
Задание 4 (ОГЭ 2020)
Найдите ширину центральной грядки, если она в два раза больше ширины узкой грядки. Ответ дайте в сантиметрах с точностью до десятых.
Решение: Ширина теплицы 3,2 м = 320 см. В теплице есть 2 дорожки по 40 см и три грядки. Пусть ширина узкой грядки х см, тогда широкой грядки – 2х см.
Составим уравнение 2х + х + х + 2 * 40 = 320 и решим его.
4х + 80 = 320,
4х = 320 – 80,
4х = 240,
х = 60 (см) – ширина узкой грядки.
Найдем ширину центральной грядки (широкой). 2х = 2 * 60 = 120 (см).
Ответ: 120.
Задание 5 (ОГЭ 2020)
Найдите высоту входа в теплицу. Ответ дайте в сантиметрах.
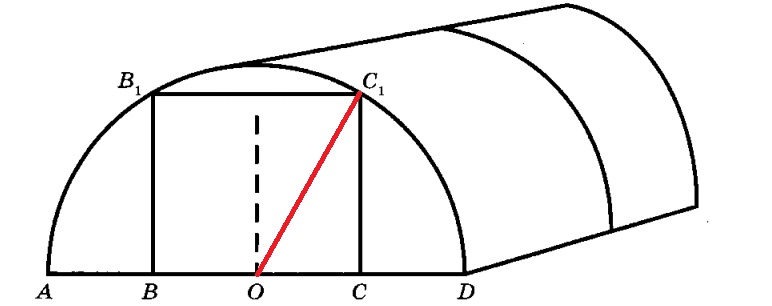
Чтобы найти высоту входа в теплицу,нужно рассмотреть прямоуголный треугольник OC1A. Применив теорему Пифагора, вычислим высоту CC1 теплицы.
По условию AB = BO = OC = CD = 320 см : 4 = 80 см.
ОС1 = OD = 160 см – радиусы.
По теореме Пифагора имеем: СС1 = 80√3 см = 136 см.
Ответ: 136.
