Как найти ширину параллелепипеда
Объемная геометрическая фигура, состоящая из шести граней, каждая из которых — параллелограмм, называется параллелепипедом. Его разновидности: прямоугольный, прямой, наклонный и куб. Осваивать вычисления лучше на примере прямоугольного параллелепипеда. В такой форме сделаны некоторые упаковочные коробки, шоколадные конфеты и т.д. Здесь все грани — прямоугольники.

Инструкция
Запишите исходные данные. Пусть известен объем параллелепипеда V = 124 см³, его длина a = 12 см и высота с = 3 см. Надо найти ширину b. На практике длина измеряется по самой длинной стороне, высота — вверх от основания. Чтобы не запутаться, положите небольшую коробку — например, спичечный коробок — на стол. Длину, высоту и ширину измеряйте от одного и того же угла.
Вспомните формулу, в которую входит неизвестная величина и все или некоторые из известных. В данном случае V = a * b * c.
Выразите неизвестную величину через остальные. По условию задачи надо найти b = V / (a * c). Когда выводите формулу, проверяйте, правильно ли расставлены скобки, в случае ошибок результат вычислений будет неверным.
Убедитесь, что исходные данные представлены в одном виде. Если это не так, преобразуйте их. Если бы на первом шаге было написано a = 0,12 м, эту величину пришлось бы перевести в см, потому что в таком виде представлены остальные размеры параллелепипеда. Важно помнить, что 1 м = 100 см, 1 см = 100 мм.
Решите задачу, подставив в результат третьего шага числовые значения — с учетом поправок, выполненных на четвертом шаге. b = 124 / (12 * 3) = 124 / 36 = 3,44 см. Результат получается примерный, потому что пришлось округлить значение до двух знаков после запятой.
Сделайте проверку, используя формулу второго шага. V = 12 * 3,44 * 3 = 123,84 см³. По условию задачи V = 124 см³. Можно сделать вывод, что решение правильное, потому что на пятом шаге результат округлялся.
Видео по теме
Обратите внимание
Чтобы уверенно решать подобные задачи, тренируйтесь несколько раз. Для этого на первом шаге берите разные числовые значения.
Полезный совет
Если имеете дело с прямым, наклонным параллелепипедом или кубом, на втором шаге возможно применение других формул. Откройте учебник математики и найдите подходящий вариант.
Источники:
- Объем параллелепипеда
Войти на сайт
или
Забыли пароль?
Еще не зарегистрированы?
This site is protected by reCAPTCHA and the Google Privacy Policy and Terms of Service apply.
Измерения прямоугольного параллелепипеда и его свойства
Содержание:
- Что такое прямоугольный параллелепипед — определение
- Свойства параллелепипеда, какими обладают противолежащие грани
- Формулы вычисления объема и площади поверхности прямоугольного параллелепипеда
- Как найти диагональ и ширину прямоугольного параллелепипеда
Что такое прямоугольный параллелепипед — определение
Определение
Параллелепипед — это призма с шестью гранями, в основании которой лежит параллелограмм.
Согласно другому определению, это многогранник, состоящий из шести сторон-параллелограммов.
В математике в целом, и в геометрии в частности, выделяют несколько основных видов параллелепипеда:
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
- прямоугольный;
- прямой — параллелепипед, у которого 4 боковые грани являются прямоугольниками;
- наклонный — боковые грани объемной фигуры не перпендикулярны основаниям;
- ромбоэдр — шестигранная призма, грани которой — это ромбы;
- куб — состоит из квадратных граней.
Определение
Прямоугольный параллелепипед — это шестигранная призма, каждая из сторон которой в общем случае является прямоугольником. Также это — многогранник, в основании которого лежит прямоугольник, а боковые грани перпендикулярны основанию.
Прямоугольных параллелепипедов в окружающем человека мире множество: комната, закрытая книга, системный блок компьютера, закрытая коробка для подарка, спичечный коробок и т. д.
Прямоугольный параллелепипед, как и любой другой, состоит из:
- основания;
- граней — противоположных, т. е. не имеющих общего ребра, и смежных — тех, которые имеют общее ребро;
- ребер — отрезков, соединяющих соседние вершины объемной шестигранной фигуры;
- диагоналей — отрезков, соединяющих противоположные вершины;
- диагоналей граней;
- высоты — отрезка, соединяющего верхнее и нижнее основания шестигранной призмы.
В некоторых базовых задачах просят найти количество составляющих элементов шестигранной призмы. Эти числа можно запомнить: объемная фигура состоит из 8 вершин, 12 ребер и 6 граней.
Определение
Измерениями прямоугольного параллелепипеда называют его длину, ширину и высоту.
Свойства параллелепипеда, какими обладают противолежащие грани
Вне зависимости от вида параллелепипеда, все они обладают 4 свойствами:
- Противолежащие грани равны друг другу и попарно параллельны.
- Все 4 диагонали шестигранника пересекаются в одной точке, которой делятся пополам. Любой отрезок, проходящий через середину диагонали, и концы которого принадлежат поверхности, также делится пополам.
- Фигура симметрична относительно середины диагонали.
- Квадрат длины диагонали равен сумме квадратов трех измерений.
Прямоугольный параллелепипед обладает всеми этими свойствами и несколькими специфичными, свойственными только ему.
- Все стороны — прямоугольники.
- Все углы, состоящие из двух граней, равны 90°.
- Любую сторону можно принять за основание.
- Если все ребра равны и перпендикулярны, то такой шестигранник считается кубом.
Формулы вычисления объема и площади поверхности прямоугольного параллелепипеда
Определение
Объем прямоугольного параллелепипеда равен длине, умноженной на ширину и высоту.
(V=acdot bcdot h,)
где V — объем, a — длина, b — ширина, h — высота.
Примечание
Площадь боковой поверхности равна сумме площадей боковых граней.
(S_{бп}=2(ab+ac))
Примечание
Площадь полной поверхности равна сумме площадей боковых граней и оснований.
(S_{пп}=2(ab+bc+ac))
Как найти диагональ и ширину прямоугольного параллелепипеда
В соответствии с одним из основных свойств параллелепипеда, квадрат длины диагонали равен сумме квадратов трех измерений. Запишем в виде формулы:
(d^2=a^2+b^2+c^2)
Следовательно, длина диагонали равна квадратному корню из суммы трех измерений фигуры:
(sqrt{a^2+b^2+c^2})
Длина, ширина и высота, как правило, вычисляются через формулу объема:
(a=frac V{bh},;b=frac V{ah},;h=frac V{ab})
Существует и второй вариант, как возможно найти одно из измерений. Если известно смежное ему измерение и диагональ общей стороны шестигранника, то можно вычислить вторую сторону через теорему Пифагора или по свойствам диагонали.
Представление о том, что такое прямоугольный параллелепипед, все имеют еще с детства, когда играли в кубики, держали в руках такие предметы, как коробка из-под сока или из- под конфет, видели аквариум такой формы. В жизни мы постоянно сталкиваемся с предметами, которые представляют собой прямоугольный параллелепипед (рисунок 1).

Рисунок 1
Определение
Прямоугольный параллелепипед – это шестигранник, у которого все грани являются прямоугольниками. Грань – плоская поверхность предмета, составляющая угол с другой такой же поверхностью. Основания параллелепипеда – это его верхняя и нижняя грани.
Так, на рисунке 2 показан прямоугольный параллелепипед ABCDEFGH. Он имеет 6 граней, основаниями являются грани ABCD и EFGH.
У параллелепипеда есть вершины, их 8. Они обозначены заглавными латинскими буквами. Также у прямоугольного параллелепипеда есть 12 ребер – это стороны граней: AB, BC, CD, AD, EF, FG, HG, EH, AE, BF, CG, HD.
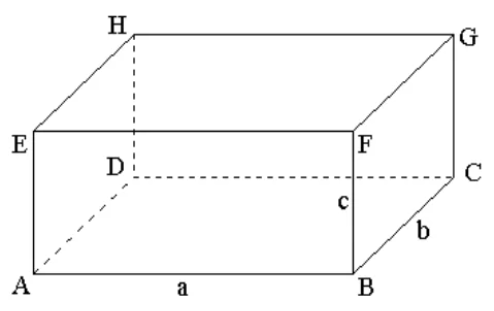
Рисунок 2
Противоположные (не имеющие общих вершин) грани прямоугольного параллелепипеда равны.
Длина, ширина, высота
Прямоугольный параллелепипед имеет три измерения – длину (а), ширину (b) и высоту (c) – рисунок 3. Зная эти измерения, можно найти не только площадь каждой грани, но и площадь всей поверхности прямоугольного параллелепипеда.
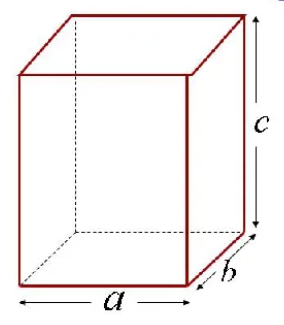
Рисунок 3
Так как каждая грань параллелепипеда – это прямоугольник, то для нахождения площади любой грани надо умножить длину и ширину этих граней, т.е S=ab, S=bc, S=ac.
Для нахождения площади поверхности прямоугольного параллелепипеда надо сложить площади всех граней, то есть S поверхности = ab+bc+ac+ab+bc+ac. Так как противоположные грани равны, то их площади тоже равны, значит S поверхности = 2ab+2bc+2ac. Это действие можно записать короче, вынося 2 за скобки, как общий множитель, то есть S поверхности = 2(ab+bc+ac). Таким образом, нахождение площади поверхности становится более быстрым.
Куб
Прямоугольный параллелепипед, у которого все измерения равны, называется кубом. Поверхность куба состоит из шести равных квадратов (рисунок 4).
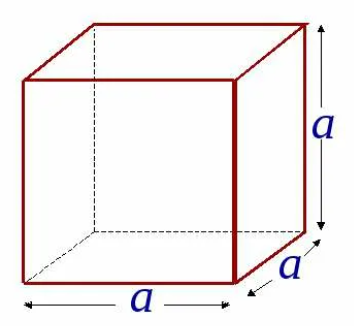
Рисунок 4
Для нахождения площади одной грани достаточно найти площадь квадрата по формуле S=a2. Тогда для нахождения площади поверхности куба надо эту площадь умножить на 6, так как шесть равных граней у куба: S=6a2
Объем прямоугольного параллелепипеда

Рисунок 5
С понятием объема люди встречаются в повседневной жизни ежедневно. Мы наливаем воду в чайник, в ванну, другие жидкости в разные ёмкости – это всё измеряется в определенных единицах и является объемом. Наши шкафы, холодильники и другие подобные предметы – имеют объемы, так как мы их заполняем определенными вещами. На рисунке 5 показаны предметы, которые мы используем и которые имеют определенный объем.
Рассмотрим объемные геометрические фигуры. Так, например, прямоугольный параллелепипед. Рассмотрим рисунок 6, где показано, что параллелепипед состоит из нескольких одинаковых кубиков. Значит, объем данного параллелепипеда равен сумме объемов его кубиков.
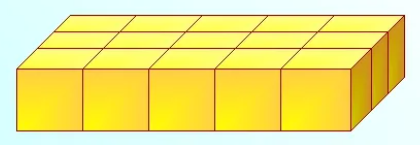
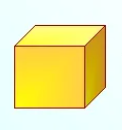
Рисунок 6
За единицу измерения объема выбирают куб, ребро которого равно единичному отрезку. Такой куб называют единичным.
Объем куба с ребром 1 мм называют кубическим миллиметром и записывают 1 мм3; с ребром 1 см – кубическим сантиметром (см3) и так далее. Измерить объем фигуры – значит подсчитать, сколько единичных кубов в ней помещается. Если объем маленького кубика на рисунке 3 принять за единицу, то объем нашего прямоугольного параллелепипеда будет равен 15 кубическим единицам.
Формула объема прямоугольного параллелепипеда
Чтобы найти объем прямоугольного параллелепипеда, надо перемножить три его измерения – длину, ширину и высоту. То есть V=abc (рисунок 4). Зная, что произведение длины и ширины – это есть площадь основания, получим, что V=(ab)h=Sh, где h – высота прямоугольного параллелепипеда. Таким образом, мы получили еще одну формулу для нахождения объема параллелепипеда.
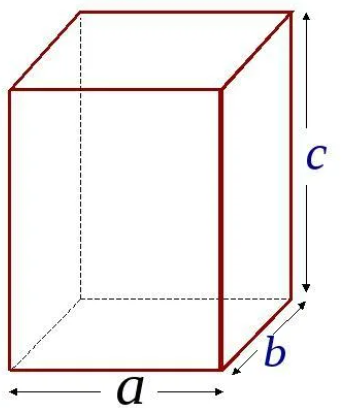
Рисунок 7
Объем куба
Поскольку у куба все ребра равны (рисунок 7), то его объем вычисляется по формуле:
V=a3
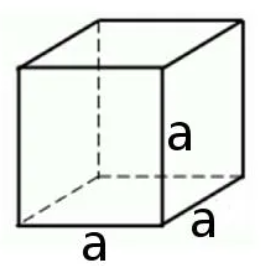
Рисунок 8
Пирамида

Рисунок 9
Прямоугольный параллелепипед является одним из видов многогранников. Также одним из видов многогранника является пирамида, образ которой также известен нам из жизни – из истории и других источников (рисунок 9).
Поверхность пирамиды состоит из боковых граней – треугольников, которые имеют общую вершину, а в её основании могут быть различные многоугольники – треугольник, четырехугольник, пятиугольник и т.д. (рисунок 10).
Рисунок 10
Таким образом, пирамиды можно классифицировать по количеству сторон основания (треугольная, четырехугольная, пятиугольная и т.д.). Если пирамида треугольная (рисунок 11), то её основанием может служить любая грань.
Рисунок 11
Даниил Романович | Просмотров: 967
Длина прямоугольного параллелепипеда равна 18 см, высота 15 см, а объем 3 240 см ^ 3. Найдем ширину данного параллелепипеда
Найдем ширину параллелепипеда
Запишем формулу объема параллелепипеда:
V = a * b * c, где:
- a – длина параллелепипеда;
- b – ширина параллелепипеда;
- c – высота параллелепипеда.
Нам известно, что а = 18 см, с = 15 см, V = 3 240 см ^ 3.
Для того, чтобы найти ширину параллелепипеда, нужно известные значения подставить в формулу объема параллелепипеда и вычислить его значение. То есть получаем:
3240 см ^ 3 = 18 см * b * 15 см;
Решим уравнение 3 240 = 18 * b * 15
3 240 = 18 * 15 * b;
3 240 = 270 * b;
Приведем уравнение к линейному виду. Для этого, перенесем все значения выражения на одну сторону. При переносе значений, их знаки меняются на противоположный знак. То есть получаем:
270 * b – 3240 = 0;
Для того, чтобы решить уравнение, определим какие свойства имеет уравнение:
- Уравнение является линейным, и записывается в виде a * x + b = 0, где a и b – любые числа;
- При a = b = 0, уравнение имеет бесконечное множество решений;
- Если a = 0, b ≠ 0, уравнение не имеет решения;
- Если a ≠ 0, b = 0, уравнение имеет решение: x = 0;
- Если, а и b – любые числа, кроме 0, то корень находится по следующей формуле x = – b/a.
Так как, a = 270 и b = – 3240, тогда находим корень уравнения по формуле x = – b/a.
b = – (- 3240)/270;
Числитель и знаменатель в дроби в правой части выражения сокращаем на 270, тогда получим:
b = – (- 12)/1;
b = – (- 12);
Раскрываем скобки. Так как, перед скобками стоит знак минус, то при ее раскрытии, знаки значений меняются на противоположный знак. То есть получаем:
b = 12;
Отсюда получили, что ширина параллелепипеда равна 12 см.
Как найти ширину параллелепипеда
Объемная геометрическая фигура, состоящая из шести граней, каждая из которых — параллелограмм, называется параллелепипедом. Его разновидности: прямоугольный, прямой, наклонный и куб. Осваивать вычисления лучше на примере прямоугольного параллелепипеда. В такой форме сделаны некоторые упаковочные коробки, шоколадные конфеты и т.д. Здесь все грани — прямоугольники.
Запишите исходные данные. Пусть известен объем параллелепипеда V = 124 см³, его длина a = 12 см и высота с = 3 см. Надо найти ширину b. На практике длина измеряется по самой длинной стороне, высота — вверх от основания. Чтобы не запутаться, положите небольшую коробку — например, спичечный коробок — на стол. Длину, высоту и ширину измеряйте от одного и того же угла.
Вспомните формулу, в которую входит неизвестная величина и все или некоторые из известных. В данном случае V = a * b * c.
Выразите неизвестную величину через остальные. По условию задачи надо найти b = V / (a * c). Когда выводите формулу, проверяйте, правильно ли расставлены скобки, в случае ошибок результат вычислений будет неверным.
Убедитесь, что исходные данные представлены в одном виде. Если это не так, преобразуйте их. Если бы на первом шаге было написано a = 0,12 м, эту величину пришлось бы перевести в см, потому что в таком виде представлены остальные размеры параллелепипеда. Важно помнить, что 1 м = 100 см, 1 см = 100 мм.
Решите задачу, подставив в результат третьего шага числовые значения — с учетом поправок, выполненных на четвертом шаге. b = 124 / (12 * 3) = 124 / 36 = 3,44 см. Результат получается примерный, потому что пришлось округлить значение до двух знаков после запятой.
Сделайте проверку, используя формулу второго шага. V = 12 * 3,44 * 3 = 123,84 см³. По условию задачи V = 124 см³. Можно сделать вывод, что решение правильное, потому что на пятом шаге результат округлялся.
