Как найти ширину реки геометрия

Добрый день, уважаемые гости и подписчики канала “Строю для Себя”!

Оказывается, узнать ширину реки также очень просто, как и определить высоту предмета (дерева, дома, столба), не поднимаясь на него, о чем была написана предыдущая статья “Как определить высоту объекта вблизи или на расстоянии? (5 способов!)”.

Ширина реки вычисляется почти теми же свойствами треугольников из школьного курса геометрии. Наше расстояние находится посредством измерения другого расстояния, которое доступно нам на берегу.

В данной статье опишу два способа, один из которых требует самоделки, а второй способ – вовсе не требует ничего, кроме школьных знаний по геометрии :-)))

Итак, первый способ:

Нам нужна дощечка и 3 острых предмета (гвоздь, иголка, булавка и т.п.). Из этих предметов на плоском основании строим прямоугольный равнобедренный треугольник, подручным способом это можно очень просто сделать.

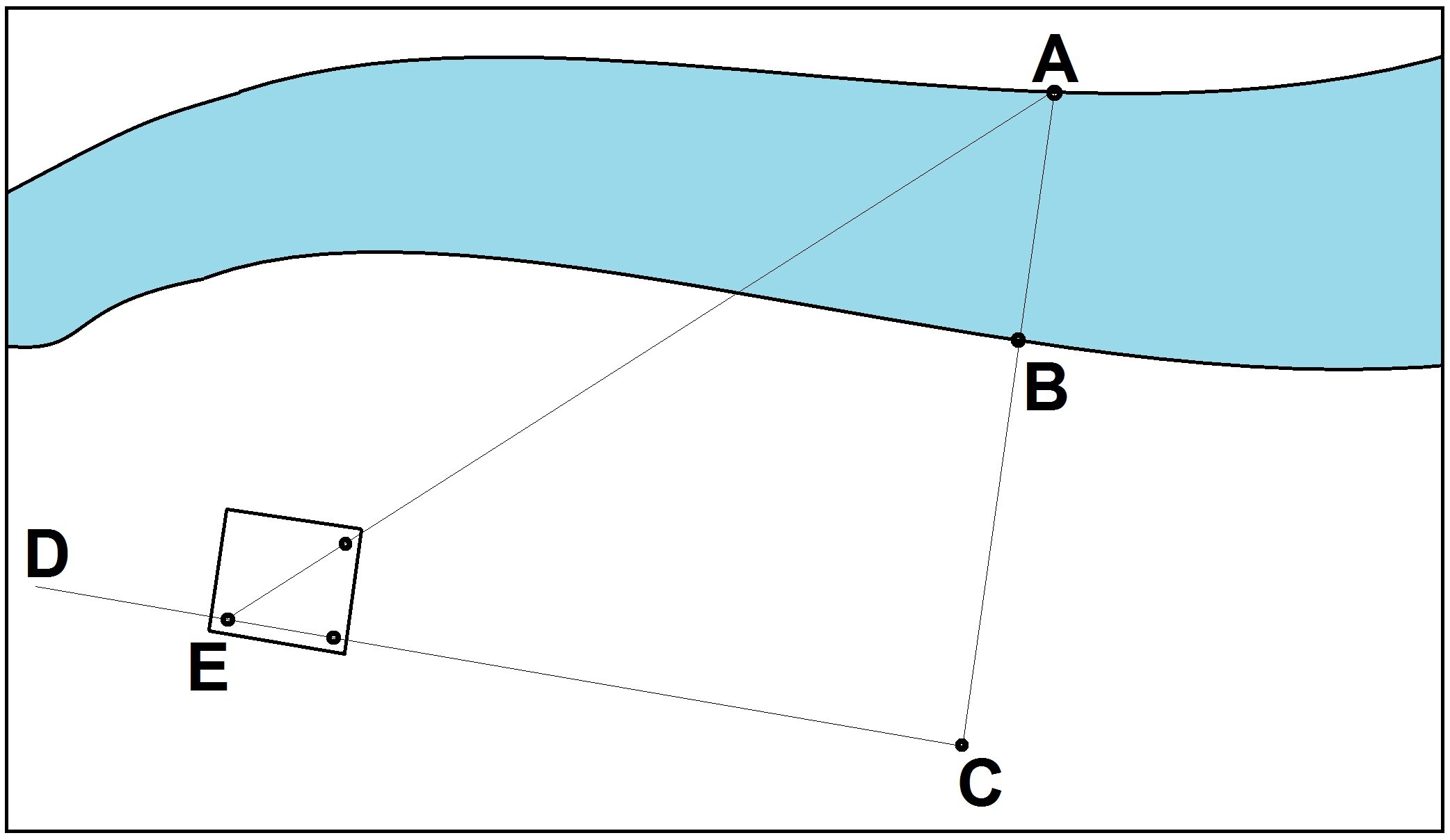
После чего, выбираем две наиболее приметные точки по обоим берегам и совмещаем с ними по линии взгляда две вершинки нашего устройства, как показано на рисунке ниже (Для удобства восприятия, буду использовать для обозначения отрезков сторон латинские буквы: A, B, C, D и т.д.).

Другими словами, нам требуется определить длину отрезка АВ.

Фиксируем приборчик на поверхности земли. Далее, не сдвигая его (рисунок ниже), определяем луч по другому из катетов построенного треугольника, и, благодаря врожденному глазомеру, выбираем на этой прямой любую точку D. Теперь, достаточно убрать прибор и в точке С воткнуть веточку.

Мы получили два перпендикулярных отрезка АС и CD. Далее, перемещаемся с нашим устройством в руках по отрезку CD в сторону точки D. Задача сводится к тому, чтобы найти такую точку на прямой СD, (пусть она будет точкой Е), чтобы точка А и точка С совпали с нашими вершинками устройства по катету и гипотенузе, т.е. лежали на прямых отрезках АЕ и СD. Для простоты, вид сверху:

Таким образом, мы нашли третью вершинку треугольника (точка Е), построенного на местности. Данный треугольник АСЕ является и прямоугольным и равнобедренным, углы А и Е равны по 45 град. И измерив отрезок СЕ, вы получите расстояние АС.

Теперь достаточно из АС вычесть ВС, в итоге, получив ширину нашей реки АВ.

Второй способ без использования самодельных приспособ:

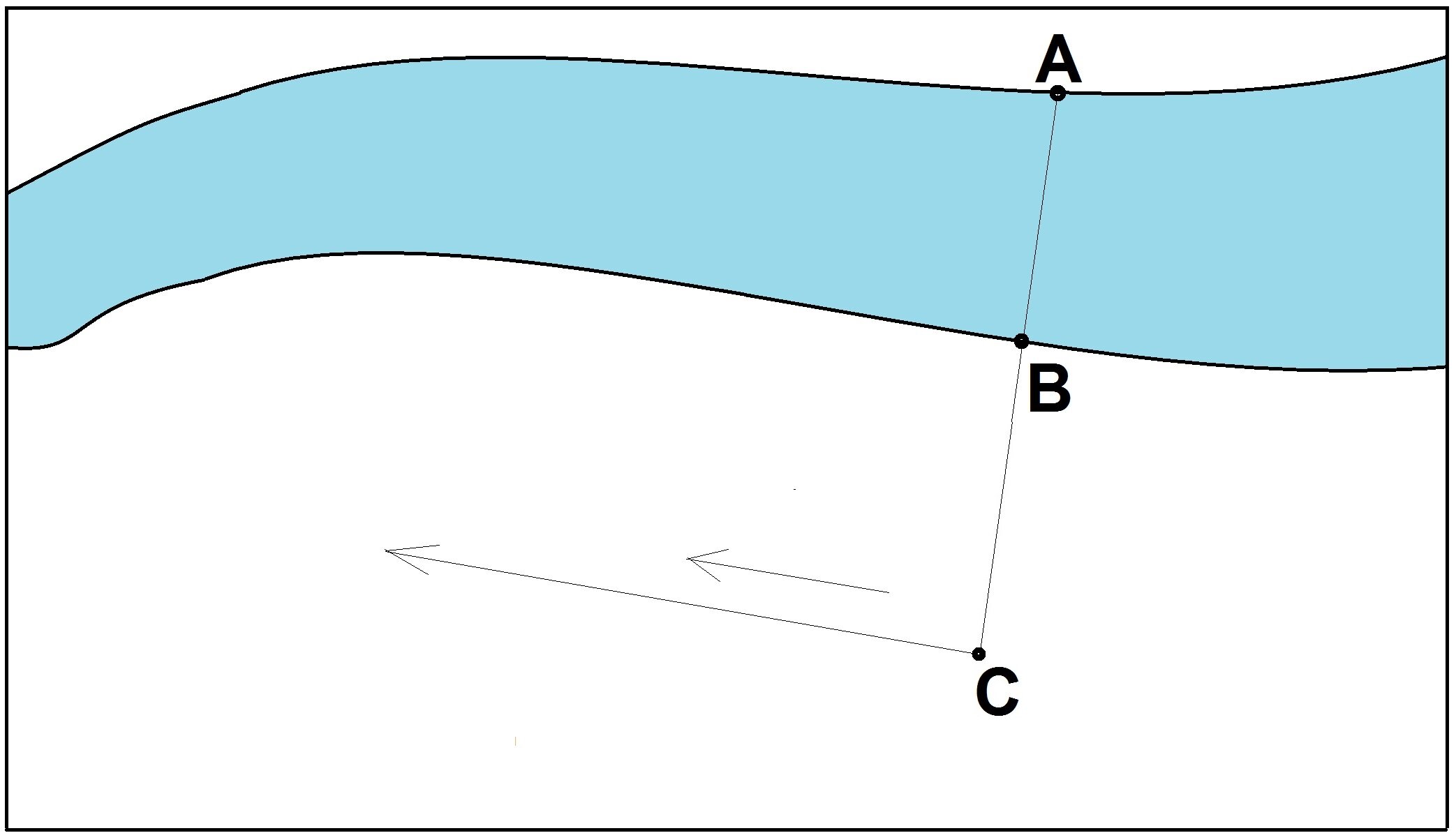
В данном способе все также выбираем наиболее приметные две точки на двух берегах А и В, и устанавливаем колышек в любую точку С, выбранную на прямой, таким образом А, В и С – лежат на одной прямой линии.

Далее, нам требуется от точки С начать движение под прямым углом, к примеру пройти 10 шагов и определить точку О. После установки очередного колышка в точку О, двигаемся по этой же прямой, но проходим в 4, 5 или 6 раз меньшее расстояние, чем отрезок СО. Например, для легкости вычислений без остатка: если СО=10 шагов, то следующий путь сократим в 5 раз, следовательно следующий отрезок ОD будет равен 2 шага.

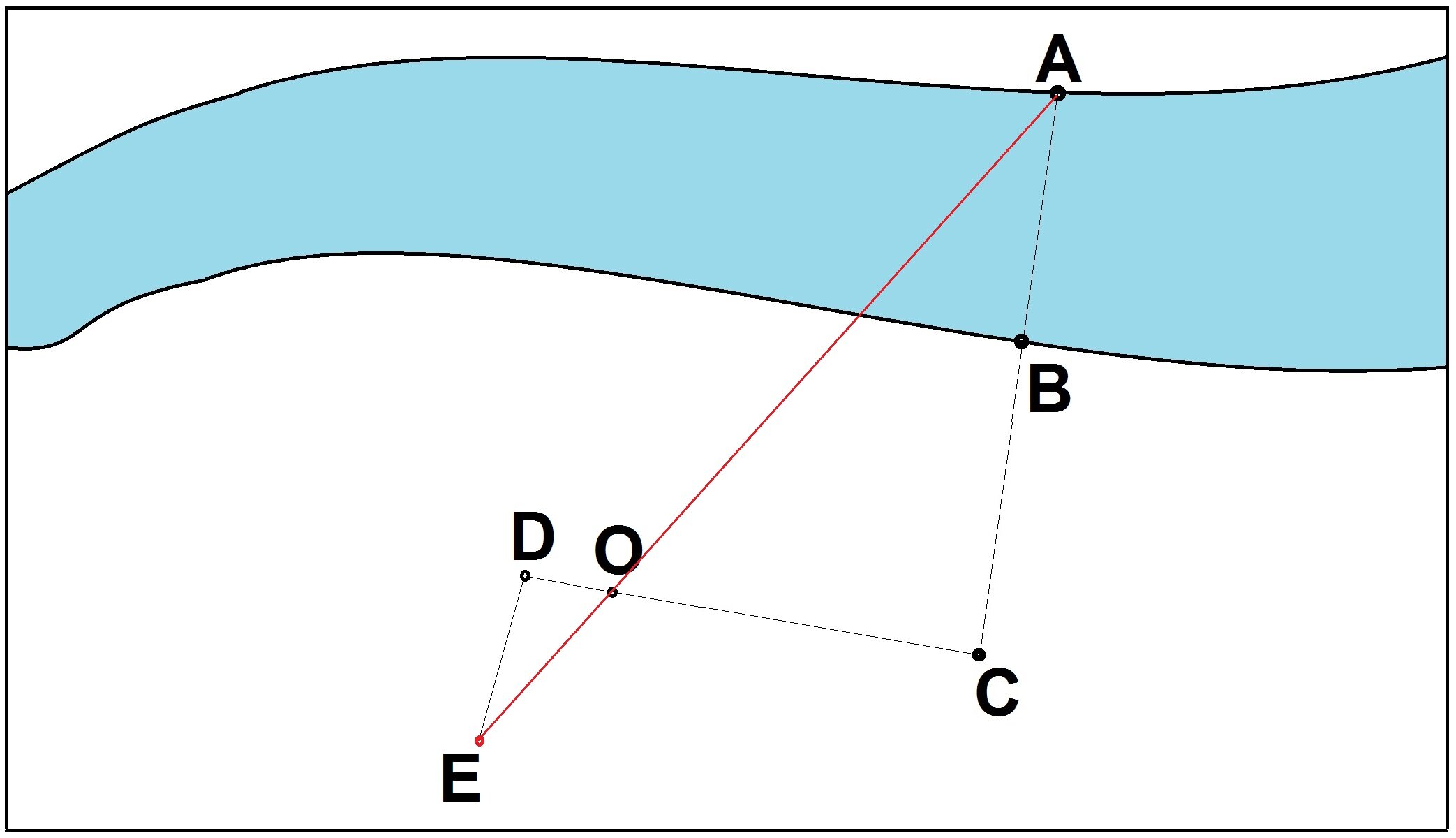
Теперь, достаточно от точки D сделать несколько шагов назад под прямым углом, чтобы совместить на одной прямой линии колышек в точке О и точку на противоположном берегу – точку А (на рисунке – красная линия).

Как только совместили А и О, значит вы стоите на точке Е и надеюсь у вас не возникает сомнений, что треугольники ODE и OAC подобны с соотношением сторон 1:5.

Другими словами, отрезок АС равен пяти отрезкам DE. Делаем необходимые вычисления, находим АС, и далее, как в первом способе из АС вычитаем ВС.

Всё, получили ширину реки.

На местности, делается всё 7-12 минут и при соблюдении действительно прямых углов – погрешность составляет от одного до трёх метров, зависит от ширины реки и четкости зрения.

Спасибо Вам за терпение и за внимание. Надеюсь, что статья оказалась для вас полезной!

Деревья с сильной корневой системой, которые не сажают около домов (минимальные расстояния от строений)

Универсальная формула для вычисления площади фигур и объема тел

Где применить на практике знания по геометрии и чего не хватает детям? (Прикладная геометрия)

Расчет деревянной балки: прогиб и допустимая нагрузка (хозяину на заметку)

Простые способы определения ширины реки, другого местного предмета или участка местности, определение дальности видимого горизонта.

Определение ширины реки, другого местного предмета или участка местности, например большого оврага, производится следующим образом. Наблюдатель становится в начальной точке А. Например на берегу реки, и выбирает на противоположном берегу или стороне какой-либо хорошо заметный ориентир. Например куст, камень,дерево и тому подобное.

После этого, идя в направлении, перпендикулярном к линии АБ, переходит в точку В, удаленную от точки А больше, чем предполагаемая ширина реки или измеряемого участка местности. В точке В устанавливает веху (палку, колышек). Затем, идя по тому же направлению, переходит в точку С. Которая находится от точки В на таком же расстоянии, как и точка В от точки А.

Далее от точки С идет под прямым углом к линии АС до точки Д, то есть до тех пор, пока веха, установленная в точке В, не окажется в створе с выбранным ориентиром (деревом) на противоположном берегу реки. Или точке измеряемого участка местности. Из равенства треугольников ВДС = ВБА видно, что отрезок СД = АБ, то есть ширине реки или измеряемого участка местности. В показанном на рисунке примере он равен 45 метров.

Способ определения ширины реки, другого местного предмета или участка местности с помощью травинки.

Определение ширины реки, другого местного предмета или участка местности может быть произведено и с помощью обычной травинки. Сорвите ее и выберите на противоположном берегу реки или стороне участка, двазаметных предмета. Встаньте лицом к этим предметам, вытяните руки с травинкой и отмерьте с ее помощью расстояние между предметами, смотря на них одним любым глазом.

После этого сложите травинку пополам (вдвое). И затем отходите от берега или условной границы участка до тех пор, пока расстояние между выбранными предметами не закроется (не уложится) сложенной вдвое травинкой. Замерьте это расстояние шагами, переведите его в метры. Это и будет расстояние, равное ширине реки или измеряемогоучастка местности.

Способ определения дальности видимого горизонта.

Для того чтобы лучшеразвить глазомер, необходимо знать, как далеко лежит от наблюдателя горизонт. С этой целью пользуются формулой : дальность горизонта = 113 х корень квадратный h, где h — высота наблюдателя (в км).

Например, стоя на равнине, человек ростом 1,6 метра видит окружающую местность на дальности равной : 113 х корень квадратный из 0,0016 = 4,52 километра. А сидя влодке и возвышаясь над водой только на 1 метр, человек может обозревать окружающую местность на дальности равной : 113 х корень квадратный из 0,001 = 3,58 километра.

По материалам книги «Карта и компас мои друзья».
Клименко А.И.

Как можно определить
ширину реки?

Первые уроки в начале учебного года в 6-м классе я провожу не в кабинете географии, а на экскурсиях по изучению родного края. Работа на местности дает возможность формировать практические умения учащихся.

Выбираем на противоположном берегу реки хорошо заметную точку А и прямо против нее на нашем берегу точку В; на некотором расстоянии от В вдоль берега реки выбираем третью точку С. Расстояние между В и С измеряем рулеткой или шагами и наносим на планшет в определенном масштабе. Затем, сориентировав планшет по компасу, из точки В наводим визирную линейку на точку А и прочерчиваем на планшете линию ВА. Потом переходим в точку С и отсюда, сориентировав опять планшет по компасу, визируем на точку А и прочерчиваем линию СА. У нас на планшете получается треугольник АВС. Потом измеряем на чертеже линию АВ и при помощи масштаба вычисляем ее действительную длину, то есть ширину реки.

Рис. 1.
Определение ширины реки
способом засечек

Если трудно найти у самых берегов реки две ясно видимые точки, находящиеся прямо одна против другой, то выбираем вдоль берега реки произвольные точки В и С, измеряем между ними расстояние и по масштабу наносим его линией ВС на планшет. Затем находим на противоположном берегу какую-нибудь хорошо видимую точку А и визируем на нее из В и из С, прочерчивая на планшете линии ВА и СА. Затем на чертеже из точки А опускаем перпендикуляр АD на линию ВС и измеряем по масштабу длину перпендикуляра, и так определяем ширину реки.

Рис. 2.
Определение ширины реки
способом засечек с опусканием
перпендикуляра

Можно найти ширину реки и еще одним способом — через построение равных треугольников.

Рис. 3.
Определение ширины реки
путем построения равных треугольников

Визируем из точки В на точку А, находящуюся на противоположном берегу, и намечаем линию АВ. Затем от точки В на местности отмеряем линию ВС (произвольной длины), перпендикулярную к линии АВ. Делим линию ВС на два равных отрезка ВЕ и ЕС, в точке Е ставим хорошо заметную вешку. Потом из точки С проводим линию, перпендикулярную к ВС, и двигаемся по ней до тех пор, пока не окажемся в точке D, которая лежит на одной прямой с точками А и Е. Линию СD точно измеряем. Ширина реки АВ равна расстоянию между точками С и D, так как полученные нами треугольники ВЕА и СЕD между собой равны.

Ребята с удовольствием выполняют эту работу.

Интегрированный проект “Геометрия у реки” (математика=география)

Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.

«Актуальность создания школьных служб примирения/медиации в образовательных организациях»

Свидетельство и скидка на обучение каждому участнику

Муниципальное бюджетное общеобразовательное учреждение «Гимназия»

Геометрия у реки

Интегрированная научно- исследовательская работа

(математика и география)

Смирнова Наталия Алексеевна и Чичканова Анастасия Павловна,

ученики 10б класса

Гребенникова Ирина Сергеевна,

учитель математики и

Щербакова Ирина Анатольевна,

1.1 Изучение маршрута по космическому снимку и

картографическая подготовка к походу……………..

2. Исследовательские работы во время похода…………….

2.1 Практические задания-исследования с помощью геометрии

2.1.1 Измерение высоты дерева………………………………

2.1.2 Измерение ширины реки…………………………………

2.1.3 Измерение глубины реки………………………………..

2.1.4 Вычисление площади водного сечения реки…………….

2.1.5 Определение крутизны склона……………………………..

2.1.6 Геометрический способ разведения костра……………….

2.2 Практическое применение географических знаний…………..

Определение сторон горизонта……………………………

2.2.3 Ориентирование по местным предметам……………….

3. Использование практических задач для подготовки к ЕГЭ…………..

3.1 Решение заданий В6……………………………………….

Природа говорит языком математики:

буквы этого языка – круги, треугольники

и иные математические фигуры.

Геометрия и география… Казалось бы, как две эти разные науки взаимосвязаны между собой? Некоторые ученые до сих пор скептически относятся к симбиозу этих двух наук. Резонанс мнений исследователей велик, от восторженных взглядов до недоверчивых мыслей на слияние этих двух дисциплин.

Зарождение геометрии было связано с различными измерительными работами, которые приходилось выполнять при разметке земельных участков, проведении дорог, строительстве зданий и других сооружений. В результате этой деятельности появились и постепенно накапливались различные правила, связанные с геометрическими измерениями и построениями. Таким образом, элементами геометрия можно воспользоваться для измерения ширины, глубины, скорости течения реки, определения крутизны склона, высоты дерева и т. д. Знания географии помогают ориентироваться на местности, использовать один из “языков” международного общения – географическую карту, самостоятельно оценивать уровень безопасности окружающей среды как сферы жизнедеятельности. Таким образом, интегрированная научно-исследовательская работа «Геометрия у реки» ярко демонстрирует связь математики с географией.

Создавая интегрированный проект, мы выдвинули гипотезу: Можно ли воспользоваться приобретёнными геометрическими и географическими знаниями на практике, например в походе? Работая по данной проблеме, пытались выяснить, помогают ли учебные знания выполнить поставленные цели и задачи туристического похода, а также выжить и сохранить здоровье?

Актуальность данной работы состоит в том, что в ней мы рассмотрели возможность практического применения основ геометрии и географии в многодневном водном походе по реке Пра. А современная жизнь делает задачи по геометрии актуальными, так как сфера их практического приложения расширяется. Вопросы инновационных технологий в строительстве, космонавтике, технике невозможны без умения производить необходимые чертежи и вычисления, которые требуют знания важных и интереснейших свойств треугольника. Решая на практике планиметрические задачи типа В6, мы готовимся к ЕГЭ по математике.

Объект исследования: река Пра и её склоны.

Предмет исследования: вода и ландшафт реки.

Цель работы: применить полученные знания по геометрии и географии в условиях дикой природы.

с помощью современных информационных технологий изучить космический снимок Рязанской области; протяжённость маршрута водного похода;

с помощью геометрии: измерить высоту дерева, определить ширину, глубину, скорость течения, крутизну склонов реки Пра;

применить географические знания ориентирования и приспособления к условиям выживания в природе, полученные в школе;

оформить результаты исследования в виде презентации, таблиц и графиков;

решая практические задачи по планиметрии и географии, подготовиться к ЕГЭ.

Методы и приёмы исследования:

Приемы разностороннего гидрологического изучения;

Полевое картирование, фотографические работы;

Знакомство с литературой местного края и архивными источниками.

1. ПОДГОТОВКА К ПОХОДУ

Успех похода во многом зависит от того, насколько подготовился к нему его руководители и как подготовлены к походу все принимающие в нем участие члены туристской группы. Каковы бы ни были цели водных исследований, необходимо, прежде чем приступить к разработке маршрута похода, ознакомиться с краеведческой литературой, имеющей близкое отношение как непосредственно к изучаемому водному объекту, так и к тому району, в котором намечается проводить исследовательские работы . Тщательно продуманный и умело спланированный маршрут во многом предопределяет успех похода. За одну – две недели до выхода на маршрут мы научились пользоваться различными специальными инструментами и самодельным оборудованием, с которым придется иметь дело при исследовательских работах.

Изучение маршрута по космическому снимку и картографическая подготовка к походу

На Земле русской есть удивительный уголок под древним названием Мещёра, включающий Мещёрский национальный парк и Окский заповедник. Неподалёку, на старинном Муромском тракте, промышлял, согласно преданиям Соловей-разбойник. Мещёра вдохновляла многих художников, поэтов, писателей, музыкантов, таких как С. Есенин, К. Паустовский, Ф. Шаляпин. Одной из многочисленных рек Мещёры является река Пра. Река Пра практически ровно пополам делит рязанскую Мещеру. “Я много видел живописных и глухих мест в России, но вряд ли когда-нибудь увижу реку более девственную и таинственную, чем Пра”, – писал К. Паустовский.

Прежде чем отправиться в многодневный байдарочный туристический поход мы с помощью прибора «Космос М-2» изучили космический снимок Рязанской области, её площадь(37374кв. км) и определили географическое положение реки Пра. Пра — река в Рязанской области, левый приток Оки. Берёт начало из озера Святое (Клепиковские озёра), течет Мещёрскими лесами на юг, юго-восток и восток. По спутниковому снимку определили географические координаты истока реки Пра: широта: 54°44’с. ш., долгота: 40°59′ в. д. Длина Пры — 192 км. На Пре расположен город Спас-Клепики— районный центр Рязанской области. Начало водного похода у города Спас-Клёпики. Определили по карте его координаты – 55°с.ш. 40°в.д. и направление маршрута по реке Пра до следующего причала у Жуковских Выселок., далее остановка у села Деулино, его координаты – 54°с. ш. 40° в.д., далее до посёлка Брыкин Бор, его координаты – 54 °с. ш . 40°с.ш. С помощью географической карты наметили протяжённость маршрута, который составил приблизительно 120 км.

2. ИССЛЕДОВАТЕЛЬСКИЕ РАБОТЫ ВО ВРЕМЯ ПОХОДА

2.1 Практические задания-исследования с помощью геометрии

2.1.1 Измерение высоты дерева

Прибрежная растительность реки Пра очень разнообразна. По берегам растёт много различных деревьев и кустарников. Существует множество различных способов измерения высоты дерева, не срубая его и не взбираясь на верхушку, при помощи весьма незамысловатых приборов и даже без всяких приспособлений.

По длине тени: способ Фалеса

Самый лёгкий и самый древний способ – без сомнения, тот, которым греческий мудрец Фалес за шесть веков до нашей эры определил в Египте высоту пирамиды. Он воспользовался её тенью. Нетрудно изменить этот способ так, чтобы в солнечный день можно было пользоваться любой тенью, какой бы длины она ни была. Измерив, и свою тень или тень какого-нибудь шеста, вычислим искомую высоту из пропорции: AB :А₁В₁= BC :В₁С₁

т.е. высота дерева во столько же раз больше вашей собственной высоты, во сколько раз тень дерева длиннее вашей тени. Это вытекает, конечно, из геометрического подобия треугольников АВС и А₁В₁С₁.

Рис.1 Измерение высоты дерева.

Измерение высоты дерева при помощи простого булавочного прибора

Вполне возможно обойтись при измерении высоты и без помощи теней. Прежде всего, мы можем воспользоваться свойством равнобедренного треугольника, обратившись к услугам весьма простого прибора, который легко изготовить из дощечки и трёх булавок. (см. приложение1)

Рис.2 Схема применения булавочного прибора. Рис.3

Приближаясь к дереву или удаляясь от него, мы нашли такое место А (рис.2), из которого, глядя на булавки А₁ и С₁ , увидели, что они показывают верхушку С дерева: это значит, что продолжение гипотенузы А₁С₁ проходит через точку С. Тогда, очевидно, расстояние А₁В = СВ, так как угол А₁=45 0 .

Следовательно, измерив расстояние А₁В и прибавив ВD, т.е. возвышение А₁А глаза над землёй, получили искомую высоту дерева.

По другому способу вы обходитесь даже и без булавочного прибора. Здесь нужен шест, который мы воткнули в землю так, чтобы выступающая часть как раз равнялась нашему росту. Место для шеста выбрали так, чтобы, лежа, как показано на рис.3, мы видели верхушку дерева на одной прямой линии с верхней точкой шеста. Так как треугольник АВ₁С₁ – равнобедренный и прямоугольный, то угол А=45 0 и, следовательно, АВ равно ВС, т.е. искомый высоте дерева. Существует ещё множество различных способов измерения высоты дерева. (см. приложение2)

Вывод: применяя различные способы измерения высоты дерева, используя различные инструменты для измерения высот, можно находить высоту различных объектов: здания, магазина, школы, частного дома. Результаты измерений занесли в таблицу и вычислили погрешность измерений (см. приложение).

2.1.2 Измерение ширины реки

Не переплывая реки, измерить её ширину – так же просто для знающего геометрию, как определить высоту дерева, не взбираясь на вершину. Неприступное расстояние измеряют теми же приёмами, какими мы измеряли недоступную высоту. Ширина реки достаточно точно может быть определена способом построения на берегу реки двух равных прямоугольных треугольников. Выбрав на противоположном берегу какой-нибудь приметный предмет А (дерево, камень и т. п.), расположенный у самой воды, вбиваем против него колышек В (рис.4). Вдоль берега, перпендикулярно к линии АВ, отмеряем рулеткой определенное расстояние (например 20 м) и вбиваем колышек С. На продолжении линии ВС в расстоянии, равном также 20 м, вбиваем еще один колышек Д. От колышка Л в направлении ДЕ, перпендикулярном к линии ДВ, надо идти от реки до тех пор, пока колышек С не окажется на одной линии с предметом А. Так как треугольники ABC = Е DC , то ширина реки будет равна расстоянию ДЕ минус ВК.

Рис.4

При помощи нитки или травинки

Очень прост и удобен приближенный прием определения ширины реки при помощи травинки или нитки. Стоя на берегу реки в точке А(рис.5), заметим на противоположном ее берегу два приметных предмета (например лодку В и дерево С), расположенных близ уреза. Затем, взяв травинку за ее концы вытянутыми перед собой руками, замечают ее длину d, которой закрывается промежуток ВС между выбранными предметами (смотреть надо одним глазом). Затем, сложив травинку (нитку) пополам, отходим от реки до тех пор (точка D), пока промежуток ВС не будет закрыт травинкой. Расстояние AD будет равно ширине реки (на основании существующей в геометрии зависимости между величинами центрального и вписанного углов, опирающихся на одну и ту же хорду).

Рис.5

Существует множество способов решения этой задачи, которые подробно рассмотрены в приложении 3.

Вывод: вот несколько легко выполнимых приёмов, при помощи которых всегда возможно, не переправляясь на другой берег, измерить не только ширину реки, но и расстояние до любого недоступного объекта со вполне удовлетворительной точностью.

2.1.3 Измерение глубины реки

Близ берега реки мы отыскали водное растение, которое доставило нам реальный материал для практической задачи: без всяких приспособлений, не замочив даже рук, определить глубину водоёма в неглубоком месте. Рис.6

Решение: Пусть растение возвышается над водой на 0,5м. перегнём его так, чтобы его надводная часть коснулась воды. Тогда расстояние от стебля (точки С) до точки В, касания с водой, составило 1,5м.

Рассмотрим прямоугольный треугольник BD С. Обозначим искомую глубину реки СD через х. (рис.6) Тогда, по теореме Пифагора, имеем:

BD ² = D С 2 +СВ 2 , значит BD ² =х 2 +СВ 2

В D = х+ 0,5, расстояние СВ=1,5м, получим

Х 2 +х+0,25=х 2 +2,25, отсюда х=2

Ответ: искомая глубина реки составила 2м.

Вывод: при помощи различных способов (см. приложение) мы измеряли глубину реки и составили таблицу глубин(см. приложение). Определили, что средняя глубина реки Пра ≈ 1,5 м.

2.2.4 Определение площади водного сечения реки

Умея измерять глубины в отдельных точках и зная положение последних по ширине реки, нетрудно определить площадь поперечного водного сечения.

Проще всего и точнее всего при определении поперечного сечения реки перетянуть через нее промерную веревку (трос) и через равные по ширине расстояния произвести измерение глубин (примерно в 10—20 точках).

По данным измерений, записанным в таблице(см.приложение) (графы 1—3), легко вычертить профиль поперечного сечения реки и вычислить его площадь. Пример построения профиля поперечного сечения реки показан на рисунке 7.

Вычисление площади поперечного сечения заключается в определении площадей отдельных отсеков между соседними промерными вертикалями, представляющих собою трапеции или треугольники (по краям сечения), и последующем суммировании этих частных площадей. Найдя полусуммы соседних глубин и помножив их на соответствующие расстояния между промерными вертикалями, получим частные площади, а просуммировав их, и общую площадь поперечного сечения. Подсчет площади живого сечения дан в графах 4—6 приведенной выше таблице(См. приложение) .

Рис.7

2.1.5 Определение крутизны склона

Для измерения крутизны склона применили самодельный прибор эклиметр,(см. приложение1) Для измерения крутизны склона прибор должен занять положение, параллельное склону, при этом отвес покажет некую величину β. Для вычисления угла α следует вычесть из 90 о эту, полученную путем измерения, величину β, тогда α=90 о -β, а сама работа по определению крутизны склона при по мощи эклиметра — на рисунке 8

Рис.8

Крутизна склона приближенно может быть определена измерением его поверхности шагами. Подняв записную книжку до уровня глаз (рис. 26) и держа ее горизонтально, замечают на склоне точку В, в которую попадает луч зрения, скользящий вдоль края книжки. Расстояние АВ измеряют парами шагов.

Частное от деления 60 градусов на количество пар шагов, пройденных от точки стояния А до точки В, расположенной на склоне на уровне глаз измеряющего, покажет примерную крутизну склона в градусах.

Например, Число 60° выражает приблизительную величину радиана, т. е. центрального угла, опирающегося на дугу окружности, равную длине радиуса ( радиан равен 57°18 ′ ). Отсюда, крутизна склона

Так, если АВ равно 4 парам шагов, а АС (рост человека) — 1 паре шагов, то крутизна склона будет равна 60:4=15 градусам.

[spoiler title=”источники:”]

http://geo.1sept.ru/article.php?ID=200700620

http://infourok.ru/integrirovanniy-proekt-geometriya-u-reki-matematikageografiya-481547.html

[/spoiler]

Всем привет!

Нашел на просторах сети эту статью, не удержался – вставил тут, чтобы не потерять.

Ширина реки вычисляется почти теме же свойствами треугольников из школьного курса геометрии. Наше расстояние находится посредством измерения другого расстояния, которое доступно нам на берегу.

В данной статье опишу два способа, один из которых требует самоделки, а второй способ – вовсе не требует ничего, кроме школьных знаний по геометрии :-)))

Итак, первый способ:

Нам нужна дощечка и 3 острых предмета (гвоздь, иголка, булавка и т.п.). Из этих предметов на плоском основании строим прямоугольный равнобедренный треугольник, подручным способом это можно очень просто сделать.

После чего, выбираем две наиболее приметные точки по обоим берегам и совмещаем с ними по линии взгляда две вершинки нашего устройства, как показано на рисунке ниже (Для удобства восприятия, буду использовать для обозначения отрезков сторон латинские буквы: A, B, C, D и т.д.).

 

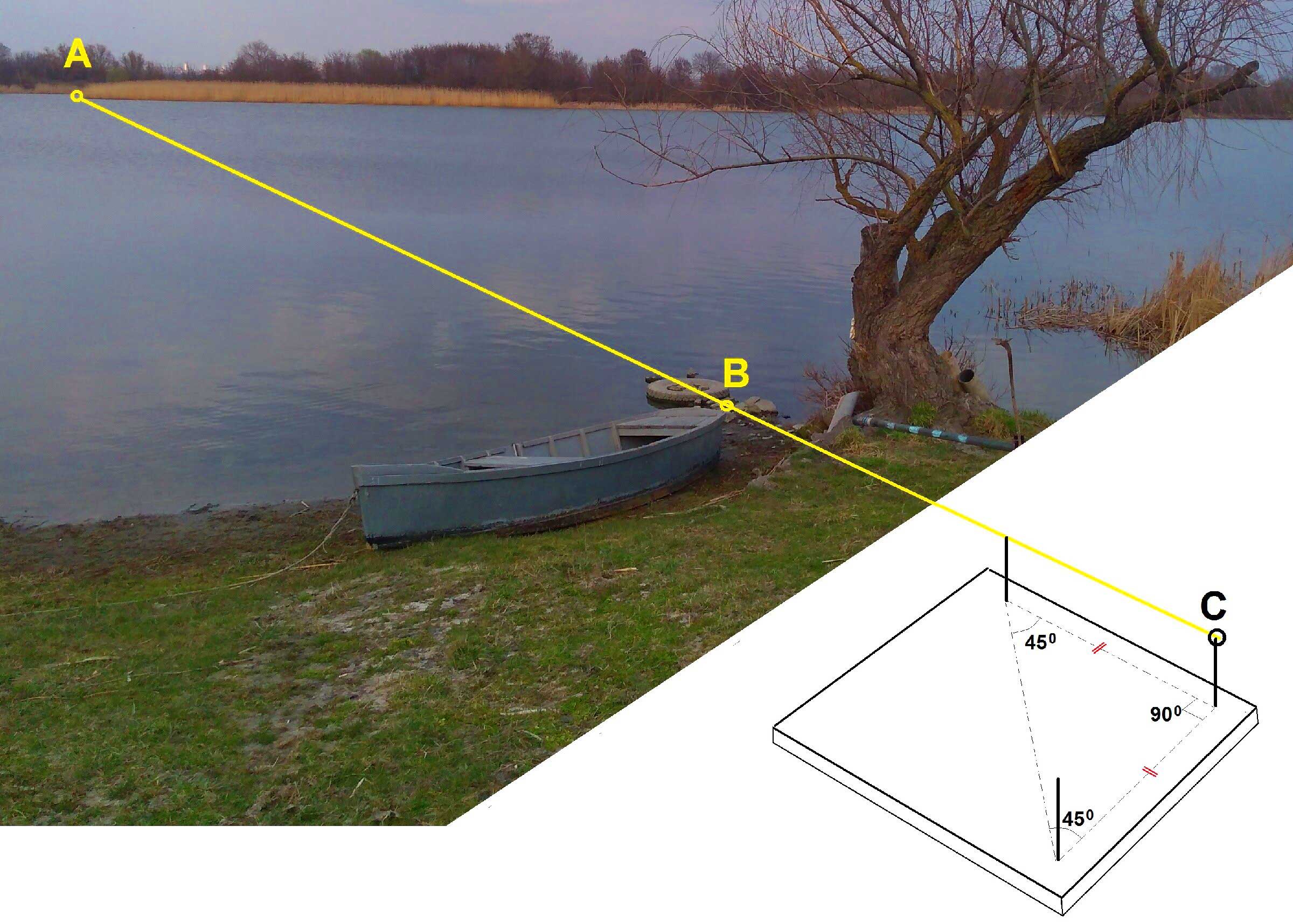
Другими словами, нам требуется определить длину отрезка АВ.

Фиксируем приборчик на поверхности земли. Далее, не сдвигая его (рисунок ниже), определяем луч по другому из катетов построенного треугольника, и, благодаря врожденному глазомеру, выбираем на этой прямой любую точку D. Теперь, достаточно убрать прибор и в точке С воткнуть веточку.

 Мы получили два перпендикулярных отрезка АС и CD. Далее, перемещаемся с нашим устройством в руках по отрезку CD в сторону точки D. Задача сводится к тому, чтобы найти такую точку на прямой СD, (пусть она будет точкой Е), чтобы точка А и точка С совпали с нашими вершинками устройства по катету и гипотенузе, т.е. лежали на прямых отрезках АЕ и СD. Для простоты, вид сверху:

Таким образом, мы нашли третью вершинку треугольника (точка Е), построенного на местности. Данный треугольник АСЕ является и прямоугольным и равнобедренным, углы А и Е равны по 45 град. И измерив отрезок СЕ, вы получите расстояние АС.

Теперь достаточно из АС вычесть ВС, в итоге, получив ширину нашей реки АВ.

Второй способ без использования самодельных приспособ:

В данном способе все также выбираем наиболее приметные две точки на двух берегах А и В, и устанавливаем колышек в любую точку С, выбранную на прямой, таким образом А, В и С – лежат на одной прямой линии.

Далее, нам требуется от точки С начать движение под прямым углом, к примеру пройти 10 шагов и определить точку О. После установки очередного колышка в точку О, двигаемся по этой же прямой, но проходим в 4, 5 или 6 раз меньшее расстояние, чем отрезок СО. Например, для легкости вычислений без остатка: если СО=10 шагов, то следующий путь сократим в 5 раз, следовательно следующий отрезок ОD будет равен 2 шага.

Теперь, достаточно от точки D сделать несколько шагов назад под прямым углом, чтобы совместить на одной прямой линии колышек в точке О и точку на противоположном берегу – точку А (на рисунке – красная линия).

Как только совместили А и О, значит вы стоите на точке Е и надеюсь у вас не возникает сомнений, что треугольники ODE и OAC подобны с соотношением сторон 1:5.

Другими словами, отрезок АС равен пяти отрезкам DE. Делаем необходимые вычисления, находим АС, и далее, как в первом способе из АС вычитаем ВС.

Всё, получили ширину реки.

На местности, делается всё 7-12 минут и при соблюдении действительно прямых углов – погрешность составляет от одного до трёх метров, зависит от ширины реки и четкости зрения.

Спасибо Вам за терпение и за внимание. Надеюсь, что статья оказалась для вас полезной!

Автор (хороший человек): Строю для себя

Всем привет!

Нашел на просторах сети эту статью, не удержался – вставил тут, чтобы не потерять.

Ширина реки вычисляется почти теме же свойствами треугольников из школьного курса геометрии. Наше расстояние находится посредством измерения другого расстояния, которое доступно нам на берегу.

В данной статье опишу два способа, один из которых требует самоделки, а второй способ – вовсе не требует ничего, кроме школьных знаний по геометрии :-)))

Итак, первый способ:

Нам нужна дощечка и 3 острых предмета (гвоздь, иголка, булавка и т.п.). Из этих предметов на плоском основании строим прямоугольный равнобедренный треугольник, подручным способом это можно очень просто сделать.

После чего, выбираем две наиболее приметные точки по обоим берегам и совмещаем с ними по линии взгляда две вершинки нашего устройства, как показано на рисунке ниже (Для удобства восприятия, буду использовать для обозначения отрезков сторон латинские буквы: A, B, C, D и т.д.).

 

Другими словами, нам требуется определить длину отрезка АВ.

Фиксируем приборчик на поверхности земли. Далее, не сдвигая его (рисунок ниже), определяем луч по другому из катетов построенного треугольника, и, благодаря врожденному глазомеру, выбираем на этой прямой любую точку D. Теперь, достаточно убрать прибор и в точке С воткнуть веточку.

 Мы получили два перпендикулярных отрезка АС и CD. Далее, перемещаемся с нашим устройством в руках по отрезку CD в сторону точки D. Задача сводится к тому, чтобы найти такую точку на прямой СD, (пусть она будет точкой Е), чтобы точка А и точка С совпали с нашими вершинками устройства по катету и гипотенузе, т.е. лежали на прямых отрезках АЕ и СD. Для простоты, вид сверху:

Таким образом, мы нашли третью вершинку треугольника (точка Е), построенного на местности. Данный треугольник АСЕ является и прямоугольным и равнобедренным, углы А и Е равны по 45 град. И измерив отрезок СЕ, вы получите расстояние АС.

Теперь достаточно из АС вычесть ВС, в итоге, получив ширину нашей реки АВ.

Второй способ без использования самодельных приспособ:

В данном способе все также выбираем наиболее приметные две точки на двух берегах А и В, и устанавливаем колышек в любую точку С, выбранную на прямой, таким образом А, В и С – лежат на одной прямой линии.

Далее, нам требуется от точки С начать движение под прямым углом, к примеру пройти 10 шагов и определить точку О. После установки очередного колышка в точку О, двигаемся по этой же прямой, но проходим в 4, 5 или 6 раз меньшее расстояние, чем отрезок СО. Например, для легкости вычислений без остатка: если СО=10 шагов, то следующий путь сократим в 5 раз, следовательно следующий отрезок ОD будет равен 2 шага.

Теперь, достаточно от точки D сделать несколько шагов назад под прямым углом, чтобы совместить на одной прямой линии колышек в точке О и точку на противоположном берегу – точку А (на рисунке – красная линия).

Как только совместили А и О, значит вы стоите на точке Е и надеюсь у вас не возникает сомнений, что треугольники ODE и OAC подобны с соотношением сторон 1:5.

Другими словами, отрезок АС равен пяти отрезкам DE. Делаем необходимые вычисления, находим АС, и далее, как в первом способе из АС вычитаем ВС.

Всё, получили ширину реки.

На местности, делается всё 7-12 минут и при соблюдении действительно прямых углов – погрешность составляет от одного до трёх метров, зависит от ширины реки и четкости зрения.

Спасибо Вам за терпение и за внимание. Надеюсь, что статья оказалась для вас полезной!

Автор (хороший человек): Строю для себя

Добрый день, уважаемые гости и подписчики канала “Строю для Себя”!

Оказывается, узнать ширину реки также очень просто, как и определить высоту предмета (дерева, дома, столба), не поднимаясь на него.

Ширина реки вычисляется почти теме же свойствами треугольников из школьного курса геометрии. Наше расстояние находится посредством измерения другого расстояния, которое доступно нам на берегу.

В данной статье опишу два способа, один из которых требует самоделки, а второй способ вовсе не требует ничего, кроме школьных знаний по геометрии!

Итак, первый способ:

Нам нужна дощечка и 3 острых предмета (гвоздь, иголка, булавка и т.п.). Из этих предметов на плоском основании строим прямоугольный равнобедренный треугольник, подручным способом это можно очень просто сделать.

После чего, выбираем две наиболее приметные точки по обоим берегам и совмещаем с ними по линии взгляда две вершинки нашего устройства, как показано на рисунке ниже (Для удобства восприятия, буду использовать для обозначения отрезков сторон латинские буквы: A, B, C, D и т.д.).

Другими словами, нам требуется определить длину отрезка АВ.

Фиксируем приборчик на поверхности земли. Далее, не сдвигая его (рисунок ниже), определяем луч по другому из катетов построенного треугольника, и, благодаря врожденному глазомеру, выбираем на этой прямой любую точку D. Теперь, достаточно убрать прибор и в точке С воткнуть веточку.

Мы получили два перпендикулярных отрезка АС и CD. Далее, перемещаемся с нашим устройством в руках по отрезку CD в сторону точки D. Задача сводится к тому, чтобы найти такую точку на прямой СD, (пусть она будет точкой Е), чтобы точка А и точка С совпали с нашими вершинками устройства по катету и гипотенузе, т.е. лежали на прямых отрезках АЕ и СD. Для простоты, вид сверху:

Таким образом, мы нашли третью вершинку треугольника (точка Е), построенного на местности. Данный треугольник АСЕ является и прямоугольным и равнобедренным, углы А и Е равны по 45 град. И измерив отрезок СЕ, вы получите расстояние АС.

Теперь достаточно из АС вычесть ВС, в итоге, получив ширину нашей реки АВ.

Второй способ без использования самодельных приспособ:

В данном способе все также выбираем наиболее приметные две точки на двух берегах А и В, и устанавливаем колышек в любую точку С, выбранную на прямой, таким образом А, В и С — лежат на одной прямой линии.

Далее, нам требуется от точки С начать движение под прямым углом, к примеру пройти 10 шагов и определить точку О. После установки очередного колышка в точку О, двигаемся по этой же прямой, но проходим в 4, 5 или 6 раз меньшее расстояние, чем отрезок СО. Например, для легкости вычислений без остатка: если СО=10 шагов, то следующий путь сократим в 5 раз, следовательно следующий отрезок ОD будет равен 2 шага.

Теперь, достаточно от точки D сделать несколько шагов назад под прямым углом, чтобы совместить на одной прямой линии колышек в точке О и точку на противоположном берегу — точку А (на рисунке — красная линия).

Как только совместили А и О, значит вы стоите на точке Е и надеюсь у вас не возникает сомнений, что треугольники ODE и OAC подобны с соотношением сторон 1:5.

Другими словами, отрезок АС равен пяти отрезкам DE. Делаем необходимые вычисления, находим АС, и далее, как в первом способе из АС вычитаем ВС.

Всё, получили ширину реки.

На местности, делается всё 7-12 минут и при соблюдении действительно прямых углов — погрешность составляет от одного до трёх метров, зависит от ширины реки и четкости зрения.

Спасибо Вам за терпение и за внимание.

Надеюсь, что статья оказалась для вас полезной!