-
-
July 1 2020, 18:00
- Образование
- Техника
- Cancel
Как измерить ширину реки без заплыва по ней

В какие ситуации только не поставит человека жизнь. Некогда не знаешь, что может пригодиться завтра утром! Возможно однажды понадобится даже умение измерять ширину реке. Благо, сделать это можно без специального оборудования и даже не переплывая водную преграду. Существует два проверенных годами способа, правда, для их реализации придется хорошенько поработать извилинами. Вычисляется ширина любой реки по свойствам треугольников из школьного курса геометрии.
Неожиданно, правда?
Способ первый
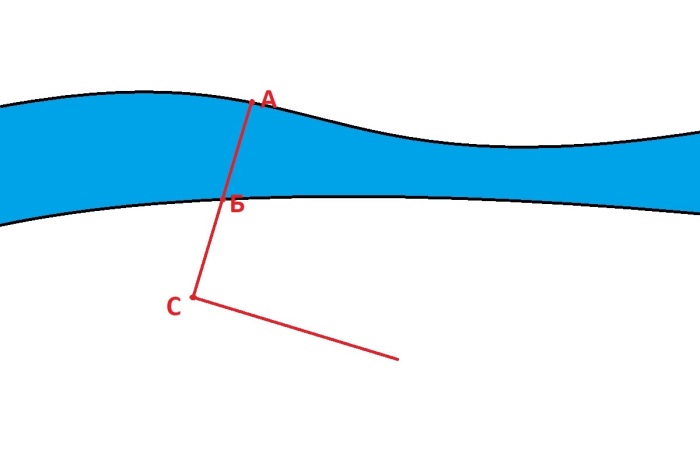
Сначала выбираем две наиболее приметные точки на берегах «А» и «Б», после чего ставим колышек в точку «С», которая должна лежать с точками «А» и «Б» в одной прямой линии на любом удалении от берега. От колышка делаем 10 шагов к следующей точке «О» так, чтобы наше движение чертило перпендикулярную линию отрезку «АС». Ставим на месте «О» еще один колышек.
Продолжаем идти по прямой еще два шага и ставим колышек «Д», делаем несколько шагов вбок от прямой так, чтобы получить отрезок «ДЕ» под прямым углом относительно отрезка «СД». После этого соединяем линией точки «Е» и «А». Если все было сделано правильно, то отрезок пройдет через точку «О», и мы получим два подобных треугольника «АСО» и «ОДЕ» с соотношением сторон 1 к 5.
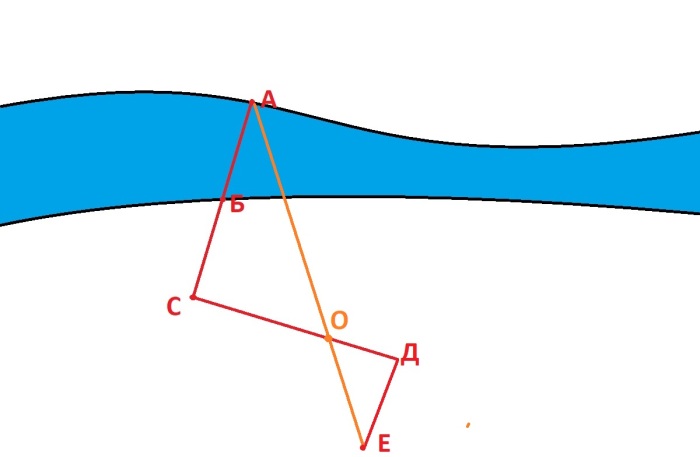
Таким образом отрезок «АС» будет равен 5 отрезкам «ДЕ». А так как расстояние от точки «Б» до точки «С» мы знаем, то можно вычесть из отрезков ширину реки.
Погрешность расчётов составит 1-3 метра.
Способ второй

Прежде всего понадобится «наколдовать» три острых предмета (например, три булавки или гвоздика) и какое-нибудь плоское основание – лучше всего дощечку. Из трех гвоздиков строим на основании прямоугольный равнобедренный треугольник, после чего нужно будет выбрать на двух берегах реки два наиболее узнаваемых предмета.
Сделанное нами устройство необходимо совместить с выбранными предметами по линии взгляда. Таким образом получаем два отрезка «АБ» и «БС», где первый – ширина нашей реки. Для этого сначала нужно зафиксировать сделанный прибор на земле так, чтобы не нарушить созданную композицию. Проводим луч по катету малого треугольника «СД», после чего убираем наше устройство, поставив на его место колышек.
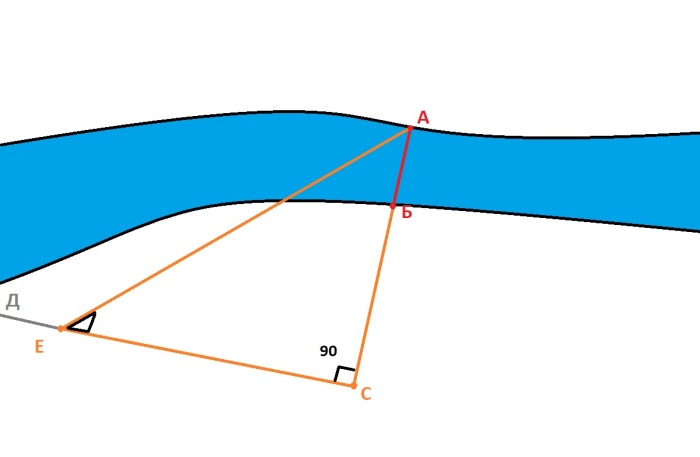
Должно получиться два перпендикулярных отрезка «АС» и «СД». Далее на отрезке «СД» нужно при помощи нашего приспособления выбрать такую точку «Е», находясь в которой точки «А» и точки «С» будут совпадать с гвоздиками на измерительном устройстве.
В итоге получаем равнобедренный прямоугольный треугольник «АСЕ» с углами 90 и 45 градусов. Измерив отрезок «СЕ» получаем расстояние «АС». Останется только вычесть из него уже известный нам отрезок «ВС».
Практическая работа
на местности
Как можно определить
ширину реки?
Первые уроки в начале учебного года в 6-м
классе я провожу не в кабинете географии, а на
экскурсиях по изучению родного края. Работа на
местности дает возможность формировать
практические умения учащихся.
Выбираем на противоположном берегу реки хорошо
заметную точку А и прямо против нее на нашем
берегу точку В; на некотором расстоянии от В
вдоль берега реки выбираем третью точку С.
Расстояние между В и С измеряем рулеткой
или шагами и наносим на планшет в определенном
масштабе. Затем, сориентировав планшет по
компасу, из точки В наводим визирную линейку
на точку А и прочерчиваем на планшете линию ВА.
Потом переходим в точку С и отсюда,
сориентировав опять планшет по компасу, визируем
на точку А и прочерчиваем линию СА. У нас
на планшете получается треугольник АВС.
Потом измеряем на чертеже линию АВ и при
помощи масштаба вычисляем ее действительную
длину, то есть ширину реки.
|
|
Рис. 1.
|
Если трудно найти у самых берегов реки
две ясно видимые точки, находящиеся прямо одна
против другой, то выбираем вдоль берега реки
произвольные точки В и С, измеряем между
ними расстояние и по масштабу наносим его линией ВС
на планшет. Затем находим на противоположном
берегу какую-нибудь хорошо видимую точку А и
визируем на нее из В и из С, прочерчивая на
планшете линии ВА и СА. Затем на чертеже
из точки А опускаем перпендикуляр АD на
линию ВС и измеряем по масштабу длину
перпендикуляра, и так определяем ширину реки.
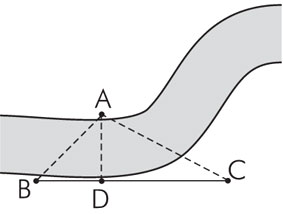 |
Рис. 2.
|
Можно найти ширину реки и еще одним
способом — через построение равных
треугольников.
|
|
Рис. 3.
|
Визируем из точки В на точку А,
находящуюся на противоположном берегу, и
намечаем линию АВ. Затем от точки В на
местности отмеряем линию ВС (произвольной
длины), перпендикулярную к линии АВ. Делим
линию ВС на два равных отрезка ВЕ и ЕС,
в точке Е ставим хорошо заметную вешку. Потом
из точки С проводим линию, перпендикулярную к
ВС, и двигаемся по ней до тех пор, пока не
окажемся в точке D, которая лежит на одной
прямой с точками А и Е. Линию СD точно
измеряем. Ширина реки АВ равна расстоянию
между точками С и D, так как полученные
нами треугольники ВЕА и СЕD между собой
равны.
Ребята с удовольствием выполняют эту работу.
Н.Г. УСТИМОВА,
ведущий учитель географии средней школы № 6,
г. Бугульма,
Республика Татарстан
Простые способы определения ширины реки, другого местного предмета или участка местности, определение дальности видимого горизонта.
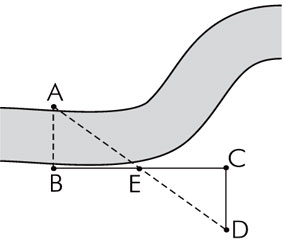
Определение ширины реки, другого местного предмета или участка местности, например большого оврага, производится следующим образом. Наблюдатель становится в начальной точке А. Например на берегу реки, и выбирает на противоположном берегу или стороне какой-либо хорошо заметный ориентир. Например куст, камень,дерево и тому подобное.
После этого, идя в направлении, перпендикулярном к линии АБ, переходит в точку В, удаленную от точки А больше, чем предполагаемая ширина реки или измеряемого участка местности. В точке В устанавливает веху (палку, колышек). Затем, идя по тому же направлению, переходит в точку С. Которая находится от точки В на таком же расстоянии, как и точка В от точки А.

Далее от точки С идет под прямым углом к линии АС до точки Д, то есть до тех пор, пока веха, установленная в точке В, не окажется в створе с выбранным ориентиром (деревом) на противоположном берегу реки. Или точке измеряемого участка местности. Из равенства треугольников ВДС = ВБА видно, что отрезок СД = АБ, то есть ширине реки или измеряемого участка местности. В показанном на рисунке примере он равен 45 метров.
Способ определения ширины реки, другого местного предмета или участка местности с помощью травинки.
Определение ширины реки, другого местного предмета или участка местности может быть произведено и с помощью обычной травинки. Сорвите ее и выберите на противоположном берегу реки или стороне участка, двазаметных предмета. Встаньте лицом к этим предметам, вытяните руки с травинкой и отмерьте с ее помощью расстояние между предметами, смотря на них одним любым глазом.

После этого сложите травинку пополам (вдвое). И затем отходите от берега или условной границы участка до тех пор, пока расстояние между выбранными предметами не закроется (не уложится) сложенной вдвое травинкой. Замерьте это расстояние шагами, переведите его в метры. Это и будет расстояние, равное ширине реки или измеряемогоучастка местности.
Способ определения дальности видимого горизонта.
Для того чтобы лучшеразвить глазомер, необходимо знать, как далеко лежит от наблюдателя горизонт. С этой целью пользуются формулой : дальность горизонта = 113 х корень квадратный h, где h — высота наблюдателя (в км).
Например, стоя на равнине, человек ростом 1,6 метра видит окружающую местность на дальности равной : 113 х корень квадратный из 0,0016 = 4,52 километра. А сидя влодке и возвышаясь над водой только на 1 метр, человек может обозревать окружающую местность на дальности равной : 113 х корень квадратный из 0,001 = 3,58 километра.
По материалам книги «Карта и компас мои друзья».
Клименко А.И.
Как можно определить
ширину реки?
Первые уроки в начале учебного года в 6-м классе я провожу не в кабинете географии, а на экскурсиях по изучению родного края. Работа на местности дает возможность формировать практические умения учащихся.
Выбираем на противоположном берегу реки хорошо заметную точку А и прямо против нее на нашем берегу точку В; на некотором расстоянии от В вдоль берега реки выбираем третью точку С. Расстояние между В и С измеряем рулеткой или шагами и наносим на планшет в определенном масштабе. Затем, сориентировав планшет по компасу, из точки В наводим визирную линейку на точку А и прочерчиваем на планшете линию ВА. Потом переходим в точку С и отсюда, сориентировав опять планшет по компасу, визируем на точку А и прочерчиваем линию СА. У нас на планшете получается треугольник АВС. Потом измеряем на чертеже линию АВ и при помощи масштаба вычисляем ее действительную длину, то есть ширину реки.
Рис. 1.
Определение ширины реки
способом засечек
Если трудно найти у самых берегов реки две ясно видимые точки, находящиеся прямо одна против другой, то выбираем вдоль берега реки произвольные точки В и С, измеряем между ними расстояние и по масштабу наносим его линией ВС на планшет. Затем находим на противоположном берегу какую-нибудь хорошо видимую точку А и визируем на нее из В и из С, прочерчивая на планшете линии ВА и СА. Затем на чертеже из точки А опускаем перпендикуляр АD на линию ВС и измеряем по масштабу длину перпендикуляра, и так определяем ширину реки.
Рис. 2.
Определение ширины реки
способом засечек с опусканием
перпендикуляра
Можно найти ширину реки и еще одним способом — через построение равных треугольников.
Рис. 3.
Определение ширины реки
путем построения равных треугольников
Визируем из точки В на точку А, находящуюся на противоположном берегу, и намечаем линию АВ. Затем от точки В на местности отмеряем линию ВС (произвольной длины), перпендикулярную к линии АВ. Делим линию ВС на два равных отрезка ВЕ и ЕС, в точке Е ставим хорошо заметную вешку. Потом из точки С проводим линию, перпендикулярную к ВС, и двигаемся по ней до тех пор, пока не окажемся в точке D, которая лежит на одной прямой с точками А и Е. Линию СD точно измеряем. Ширина реки АВ равна расстоянию между точками С и D, так как полученные нами треугольники ВЕА и СЕD между собой равны.
Ребята с удовольствием выполняют эту работу.
Интегрированный проект “Геометрия у реки” (математика=география)
Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.
«Актуальность создания школьных служб примирения/медиации в образовательных организациях»
Свидетельство и скидка на обучение каждому участнику
Муниципальное бюджетное общеобразовательное учреждение «Гимназия»
Геометрия у реки
Интегрированная научно- исследовательская работа
(математика и география)
Смирнова Наталия Алексеевна и Чичканова Анастасия Павловна,
ученики 10б класса
Гребенникова Ирина Сергеевна,
учитель математики и
Щербакова Ирина Анатольевна,
1.1 Изучение маршрута по космическому снимку и
картографическая подготовка к походу……………..
2. Исследовательские работы во время похода…………….
2.1 Практические задания-исследования с помощью геометрии
2.1.1 Измерение высоты дерева………………………………
2.1.2 Измерение ширины реки…………………………………
2.1.3 Измерение глубины реки………………………………..
2.1.4 Вычисление площади водного сечения реки…………….
2.1.5 Определение крутизны склона……………………………..
2.1.6 Геометрический способ разведения костра……………….
2.2 Практическое применение географических знаний…………..
Определение сторон горизонта……………………………
2.2.3 Ориентирование по местным предметам……………….
3. Использование практических задач для подготовки к ЕГЭ…………..
3.1 Решение заданий В6……………………………………….
Природа говорит языком математики:
буквы этого языка – круги, треугольники
и иные математические фигуры.
Геометрия и география… Казалось бы, как две эти разные науки взаимосвязаны между собой? Некоторые ученые до сих пор скептически относятся к симбиозу этих двух наук. Резонанс мнений исследователей велик, от восторженных взглядов до недоверчивых мыслей на слияние этих двух дисциплин.
Зарождение геометрии было связано с различными измерительными работами, которые приходилось выполнять при разметке земельных участков, проведении дорог, строительстве зданий и других сооружений. В результате этой деятельности появились и постепенно накапливались различные правила, связанные с геометрическими измерениями и построениями. Таким образом, элементами геометрия можно воспользоваться для измерения ширины, глубины, скорости течения реки, определения крутизны склона, высоты дерева и т. д. Знания географии помогают ориентироваться на местности, использовать один из “языков” международного общения – географическую карту, самостоятельно оценивать уровень безопасности окружающей среды как сферы жизнедеятельности. Таким образом, интегрированная научно-исследовательская работа «Геометрия у реки» ярко демонстрирует связь математики с географией.
Создавая интегрированный проект, мы выдвинули гипотезу: Можно ли воспользоваться приобретёнными геометрическими и географическими знаниями на практике, например в походе? Работая по данной проблеме, пытались выяснить, помогают ли учебные знания выполнить поставленные цели и задачи туристического похода, а также выжить и сохранить здоровье?
Актуальность данной работы состоит в том, что в ней мы рассмотрели возможность практического применения основ геометрии и географии в многодневном водном походе по реке Пра. А современная жизнь делает задачи по геометрии актуальными, так как сфера их практического приложения расширяется. Вопросы инновационных технологий в строительстве, космонавтике, технике невозможны без умения производить необходимые чертежи и вычисления, которые требуют знания важных и интереснейших свойств треугольника. Решая на практике планиметрические задачи типа В6, мы готовимся к ЕГЭ по математике.
Объект исследования: река Пра и её склоны.
Предмет исследования: вода и ландшафт реки.
Цель работы: применить полученные знания по геометрии и географии в условиях дикой природы.
с помощью современных информационных технологий изучить космический снимок Рязанской области; протяжённость маршрута водного похода;
с помощью геометрии: измерить высоту дерева, определить ширину, глубину, скорость течения, крутизну склонов реки Пра;
применить географические знания ориентирования и приспособления к условиям выживания в природе, полученные в школе;
оформить результаты исследования в виде презентации, таблиц и графиков;
решая практические задачи по планиметрии и географии, подготовиться к ЕГЭ.
Методы и приёмы исследования:
Приемы разностороннего гидрологического изучения;
Полевое картирование, фотографические работы;
Знакомство с литературой местного края и архивными источниками.
1. ПОДГОТОВКА К ПОХОДУ
Успех похода во многом зависит от того, насколько подготовился к нему его руководители и как подготовлены к походу все принимающие в нем участие члены туристской группы. Каковы бы ни были цели водных исследований, необходимо, прежде чем приступить к разработке маршрута похода, ознакомиться с краеведческой литературой, имеющей близкое отношение как непосредственно к изучаемому водному объекту, так и к тому району, в котором намечается проводить исследовательские работы . Тщательно продуманный и умело спланированный маршрут во многом предопределяет успех похода. За одну – две недели до выхода на маршрут мы научились пользоваться различными специальными инструментами и самодельным оборудованием, с которым придется иметь дело при исследовательских работах.
Изучение маршрута по космическому снимку и картографическая подготовка к походу
На Земле русской есть удивительный уголок под древним названием Мещёра, включающий Мещёрский национальный парк и Окский заповедник. Неподалёку, на старинном Муромском тракте, промышлял, согласно преданиям Соловей-разбойник. Мещёра вдохновляла многих художников, поэтов, писателей, музыкантов, таких как С. Есенин, К. Паустовский, Ф. Шаляпин. Одной из многочисленных рек Мещёры является река Пра. Река Пра практически ровно пополам делит рязанскую Мещеру. “Я много видел живописных и глухих мест в России, но вряд ли когда-нибудь увижу реку более девственную и таинственную, чем Пра”, – писал К. Паустовский.
Прежде чем отправиться в многодневный байдарочный туристический поход мы с помощью прибора «Космос М-2» изучили космический снимок Рязанской области, её площадь(37374кв. км) и определили географическое положение реки Пра. Пра — река в Рязанской области, левый приток Оки. Берёт начало из озера Святое (Клепиковские озёра), течет Мещёрскими лесами на юг, юго-восток и восток. По спутниковому снимку определили географические координаты истока реки Пра: широта: 54°44’с. ш., долгота: 40°59′ в. д. Длина Пры — 192 км. На Пре расположен город Спас-Клепики— районный центр Рязанской области. Начало водного похода у города Спас-Клёпики. Определили по карте его координаты – 55°с.ш. 40°в.д. и направление маршрута по реке Пра до следующего причала у Жуковских Выселок., далее остановка у села Деулино, его координаты – 54°с. ш. 40° в.д., далее до посёлка Брыкин Бор, его координаты – 54 °с. ш . 40°с.ш. С помощью географической карты наметили протяжённость маршрута, который составил приблизительно 120 км.
2. ИССЛЕДОВАТЕЛЬСКИЕ РАБОТЫ ВО ВРЕМЯ ПОХОДА
2.1 Практические задания-исследования с помощью геометрии
2.1.1 Измерение высоты дерева
Прибрежная растительность реки Пра очень разнообразна. По берегам растёт много различных деревьев и кустарников. Существует множество различных способов измерения высоты дерева, не срубая его и не взбираясь на верхушку, при помощи весьма незамысловатых приборов и даже без всяких приспособлений.
По длине тени: способ Фалеса
Самый лёгкий и самый древний способ – без сомнения, тот, которым греческий мудрец Фалес за шесть веков до нашей эры определил в Египте высоту пирамиды. Он воспользовался её тенью. Нетрудно изменить этот способ так, чтобы в солнечный день можно было пользоваться любой тенью, какой бы длины она ни была. Измерив, и свою тень или тень какого-нибудь шеста, вычислим искомую высоту из пропорции: AB :А1В1= BC :В1С1
т.е. высота дерева во столько же раз больше вашей собственной высоты, во сколько раз тень дерева длиннее вашей тени. Это вытекает, конечно, из геометрического подобия треугольников АВС и А1В1С1.
 Рис.1 Измерение высоты дерева.
Рис.1 Измерение высоты дерева.
Измерение высоты дерева при помощи простого булавочного прибора
Вполне возможно обойтись при измерении высоты и без помощи теней. Прежде всего, мы можем воспользоваться свойством равнобедренного треугольника, обратившись к услугам весьма простого прибора, который легко изготовить из дощечки и трёх булавок. (см. приложение1)


Рис.2 Схема применения булавочного прибора. Рис.3
Приближаясь к дереву или удаляясь от него, мы нашли такое место А (рис.2), из которого, глядя на булавки А1 и С1 , увидели, что они показывают верхушку С дерева: это значит, что продолжение гипотенузы А1С1 проходит через точку С. Тогда, очевидно, расстояние А1В = СВ, так как угол А1=45 0 .
Следовательно, измерив расстояние А1В и прибавив ВD, т.е. возвышение А1А глаза над землёй, получили искомую высоту дерева.
По другому способу вы обходитесь даже и без булавочного прибора. Здесь нужен шест, который мы воткнули в землю так, чтобы выступающая часть как раз равнялась нашему росту. Место для шеста выбрали так, чтобы, лежа, как показано на рис.3, мы видели верхушку дерева на одной прямой линии с верхней точкой шеста. Так как треугольник АВ1С1 – равнобедренный и прямоугольный, то угол А=45 0 и, следовательно, АВ равно ВС, т.е. искомый высоте дерева. Существует ещё множество различных способов измерения высоты дерева. (см. приложение2)
Вывод: применяя различные способы измерения высоты дерева, используя различные инструменты для измерения высот, можно находить высоту различных объектов: здания, магазина, школы, частного дома. Результаты измерений занесли в таблицу и вычислили погрешность измерений (см. приложение).
2.1.2 Измерение ширины реки
Не переплывая реки, измерить её ширину – так же просто для знающего геометрию, как определить высоту дерева, не взбираясь на вершину. Неприступное расстояние измеряют теми же приёмами, какими мы измеряли недоступную высоту. Ширина реки достаточно точно может быть определена способом построения на берегу реки двух равных прямоугольных треугольников. Выбрав на противоположном берегу какой-нибудь приметный предмет А (дерево, камень и т. п.), расположенный у самой воды, вбиваем против него колышек В (рис.4). Вдоль берега, перпендикулярно к линии АВ, отмеряем рулеткой определенное расстояние (например 20 м) и вбиваем колышек С. На продолжении линии ВС в расстоянии, равном также 20 м, вбиваем еще один колышек Д. От колышка Л в направлении ДЕ, перпендикулярном к линии ДВ, надо идти от реки до тех пор, пока колышек С не окажется на одной линии с предметом А. Так как треугольники ABC = Е DC , то ширина реки будет равна расстоянию ДЕ минус ВК.
 Рис.4
Рис.4
При помощи нитки или травинки
Очень прост и удобен приближенный прием определения ширины реки при помощи травинки или нитки. Стоя на берегу реки в точке А(рис.5), заметим на противоположном ее берегу два приметных предмета (например лодку В и дерево С), расположенных близ уреза. Затем, взяв травинку за ее концы вытянутыми перед собой руками, замечают ее длину d, которой закрывается промежуток ВС между выбранными предметами (смотреть надо одним глазом). Затем, сложив травинку (нитку) пополам, отходим от реки до тех пор (точка D), пока промежуток ВС не будет закрыт травинкой. Расстояние AD будет равно ширине реки (на основании существующей в геометрии зависимости между величинами центрального и вписанного углов, опирающихся на одну и ту же хорду).
 Рис.5
Рис.5
Существует множество способов решения этой задачи, которые подробно рассмотрены в приложении 3.
Вывод: вот несколько легко выполнимых приёмов, при помощи которых всегда возможно, не переправляясь на другой берег, измерить не только ширину реки, но и расстояние до любого недоступного объекта со вполне удовлетворительной точностью.
2.1.3 Измерение глубины реки
Близ берега реки мы отыскали водное растение, которое доставило нам реальный материал для практической задачи: без всяких приспособлений, не замочив даже рук, определить глубину водоёма в неглубоком месте.  Рис.6
Рис.6
Решение: Пусть растение возвышается над водой на 0,5м. перегнём его так, чтобы его надводная часть коснулась воды. Тогда расстояние от стебля (точки С) до точки В, касания с водой, составило 1,5м.
Рассмотрим прямоугольный треугольник BD С. Обозначим искомую глубину реки СD через х. (рис.6) Тогда, по теореме Пифагора, имеем:
BD ² = D С 2 +СВ 2 , значит BD ² =х 2 +СВ 2
В D = х+ 0,5, расстояние СВ=1,5м, получим
Х 2 +х+0,25=х 2 +2,25, отсюда х=2
Ответ: искомая глубина реки составила 2м.
Вывод: при помощи различных способов (см. приложение) мы измеряли глубину реки и составили таблицу глубин(см. приложение). Определили, что средняя глубина реки Пра ≈ 1,5 м.
2.2.4 Определение площади водного сечения реки
Умея измерять глубины в отдельных точках и зная положение последних по ширине реки, нетрудно определить площадь поперечного водного сечения.
Проще всего и точнее всего при определении поперечного сечения реки перетянуть через нее промерную веревку (трос) и через равные по ширине расстояния произвести измерение глубин (примерно в 10—20 точках).
По данным измерений, записанным в таблице(см.приложение) (графы 1—3), легко вычертить профиль поперечного сечения реки и вычислить его площадь. Пример построения профиля поперечного сечения реки показан на рисунке 7.
Вычисление площади поперечного сечения заключается в определении площадей отдельных отсеков между соседними промерными вертикалями, представляющих собою трапеции или треугольники (по краям сечения), и последующем суммировании этих частных площадей. Найдя полусуммы соседних глубин и помножив их на соответствующие расстояния между промерными вертикалями, получим частные площади, а просуммировав их, и общую площадь поперечного сечения. Подсчет площади живого сечения дан в графах 4—6 приведенной выше таблице(См. приложение) .
 Рис.7
Рис.7
2.1.5 Определение крутизны склона
Для измерения крутизны склона применили самодельный прибор эклиметр,(см. приложение1) Для измерения крутизны склона прибор должен занять положение, параллельное склону, при этом отвес покажет некую величину β. Для вычисления угла α следует вычесть из 90 о эту, полученную путем измерения, величину β, тогда α=90 о -β, а сама работа по определению крутизны склона при по мощи эклиметра — на рисунке 8
 Рис.8
Рис.8
Крутизна склона приближенно может быть определена измерением его поверхности шагами. Подняв записную книжку до уровня глаз (рис. 26) и держа ее горизонтально, замечают на склоне точку В, в которую попадает луч зрения, скользящий вдоль края книжки. Расстояние АВ измеряют парами шагов. 
Частное от деления 60 градусов на количество пар шагов, пройденных от точки стояния А до точки В, расположенной на склоне на уровне глаз измеряющего, покажет примерную крутизну склона в градусах.
Например, Число 60° выражает приблизительную величину радиана, т. е. центрального угла, опирающегося на дугу окружности, равную длине радиуса ( радиан равен 57°18 ′ ). Отсюда, крутизна склона
Так, если АВ равно 4 парам шагов, а АС (рост человека) — 1 паре шагов, то крутизна склона будет равна 60:4=15 градусам.
[spoiler title=”источники:”]
http://geo.1sept.ru/article.php?ID=200700620
http://infourok.ru/integrirovanniy-proekt-geometriya-u-reki-matematikageografiya-481547.html
[/spoiler]
поделиться знаниями или
запомнить страничку
- Все категории
-
экономические
43,653 -
гуманитарные
33,653 -
юридические
17,917 -
школьный раздел
611,904 -
разное
16,900
Популярное на сайте:
Как быстро выучить стихотворение наизусть? Запоминание стихов является стандартным заданием во многих школах.
Как научится читать по диагонали? Скорость чтения зависит от скорости восприятия каждого отдельного слова в тексте.
Как быстро и эффективно исправить почерк? Люди часто предполагают, что каллиграфия и почерк являются синонимами, но это не так.
Как научится говорить грамотно и правильно? Общение на хорошем, уверенном и естественном русском языке является достижимой целью.
Содержание
- Контрольная работа №4. Подобные треугольники. Вариант 1. Контрольная работа №4. Подобные треугольники. Вариант 2
- Дистанционные курсы для педагогов
- Дистанционные курсы Повышения квалификации и профессиональной переподготовки
- Разговоры о важном
- Контрольная работа по геометрии Подобные треугольники
- Методические и практические аспекты развития пространственного мышления школьников на уроках математики
- Система работы учителя математики по подготовке учащихся основной школы к математическим конкурсам и олимпиадам в рамках обновленного ФГОС ООО
- Математика: теория и методика преподавания с применением дистанционных технологий
- Формирование математической грамотности с целью развития общих компетенций
- Опытные онлайн-репетиторы
- Дистанционные курсы для педагогов
- Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:
- Другие материалы
- Вам будут интересны эти курсы:
- Оставьте свой комментарий
- Автор материала
- Дистанционные курсы для педагогов
- Онлайн-занятия с репетиторами
- Подарочные сертификаты
- Искусство производить измерения
Контрольная работа №4. Подобные треугольники. Вариант 1. Контрольная работа №4. Подобные треугольники. Вариант 2
Контрольная работа №4
Подобные треугольники
Вариант 1
А1. Отрезки АВ и СМ пересекаются в точке О так, что АС || ВМ. Найдите длину отрезка СМ, если АО=16 см, ОВ=4 см, СО=12 см.
А2. В треугольнике АВС точка К принадлежит стороне АВ, а точка Р – стороне АС. Отрезок КР|| BC. Найдите периметр треугольника АКР, если АВ=9 см, ВС=12 см, АС=15 см и АК : КВ=2:1.
А3. В треугольнике АВС угол С=90 0 . АС=3 см, ВС=4 см. Найдите 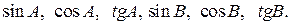
В1. Между пунктами А и В находится болото. Чтобы найти расстояние между А и В, отметили вне болота произвольную точку С, измерили расстояние АС = 600 м и ВС = 400 м, а также 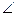 АСВ = 62°.
АСВ = 62°.
Начертите план в масштабе 1 : 10 000 и найдите по нему расстояние между пунктами А и В.
____________________________________________________________________
Контрольная работа №4
Подобные треугольники
Вариант 2
А1. Отрезки АВ и СМ пересекаются в точке О так, что АС || ВМ. Найдите длину отрезка СМ, если АС=15 см, ВМ=3 см, СО=10 см.
А2. В треугольнике АВС точка К принадлежит стороне АВ, а точка Р – стороне АС. Отрезок КР|| BC. Найдите периметр треугольника АКР, если АВ=16 см, ВС=8 см, АС=15 см и АК =4 см.
 А3. В треугольнике АВС угол С=90 0 . АС=4 см, АВ=5 см. Найдите
А3. В треугольнике АВС угол С=90 0 . АС=4 см, АВ=5 см. Найдите 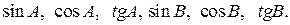
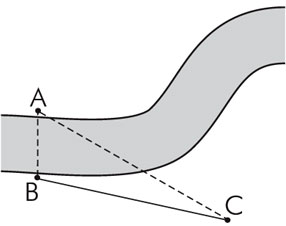
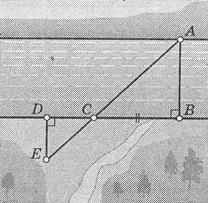
В1. На рисунке показано, как можно определить ширину реки АВ, построив на местности подобные треугольники. Обоснуйте: какие построения выполнены; чем мы пользуемся для определения ширины реки? Выполните необходимые измерения и определите ширину реки
Источник
Дистанционные курсы для педагогов
650 курсов повышения квалификации от 590 руб.
253 курса профессиональной переподготовки от 2190 руб.
Входим в перечень Министерства просвещения Российской Федерации
Дистанционные курсы Повышения квалификации и профессиональной переподготовки
900 курсов от 770 рублей
Разговоры о важном
Рекомендуем всем учителям 1-11 классов
Войти с помощью:
Контрольная работа по геометрии Подобные треугольники
Контрольная работа №4
А1. Отрезки АВ и СМ пересекаются в точке О так, что АС || ВМ. Найдите длину отрезка СМ, если АО=12 см, ОВ=3 см, СО=8 см.
А2. В треугольнике АВС точка К принадлежит стороне АВ, а точка Р – стороне АС. Отрезок КР|| BC . Найдите периметр треугольника АКР, если АВ=9 см, ВС=12 см, АС=15 см и АК : КВ=2:1.
А3. В треугольнике АВС угол С=90 0 . АС=15см, ВС=8 см. Найдите 
В1. Между пунктами А и В находится болото. Чтобы найти расстояние между А и В, отметили вне болота произвольную точку С, измерили расстояние АС = 600 м и ВС = 400 м, а также  АСВ = 62°.
АСВ = 62°.
Начертите план в масштабе 1 : 10 000 и найдите по нему расстояние между пунктами А и В.
Контрольная работа №4
А1. Отрезки АВ и СМ пересекаются в точке О так, что АС || ВМ. Найдите длину отрезка СМ, если АС=15 см, ВМ=3 см, СО=10 см.
А2. В треугольнике АВС точка К принадлежит стороне АВ, а точка Р – стороне АС. Отрезок КР|| BC . Найдите периметр треугольника АКР, если АВ=16 см, ВС=8 см, АС=15 см и АК =4 см.
 А3. В треугольнике АВС угол С=90 0 . АС=4 см, АВ=5 см. Найдите
А3. В треугольнике АВС угол С=90 0 . АС=4 см, АВ=5 см. Найдите 
В1. На рисунке показано, как можно определить ширину реки АВ, построив на местности подобные треугольники. Обоснуйте: какие построения выполнены; чем мы пользуемся для определения ширины реки? Выполните необходимые измерения и определите ширину реки
(масштаб рисунка 1 : 1000).


Курс повышения квалификации
Методические и практические аспекты развития пространственного мышления школьников на уроках математики
- Сейчас обучается 37 человек из 28 регионов


Курс повышения квалификации
Система работы учителя математики по подготовке учащихся основной школы к математическим конкурсам и олимпиадам в рамках обновленного ФГОС ООО
- Сейчас обучается 82 человека из 35 регионов


Курс профессиональной переподготовки
Математика: теория и методика преподавания с применением дистанционных технологий


Формирование математической грамотности с целью развития общих компетенций


Лучшее для учеников, педагогов и родителей
Опытные
онлайн-репетиторы
- По любым предметам 1-11 классов
- Подготовка к ЕГЭ и ОГЭ
Рабочие листы и материалы для учителей и воспитателей
Более 6 500 дидактических материалов для школьного и домашнего обучения
Самые массовые международные дистанционные
29 конкурсов на разные темы для учеников 1–11 классов и дошкольников
29 конкурсов для учеников 1–11 классов и дошкольников от проекта «Инфоурок»
Дистанционные курсы для педагогов
Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:
6 127 428 материалов в базе
Другие материалы






Вам будут интересны эти курсы:
Оставьте свой комментарий
Авторизуйтесь, чтобы задавать вопросы.
Добавить в избранное
- 07.02.2018 4327
- DOCX 197.5 кбайт
- 24 скачивания
- Оцените материал:
Настоящий материал опубликован пользователем Усманова Олеся Тимербаевна. Инфоурок является информационным посредником и предоставляет пользователям возможность размещать на сайте методические материалы. Всю ответственность за опубликованные материалы, содержащиеся в них сведения, а также за соблюдение авторских прав несут пользователи, загрузившие материал на сайт
Если Вы считаете, что материал нарушает авторские права либо по каким-то другим причинам должен быть удален с сайта, Вы можете оставить жалобу на материал.
Автор материала

- На сайте: 6 лет и 3 месяца
- Подписчики: 1
- Всего просмотров: 45289
- Всего материалов: 26
Московский институт профессиональной
переподготовки и повышения
квалификации педагогов
Дистанционные курсы
для педагогов
663 курса от 490 рублей
Выбрать курс со скидкой
Выдаём документы
установленного образца!
Онлайн-занятия с репетиторами

о которых мечтает каждая женщина
Способы организации, средства и методы развития физических качеств в период дистанционного обучения
Путешествие в Японию. Особенности традиционное японского жилища
Риск и экологический риск. Методология оценки риска
Подарочные сертификаты
Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.
Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.
Источник
Искусство производить измерения
Джайб
| Предметное поле | Математика, литература, история, русский язык, черчение, воспитательная работа |
| Класс | 9-11 |
| Типология | Обучающая |
| Личностно-значимый познавательный вопрос | По своему правы те, кто говорит, что тригонометрия в реальной жизни не нужна. Ну, каковы ее обычные прикладные задачи? Измерять расстояние между недоступными объектами. С помощью тригонометрии составляют карты, измеряют высоту гор или деревьев, ширину рек и озер, расстояния до звезд. Простому дворнику все эти измерения и не нужны. Но однажды у нас сломался старенький бабушкин телевизор со стеклянным экраном и электронно-лучевой трубкой. И решили мы купить новый, жидкокристаллический. Старый телевизор был 29 дюймов по диагонали. Идем мы в магазин и покупаем бабушке новый телевизор. 29 дюймов сейчас не делают, возьмем 32, пусть бабушка порадуется. Приносим подарок, включаем, а бабушка нам и говорит: «Чой-то маленький какой-то телевизор, мой-то больше был, милые!» Можно было бы эти бабушкины высказывания пропустить мимо ушей, но мы знаем тригонометрию (!) и решили разобраться в этом вопросе. У старого телевизора отношение сторон – 4:5, а у нового – 9:16. Высота экрана бабушкиного телевизора была чуть больше 18 дюймов, а мы ей купили экран с высотой менее 16 дюймов. Вот он ей и кажется маленьким. Интернет-блогер Матвей Павлов Как мы это посчитали? Давайте разбираться в этой ситуации вместе. А где ещё в реальной жизни Вам могут пригодиться знания из тригонометрии? |
| Информация по данному вопросу | Текст 1. Определение синуса, косинуса, тангенса и котангенса острого угла прямоугольного треугольника: Синусом α острого угла прямоугольного треугольника называется отношение AB/OB (противолежащего катета к гипотенузе). 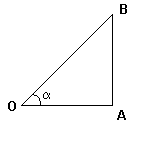 Косинусом α острого угла прямоугольного треугольника называется отношение ОА/OB (прилежащего катета к гипотенузе). Тангенсом α острого угла прямоугольного треугольника называется отношение AB/OA (отношение противолежащего катета к прилежащему). Учебник «Геометрия 7-9 класс» Текст 2. В строительстве очень важно знать площадь участка, отведённого на застройку. Для измерения площади древние египтяне использовали особый треугольник, у которого были фиксированные длины сторон. Занимались измерениями особые специалисты, которые назывались «натягивателями каната» (гарпедонаптай). Они брали длинную верёвку, делили её на 12 равных частей узелками или какими – то другими метками, а концы верёвки связывали. На направлении север – юг они устанавливали два кола на расстоянии четырёх частей, отмеченных на верёвке. Затем при помощи третьего кола натягивали связанную верёвку так, чтобы образовался треугольник, у которого одна сторона имела три части, другая – четыре, а третья пять частей. Получался прямоугольный треугольник, площадь которого могла быть принята за эталон, если ремесленники пользовались верёвкой всегда одной и той же строго определённой длины. При этом одна сторона, имеющая три части, указывала восточно-западное направление. История математики, 2012 год Текст 3. «- Сегодня нам надо измерить высоту площади далёкого Вида, – сказал инженер. – Вам понадобится для этого инструмент? – спросил Герберт. — Нет, не понадобится. Мы будем действовать несколько иначе, обратившись к не менее простому и точному способу. Юноша, стараясь научиться возможно большему, последовал за инженером, который спустился с гранитной стены до окраины берега. Взяв прямой шест, футов 12 длиною, инженер измерил его возможно точнее, сравнивая со своим ростом, который был ему хорошо известен. Герберт же нес за ним отвес, вручённый ему инженером: просто камень, привязанный к концу веревки. Не доходя футов 500 до гранитной стены, поднимавшейся отвесно, инженер воткнул шест в песок фута на 2 и, прочно укрепив его, поставил вертикально с помощью отвеса. Затем он отошёл от шеста на такое расстояние, чтобы, лёжа на песке, можно было на одной прямой линии видеть и конец шеста, и край гребня. Эту точку он тщательно пометил колышком. — Тебе знакомы начатки геометрии? – спросил он Герберта, поднимаясь с земли. — Да. — Помнишь свойства подобных треугольников? — Их сходственные стороны пропорциональны. — Правильно. Так вот, сейчас я построю два подобных прямоугольных треугольника. У меньшего одним из катетов будет отвесный шест, другим – расстояние от колышка до основания шеста; гипотенуза же – мой луч зрения. У другого треугольника катетами будут отвесная стена, высоту которой мы хотим определить, и расстояние от колышка до основания этой стены; гипотенуза же – мой луч зрения, совпадающий с направлением гипотенузы первого треугольника. — Понял! – воскликнул юноша. – Расстояние от колышка до шеста так относится к расстоянию от колышка до основания стены, как высота шеста к высоте стены. — Да. И следовательно, если мы измерим два первых расстояния, то зная высоту шеста, сможем вычислить четвёртый, неизвестный член пропорции, то есть высоту стены. — Оба горизонтальных расстояния были измерены: меньшее равнялось 15 футам, большее – 500 футам. По окончании измерений инженер составил следующую запись: 15 : 500 = 10 : х, 500 × 10 = 5000, 5000 : 15 = 333,8. Значит, высота гранитной стены равнялась 333 футам». Ж.Верн «Таинственный остров» Текст 4. Наибольшее внимание ученых привлекали тригонометрические соотношения на сферических поверхностях. Это было продиктовано нуждами астрономии и географии. Дело в том, что преобладающей гипотезой о строении вселенной была геоцентристская. Согласно этой гипотезе земля есть шар, расположенный в центре небесной сферы, которая равномерно вращается вокруг своей оси. Светила расположены на этой сфере. Их движения и подвергаются изучению. При этом большое значение приобретают математические задачи о расположении точек и фигур на сферах и об их движениях (перемещениях). Работы, в которых подобные задачи решаются, получили название сферики. В сферику включались теоремы об окружностях и сферах, графические приемы построения сферических треугольников, сферопея или объединение кинематических моделей, изображающих мир (армиллы), и др. В сферике, таким образом, сочетались элементы практической астрономии, географии (определение места наблюдения, направления пути по положению небесных светил) и геометрии на сферах. Плоская тригонометрия при таких условиях отнюдь не играла лишь второстепенную роль по сравнению с тригонометрией сферической. У нее была своя область приложений. Кроме того, она являлась частью практической астрономии, так как в последней широко используются ортогональные проектирования. Фигуры, находящиеся или передвигающиеся на сфере, проектируются на плоскости, избранные для отсчетов: плоскости горизонта, меридиана или др. Тем самым многие задачи сводятся к плоским случаям. Измерительные операции при этом чаще всего прилагаются к хордам. Многократное применение подобных операций неизбежно порождало стремление табулировать значения хорд, составлять таблицы их значений. Сипливец Алексей, г. Нежина Текст 5. Синус – одна из тригонометрических функций, обозначение sin. Синус острого угла в прямоугольном треугольнике называется отношение катета, лежащего против этого угла, к гипотенузе. Индийские математики Синус обозначали словом «джива» (буквально — тетива лука). Арабы переделали этот термин в «джиба», который в дальнейшем превратился в «джайб» — обиходное слово арабского языка, означающее изгиб, пазуха, складка одежды, что соответствует латинскому слову sinus. Большая советская энциклопедия, 1969—1978 Косинусом α острого угла прямоугольного треугольника называется отношение ОА/OB (прилежащего катета к гипотенузе). Тангенсом α острого угла прямоугольного треугольника называется отношение AB/OA (отношение противолежащего катета к прилежащему). Учебник «Геометрия 7-9 класс» Текст 2. В строительстве очень важно знать площадь участка, отведённого на застройку. Для измерения площади древние египтяне использовали особый треугольник, у которого были фиксированные длины сторон. Занимались измерениями особые специалисты, которые назывались «натягивателями каната» (гарпедонаптай). Они брали длинную верёвку, делили её на 12 равных частей узелками или какими – то другими метками, а концы верёвки связывали. На направлении север – юг они устанавливали два кола на расстоянии четырёх частей, отмеченных на верёвке. Затем при помощи третьего кола натягивали связанную верёвку так, чтобы образовался треугольник, у которого одна сторона имела три части, другая – четыре, а третья пять частей. Получался прямоугольный треугольник, площадь которого могла быть принята за эталон, если ремесленники пользовались верёвкой всегда одной и той же строго определённой длины. При этом одна сторона, имеющая три части, указывала восточно-западное направление. История математики, 2012 год Текст 3. «- Сегодня нам надо измерить высоту площади далёкого Вида, – сказал инженер. – Вам понадобится для этого инструмент? – спросил Герберт. — Нет, не понадобится. Мы будем действовать несколько иначе, обратившись к не менее простому и точному способу. Юноша, стараясь научиться возможно большему, последовал за инженером, который спустился с гранитной стены до окраины берега. Взяв прямой шест, футов 12 длиною, инженер измерил его возможно точнее, сравнивая со своим ростом, который был ему хорошо известен. Герберт же нес за ним отвес, вручённый ему инженером: просто камень, привязанный к концу веревки. Не доходя футов 500 до гранитной стены, поднимавшейся отвесно, инженер воткнул шест в песок фута на 2 и, прочно укрепив его, поставил вертикально с помощью отвеса. Затем он отошёл от шеста на такое расстояние, чтобы, лёжа на песке, можно было на одной прямой линии видеть и конец шеста, и край гребня. Эту точку он тщательно пометил колышком. — Тебе знакомы начатки геометрии? – спросил он Герберта, поднимаясь с земли. — Да. — Помнишь свойства подобных треугольников? — Их сходственные стороны пропорциональны. — Правильно. Так вот, сейчас я построю два подобных прямоугольных треугольника. У меньшего одним из катетов будет отвесный шест, другим – расстояние от колышка до основания шеста; гипотенуза же – мой луч зрения. У другого треугольника катетами будут отвесная стена, высоту которой мы хотим определить, и расстояние от колышка до основания этой стены; гипотенуза же – мой луч зрения, совпадающий с направлением гипотенузы первого треугольника. — Понял! – воскликнул юноша. – Расстояние от колышка до шеста так относится к расстоянию от колышка до основания стены, как высота шеста к высоте стены. — Да. И следовательно, если мы измерим два первых расстояния, то зная высоту шеста, сможем вычислить четвёртый, неизвестный член пропорции, то есть высоту стены. — Оба горизонтальных расстояния были измерены: меньшее равнялось 15 футам, большее – 500 футам. По окончании измерений инженер составил следующую запись: 15 : 500 = 10 : х, 500 × 10 = 5000, 5000 : 15 = 333,8. Значит, высота гранитной стены равнялась 333 футам». Ж.Верн «Таинственный остров» Текст 4. Наибольшее внимание ученых привлекали тригонометрические соотношения на сферических поверхностях. Это было продиктовано нуждами астрономии и географии. Дело в том, что преобладающей гипотезой о строении вселенной была геоцентристская. Согласно этой гипотезе земля есть шар, расположенный в центре небесной сферы, которая равномерно вращается вокруг своей оси. Светила расположены на этой сфере. Их движения и подвергаются изучению. При этом большое значение приобретают математические задачи о расположении точек и фигур на сферах и об их движениях (перемещениях). Работы, в которых подобные задачи решаются, получили название сферики. В сферику включались теоремы об окружностях и сферах, графические приемы построения сферических треугольников, сферопея или объединение кинематических моделей, изображающих мир (армиллы), и др. В сферике, таким образом, сочетались элементы практической астрономии, географии (определение места наблюдения, направления пути по положению небесных светил) и геометрии на сферах. Плоская тригонометрия при таких условиях отнюдь не играла лишь второстепенную роль по сравнению с тригонометрией сферической. У нее была своя область приложений. Кроме того, она являлась частью практической астрономии, так как в последней широко используются ортогональные проектирования. Фигуры, находящиеся или передвигающиеся на сфере, проектируются на плоскости, избранные для отсчетов: плоскости горизонта, меридиана или др. Тем самым многие задачи сводятся к плоским случаям. Измерительные операции при этом чаще всего прилагаются к хордам. Многократное применение подобных операций неизбежно порождало стремление табулировать значения хорд, составлять таблицы их значений. Сипливец Алексей, г. Нежина Текст 5. Синус – одна из тригонометрических функций, обозначение sin. Синус острого угла в прямоугольном треугольнике называется отношение катета, лежащего против этого угла, к гипотенузе. Индийские математики Синус обозначали словом «джива» (буквально — тетива лука). Арабы переделали этот термин в «джиба», который в дальнейшем превратился в «джайб» — обиходное слово арабского языка, означающее изгиб, пазуха, складка одежды, что соответствует латинскому слову sinus. Большая советская энциклопедия, 1969—1978 |
| Задания для работы и информацией | |
| Ознакомление | Дайте лексическое толкование слова «Джайб». |
| Понимание | Постройте египетский треугольник с помощью циркуля и линейки без шкалы. Опишите шаги, необходимые для его построения. Предложите Герберту способ измерения высоты гранитной стены, позволяющий использовать определение синуса угла. |
| Применение | Проанализируйте особенности построения углов в 30°, 60°, 45° на основе определения синуса, косинуса и тангенса углов. Предложите дизайнеру несколько способов построения таких элементов в дизайне помещений. |
| Анализ | Разработайте план (эскиз) комнаты школьника, позволяющий показать применение нестандартных элементов дизайна интерьера. |
| Синтез | Проведите экспертизу ситуации с телевизором. Сделайте расчёты, доказывающие праводу рассуждений Матвея Павлова. |
| Оценка | Оцените значимость тригонометрических знаний для реальной жизни. Запишите свои рассуждения в форме связного текста. |
Лубнина В.А.,
МБОУ «СОШ с УИОП № 66» г. Киров
| Предметное поле | Математика, география, ОБЖ |
| Класс | |
| Типология | Обучающая |
| Личностно–значимый познавательный вопрос | В современном мире мы определяем значения различных величин (длину, массу, температуру и т. п.) с помощью различных инструментов и приборов. Так, в своей профессиональной деятельности строители, архитекторы, лесоводы, военные для определения высоты объекта используют специальные сложные и дорогостоящие приборы – высотомеры. Можете ли Вы определить высоту здания или дерева без использования технических средств, полагаясь только на то, что есть «под руками»? Такое умение необходимо многим людям, находящимся в лесу: туристам, охотникам, лесникам. |
| Информация по данному вопросу | Текст 1. С пропорциями имели дело древние строители. Правильные соотношения, возводимых ими дворцов и храмов придавало этим зданиям ту необыкновенную красоту, которая восхищает нас и сегодня. Древнегреческие математики очень искусно преобразовывали пропорции, доказывали с их помощью самые сложные утверждения, решали самые сложные задачи. Говорят, что отрезки AB и СD пропорциональны отрезкам A1B1 и C1D1, если 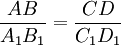 . Два треугольника называются подобными, если их углы соответственно равны и стороны одного треугольника пропорциональны сходственным сторонам другого. Коэффициентом подобия называется число k, равное отношению сходственных сторон. Признаки подобия треугольников: I. Два треугольника подобны, если два угла одного треугольника соответственно равны двум углам другого. II. Два треугольника подобны, если две стороны одного треугольника пропорциональны двум сторонам другого треугольника и углы, лежащие между ними, равны. III. Два треугольника подобны, если три стороны одного треугольника пропорциональны трём сторонам другого треугольника. Отношение периметров двух подобных треугольников равно коэффициенту подобия. Отношение площадей двух подобных треугольников равно квадрату коэффициента подобия. Источник: Атанасян Л. С., Геометрия 7-9 класс . Два треугольника называются подобными, если их углы соответственно равны и стороны одного треугольника пропорциональны сходственным сторонам другого. Коэффициентом подобия называется число k, равное отношению сходственных сторон. Признаки подобия треугольников: I. Два треугольника подобны, если два угла одного треугольника соответственно равны двум углам другого. II. Два треугольника подобны, если две стороны одного треугольника пропорциональны двум сторонам другого треугольника и углы, лежащие между ними, равны. III. Два треугольника подобны, если три стороны одного треугольника пропорциональны трём сторонам другого треугольника. Отношение периметров двух подобных треугольников равно коэффициенту подобия. Отношение площадей двух подобных треугольников равно квадрату коэффициента подобия. Источник: Атанасян Л. С., Геометрия 7-9 класс  Текст 2. Измерение высоты дерева с помощью лужи можно удачно применять после дождя (в случае, когда луж нет, можно использовать зеркало). Измерение производят таким образом: находят невдалеке от измеряемого предмета лужицу и становятся около неё так, чтобы она помещалась между вами и предметом. После этого находят точку, из которой видна отражённая в воде вершинка предмета. Измеряемый предмет, например дерево, будет во столько раз выше вас, во сколько расстояние от него до лужицы больше, чем расстояние от лужицы до вас. Источник: http://piterhunt.ru Текст 3. Притча о Фалесе. Усталый пришел северный чужеземец в страну Великого Хапи. Солнце уже садилось, когда он подошел к великолепному дворцу фараона, что-то сказал слугам. Те мгновенно распахнули перед ним двери и провели его в приемную залу. И вот он стоит в запыленном походном плаще, а перед ним на золоченном троне сидит фараон. Рядом стоят высокомерные жрецы, хранители вечных тайн природы. – Кто ты? – спросил верховный жрец? – Зовут меня Фалес. Родом я из Милета. Жрец надменно продолжал: – Так это ты похвалялся, что сможешь измерить высоту пирамиды, не взбираясь на нее? – жрецы согнулись от хохота. – Будет хорошо, – насмешливо продолжал жрец, – если ты ошибешься не более, чем на сто локтей. – Я могу измерить высоту пирамиды и ошибусь не более чем на пол-локтя. Я сделаю это завтра. Лица жрецов потемнели. Какая наглость! Этот чужестранец утверждает, что может вычислить то, чего не могут они – жрецы Великого Египта. – Хорошо, сказал фараон. – Около дворца стоит пирамида, мы знаем ее высоту. Завтра проверим твое искусство. На следующий день Фалес нашёл длинную палку, воткнул её в землю чуть поодаль пирамиды. Провёл некоторые измерения и назвал высоту пирамиды. Источник: http://www.myshared.ru Текст 2. Измерение высоты дерева с помощью лужи можно удачно применять после дождя (в случае, когда луж нет, можно использовать зеркало). Измерение производят таким образом: находят невдалеке от измеряемого предмета лужицу и становятся около неё так, чтобы она помещалась между вами и предметом. После этого находят точку, из которой видна отражённая в воде вершинка предмета. Измеряемый предмет, например дерево, будет во столько раз выше вас, во сколько расстояние от него до лужицы больше, чем расстояние от лужицы до вас. Источник: http://piterhunt.ru Текст 3. Притча о Фалесе. Усталый пришел северный чужеземец в страну Великого Хапи. Солнце уже садилось, когда он подошел к великолепному дворцу фараона, что-то сказал слугам. Те мгновенно распахнули перед ним двери и провели его в приемную залу. И вот он стоит в запыленном походном плаще, а перед ним на золоченном троне сидит фараон. Рядом стоят высокомерные жрецы, хранители вечных тайн природы. – Кто ты? – спросил верховный жрец? – Зовут меня Фалес. Родом я из Милета. Жрец надменно продолжал: – Так это ты похвалялся, что сможешь измерить высоту пирамиды, не взбираясь на нее? – жрецы согнулись от хохота. – Будет хорошо, – насмешливо продолжал жрец, – если ты ошибешься не более, чем на сто локтей. – Я могу измерить высоту пирамиды и ошибусь не более чем на пол-локтя. Я сделаю это завтра. Лица жрецов потемнели. Какая наглость! Этот чужестранец утверждает, что может вычислить то, чего не могут они – жрецы Великого Египта. – Хорошо, сказал фараон. – Около дворца стоит пирамида, мы знаем ее высоту. Завтра проверим твое искусство. На следующий день Фалес нашёл длинную палку, воткнул её в землю чуть поодаль пирамиды. Провёл некоторые измерения и назвал высоту пирамиды. Источник: http://www.myshared.ru |
| Задания на работу с данной информацией | |
| Ознакомление | 1. Отрезки AB,CD и EF,MN пропорциональны друг другу. Найти EF,если AB= 5 см, CD= 80 мм, MN= 1 дм. 2. Что показывает коэффициент подобия? 3. Если в определении подобных треугольников поменять условие и заключение, будет ли оно верным? 4. Площадь одного подобного треугольника в четыре раза больше площади другого. Найдите коэффициент подобия. 5. Подобны ли треугольники ABC и A1B1C1, если известно, что: AB=10 см, BC=8 см, A1B1=5 см, A1C1=3 см, ÐC=ÐC1=90 0 ? |
| Понимание |  Короткое плечо шлагбаума имеет длину 1м, а длинное плечо 4м. На какую высоту (в метрах) поднимается конец длинного плеча, когда конец короткого опускается на 0,5м? Короткое плечо шлагбаума имеет длину 1м, а длинное плечо 4м. На какую высоту (в метрах) поднимается конец длинного плеча, когда конец короткого опускается на 0,5м? |
| Применение | В деревне у бабушки растёт старый тополь, который Вам необходимо спилить. В 10 м от тополя стоит забор. Определите, упадёт ли тополь на забор, если в 8 м от дерева находится лужа, отойдя от которой на 1,5 м вы видите верхушку тополя (рост человека 1м 70 см). |
| Анализ | 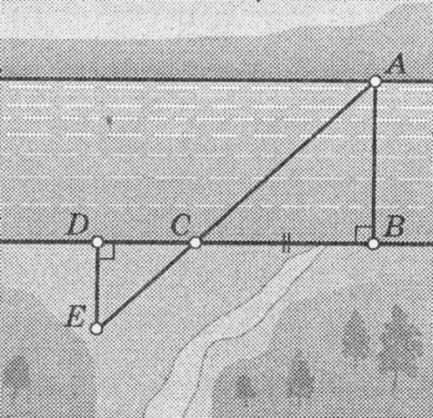 Из воспоминаний участника Великой Отечественной войны: «Нашему отделению было приказано измерить ширину реки, через которую предстояло организовать переправу. Подобравшись к кустарнику вблизи реки, отделение залегло, а я вместе с другим солдатом выдвинулся ближе к реке, откуда был хорошо виден противоположный берег. В таких условиях измерить ширину реки можно было и на глаз. Но мы поступили следующим образом. » На рисунке показано, как можно определить ширину реки АВ, построив на местности подобные треугольники. Проанализируйте: какие построения выполнены; чем мы пользуемся для определения ширины реки? Выполните необходимые измерения и определите ширину реки (масштаб рисунка 1 : 1000). Из воспоминаний участника Великой Отечественной войны: «Нашему отделению было приказано измерить ширину реки, через которую предстояло организовать переправу. Подобравшись к кустарнику вблизи реки, отделение залегло, а я вместе с другим солдатом выдвинулся ближе к реке, откуда был хорошо виден противоположный берег. В таких условиях измерить ширину реки можно было и на глаз. Но мы поступили следующим образом. » На рисунке показано, как можно определить ширину реки АВ, построив на местности подобные треугольники. Проанализируйте: какие построения выполнены; чем мы пользуемся для определения ширины реки? Выполните необходимые измерения и определите ширину реки (масштаб рисунка 1 : 1000). |
| Синтез | Как, по Вашему мнению, Фалес вычислил высоту египетской пирамиды? Найдите её высоту, если высота шеста – 4 локтя; длина тени шеста – 6 локтей; длина тени пирамиды – 200 локтей. |
| Оценка | На каком оптимальном расстоянни от грядок необходимо построить домик высотой 6 м, чтобы грядки как можно больше времени были освещены солнцем. |
Лямина О.В.,
учитель математики, МОАУ СОШ с УИОП №10, г. Киров
Источник