Правильный шестиугольник, многоугольнике с 6 вершинами, вычислить его параметры. Шестиугольник-это фигура, из которой можно складывать мозаику (черепицу). Введите одно из известных значений. Затем нажмите кнопку вычислить.
.
Поделиться расчетом:
Калькулятор шестиугольников
Длина стороны(a)
Большая диагональ(d1)
Меньшая диагональ(d2)
Периметр(p)
Площадь(S)
Радиус вписанной окружности(r)
Вычислить
Очистить
Формулы:

d2 = √3 * a
p = 6 * a
S = 3/2 * √3 * a2
r = √3 / 2 * a
Высота = d2 = 2 * r
Радиус окружности = a
Внутренние углы: 120°, 9 диагоналей





Ширина шестиугольника Решение
ШАГ 0: Сводка предварительного расчета
ШАГ 1. Преобразование входов в базовый блок
Длина края шестиугольника: 6 метр –> 6 метр Конверсия не требуется
ШАГ 2: Оцените формулу
ШАГ 3: Преобразуйте результат в единицу вывода
12 метр –> Конверсия не требуется
9 Ширина шестиугольника Калькуляторы
2 Ширина шестиугольника Калькуляторы
Ширина шестиугольника формула
Ширина шестиугольника = 2*Длина края шестиугольника
w = 2*le
Что такое шестиугольник?
Правильный шестиугольник определяется как равносторонний и равноугольный шестиугольник. Просто это шестисторонний правильный многоугольник. Он бицентрический, что означает, что он одновременно циклический (имеет описанную окружность) и тангенциальный (имеет вписанную окружность). Общая длина сторон равна радиусу описанной окружности или описанной окружности, которая равна 2/sqrt(3), умноженной на апофему (радиус вписанной окружности). Все внутренние углы равны 120 градусов. Правильный шестиугольник имеет шесть вращательных симметрий.
The six-sided hexagon shape pops up in some unlikely places: the cells of honeycombs, the shapes soap bubbles make when they’re smashed together, the outer edge of bolts, and even the hexagon-shaped basalt columns of the Giant’s Causeway, a natural rock formation on the north coast of Ireland. Assuming you’re dealing with a regular hexagon, which means all its sides are of the same length, you can use the hexagon’s perimeter or its area to find the length of its sides.
TL;DR (Too Long; Didn’t Read)
The simplest, and by far most common, way of finding the length of a regular hexagon’s sides is using the following formula:
s = P ÷ 6, where P is the perimeter of the hexagon, and s is the length of any one of its sides.
Calculating Hexagon Sides From the Perimeter
Because a regular hexagon has six sides of the same length, finding the length of any one side is as simple as dividing the hexagon’s perimeter by 6. So if your hexagon has a perimeter of 48 inches, you have:
frac{48 text{ inches}}{6} = 8 text{ inches}
Each side of your hexagon measures 8 inches in length.
Calculating Hexagon Sides From the Area
Just like squares, triangles, circles and other geometric shapes you may have dealt with, there is a standard formula for calculating the area of a regular hexagon. It is:
A = (1.5 × sqrt{3}) × s^2
where A is the hexagon’s area and s is the length of any one of its sides.
Obviously, you can use the length of the hexagon’s sides to calculate the area. But if you know the hexagon’s area, you can use the same formula to find the length of its sides instead. Consider a hexagon that has an area of 128 in2:
Start by substituting the area of the hexagon into the equation:
128 = (1.5 × sqrt{3}) × s^2
The first step in solving for s is to isolate it on one side of the equation. In this case, dividing both sides of the equation by (1.5 × √3) gives you:
frac{128}{1.5 × sqrt{3}} = s^2
Conventionally the variable goes on the left side of the equation, so you can also write this as:
s^2=frac{128}{1.5 × sqrt{3}}
Simplify the term on the right. Your teacher might let you approximate √3 as 1.732, in which case you’d have:
s^2=frac{128}{1.5 × 1.732}
Which simplifies to:
s^2=frac{128}{2.598}
Which, in turn, simplies to:
s^2 = 49.269
You can probably tell, by examination, that s is going to be close to 7 (because 72 = 49, which is very close to the equation you’re dealing with). But taking the square root of both sides with a calculator will give you a more exact answer. Don’t forget to write in your units of measure, too:
sqrt{s^2} = sqrt{49.269}
then becomes:
s = 7.019 text{ inches}
Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 28 февраля 2022 года; проверки требуют 2 правки.
| Шестиугольник | |
|---|---|
 Правильный шестиугольник |
|
| Тип | Правильный многоугольник |
| Рёбра | 6 |
| Символ Шлефли | {6}, t{3} |
| Диаграмма Коксетера — Дынкина |
|
| Вид симметрии | Диэдрическая группа (D6) |
| Площадь |
   |
| Внутренний угол | 120° |
| Свойства | |
| выпуклый, вписанный, Равносторонний, равноугольный[en], изотоксальный | |
Правильный шестиугольник (или гексагон от греч. εξάγωνο) — правильный многоугольник с шестью сторонами.
Свойства[править | править код]
Построение[править | править код]
Правильный шестиугольник можно построить с помощью циркуля и линейки. Ниже приведён метод построения, предложенный Евклидом в «Началах», книга IV, теорема 15.
Правильный шестиугольник в природе, технике и культуре[править | править код]
- Пчелиные соты показывают разбиение плоскости на правильные шестиугольники.
- Некоторые сложные молекулы углерода (напр., графит) имеют гексагональную кристаллическую решётку.
- Гигантский гексагон — атмосферное явление на Сатурне.
- Сечение гайки и многих карандашей имеет вид правильного шестиугольника.
- Игровое поле гексагональных шахмат составляют шестиугольники, в отличие от квадратов традиционной шахматной доски.
- Гексаграмма — шестиконечная звезда, образованная двумя правильными треугольниками. Под названием звезда Давида она является символом иудаизма.
- Гексагоном[fr] иногда называют материковую часть Франции, потому что её географические очертания напоминают данную геометрическую фигуру.
Примечания[править | править код]
- ↑ А. М. Райгородский. Проблема Борсука. — М.: Издательство МЦНМО, 2006. — С. 9. — 56 с. — (Библиотека „Математическое просвещение“). — ISBN ISBN 5-94057-249-9.
См. также[править | править код]
- Шестиугольник
- Упаковка кругов на плоскости
Ссылки[править | править код]
- Шестиугольный мир (ЖЖ-сообщество)
Правильный шестиугольник
Правильный шестиугольник — это такой шестиугольник у которого все шесть сторон равны и его шесть углов равны.
Правильный шестиугольник
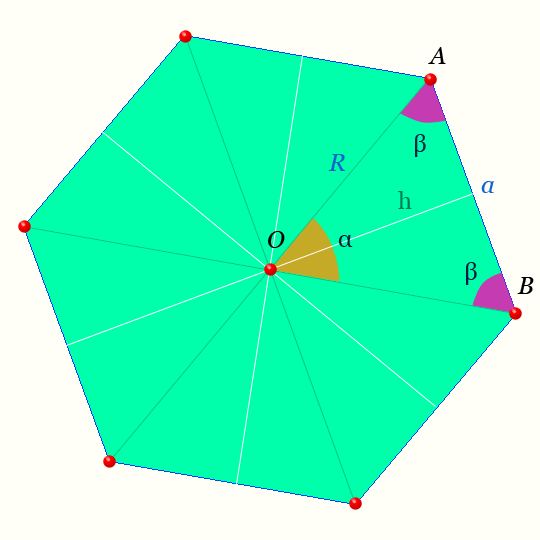
Центр правильного шестиугольника — на рисунке точка O равноудалена от вершин.
Светлая линия обозначающая высоту треугольника AOB : h называется — апофемой.
Отрезки OA, OB — радиусы правильного шестиугольника.
Обозначения на рисунке для правильного шестиугольника
| n=6 | число сторон и вершин правильного шестиугольника, | шт |
|---|---|---|
| α | центральный угол правильного шестиугольника, | радианы, ° |
| β | половина внутреннего угла правильного шестиугольника, | радианы, ° |
| γ | внутренний угол правильного шестиугольника, | радианы, ° |
| a | сторона правильного шестиугольника, | м |
| R | радиусы правильного шестиугольника, | м |
| p | полупериметр правильного шестиугольника, | м |
| L | периметр правильного шестиугольника, | м |
| h | апофемы правильного шестиугольника, | м |
Основные формулы для правильного шестиугольника
Периметр правильного шестиугольника
[ L = 6a ]
Полупериметр правильного шестиугольника
[ p = 3a ]
Центральный угол правильного шестиугольника в радианах
[ α = frac{π}{3} ]
Центральный угол правильного шестиугольника в градусах
[ α = frac{180°}{3} = 60° ]
Половина внутреннего угла правильного шестиугольника в радианах
[ β = frac{π}{3} ]
Половина внутреннего угла правильного шестиугольника в градусах
[ β = frac{180°}{3} = 60° ]
Внутренний угол правильного шестиугольника в радианах
[ γ = 2β = frac{2}{3}π ]
Внутренний угол правильного шестиугольника в градусах
[ γ = frac{2}{3}180° = 120° ]
Площадь правильного шестиугольника
[ S = ph = 3ha ]
Или учитывая формулу Площади правильного шестиугольника получим
[ S = frac{3sqrt{3}}{2}a^2 ]
Отсюда получим апофему правильного шестиугольника
[ h = frac{sqrt{3}}{2}a ]
Правильный шестиугольник |
стр. 270 |
|---|