Какова ширина всего спектра первого порядка (длины волн заключены в пределах от 0,38 до 0,76 мкм), полученного на экране, отстоящем на 3 м от дифракционной решетки с периодом 0,01 мм?
Спрятать решение
Решение.
Условие дифракционного максимума причем для малых углов дифракции
Тогда ширина спектра первого порядка
Ответ: 11 см.
————-
Дублирует задание № 3137.
Спрятать критерии
Источник: Рымкевич А. П. Сборник задач по физике для 9−11 классов, М.: «Просвещение», 1990 (№ 1070)
Источник: сайт Решу урок — физика 10-11, задание № 3137.
Предмет: Физика,
автор: 45765418
Ответы
Автор ответа: DedStar
16
Ответ:
Объяснение:
Дано:
d = 0,01 мм = 1·10⁻⁵ м
λ₁ = 380 нм = 380·10⁻⁹ м
λ₂ = 760 нм = 760·10⁻⁹ м
m = 1
L = 170 см = 1,70 м
__________________
Δx – ?
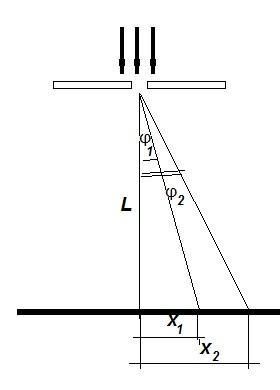
Сделаем чертеж.
Для малых углов:
sin φ ≈ tg φ = x / L
Формула дифракционной решетки:
d·sin φ = m·λ
d·x / L = m·λ
имеем:
x₁ = m·L·λ₁ / d
x₂ = m·L·λ₂ / d
Тогда:
Δx = x₂ – x₁ = (m·L/d)· (λ₂ – λ₁)
Δx = (1·1,70/1·10⁻⁵)· (760 – 380)·10⁻⁹ ≈ 0,065 м или 65 мм
Приложения:
Предыдущий вопрос
Следующий вопрос
Интересные вопросы
Предмет: Русский язык,
автор: konl55
то что наверху помогите там написано
1 месяц назад
Предмет: Русский язык,
автор: Яночка20045
Придумайте заголовок к этому стихотворению.
Этот мальчик-рисовальщик
По краснел он до ушей
Потому что не умеет
Он чинить карандашей.
Искрошились
Еле-еле
Заострились
И взмолилися они
-Отпусти нас,не чини!
В любом из слов,подчеркните орфограммы
Помогитее с:
1 месяц назад
Предмет: Английский язык,
автор: vikarotaru09
ребята там прослушивание было в классе и я не прослушала про англ яз и незнаю что делать
1 месяц назад
Предмет: Геометрия,
автор: Аноним
Определите вид Четырехугольника DANB и найдите его пириметр если MN = NK = 26 см, AD||NK, DB||MN и MD=DK. Дам за ответ 20 баллов! Помогите пожалуйста)
6 лет назад
Предмет: Алгебра,
автор: Nellity
Как по графику функции y=✔x можно построить график функции :
6 лет назад
2016-12-18
Найти ширину спектра первого порядка с длинами волн в диапазоне от $lambda_{ф} = 0,38 мкм$ до $lambda_{кр} = 0,76 мкм$, полученного на экране с помощью линзы с фокусным расстоянием $F = 3 м$. Дифракционная решетка имеет 100 штрихов на 1 мм.
Решение:
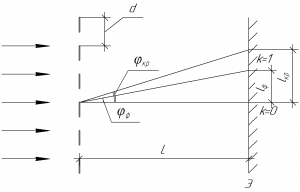
Прошедший через дифракционную решетку свет разлагается на параллельные пучки, которые направлены под углами, определяемыми формулой дифракционной решетки. Как известно, параллельный пучок света, падающий на собирающую линзу, фокусируется в ее фокальной плоскости (то есть в плоскости, перпендикулярной главной оптической оси и проходящей через фокус линзы). Следовательно, для получения четкого изображения спектра необходимо расположить экран в фокальной плоскости линзы (расстояние между линзой и экраном равно фокусному расстоянию линзы). Для спектра первого ($k = 1$) порядка имеем картину, представленную на рисунке.
Запишем формулу дифракционной решетки для спектра первого порядка для длин волн $lambda_{ф}$ и $lambda_{кр}$:
$d sin phi_{кр} = lambda_{кр}$ (1)
$d sin phi_{ф} = lambda_{ф}$. (2)
Из геометрических соображений ширина спектра $l$ определяется соотношением:
$l = F ( tg phi_{кр} – tg phi_{ф})$. (3)
Учитывая, что для малых $phi sin phi approx tg phi approx phi$, из (3) находим:
$l = frac{F}{d}( lambda_{кр} – lambda_{ф}) = 11 см$.
1)
Радиус к-й
зоны Френеля:
–
для сферической волны
r
,
где
a
– расстояние между диафрагмой с круглым
отверстием и точечным источником света;
b
– расстояние между диафрагмой и экраном,
на котором ведется наблюдение дифракционной
картины; к
–
номер зоны Френеля; l
–
длина
волны.
–
для плоской волны
r
.
2)
Дифракция света на одной щели при
нормальном падении света (дифракция
Фраунгофера).
Угол
j
отклонения лучей, соответствующих
минимуму интенсивности света, определяется
из условия
asin
,
к
=
0,
1, 2 …,
где
a
– ширина щели;
к
– порядковый
номер минимума; l
–
длина волны.
Угол
j
отклонения
лучей, соответствующий максимуму
интенсивности света, определяется из
условия
asin
,
к
=
0, 1, 2 …,
где
j
– приближенное значение угла дифракции.
3)
Дифракция света на дифракционной решетке
при нормальном падении лучей.
Условие главных
максимумов интенсивности
d
sin
,
к = 0,
1, 2 …,
где
d
– период (постоянная решетки); к
–
номер главного дифракционного максимума
в случае монохроматического света или
порядок спектра в случае белого света;
j
–
угол отклонения лучей, соответствующий
максимуму интенсивности.
4)
Разрешающая способность дифракционной
решетки
R
=
= к
N,
где
Dl
– наименьшая разность длин волн двух
соседних спектральных линий
(l
и l
+
Dl),
при которой эти линии могут быть видны
раздельно в спектре, полученном
посредством данной решетки; N
–
число щелей решетки.
5)
Формула Вульфа-Брэггов
2dsin
,
где
q
–
угол скольжения (угол между направлением
параллельного пучка рентгеновского
излучения, падающего на кристалл, и
атомной плоскостью в кристалле); d
– расстояние между атомными плоскостями
кристалла.
Примеры решения задач
Задача
1
На
дифракционную решетку длиной 10 мм,
имеющую 400 штрихов на 1 мм, падает
нормально свет от разрядной трубки.
Помещенная вблизи решетки линза
проецирует дифракционную картину (рис.
4) на плоский экран Э,
удаленный от линзы на расстояние 1м.
Определить: 1) ширину спектра первого
порядка, если границы видимого спектра
составляют 780 нм (красный край спектра)
и 400 нм (фиолетовый край спектра); 2) число
спектральных линий красного цвета,
которые теоретически можно наблюдать
с помощью данной дифракционной решетки;
3) в спектре какого порядка эта решетка
может разрешить две линии с
длиной волны, равной 500 нм и 500,1 нм?
|
Дано:
l0
n
L кр ф 10-7 1
2 |
Решение:
Угол
d следовательно, sin = (2) |
|
l1 |
Аналогично
для дифракционного максимума красного
цвета получим:
sin
=
.
(3)
Из
рис. 4 следует, что расстояние от центра
дифракционной картины до фиолетовой
спектральной линии равно
l1
= Ltg
,
(4)
соответственно
для красной спектральной линии
l2
= L
tg
.
(5)
0
линза
L
Э
1
2
Рис.
4
Ширина
спектра первого порядка будет Δl
=
l2
– l1
или
с учетом
формул (4) и (5)
Δl
= L
(tg
–
tg
).
(6)
В
случае малых углов
,
что имеет место для спектра первого
порядка
tg
sin
.
Поэтому,
подставив выражения (2) и (3) в формулу
(6), получим:
(7)
Зная
число штрихов n
на 1 мм решетки, найдем период решетки:
d
=
.
(8)
Подставляя
(8) в формулу (7), получим:
.
(9)
Произведем
вычисления
м
= 15,2 см.
Для
определений числа спектральных линий
красного цвета найдем максимальное
значение кmах,
исходя из того, что максимальный угол
отклонения лучей не может превышать
90° (sin 90° = 1). Из формулы (1) напишем:
к
=
,
следовательно,
кmax
.
С
учетом (8) получим:
.
Так
как число кmах
должно быть обязательно целым, то кmах=
3. Влево и вправо от центра картины будет
наблюдаться одинаковое число спектральных
линий, равное 2кmах.
Таким образом, общее число спектральных
линий равно 2кmах
=
6.
Так как разрешающая
способность дифракционной решетки
R
=
=
кN,
(10)
то
минимальная разница длин волн
двух
спектральных линий, разрешаемых решеткой,
.
(11)
Две спектральные
линии разрешены, если
.
(12)
Полагая
l
= l1,
получаем
.
(13)
Из
выражения (13) следует, что спектральные
линии разрешены в спектрах с порядком
.
(14)
Число
щелей решетки определяется выражением
,
или с учетом формулы (8)
N
=
n.
(15)
Подставляя
(15) в (14), получим:
.
(16)
Произведем
вычисления
.
Так
как к
– целое число, то к
2.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Условие задачи:
Дифракционная решетка, имеющая 100 штрихов на 1 мм, находится на расстоянии 1 м от экрана и освещается белым светом. Найти ширину дифракционного спектра первого порядка на экране, если (lambda_{ф} = 0,4) мкм, а (lambda_{кр} = 0,76) мкм.
Задача №10.7.26 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»
Дано:
(N=100), (l=1) мм, (L=1) м, (k=1), (lambda_{ф}=0,4) мкм, (lambda_{к}=0,76) мкм, (a-?)
Решение задачи:
[dsin varphi = klambda;;;;(1)]
В этой формуле (d) – период решетки (также называют постоянной решетки), (varphi) – угол дифракции, (k) – порядок максимума (в данной задаче (k=1)), (lambda) – длина волны, падающей нормально на решетку.
Кстати, из формулы (1) прекрасно видно, что чем больше длина волны, тем больше угол дифракции, поэтому дифракционный максимум красного цвета находится выше дифракционного максимума фиолетового цвета (для максимумов одного порядка, разумеется). Поэтому искомую ширину дифракционного спектра первого порядка (a) будем искать по формуле:
[a = {l_{кр}} – {l_ф};;;;(2)]
Запишем формулу (1) для крайних цветов видимого спектра излучения (т.е. для красного и фиолетового), естественно, свет каждой длины волны будет иметь свой собственный угол дифракции и свой дифракционный максимум:
[left{ begin{gathered}
dsin {varphi _{кр}} = k{lambda _{кр}} hfill \
dsin {varphi _ф} = k{lambda _ф} hfill \
end{gathered} right.]
Если расписать синусы углов дифракции, учитывая их малость (то есть (sin varphi approx tgvarphi)), то имеем:
[left{ begin{gathered}
dfrac{{{l_{кр}}}}{L} = k{lambda _{кр}} hfill \
dfrac{{{l_ф}}}{L} = k{lambda _ф} hfill \
end{gathered} right.]
Тогда:
[left{ begin{gathered}
{l_{кр}} = frac{{k{lambda _{кр}}L}}{d} hfill \
{l_ф} = frac{{k{lambda _ф}L}}{d} hfill \
end{gathered} right.]
В таком случае формула (2) примет вид:
[a = frac{{k{lambda _{кр}}L}}{d} – frac{{k{lambda _ф}L}}{d}]
[a = frac{{kL}}{d}left( {{lambda _{кр}} – {lambda _ф}} right)]
Период (постоянную) решетки (d) можно определить, разделив некоторую длину решетки (l) на количество содержащихся на этой длине штрихов (N), то есть:
[d = frac{l}{N};;;;(3)]
Учитывая формулу (3), окончательно имеем:
[a = frac{{kLN}}{l}left( {{lambda _{кр}} – {lambda _ф}} right)]
Задача решена в общем виде, подставим данные из условия в полученную формулу и посчитаем численный ответ:
[a = frac{{1 cdot 1 cdot 100}}{{{{10}^{ – 3}}}}left( {0,76 cdot {{10}^{ – 6}} – 0,4 cdot {{10}^{ – 6}}} right) = 0,036;м = 3,6;см]
Ответ: 3,6 см.
Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.
Смотрите также задачи:
10.7.25 Определите оптическую разность хода волн длиной 540 нм, падающих на дифракционную
10.7.27 На дифракционную решетку с периодом 4 мкм падает нормально монохроматическая волна
10.7.28 При помощи дифракционной решетки с периодом 0,02 мм получено первое дифракционное



