Как найти ширину спектральной линии

Естественная
ширина спектральной линии.
До сих пор предпо­лагалось, что
энергетические уровни бесконечно узкие.
Однако даже в идеализированном случае,
когда на частицу не действуют внешние
силы, ширина энергетических уровней
конечна. Други­ми словами, излучение
для данного перехода не монохроматиче­ское,
а имеет некоторый спектр частот.
Зависимость интенсивно­сти излучения
(поглощения) от частоты называют
спектральной
линией излучения
(поглощения), а графическое изображение
ее — контуром
спектральной линии.

Минимальная ширина
уровней, а следовательно, и минималь­ная
ширина спектральной линии определяются
соотношением не­определенностей
Гейзенберга, которое в данном случае
лучше записать в виде

,
(9.25)

где

и

—
неопределенности энергии и времени.

Предположим,
что необходимо определить частоту
излучения при переходе с уровня
на основной уровень(рис. 9.3а). Вре­мя жизни частиц в
возбужденном состоянии определяется
(9.5):
.
Следует считать, что неопределенность
времени равна времени жизни частицы,
т. е.
.
Подставляя

в (9.25), по­лучаем неопределенность
энергии уровня

(рис. 9.36). Это рассуждение можно применить
и к многоуровневой системе. Неопределенность
энергии любого уровня

,
(9.26)

где

— время жизни частицы на уровне
,
определяемое по (9.9) вероятностями
спонтанных переходов с него на нижние
уровни.

Соотношение
(9.26) определяет зависимость ширины
любого энергетического уровня
от
среднего времени жизни частиц на этом
уровне
.
Если последнее бесконечно велико
то

,
т. е. неопределенность энергии, или
ширина уровня, бес­конечно мала.
Такими будут основной энергетический
уровень,

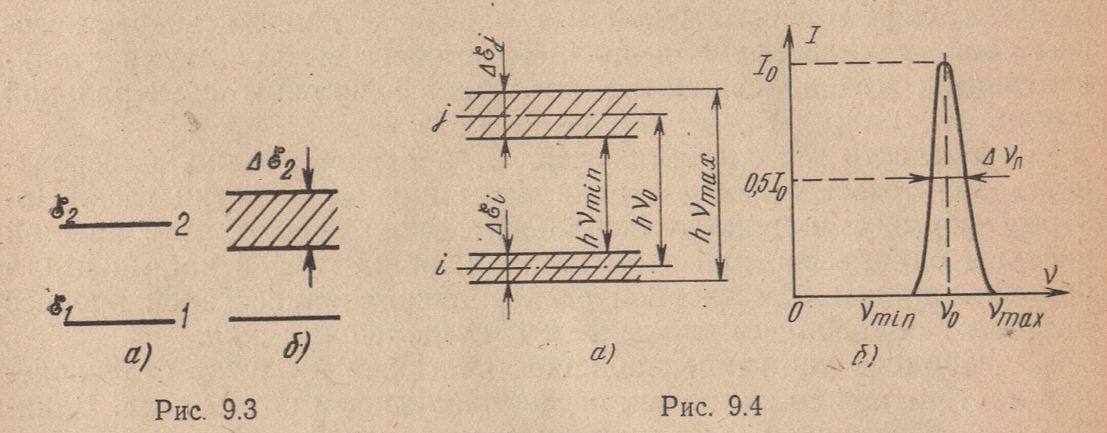
нижний
уровень системы (уровень
на рис. (9.36). Наиболее ши­рокими
оказываются уровни с малым временем
жизни. Неопре­деленность частоты
перехода между «размытыми» уровнями

и

)
с ширинами

и

(рис. 9.4а) находится из соотношения:

(9.27)

и
определяется суммой неопределенностей
энергии обоих уров­ней. Ширина
спектральной линии изолированного и
неподвижно­го атома, определяемая
только временем жизни частицы по
спон­танному излучению, минимальна
и называется естественной
ши­риной спектральной линии.
Ширину контура спектральной линии
принято определять как разность частот,
на которых интенсив­ность

равна половине максимального значения

(,
рис. 9.46). Частотой
перехода
(центральной частотой перехода) назы­вают
частоту, соответствующую максимуму
спектральной линии. Форма спектральной
линии может быть представлена так
назы­ваемой лоренцевой
кривой

,

совпадающей с
резонансной кривой колебательного
контура. Реальные наблюдаемые спектральные
линии имеют ширину боль­ше естественной.
Рассмотрим причины, вызывающие «уширение»
спектральных линий.

Уширение
спектральной линии из-за столкновений.
В газе про­исходят упругие и неупругие
столкновения частиц. При упругих
столкновениях суммарная кинетическая
энергия сталкивающихся частиц не
изменяется: частицы не обмениваются
внутренней энер­гией и не переходят
на другие энергетические уровни. При
не­упругих столкновениях суммарная
кинетическая энергия сталкивающихся
частиц либо возрастает (прямые
соударения,
или со­ударения первого рода), либо
убывает (обратные
соударения
или соударения второго рода). В этом
случае изменяется внут­ренняя энергия
сталкивающихся частиц, связанная с
электронны­ми, колебательными и
вращательными уровнями.

В результате
неупругих столкновений происходит
сокращение времени жизни рассматриваемых
частиц в данном энергетичес­ком
состоянии до времени среднего пробега
между двумя столк­новениями, что
эквивалентно увеличению ширины
спектральной линии.

Вероятность
столкновений частиц, а следовательно,
и вероят­ность квантовых переходов
одинаковы для всех частиц газа. По­этому
форма и ширина спектральной линии всего
газа и каждой частицы одинаковы, при
этом ширина линии газа и частиц стала
больше ширины естественной спектральной
линии. Такой процесс называют однородным
уширением спектральной линии.

Однородное уширение
наблюдается также в случае столкнове­ния
частиц газа со стенками, ограничивающими
объем газа. Влия­ние этих столкновений
на ширину спектральной линии становится
основным при малом давлении газа, когда
вероятность столкно­вений частиц
мала.

Доплеровское
уширение спектральной линии.
Это уширение связано с эффектом Доплера,
т. е. с зависимостью наблюдаемой частоты
излучения от скорости движения излучателя.
Если источ­ник, создающий в неподвижном
состоянии монохроматическое излучение
с частотой
,
движется со скоростью

в сторону к наблюдателю так, что проекция
скорости на направление наблю­дения
составляет

(рис. 9.5), то наблюдатель регистрирует
бо­лее высокую частоту излучения

,
(9.28)

где

—
фазовая скорость распространения волны;

— угол меж­ду направлениями скорости
излучателя и наблюдения.

В
квантовых системах источниками излучения
являются ато­мы или молекулы. В
газообразной среде при термодинамическом
равновесии скорости частиц распределены
по закону Максвелла — Больцмана. Поэтому
и форма спектральной линии всего вещества
будет связана с этим распределением. В
спектре, регистрируемом наблюдателем,
должен быть непрерывный набор частот,
так как разные атомы движутся с разными
скоростями относительно наблюдателя.
Учитывая лишь проекции скорости

в распределении Максвелла—Больцмана,
можно получить следующее выражение для
формы доплеровской спектральной линии:

.
(9.29)

Эта
зависимость является гауссовой функцией.
Соответствующая значению
ширина
линии

.
(9.30)

С
увеличением массы частиц

и понижением температуры

ширина линии

уменьшается.

Вследствие
эффекта Доплера спектральная линия
всего ве­щества не совпадает со
спектральной линией отдельной частицы.
Наблюдаемая спектральная линия вещества
представляет собой суперпозицию
спектральных линий всех частиц вещества,
т. е. ли­ний с различными центральными
частотами. Для легких частиц при обычной
температуре ширина доплеровской линии
в оптиче­ском диапазоне может превышать
естественную ширину линии на несколько
порядков и достигать значе­ния более

.

Процесс,
при котором форма спект­ральной линии
всего вещества не сов­падает с формой
спектральной линии каждой частицы,
называют неоднород­ным
уширением спектральной линии.
В рассмотренном случае причиной
не­однородного уширения был эффект
Доплера. Форма доплеровской спект­ральной
линии описывается гауссовой функцией
(9.29). Если распределение скоростей частиц
отличается от максвелловского, то и
форма доп­леровской спектральной
линии будет отличаться от гауссовой
функ­ции, но уширение останется
неоднородным.

Другие
причины уширения спектральной линии.
В квантовых приборах широко используют
твердые вещества с примесными ионами,
квантовые переходы которых являются
рабочими. Коле­бания кристаллической
решетки модулируют электрическое поле
в том месте, где находится ион, и,
следовательно, модулируют по­ложение
его энергетических уровней и увеличивают
ширину спек­тральной линии. Кроме
того, ширина линии увеличивается
вслед­ствие тепловых колебаний самих
ионов. Причиной уширения спек­тральной
линии твердого тела может быть также
пространствен­ная неоднородность
физических параметров среды или
неоднород­ности электрического и
магнитного полей. Эти неоднородности
будут вызывать неоднородное уширение
спектральной линии. При­чиной уширения
спектральной линии может быть также
электро­магнитное излучение, вызывающее
вынужденные переходы между рассматриваемыми
уровнями и приводящее к изменению
времени жизни частицы. Поэтому, например,
процесс генерации излучения в квантовых
приборах будет приводить к изменению
ширины линии.

Спектральные
коэффициенты Эйнштейна.
Введенные ранее ко­эффициенты Эйнштейна

определяют
мощность, излу­чаемую или поглощаемую
во всем спектральном диапазоне дан­ного
перехода между уровнями

и
.
Поэтому их называют инте­гральными
коэффициентами Эйнштейна. Если необходимо
учиты­вать частотное распределение
излучаемой или поглощаемой мощ­ности,
то используют спектральные коэффициенты
Эйнштейна

которые связаны с
соотношениями

(9.31)

Частотная
зависимость всех спектральных
коэффициентов оди­накова и совпадает
с формой контура спектральной линии
дан­ного перехода — лоренцевой или
гауссовой кривыми. Однако с введением
коэффициентов

следует уточнить также понятие
населенности уровней. Под населенностью

–
любого уровня

следует понимать число частиц в единице
объема, энер­гия которых попадает в
пределы размытости уровня

по энергии
.
Таким образом, число спонтанных и
вынужденных перехо­дов в единичном
частотном интервале вблизи частоты

в едини­цу времени можно записать с
использованием дифференциальных
коэффициентов Эйнштейна в виде

.
(9.32)

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

1

Спектра́льная ли́ния — узкий участок энергетического спектра (например, спектра электромагнитного излучения), где интенсивность излучения усилена либо ослаблена по сравнению с соседними областями спектра. В первом случае линия называется эмиссионной линией, во втором — линией поглощения. Положение линии в электромагнитном спектре обычно задаётся длиной волны, частотой или энергией фотона. Кроме электромагнитного спектра, спектральные линии могут возникать в спектрах энергии частиц (например, в альфа-спектре при альфа-распаде радиоактивных ядер), в спектрах звуковых колебаний и вообще любых волновых процессов. Ниже, если нет специальных оговорок, имеются в виду электромагнитные спектры.

Чаще всего спектральные линии возникают при переходах между дискретными уровнями энергии в квантовых системах: молекулах, атомах и ионах, а также атомных ядрах. У каждого химического элемента атомы и ионы имеют собственную структуру энергетических уровней, и набор спектральных линий у них уникален, что позволяет по спектральным линиям определять присутствие и количественное содержание тех или иных химических элементов в исследуемом объекте.

Спектральные линии имеют малую ширину, но они не монохромны. Распределение интенсивности излучения в линии называется профилем или контуром спектральной линии, вид которого зависит от множества факторов, называемых механизмами уширения. Среди них — естественная ширина спектральной линии, доплеровское уширение и другие эффекты.

Спектральные линии наблюдаются во всех диапазонах электромагнитного излучения: от гамма-лучей до радиоволн, причём линии в разных диапазонах обусловлены различными процессами: например, линии атомных ядер попадают в гамма- и рентгеновский диапазоны, а различные линии молекул — в основном в инфракрасный и радиоволновой диапазоны. Профили и характеристики спектральных линий содержат различную информацию об условиях среды, где они возникли.

Описание[править | править код]

Спектральные линии представляют собой узкие участки спектра электромагнитного излучения, на которых интенсивность излучения усилена либо ослаблена по сравнению с соседними областями спектра. В первом случае линии называются эмиссионными линиями, во втором — линиями поглощения. Положение линии в спектре обычно задаётся либо длиной волны либо частотой где  — скорость света, или же энергией фотона где  — постоянная Планка^[1][2][3].

Название термина «спектральная линия» объясняется внешним видом спектра при наблюдении его с помощью спектрографа с призмой или дифракционной решёткой: узкие максимумы или минимумы в спектре выглядят как яркие или тёмные линии на фоне полосы непрерывной яркости^[1][4].

Механизм возникновения[править | править код]

В большинстве случаев спектральные линии возникают из-за переходов между дискретными уровнями энергии в квантовых системах: молекулах, атомах и ионах, а также атомных ядрах. Также спектральные линии могут порождаться, например, циклотронным излучением и процессами в плазме^[2][3][5]. Излучение в линиях кристаллами рассматривается как излучение экситонов — квазичастиц, представляющих собой связанное состояние электрона и дырки^[6].

В атомах и других квантовых системах переходы с более высокого энергетического уровня на более низкий могут происходить самопроизвольно, в таком случае при переходе излучается фотон с энергией, равной разности энергии уровней, а такие переходы называются спонтанными. Если фотон с такой же энергией попадает в такой же атом на энергетическом уровне то фотон поглощается, а атом переходит на энергетический уровень Если же такой фотон попадает в атом на уровне то происходит вынужденное излучение ещё одного фотона с той же длиной волны и направлением движения, а атом переходит на уровень При постоянно идущих переходах в одну сторону излучаются либо поглощаются фотоны одной и той же энергии, поэтому на фоне непрерывного спектра наблюдается светлая или тёмная линия^[7][8].

Таким образом, длины волн спектральных линий характеризуют структуру энергетических уровней квантовой системы. В частности, каждый химический элемент и ион имеет собственную структуру энергетических уровней, а значит, уникальный набор спектральных линий^[1][4]. Линии в наблюдаемом спектре могут быть отождествлены с линиями известных химических элементов, следовательно, по спектральным линиям можно определять присутствие тех или иных химических элементов в исследуемом объекте^[9]. Количественное определение химического состава источника спектра по линиям является предметом спектрального анализа^[10].

Кроме длины волны, линии характеризуются эйнштейновскими коэффициентами перехода. Можно рассмотреть спонтанные переходы с уровня на количество таких переходов, а значит, число испущенных фотонов в этой линии единичным объёмом (берётся 1 см³) пропорционально количеству атомов в этом объёме, находящихся на уровне Эйнштейновский коэффициент спонтанного перехода является таким коэффициентом пропорциональности: количество фотонов, излучаемых в линии атомами за промежуток времени равняется Число обратных переходов с уровня на уровень в этом объёме, вызванных поглощением фотона, пропорционально не только количеству атомов на уровне но и плотности излучения соответствующей частоты в линии: Количество поглощённых фотонов выражается эйнштейновским коэффициентом поглощения и за промежуток времени равно . Аналогично и для вынужденных переходов с уровня на число излученных таким образом фотонов равняется ^[2][11].

Среди спектральных линий выделяют запрещённые линии. Запрещённые линии соответствуют переходам, которые запрещены правилами отбора, поэтому эйнштейновские коэффициенты для них очень малы и вероятность перехода в единицу времени у них существенно меньше, чем у остальных переходов, называемых разрешёнными. Энергетические уровни, с которых возможны только запрещённые переходы, называются метастабильными: обычно время нахождения атома на метастабильном уровне составляет от 10⁻⁵ секунд до нескольких суток, а на обычном ― порядка 10⁻⁸ секунд. Это приводит к тому, что в обычных условиях такие линии не наблюдаются, поскольку за время нахождения атома на метастабильном уровне он многократно сталкивается с другими атомами и передаёт им свою энергию возбуждения. Однако при низкой плотности вещества столкновения атомов происходят достаточно редко, поэтому накапливается большое количество атомов в метастабильных состояниях, спонтанные переходы из них становятся частыми и запрещённые эмиссионные линии становятся такими же интенсивными, как и разрешённые^[12][13].

Профиль спектральной линии[править | править код]

Линии в спектре имеют малую ширину, но не монохромны: распределение интенсивности излучения в линии называется профилем или контуром спектральной линии, вид которого зависит от множества факторов (см. ниже^[⇨])^[1][14]. Интенсивность излучения в спектре описывается функцией распределения энергии по длинам волн или частотам. Для отделения излучения или поглощения в линии от излучения в непрерывном спектре проводится экстраполяция соседних с линией областей спектра на область, где наблюдается линия, как если бы она отсутствовала. Можно обозначить интенсивность излучения наблюдаемого спектра на частоте как а экстраполированного — как Для эмиссионных линий разность этих величин называется интенсивностью излучения в линии на частоте для линий поглощения — глубиной линии. Другой параметр — остаточная интенсивность — выражается как ^[3][15][16]. Если в линии поглощения интенсивность спектра доходит до нуля, то линия называется насыщенной^[17].

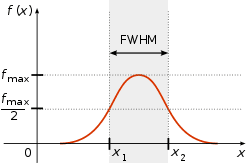
Полуширина, или же ширина линии — это разность между длинами волн или частотами, на которых интенсивность излучения или глубина линии составляет половину от максимальной. Этот параметр обозначается как (от англ. Full Width at Half Maximum). Область линии, находящаяся внутри полуширины, называется центральной частью, а области, находящиеся по сторонам ― крыльями^[3][14][16].

Для описания интенсивности линий поглощения используется понятие эквивалентной ширины это размер области в длинах волн () или в частотах (), в котором непрерывный спектр излучает суммарно столько же энергии, сколько поглощается во всей линии. Формально она определяется через остаточную интенсивность как или  — аналогичные рассуждения можно провести для спектра по длинам волн, а не частотам. Теоретически, интегрирование должно производиться от до но на практике интегрируют на конечном интервале, включающем в себя основные части линии — как правило, ширина интервала составляет не более нескольких десятков нанометров^[18][19]. Иными словами, это ширина прямоугольника с высотой, равной интенсивности непрерывного спектра, площадь которого равна площади над спектральной линией^[3][16][20].

Поскольку количество фотонов, поглощаемых или излучаемых в линии, зависит только от количества атомов в соответствующем состоянии и плотности излучения (см. выше^[⇨]), то, при прочих равных, чем больше ширина линии, тем меньше её глубина или интенсивность^[21].

Механизмы уширения[править | править код]

Существует множество факторов, которые приводят к увеличению ширины линии и из-за которых спектральные линии не являются монохроматическими ― они называются механизмами уширения^[1][3][14].

Естественная ширина[править | править код]

Естественная ширина спектральной линии, также называемая минимальной, обусловлена квантовыми эффектами^[22]. В рамках классической механики такое явление объясняется радиационным затуханием, поэтому естественная ширина также называется радиационной^[23]. Если среднее время жизни состояния, из которого переходит атом, равно то в силу принципа неопределённости энергия этого состояния определена с точностью до где  — приведённая постоянная Планка,  — постоянная Планка. Тогда неопределённость частоты излучения, соответствующей этой энергии, составляет Поскольку энергия фотона в линии зависит от энергии и начального, и конечного состояния, то полуширина линии выражается следующим образом^[24]:

где индексы обозначают уровни и ^[24]. Естественная ширина обязательно присутствует у всех линий, но, как правило, она очень мала по сравнению с остальными эффектами при их наличии^[25]. Типичное значение естественной ширины линии составляет 10⁻³ Å^[23], а особо малые естественные ширины имеют запрещённые линии^[26].

Доплеровское уширение[править | править код]

Вклад в уширение линий может вносить эффект Доплера — в таком случае уширение называется доплеровским. Если источник излучения имеет ненулевую лучевую скорость относительно наблюдателя, то длина волны излучения, которое принимает наблюдатель, изменяется относительно той, которую излучает источник: в частности, наблюдается смещение линий в спектре. Если разные части источника движутся с разной лучевой скоростью, например, при его вращении, то смещение линий от различных частей источника оказывается разным, в спектре источника складываются линии с разным смещением и линии оказываются уширенными. Также, кроме движения отдельных частей источника, вклад в доплеровское уширение может вносить тепловое движение частиц, излучающих в линии^[16][27].

Доплеровское смещение для небольших лучевых скоростей выражается формулой где  — смещение линии по частоте,  — частота линии,  — лучевая скорость,  — скорость света. При максвелловском распределении атомов по скоростям средняя скорость атома при температуре и массе атома составляет где  — постоянная Больцмана. Средняя скорость соответствует смещению от центра линии, на котором интенсивность линии в e раз меньше, чем в центре, а этот параметр достаточно близок к половине полуширины^[27][28]. При температурах порядка нескольких тысяч кельвинов ширина линий в оптическом диапазоне принимает значения 10⁻²—10⁻¹ Å^[3][29].

Эффекты давления[править | править код]

Механизмы уширения линий, которые обусловлены влиянием посторонних частиц, называются эффектами давления, так как при увеличении давления увеличивается и влияние этих частиц. Например, к эффектам давления относятся столкновения возбуждённых атомов с другими частицами, в результате которых атомы теряют свою энергию возбуждения. В результате среднее время жизни атома в возбуждённом состоянии уменьшается, и, в соответствии с принципом неопределённости, увеличивается размытость уровня по сравнению с естественной (см. выше^[⇨])^[3][30]. Однако столкновения могут и делать линии более узкими: в случае, если эффекты давления ещё не слишком сильны, но длина свободного пробега атома оказывается меньше, чем длина волны излучаемого фотона, то за время излучения скорость атома может меняться, что уменьшает величину доплеровского уширения. Это явление известно как эффект Дикке^[31].

Не меньшее влияние оказывает и прохождение частиц мимо излучающих атомов. При сближении частицы с атомом силовое поле вблизи последнего меняется, что приводит к смещению энергетических уровней в атоме. Из-за движения частиц смещение уровней постоянно меняется и различается между атомами в определённый момент времени, поэтому линии также оказываются уширенными. Наиболее сильно влияет эффект Штарка: прохождение заряженных частиц, таких как ионы и свободные электроны, вызывает переменное смещение энергетических уровней в атоме^[32].

Эффект Зеемана и эффект Штарка[править | править код]

При воздействии магнитного поля энергетические уровни атомов расщепляются на несколько подуровней с близкими значениями энергии. С разных подуровней одного уровня возможны переходы на разные подуровни другого уровня, причём энергии таких переходов отличаются, и, следовательно, спектральная линия расщепляется на три или больше спектральных линии, каждая из которых соответствует определённому переходу между подуровнями. Это явление известно как эффект Зеемана. При эффекте Зеемана профили расщеплённых частей линии зачастую сливаются между собой, что вызывает наблюдаемое уширение линии, а не расщепление^[3][33][34].

Эффект Штарка, возникающий в постоянном электрическом поле, также приводит к расщеплению энергетических уровней, и, как следствие — к расщеплению спектральных линий, как и эффект Зеемана^[35].

Инструментальный профиль[править | править код]

Кроме механизмов уширения (см. выше^[⇨]), на профиль линии влияет аппаратная функция приборов и их спектральное разрешение. Оптические инструменты имеют конечное разрешение, в частности, из-за дифракции, поэтому даже достаточно узкая линия всё равно будет иметь некоторую ширину и профиль, называемый инструментальным — зачастую инструментальный профиль и определяет наблюдаемую ширину линии^[2][3][36].

Наблюдение и анализ[править | править код]

Спектральные линии встречаются во всех областях электромагнитного спектра: например, в гамма-диапазон попадает линия, образующаяся при аннигиляции электрона и позитрона, а также различные линии атомных ядер. К рентгеновскому диапазону относятся линии атомных ядер либо ионов с высокой степенью ионизации, в ультрафиолетовом и оптическом диапазоне наблюдаются линии различных ионов и атомов. В инфракрасном диапазоне преобладают линии вращательных и колебательных переходов молекул и присутствуют линии атомных переходов между высокими уровнями энергии. В диапазон радиоволн попадают линии молекул и линии переходов между высокими уровнями энергии атомов, а также линии переходов между уровнями сверхтонкого расщепления, например, радиолиния нейтрального водорода^[3][5].

Эмиссионные линии можно наблюдать, например, в спектре нагретого разреженного газа. Если же пропустить излучение источника с непрерывным спектром через тот же самый газ в охлаждённом состоянии, то на фоне непрерывного спектра будут наблюдаться линии поглощения на тех же длинах волн^[37].

Параметры спектральных линий и их профили содержат большое количество информации об условиях в среде, где они возникли, поскольку разные механизмы уширения приводят к образованию различных профилей^[1][3][38]. Кроме того, интенсивность линии зависит от концентрации атомов или ионов, излучающих или поглощающей в этой линии. Например, для линий поглощения зависимость эквивалентной ширины линии от концентрации вещества называется кривой роста — следовательно, по интенсивности линии можно определять концентрацию того или иного вещества^[39][40].

Кроме того, на длины волн спектральных линий может влиять красное смещение: доплеровское, гравитационное или космологическое, причём красное смещение для всех линий одинаково. Например, если известно, что красное смещение вызвано эффектом Доплера и известна его величина, можно определить лучевую скорость источника излучения^[4][41][42].

История изучения[править | править код]

Задолго до открытия спектральных линий, в 1666 году Исаак Ньютон впервые наблюдал спектр Солнца, а в 1802 году Уильям Волластон создал щелевой спектроскоп. В 1814 году Йозеф Фраунгофер обнаружил в спектре Солнца спектральные линии поглощения, которые впоследствии стали называться фраунгоферовыми^[43][44].

В 1842 году Кристиан Доплер предложил метод определения лучевых скоростей звёзд по смещению линий в их спектрах. В 1868 году Уильям Хаггинс впервые применил этот метод на практике^[44].

В 1860 году Густав Кирхгоф и Роберт Бунзен определили, что каждая спектральная линия порождается определённым химическим элементом. В 1861 году Кирхгоф смог определить химический состав Солнца по линиям в его спектре, а в 1869 году Норман Локьер открыл неизвестный ранее элемент в спектре Солнца, названный гелием — на Земле этот элемент был обнаружен только в 1895 году^[43][44].

В 1885 году Иоганн Бальмер эмпирически вывел формулу для длин волн некоторых спектральных линий водорода. В 1888 году Йоханнес Ридберг обобщил эту формулу для переходов между любыми двумя уровнями в атоме водорода — формулу Ридберга. В 1896 году Питер Зееман обнаружил расщепление спектральных линий в магнитном поле — эффект, позже названный в его честь^[45][46].

Эти и другие открытые явления нуждались в теоретическом объяснении. После появления квантовой механики, в 1913 году Нильс Бор выдвинул свою квантовую теорию строения атома, которая объясняла формулу Ридберга, а в 1924 году Вольфганг Паули сформулировал принцип запрета, позволивший объяснить эффект Зеемана. В 1927 году Вернер Гейзенберг сформулировал принцип неопределённости, который обуславливает естественную ширину линии^[45][47].

Дальнейшему изучению спектральных линий способствовало изобретение более совершенных оптических приборов. Кроме того, в 1958 году был изобретён лазер, который создаёт излучение в очень узких линиях, что позволяет эффективно использовать приборы с высоким спектральным разрешением^[45][48].

Примечания[править | править код]

Литература[править | править код]

• Кононович Э. В., Мороз В. И. Общий курс астрономии. — 2-е, исправленное. — М.: УРСС, 2004. — 544 с. — ISBN 5-354-00866-2.
• Соболев В. В. Курс теоретической астрофизики. — 3-е, переработанное. — М.: Наука, 1985. — 504 с.
• Karttunen H., Kroger P., Oja H., Poutanen M., Donner K. J. Fundamental Astronomy. — 5th Edition. — Berlin; Heidelberg; N. Y.: Springer, 2007. — 510 p. — ISBN 978-3-540-34143-7.

Ширина спектральной линии – мера немонохроматичности спектральной линии. Ширину спектральной линии определяют как расстояние между точками контура спектральной линии, в к-рых интенсивность равна половине её макс, значения. В научной литературе вместо термина “Ширина спектральной линии” иногда используют англ. аббревиатуру FWHM – Full Width at Half Maximum. Ширину спектральной линии выражают в единицах круговой частоты – dw (с-1), частоты – dv (Гц), длины волны – dl (нм) или волнового числа – d(1/l) = dv/c (см-1). Иногда под Шириной спектральной линии понимают полуширину g = dw/2; для классич. осциллятора g есть константа затухания амплитуды свободных колебаний.

Источник: Konjevic N., Dimitrijevic M.S., Wiese W. L., Experimental stark widths and shifts for spectral lines of neutral atoms, “J. Phys. Chem. Ref. Data”, 1984, v. 13, № 3, p. 619: Konjevic N., DimitrijevicM. S., Experimental stark widths and shifts for spectral lines of positive ions, там же, p. 649.

Ширина спектральных линий, интервал частот v (или длин волн l = c/n, с — скорость света), характеризующий спектральные линии в спектрах оптических атомов, молекул и др. квантовых систем.

Ширина спектральных линий равна: (Dnki) рад = (Ak + Ai)/2p (где Ak и Ai— полные вероятности спонтанных переходов с уровней Ek и Ei на все нижележащие уровни); она очень мала и обычно Ширина спектральных линий для атомов и молекул определяется в основном уширением их уровней энергии при взаимодействии с окружающими частицами (в газе и плазме — при столкновениях), а также уширением спектральных линий вследствие эффекта Доплера.

Источник: Гайтлер В., Квантовая теория излучения, пер. с англ., М., 1956; Собельман И. И., Введение в теорию атомных спектров, 2 изд., М., 1977.   М. А. Ельяшевич.

1. Вспомним соотношение неопределенностей. Если под величиной Δt = τ понимать среднее время жизни атома в возбужден­ном состоянии, то ΔE имеет смысл неопределенности значения энергии этого состояния. В основном состоя­нии атом может находиться без внеш­них воздействий бесконечно долгое время: Δt = ∞ Тогда ΔE = 0, т. е. в основном состоянии энергия атома является строго определенной величиной. Однако каждый возбужден­ный уровень энергии имеет конечную ширину, которая определяется време­нем жизни атома в этом состоянии. Но тогда и спектральная линия излу­чающего атома не является строго монохроматической, а имеет конечную ширину (рис. 8 ).

Р и с. 8

Ширина спектральной линии определяется шириной уровней энергии, между которыми происходит переход. Обычно ширина уровней энергии очень мала. Например, для оптических переходов

Так же мала относительная неопределенность в частоте или длине волны излучения:

Ширина спектральной линии, обусловленная конечным временем жизни атома в возбужденных состояниях, называется Естественной шириной.

2. Интенсивность излучения атома уменьшается со временем по закону. Вследствие конечного времени жизни атома частота линии излучения оказывается “размазанной” в интервале Δω соглас­но . Это означает, что интенсивность излучения зависит от частоты. Зависимость интенсивности излучения от частоты определя­ет форму спектральной линии. Для нахождения формы спектральной ли­нии будем пользоваться полуклассическими рассуждениями, которые приводят к тем же результатам, что и строгий квантово–механический расчет.

Мы видели, что основным типом излучения атома является элек­трическое дипольное излучение. Это позволяет использовать модель атома в виде колеблющегося диполя. Если бы колебания дипо­ля продолжались бесконечно дол­го, то излучение диполя было бы монохроматическим с частотой ω0.

Р и с. 9

Так как излучение атома происходит в течение конечного времени жизни τ, то естественно исполь­зовать модель диполя, совершающего затухающие колебания (рис.9). Затухание колебаний является слабым, поскольку частота излучения атома достаточно велика: . Итак, будем считать, что диполь колеблется с момента t = 0 с частотой ω0, но колебания являются затухающими, т. е.

Здесь используется комплексная форма записи колебаний. Эта форму­ла отражает зависимость интенсивности излучения по закону Рассмотрим спектральное разложение колебаний диполя, поль­зуясь преобразованием Фурье. Спектр Фурье d(ω) функции d(t) определяется формулой:

Интенсивность излучения на частоте ω пропорциональна, т. е.

Отсюда следует, что форма спектральной линии описывается функцией

Функцию g(ω) называют Форм–фактором спектральной линии, или формой линии. Она имеет вид кривой Лоренца (рис.10). Форм–фактор нормируют таким образом, чтобы

Лоренцева кривая имеет острый максимум при ω = ω0, и быстро спадает с удалением от частоты ω0. Ширина лоренцевой кривой определяется по половине ее максимального значения. Нетрудно ви­деть, что τΔω = 1. Это соответствует (). Если излучение воз­никает при переходе между возбужденными уровнями энергии Em и En, то под величиной 1/τ понимают сумму , где τm, τn –времена жизни уровней Em En, соответственно. Такимобразом, естественное уширение спектральной линии, обусловленное конечным вре­менем жизни атома в возбужденном состоянии, описывается кривой Лоренца. Она отражает наименьшую “размытость” спектральной линии. При этом уширенными являются как линии излучения, так и линии по­глощения. Однако далеко не всегда наблюдаемая на опыте ширина спек­тральной линии совпадает с естественной шириной.

Р и с.10

Уширение спектральных линий вызывают различные процессы, приводя­щие к уменьшению времени жизни атома. Обычно это уширение значи­тельно перекрывает естественную ширину.

3. Естественная ширина характеризует излучение отдельного и неподвижного атома. Если же атомы образуют газ, находящийся при температуре Т и давлении Р, то каждый атом совершает тепловое дви­жение. В этом случае частота излучения ω атома, движущегося в направлении наблюдателя со скоростью V, смещается из–за эффекта Допплера

Где ω0 – частота излучения неподвижного атома. Форма линии излучения газа атомов будет определяться одномерной функцией распределения по скоростям f(v). При нормировке функции распределения на единицу с учетом условия можно положить

Учитывая, отсюда находим форс–фактор спектральной линии газа атомов

Допустим, что распределение атомов по скоростям является максвелловским, т. е.

Где – скорость теплового движения атомов, M – масса атома. Тогда форм–фактор описывается Гауссовой кривой

Параметр определяет ширину спектральной линии при допплеровском уширении.

4. Уширение спектральной линии происходит также вследствие столкновений между атомами. Из элементарной кинетической теории газов следует, что время между двумя последовательными столкновениями частиц – время свободного пробега – определяется формулой

Где σ – эффективное сечение столкновений, N – число атомов в единице объема, vT – средняя скорость теплового движения ато­мов. Предполагается, что при каждом столкновении процесс излуче­ния прерывается. В этом случае величину τc можно считать эффек­тивным временем жизни атома в возбужденном состоянии. Тогда шири­на спектральной линии равна

Для оценок можно принять:σ ≈ π(2a)2, где a – характерный размер, атома: N = P/(kT), где P – давление газа. Следовательно, ширина спектральной линии, обусловленная столкновениями между ато­мами, описывается формулой

При малом давлении газа роль уширения из–за столкновений стано­вится более слабой, чем допплеровское уширение, которое главным образом и определяет ширину спектральных линий газа излучающих атомов.

5. Измерение времени жизни атома в возбужденном состоянии
проводится различными методами. Существуют Прямые и Косвенные методы. Прямыми методами непосредственно измеряется время жизни по наблюдению затухания интенсивности излучения в соответствии с формулой. Таким образом можно измерять время жизни сравнительно долго живущих возбужденных уровней энер­гии порядка 10-6 с. Точность таких измерений сравнительно невы­сока. Косвенные методы основаны, главным образом, на измерении времени жизни по кривым погло­щения.

Сложение моментов импульса. Типы связей электронных моментов в атоме.

1. Состояния атома, состоящего из N электронов, описываются

Волновой функцией . Эта функция удовлетворяет уравнению Шредингера с оператором Гамильтона

Здесь – энергия взаимодействия i – го электрона с ядром, находящегося на расстоянии – – энергия электростатического взаимодействия между электронами. Энергия взаимодей­ствия между электронами гораздо слабее взаимодействия каждого электрона с ядром, поэтому в нулевом приближении электростатическим взаимодействием между электронами можно пренеб­речь. Тогда все электроны можно считать независимыми, так что каждый из них описывается сохраняющимся орбитальным моментом . Это значит, что сохраняется со временем длина каждого вектора и его проекция на ось Z. Полный (суммарный) вектор орбитального момента импульса также является сохраняющейся величиной:

Наличие кулоновского взаимодействия между электронами приводит к тому, что векторы , не сохраняются, но полный момент орбиталь­ного движения является сохраняющейся величиной, т. к. система изоли­рована. Это значит, что оператор полного орбитального момента им­пульса коммутирует с оператором Гамильтона. В этом случае не изме­няется длина каждого вектора , которая определяется орбиталь­ным квантовым числом Li :

Сохранение длин векторов означает, что каждый из них прецессирует вокруг направления вектора . Сам же вектор полного орбиталь­ного момента импульса характеризуется длиной, которая определяется квантовым числом L:

А также проекцией на ось Z:

Здесь ML — магнитное квантовое число, пробегающее 2L+1 значение:

ML = L, L-1,…-(L-1), —L

Отметим, что поскольку энергия взаимодействия электронов с ядром и друг с другом имеют разные знаки, то учет кулоновского взаимодейст­вия между электронами приводит к сдвигу уровней энергии “вверх”, т. е. к уменьшению энергии по абсолютной величине.

Далее рассмотрим систему двух электронов, состояния которых
характеризуется квантовыми числами L1, M1 И L2 , M2. При заданных числах L1,L2 числа M1,M2 пробегают по 2L1+1 и 2L2+1 значений, соответственно, т. е. имеется всего (2L1+1)(2L2+1) различных состояний. Эти состояния описываются волновыми функциями При учете слабого кулоновского взаимодействия между электронами их состояния описываются волновыми функциями Естественно, что этих состояний при заданных числах L1,L2 По — прежнему должно быть (2L1+1)(2L2+1), т. е. столько пар значений может пробегать пара чисел L,ML. Определим эти значения. По определению оператор полного орбитального момента импульса равен . Отсюда . Следовательно, ML= M1 + M2. Это равенство определяет также соотношение между наибольшими значениями магнитных квантовых чисел . Так как максимальное значение магнитного квантового числа равно соот­ветствующему орбитальному квантовому числу, то получаем, что . Вспомним далее, что квантовые числа M1,M2 изменяются на единицу, так что и число ML может изменяться на единицу. Так как L1+ L2 это максимальное значение числа ML, то следующее его значение должно быть ML= L1 + L2 — 1. Такому значению числа ML отвечает два состояния: либо M1= L1, M2= L2 – 1, либо M1= L1 — 1, M2= L2.

Отсюда следует, что эти два состояния характеризуются числами L= L1 + L2 (при этом ML= L — 1) и L= L1 + L2 — 1 (при этом ML= L). При уменьшении значения ML еще на единицу имеем три состояния:

M1= l1, m2= l2 — 2; m1= l1 — 1 и m2= l2 — 1; m1= l1 — 2 , m2= l2 .

Это значит, что число L может принимать значения L= L1 + L2 , L1 + L2 – 1, L1 + L2 — 2. Эти рассуждения можно продолжить и придти к выводу, что минимальное значение числа LMin = L1 + L2 (при L1 > L2). Таким образом, при заданных числах L1,L2 число L пробегает значения:

L= L1 + L2 , L1 + L2 – 1, …, |L1 — L2|.

Этих значений всего 2L2 + 1 (при L1 > L2) или 2L1 + 1 (при L2 > L1).
Нетрудно убедиться, что полное число состояний, отвечающих данным
числам L1 , L2 , равно (2L1+1)(2L2+1):

Формула определяет Правило сложения моментов. Это правило было найдено еще до построения квантовой механики. Если нужно сложить три и более моментов импульса, то можно пользоваться правилом с помощью его повторного применения. Это правило является универсаль­ным. Оно не зависит от природы момента импульса. Например, сложение орбитального и спинового моментов является частным случаем правила.

Определим четность состояний многоэлектронного атома. Четность состояний одноэлектронного атома опреде­ляется орбитальным квантовым числом как (-1)L . Так как взаимодействие электронов друг с другом является достаточно слабым, то их можно счи­тать независимыми. Тогда волновая функция системы электронов в цен­трально-симметричном поле ядра разбивается на произведение волновых функций отдельных электронов. Это значит, что четность состояний всей системы равна произведению .

2.Учтем теперь спин электронов. В этом случае каждый из элект — ронов обладает своим орбитальным моментом и спиновым моментом . Тогда потенциальная энергия системы электронов складывается не только из энергии взаимодействия каждого из электронов с ядром и друг с другом, но также из спин-орбитального и спин-спинового взаимодей­-
ствия. Последние взаимодействия связывают с соответствующими то-­
ками. Одновременный учет всех типов взаимодействий практически не-­
возможен. Из экспериментальных данных следует, что часто электроста-­
тическое взаимодействие между электронами гораздо сильнее спин-орби­-
тального и спин-спинового взаимодействия, так что в нулевом прибли-­
жении ими можно пренебречь. Средняя энергия электростатического
взаимодействия электронов, находящихся в поле ядра с зарядом Zl,
равная , примерно пропорциональна Z. Энергия спин-

Орбитального взаимодействия пропорциональна Z4. Таким образом, пренебрежение спин-орбитальным взаимодействием оправдано для достаточно легких элементов, а для тяжелых элементов преобладающим становится спин-орби­тальное взаимодействие, которое превосходит спин-спиновое взаимодей­ствие. При пренебрежении спин-орбитальным взаимодействием орбиталь­ный и спиновый моменты каждого электрона складываются по отдельности, образуя полный орбитальный момент и полный спиновый момент

При учете слабого взаимодействия между спинами полный спин сохраня­ется, при этом векторы спина отдельных электронов прецессируют вок­руг направления вектора . Сохранение полного спина означает, что оператор полного спина коммутирует с оператором Гамильтона.

Полный момент импульса всех электронов является суммой пол­ного орбитального и полного спинового моментов:

Такой тип сложения моментов отвечает нормальной связи, или связи Рассела – Саундерса (B. Russel, E. A. Saunders, 1904)

Этот тип связи моментов называют также LS связью. Для замкнутой системы вектор полного момента импульса сохраняется, т. е. оператор полного мо­мента импульса коммутирует с гамильто­нианом. Векторы же и изменяют­ся из-за спин-орбитального взаимодей­ствия. Однако величины этих векторов и их проекции на направление полного мо­мента имеют определенные значения. Это значит, что векторы и прецессиру­ют вокруг направления вектора ( рис. 1).

Р и с. 1

Когда спин-орбитальное взаимодействие для отдельного электрона оказывается более сильным, чем взаимодействие между моментами разных электронов, то складываются орбитальный и спиновый моменты для каждого электрона и образуется его полный момент импульса: . Полный момент импульса всех электро­нов является векторной суммой полных моментов отдельных электронов:

.

Векторы, не сохраняются

Р и с. 2

Они прецессируют вокруг направления вектора полного момента импульса (рис. 2). Такой тип сложения моментов отвечает J — J связи. В чис­том виде этот тип связи моментов встречается редко. Часто реализу­ются другие, более сложные типы связей электронных моментов. Наибо­лее распространенным среди атомов периодической системы элементов является нормальный тип связи. Рассмотрим его подробнее.

3. Квантовые векторы моментов характеризуются соответствующими квантовыми числами. Полному орбитальному моменту согласно отвечает квантовое число L, возможные значения которого определяются правилом. Величина (длина) вектора полного спина определяется квантовым числом полного спина S :

При этом магнитное спиновое квантовое число MS, принимает 2S+1 значение:

MS=S,…,0,…-S.

Квантовое число J полного момента импульса определяет величину (длину) вектора :

Проекция полного момента на ось Z имеет квантованные значения JZ=ћMJ. Магнитное квантовое число MJ пробегает 2J +1 значение:

MJ=J,…,0,…-J.

Квантовое число J определяется на основании если Известны числа L,S:

J=L+S, L+S-1,…,|L—S|

Отсюда видно, что число J принимает 2S +1 значение; если L ≥ S , или 2L +1 значение, если L ≤ S. Сами квантовые числа L, S опреде­ляются в соответствии с правилом сложения . Отметим, что все числа L, S, J по своему смыслу являются неотрицательными.

Определим возможные значения квантового числа полного спина.
В случае двух электронов имеем:. По правилу сложения моментов получаем, что число S принимает значения:

S=S1+ S2 ,…,|S1 – S2 | . Так как спиновое квантовое число для каж­дого электрона S1+ S2 равно 1/2, то квантовое число полного спина принимает два значения, соответственно при противоположной и параллельной ориентации спинов:

В случае трех электронов получаем также два значения полного спинового числа:

В случае четырех электронов полный спин имеет три значения:

Вспомним теперь обозначение состояний электрона в атоме водо­рода. Аналогичные обозначения принимают для электрон­ных состояний других атомов. Состоянию с данным значением числа приписывают соответствующую букву, только не строчную, а прописную:

Значение L 0 1 2 3 4 5 6 7 8 9 10

Состояние S P D F G H I K L M N

Уровни энергии, определяемые заданными значениями чисел L И S
называются Спектральными термами, или просто Термами. К терму LS
относятся (2L + 1)(2S + 1) состояний, которые различаются значениями проекций орбитального и спинового моментов на ось Z. Учет спина и релятивистских эффектов приводит к расщеплению терма LS на ряд компонент, соответствующих значениям полного момента J. Это тонкое, или Мультиплетное расщепление. В этом случае справа от буквы, обозначающей состояние, внизу пишут значение числа J, а
слева вверху – Мультиплетность 2S + 1, т. е. общее число значений,
которое принимает квантовое число J (при L ≥ S). Таким образом,
состояние обозначается как . Например, символ означает,
что числа L = 1, J = 1, S = 1. Читают так: “триплет P — единица”.

При L ≤ S число компонент равно 2L + 1. Таким образом, энергия ато­ма определяется числами L, J, S и не зависит от квантового числа MJ, принимающего 2J + 1 значение. Это значит, что каждый уровень
энергии имеет кратность вырождения 2J + 1, при этом при заданных
числах L, S имеется, как и должно быть, (2L + 1) (2S + 1) разлиичных состояний:

В обозначениях состояний отмечают также их четность: если состояние нечетно, то справа вверху добавляют индекс 0 (0dd — нечетный). Например, . Четное состояние обычно никак не отмечают.

Мультиплетность состояний (и термов) определяется спиновым квантовым числом как 2S + 1 (при L ≥ S ). Возможные значения числа S Зависят от количества электронов согласно — .

В случае одного электрона термы являются Дублетами. В случае двух электронов число S = 0 или 1. Тогда мультиплетность равна: 2·0+1=1

Или 2·1+1=3. Состояния с мультиплетностью 1 называют Синглетами, а с мультиплетностью 3 — Триплетами. В случае трех элек­тронов число S=1/2 или 3/2. Тогда состояния являются Дублетами и Квартетами. В случае четырех электронов S=0,1,2. Состояния ато­мов являются синглетами, триплетами и Квинтетами. Аналогично опреде­ляется мультиплетность в случае большого числа электронов.

4. Возможные радиационные переходы между различными состояниями атома LSJmJ → L’S’J’M’J Определяются правилами отбора. При излучении или поглощении фотона в системе “атом+фотон” выполняется закон сохранения момента импульса:

Где — собственный механический момент импульса (спин) фотона.

Отсюда в дипольном приближении следуют правила отбора для кванто­вого числа J:

∆J = 0, ±1.

При ∆J = 0 происходит поворот вектора Без изменения его величины (см. рис. 3в). Когда одно из квантовых чисел Или обращается в нуль, то треугольники на рис. 3 вырождаются в два равных отрезка прямых, направленных в одну сторону или противоположно. Равенство нулю и другого квантового числа, очевидно, невозможно, поскольку это нарушает закон сохранения момента импульса. Гово­рят, что по квантовому числу J Переход строго запрещен (A. Lande, 1921).

Р и с.3

Чтобы учесть запрещение таких переходов, правило дополняют условием: J + J’ ≥ 1.

Запишем теперь закон сохранения момента импульса в другой
форме: Отсюда следует, что момент импульса, уносимый (или приносимый) фотоном, складывается из изменений орби­тального и спинового моментов атома. Эти изменения определяются характером взаимодействия электронов с фотоном. Эксперименты и рас­четы показывают, что по крайней мере в оптическом диапазоне м и при дипольном излучении (или поглощении) фотона, не происходит измене­ния числа электронов в атоме, а также ориентации их спинов, т. е. полный спин электронов атома не изменяется. Это значит, что для спи­нового квантового числа существует правило отбора:

∆S = 0

Поскольку число S определяет мультиплетность термов (и состояний), то правило означает, что переходы между состояниями с раз­личной мультиплетностью запрещены. Это так называемый Принцип за­прета интеркомбинаций. Отметим, что этот принцип не является абсолют­но жестким – в спектрах атомов наблюдаются его нарушения. Из закона сохранения момента импульса и правила следуют также правила отбора для квантового числа L:

ΔL=0,±1

При этом 0 – 0 переходы запрещены, т. е. L + L’ ≥ 1. Отметим, что переходы без изменения орбитального квантового числа совершенно не­возможны для водородоподобных атомов и для атомов с одним электроном сверх заполненных оболочек. Этот запрет вытекает из закона сохране­ния четности волновых функций одно электронных состояний атомов