Как найти ширину треугольника 3 класс

Треугольник

Треугольник является базовой фигурой геометрии, встречающейся повсеместно. Расчет всех геометрических фигур и тел основаны на наличии в них тех или иных треугольников, благодаря чему становится возможным применить множество теорем и формул, несвойственных конкретным фигурам по отдельности. Равносторонние треугольники, равнобедренные треугольники и прямоугольные треугольники составляют каркас решения геометрических задач, и обладая множеством дополнительных построений внутри треугольника, они предоставляют огромное количество значений тех или иных длин. Все биссектрисы, медианы, высоты, радиусы окружностей, вписанных или описанных около таких треугольников, можно рассчитать в этом разделе через геометрический калькулятор. Для этого необходимо ввести любые имеющиеся вводные данные, и калькулятор выдаст не только значения всех остальных параметров треугольника, но и объяснит преобразования формул, использованные для этих расчетов.

Формулы определения периметра, площади и сторон треугольника

Треугольник — это элементарная геометрическая фигура, содержащая минимально возможное количество составляющих — три.

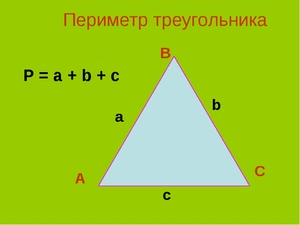
Точки соприкосновения сторон являются вершинами его углов, обозначаются заглавными латинскими символами A; B и C. Отрезки между вершинами являются сторонами или гранями треугольника и обозначаются названиями этих вершин: AB; BC; CA или прописной буквой противолежащего угла (вершины): AB=c; BC=a; CA=b.

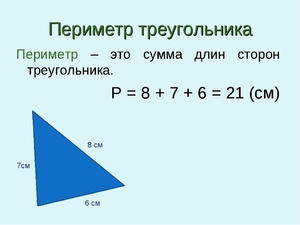
Периметр равен длине всех сторон фигуры, у треугольника он равен сумме трех сторон:

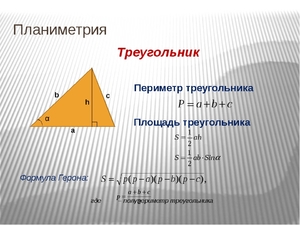
Высота треугольника — это перпендикуляр от прямой, на которой лежит основание, до одноименной вершины, обозначается h.

Площадь составляет величину поверхности, заключенной внутри фигуры, обозначается S. Произведение основания на высоту дает значение площади. Ее можно определить и по формуле Герона:

Из этого видео вы узнаете, как найти площадь треугольника.

Классификация треугольников

Треугольник состоит из сторон и углов, сумма его углов всегда равна 180 градусов: A+B+C=180°.

1. Равноугольный: все вершины равны 60°, будет и равносторонним.
2. Равнобедренный: при равенстве двух граней углы на основании равны.
3. Разноугольный: все вершины разные, ребра у него тоже разные.
4. Прямоугольный: один угол равен 90°, примыкающие грани называются катеты, противолежащая — гипотенуза. Бывает равнобедренным (катеты равны) или разноугольным (катеты разные).
5. Тупоугольный: один угол больше 90°. Может быть равнобедренным или разноугольным.

Описание

Чтобы описать любой треугольник, достаточно указать:

1. Одну сторону и прилегающие к ней углы.
2. Две стороны и угол между ними.
3. Три стороны.

Данных из любого пункта достаточно для построения заданной фигуры и вычисления всех ее параметров, используя теорему косинусов:

Подставляя известные значения, получим уравнение, решив которое узнаем неизвестные величины.

Cos90°=0, поэтому для прямоугольного треугольника c*c=a*a+b*b, где a и b — катеты, c — гипотенуза, сторона, лежащая напротив прямого угла.

Примеры

Известно, что одна грань равна 9 см и прилегающие углы по 60 градусов. Тогда из того, что сумма углов всегда равна 180°, получаем: 180=60+60+x; x=180—120=60. Все три вершины по 60°, значит, все стороны равны. Периметр составляет P=9+9+9=27 см, полупериметр p=13,5 см. Чтобы найти высоту, нужно опустить перпендикуляр из вершины на основание, получим прямоугольный треугольник с гипотенузой 9 см, катетом 4,5 см и катетом неизвестной длины, равным искомой высоте: 9*9—4,5*4,5=60,75=h 2 .

Высота равна корню квадратному из 60,75 или 7,79422863406 см. Умножаем основание на высоту, делим пополам и получаем площадь: 7,79422863406*9/2=35,074028853 см 2 . Если находить площадь по формуле Герона через полупериметр и ребра, ответ будет одинаковый:

S=√(13,5·(13,5—9)·(13,5—9)·(13,5—9))=35,074028853 см 2 .

Следующий пример с разносторонним треугольником. Дано: AB=12 см, BC=10 см, CA=8 см. Требуется найти периметр и площадь фигуры. P=a+b+c=BC+CA+AB=10 см+8 см+12 см=30 см. Площадь находим по формуле Герона, подставляя в нее уже известные значения, учитывая, что p=0,5Р; p=15 см. S=√(p·(p—a)·(p—b)·(p—c))=√(15·(15—10)·(15—8)·(15—12))=√15·5·7·3=√1575=39,686269666 см 2 .

Рассмотрим пример, когда известны два катета прямоугольного треугольника. Допустим, они имеют значения два и четыре метра. Тогда гипотенуза будет равна корню квадратному из суммы квадратов катетов √2 2 +4 2 =4,472135955 м. Периметр 2+4+4,472135955=10,472135955. Площадь равна половине произведения катетов S=2·4=8м 2 .

Когда известны две стороны и угол между ними, остается найти только третью сторону по теореме косинусов. Пусть известные стороны составляют значения 16 и 28 метров, а угол между ними будет в 60 градусов, тогда третья сторона будет равна корню квадратному из этого выражения 16 2 +28 2 — 2·16·28·0,5, что составит значение в 24,3310501212 м. Периметр равен 16+28+24,3310501212=68,3310501212≈68,33 м. Полупериметр будет 34,165 м. Подставляя полученные значения в формулу Герона, найдем площадь S=√(34,165·(34,165—16)·(34,165—28)·(34,165—24,33))=193,982314238 м 2 .

Если известно три параметра любого треугольника — два угла и сторона или две стороны и угол между ними, то ничего особенно сложного в нахождении неизвестных параметров треугольника — периметра, площади или высоты — нет. Нужно только внимательно производить простые вычисления. Иногда можно проявить и смекалку, разбив фигуру на несколько более простых в вычислении, например, прямоугольных треугольников. В каждом конкретном случае все зависит от исходных данных. Все формулы и вычисления, приведенные выше, верны для плоских фигур; для расположенных на сферической поверхности ход вычислений будет иным.

Видео

Это видео поможет вам закрепить полученные знания.

Треугольник. Формулы и свойства треугольников.

Типы треугольников

По величине углов

По числу равных сторон

Вершины углы и стороны треугольника

Свойства углов и сторон треугольника

Сумма углов треугольника равна 180°:

В треугольнике против большей стороны лежит больший угол, и обратно. Против равных сторон лежат равные углы:

если α > β , тогда a > b

если α = β , тогда a = b

Сумма длин двух любых сторон треугольника больше длины оставшейся стороны:

a + b > c
b + c > a
c + a > b

Теорема синусов

Стороны треугольника пропорциональны синусам противолежащих углов.

a	=	b	=	c	= 2R
sin α	sin β	sin γ

Теорема косинусов

Квадрат любой стороны треугольника равен сумме квадратов двух других сторон треугольника минус удвоенное произведение этих сторон на косинус угла между ними.

a 2 = b 2 + c 2 – 2 bc · cos α

b 2 = a 2 + c 2 – 2 ac · cos β

c 2 = a 2 + b 2 – 2 ab · cos γ

Теорема о проекциях

Для остроугольного треугольника:

a = b cos γ + c cos β

b = a cos γ + c cos α

c = a cos β + b cos α

Формулы для вычисления длин сторон треугольника

Медианы треугольника

Свойства медиан треугольника:

В точке пересечения медианы треугольника делятся в отношении два к одному (2:1)

Медиана треугольника делит треугольник на две равновеликие части

Треугольник делится тремя медианами на шесть равновеликих треугольников.

Формулы медиан треугольника

Формулы медиан треугольника через стороны

m_a = 1 2 √ 2 b 2 +2 c 2 – a 2

m_b = 1 2 √ 2 a 2 +2 c 2 – b 2

m_c = 1 2 √ 2 a 2 +2 b 2 – c 2

Биссектрисы треугольника

Свойства биссектрис треугольника:

Биссектриса треугольника делит противолежащую сторону на отрезки, пропорциональные прилежащим сторонам треугольника

Угол между биссектрисами внутреннего и внешнего углов треугольника при одной вершине равен 90°.

Формулы биссектрис треугольника

Формулы биссектрис треугольника через стороны:

l_a = 2√ bcp ( p – a ) b + c

l_b = 2√ acp ( p – b ) a + c

l_c = 2√ abp ( p – c ) a + b

где p = a + b + c 2 – полупериметр треугольника

Формулы биссектрис треугольника через две стороны и угол:

l_a = 2 bc cos α 2 b + c

l_b = 2 ac cos β 2 a + c

l_c = 2 ab cos γ 2 a + b

Высоты треугольника

Свойства высот треугольника

Формулы высот треугольника

h_a = b sin γ = c sin β

h_b = c sin α = a sin γ

h_c = a sin β = b sin α

Окружность вписанная в треугольник

Свойства окружности вписанной в треугольник

Формулы радиуса окружности вписанной в треугольник

r = ( a + b – c )( b + c – a )( c + a – b ) 4( a + b + c )

Окружность описанная вокруг треугольника

Свойства окружности описанной вокруг треугольника

Формулы радиуса окружности описанной вокруг треугольника

R = S 2 sin α sin β sin γ

R = a 2 sin α = b 2 sin β = c 2 sin γ

Связь между вписанной и описанной окружностями треугольника

Средняя линия треугольника

Свойства средней линии треугольника

MN = 1 2 AC KN = 1 2 AB KM = 1 2 BC

MN || AC KN || AB KM || BC

Периметр треугольника

Периметр треугольника ∆ ABC равен сумме длин его сторон

Формулы площади треугольника

Формула Герона

Равенство треугольников

Признаки равенства треугольников

Первый признак равенства треугольников — по двум сторонам и углу между ними

Второй признак равенства треугольников — по стороне и двум прилежащим углам

Третий признак равенства треугольников — по трем сторонам

Подобие треугольников

∆MNK => α = α ₁, β = β ₁, γ = γ ₁ и AB MN = BC NK = AC MK = k ,

где k – коэффициент подобия

Признаки подобия треугольников

Первый признак подобия треугольников

Второй признак подобия треугольников

Третий признак подобия треугольников

Любые нецензурные комментарии будут удалены, а их авторы занесены в черный список!

Добро пожаловать на OnlineMSchool.
Меня зовут Довжик Михаил Викторович. Я владелец и автор этого сайта, мною написан весь теоретический материал, а также разработаны онлайн упражнения и калькуляторы, которыми Вы можете воспользоваться для изучения математики.

[spoiler title=”источники:”]

http://liveposts.ru/articles/education-articles/matematika/formuly-opredeleniya-perimetra-ploshhadi-i-storon-treugolnika

http://ru.onlinemschool.com/math/formula/triangle/

[/spoiler]

Вы зашли на страницу вопроса Как найти ширину треугольника?, который относится к
категории Математика. По уровню сложности вопрос соответствует учебной
программе для учащихся 1 – 4 классов. В этой же категории вы найдете ответ
и на другие, похожие вопросы по теме, найти который можно с помощью
автоматической системы «умный поиск». Интересную информацию можно найти в
комментариях-ответах пользователей, с которыми есть обратная связь для
обсуждения темы. Если предложенные варианты ответов не удовлетворяют,
создайте свой вариант запроса в верхней строке.

Математика

Компоненты арифметических действий и их взаимосвязь.

1. Компоненты при сложении:

1слагаемое, 2слагаемое, сумма.

1. Компоненты при вычитании:

уменьшаемое, вычитаемое, разность.

1. Компоненты при умножении:

1 множитель, 2множитель, произведение.

1. Компоненты при делении:

делимое, делитель ,частное.

1. Назвать результаты всех действий:

при сложении – сумма

при вычитании – разность

при умножении – произведение

при делении – частное

1. Как найти неизвестное слагаемое?

Чтобы найти неизвестное слагаемое, нужно из суммы вычесть известное слагаемое.

Х+4=12                        или                4+х=12

Х=12-4                                        х=12-4                                        

Х=8                                                 х=8

8+4=12                                        4+8=12

  12=12                                        12=12

1. Как найти неизвестное уменьшаемое?

Чтобы найти неизвестное уменьшаемое, надо к разности прибавить вычитаемое.

Х-7=3

Х=3+7

Х=10

10-7=3

        3=3

1. Как найти неизвестное вычитаемое?

Чтобы найти неизвестное вычитаемое, надо из уменьшаемого вычесть разность.

8-х =5

х=8-5

х=3

8-3=5

   5=5

9                Как найти неизвестный множитель?        

Чтобы найти неизвестный множитель, надо произведение разделить на известный множитель.

х·3=6                                4·х=8

х=6:3                                х=8:4

х=2                                х=2        

2·3=6                                4·2=8

   6=6                                   8=8

10           Как найти неизвестное делимое?

Чтобы найти неизвестное делимое, надо частное умножить на делитель.

х:5=3

х=3·5

х=15

15:5=3

     3=3

1. Как найти неизвестный делитель?

Чтобы найти неизвестный делитель, надо делимое разделить на частное.

6:х=2

х =6:2

х=3

6:3=2

   2=2

Геометрический материал.

1. Что такое квадрат?

Квадрат – это прямоугольник, у которого все стороны равны.

1. Что такое прямоугольник?

Прямоугольник – это четырёхугольник, у которого все углы прямые. Противоположные стороны прямоугольника  равны.

1. Что такое треугольник?

Треугольник – многоугольник, у которого три угла и три стороны.

15     Что такое четырёхугольник?

Четырёхугольник – геометрическая фигура, у которой четыре угла и четыре стороны.

1. Что такое периметр?

Периметр( Ρ) – это сумма длин сторон какой-нибудь геометрической фигуры.

1. Что такое площадь?

Площадь(S) – это внутренняя часть какой-нибудь геометрической  фигуры

(прямоугольника, квадрата и т.д)

1. Как найти периметр квадрата?

У квадрата 4 стороны, равные между собой. Чтобы найти сторону квадрата, нужно Ρ□ разделить на 4.

a□ = Ρ□ : 4

1. Как найти периметр прямоугольника?

Чтобы найти периметр прямоугольника, нужно сложить все 4 стороны   прямоугольника

 Или

сложить длину и ширину прямоугольника и умножить на 2.

        Ρ▬=a+b+a+b

или

    Ρ▬=(a+b)·2

1. Как найти периметр треугольника?

Чтобы найти периметр треугольника, нужно сложить все 3 стороны.

1. Как найти сторону квадрата, если известен периметр? 

У квадрата 4 стороны, равные между собой. Чтобы найти сторону квадрата, нужно Ρ разделить на 4.

a=Ρ:4

1.         Как найти сторону прямоугольника, если известен периметр и другая сторона? 

Чтобы найти сторону прямоугольника, нужно Ρ▬разделить на 2  и  вычесть другую сторону.

a▬=Ρ▬:2 – b

b▬=Ρ▬:2 – a

22        В каких единицах измеряется периметр?

    Периметр измеряется в мм, см, дм, метрах.

23         Как найти площадь квадрата?

Площадь квадрата равна произведению двух его сторон.

S□ =  a · a

24          Как найти площадь прямоугольника?

Чтобы найти площадь прямоугольника, надо длину прямоугольника умножить на его ширину.

S█ =  a · b

25          Как найти сторону прямоугольника, если известна площадь и другая его сторона?

Чтобы найти одну из сторон прямоугольника,  нужно площадь прямоугольника разделить на известную сторону.

a▬=S▬ :  b

b▬= S ▬ : a

   26        В каких единицах измеряется площадь?

   Площадь измеряется в квадратных единицах: мм², см², дм², м².

27      Назвать единицы длины.

Единицы длины – мм, см, дм, м, км.

28           Рассказать таблицу мер длины.

1см  =  10мм

1дм  =  10см

1дм  =  100мм

1м  =    10 дм

1м  =  100 см

1км = 1000м

29       Сколько  квадратных сантиметров

в 1квадратном метре?

1м²  =  10 000см²  

30      Сколько  квадратных  дециметров  

в 1 квадратном  метре?

1м²  =  100дм²  

31            Рассказать  таблицу мер площади.

1м²  =  100дм²  = 10 000см²  

1дм²  = 100см²  =  10 000мм²

1см²  =  100мм²

Масса.

32            Назвать единицы массы.

Масса измеряется в граммах, килограммах, центнерах, тоннах.

33           Рассказать таблицу мер массы.

1кг  = 1000г

1ц  =  100кг

1т  =  10ц

1т  =  1000кг

Время.

34        Назвать  единицы измерения времени.

Время  измеряется секундами, минутами, часами, сутками, неделями, месяцами, годами, веками.

35           Рассказать таблицу мер времени.

1мин  =  60сек.

1час  =  60мин

1час  =  3600сек.

1сут.  =  24часа

1год  =  12мес.  =  365сут.  или  366сут.

1век  =  100лет

Взаимосвязь скорости, времени и расстояния.

36     Как  найти  скорость?

Чтобы найти скорость ( v ), надо расстояние ( S ) разделить на время ( t ), затраченное в пути.

v = S : t

37    Как найти время?

Чтобы найти время ( t ), надо расстояние ( S ) разделить на скорость ( v ).

t = S : v

38    Как найти расстояние?

Чтобы найти расстояние ( S ),  нужно скорость ( v ) умножить на время ( t ).

S = v · t

Взаимосвязь цены, количества, стоимости.

39    Что такое цена?

Цена – стоимость одного предмета, единицы товара.

40     Как найти стоимость?

Чтобы найти стоимость, нужно цену умножить на количество.

Ст = Ц · К

41     Как найти цену?

Чтобы найти цену, нужно стоимость разделить на количество.

Ц  =  Ст : К

42   Как найти  количество?

Чтобы найти количество, нужно стоимость разделить на цену.

К = Ст : Ц

Задачи на дроби.

43

Дробь  – ⅔

2 – числитель

3 – знаменатель

44  Как найти дробь числа?

Чтобы найти дробь числа, нужно число разделить на знаменатель, а потом умножить на числитель.

45      Как найти число по дроби?

Чтобы  найти число по дроби, нужно число разделить на числитель и умножить на знаменатель.

Взаимосвязь работы, времени и производительности.

46    Что такое производительность?

         Как найти производительность?

Производительностью ( v ) называют работу, выполненную за единицу времени.

Чтобы найти производительность ( v ), надо всю выполненную работу разделить на время.

v  =  A  :  t

47    Как найти выполненную работу?

Выполненная работа равна производительности, умноженной на время работы.

A  =  v  · t

48   Как найти время работы?

Чтобы узнать время работы, надо работу разделить на производительность.

t  =  A  :  v

49   Как  найти среднее арифметическое?

Чтобы найти среднее арифметическое надо сумму разделить на число слагаемых.