Как найти сходимость ряда с корнями

Исследовать на сходимость числовой ряд

Числовой ряд в общем виде задаётся следующей формулой: $$sum_{n=1}^infty a_n.$$ Разберем из чего состоит ряд. $a_n$ – это общий член ряда. $n$ – это переменная суммирования, которая может начинаться с нуля или любого натурального числа. Таким образом ряд расписывается следующим образом: $$sum_{n=1}^infty a_n = a_1+a_2+a_3+…$$ Слагаемые $a_1,a_2,a_3,…$ называются членами ряда. Если они неотрицательные, то ряд называется положительными числовым рядом.

Ряд расходится, если сумма его членов равна бесконечности: $$sum_{n=1}^infty n^2+1 = 2+5+10+…$$Ряд сходится, если сумма его членов равна конечному числу. Например, бесконечно убывающая геометрическая прогрессия: $$sum_{n=0}^infty frac{1}{2^n} = 1+frac{1}{2} + frac{1}{4}+frac{1}{8}+…$$ Её сумма вычисляется по следующей формуле $S = frac{A}{1-q}$, где $A$ – первый член прогрессии, а $q$ – основание. В данном случае сумма равна $S = frac{1}{1 – frac{1}{2}} = 2$.

Стоит заметить, что вычислить сумму ряда в большинстве случаев просто так не получится. Поэтому используют признаки сходимости, выполнение которых достаточно для установления сходимости ряда. Например, признаки Коши и Даламбера. Зависит это от общего члена ряда.

Необходимый признак сходимости ряда

Необходимый признак сходимости ряда нужно применять мысленно перед тем, как использовать достаточные признаки. Именно благодаря ему, можно заранее установить, что ряд расходится и не тратить время на проверку достаточными признаками. Для этого, нужно найти предел общего члена ряда и в зависимости от его значения сделать вывод.

1. Если ряд сходится, то $limlimits_{nto infty} a_n = 0$
2. Если $limlimits_{nto infty} a_n neq 0$ или не существует, то ряд расходится

ЗАМЕЧАНИЕ ! Первый пункт не работает в обратную сторону и нужно использовать достаточный признак сходимости. То есть, если предел общего члена ряда равен нулю, то это ещё не значит, что ряд сходится! Требуется использовать один из достаточных признаков сходимости.

Признаки сравнения

Обобщенный гармонический ряд записывается следующим образом $ sum_{n=1} ^infty frac{1}{n^p} $.

1. Если $ p = 1 $, то ряд $ sum_{n=1} ^infty frac{1}{n} $ расходится
2. Если $ p leqslant 1 $, то ряд расходится. Пример,$ sum_{n=1} ^infty frac{1}{sqrt{n}} $, в котором $ p = frac{1}{2} $
3. Если $ p > 1 $, то ряд сходится. Пример, $ sum_{n=1} ^infty frac{1}{sqrt{n^3}} $, в котором $ p = frac{3}{2} > 1 $

Этот ряд пригодится нам при использовании признаков сравнения, о которых пойдет речь дальше.

Признак сравнения

Пусть даны два знакоположительных числовых ряда $sum_{n=1}^infty a_n$ и $sum_{n=1}^infty b_n$, причем второй ряд сходящийся. Тогда, если начиная с некоторого номера $n$ выполнено неравенство $a_n le b_n$, то ряд $sum_{n=1}^infty a_n$ сходится вместе с $sum_{n=1}^infty b_n$.

Предельный признак сравнения

Если предел отношения общих членов двух рядов $sum_{n=1}^infty a_n$ и $sum_{n=1}^infty b_n$ равен конечному числу и отличается от нуля $$lim_{ntoinfty} frac{a_n}{b_n} = A,$$то оба ряда сходятся или расходятся одновременно.

ЗАМЕЧАНИЕ. Предельный признак удобно применять когда хотя бы один из общих членов ряда представляет собой многочлен.

Сообщения без ответов | Активные темы

Похожие темы	Автор	Ответы	Просмотры	Последнее сообщение
Исследовать на сходимость числовой ряд в форуме Ряды	Brunetka25	1	361	07 дек 2015, 15:39
Исследовать числовой ряд на сходимость в форуме Ряды	ALENA17	1	162	13 апр 2020, 08:48
Исследовать числовой ряд на сходимость в форуме Ряды	Inkvize	6	401	02 апр 2018, 23:06
Исследовать на сходимость числовой ряд в форуме Ряды	kykyky	1	384	27 ноя 2015, 19:00
Исследовать числовой ряд на сходимость в форуме Ряды	351w	5	375	27 май 2018, 19:22
Исследовать на сходимость числовой ряд с помощью достаточных в форуме Ряды	Kashirov+++	2	350	07 май 2014, 13:38
Исследовать на абсолютную и условную сходимость числовой ряд в форуме Ряды	Brunetka25	1	356	07 дек 2015, 15:44
Исследовать на абсолютную и условную сходимость числовой ряд в форуме Ряды	Ann1993	2	472	27 май 2014, 07:56
Дроби под корнем в форуме Алгебра	Tipok	4	503	02 сен 2014, 12:59
Доказать сходимость числовой последовательности в форуме Пределы числовых последовательностей и функций, Исследования функций	oksanakurb	9	424	07 янв 2014, 17:41

Кто сейчас на конференции

Сейчас этот форум просматривают: нет зарегистрированных пользователей и гости: 2

Вы не можете начинать темы Вы не можете отвечать на сообщения Вы не можете редактировать свои сообщения Вы не можете удалять свои сообщения Вы не можете добавлять вложения

Лекция
4 1

4.1.
Функциональные ряды: основные понятия,
область сходимости 1

4.2.
Степенные ряды: основные понятия,
теорема Абеля 2

4.3.
Свойства степенных рядов 5

4.4.
Формула Тейлора 5

4.1. Функциональные ряды: основные понятия, область сходимости

Определение
1.
Ряд, члены которого являются функциями
одной
или нескольких независимых переменных,
определёнными
на некотором множестве,
будем называть функциональным
рядом.

Рассмотрим
функциональный ряд,
члены которого являются функциями одной
независимой переменной х.
Сумма первых n
членов ряда

является частичной суммой данного
функционального ряда. Общий член

есть функция от х,
определенная в некоторой области. Если
положить
,
получим числовой ряд
,
и если он сходится, т.е. существует предел
частичных сумм этого ряда,
где

− сумма числового ряда, тогда говорят,
что

− точка сходимости функционального
ряда
,
а если числовой ряд

расходится, то

называется точкой расходимости
функционального ряда.

Определение
2.
Областью
сходимости
функционального ряда

называется множество всех таких значений
х,
при которых функциональный ряд сходится.
Область сходимости, состоящая из всех
точек сходимости, обозначается
.
Отметим, что
.

Будем
говорить, что функциональный ряд сходится
в области
,
если для любого

он сходится как числовой, при этом его
сумма будет некоторой функцией

(это так называемая предельная
функция
последовательности
:
).

Как
находить область сходимости функционального
ряда
?
Можно использовать признак, аналогичный
признаку Даламбера. Для ряда

составляем

и рассматриваем предел при фиксированном
х:
.
Тогда

является решением неравенства

и решением уравнения

(берем только те решения уравнения, в
которых соответствующие числовые ряды
сходятся).

Пример
1.
Найти область сходимости ряда
.

Решение.
Обозначим
,
.
Составим и вычислим предел
,
тогда область сходимости определяется
неравенством

и уравнением
.
Исследуем дополнительно сходимость
исходного ряда в точках, являющимися
корнями уравнения: а) если
,
,
то получается расходящийся ряд
;
б) если
,
,
то ряд

сходится условно (по признаку Лейбница,
пример 1, лекция 3).
Таким образом,
область сходимости

ряда

имеет вид:
.

4.2. Степенные ряды: основные понятия, теорема Абеля

Рассмотрим
частный случай функционального ряда,
так называемый степенной
ряд:
,
где
.

Определение
3.
Степенным
рядом
называется функциональный ряд вида
,
где

−
постоянные числа, называемые
коэффициентами
ряда.

Степенной
ряд есть «бесконечный многочлен»,
расположенный по возрастающим степеням
.
(Любой числовой ряд

является частным случаем степенного
ряда при
.)

Рассмотрим
частный случай степенного ряда при
:
.
Выясним, какой вид имеет область
сходимости данного ряда
.

Теорема
1 (теорема Абеля).
1) Если степенной ряд
(*)
сходится в точке
,
то он абсолютно сходится при всяком х,
для которого справедливо неравенство
.
2)
Если же степенной ряд расходится при
,
то он расходится при всяком х,
для
которого
.

Доказательство.
1) По условию степенной ряд сходится в
точке
,
т е. сходится числовой ряд
(**),
а значит, по необходимому признаку
сходимости его общий член стремится к
0, т.е.
.
Следовательно, существует такое число
,
что все члены ряда ограничены этим
числом:
.

Рассмотрим
теперь любое х,
для которого
,
и составим ряд из абсолютных величин:
.
Запишем этот ряд в другом виде: т.к.
,
то
(***).

Из
неравенства

получаем
,
т.е. ряд
(****)
состоит из членов, которые больше
соответствующих членов ряда (***). Ряд

представляет собой сходящийся ряд
геометрической прогрессии с знаменателем
,
причем
,
т.к.
.
Следовательно, ряд (***) сходится при
.
Таким образом, степенной ряд

абсолютно сходится.

2)
Пусть теперь ряд

расходится при
,
иными словами, расходится числовой ряд
.
Докажем, что для любого х
()
ряд расходится. Доказательство ведется
от противного. Пусть при некотором
фиксированном

()
ряд сходится, тогда он сходится при всех

(см. первую часть данной теоремы), в
частности, при
,
что противоречит условию 2 теоремы.
Теорема доказана.

Следствие.
Теорема Абеля позволяет судить о
расположении точки сходимости степенного
ряда.
Если точка

является точкой сходимости степенного
ряда, то интервал

заполнен точками сходимости; если точкой
расходимости является точка
,
то бесконечные интервалы

заполнены точками расходимости (см.
рис. 1).

Рис.
1.

Можно
показать, что существует такое число
,
что при всех

степенной ряд

абсолютно сходится, а при

− расходится. Будем считать, что если
ряд сходится только в одной точке 0, то
,
а если ряд сходится при всех
,
то
.

Определение
4.
Интервалом
сходимости
степенного ряда

называется такой интервал
,
что при всех

этот ряд сходится и притом абсолютно,
а для всех х,
лежащих вне этого интервала, ряд
расходится. Число R
называется радиусом
сходимости
степенного ряда.

Замечание.
На концах интервала

вопрос о сходимости или расходимости
степенного ряда решается отдельно для
каждого конкретного ряда.

Покажем
один из способов определения интервала
и радиуса сходимости степенного ряда.

Рассмотрим
степенной ряд

и обозначим
.
Составим ряд из абсолютных величин его
членов:

и применим к нему признак
Даламбера.

Пусть
существует
,
где
.
По признаку Даламбера ряд сходится,
если
,
и расходится, если
.
Отсюда ряд сходится при
,
тогда интервал сходимости:
.
При

ряд расходится, т.к.
.
Используя обозначение
,
получим формулу для определения радиуса
сходимости степенного ряда:
,
где

− коэффициенты степенного ряда. Если
окажется, что предел
,
то полагаем
.

Для
определения интервала и радиуса
сходимости степенного ряда также можно
использовать радикальный признак Коши,
радиус сходимости ряда определяется
из соотношения
.

Определение
5.
Обобщенным
степенным рядом называется ряд вида
.
Его также называют рядом по степеням
.
Для такого ряда интервал сходимости
имеет вид:
,
где

− радиус сходимости.

Покажем,
как находится радиус сходимости для
обобщенного степенного ряда.

,
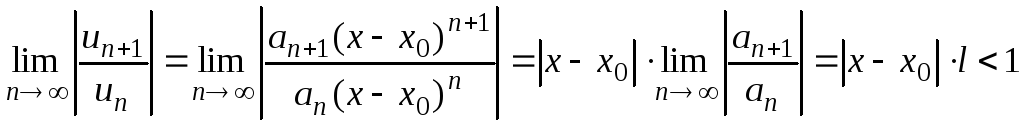
т.е.
,
где
.

Если
,
то
,
;
если
,
то

и область сходимости
.

Пример
2.
Найти область сходимости ряда
.

Решение.
Обозначим
.
Составим предел
.
Решаем неравенство:
,

,
следовательно, интервал сходимости
имеет вид:
,
причем R
= 5. Дополнительно исследуем концы
интервала сходимости: а)
,
,
получаем ряд
,
который
расходится;
б)
,

,
получаем ряд
,
который сходится условно. Таким образом,
область сходимости:
,
.

Пример
3.
Ряд

расходится для всех
,
т.к.

при
,
радиус сходимости
.

Пример
4.
Ряд

сходится при всех
,
радиус сходимости
.

Признаки сравнения числовых рядов. Вторая часть.

В первой части этой темы мы начали разбирать примеры применения признаков сравнения для исследования вопроса сходимости положительных рядов. Вот два этих признака:

Первый признак сравнения

Второй признак сравнения

Пусть заданы два положительных ряда $sumlimits_{n=1}^{infty}u_n$ и $sumlimits_{n=1}^{infty}v_n$. Если при условии $v_nneq 0$ существует предел
$$lim_{ntoinfty}frac{u_n}{v_n}=K,$$
где $0 < K < infty$, то ряды $sumlimits_{n=1}^{infty}u_n$ и $sumlimits_{n=1}^{infty}v_n$ сходятся либо расходятся одновременно.

И вот два ряда, с которыми мы и будем сравнивать исследуемые в задачах ряды: обобщённый гармонический ряд

$$
begin{equation}
sumlimits_{n=1}^{infty}frac{1}{n^alpha}
end{equation}
$$

который сходится если $alpha > 1$ и расходится при $alpha ≤ 1$, а также сумма геометрической прогрессии

$$
begin{equation}
sumlimits_{n=1}^{infty}aq^n
end{equation}
$$

Ряд (2) сходится если $|q| < 1$ и расходится если $|q|≥ 1$.

На этой странице поговорим о рядах, у которых выражение общего члена ряда включает в себя некий “несущественный” элемент: $arcsin x$, $arccos x$, $arctg x$, $arcctg x$, $cos x$ или $sin x$. В вопросе исследования сходимости таких рядов нам помогут записанные ниже неравенства. Для начала отметим, что при любом $xin R$ верны такие неравенства:

$$
begin{equation}
-1≤sin x≤ 1
end{equation}
$$

$$
begin{equation}
-1≤cos x≤ 1
end{equation}
$$

$$
begin{equation}
-frac{pi}{2}<arctg x<frac{pi}{2}
end{equation}
$$

$$
begin{equation}
0<arcctg x<pi
end{equation}
$$

Если $-1≤ x≤ 1$, то:

$$
begin{equation}
-frac{pi}{2}≤arcsin x≤frac{pi}{2}
end{equation}
$$

$$
begin{equation}
0≤arccos x≤pi
end{equation}
$$

На неравества с арксинусом и арккосинусом стоит обратить особое внимание. Дело в том, что их можно применять только когда $-1≤ x≤ 1$. Поэтому перед применением неравенств (7) и (8) нужно проверить выполнение условия $-1≤ x≤ 1$. Да и вообще, если в записи общего члена ряда указан арксинус или арккосинус, то нелишне проверить его аргумент: лежит ли этот аргумент в положенном ему интервале $-1≤ x≤ 1$ или нет? То же самое касается, кстати, и иных выражений. Например, ряд $sumlimits_{n=1}^{infty}frac{5n}{n-9}$ записан с ошибкой. Посудите сами: если $n=9$, то $n-9=0$ и значит значение выражения $frac{5n}{n-9}$ будет попросту неопределено, – мы же не можем делить на ноль! Подобного рода ошибками часто страдают стандартные типовые расчёты и контрольные работы. Поэтому предварительная (пусть и устная) проверка не помешает.

В первой части мы решали все примеры двумя способами: с помощью первого и второго признаков сравнения. В этой части станем решать примеры с помощью какого-либо одного признака, – так как все эти решения, по сути, однотипны. Хотя есть примеры, где нужно применять какой-то один признак, ибо применение иного признака сравнения будет невозможным (см. пример №7) или нецелесообразным (см. пример №8).

Для вычисления пределов будем использовать методы, изложенные в теме “Пределы с иррациональностями”, а также “Предел отношения двух многочленов”.

Пример №5

Исследовать сходимость ряда $sumlimits_{n=1}^{infty}frac{arcsinfrac{7n-1}{9n}}{sqrt[6]{4n^2-3}}$.

Решение

Так как нижний предел суммирования равен 1, то общий член ряда записан под знаком суммы: $u_n=frac{arcsinfrac{7n-1}{9n}}{sqrt[6]{4n^2-3}}$. Сразу обратим внимание, что общий член ряда записан корректно. Ноль в знаменателе или отрицательное число под корнем невозможны так как $4n^2-3 > 0$. Так как $0<7n-1<9n$, то выражение $frac{7n-1}{9n}$, которое является аргументом арксинуса, удовлетворяет неравенству $0<frac{7n-1}{9n}<1$. Т.е. аргумент арксинуса не выходит за пределы отрезка $[-1;1]$, что говорит о корректности выражения общего члена ряда. В дальнейшем такие рассуждения будем пропускать, однако проводить их (хотя бы устно) всё-таки желательно.

Ну, и так как и числитель и знаменатель общего члена ряда положительны, то $u_n > 0$, т.е. наш ряд положительный.

Выполнение необходимого условия сходимости проверять не будем. В принципе, очевидно, что так арксинус в числителе ограничен (см. формулу (7)), а знаменатель стремится к бесконечности, то $lim_{ntoinfty}u_n=0$. Обычно дело и ограничивается устной проверкой, после которой переходят к одному из признаков сходимости. В данном случае переходим к применению признаков сравнения.

Выберем ряд для сравнения. Для этого сначала проведём пару неформальных рассуждений. Если $ntoinfty$, то выражение в знаменателе общего члена ряда будет стремиться к бесконечности, т.е. $sqrt[6]{4n^2-3}toinfty$. Но что будет с числителем? А в числителе мы имеем арксинус, который удовлетворяет неравенству (7):

$$-frac{pi}{2}≤arcsinfrac{7n-1}{9n}≤frac{pi}{2}$$

В принципе, так как $0<frac{7n-1}{9n}<1$, то указанное выше неравенство можно записать более точно:

$$0<arcsinfrac{7n-1}{9n}<frac{pi}{2}$$

Иными словами, если $ntoinfty$, то арксинус не сможет выйти даже за пределы $frac{pi}{2}$, в то время как знаменатель будет уходить в бесконечность. Мысленно отбросим арксинус в числителе. А в знаменателе оставим лишь наибольшую степень $n$ (как это делалось с предыдущих примерах). Дробь $frac{arcsinfrac{7n-1}{9n}}{sqrt[6]{4n^2-3}}$ после таких преобразований примет вид $frac{1}{sqrt[6]{n^2}}=frac{1}{sqrt[3]{n}}$. Именно с рядом $sumlimits_{n=1}^{infty}frac{1}{sqrt[3]{n}}$ мы и станем сравнивать наш ряд. Так как $sumlimits_{n=1}^{infty}frac{1}{sqrt[3]{n}}=sumlimits_{n=1}^{infty}frac{1}{n^frac{1}{3}}$ и $frac{1}{3}≤ 1$, то ряд $sumlimits_{n=1}^{infty}frac{1}{sqrt[3]{n}}$ расходится. А значит будет расходиться и наш ряд. Остаётся лишь формально провести доказательство этого утверждения.

В этот раз применим признак сравнения в предельной форме. Сравнивать станем с рядом $sumlimits_{n=1}^{infty}frac{1}{sqrt[3]{n}}$. Оба общих члена сравниваемых рядов не равны нулю, поэтому в знаменателе можем размещать общий член любого ряда. В предыдущих примерах общий член “эталонного” ряда попадал всегда в знаменатель, а здесь, сугубо для разнообразия, поместим его в числитель:

$$
lim_{ntoinfty}frac{frac{1}{sqrt[3]{n}}}{frac{arcsinfrac{7n-1}{9n}}{sqrt[6]{4n^2-3}}}=lim_{ntoinfty}frac{sqrt[6]{4n^2-3}}{sqrt[3]{n}cdotarcsinfrac{7n-1}{9n}}=left|frac{infty}{infty} right|
=lim_{ntoinfty}frac{sqrt[6]{4-frac{3}{n^2}}}{arcsinfrac{7n-1}{9n}}=
frac{sqrt[6]{4-0}}{arcsinfrac{7}{9}}=frac{sqrt[3]{2}}{arcsinfrac{7}{9}}.
$$

Так как $0<frac{sqrt[3]{2}}{arcsinfrac{7}{9}}<infty$, то ряды $sumlimits_{n=1}^{infty}frac{arcsinfrac{7n-1}{9n}}{sqrt[6]{4n^2-3}}$ и $sumlimits_{n=1}^{infty}frac{1}{sqrt[3]{n}}$ сходятся либо расходятся одновременно. Так как ряд $sumlimits_{n=1}^{infty}frac{1}{sqrt[3]{n}}$ расходится, то одновременно с ним будет расходиться и ряд $sumlimits_{n=1}^{infty}frac{arcsinfrac{7n-1}{9n}}{sqrt[6]{4n^2-3}}$.

Ответ: ряд расходится.

Пример №6

Исследовать сходимость ряда $sumlimits_{n=1}^{infty}frac{arctg^2sqrt{2n^3-1}}{sqrt[4]{3n^5-2}}$.

Решение

Так как нижний предел суммирования равен 1, то общий член ряда записан под знаком суммы: $u_n=frac{arctg^2sqrt{n^3-1}}{sqrt[4]{3n^5-2}}$. При этом и числитель и знаменатель положительны, т.е. $u_n > 0$. Следовательно, заданный нам ряд – положительный. Так как арктангенс в числителе ограничен (см. формулу (5)), а $sqrt[4]{3n^5-2}toinfty$ при $ntoinfty$, то при проверке необходимого условия сходимости мы получим, что $lim_{ntoinfty}u_n=0$. Так как эта проверка нам ничего нового не даёт (ряд может как сходиться, так и расходиться), то переходим к использованию признака сравнения.

Начнём с неформальных рассуждений для выбора ряда, с которым станем сравнивать. Если $ntoinfty$, то выражение в знаменателе общего члена ряда будет стремиться к бесконечности, т.е. $sqrt[4]{3n^5-2}toinfty$. Но что будет с числителем? А в числителе мы имеем арктангенс. Согласно формуле (5) можно записать такое неравенство:

$$
-frac{pi}{2}<arctgsqrt{2n^3-1}<frac{pi}{2}
$$

А для $arctg^2sqrt{2n^3-1}$ получим:

$$
0≤arctg^2sqrt{2n^3-1}<left(frac{pi}{2}right)^2
$$

Данное неравенство можно и уточнить. Начальное значение $arctg^2sqrt{2n^3-1}$ при $n=1$ равно

$$arctg^2sqrt{2n^3-1}=arctg^2sqrt{2-1}=arctg^21=left(frac{pi}{4}right)^2.$$

Так как арктангенс – возрастающая функция, то записанное выше неравенство станет таким:

$$
left(frac{pi}{4}right)^2≤arctg^2sqrt{2n^3-1}<left(frac{pi}{2}right)^2
$$

Итак, что мы имеем? Знаменатель стремится в бесконечность, а числитель не может превысить даже $left(frac{pi}{2}right)^2$. Мысленно отбросим арктангенс в числителе. В знаменателе оставим под корнем лишь $n^5$. Тогда дробь $frac{arctg^2sqrt{n^3-1}}{sqrt[4]{3n^5-2}}$ станет такой: $frac{1}{sqrt[4]{n^5}}$. Именно с рядом $sumlimits_{n=1}^{infty}frac{1}{sqrt[4]{n^5}}$ мы и станем сравнивать заданный ряд. Так как $sumlimits_{n=1}^{infty}frac{1}{sqrt[4]{n^5}}=sumlimits_{n=1}^{infty}frac{1}{n^frac{5}{4}}$ и $frac{5}{4} > 1$, то ряд $sumlimits_{n=1}^{infty}frac{1}{sqrt[4]{n^5}}$ сходится. Значит, и наш ряд будет сходиться. Осталось лишь строго доказать эту сходимость.

Здесь можно применять как первый, так и второй признаки сравнения. Мне удобнее применить признак сравнения в предельной форме (т.е., второй признак). Однако я укажу и решение с помощью первого признака сравнения, только скрою его под примечание в конце решения этого примера. Сравнивать станем с рядом $sumlimits_{n=1}^{infty}frac{1}{sqrt[4]{n^5}}$. Оба общих члена сравниваемых рядов не равны нулю, поэтому в знаменателе можем размещать общий член любого ряда.

$$
lim_{ntoinfty}frac{frac{arctg^2sqrt{2n^3-1}}{sqrt[4]{3n^5-2}}}{frac{1}{sqrt[4]{n^5}}}=
lim_{ntoinfty}frac{sqrt[4]{n^5}cdotarctg^2sqrt{2n^3-1}}{sqrt[4]{3n^5-2}}=left|frac{infty}{infty}right|=
lim_{ntoinfty}frac{arctg^2sqrt{2n^3-1}}{sqrt[4]{3-frac{2}{n^5}}}=frac{left(frac{pi}{2}right)^2}{sqrt[4]{3}}=
frac{pi^2}{4cdotsqrt[4]{3}}.
$$

При вычислении предела был использован тот факт, что $lim_{tto +infty}arctg t=frac{pi}{2}$. Так как $0<frac{pi^2}{4cdotsqrt[4]{3}}<infty$, то ряды $sumlimits_{n=1}^{infty}frac{arctg^2sqrt{2n^3-1}}{sqrt[4]{3n^5-2}}$ и $sumlimits_{n=1}^{infty}frac{1}{sqrt[4]{n^5}}$ сходятся либо расходятся одновременно. Так как ряд $sumlimits_{n=1}^{infty}frac{1}{sqrt[4]{n^5}}$ сходится, то одновременно с ним будет сходиться и ряд $sumlimits_{n=1}^{infty}frac{arctg^2sqrt{2n^3-1}}{sqrt[4]{3n^5-2}}$.

Как решить этот пример с помощью первого признака сравнения? показатьскрыть

Ответ: ряд сходится.

Пример №7

Исследовать сходимость ряда $sumlimits_{n=1}^{infty}frac{1}{n}sinleft(frac{2+(-1)^n}{6}cdotpiright)$.

Решение

Так как нижний предел суммирования равен 1, то общий член ряда записан под знаком суммы: $u_n=frac{1}{n}sinleft(frac{2+(-1)^n}{6}cdotpiright)$.

Посмотрим, какие значения может принимать $sinleft(frac{2+(-1)^n}{6}cdotpiright)$. Если $n$ – чётное число, то $(-1)^n=1$, поэтому:

$$
sinleft(frac{2+(-1)^n}{6}cdotpiright)=sinleft(frac{2+1}{6}cdotpiright)=sinfrac{pi}{2}=1.
$$

Если же $n$ – нечётное число, то $(-1)^n=-1$, тогда синус станет таким:

$$
sinleft(frac{2+(-1)^n}{6}cdotpiright)=sinleft(frac{2-1}{6}cdotpiright)=sinfrac{pi}{6}=frac{1}{2}.
$$

Как видите, синус в данной ситуации выступает как простой числовой коэффициент, который равен то 1, то $frac{1}{2}$. Кстати, отсюда следует, что наш ряд положительный и мы можем применить признаки сравнения. Выберем ряд для сравнения. Отбросив синус, который, по сути, является простым числовым коэффициентом, получим ряд для сравнения: $sumlimits_{n=1}^{infty}frac{1}{n}$. Это гармонический ряд. Он расходится, поэтому и наш ряд будет расходиться. Однако применить второй признак сравнения (предельный признак) мы в этой ситуации не можем. Судите сами:

$$
lim_{ntoinfty}frac{frac{1}{n}sinleft(frac{2+(-1)^n}{6}cdotpiright)}{frac{1}{n}}=
lim_{ntoinfty}sinleft(frac{2+(-1)^n}{6}cdotpiright)
$$

Полученный предел не существует, так как при $ntoinfty$ синус для четных $n$ принимает значение 1, а для нечётных – значение $frac{1}{2}$. Значит ли это, что наш ряд расходится? Вовсе нет, – это говорит лишь о том, что нужно применять первый признак сравнения. Так как $sinleft(frac{2+(-1)^n}{6}cdotpiright)≥frac{1}{2}$, то:

$$
frac{1}{n}sinleft(frac{2+(-1)^n}{6}cdotpiright)≥frac{1}{2}cdotfrac{1}{n}.
$$

Так как ряд $sumlimits_{n=1}^{infty}frac{1}{n}$ расходится, то будет расходиться и ряд $sumlimits_{n=1}^{infty}left(frac{1}{2}cdotfrac{1}{n}right)$. Так как ряд $sumlimits_{n=1}^{infty}left(frac{1}{2}cdotfrac{1}{n}right)$ расходится и $frac{1}{n}sinleft(frac{2+(-1)^n}{6}cdotpiright)≥frac{1}{2}cdotfrac{1}{n}$, то согласно первому признаку сравнения (пункт №1) ряд $sumlimits_{n=1}^{infty}frac{1}{n}sinleft(frac{2+(-1)^n}{6}cdotpiright)$ расходится.

Ответ: ряд расходится.

Пример №8

Исследовать сходимость ряда $sumlimits_{n=1}^{infty}frac{2^{3n}+cos n!}{5^{2n+1}-n}$.

Решение

Так как нижний предел суммирования равен 1, то общий член ряда записан под знаком суммы: $u_n=frac{2^{3n}+cos n!}{5^{2n+1}-n}$. Так как согласно формуле (4) имеем $-1≤cos n!≤ 1$, то $2^{3n}+cos n!≥ 1$. Так как $5^{2n+1}-n > 0$ (это легко доказать, например, методом математической индукции), то наш ряд – положительный, т.е. $u_n≥ 0$.

С каким рядом станем сравнивать заданный ряд? Давайте отбросим все “несущественные” элементы для дроби $frac{2^{3n}+cos n!}{5^{2n+1}-n}$. В числителе выкинем косинус, а в знаменателе отбросим $n$. Дело в том, что порядок роста $n$ меньше, чем $5^{2n+1}$. Например, если $n=5$, то $5^{2n+1}=48,828,125$. После всех “отбрасываний” у нас останется $frac{2^{3n}}{5^{2n+1}}=frac{left(2^3right)^n}{5cdot left(5^2right)^n}=frac{1}{5}left(frac{8}{25}right)^n$. В принципе, и множитель $frac{1}{5}$ можно смело убрать, так как на сходимость он не повлияет.

Итак, мы станем сравнивать наш ряд с рядом $sumlimits_{n=1}^{infty}left(frac{8}{25}right)^n$. Это ряд вида (2), т.е. сумма элементов геометрической прогрессии с знаменателем $frac{8}{25}$. Так как $left|frac{8}{25}right|< 1$, то ряд $sumlimits_{n=1}^{infty}left(frac{8}{25}right)^n$ сходится.

Здесь можно применять как первый признак сравнения, так и второй. Однако проще использовать неравенства, т.е. применить первый признак сравнения (если есть необходимость рассмотреть применение второго признака сравнения, то отпишите об этом на форум). Если мы вместо $cos n!$ в числителе напишем $2^{3n}$, то увеличим данную дробь:

$$
frac{2^{3n}+cos n!}{5^{2n+1}-n} < frac{2^{3n}+2^{3n}}{5^{2n+1}-n}=2cdotfrac{2^{3n}}{5^{2n+1}-n}.
$$

Так как $n < frac{1}{2}5^{2n+1}$ (это можно доказать методом математической индукции, если есть необходимость рассмотреть здесь это доказательство, то отпишите об этом на форум), то $5^{2n+1}-n > 5^{2n+1}-frac{1}{2}5^{2n+1}=frac{1}{2}5^{2n+1}$. Уменьшая знаменатель мы увеличиваем дробь:

$$
frac{2^{3n}+cos n!}{5^{2n+1}-n} < 2cdotfrac{2^{3n}}{5^{2n+1}-n} < 2cdotfrac{2^{3n}}{frac{1}{2}cdot 5^{2n+1}}=4cdot frac{2^{3n}}{5^{2n+1}}=frac{4}{5}cdotleft(frac{8}{25}right)^n.
$$

Так как ряд $sumlimits_{n=1}^{infty}left(frac{4}{5}cdotleft(frac{8}{25}right)^nright)$ сходится и $frac{2^{3n}+cos n!}{5^{2n+1}-n} < frac{4}{5}cdotleft(frac{8}{25}right)^n$, то согласно первому признаку сравнения (пункт №2) ряд $sumlimits_{n=1}^{infty}frac{2^{3n}+cos n!}{5^{2n+1}-n}$ сходится.

Ответ: ряд сходится.

Продолжение темы исследования сходимости рядов с помощью признаков сравнения рассмотрим в третьей части.

Содержание:

1. Радиус сходимости и круг сходимости степенного ряда
2. Регулярные функции
3. Примеры с решением

Радиус сходимости и круг сходимости степенного ряда

Функциональные ряды вида (1) и — заданные комплексные числа, — комплексное переменное, называются степенными рядами. Числа называются коэффициентами степенного ряда (1). Полагая в (1) получим ряд (2) исследование сходимости которого эквивалентно исследованию сходимости ряда (1).

Теорема 1. (Абеля).

Если степенной ряд (2) сходится при , то он сходится и притом абсолютно при любом таком, что а если этот ряд расходится при то он расходится при всяком для которого

Теорема 2.

Для всякого степенного ряда (2) существует — число или ) такое, что ряд (2) абсолютно сходится в круге если Этот круг называется кругом сходимости степенного ряда, a радиусом сходимости этого ряда. Если то ряд (2) сходится в одной точке а если то этот ряд сходится во всей комплексной плоскости. В точках границы кругаряд (2) может как сходиться, так и расходиться. В любом меньшем круге ряд (2) сходится абсолютно и равномерно. Для степенного ряда круг сходимости имеет вид

По этой ссылке вы найдёте полный курс лекций по высшей математике:

Теорема 3 (Абеля).

Если — радиус сходимости степенного ряда (2), причем и если этот ряд сходится при то он сходится равномерно на отрезке а его сумма непрерывна на этом отрезке. Для радиуса сходимости степенного ряда (3) справедлива формула Коши-Адамара: (4) Если существует (конечный или бесконечный) то (5) а если существует (конечный или бесконечный) то (6) Для степенного ряда (7) где — заданные действительные числа, — действительное переменное, существует — число или такое, что при ряд (7) абсолютно сходятся, если и расходится, если Интервал называют интервалом, сходимости, а радиусом сходимости ряда (7). Радиус сходимости ряда (7) совпадает с радиусом сходимости ряда где комплексное переменное. При ряд (7) сходится лишь в точке а при — при всех

Исследовать степенной ряд (7) на сходимость — значит найти его интервал сходимости и выяснить, сходится или расходится этот ряд в концах его интервала сходимости. Область сходимости степенного ряда (7) состоит из его интервала сходимости и, быть может, некоторых граничных точек этого интервала.

Возможно вам будут полезны данные страницы:

Регулярные функции

Функция комплексного переменного называется регулярной (однозначной аналитической, голоморфной) в точке а, если она определена в некоторой окрестности точки а и представима в круге где сходящимся к степенным рядом: (8) Отметим, что любой многочлен функция, регулярная в каждой точке комплексной плоскости.

Рациональная функция где и — многочлены степени п и т соответственно, регулярна в каждой точке где

В теории функций комплексного переменного доказывается (см., например, [14]), что на границе круга сходимости степенного ряда (8) лежит хотя бы одна “особая” точка его суммы Отсюда следует, что радиус степенного ряда (8) равен расстоянию от точки до ближайшей к а особой точки функции В частности, если где многочлены и не имеют общих корней, то для этой функции радиус сходимости степенного ряда (8) равен расстоянию от точки до ближайшего к этой точке корня многочлена т. е. (9) где — корни многочлена Дифференцирование и интегрирование степенного ряда. Вычисление суммы ряда. Если степенной ряд (10) где — заданные действительные числа, — действительное переменное, имеет радиус сходимости то: 1) в интервале сходимости функция имеет производные любого порядка, получаемые почленным дифференцированием ряда (10);

2) внутри интервала сходимости этот ряд можно почленно интегрировать, т. е. 3) степенные ряды, получаемые из ряда (10) при почленном дифференцировании и интегрировании, имеют тот же радиус сходимости, что и ряд (10).

Показано пространство степенных рядов с одной переменной и коэффициентом. Пространство имеет структуру дифференциальной алгебры на кольце (если кольца одинаковы, с коммутативным, интегральным и единичным).

Примеры с решением

Пример 1.

Найти радиус сходимости Я степенного ряда:

1) Так как существует то по формуле (5) находим 2) В этом случае и поэтому (формула (5)). 3) Так как и существует то по формуле (б) получаем 4) Обозначим тогда Заметим, что ряд сходится, если и расходится, если Следовательно, ряд nz3n сходится, если т. е. при и расходится при . Итак, радиус сходимости ряда Заметим, что Я можно найти и по формуле (4). В самом деле, так как то по формуле (4) получаем

Пример 2.

Найти область сходимости степенного ряда: 1) По формуле (5) находим радиус сходимости ряда Ряд сходится в интервале (0;2). При ряд расходится, так как для его п-го члена ап справедлива асимптотическая формула При получаем сходящийся по признаку Лейбница ряд Следовательно, область сходимости ряда — полуинтервал 2) Радиус сходимости ряда равен (формула (5)). При и ряд абсолютно сходится, так как по интегральному признаку сходится ряд Поэтому область сходимости ряда отрезок 3) По формуле (4) находим, что радиус сходимости ряда При ряд расходится (не выполняется необходимое условие сходимости). Следовательно, область сходимости ряда — интервал

Пример 3.

Пользуясь формулой (9), найти радиус сходимости степенного ряда (8), для функции 1) Многочлен имеет корни , а наименьшее из чисел равно Поэтому 2) Многочлен имеет корни причем Поэтому 3) Из равенства следует, что многочлен имеет корни Так как то

При использовании эти соотношения превращаются в алгебраические уравнения для коэффициентов ряда.

Пример 4.

Найти сумму ряда Рассмотрим ряд Этот ряд сходится, если (его радиус сходимости ), а сумма ряда равна Дифференцируя почленно ряд получаем откуда Степенные ряды можно использовать при вычислении сумм числовых рядов. Если известно, что ряд сходится, то его сумму можно найти по формуле (11)

Пример 5.

Доказать, что

Рассмотрим степенной ряд Его сумма равна Радиус сходимости этого ряда равен 1, в точке ряд сходится (признак Лейбница). Применив формулу (11), получаем равенство (12). (пример 3). Отсюда следует, что (14) Так как этот ряд сходится при то из (14) по формуле (11) следует равенство (13).