Skip to content
В этой статье мы рассмотрим разные подходы к одной из самых распространенных и, по моему мнению, важных задач в Excel – как найти в ячейках и в столбцах таблицы повторяющиеся значения.
Работая с большими наборами данных в Excel или объединяя несколько небольших электронных таблиц в более крупные, вы можете столкнуться с большим числом одинаковых строк.
И сегодня я хотел бы поделиться несколькими быстрыми и эффективными методами выявления дубликатов в одном списке. Эти решения работают во всех версиях Excel 2016, Excel 2013, 2010 и ниже. Вот о чём мы поговорим:
- Поиск повторяющихся значений включая первые вхождения
- Поиск дубликатов без первых вхождений
- Определяем дубликаты с учетом регистра
- Как извлечь дубликаты из диапазона ячеек
- Как обнаружить одинаковые строки в таблице данных
- Использование встроенных фильтров Excel
- Применение условного форматирования
- Поиск совпадений при помощи встроенной команды “Найти”
- Определяем дубликаты при помощи сводной таблицы
- Duplicate Remover – быстрый и эффективный способ найти дубликаты
Самой простой в использовании и вместе с тем эффективной в данном случае будет функция СЧЁТЕСЛИ (COUNTIF). С помощью одной только неё можно определить не только неуникальные позиции, но и их первые появления в столбце. Рассмотрим разницу на примерах.
Поиск повторяющихся значений включая первые вхождения.
Предположим, что у вас в колонке А находится набор каких-то показателей, среди которых, вероятно, есть одинаковые. Это могут быть номера заказов, названия товаров, имена клиентов и прочие данные. Если ваша задача – найти их, то следующая формула для вас:
=СЧЁТЕСЛИ(A:A; A2)>1
Где А2 – первая ячейка из области для поиска.
Просто введите это выражение в любую ячейку и протяните вниз вдоль всей колонки, которую нужно проверить на дубликаты.
Как вы могли заметить на скриншоте выше, формула возвращает ИСТИНА, если имеются совпадения. А для встречающихся только 1 раз значений она показывает ЛОЖЬ.
Подсказка! Если вы ищите повторы в определенной области, а не во всей колонке, обозначьте нужный диапазон и “зафиксируйте” его знаками $. Это значительно ускорит вычисления. Например, если вы ищете в A2:A8, используйте
=СЧЕТЕСЛИ($A$2:$A$8, A2)>1
Если вас путает ИСТИНА и ЛОЖЬ в статусной колонке и вы не хотите держать в уме, что из них означает повторяющееся, а что – уникальное, заверните свою СЧЕТЕСЛИ в функцию ЕСЛИ и укажите любое слово, которое должно соответствовать дубликатам и уникальным:
=ЕСЛИ(СЧЁТЕСЛИ($A$2:$A$17; A2)>1;”Дубликат”;”Уникальное”)
Если же вам нужно, чтобы формула указывала только на дубли, замените “Уникальное” на пустоту (“”):
=ЕСЛИ(СЧЁТЕСЛИ($A$2:$A$17; A2)>1;”Дубликат”;””)
В этом случае Эксель отметит только неуникальные записи, оставляя пустую ячейку напротив уникальных.
Поиск неуникальных значений без учета первых вхождений
Вы наверняка обратили внимание, что в примерах выше дубликатами обозначаются абсолютно все найденные совпадения. Но зачастую задача заключается в поиске только повторов, оставляя первые вхождения нетронутыми. То есть, когда что-то встречается в первый раз, оно однозначно еще не может быть дубликатом.
Если вам нужно указать только совпадения, давайте немного изменим:
=ЕСЛИ(СЧЁТЕСЛИ($A$2:$A2; A2)>1;”Дубликат”;””)
На скриншоте ниже вы видите эту формулу в деле.
Нетрудно заметить, что она не обозначает первое появление слова, а начинает отсчет со второго.
Чувствительный к регистру поиск дубликатов
Хочу обратить ваше внимание на то, что хоть формулы выше и находят 100%-дубликаты, есть один тонкий момент – они не чувствительны к регистру. Быть может, для вас это не принципиально. Но если в ваших данных абв, Абв и АБВ – это три разных параметра – то этот пример для вас.
Как вы могли уже догадаться, выражения, использованные нами ранее, с такой задачей не справятся. Здесь нужно выполнить более тонкий поиск, с чем нам поможет следующая функция массива:
{=ЕСЛИ(СУММ((–СОВПАД($A$2:$A$17;A2)))<=1;””;”Дубликат”)}
Не забывайте, что формулы массива вводятся комбиинацией Ctrl + Shift + Enter.
Если вернуться к содержанию, то здесь используется функция СОВПАД для сравнения целевой ячейки со всеми остальными ячейками с выбранной области. Результат возвращается в виде ИСТИНА (совпадение) или ЛОЖЬ (не совпадение), которые затем преобразуются в массив из 1 и 0 при помощи оператора (–).
После этого, функция СУММ складывает эти числа. И если полученный результат больше 1, функция ЕСЛИ сообщает о найденном дубликате.
Если вы взглянете на следующий скриншот, вы убедитесь, что поиск действительно учитывает регистр при обнаружении дубликатов:
Смородина и арбуз, которые встречаются дважды, не отмечены в нашем поиске, так как регистр первых букв у них отличается.
Как извлечь дубликаты из диапазона.
Формулы, которые мы описывали выше, позволяют находить дубликаты в определенном столбце. Но часто речь идет о нескольких столбцах, то есть о диапазоне данных.
Рассмотрим это на примере числовой матрицы. К сожалению, с символьными значениями этот метод не работает.
При помощи формулы массива
{=ИНДЕКС(НАИМЕНЬШИЙ(ЕСЛИ(СЧЁТЕСЛИ($A$2:$E$11;$A$2:$E$11)>1;$A$2:$E$11);СТРОКА($1:$100)); НАИМЕНЬШИЙ(ЕСЛИОШИБКА(ЕСЛИ(ПОИСКПОЗ(НАИМЕНЬШИЙ(ЕСЛИ( СЧЁТЕСЛИ($A$2:$E$11;$A$2:$E$11)>1;$A$2:$E$11);СТРОКА($1:$100)); НАИМЕНЬШИЙ(ЕСЛИ(СЧЁТЕСЛИ($A$2:$E$11;$A$2:$E$11)>1;$A$2:$E$11); СТРОКА($1:$100));0)=СТРОКА($1:$100);СТРОКА($1:$100));””);СТРОКА()-1))}
вы можете получить упорядоченный по возрастанию список дубликатов. Для этого введите это выражение в нужную ячейку и нажмите Ctrl+Alt+Enter.
Затем протащите маркер заполнения вниз на сколько это необходимо.
Чтобы убрать сообщения об ошибке, когда дублирующиеся значения закончатся, можно использовать функцию ЕСЛИОШИБКА:
=ЕСЛИОШИБКА(ИНДЕКС(НАИМЕНЬШИЙ(ЕСЛИ(СЧЁТЕСЛИ($A$2:$E$11;$A$2:$E$11)>1;$A$2:$E$11); СТРОКА($1:$100));НАИМЕНЬШИЙ(ЕСЛИОШИБКА(ЕСЛИ(ПОИСКПОЗ( НАИМЕНЬШИЙ(ЕСЛИ(СЧЁТЕСЛИ($A$2:$E$11;$A$2:$E$11)>1;$A$2:$E$11); СТРОКА($1:$100));НАИМЕНЬШИЙ(ЕСЛИ(СЧЁТЕСЛИ($A$2:$E$11;$A$2:$E$11)>1;$A$2:$E$11); СТРОКА($1:$100));0)=СТРОКА($1:$100);СТРОКА($1:$100));””);СТРОКА()-1));””)
Также обратите внимание, что приведенное выше выражение рассчитано на то, что оно будет записано во второй строке. Соответственно выше него будет одна пустая строка.
Поэтому если вам нужно разместить его, к примеру, в ячейке K4, то выражение СТРОКА()-1 в конце замените на СТРОКА()-3.
Обнаружение повторяющихся строк
Мы рассмотрели, как обнаружить одинаковые данные в отдельных ячейках. А если нужно искать дубликаты-строки?
Есть один метод, которым можно воспользоваться, если вам нужно просто выделить одинаковые строки, но не удалять их.
Итак, имеются данные о товарах и заказчиках.
Создадим справа от наших данных формулу, объединяющую содержание всех расположенных слева от нее ячеек.
Предположим, что данные хранятся в столбцах А:C. Запишем в ячейку D2:
=A2&B2&C2
Добавим следующую формулу в ячейку E2. Она отобразит, сколько раз встречается значение, полученное нами в столбце D:
=СЧЁТЕСЛИ(D:D;D2)
Скопируем вниз для всех строк данных.
В столбце E отображается количество появлений этой строки в столбце D. Неповторяющимся строкам будет соответствовать значение 1. Повторам строкам соответствует значение больше 1, указывающее на то, сколько раз такая строка была найдена.
Если вас не интересует определенный столбец, просто не включайте его в выражение, находящееся в D. Например, если вам хочется обнаружить совпадающие строки, не учитывая при этом значение Заказчик, уберите из объединяющей формулы упоминание о ячейке С2.
Обнаруживаем одинаковые ячейки при помощи встроенных фильтров Excel.
Теперь рассмотрим, как можно обойтись без формул при поиске дубликатов в таблице. Быть может, кому-то этот метод покажется более удобным, нежели написание выражений Excel.
Организовав свои данные в виде таблицы, вы можете применять к ним различные фильтры. Фильтр в таблице вы можете установить по одному либо по нескольким столбцам. Давайте рассмотрим на примере.
В первую очередь советую отформатировать наши данные как «умную» таблицу. Напомню: Меню Главная – Форматировать как таблицу.
После этого в строке заголовка появляются значки фильтра. Если нажать один из них, откроется выпадающее меню фильтра, которое содержит всю информацию по данному столбцу. Выберите любой элемент из этого списка, и Excel отобразит данные в соответствии с этим выбором.
Вы можете убрать галочку с пункта «Выделить все», а затем отметить один или несколько нужных элементов. Excel покажет только те строки, которые содержат выбранные значения. Так можно обнаружить дубликаты, если они есть. И все готово для их быстрого удаления.
Но при этом вы видите дубли только по отфильтрованному. Если данных много, то искать таким способом последовательного перебора будет несколько утомительно. Ведь слишком много раз нужно будет устанавливать и менять фильтр.
Используем условное форматирование.
Выделение цветом по условию – весьма важный инструмент Excel, о котором достаточно подробно мы рассказывали.
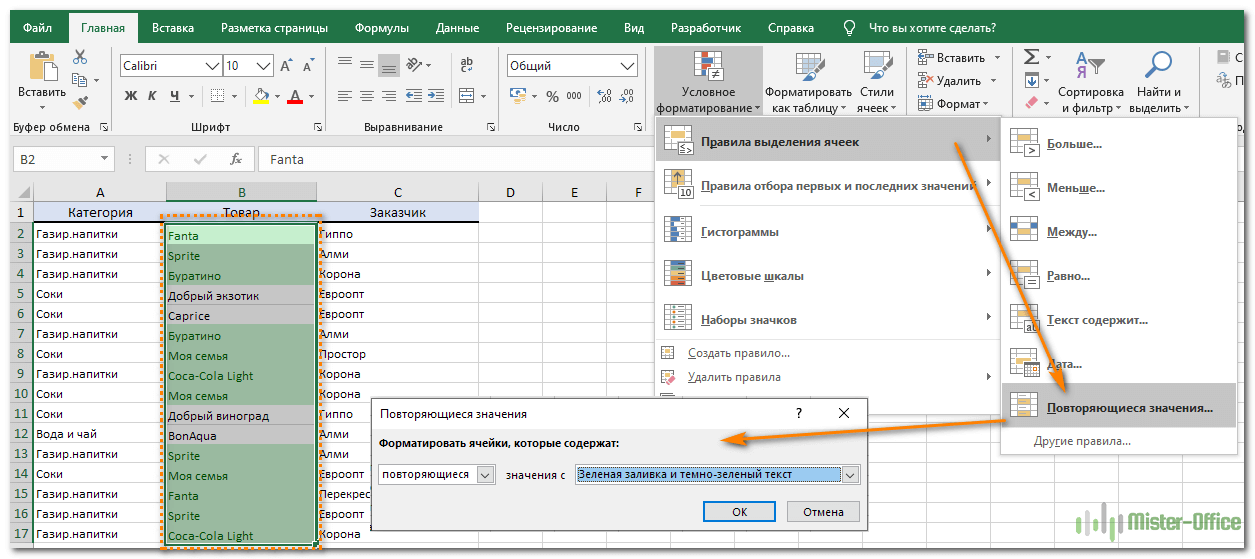
Сейчас я покажу, как можно в Экселе найти дубли ячеек, просто их выделив цветом.
Как показано на рисунке ниже, выбираем Правила выделения ячеек – Повторяющиеся. Неуникальные данные будут подсвечены цветом.
Но здесь мы не можем исключить первые появления – подсвечивается всё.
Но эту проблему можно решить, использовав формулу условного форматирования.
=СЧЁТЕСЛИ($B$2:$B2; B2)>1
Результат работы формулы выденения повторяющихся значений вы видите выше. Они выделены зелёным цветом.
Чтобы освежить память, можете руководствоваться нашим материалом «Как изменить цвет ячейки в зависимости от значения».
Поиск совпадений при помощи команды «Найти».
Еще один простой, но не слишком технологичный способ – использование встроенного поиска.
Зайдите на вкладку Главная и кликните «Найти и выделить». Откроется диалоговое окно, в котором можно ввести что угодно для поиска в таблице. Чтобы избежать опечаток, можете скопировать искомое прямо из списка данных.
Затем нажимаем «Найти все», и видим все найденные дубликаты и места их расположения, как на рисунке чуть ниже.
В случае, когда объём информации очень велик и требуется ускорить работу поиска, предварительно выделите столбец или диапазон, в котором нужно искать, и только после этого начинайте работу. Если этого не сделать, Excel будет искать по всем имеющимся данным, что, конечно, медленнее.
Этот метод еще более трудоемкий, нежели использование фильтра. Поэтому применяют его выборочно, только для отдельных значений.
Как применить сводную таблицу для поиска дубликатов.
Многие считают сводные таблицы слишком сложным инструментом, чтобы постоянно им пользоваться. На самом деле, не все так запутано, как кажется. Для новичков рекомендую к ознакомлению наше руководство по созданию и работе со сводными таблицами.
Для более опытных – сразу переходим к сути вопроса.
Создаем новый макет сводной таблицы. А затем в качестве строк и значений используем одно и то же поле. В нашем случае – «Товар». Поскольку название товара – это текст, то для подсчета таких значений Excel по умолчанию использует функцию СЧЕТ, то есть подсчитывает количество. А нам это и нужно. Если будет больше 1, значит, имеются дубликаты.
Вы наблюдаете на скриншоте выше, что несколько товаров дублируются. И что нам это дает? А далее мы просто можем щелкнуть мышкой на любой из цифр, и на новом листе Excel покажет нам, как получилась эта цифра.
К примеру, откуда взялись 3 дубликата Sprite? Щелкаем на цифре 3, и видим такую картину:
Думаю, этот метод вполне можно использовать. Что приятно – никаких формул не требуется.
Duplicate Remover – быстрый и эффективный способ найти дубликаты в Excel
Теперь, когда вы знаете, как использовать формулы для поиска повторяющихся значений в Excel, позвольте мне продемонстрировать вам еще один быстрый, эффективный и без всяких формул способ: инструмент Duplicate Remover для Excel.
Этот универсальный инструмент может искать повторяющиеся или уникальные значения в одном столбце или же сравнивать два столбца. Он может находить, выбирать и выделять повторяющиеся записи или целые повторяющиеся строки, удалять найденные дубли, копировать или перемещать их на другой лист. Я думаю, что пример практического использования может заменить очень много слов, так что давайте перейдем к нему.
Как найти повторяющиеся строки в Excel за 2 быстрых шага
Сначала посмотрим в работе наиболее простой инструмент — быстрый поиск дубликатов Quick Dedupe. Используем уже знакомую нам таблицу, в которой мы выше искали дубликаты при помощи формул:
Как видите, в таблице несколько столбцов. Чтобы найти повторяющиеся записи в этих трех столбцах, просто выполните следующие действия:
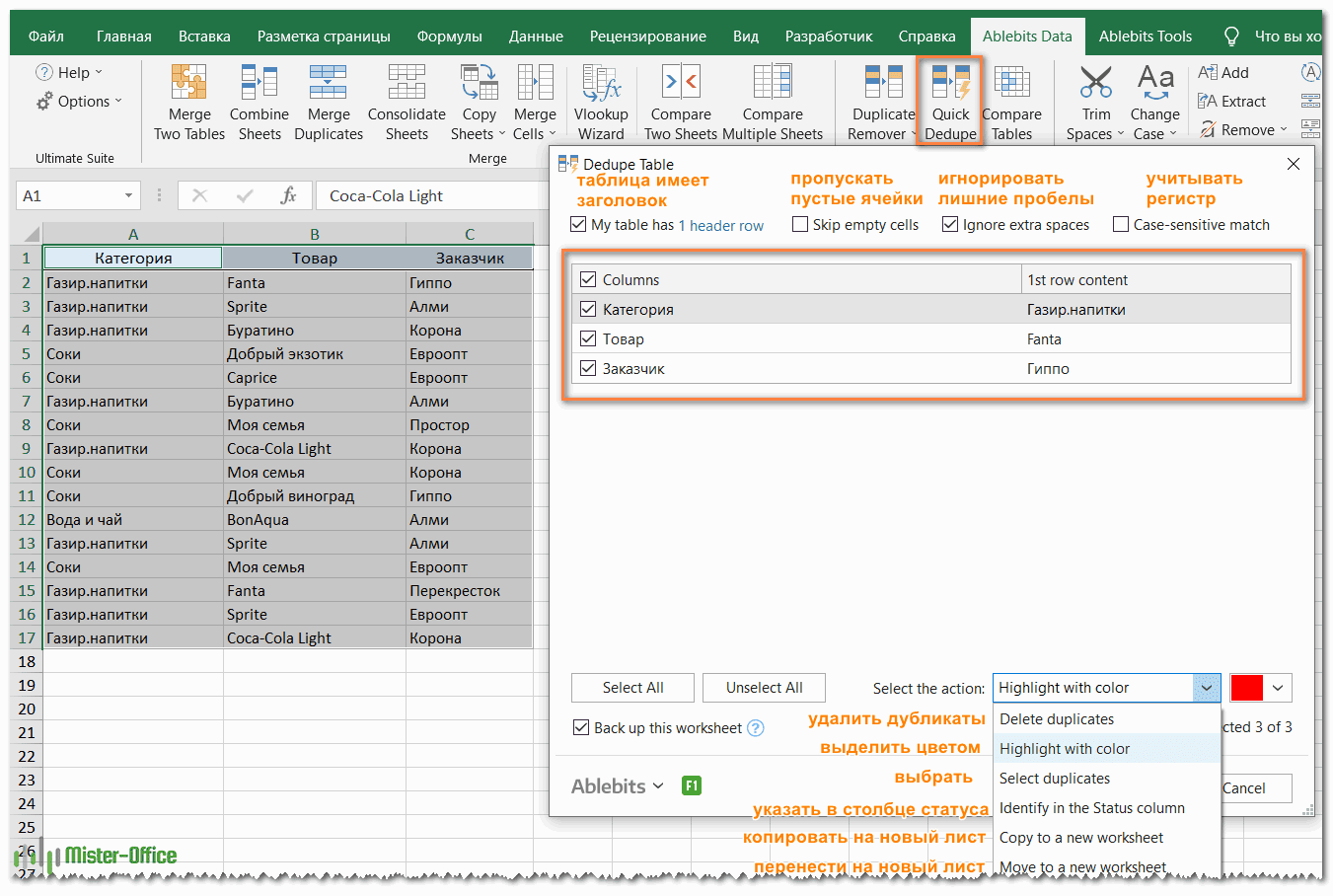
- Выберите любую ячейку в таблице и нажмите кнопку Quick Dedupe на ленте Excel. После установки пакета Ultimate Suite для Excel вы найдете её на вкладке Ablebits Data в группе Dedupe. Это наиболее простой инструмент для поиска дубликатов.
- Интеллектуальная надстройка возьмет всю таблицу и попросит вас указать следующие две вещи:
- Выберите столбцы для проверки дубликатов (в данном примере это все 3 столбца – категория, товар и заказчик).
- Выберите действие, которое нужно выполнить с дубликатами. Поскольку наша цель – выявить повторяющиеся строки, я выбрал «Выделить цветом».
Помимо выделения цветом, вам доступен ряд других опций:
- Удалить дубликаты
- Выбрать дубликаты
- Указать их в столбце статуса
- Копировать дубликаты на новый лист
- Переместить на новый лист
Нажмите кнопку ОК и подождите несколько секунд. Готово! И никаких формул 😊.
Как вы можете видеть на скриншоте ниже, все строки с одинаковыми значениями в первых 3 столбцах были обнаружены (первые вхождения не идентифицируются как дубликаты).
Если вам нужны дополнительные возможности для работы с дубликатами и уникальными значениями, используйте мастер удаления дубликатов Duplicate Remover, который может найти дубликаты с первыми вхождениями или без них, а также уникальные значения. Подробные инструкции приведены ниже.
Мастер удаления дубликатов – больше возможностей для поиска дубликатов в Excel.
В зависимости от данных, с которыми вы работаете, вы можете не захотеть рассматривать первые экземпляры идентичных записей как дубликаты. Одно из возможных решений – использовать разные формулы для каждого сценария, как мы обсуждали в этой статье выше. Если же вы ищете быстрый, точный метод без формул, попробуйте мастер удаления дубликатов — Duplicate Remover. Несмотря на свое название, он не только умеет удалять дубликаты, но и производит с ними другие полезные действия, о чём мы далее поговорим подробнее. Также умеет находить уникальные значения.
- Выберите любую ячейку в таблице и нажмите кнопку Duplicate Remover на вкладке Ablebits Data.
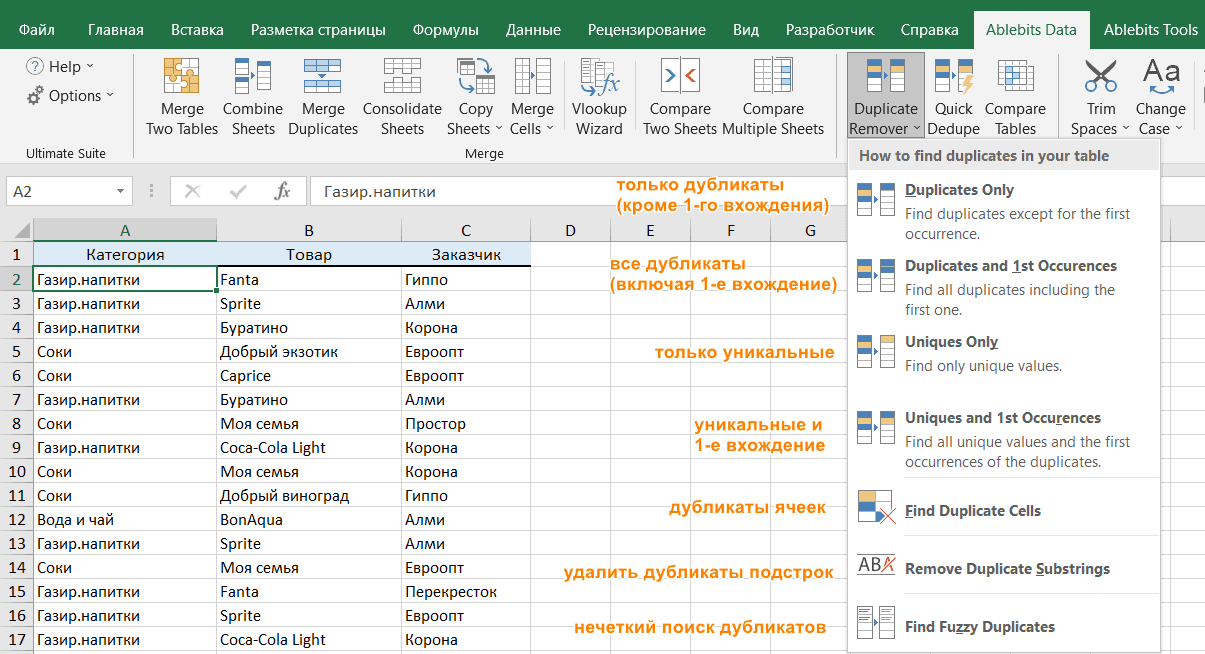
- Вам предложены 4 варианта проверки дубликатов в вашем листе Excel:
- Дубликаты без первых вхождений повторяющихся записей.
- Дубликаты с 1-м вхождением.
- Уникальные записи.
- Уникальные значения и 1-е повторяющиеся вхождения.
В этом примере выберем второй вариант, т.е. Дубликаты + 1-е вхождения:
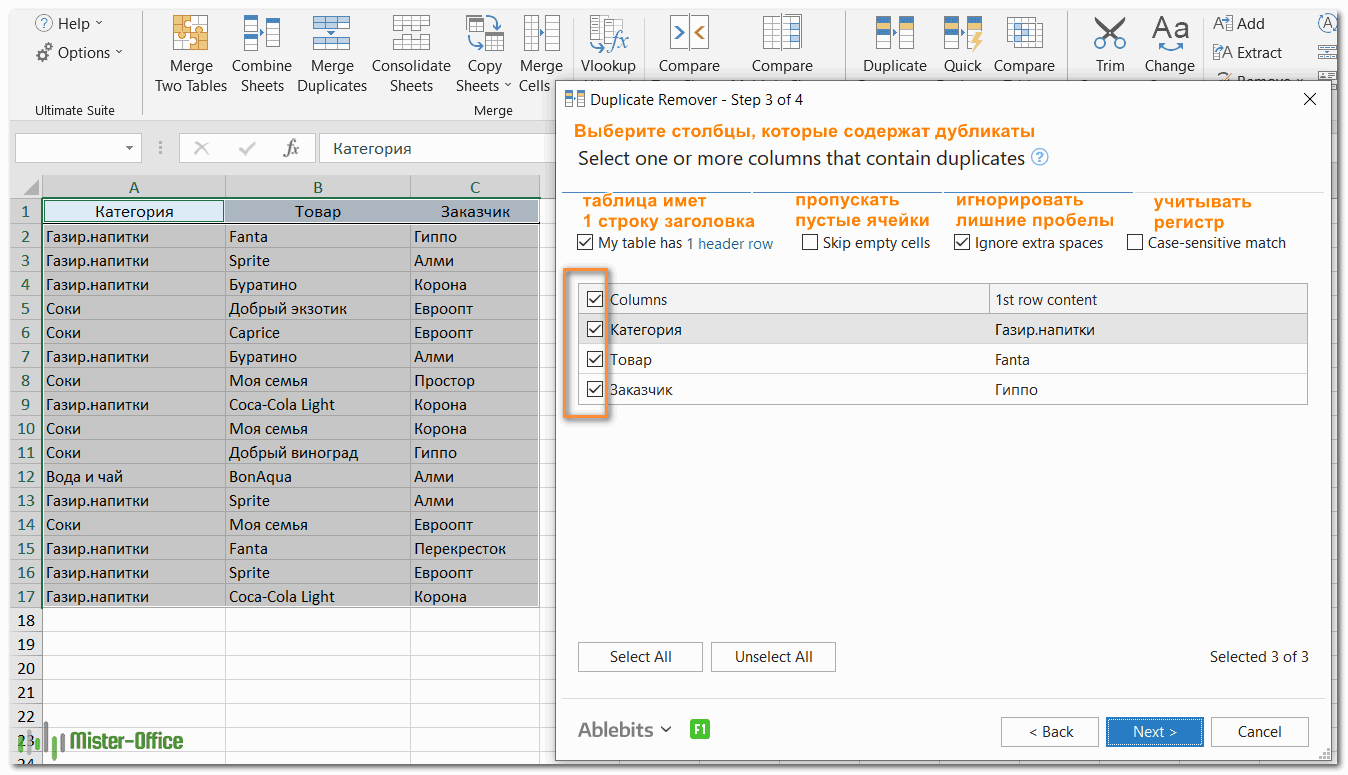
- Теперь выберите столбцы, в которых вы хотите проверить дубликаты. Как и в предыдущем примере, мы возьмём первые 3 столбца:
- Наконец, выберите действие, которое вы хотите выполнить с дубликатами. Как и в случае с инструментом быстрого поиска дубликатов, мастер Duplicate Remover может идентифицировать, выбирать, выделять, удалять, копировать или перемещать повторяющиеся данные.
Поскольку цель этого примера – продемонстрировать различные способы определения дубликатов в Excel, давайте отметим параметр «Выделить цветом» (Highlight with color) и нажмите Готово.
Мастеру Duplicate Remover требуется всего лишь несколько секунд, чтобы проверить вашу таблицу и показать результат:
Как видите, результат аналогичен предыдущему. Но здесь мы выделили дубликаты, включая и первое появление повторяющихся записей.
Никаких формул, никакого стресса, никаких ошибок – всегда быстрые и безупречные результаты 🙂
Итак, мы с вам научились различными способами обнаруживать повторяющиеся записи в таблице Excel. В следующих статьях разберем, что мы с этим можем полезного сделать.
Если вы хотите попробовать эти инструменты для поиска дубликатов в таблицах Excel, вы можете загрузить полнофункциональную ознакомительную версию программы. Будем очень признательны за ваши отзывы в комментариях!

В материале, переводом которого мы решили поделиться к старту курса о машинном и глубоком обучении, простым языком рассказывается о семантическом поиске, статья охватывает шесть его методов; начиная с простых сходства по Жаккару, алгоритма шинглов и расстояния Левенштейна, автор переходит к поиску с разреженными векторами — TF-IDF и BM25 и заканчивает современными представлениями плотных векторов и Sentence-BERT. Простые примеры сопровождаются кодом и иллюстрациями, а в конце вы найдёте ссылки на соответствующие блокноты Jupyter.
Поиск сходства — одна из самых быстрорастущих областей в ИИ и машинном обучении. По своей сути, это процесс сопоставления релевантных частей информации друг с другом. Велика вероятность, что вы нашли эту статью через поисковую систему — скорее всего, Google. Возможно, вы искали что-то вроде “what is semantic similarity search?” или “traditional vs vector similarity search”. Google обработал ваш запрос и использовал многие основные принципы поиска по сходству, о которых рассказывается в этой статье.
Если поиск сходства лежит в основе успеха компании стоимостью $ 1,65 Т — пятой по стоимости в мире[1], есть большой шанс, что о нём стоит узнать больше. Поиск сходства — сложная тема, есть бесчисленное множество методик построения эффективных поисковых систем. В этой статье мы рассмотрим несколько наиболее интересных и мощных из этих методов, уделяя особое внимание семантическому поиску. Посмотрим, как они работают, чем они хороши и как мы можем применять их самостоятельно. Можно посмотреть это видео или прочитать статью.
Два видео о двух классах подходов
Традиционный поиск
Мы начинаем с лагеря традиций и там находим нескольких ключевых игроков:
-
Сходство Жаккара.
-
Алгоритм шинглов.
-
Расстояние Левенштейна.
Все это показатели отлично работают при поиске сходства, из них мы рассмотрим три самых популярных: сходство по Жаккару, алгоритм шинглов и расстояние Левенштейна.
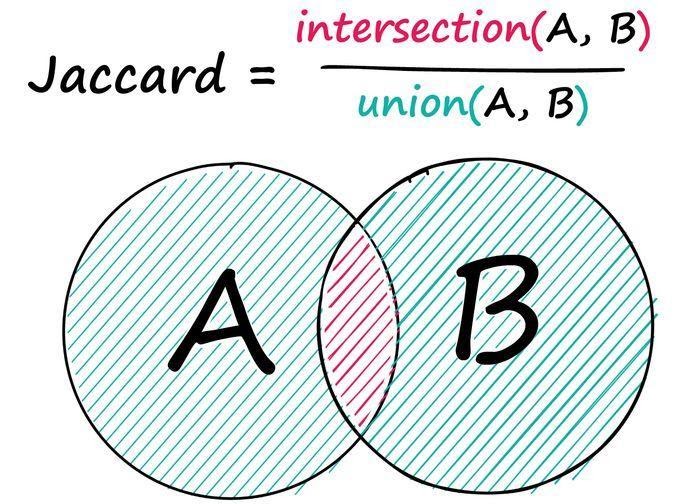
Сходство Жаккара
Сходство Жаккара — это простая, но иногда мощная метрика сходства. Даны две последовательности A и B: находим число общих элементов в них и делим найденное число на количество элементов обеих последовательностей.
Пример: даны две последовательности целых чисел, запишем:
Здесь мы определили два общих неодинаковых целых числа, 3 и 4 — между двумя последовательностями с общим количеством десяти целых чисел в обеих, где восемь чисел являются уникальными значениями — 2/8 даёт нам оценку сходства по Жаккарду 0,25. Ту же операцию можно выполнить и для текстовых данных: всё, что мы делаем, — заменяем целые числа на токены.
Мы обнаружили, что, как и ожидалось, предложения b и c набрали гораздо больше баллов. Конечно, это не лучшее решение — два предложения, в которых нет ничего общего, кроме слов ‘the’, ‘a’, ‘is’ и т. д., могут получить высокие оценки Жаккара, несмотря на то, что они неодинаковы по смыслу. Эти недостатки могут быть частично устранены с помощью методов предварительной обработки, таких как удаление стоп-слов, стемминг/лемматизация и т. д. Однако, как мы скоро увидим, некоторые методы позволяют полностью избежать этих проблем.
Алгоритм шинглов
Другая похожая техника — алгоритм использует точно такую же логику пересечения/объединения — но с “шинглом”. 2-шингловое предложение a будет выглядеть так:
a = {'his thought', 'thought process', 'process is', ...}После можно применить тот же расчёт пересечения/объединения между разбитыми на шинглы предложениями:
При помощи двух шинглов находим три совпадающих шингла между предложениями b и c, в результате сходство составляет 0,125.
Расстояние Левенштейна
Другая популярная метрика сравнения двух строк — расстояние Левенштейна — это количество операций, необходимых для преобразования одной строки в другую, вот его формула:
На вид она довольно сложна; если вы её поняли, это прекрасно! Если нет, не волнуйтесь — мы разберём её. Переменные a и b представляют две наши строки, i и j — позиции символов в a и b соответственно. Итак, даны строки:
Мы найдём, что:
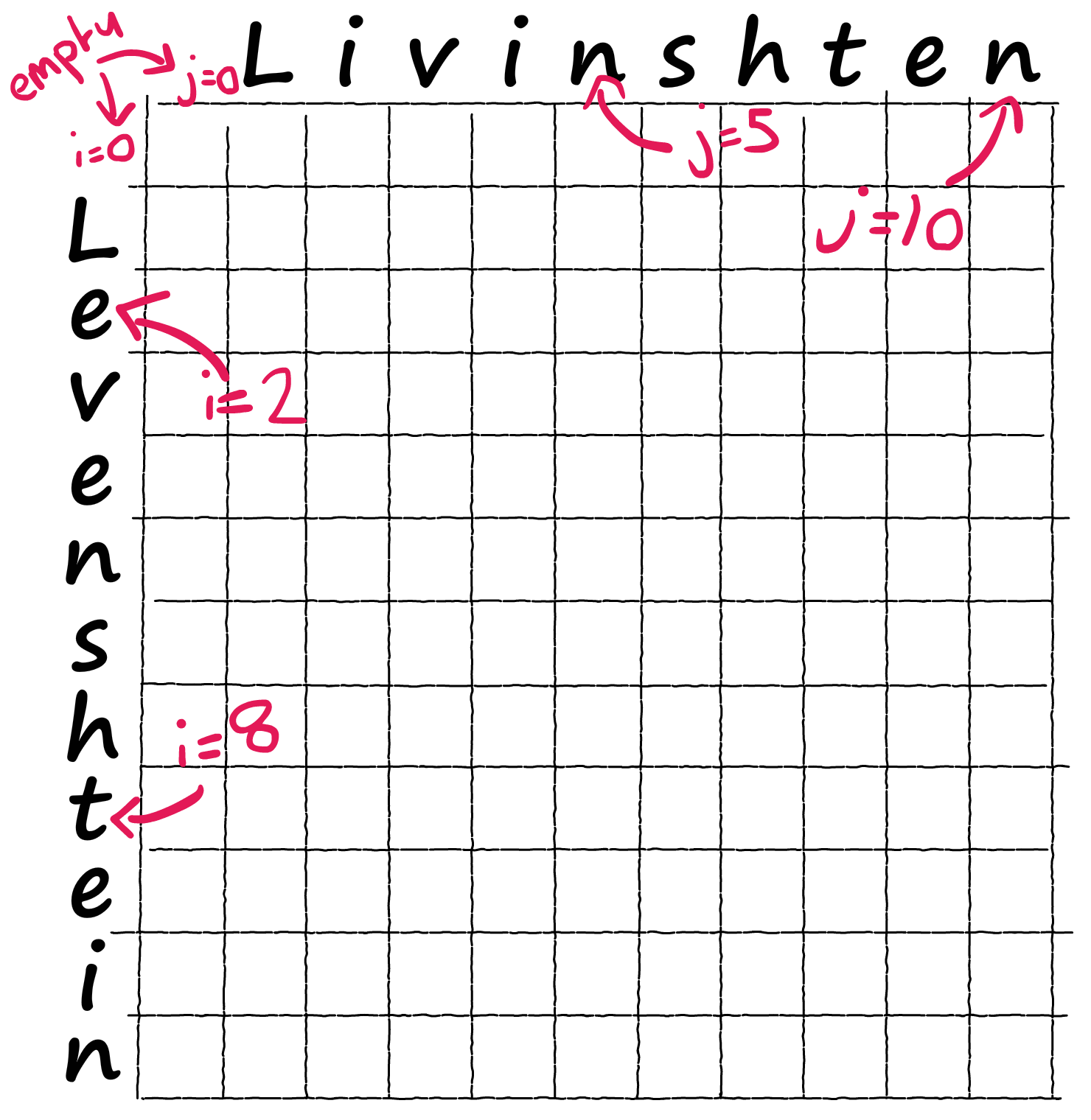
Это легко! Прекрасный способ понять логику этой формулы — визуализировать алгоритм Вагнера — Фишера, рассчитывающий расстояние Левенштейна при помощи простой матрицы. Мы берём два слова a и b и размещаем их по обеим осям нашей матрицы, включая символ ничего как пустое пространство:
Код инициализации пустой матрицы Вагнера — Фишера:
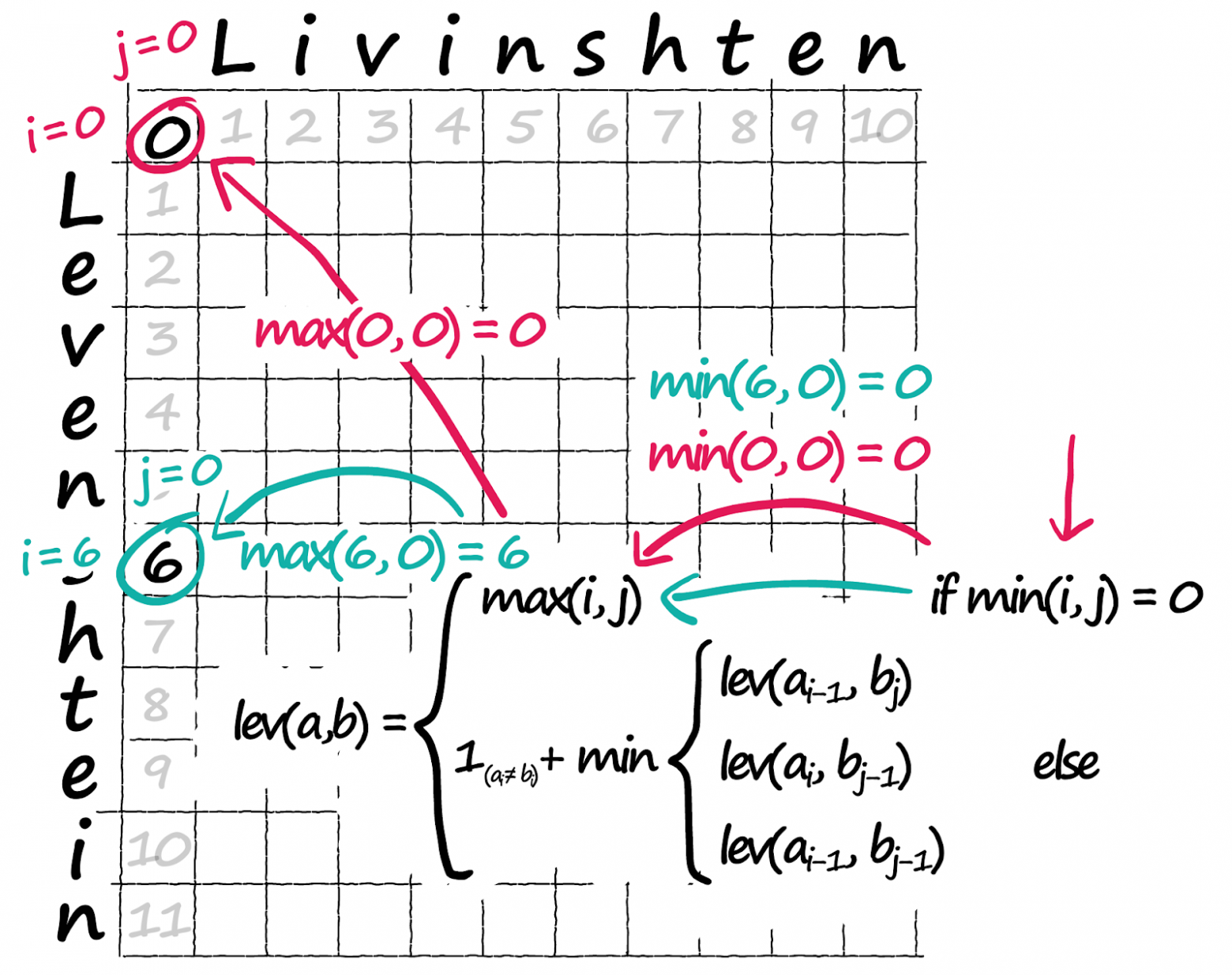
Переберём все позиции в матрице и применим ту сложную формулу, которую видели ранее. Первый шаг в нашей формуле if min(i, j) = 0 — здесь мы уточняем, не равны ли i и j нулю? Если да, переходим к функции max(i, j), которая присваивает текущей позиции в нашей матрице больше из двух значений — i и j:
Код операций min(i, j) == 0, за которой следует визуализированная выше max(i, j).
С внешними краями нашей матрицы мы разобрались, но нам всё ещё нужно вычислить внутренние значения — именно там будет проходить оптимальный путь. Вернёмся к if min(i, j) = 0 — что, если ни одно из них не равно 0? Затем переходим к сложной части уравнения в разделе min {. Нам нужно вычислить значение для каждой строки, а после взять минимальное значение. Сейчас эти значения известны — они находятся в нашей матрице:
lev(i-1, j), а все остальные операции — это операции индексации, когда мы извлекаем значение в данной позиции. Затем берём минимальное значение из трёх. Остаётся только одна операция. +1 слева должно применяться только в том случае, если a[i] != b[i] — это штраф за несовпадение символов.
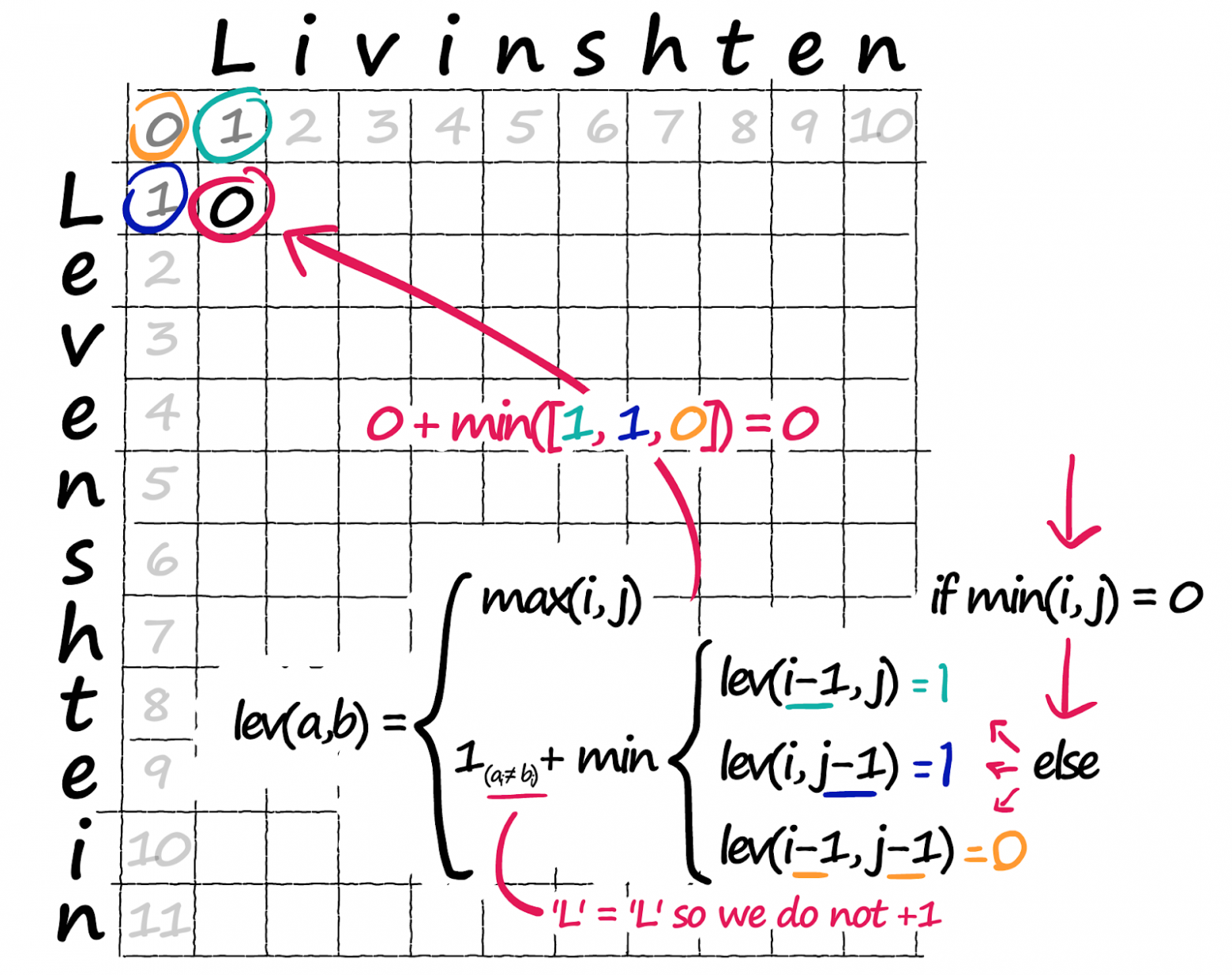
Эта операция в цикле по всей матрице выглядит так:
Полная реализация расчёта расстояния Левенштейна при помощи матрицы Вагнера — Фишера.
Итак, мы вычислили каждое значение в матрице — эти значения представляют собой количество операций, необходимых для преобразования из строки a до позиции i в строку b до позиции j. Мы ищем количество операций для преобразования a в b, поэтому мы берём правое нижнее значение нашего массива lev[-1, -1].
Векторное сходство
Для поиска на основе вектора мы обычно используем один из нескольких методов построения векторов:
-
TF-IDF.
-
BM25.
-
word2vec/doc2vec.
-
BERT.
-
USE.
В тандеме с некоторыми реализациями приблизительных ближайших соседей (ANN) эти векторные методы в мире поиска сходства, если говорить терминами программирования, — минимально жизнеспособные продукты. Рассмотрим подходы на основе TF-IDF, BM25 и BERT, поскольку они являются наиболее распространёнными и охватывают как разреженные, так и плотные векторные представления.
1. TF-IDF
Почтенный дедушка векторного поиска сходства, родившийся ещё в 1970-х годах. Он состоит из двух частей: Term Frequency (TF) и Inverse Document Frequency (IDF). Компонент TF подсчитывает, сколько раз термин встречается в документе, и делит его на общее количество терминов этого же документа.
Это первая половина нашего расчёта, мы имеем частоту запроса в рамках текущего документа f(q, D) в числителе и частоту всех терминов в рамках текущего документа f(t, D) в знаменатели дроби. TF — хороший показатель, но не позволяет нам провести различие между распространёнными и необычными словами. Если бы мы искали слово “the”, используя только TF, мы бы присвоили этому предложению ту же релевантность, что и при поиске “bananas”. Это хорошо, пока мы не начнём сравнивать документы или искать что-то с помощью длинных запросов. Мы не хотим, чтобы такие слова, как ‘the’, ‘is’ или ‘it’, были оценены так же высоко, как ‘bananas’ или ‘street’.
В идеале хочется, чтобы совпадения между более редкими словами оценивались выше. Для этого мы можем умножить TF на второй член — IDF. Обратная частота документа измеряет, насколько часто встречается слово во всех наших документах.
Здесь три предложения. Вычислив IDF для нашего распространённого слова ‘is’, получаем гораздо меньшее число, чем в случае более редкого слова ‘forest’. Если бы после мы искали оба слова ‘is’ и ‘forest’, то объединили бы TF и IDF следующим образом:
Мы вычисляем оценки TF(‘is’, D) и TF(‘forest’, D) для документов a, b и c. Значение IDF относится ко всем документам, поэтому IDF(‘is’) и IDF(‘forest’) вычисляются только один раз. Затем мы получаем значения TF-IDF для обоих слов в каждом документе путём умножения компонентов TF и IDF. Предложение a набирает наибольшее количество баллов для ‘forest’, а ‘is’ всегда набирает 0, поскольку IDF(‘is’) равно 0.
Это замечательно, но где здесь применяется векторное сходства? Итак, мы берём наш словарный запас (большой список всех слов в нашем наборе данных) и вычисляем TF-IDF для каждого слова.
Чтобы сформировать векторы TF-IDF, мы можем собрать это воедино:
Отсюда мы получаем вектор TF-IDF. Стоит отметить, что словарь легко может иметь более 20 000 слов, поэтому созданные этим методом векторы невероятно разрежены, а это означает, что закодировать какой-либо семантический смысл мы не можем.
2. BM25
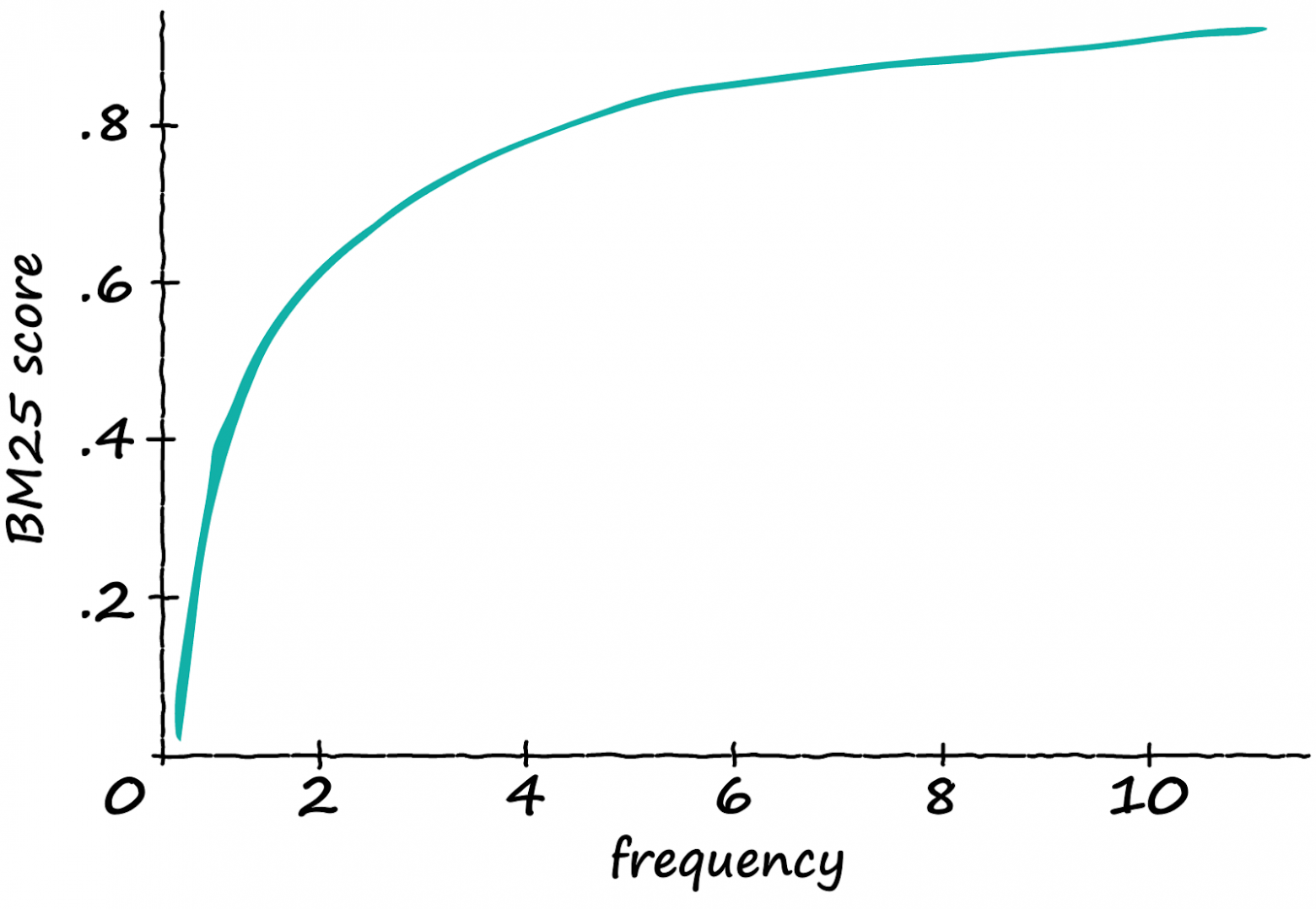
Преемник TF-IDF, Okapi BM25, является результатом оптимизации TF-IDF в первую очередь для нормализации результатов на основе длины документа. TF-IDF — отличный инструмент, но он может давать сомнительные результаты, когда мы начинаем сравнивать несколько упоминаний. Если мы возьмём две статьи по 500 слов и обнаружим, что “Черчилль” в статье А упоминается 6 раз, а в статье Б — 12 раз, должны ли мы считать статью А в два раза менее релевантной? Скорее всего, нет. BM25 решает эту проблему путём модификации TF-IDF:
Уравнение выглядит довольно неприятно, но это не что иное, как наша формула TF-IDF с несколькими новыми параметрами! Давайте сравним два компонента TF:
И затем часть IDF, которая даже не вводит никаких новых параметров — она просто переставляет IDF из TF-IDF.
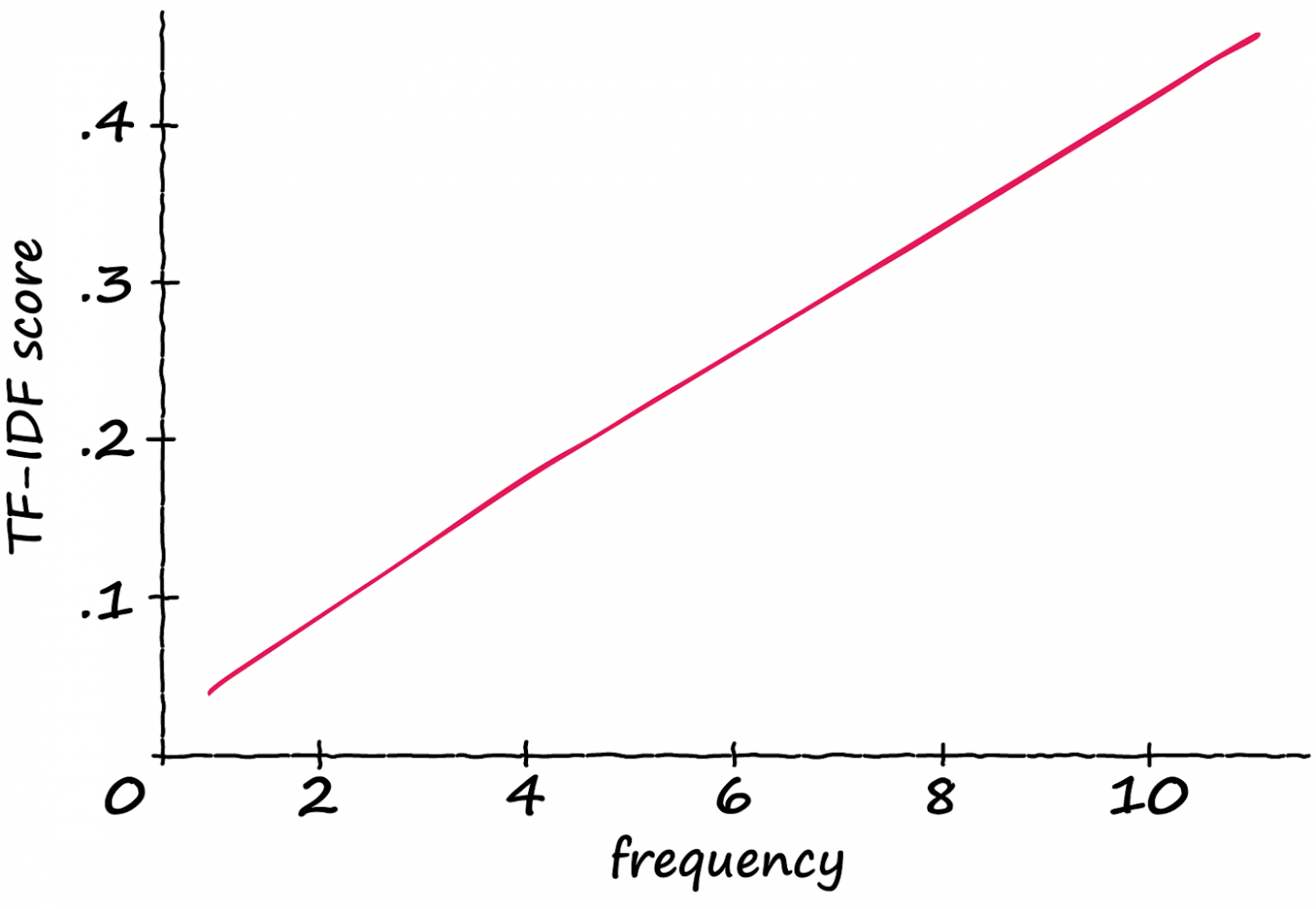
Итак, каков результат этой модификации? Если взять последовательность из 12 лексем и постепенно подавать в неё всё больше и больше “подходящих” лексем, то получим следующие результаты:
Показатель TF-IDF линейно увеличивается с ростом числа релевантных лексем. Таким образом, если частота удваивается — увеличивается и показатель TF-IDF. Звучит круто! Но как реализовать это на Python? Опять же напишем простую и понятную реализацию, как с TF-IDF.
Мы использовали параметры по умолчанию для k и b, и наши результаты выглядят многообещающе. Запрос ‘purple’ соответствует только предложению a, а ‘bananas’ набирает приемлемые баллы и для b, и для c, но для c — немного выше благодаря меньшему количеству слов. Чтобы построить векторы на основе этих данных, сделаем то же самое, что и с TF-IDF.
Опять же, как и в случае с векторами TF-IDF, эти векторы разрежены. Мы не сможем кодировать семантическое [смысловое] значение, вместо этого сосредоточимся на синтаксисе.
Теперь давайте посмотрим, как можно начать рассматривать семантику.
3. BERT
BERT (Bidirectional Encoder Representations from Transformers) — это чрезвычайно популярная модель трансформатора, в NLP она используется почти для всего. Посредством 12 (или около того) уровней кодера BERT кодирует огромное количество информации в набор плотных векторов.
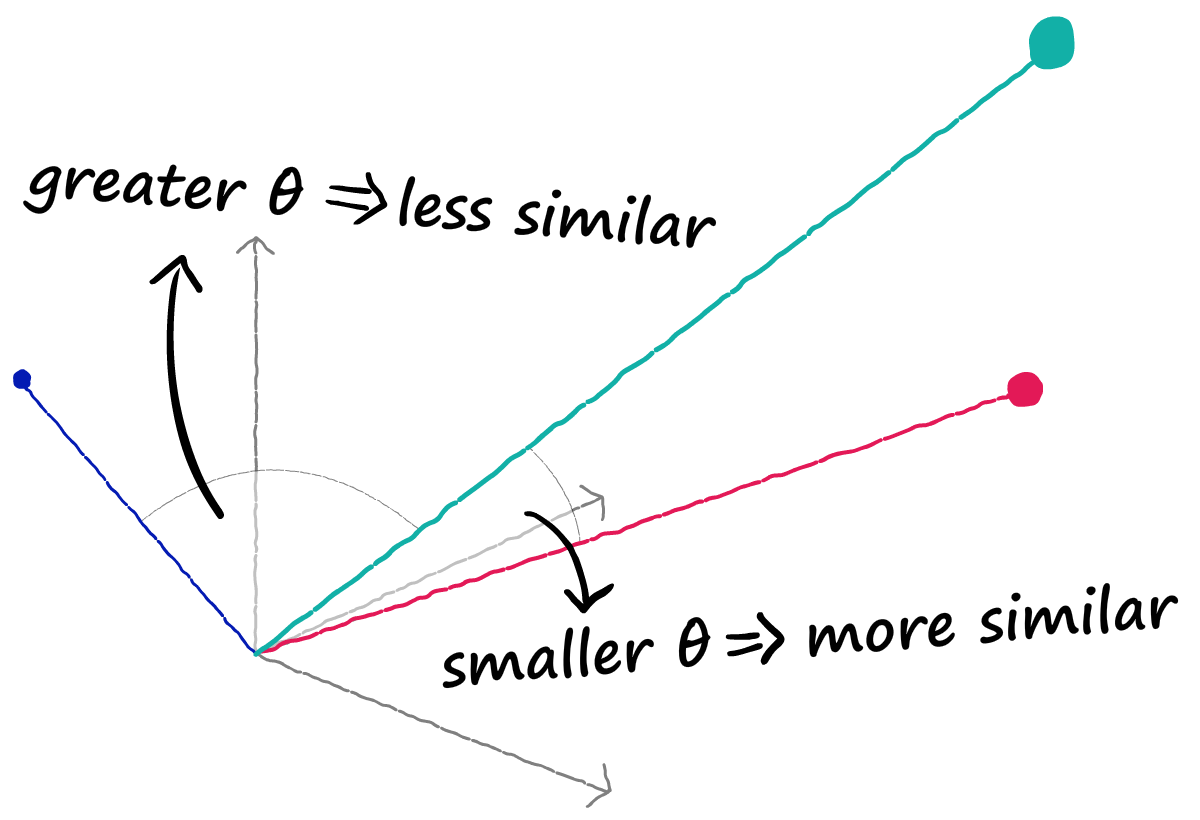
Каждый плотный вектор обычно содержит 768 значений, и мы обычно имеем 512 таких векторов для каждого закодированного BERT предложения. Эти векторы содержат то, что мы можем рассматривать как числовые представления языка. Эти векторы также возможно извлечь (если этого захочется) из разных слоёв, но обычно из последнего слоя. Теперь, имея два правильно закодированных плотных вектора, мы можем использовать метрику сходства, такую как косинусное сходство, чтобы рассчитать теперь уже семантическое сходство. Более выровненные векторы семантически схожи, и наоборот.
Но есть одна проблема: каждая последовательность представлена 512 векторами — не одним вектором. Вот здесь-то и появляется ещё одна — блестящая — адаптация BERT. Sentence-BERT позволяет нам создать один вектор, который представляет нашу полную последовательность, иначе известную как вектор предложений[2]. У нас есть два способа реализации SBERT: простой способ с использованием библиотеки sentence-transformers или уже не столько простой способ с использованием transformers и PyTorch.
Рассмотрим оба варианта, начиная с подхода через transformers и PyTorch, чтобы получить интуитивное представление о построении векторов. Если вы уже использовали библиотеку трансформаторов HF, первые несколько шагов покажутся вам очень знакомыми: инициализируем SBERT и токенизатор, токенизируем наш текст и обработаем токены моделью.
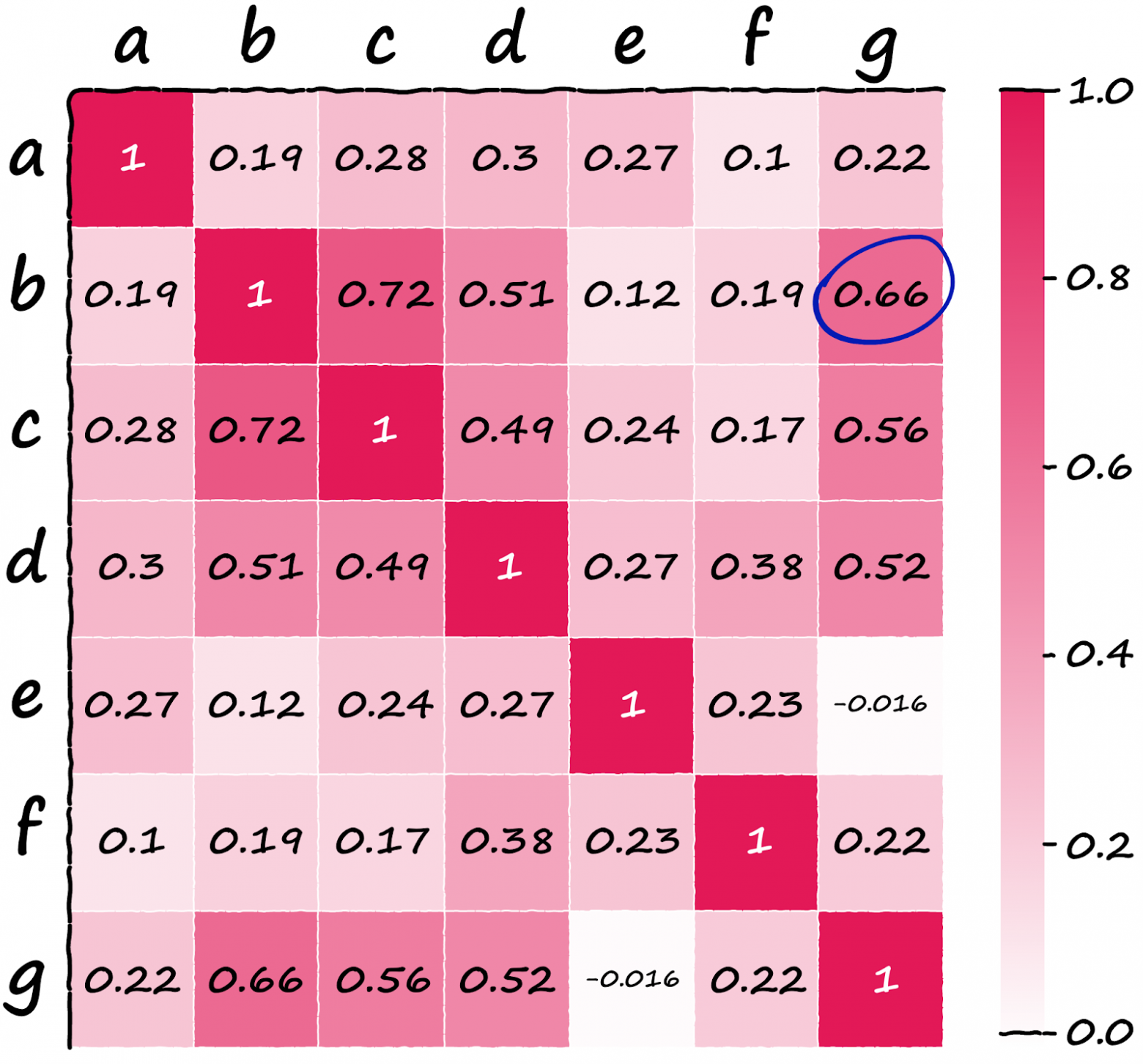
Мы добавили сюда новое предложение, предложение g несёт тот же семантический смысл, что и b, — без тех же ключевых слов. Из-за отсутствия общих слов все наши предыдущие методы не смогли бы найти сходство между этими двумя последовательностями — запомните это на будущее.
У нас есть векторы длины 768, но это не векторы предложений, так как мы имеем векторное представление каждой лексемы в последовательности (поскольку мы работаем SBERT, их здесь 128, а в случае BERT их 512). Для создания вектора предложений нам необходимо выполнить вычислить среднее значение.
Первое, что мы делаем, — умножаем каждое значение в тензоре embeddings на соответствующее значение attention_mask. Маска attention_mask содержит единицы там, где у нас есть “настоящие токены” (например, не токен заполнения), и нули в других местах — эта операция позволяет нам игнорировать ненастоящие токены.
И вот наши векторы предложений, при помощи которых мы можем измерить сходство, вычислив косинусное сходство между всеми векторами.
Визуализировав массив, можно легко определить предложения с более высоким уровнем сходства:
Теперь вспомните замечание о том, что предложения b и g имеют по сути одинаковый смысл, но не имеют ни одного одинакового ключевого слова. Мы надеемся, что SBERT с его превосходными семантическими представлениями языка определит эти два предложения как похожие — и вот, пожалуйста, сходство между ними составляет 0,66 балла (обведено выше). Итак, альтернативный (простой) подход заключается в применении SBERT. Чтобы получить точно такой же результат, как выше, напишем:
Что, конечно, гораздо проще. На этом завершаем прогулку по истории с Жаккаром, Левенштейном и Bert!
Ссылки
-
[1] Market Capitalization of Alphabet (GOOG), Companies Market Cap.
-
[2] N. Reimers, I. Gurevych, Sentence-BERT: Sentence Embeddings using Siamese BERT-Networks (2019), Proceedings of the 2019 Conference on Empirical Methods in 2019.
-
Репозиторий блокнотов
Блокноты Colab
Эта статья — живая иллюстрация развития технологий анализа текста и искусственного интеллекта. Если вы не хотите оставаться в стороне от области ИИ, то вы можете обратить внимание на наш курс «Machine Learning и Deep Learning». Или же прокатайтесь в работе с данными на нашем курсе о Data Science.
Узнайте, как прокачаться и в других специальностях или освоить их с нуля:
-
Профессия Data Scientist
-
Профессия Data Analyst
-
Курс по Data Engineering
Другие профессии и курсы
Математическое совпадение — ситуация, когда два выражения дают почти одинаковые значения, хотя теоретически это совпадение никак объяснить нельзя. Например, существует близость круглого числа 1000, выраженного как степень 2 и как степень 10: 
Введение[править | править код]
Математическое совпадение часто связано с целыми числами, и удивительные («случайные») примеры отражают факт, что вещественные числа, возникающие в некоторых контекстах, оказываются по некоторым стандартам «близкой» аппроксимацией малых целых чисел или степени десятки, или, более общо, рационального числа с малым знаменателем. Другой вид математических совпадений, таких как целые числа, одновременно удовлетворяющие нескольким, внешне не связанным, критериям или совпадения, относящиеся к единицам измерения. В классе чисто математических совпадений некоторые простые результаты имеют глубокое математическое основание, в то время как другие появляются «нежданно-негаданно».
Если дано счётное число путей образования математических выражений, использующих конечное число символов, совпадение числа используемых символов и точности приближения может быть наиболее очевидным путём получения математического совпадения. Стандарта, однако, нет и сильный закон малых чисел[en] является видом аргумента, к которому прибегают, когда нет формального математического понимания. Необходимо некоторое эстетическое математическое чувство для вынесения решения о значении математического совпадения, является ли это исключительным явлением, либо это важный математический факт (например, постоянная Рамануджана[en] ниже о константе, которая появилась в печати несколько лет назад как научная первоапрельская шутка[1]). Подводя итог, эти случайные совпадения рассматриваются из-за их курьёзности или для ободрения любителей математики на элементарном уровне.
Некоторые примеры[править | править код]
Рациональные приближения[править | править код]
Иногда простые рациональные приближения исключительно близки к интересным иррациональным значениям. Факт объясним в терминах представления иррациональных значений непрерывными дробями, но почему эти невероятные совпадения случаются, часто остаётся неясным.
Часто используется рациональное приближение (непрерывными дробями) к отношению логарифмов различных чисел, что даёт (приближённое) совпадение степеней этих чисел[2].
Некоторые совпадения с числом 
- первая подходящая дробь числа
, [3; 7] = 22/7 = 3,1428…, известна с времён Архимеда [3], и даёт точность около 0,04 %. Третья подходящая дробь, [3; 7, 15, 1] = 355/113 = 3,1415929…, которую нашёл Цзу Чунчжи [4], верна до шести десятичных знаков[3]. Эта высокая точность получается из-за того, что следующий член непрерывной дроби имеет необычно большое значение:
= [3; 7, 15, 1, 292, …][5];
- совпадение, в котором участвует
и золотое сечение φ, задаётся формулой
. Это соотношение связано с треугольником Кеплера; некоторые исследователи считают, что это совпадение найдено в пирамидах Гизы, но крайне невероятно, что оно является преднамеренным[6];
- существует последовательность шести девяток, которая начинается с 762-й позиции десятичного представления числа
. Для случайно выбранного нормального числа вероятность любой выбранной последовательности шести цифр (например, 658 020) встречается редко в десятичном представлении, только 0,08 %. Есть гипотеза, что
является нормальным числом, но это не доказано;
; верно с точностью до 0,002 %.
Совпадения с числом 
Также широко используется совпадение 






Совпадения с музыкальными интервалами[править | править код]
Совпадение 



Совпадение ![{displaystyle {sqrt[{12}]{2}}{sqrt[{7}]{5}}=1,33333319ldots approx {frac {4}{3}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/288213e10bc60f1985ec16cd9860bb27e489fbd4)
Совпадение ![{displaystyle {sqrt[{8}]{5}}{sqrt[{3}]{35}}=4,00000559ldots approx 4}](https://wikimedia.org/api/rest_v1/media/math/render/svg/19c696c2632a25a3fc7371a0d8f978202ba1e2a9)
Совпадение ![{displaystyle {sqrt[{9}]{0,6}}{sqrt[{28}]{4,9}}=0,99999999754ldots approx 1}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d900f2f2750d9e6cc5a6e426d7bd00d887e12867)

Совпадение со степенью 2 приводит к тому, что три большие терции составляют октаву, 
Числовые выражения[править | править код]
Выражения со степенями 
;
;
;
;
Некоторые правдоподобные связи выполняются с высокой степени точности, но тем не менее остаются совпадениями. Примером служит:
.
Две стороны этого выражения отличаются лишь в 42-м десятичном знаке[15].
Выражения со степенями 

Выражения с 

Выражение с логарифмами:
(точность 0,00024 %).
В обсуждении парадокса дней рождения возникает число 

Числовые совпадения в физическом мире[править | править код]
Длина шести недель[править | править код]
Число секунд в шести неделях, или 42 днях, равно в точности 10! (факториал) секунд (так как 


Скорость света[править | править код]
Скорость света (по определению) равна в точности
299 792 458 м/с, очень близко к 300 000 000 м/с. Это чисто совпадение, поскольку метр был первоначально определён как 1/10 000 000 расстояния между земным полюсом и экватором на уровне моря, длина земной окружности получилась около 2/15 световой секунды[20].
Гравитационное ускорение[править | править код]
Не являясь константной, а зависящей от широты и долготы, числовое значение ускорение свободного падения на поверхности лежит между 9,74 и 9,87, что достаточно близко к 10. Это означает, что в результате второго закона Ньютона вес килограмма массы на земной поверхности Земли соответствует примерно 10 ньютонам приложено на объект силы [21].
Это совпадение на самом деле связано с вышеупомянутым совпадением квадрата 

Когда было обнаружено, что длина окружности Земли очень близка 40 000 000 метрам, определение метра было изменено, чтобы отразить этот факт, поскольку это был более объективный стандарт (гравитационная постоянная на поверхности Земли не постоянна). Это привело к увеличению длины метра чуть меньше чем на 1 %, что попадало в пределы экспериментальных ошибок измерения.
Ещё одно совпадение — что величина g, равная примерно 9,8 м/с2, равна 1,03 светового года/год2, что близко к 1. Это совпадение связано с фактом, что g близко к 10 в системе единиц СИ (м/с2), как упоминалось выше, вместе с фактами, что число секунд в году близко к численному значению c/10, где c — скорость света в м/с.
Константа Ридберга[править | править код]
Постоянная Ридберга, умноженная на скорость света и выраженная как частота, близка к 
Гц
[23].
Постоянная тонкой структуры[править | править код]
Постоянная тонкой структуры 


Хотя это совпадение не столь строго, как некоторые выше, замечательно, что 
См. также[править | править код]
- Треугольник Кеплера#Математическое совпадение
- Формула Коидэ
Примечания[править | править код]
- ↑ Gardner, 2001, с. 674–694.
- ↑ 1 2 3 Schroeder, 2008, с. 26–28.
- ↑ 1 2 Beckmann, 1971, с. 101, 170.
- ↑ Mikami, 1913, с. 135.
- ↑ Weisstein, 2003, с. 2232.
- ↑ Herz-Fischler, 2000, с. 67.
- ↑ В 1828 году родился Лев Толстой, это позволяет запомнить число e с точностью до 10 знаков.
- ↑ The Number e to 1 Million Digits. NASA. Дата обращения: 14 февраля 2017. Архивировано 2 июля 2017 года.
- ↑ Beucher, 2008, с. 195.
- ↑ Ayob, 2008, с. 278.
- ↑ 1 2 Frank Rubin, The Contest Center — Pi Архивная копия от 8 октября 2017 на Wayback Machine.
- ↑ Why is
so close to 10? Архивная копия от 9 августа 2017 на Wayback Machine (Почему
так близок к 10?), Noam Elkies
- ↑ 1 2 3 4 5 6 Weisstein, Eric W. Almost Integer (англ.) на сайте Wolfram MathWorld.
- ↑ согласно Рамануджану: Quarterly Journal of Mathematics, XLV, 1914, pp. 350—372. Рамануджан утверждает, что эта «любопытная аппроксимация» для
была «получена эмпирически» и не имеет связи с теорией, которая развивалась в статье
- ↑ Архивированная копия. Дата обращения: 25 февраля 2017. Архивировано из оригинала 20 июля 2011 года.
- ↑ Joseph Clarke, 2015)
- ↑ Конвей, Слоун, Плоуф, 1988
- ↑ Barrow, 2002.
- ↑ Arratia, Goldstein, Gordon, 1990, с. 403–434.
- ↑ 1 2 Michon, Gérard P. Numerical Coincidences in Man-Made Numbers. Mathematical Miracles. Дата обращения: 29 апреля 2011. Архивировано 22 октября 2017 года.
- ↑ Leduc, 2003, с. 25.
- ↑ What Does Pi Have To Do With Gravity? Wired (8 марта 2013). Дата обращения: 15 октября 2015. Архивировано 10 ноября 2017 года.
- ↑ NIST.
Литература[править | править код]
- Martin Gardner. Six Sensational Discoveries // The Colossal Book of Mathematics. — New York: W. W. Norton & Company, 2001. — С. 674–694. — ISBN 0-393-02023-1.
- Yoshio Mikami. Development of Mathematics in China and Japan. — B. G. Teubner, 1913. — С. 135.
- Petr Beckmann. A History of Pi. — Macmillan, 1971. — С. 101, 170. — ISBN 978-0-312-38185-1.
- Roger Herz-Fischler. The Shape of the Great Pyramid. — Wilfrid Laurier University Press, 2000. — С. 67. — ISBN 978-0-889-20324-2.
- Ottmar Beucher. Matlab und Simulink. — Pearson Education, 2008. — С. 195. — ISBN 978-3-8273-7340-3.
- K. Ayob. Digital Filters in Hardware: A Practical Guide for Firmware Engineers. — Trafford Publishing, 2008. — С. 278. — ISBN 978-1-4251-4246-9.
- Manfred Robert Schroeder. Number theory in science and communication. — 2nd. — Springer, 2008. — С. 26–28. — ISBN 978-3-540-85297-1.
- John D Barrow. The Constants of Nature. — London: Jonathan Cape, 2002. — ISBN 0-224-06135-6.
- Richard Arratia, Larry Goldstein, Louis Gordon. Poisson approximation and the Chen-Stein method // Statistical Science. — 1990. — Т. 5, вып. 4. — С. 403–434. — doi:10.1214/ss/1177012015. — JSTOR 2245366.
- Charles Smythe. Our Inheritance in the Great Pyramid. — Kessinger Publishing, 2004. — С. 39. — ISBN 1-4179-7429-X.
- Steven A. Leduc. Cracking the AP Physics B & C Exam, 2004–2005 Edition. — Princeton Review Publishing, 2003. — С. 25. — ISBN 0-375-76387-2.
- Rydberg constant times c in Hz. Fundamental physical constants. NIST. Дата обращения: 25 июля 2011.
- Randall Munroe. What If?. — 2014. — ISBN 9781848549562.
- Roger Herz-Fischler. The Shape of the Great Pyramid. — Wilfrid Laurier University Press, 2000. — С. 67. — ISBN 978-0-889-20324-2.
- Eric W. Weisstein. CRC concise encyclopedia of mathematics. — CRC Press, 2003. — С. 2232. — ISBN 978-1-58488-347-0.
Ссылки[править | править код]
- В. Левшин. Магистр рассеянных наук. — Москва: Детская Литература, 1970. — С. 256.
- Hardy, G. H. — A Mathematician’s Apology. — New York: Cambridge University Press, 1993, (ISBN 0-521-42706-1)
- Weisstein, Eric W. Almost Integer (англ.) на сайте Wolfram MathWorld.
- Various mathematical coincidences in the «Science & Math» section of futilitycloset.com
- Press, W. H., Seemingly Remarkable Mathematical Coincidences Are Easy to Generate
При анализе данных с помощью Excel очень часто приходится искать некоторые значения по определенным критериям и подставлять их в другие таблицы. В таких задачах на помощью приходит функция ВПР, но у нее есть два существенных недостатка. Во-первых, функция ВПР возвращает только первое найденное значение. Например, у меня есть перечень заказов и необходимо получить номера всех заказов, которые оформил конкретный менеджер. Фамилия менеджера выбирается из выпадающего списка (выделено желтым) и ниже должны выводиться соответствующие номера заказов (зеленая область).
Если использовать стандартную функцию ВПР, то она найдет первый подходящий заказ и вернет ТОЛЬКО его номер.
Еще одним недостатком функции ВПР является то, что она ищет значения только в левом крайнем столбце выделенного диапазона. То есть если бы столбец с фамилиями менеджеров находился правее столбца с номерами заказов, то функцию ВПР вообще не удалось бы использовать.
Этот недостаток устраняется с помощью сочетания функций ИНДЕКС и ПОИСКПОЗ, которые являются более гибкой альтернативой функции ВПР, но и эти функции не решают поставленную задачу.
Как же быть, если нужно вернуть все значения, соответсвующие определенному критерию? В этом также поможет функция ИНДЕКС.
Напомню, что функция ИНДЕКС возвращает значение, которое находится в указанном номере строки выделенного диапазона. То есть мы должны выбрать некоторый диапазон значений и вторым аргументом указать номер строки в этом диапазоне. Подчеркиваю, не номер строки листа Эксель, а номер строки выделенного диапазона значений.
Функция ИНДЕКС может возвращать не только одно значение, а массив значений. И именно это нам и нужно. Чтобы функция вернула массив значений, мы должны в нее подставить массив номеров нужным нам строк. Поэтому основной задачей для нас сейчас как раз и будет получение этого массива.
Давайте рассмотрим упрощенную таблицу, чтобы в ней не было отвлекающей информации. У нас есть таблица, состоящая из двух столбцов – Менеджер и Номер заказа. Также есть выпадающий список с фамилиями менеджеров и некоторая область листа, в которую мы будем выводить все заказы, связанные с выбранным менеджером.
Итак, сначала мы должны определить все строки в основной таблице, относящиеся к выбранному в списке менеджеру. Давайте сделаем это с помощью вспомогательного столбца и функции ЕСЛИ.
Если значение из текущей ячейки первого столбца таблицы (А2) равно значению, выбранному в выпадающем списке (L1), то определим номер строки, в котором это значение находится. Для этого воспользуемся функцией СТРОКА, которая как раз и предназначена для решения этой задачи. Так как формулу мы будем протягивать по диапазону, то не забываем зафиксировать ссылку на ячейку с выпадающем списком.
Протягиваем формулу.
Так как мы не указали в функции ЕСЛИ значение, которое появится в случае невыполнения условия, то в соответствующих ячейках выводится логическое выражение ЛОЖЬ. Это неважно, так как нас будут интересовать только цифры.
Мы получили номера строк листа Эксель, но в функцию ИНДЕКС необходимо подставить номер строки в выделенном диапазоне. В данном примере основная таблица располагается в верху листа и в первой строке находится шапка с названиями столбцов, поэтому, чтобы получить необходимые значения, мы можем откорректировать формулу и отнять единицу от полученного значения. В итоге во вспомогательном столбце появится массив необходимых нам чисел.
Если же таблица находится в другой части листа, то нужно будет либо вручную прописать необходимое корректировочное значение (то есть отступ от первой строки листа), либо можно автоматизировать этот процесс с помощью все той же функции СТРОКА, но об этом я расскажу чуть позже, чтобы сейчас не усложнять формулу.
Итак, теперь нам нужно отсортировать столбец, чтобы в начале были цифры. Сделать это можно, например, с помощью функции НАИМЕНЬШИЙ, которая возвращает указанное по счету наименьшее значение в выбранном диапазоне.
Выбираем диапазон (С2:С18) и затем необходимо указать цифру, определяющую, какое по порядку наименьшее число нужно вывести. Если укажем 1, то получим первое наименьшее значение в диапазоне, если 2, то второе, и так далее. Именно таким образом мы и сможем отсортировать полученный список с помощью формулы. Создадим вспомогательный столбец со значениями по порядку и подставим эти значения в функцию НАИМЕНЬШИЙ.
Мы получили необходимый нам перечень номеров строк и можем вернуться к функции ИНДЕКС. Фактически нам нужно подтянуть значения из второго столбца основной таблицы, поэтому в качестве диапазона указываем его. В качестве строки, соответственно, только что рассчитанные значения.
Чтобы избавиться от ошибки ЧИСЛО! воспользуемся функцией ЕСЛИОШИБКА. Обернем ей полученную функцию и в случае ошибки выведем пустоту.
Мы достигли необходимого результата, но для этого пришлось создать несколько вспомогательных столбцов. Давайте свернем все промежуточные вычисления в одну формулу, но это будет не простая формула, а формула массива, поэтому нам нужно будет поменять некоторые ссылки на диапазоны, к которым они относятся. А если точнее, то в функции ЕСЛИ нужно будет заменить относительные ссылки на ячейки столбца А соответствующим диапазоном и не забываем зафиксировать его. Также не забываем сделать формулу формулой массива, нажав сочетание клавиш Ctrl + Shift + Enter. Растянем формулу на весь зарезервированный диапазон таблицы и получаем необходимый результат.
Все вспомогательные столбцы, кроме столбца с нумерацией (столбец F) можно удалить. Давайте сделаем так, чтобы и этот столбец был не нужен. Значения столбца F используются в функции НАИМЕНЬШИЙ и нам нужно сделать так, чтобы подобный ряд чисел создавался автоматически и не зависел от того, где находится таблица с формулами. Для этого можно воспользоваться функцией СТРОКА и определить номер строки листа Эксель первой ячейки основной таблицы. Затем этот номер будем вычитать из номера последующих строк. Чтобы значения «не сползали» при протягивании формулы, зафиксируем ссылку на первую ячейку диапазона.
Все отлично, кроме того, что все значения нужно увеличить на единицу. Дополним формулу и получим нужный нам результат.
Осталось скопировать формулу и подставить ее в формулу массива, после чего и последний вспомогательный столбец можно будет удалить.
Ну и по аналогии можно решить проблему зависимости формулы от расположения исходной таблицы. Сейчас ее заголовки расположены в первой строке листа и поэтому формула четко привязана к этому положению.
Мы можем внести в функцию ЕСЛИ аналогичную формулу с двумя функциями СТРОКА. То есть отнимем от уже имеющейся функции СТРОКА со всем диапазоном столбца номер строки первой ячейки этого диапазона и прибавим единицу.
Теперь формула никак не привязана к положению исходной таблице на листе и она выполняет поставленную задачу – возвращает все искомые значения из указанного диапазона.
Ссылки на мои ресурсы по Excel
★ YouTube-канал по Excel
★ Телеграм
★ Серия видеокурсов “Microsoft Excel Шаг за Шагом”
★ Авторские книги и курсы
Функция ПОИСКПОЗ в Excel используется для поиска точного совпадения или ближайшего (меньшего или большего заданному в зависимости от типа сопоставления, указанного в качестве аргумента) значения заданному в массиве или диапазоне ячеек и возвращает номер позиции найденного элемента.
Примеры использования функции ПОИСКПОЗ в Excel
Например, имеем последовательный ряд чисел от 1 до 10, записанных в ячейках B1:B10. Функция =ПОИСКПОЗ(3;B1:B10;0) вернет число 3, поскольку искомое значение находится в ячейке B3, которая является третьей от точки отсчета (ячейки B1).
Данная функция удобна для использования в случаях, когда требуется вернуть не само значение, содержащееся в искомой ячейке, а ее координату относительно рассматриваемого диапазона. В случае использования для констант массивов, которые могут быть представлены как массивы элементов «ключ» – «значение», функция ПОИСКПОЗ возвращает значение ключа, который явно не указан.
Например, массив {“виноград”;”яблоко”;”груша”;”слива”} содержит элементы, которые можно представить как: 1 – «виноград», 2 – «яблоко», 3 – «груша», 4 – «слива», где 1, 2, 3, 4 – ключи, а названия фруктов – значения. Тогда функция =ПОИСКПОЗ(“яблоко”;{“виноград”;”яблоко”;”груша”;”слива”};0) вернет значение 2, являющееся ключом второго элемента. Отсчет выполняется не с 0 (нуля), как это реализовано во многих языках программирования при работе с массивами, а с 1.
Функция ПОИСКПОЗ редко используется самостоятельно. Ее целесообразно применять в связке с другими функциями, например, ИНДЕКС.
Формула для поиска неточного совпадения текста в Excel
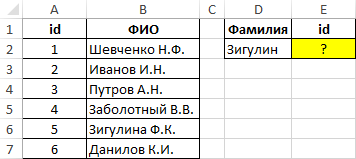
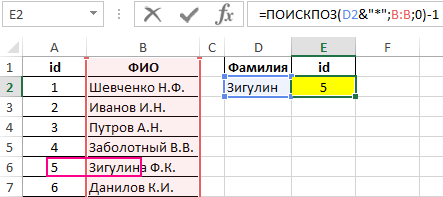
Пример 1. Найти позицию первого частичного совпадения строки в диапазоне ячеек, хранящих текстовые значения.
Вид исходной таблицы данных:
Для нахождения позиции текстовой строки в таблице используем следующую формулу:
=ПОИСКПОЗ(D2&”*”;B:B;0)-1
Описание аргументов:
- D2&”*” – искомое значение, состоящее и фамилии, указанной в ячейке B2, и любого количества других символов (“*”);
- B:B – ссылка на столбец B:B, в котором выполняется поиск;
- 0 – поиск точного совпадения.
Из полученного значения вычитается единица для совпадения результата с id записи в таблице.
Пример поиска:
Сравнение двух таблиц в Excel на наличие несовпадений значений
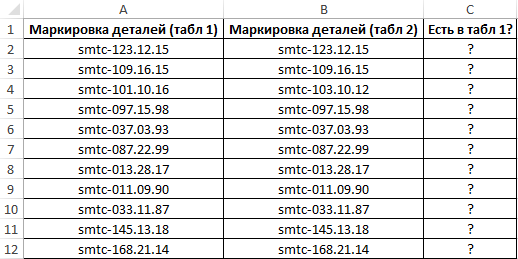
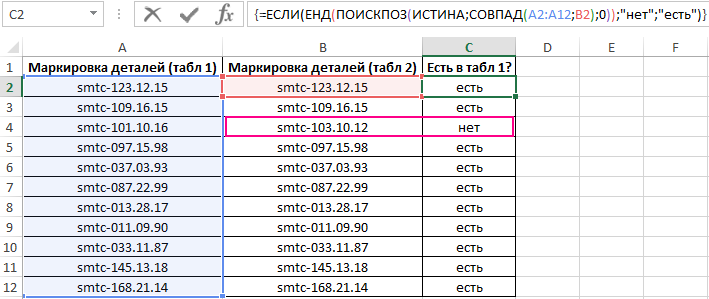
Пример 2. В Excel хранятся две таблицы, которые на первый взгляд кажутся одинаковыми. Было решено сравнить по одному однотипному столбцу этих таблиц на наличие несовпадений. Реализовать способ сравнения двух диапазонов ячеек.
Вид таблицы данных:
Для сравнения значений, находящихся в столбце B:B со значениями из столбца A:A используем следующую формулу массива (CTRL+SHIFT+ENTER):
Функция ПОИСКПОЗ выполняет поиск логического значения ИСТИНА в массиве логических значений, возвращаемых функцией СОВПАД (сравнивает каждый элемент диапазона A2:A12 со значением, хранящимся в ячейке B2, и возвращает массив результатов сравнения). Если функция ПОИСКПОЗ нашла значение ИСТИНА, будет возвращена позиция его первого вхождения в массив. Функция ЕНД возвратит значение ЛОЖЬ, если она не принимает значение ошибки #Н/Д в качестве аргумента. В этом случае функция ЕСЛИ вернет текстовую строку «есть», иначе – «нет».
Чтобы вычислить остальные значения «протянем» формулу из ячейки C2 вниз для использования функции автозаполнения. В результате получим:
Как видно, третьи элементы списков не совпадают.
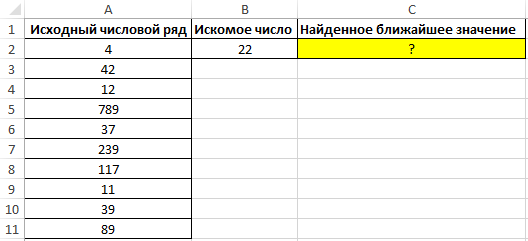
Поиск ближайшего большего знания в диапазоне чисел Excel
Пример 3. Найти ближайшее меньшее числу 22 в диапазоне чисел, хранящихся в столбце таблицы Excel.
Вид исходной таблицы данных:
Для поиска ближайшего большего значения заданному во всем столбце A:A (числовой ряд может пополняться новыми значениями) используем формулу массива (CTRL+SHIFT+ENTER):
Функция ПОИСКПОЗ возвращает позицию элемента в столбце A:A, имеющего максимальное значение среди чисел, которые больше числа, указанного в ячейке B2. Функция ИНДЕКС возвращает значение, хранящееся в найденной ячейке.
Результат расчетов:
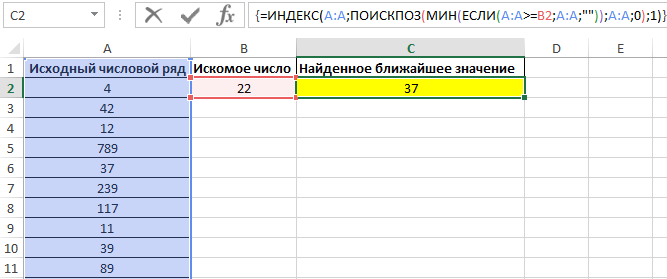
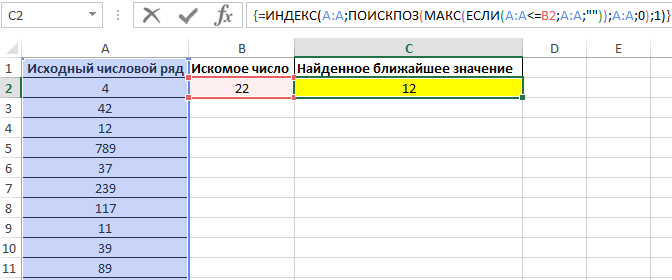
Для поиска ближайшего меньшего значения достаточно лишь немного изменить данную формулу и ее следует также ввести как массив (CTRL+SHIFT+ENTER):
Результат поиска:
Особенности использования функции ПОИСКПОЗ в Excel
Функция имеет следующую синтаксическую запись:
=ПОИСКПОЗ(искомое_значение;просматриваемый_массив;[тип_сопоставления])
Описание аргументов:
- искомое_значение – обязательный аргумент, принимающий текстовые, числовые значения, а также данные логического и ссылочного типов, который используется в качестве критерия поиска (для сопоставления величин или нахождения точного совпадения);
- просматриваемый_массив – обязательный аргумент, принимающий данные ссылочного типа (ссылки на диапазон ячеек) или константу массива, в которых выполняется поиск позиции элемента согласно критерию, заданному первым аргументом функции;
- [тип_сопоставления] – необязательный для заполнения аргумент в виде числового значения, определяющего способ поиска в диапазоне ячеек или массиве. Может принимать следующие значения:
- -1 – поиск наименьшего ближайшего значения заданному аргументом искомое_значение в упорядоченном по убыванию массиве или диапазоне ячеек.
- 0 – (по умолчанию) поиск первого значения в массиве или диапазоне ячеек (не обязательно упорядоченном), которое полностью совпадает со значением, переданным в качестве первого аргумента.
- 1 – Поиск наибольшего ближайшего значения заданному первым аргументом в упорядоченном по возрастанию массиве или диапазоне ячеек.
Скачать примеры ПОИСКПОЗ для поиска совпадения значений в Excel
Примечания:
- Если в качестве аргумента искомое_значение была передана текстовая строка, функция ПОИСКПОЗ вернет позицию элемента в массиве (если такой существует) без учета регистра символов. Например, строки «МоСкВа» и «москва» являются равнозначными. Для различения регистров можно дополнительно использовать функцию СОВПАД.
- Если поиск с использованием рассматриваемой функции не дал результатов, будет возвращен код ошибки #Н/Д.
- Если аргумент [тип_сопоставления] явно не указан или принимает число 0, для поиска частичного совпадения текстовых значений могут быть использованы подстановочные знаки («?» – замена одного любого символа, «*» – замена любого количества символов).
- Если в объекте данных, переданном в качестве аргумента просматриваемый_массив, содержится два и больше элементов, соответствующих искомому значению, будет возвращена позиция первого вхождения такого элемента.















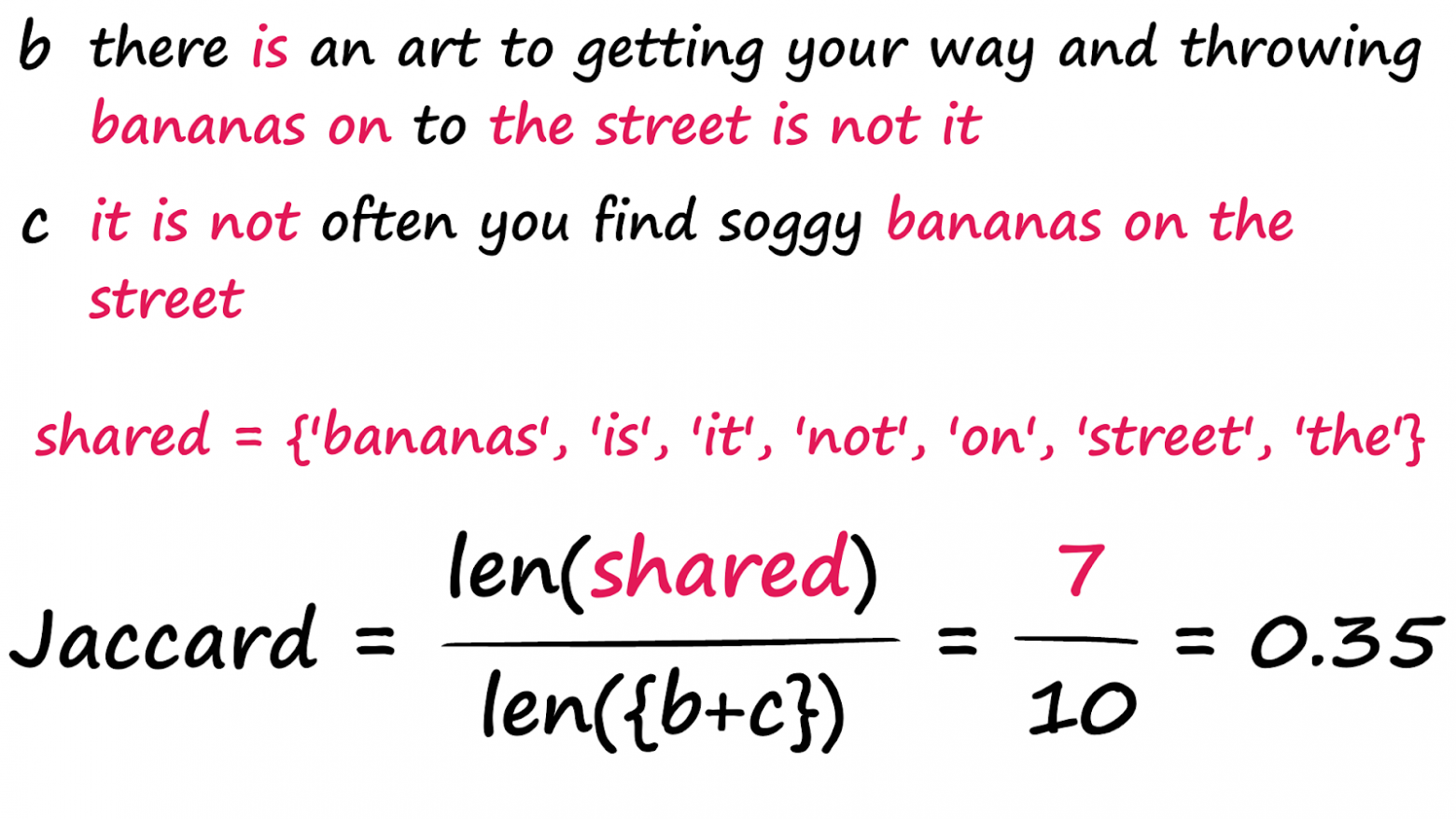
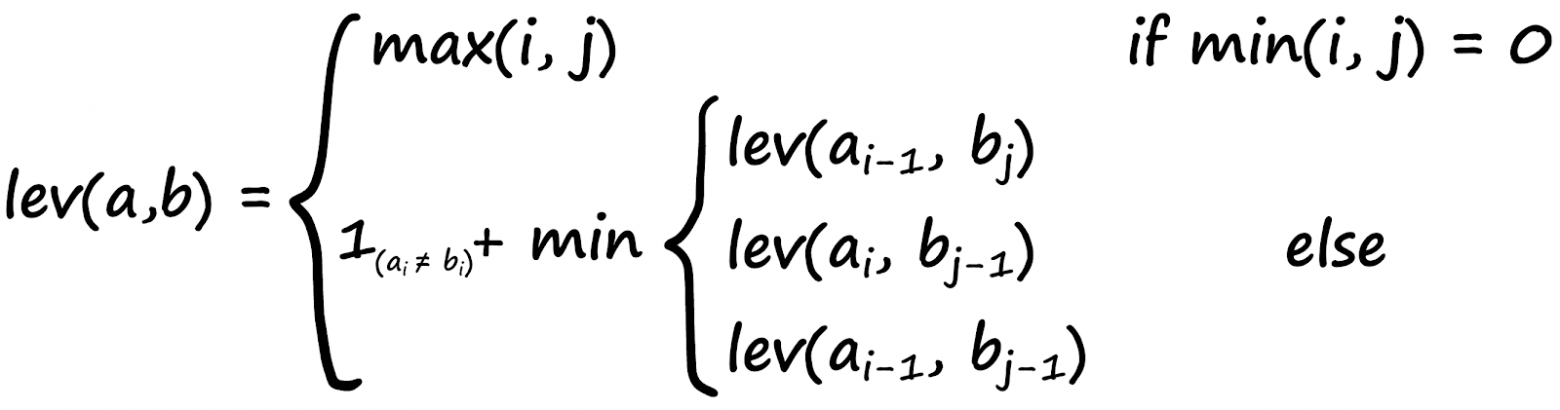

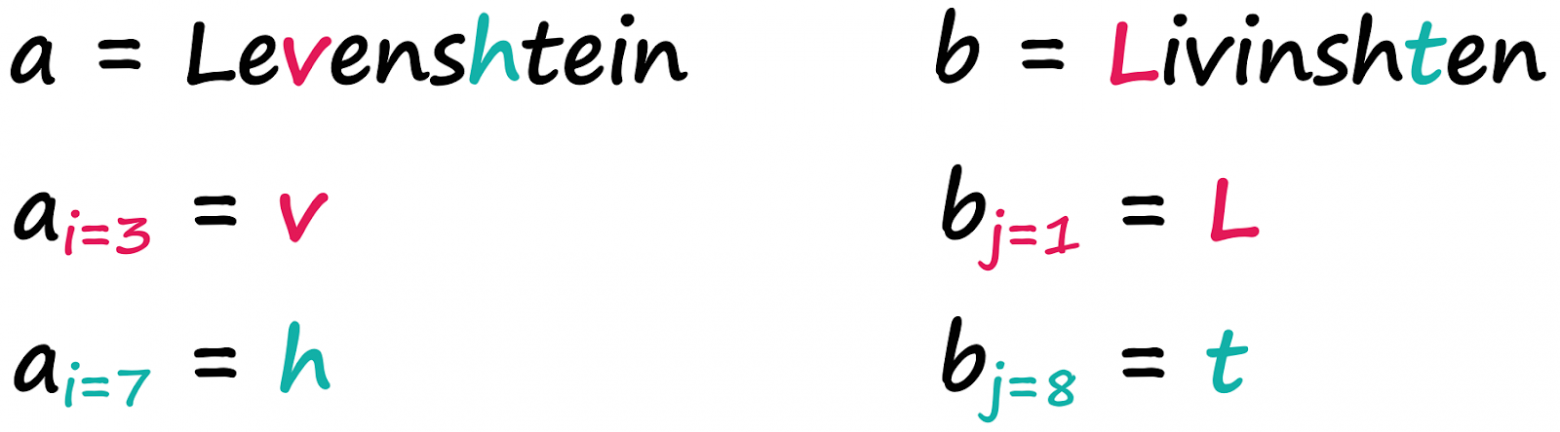
![Если a[i] != b[j], прибавляем 1 к нашему минимальному значению — это штраф за несовпадение символов Если a[i] != b[j], прибавляем 1 к нашему минимальному значению — это штраф за несовпадение символов](https://habrastorage.org/r/w1560/getpro/habr/upload_files/12c/fbc/914/12cfbc914c84442521dd0be415c77d46.png)
![Оптимальный путь по матрице — в позиции [-1, -1] внизу — справа мы имеем расстояние Левенштейна между двумя строками Оптимальный путь по матрице — в позиции [-1, -1] внизу — справа мы имеем расстояние Левенштейна между двумя строками](https://habrastorage.org/r/w1560/getpro/habr/upload_files/c9d/56c/572/c9d56c5721de0206c637ddecac7be442.png)
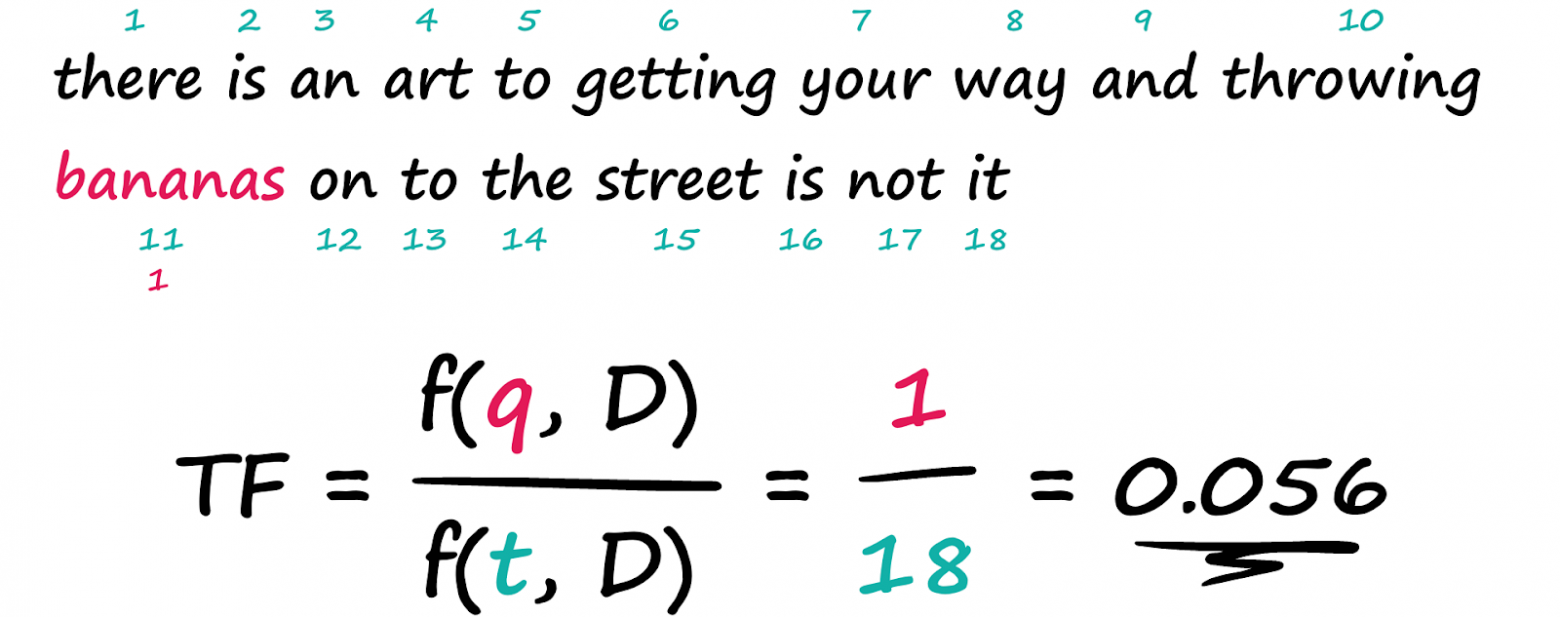



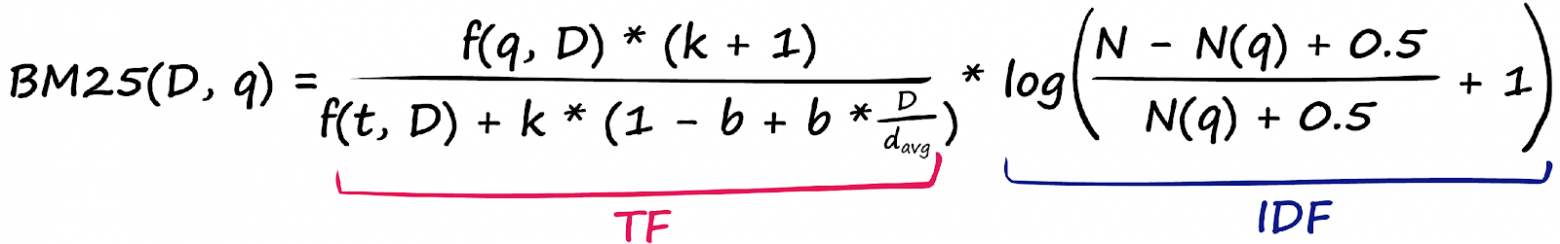
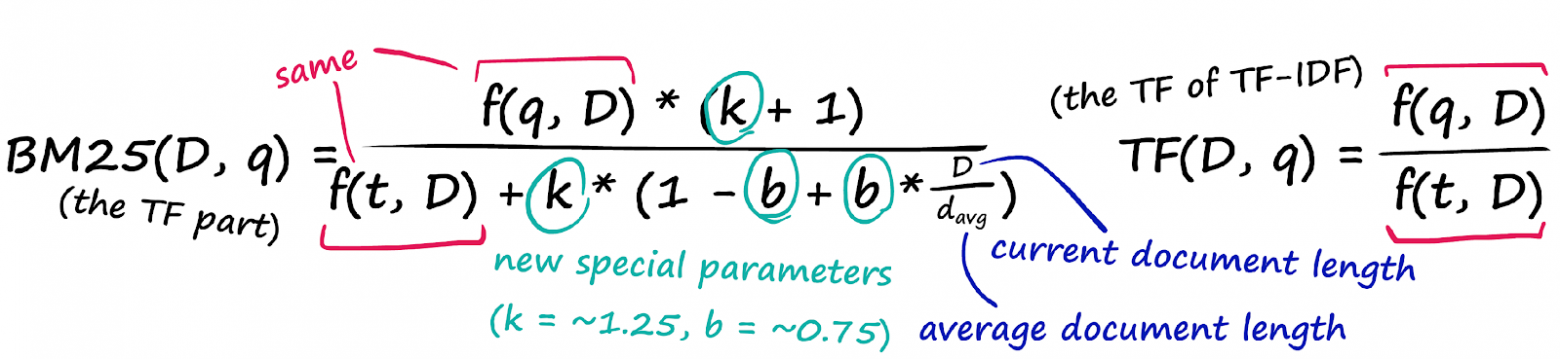
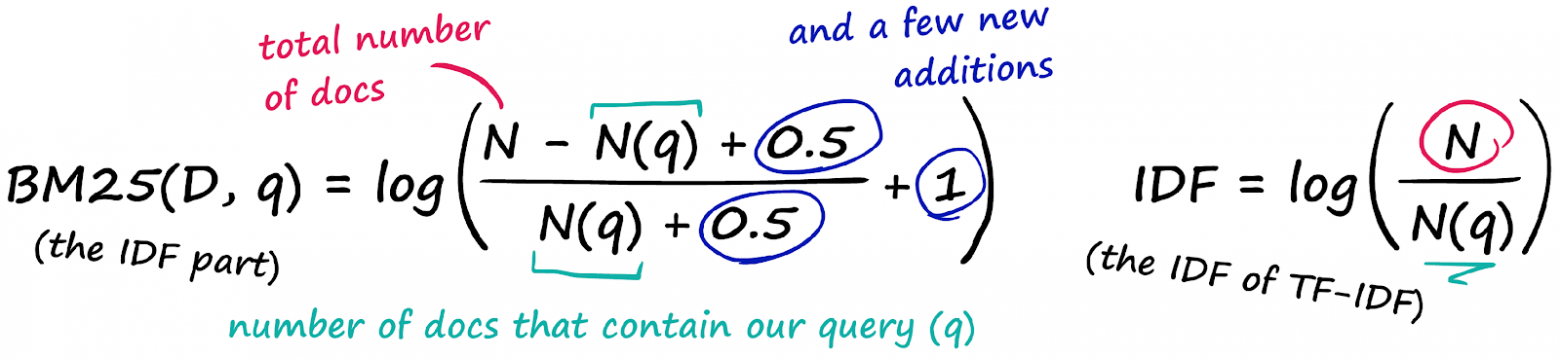



![{displaystyle {sqrt[{4}]{frac {2143}{22}}}=3,1415926525dots }](https://wikimedia.org/api/rest_v1/media/math/render/svg/e9f43b670a8ab4444d742eb55c2a29127d8310f2)
![{displaystyle {sqrt[{5}]{306}}=3,14155dots }](https://wikimedia.org/api/rest_v1/media/math/render/svg/e5ef398db34ea93321e931c75d432dc48bf076a4)
![{displaystyle {sqrt[{6}]{frac {17305}{18}}}=3,1415924dots }](https://wikimedia.org/api/rest_v1/media/math/render/svg/41c1d80c99df2ecbe58f01788af19db161c2b97b)
![{displaystyle {sqrt[{7}]{frac {21142}{7}}}=3,14159dots }](https://wikimedia.org/api/rest_v1/media/math/render/svg/ad97c13ca06cc0a390edc6b03b248bb91d0af160)