Сегодня я подготовил для вас подробную статью о несобственных интегралах.
Определенные интегралы  , для которых отрезок [a; b] конечен, а функция f(x) – непрерывна на этом отрезке, называют собственными.
, для которых отрезок [a; b] конечен, а функция f(x) – непрерывна на этом отрезке, называют собственными.
С целью обобщения понятия интеграла рассмотрим:
1) определенные интегралы от непрерывных функций, но с бесконечными пределами интегрирования;
2) определенные интегралы с конечными пределами интегрирования, но от функций, имеющих бесконечный разрыв на промежутке интегрирования. Такие определенные интегралы называют несобственными.
1. Интегралы с бесконечными пределами.
Пусть функция f(x) определена на промежутке [a; +∞) и пусть f(x) интегрирована на любом отрезке [a; b] (b> a– произвольные действительные числа).
Определение 1.1. Предел  интеграла при b→+∞ называется несобственными интегралом функции f(x) от а до +∞ и обозначается символом:
интеграла при b→+∞ называется несобственными интегралом функции f(x) от а до +∞ и обозначается символом: 

Если предел (1.1) есть конечное число, то несобственный интеграл  называют сходящимся. Если предел (1.1) не существует или равен бесконечности, то несобственный интеграл
называют сходящимся. Если предел (1.1) не существует или равен бесконечности, то несобственный интеграл  называют расходящимся.
называют расходящимся.
Пример 1.1. Исследовать на сходимость интеграл

Решение. Вычислим определенный интеграл

Имеем

Следовательно, заданный интеграл сходится и он равен

Из рассмотренного следует, что вопрос о сходимости (расходимости) несобственных интегралов решается с помощью первоначальной функции для подынтегральной функции. Это обстоятельство сильно сужает круг практического использования понятия несобственного интеграла. В отдельных случаях вопрос о сходимости (расхождении) несобственного интеграла можно решить, не находя первообразной для подынтегральной функции. При этом пользуются так называемыми признаками сходимости несобственных интегралов. Простейшим признаком сходимости является признак сравнения.
Теорема 1.1. Пусть для всех x ≥ a функции f(x) и g(x) определены и выполняются неравенства 0 ≤ f(x) ≤ g(x). Тогда:

Для функции f(x), непрерывной на бесконечном промежутке -∞ < x ≤ b, определяется несобственный интеграл 

Для функции f(x), непрерывной на всей числовой оси, несобственный интеграл  определяется равенством:
определяется равенством:

где с – произвольное действительное число.
2. Интегралы от неограниченных функций.
Пусть функция f(x) такая, что для произвольного малого ɛ>0 она определена, ограничена и интегрирована на отрезке [a+ɛ; b] и неограниченна на (a; b].
Определение 1.2. Предел определенного интеграла  при ɛ→0 называется несобственным интегралом функции f(x) на отрезке [a; b] и обозначается символом
при ɛ→0 называется несобственным интегралом функции f(x) на отрезке [a; b] и обозначается символом

Аналогично для функции f(x), определенной, непрерывной и интегрированной на отрезке [a; b- ɛ] и неограниченной на [a; b) обозначается несобственный интеграл:

Если пределы (1.4), (1.5) есть конечные числа, то несобственные интегралы называются сходящимися, а если эти пределы не существуют, то несобственные интегралы называются расходящимися.
В конце отметим, что для функции f(x), которая имеет на промежутке (a; b) точку с, в окрестности которой f(x) неограниченная, но является ограниченной и интегрированной на каждом из отрезков [a; c- ɛ] и [ñ + ɛ; b], интеграл определяется равенством.
Аналогично обозначается несобственный интеграл на отрезке [a; b] от функции, которая непрерывна на нем всюду, кроме конечного числа точек, и неограниченной вблизи этих точек.
Пример 1.2.Исследовать сходимость интегралов. Для сходящихся интегралов найти их значение:

Решение.
а) функция 
ограничена и непрерывна, а потому и интегрируемая. Предельное значение

существует; таким образом,


ограничена и непрерывна, но

 расходится.
расходится.
Пример 1.3. Исследовать сходимость интегралов. Для сходящихся интегралов найти их значение

Решение.

если α > 0, интеграл сходится; если α ≤ 0, то интеграл расходится;

если α > 1; если 0 < α ≤ 1, интеграл расходится как и при α = 1:

так и при 0 < α < 1:

Пример 1.4. Найти несобственный интеграл 
Решение. Функция  непрерывна при 0 ≤ x < 2 и имеет бесконечный разрыв в точке x=2, поэтому имеем
непрерывна при 0 ≤ x < 2 и имеет бесконечный разрыв в точке x=2, поэтому имеем

Поэтому данный интеграл сходится и равен 2√2.
Пример 1.5. Исследовать сходимость интегралы. Для сходящихся интегралов найти их значение:

Решение.

то есть, несобственный интеграл расходится

то есть, несобственный интеграл I2 сходится и равен  .
.
Пример 1.5. Исследовать на сходимость интегралы:

Решение.
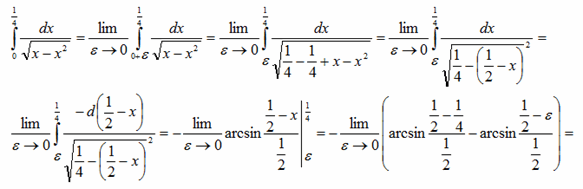
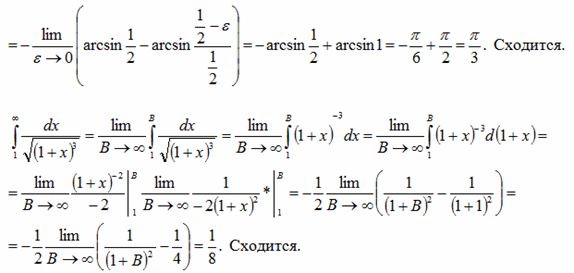
Если у Вас есть ко мне вопросы, или нужна помощь, консультация по решению несобственных интегралов, записывайтесь на мои занятия. Буду рад Вам помочь.
© blog.tutoronline.ru,
при полном или частичном копировании материала ссылка на первоисточник обязательна.
Пример
1.
Исследовать сходимость интеграла

.
Функция
![]()
на
промежутке
![]()
имеет
одну особую точку
.
Воспользуемся
определением несобственного интеграла

–
не
существует
![]()
расходится.
Пример
2.
Исследовать сходимость и вычислить ( в
случае сходимости ) интеграл

.

Пример
3.
Исследовать сходимость

.
Заметим,
что так как подынтегральная функция
рациональна, то её первообразная
выражается элементарной функцией. Но
вычисление первообразной здесь громоздко
и для ответа на вопрос воспользуемся
не определением несобственного интеграла,
а признаком сравнения, так как
подынтегральная функция положительна.
Так как особой точкой является
,
интеграл
![]()
сходится
и

,
то
в силу признака сравнения исходный
интеграл сходится.
Пример
4.
Исследовать сходимость интеграла

.
Функция

имеет
на промежутке интегрирования две особые
точки
![]()
и
![]()
.
Следовательно
необходимо рассмотреть сходимость
каждого из
интегралов

и
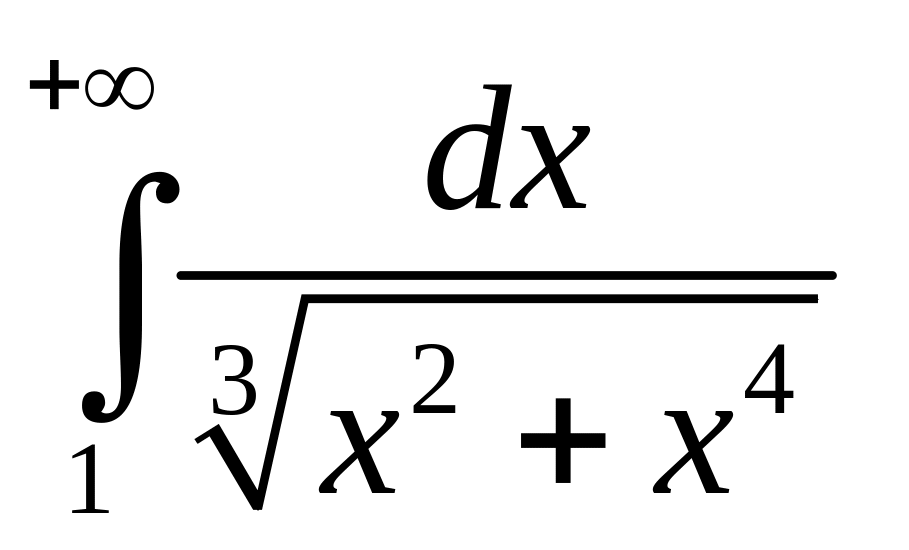
.
Воспользуемся
признаком сравнения

;

.
Так
как оба интеграла
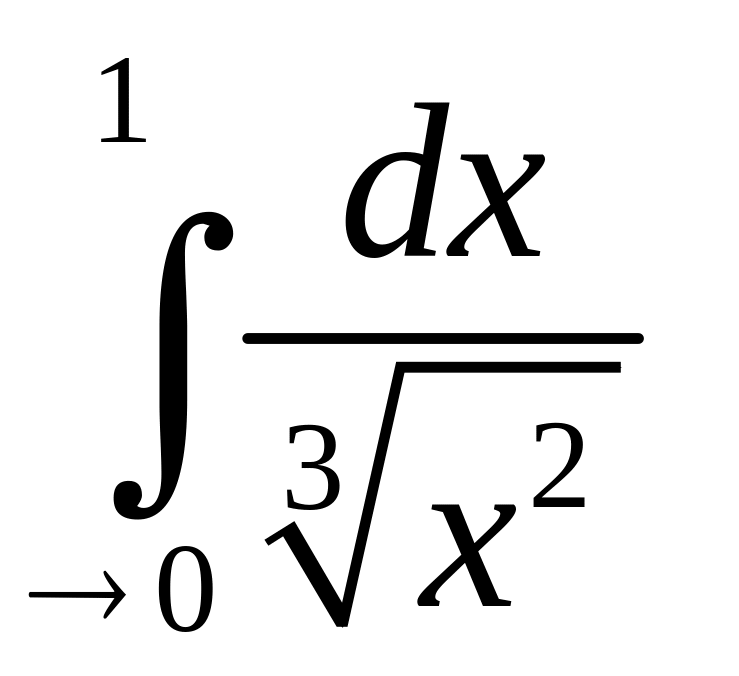
и

сходятся,
то сходится и исходный.
Пример
5.
Исследовать сходимость интеграла

.
Подынтегральная
функция имеет на промежутке
![]()
две
особые точки
и
![]()
.
Разобьем
наш интеграл на два

.
Так
как

и
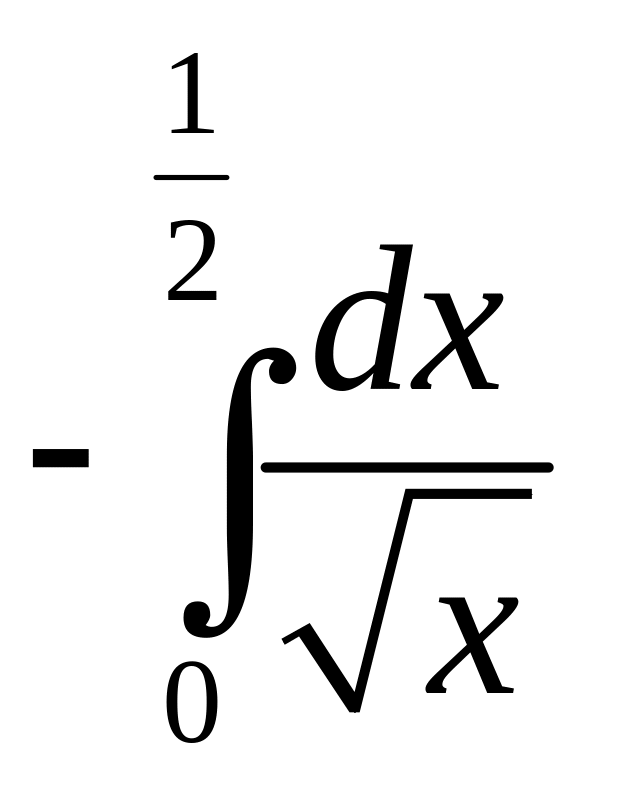
сходится,
то сходится

.
Так
как

и

расходится,
то

расходится.
Следовательно, исходный интеграл
расходится.
Пример
6.
Исследовать сходимость интеграла

.
Особая
точка
.
Так
как
![]()
при
,
то
при достаточно малых
![]()
имеет
место оценка
![]()

.
Подберём
так,
чтобы

.
Тогда
интеграл от «большей» функции
будет
сходится. По признаку сравнения
исходный
интеграл сходится.
Пример
7.
Исследовать абсолютную или условную
сходимость интеграла

.
Функция
![]()
имеет
на
одну
особую точку
,
является
знакопроизвольной. Исследуем сходимость
интеграла по признаку Дирихле.

-ограничена
на
,
функция
![]()
-монотонно
убывает слева в точке
,
так
как

при
![]()
и
![]()
.
Итак,
в силу признака Дирихле, интеграл
сходится.
Для
исследования абсолютной сходимости
данного интеграла воспользуемся оценкой
![]()
.
Имеем

.
Дословно
повторяя приведённые выше рассуждения,
получим, что интеграл

сходится. Так как
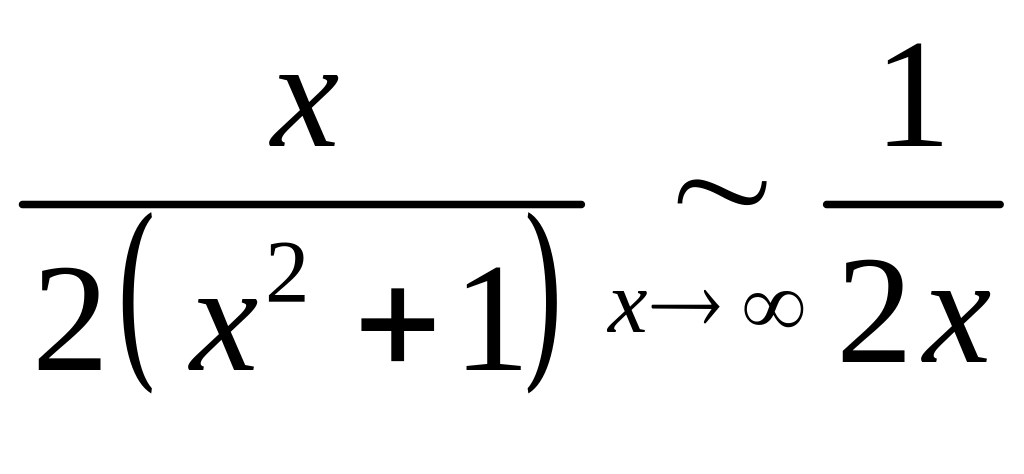
,
то
по признаку сравнения

расходится. Следовательно, интеграл
расходится
и
исходный интеграл сходится условно.
Пример
8.
Исследовать на сходимость несобственные
интегралы
а)
сходится.
б)
расходится.
в)
сходится.
г)
,
(где
![]()
,
так
как
![]()
при
достаточно большом значении
![]()
верна
оценка
![]()
)
Подберём
так,
чтобы
![]()
(тогда интеграл от «большей» функции
будет
сходящимся). При

данный
интеграл сходится.
д)
и интеграл от «меньшей» функции
расходится
исходный интеграл расходится.
е)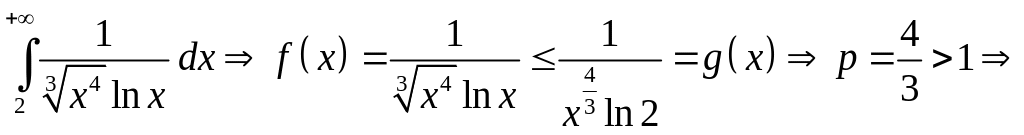
сходится.
«Большая»
функция
,
интеграл
от неё сходится
исходный интеграл сходится.
ж)
.
Подберём
так,
чтобы
![]()
(тогда
интеграл от «меньшей» функции
будет
расходящимся). При
![]()
данный интеграл расходится.
з)
.
Особая точка
,
так
как

.
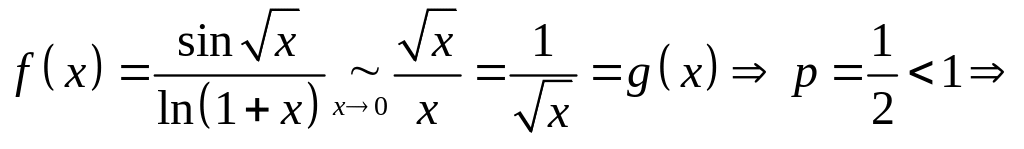
интеграл
сходится.
и)
.
Исследуем на сходимость каждый интеграл.

первый
интеграл сходится.

.
Исследуем
на сходимость интеграл

.
Сделаем
замену в интеграле
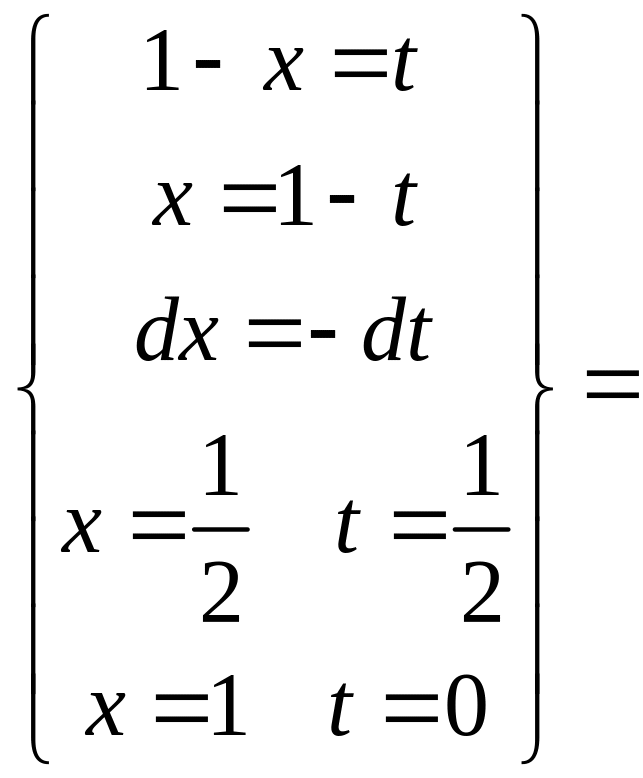

второй
интеграл сходится.
Следовательно,
исходный интеграл сходится.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Определённый интеграл называется несобственным, если выполняется по крайней мере одно из следующих условий.
- Область интегрирования является бесконечной. Например, является бесконечным промежутком
.
- Функция
является неограниченной в окрестности некоторых точек области интегрирования.
Если интервал ![[a,b]](https://wikimedia.org/api/rest_v1/media/math/render/svg/9c4b788fc5c637e26ee98b45f89a5c08c85f7935)
Несобственные интегралы I рода[править | править код]

Несобственный интеграл первого рода
Пусть 


- Если
, то используется обозначение
и интеграл называется несобственным интегралом Римана первого рода. В этом случае
называется сходящимся.
- Если не существует конечного
(
или
), то интеграл
называется расходящимся к «
», «
», или просто расходящимся.
Пусть 
![(-infty, b]](https://wikimedia.org/api/rest_v1/media/math/render/svg/7a9d3156528d17e410760f1d0cd5034f6011a635)

- Если
, то используется обозначение
и интеграл называется несобственным интегралом Римана первого рода. В этом случае
называется сходящимся.
- Если не существует конечного
(
или
), то интеграл
называется расходящимся к «
», «
», или просто расходящимся.
Если функция 

Геометрический смысл несобственного интеграла I рода[править | править код]
Несобственный интеграл первого рода выражает площадь бесконечно длинной криволинейной трапеции.
Примеры[править | править код]

Несобственные интегралы II рода[править | править код]

Несобственный интеграл Римана второго рода
Пусть 
![(a,b]](https://wikimedia.org/api/rest_v1/media/math/render/svg/6a6969e731af335df071e247ee7fb331cd1a57ae)

- Если
, то используется обозначение
и интеграл называется несобственным интегралом Римана второго рода. В этом случае интеграл называется сходящимся.
- Если
или
, то обозначение сохраняется, а
называется расходящимся к «
», «
», или просто расходящимся.
Пусть 


- Если
, то используется обозначение
и интеграл называется несобственным интегралом Римана второго рода. В этом случае интеграл называется сходящимся.
- Если
или
, то обозначение сохраняется, а
называется расходящимся к «
», «
», или просто расходящимся.
Если функция 

![[a;b]](https://wikimedia.org/api/rest_v1/media/math/render/svg/68e776d74130a8890a814c1f4e74372a9110d2f9)

Геометрический смысл несобственных интегралов II рода[править | править код]
Несобственный интеграл второго рода выражает площадь бесконечно высокой криволинейной трапеции.
Пример[править | править код]

Отдельный случай[править | править код]
Пусть функция 

Тогда можно найти несобственный интеграл 
Критерий Коши[править | править код]
1. Пусть 


- Тогда
сходится
2. Пусть 
![(a,b]](https://wikimedia.org/api/rest_v1/media/math/render/svg/6a6969e731af335df071e247ee7fb331cd1a57ae)

- Тогда
сходится
Абсолютная сходимость[править | править код]
Интеграл 

Если интеграл сходится абсолютно, то он сходится.
Условная сходимость[править | править код]
Интеграл 


См. также[править | править код]
- Интеграл Римана
- Интеграл Лебега
- Метод Самокиша — численный метод для вычисления интегралов с особенностями.
Литература[править | править код]
Дмитрий Письменный. Конспект лекций по высшей математике, часть 1. — Айрис Пресс, 2007. — С. 233-237.
Это «родственник» определённого интеграла. …Нормальное такое определение :). И сразу возникает вопрос: чем отличается несобственный интеграл от «собрата»? Он может отличаться пределами интегрирования:
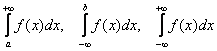 – то есть, один или даже оба предела бесконечны, при этом подынтегральная функция непрерывна на промежутке интегрирования.
– то есть, один или даже оба предела бесконечны, при этом подынтегральная функция непрерывна на промежутке интегрирования.
Такие интегралы получили название несобственные интегралы первого рода.
Кроме того, несобственный интеграл может быть «внешне похож» на определённый интеграл и иметь вид 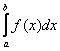 . Но есть один нюанс. Подынтегральная функция не определена в точке
. Но есть один нюанс. Подынтегральная функция не определена в точке ![]() или
или ![]() . Или на обоих концах. Или даже во внутренних точках отрезка
. Или на обоих концах. Или даже во внутренних точках отрезка ![]() .
.
Это так называемые несобственные интегралы второго рода.
Что значит решить несобственный интеграл? В отличие от определённого интеграла, тут есть три варианта. Решить несобственный интеграл – это значит найти конечное число, либо получить бесконечность, либо выяснить, что несобственного интеграла не существует.
1) Если несобственный интеграл равен конечному числу, то говорят, что он сходится. Число может быть как положительным, так и отрицательным. Или нулём.
2) Если несобственный интеграл равен бесконечности (со знаком «плюс» или «минус»), то говорят, он расходится.
3) И в ряде случаев несобственного интеграла может вовсе не существовать. Даже если подынтегральная функция непрерывна на промежутке интегрирования! (вспоминаем, что определённый интеграл при этом условии существует всегда).
Как решить несобственный интеграл? С помощью той же формулы Ньютона-Лейбница. С некоторыми особенностями.
И здесь вы должны понимать и уметь решать несложные пределы функций.
В чём смысл несобственного интеграла? Геометрически – это тоже площадь (если интеграл существует). Но площадь своеобразная. И с этим своеобразием мы познакомимся прямо на следующей странице:
 2.2. Несобственный интеграл первого рода
2.2. Несобственный интеграл первого рода
 1.11. А если подынтегральная функция нечётная?
1.11. А если подынтегральная функция нечётная?
| Оглавление |
Полную и свежую версию данного курса в pdf-формате,
а также курсы по другим темам можно найти здесь.
Также вы можете изучить эту тему подробнее – просто, доступно, весело и бесплатно!
С наилучшими пожеланиями, Александр Емелин
Содержание:
Несобственные интегралы:
При введении понятия определенного интеграла Римана предполагалось что:
- промежуток интегрирования является конечным;
- подынтегральная функция f(х) является ограниченной.
Обобщим понятие определенного интеграла на два случая, когда:
- промежуток итерирования является бесконечным;
- подынтегральная функция f(x) неограниченна в окрестности некоторых точек отрезка интегрирования.
Несобственные интегралы с бесконечными пределами интегрирования
Обобщим понятие интеграла на случай бесконечных промежутков. На прямой 
Рассмотрим для определенности полупрямую 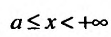 . Для этого предположим, что функция f(x) определена для всех
. Для этого предположим, что функция f(x) определена для всех 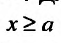 и пусть она интегрируема на любом конечном отрезке
и пусть она интегрируема на любом конечном отрезке 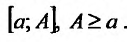
Тогда на отрезке 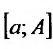 существует определенный интеграл Римана
существует определенный интеграл Римана
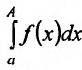 . Этот определенный интеграл является функцией верхнего предела А:
. Этот определенный интеграл является функцией верхнего предела А:
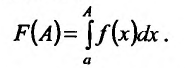
Рассмотрим предел этой функции F(a) при 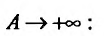

Определение 21.1.1. Предел (21.1.1) в случае, если он существует, называется несобственным интегралом первого рода от функции f(x) на полупрямой 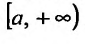 и обозначается символом
и обозначается символом

При этом говорят, что несобственный интеграл (21.1.2) сходится, и пишут равенство:
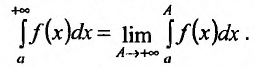
Символ (21.1.2) употребляют и в случае, если предела (21.1.1) не существует, но в этом случае говорят, что несобственный интеграл (21.1.2) расходится.
Аналогично определяется и несобственный интеграл 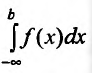 для функции f(x), определенной на полупрямой
для функции f(x), определенной на полупрямой 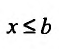 и интегрируемой по Риману на любом отрезке
и интегрируемой по Риману на любом отрезке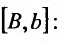
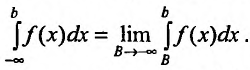
Если для функции f(х) имеют смысл несобственные интегралы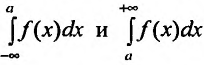 , т.е. каждый из этих интегралов сходится, где а – любое действительное число, то несобственный интеграл
, т.е. каждый из этих интегралов сходится, где а – любое действительное число, то несобственный интеграл 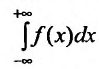 сходится и справедливо равенство:
сходится и справедливо равенство:
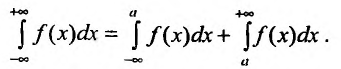
Следует отмстить, что в приложениях важную роль играет интеграл Пуассона:
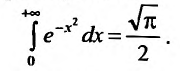
Геометрически, он равен площади неограниченной криволинейной трапеции (см. рис. 21.1) 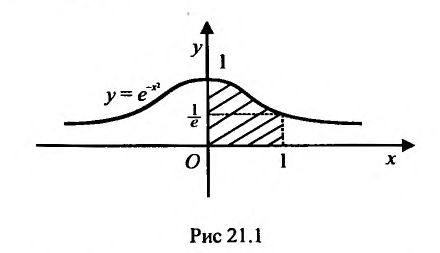
Пример:
Исследовать сходимость несобственного интеграла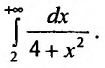
Решение:
Поскольку функция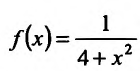 интегрируема на отрезке [2;A], где
интегрируема на отрезке [2;A], где 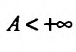 , применяя определение 25.1.1, получим:
, применяя определение 25.1.1, получим:
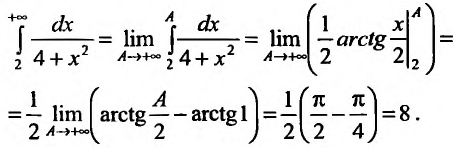
Следовательно, несобственный интеграл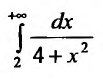 сходится и справедливо равенство:
сходится и справедливо равенство: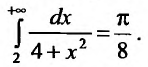
Пример:
Исследовать сходимость несобственного интеграла: 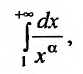 где а – произвольное действительное число.
где а – произвольное действительное число.
Решение:
Поскольку функция 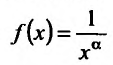 интегрируема на любом отрезке
интегрируема на любом отрезке 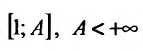 то, применяя определение 21.1.1, получим:
то, применяя определение 21.1.1, получим:
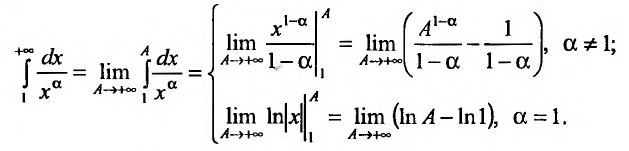 Так как
Так как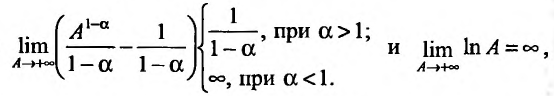
а = 1, то при а > 1 несобственный интеграл 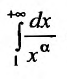 сходится, а при
сходится, а при
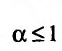 – расходится.
– расходится.
При исследовании сходимости несобственных интегралов целесообразно применять достаточные признаки сходимости.
Предполагая, что функции f(х) и g(x) определены, неотрицательны и интегрируемы по Риману на любом отрезке [а,А],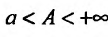 , сформулируем признаки сравнения.
, сформулируем признаки сравнения.
Теорема 21.1.1. Пусть на полупрямой 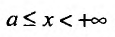 выполняется неравенство:
выполняется неравенство: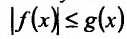 . Тогда из сходимости интеграла
. Тогда из сходимости интеграла
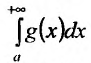 следует сходимость интеграла
следует сходимость интеграла 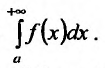
Теорема 21.1.2. Пусть на полупрямой 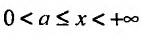 функция f(x) удовлетворяет неравенству
функция f(x) удовлетворяет неравенству 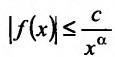 , где с и а – постоянные величины, а > 1. Тогда интеграл
, где с и а – постоянные величины, а > 1. Тогда интеграл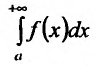 сходится. Если же существует такая постоянная с > 0, что на полупрямой
сходится. Если же существует такая постоянная с > 0, что на полупрямой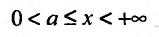 справедливо неравенство
справедливо неравенство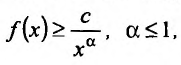 то интеграл
то интеграл 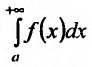 расходится.
расходится.
Теорема 21.1.3. Пусть функция f(x) является ограниченной по сравнению с g(x) при 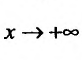 , тогда, если интеграл
, тогда, если интеграл 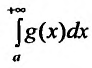 сходится, то сходится и
сходится, то сходится и 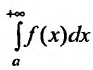 , а если интеграл
, а если интеграл 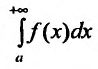 расходится, то расходится и интеграл
расходится, то расходится и интеграл 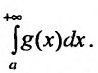
Введем понятие абсолютной и условной сходимости несобственных интегралов.
Несобственный интеграл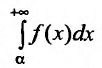 называется абсолютно сходящимся, если сходится интеграл
называется абсолютно сходящимся, если сходится интеграл 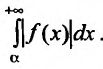 Если же интеграл
Если же интеграл
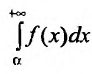 сходится, а интеграл
сходится, а интеграл 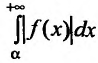 расходится, то несобственный интеграл
расходится, то несобственный интеграл 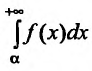 называется условно сходящимся.
называется условно сходящимся.
Интегралы от неограниченных функций
Во всех предыдущих рассуждениях мы предполагали, что подынтегральная функция f(х) непрерывна на промежутке интегрирования. Поэтому, если мы хотим, чтобы некоторые неограниченные функции интегрировались в каком-то смысле, то нам нужно обобщить понятие определенного интеграла.
Пусть функция f(x) определена и неограниченна на полуинтервале [а,b), причем она ограничена на любом отрезке 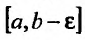 ,
,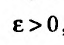 , заключенном в интервале
, заключенном в интервале 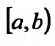 Точку b при этом будем называть особой. Будем также предполагать, что функция f(x) интегрируема на отрезке
Точку b при этом будем называть особой. Будем также предполагать, что функция f(x) интегрируема на отрезке 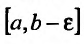 . Тогда можно говорить о функции:
. Тогда можно говорить о функции:
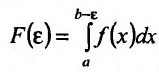
значение которой зависит от 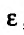 следовательно, можно рассматривать правый предел
следовательно, можно рассматривать правый предел 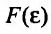 при
при 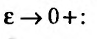

Определение 21.2.1. Правый предел (21.2.1) в случае, если он существует, называется несобственным интегралом второго рода от функции f(х) на отрезке 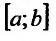 и обозначается символом:
и обозначается символом:

При этом говорят, что несобственный интеграл (21.2.2) сходится, и пишут равенство:

Символ (21.2.2) применяют и в случае, если указанного предела (21.2.3) не существует, но в этом случае говорят, что несобственный интеграл (21.2.3) расходится.
Из определения 21.2.1. следует, что если f(x) > 0 на [a,b), то несобственный интеграл 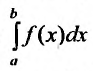 численно равен площади неограниченной области G (см. рис. 21.2).
численно равен площади неограниченной области G (см. рис. 21.2).
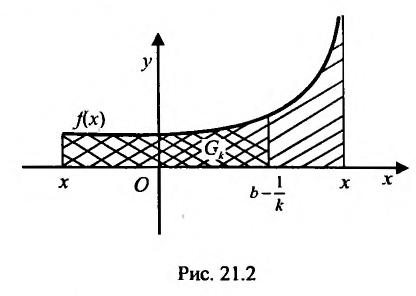
Действительно,
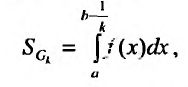
где 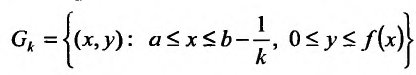 , а если
, а если 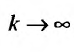 то
то
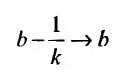 и площадь
и площадь 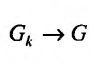 . В свою очередь,
. В свою очередь, 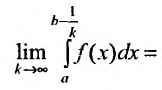
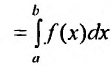 согласно определению несобственного интеграла.
согласно определению несобственного интеграла.
Итак, под несобственным интегралом будем понимать интеграл, определенный формулой (21.2.3).
Аналогично определяется и несобственный интеграл 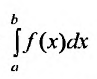
от функции f(x), определенной на полуинтервале (a,b] и интегрируемой на всех отрезках

Если же функция f(x) определена на интервале (a, b) и если при некотором выборе точки 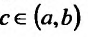 существуют несобственные
существуют несобственные
интегралы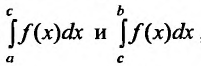 , то по определению положим:
, то по определению положим:
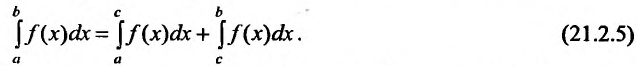
При этом в рассматриваемом случае существование и величина
интеграла 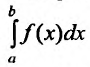 не зависит от выбора точки
не зависит от выбора точки 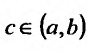 . Действительно, в этом случае функция f(x), очевидно, интегрируема на любом отрезке
. Действительно, в этом случае функция f(x), очевидно, интегрируема на любом отрезке 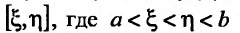 и равенство (21.2.5) равносильно равенству:
и равенство (21.2.5) равносильно равенству:
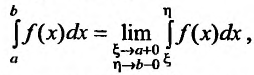
причем переменные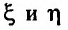 стремятся к своим пределам независимо друг от друга. Поэтому, естественно ограничиться изучением несобственных интегралов определяемых (21.2.3) и (21.2.4).
стремятся к своим пределам независимо друг от друга. Поэтому, естественно ограничиться изучением несобственных интегралов определяемых (21.2.3) и (21.2.4).
Пример №1
Функция 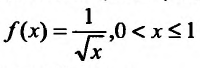 неограниченна и, следовательно, не интегрируема по Риману.
неограниченна и, следовательно, не интегрируема по Риману.
Несобственный же интеграл 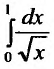 существует:
существует:
Пример №2
Для функции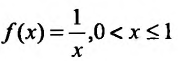 несобственный интеграл
несобственный интеграл 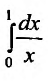 не существует, так как
не существует, так как 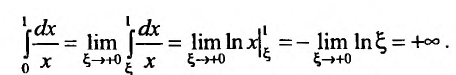
На несобственные интегралы легко переносятся многие свойства интеграла Римана. Так, например, если функция f(x) непрерывна на полуинтервале
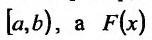 какая-либо первообразная функция f(х) на полуинтервале [a,b), то
какая-либо первообразная функция f(х) на полуинтервале [a,b), то

где 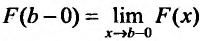 Равенство (21.2.6) понимается в том смысле, что или обе части равенства одновременно имеют смысл и тогда они равны, или они одновременно не имеют смысла.
Равенство (21.2.6) понимается в том смысле, что или обе части равенства одновременно имеют смысл и тогда они равны, или они одновременно не имеют смысла.
Сформулируем и докажем критерий сходимости несобственных интегралов:
Теорема 21.2.2. Пусть функция f(x) определена и неотрицательна на полуинтервале [a,b). Тогда для того чтобы несобственный интеграл 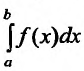 сходился, необходимо и достаточно,чтобы интегралы
сходился, необходимо и достаточно,чтобы интегралы 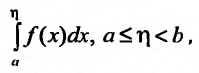 были ограничены в совокупности, т. е. чтобы существовала постоянная М > 0, такая, что
были ограничены в совокупности, т. е. чтобы существовала постоянная М > 0, такая, что 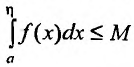 , для любого числа
, для любого числа 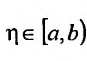 , причем в этом случае
, причем в этом случае 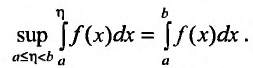
Доказательство. Обозначим через 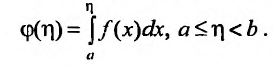
Если 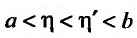 , то в силу неотрицательности функции f(x) значение интеграла является неотрицательным числом:
, то в силу неотрицательности функции f(x) значение интеграла является неотрицательным числом:
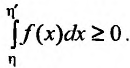
Поэтому справедливо неравенство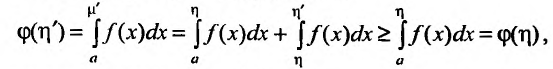 из которого следует, что
из которого следует, что 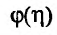 – монотонно возрастающая функция. Поэтому предел
– монотонно возрастающая функция. Поэтому предел 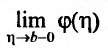 существует и он будет конечный, если
существует и он будет конечный, если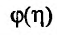 – ограничена сверху, т. е. когда выполняется условие:
– ограничена сверху, т. е. когда выполняется условие:
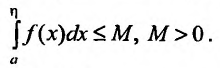
Ясно, что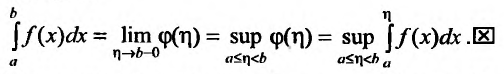
Из теоремы следует, что для того, чтобы несобственный интеграл 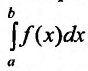 расходился, необходимо и достаточно, чтобы функция
расходился, необходимо и достаточно, чтобы функция  была не ограничена сверху:
была не ограничена сверху: 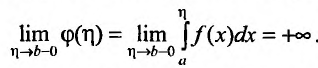
Поэтому когда несобственный интеграл расходится, то пишут: 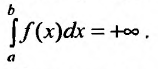
Сформулируем далее теоремы, которые называются признаками сравнения несобственных интегралов. Для этого предположим, что: 1) функции f(x) и g(x) определены и f(x) > 0, g(x) >0 на 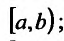 , 2) f(x) и g(x) интегрируемы по Риману на любом отрезке
, 2) f(x) и g(x) интегрируемы по Риману на любом отрезке 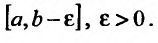
Теорема 21.2.3. Пусть функция f(x) является ограниченной по сравнению с функцией g(x) в некоторой окрестности точки Ь: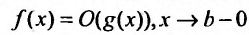 , тогда, если:
, тогда, если: 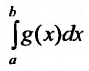 сходится, то сходится и интеграл
сходится, то сходится и интеграл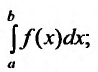
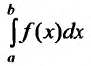 расходится, то расходится и интеграл
расходится, то расходится и интеграл 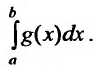
Следствие. Пусть 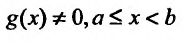 и l
и l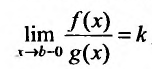 тогда:
тогда:
1) если интеграл 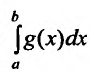 сходится и
сходится и 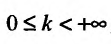 то и интеграл
то и интеграл 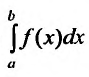 также сходится;
также сходится;
2) если интеграл 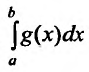 расходится и
расходится и 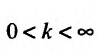 , то и иитеграл
, то и иитеграл 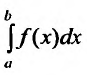 также расходится.
также расходится.
В частности, если 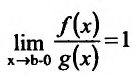 . то интегралы
. то интегралы 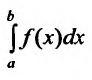 и
и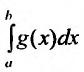 сходятся или расходятся одновременно.
сходятся или расходятся одновременно.
Пример №3
Исследовать сходимость несобственного интеграла:
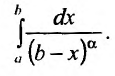
Решение:
На полуинтервале 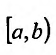 для функции
для функции 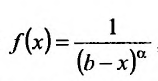
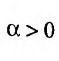 , точка b является особой. Так как эта функция интегрируема на любом отрезке
, точка b является особой. Так как эта функция интегрируема на любом отрезке 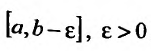 , то, согласно определению 21.2.1, получим:
, то, согласно определению 21.2.1, получим:
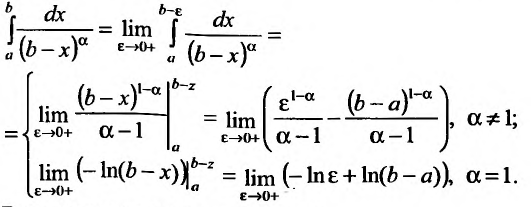
Вычислим полученные пределы:
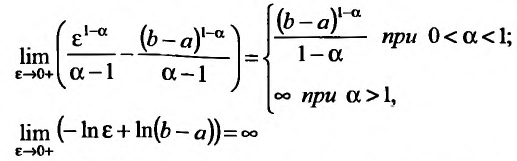
Следовательно, рассматриваемый несобственный интеграл сходится при 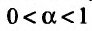 и расходится при
и расходится при 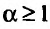
В качестве функции сравнения часто бывает достаточно брать
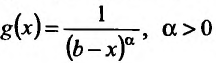 , так как известно поведение интеграла:
, так как известно поведение интеграла:
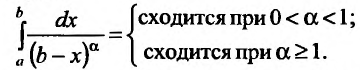
Отметим, что если функция f(x) непрерывна на полуинтервале 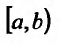 и b – особая точка, то интегралы второго рода сводятся к интегралам первого рода при помощи замены:
и b – особая точка, то интегралы второго рода сводятся к интегралам первого рода при помощи замены:
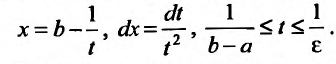
В результате этой замены переменной, получим равенство: 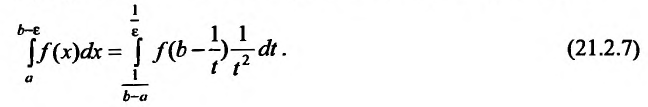
Из этого равенства следует, что если сходится интеграл
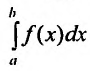 , т.е. существует предел:
, т.е. существует предел: 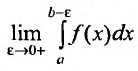 , то существует и предел
, то существует и предел 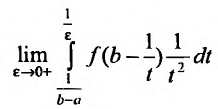 , что означает сходимость несобственного интеграла первого рода
, что означает сходимость несобственного интеграла первого рода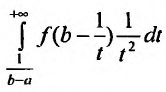 и равенство этого интеграла интегралу
и равенство этого интеграла интегралу 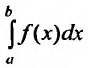 . И обратно, из сходимости несобственного интеграла первого рода следует сходимость несобственного интеграла второго рода и равенство этих двух интегралов.
. И обратно, из сходимости несобственного интеграла первого рода следует сходимость несобственного интеграла второго рода и равенство этих двух интегралов.
Отмстим, что несобственные интегралы первого рода широко применяются в экономических исследованиях. Так эффективность функционирования розничной торговли; валовой доход (сумму торговых сделок) розничной торговли от реализации товаров и услуг; общая сумма текущих издержек обращения и капиталовложений, сводимых к текущим затратам; совокупная денежная оценка полезности времени, расходуемого населением на приобретение товаров в розничной торговле и др. описывается при помощи несобственных интегралов.
Несобственные интегралы в высшей математике
Определенные интегралы с одним или двумя бесконечными пределами интегрирования от непрерывной на интервале интегрирования функции.(Несобственные интегралы I рода).
Теорема: Пусть функция f(х) непрерывна на интервале 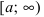 (или интервалах
(или интервалах 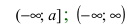 ). Если существует предел
). Если существует предел 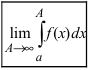 (или пределы
(или пределы 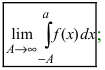
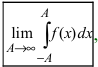 соответственно), то существует интеграл
соответственно), то существует интеграл 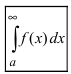 (или интегралы
(или интегралы 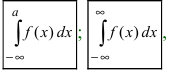 соответственно).
соответственно).
Определение: Определенный интеграл с одним или двумя бесконечными пределами интегрирования от непрерывной на интервале интегрирования функции называется несобственным интегралом I рода
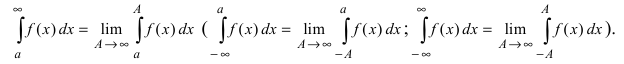
Замечание: Несобственный интеграл I рода вычисляется в смысле главного значения.
В дальнейшем будем изучать только интегралы  другие интегралы рассматриваются аналогично.
другие интегралы рассматриваются аналогично.
Пример:
Вычислить интеграл 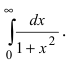
Решение:
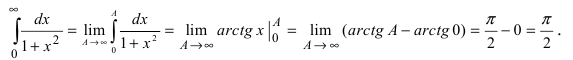
Пример:
Вычислить интеграл 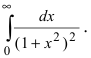
Решение:
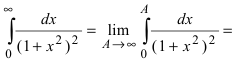 (применим метод замены переменной интегрирования) =
(применим метод замены переменной интегрирования) = 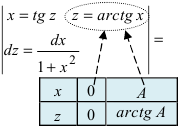 (пересчитаем пределы интегрирования)
(пересчитаем пределы интегрирования)
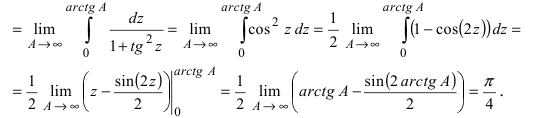
Определение: Несобственный интеграл I рода называется сходящимся, если пределы в указанных выше равенствах конечны, в противном случае несобственный интеграл I рода называется расходящимся.
Пример:
Выяснить сходимость интеграла 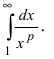
Решение:
Рассмотрим возможные случаи:
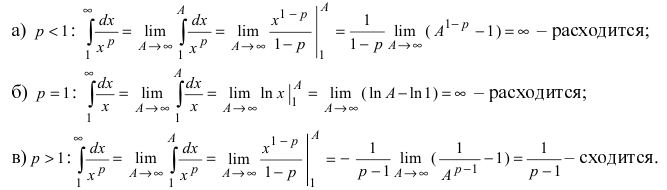
Следовательно, данный несобственный интеграл расходится при 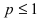 и сходится при
и сходится при 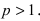 Этот интеграл часто используется в теории рядов (см. ниже). Рассмотрим признак сходимости несобственного интеграла I рода:
Этот интеграл часто используется в теории рядов (см. ниже). Рассмотрим признак сходимости несобственного интеграла I рода:
Теорема: Пусть функции f(x) и g(x) непрерывны на интервале 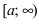 и удовлетворяют неравенству
и удовлетворяют неравенству 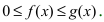 Тогда: из сходимости интеграла
Тогда: из сходимости интеграла 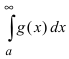 вытекает сходимость интеграла
вытекает сходимость интеграла 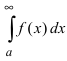 , а из расходимости интеграла
, а из расходимости интеграла 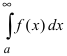 следует расходимость интеграла
следует расходимость интеграла 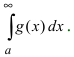
Пример:
Исследовать на сходимость интеграл 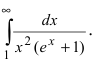
Решение:
На интервале 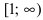 справедливы неравенства
справедливы неравенства 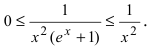 Так как
Так как 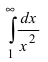
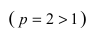 сходится, то по признаку сходимости сходится и интеграл
сходится, то по признаку сходимости сходится и интеграл 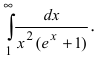
Пример:
Исследовать на сходимость интеграл 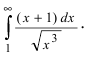
Решение:
На интервале  справедливы неравенства
справедливы неравенства 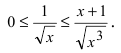 Так как
Так как 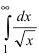
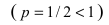 расходится то по признаку сходимости расходится и интеграл
расходится то по признаку сходимости расходится и интеграл 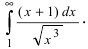
Следствие из теоремы. Если сходится интеграл 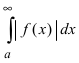 , то сходится и интеграл
, то сходится и интеграл 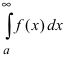 .
.
Пример:
Исследовать на сходимость интеграл 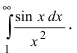
Решение:
Так как 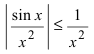 и интеграл
и интеграл 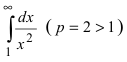 сходится, то по признаку сходимости сходится и интеграл
сходится, то по признаку сходимости сходится и интеграл 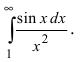
Определенные интегралы с конечными пределами интегрирования от функций, имеющих точки разрыва второго рода на интервале интегрирования. (Несобственные интегралы II рода).
Определение: Если функция f(х) не существует хотя бы в одной точке 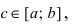 то интеграл
то интеграл 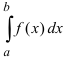 называется несобственным интегралом II рода.
называется несобственным интегралом II рода.
32. Если функция f(х) в точке 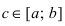 терпит разрыв II рода, то обычное определение определенного интеграла как предела интегральной суммы непригодно.
терпит разрыв II рода, то обычное определение определенного интеграла как предела интегральной суммы непригодно.
Вычисление определенного интеграла с конечными пределами от разрывной на интервале интегрирования функции производится посредством предельного перехода 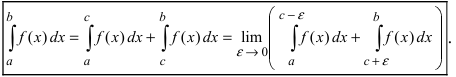
Определение: Если приведенные пределы существуют и конечны, то несобственный интеграл II рода называется сходящимся, в противном случае – расходящимся.
Пример:
Вычислить интеграл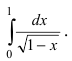
Решение:
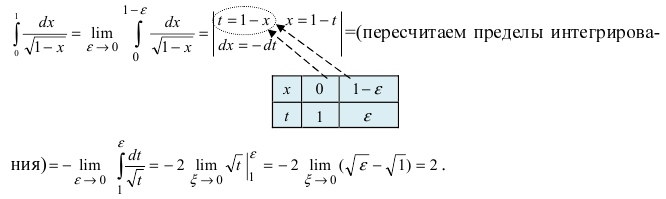
Рассмотрим признак сходимости несобственных интегралов II рода:
Теорема: Пусть функции f(х) и g(x) непрерывны на интервале 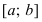 и удовлетворяют неравенству
и удовлетворяют неравенству 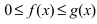 , а в точке
, а в точке 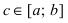 обе функции терпят разрыв II рода.
обе функции терпят разрыв II рода.
Тогда:
Применение определенного интеграла в науке и технике
1. Работа по сжатию пружины
Пусть тело массой m прикреплено к пружине с коэффициентом упругости k. Требуется вычислить работу, которую совершит сила упругости при растяжении пружины от а до b (Рис. 13):
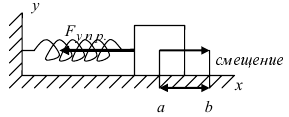 Рис. 13. Вычисление работы упругой силы. Из физики известно, что сила упругости
Рис. 13. Вычисление работы упругой силы. Из физики известно, что сила упругости 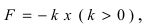 а работа
а работа 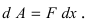
Отсюда находим, что 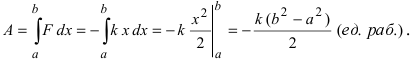 Если выполняется неравенство
Если выполняется неравенство 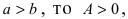 т.е. она совершается против силы упругости. В противном случае работа совершается силой упругости.
т.е. она совершается против силы упругости. В противном случае работа совершается силой упругости.
Работа по откачке жидкости из резервуара
Пусть резервуар представляет собой параболоид вращения и имеет высоту Л. Резервуар заполнен жидкостью с плотностью р. Вычислить работу, которую надо совершить при полной откачке жидкости из резервуара (Рис. 14). 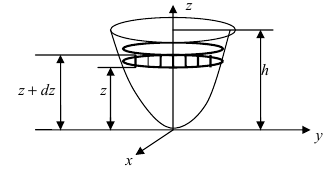
Рис. 14. Вычисление работы по откачке жидкости из параболоида.
Параболоид вращения задается уравнением 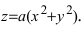 На слой жидкости, расположенный на высоте между
На слой жидкости, расположенный на высоте между 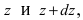 действует сила тяжести
действует сила тяжести 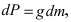 где g – ускорение свободного падения, dm – масса рассматриваемого слоя жидкости. В силу того, что
где g – ускорение свободного падения, dm – масса рассматриваемого слоя жидкости. В силу того, что 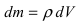 (dV – объем рассматриваемого слоя жидкости), то
(dV – объем рассматриваемого слоя жидкости), то 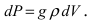 Для тела вращения, которым является резервуар с жидкостью, элемент объема
Для тела вращения, которым является резервуар с жидкостью, элемент объема 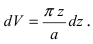 Работу, которую надо совершить по откачке этого слоя жидкости, равна
Работу, которую надо совершить по откачке этого слоя жидкости, равна 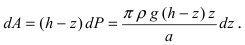 Следовательно, работа по откачке всей жидкости из резервуара равна
Следовательно, работа по откачке всей жидкости из резервуара равна
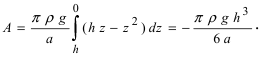
3. Работа по постройке пирамиды
Пусть необходимо построить пирамиду высотой h со стороной основания а из материала с плотностью р . Требуется найти работу по возведению этой пирамиды (Рис. 15, обозначения расставить самостоятельно). 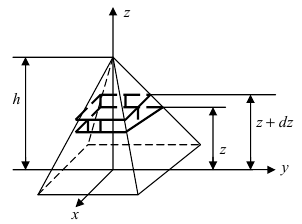
Рис. 15. Вычисление работы по постройке пирамиды.
Для того, чтобы увеличить высоту пирамиды на 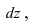 надо затратить материал массой
надо затратить материал массой 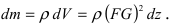 Так как треугольник ЕОВ подобен треугольнику
Так как треугольник ЕОВ подобен треугольнику 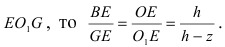 В силу того, что треугольник ЕАВ подобен треугольнику
В силу того, что треугольник ЕАВ подобен треугольнику 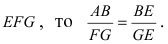 Отсюда следует, что
Отсюда следует, что 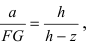 т.е. FG =
т.е. FG =
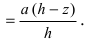 Таким образом, сила тяжести, действующая на выделенный слой материала, будет равна
Таким образом, сила тяжести, действующая на выделенный слой материала, будет равна 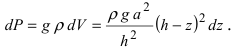 Элемент работы определяется формулой
Элемент работы определяется формулой 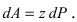 Тогда работа по возведению всей пирамиды будет равна
Тогда работа по возведению всей пирамиды будет равна 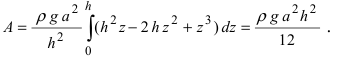
4. Давление жидкости на вертикально погруженную стенку
Пусть в жидкость с плотностью р вертикально погрузили пластину. Требуется вычислить давление, оказываемое со стороны жидкости на пластину (Рис. 16). Давление на глубине х обозначим через Р(х), тогда давление в слое жидкости от х до х + dx будет равно 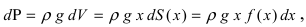 где
где
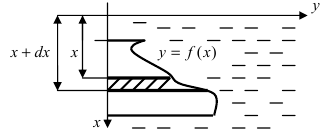
Рис. 16. Вычисление давления жидкости на вертикально погруженную жидкость.
f(x) – функция которая описывает форму пластины. Отсюда находим давление, оказываемое со стороны жидкости на пластину:
- Заказать решение задач по высшей математике
Пример №4
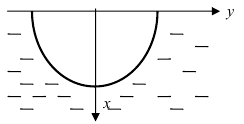
Вычислить давление жидкости на пластину, имеющую форму полуокружности с радиусом R, диаметр которой совпадает с поверхностью (Рис. 17).
Решение:
Рис. 17. Вычисление давления жидкости на пластину, имеющую форму полуокружности с радиусом R.
В данном примере 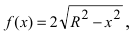 следовательно, давление жидкости на пластину равно
следовательно, давление жидкости на пластину равно 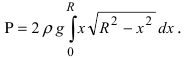 Используя метод замены переменной интегрирования, показать самостоятельно, что давление равно
Используя метод замены переменной интегрирования, показать самостоятельно, что давление равно 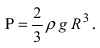
5. Вторая космическая скорость
Известно, что на любое тело массой m, которое находится на высоте х над поверхностью Земли, имеющей массу M и форму шара радиусом R, действует сила притяжения Земли 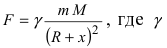 – гравитационная постоянная. Второй космической скоростью называется такая скорость, при которой тело не возвращается на Землю. Это означает, что телу придается такая кинетическая энергия
– гравитационная постоянная. Второй космической скоростью называется такая скорость, при которой тело не возвращается на Землю. Это означает, что телу придается такая кинетическая энергия 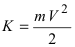 (y – скорость движения), что оно может быть удалено в бесконечно удаленную точку по отношению к Земле. Для того чтобы удалить тело в бесконечно удаленную точку по отношению к Земле, необходимо совершить работу против сил гравитации
(y – скорость движения), что оно может быть удалено в бесконечно удаленную точку по отношению к Земле. Для того чтобы удалить тело в бесконечно удаленную точку по отношению к Земле, необходимо совершить работу против сил гравитации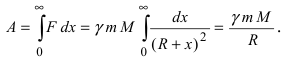
Приравнивая полученное выражение для работы значению кинетической энергии, получим выражение для второй космической скорости
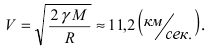
Несобственные интегралы первого рода
Несобственный интеграл первого рода – обобщение понятия интеграла Римана на бесконечный промежуток. Для бесконечного промежутка Δ составить суммы
Римана вида (1) § 24 нельзя.
Определение 1. Пусть функция y=f(x) определена на промежутке 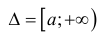 и интегрируема на любом конечном отрезке
и интегрируема на любом конечном отрезке 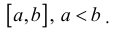
Несобственным интегралом 1-го рода функции y=f(x) на промежутке Δ называется 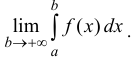 Несобственный интеграл обозначается
Несобственный интеграл обозначается 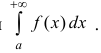
Таким образом:
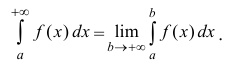 (1)
(1)
Если предел (1) существует, то интеграл называется сходящимся, в противном случае – расходящимся.
Аналогично:
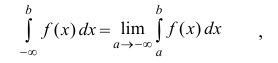 (2)
(2)
для функции y=f(x), определенной на промежутке 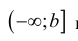 и интегрируемой на
и интегрируемой на
любом конечном промежутке [a b] и 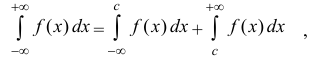 (3)
(3)
где с – промежуточная точка , и интегралы в правой части формулы (3) вычисляются по формулам (1) и (2).
Пример:
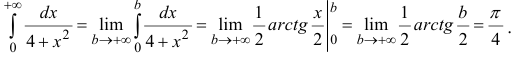
Пример:
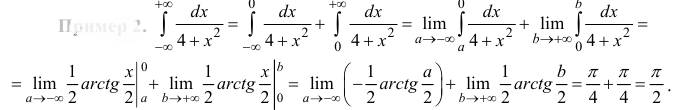
Пример:
Исследовать на сходимость 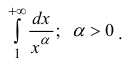
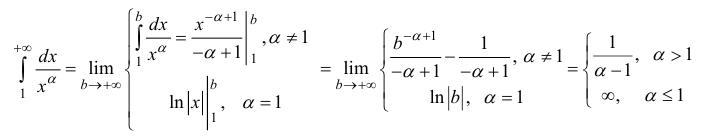
Таким образом, интеграл сходится, если α > 1 и расходится, если α ≤ 1.
Теорема 1 (признак сравнения). Пусть функции 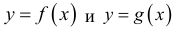 определены на промежутке
определены на промежутке 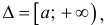 , интегрируемы на любом конечном промежутке [a b] и пусть
, интегрируемы на любом конечном промежутке [a b] и пусть 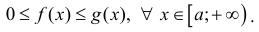
Тогда из сходимости 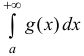 следует сходимость
следует сходимость 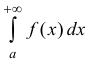 , а из расходимости
, а из расходимости
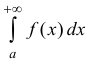 следует расходимость
следует расходимость 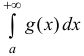 .
.
Доказательство следует из неравенства: 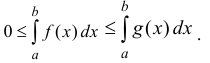
Теорема 2 (предельный признак сравнения). Пусть 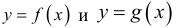 – положительны
– положительны 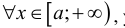 удовлетворяют условиям определения 1 на этом
удовлетворяют условиям определения 1 на этом
промежутке и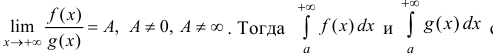 сходятся или расходятся одновременно.
сходятся или расходятся одновременно.
Доказательство. Пусть ε >0 и такое, что A -ε − > 0, тогда из определения предела
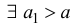 такое, что
такое, что 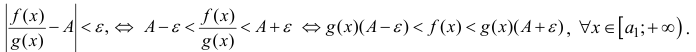
И далее доказательство следует из теоремы 1.
На практике, при исследовании на сходимость по предельному признаку в
качестве g(x) часто используют функцию 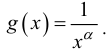
Пример:
Исследовать на сходимость интеграл 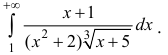
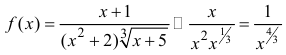 при
при 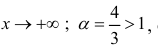 следовательно, (см. пример 3), интеграл сходится.
следовательно, (см. пример 3), интеграл сходится.
Определение 2. Несобственный интеграл 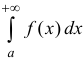 называется абсолютно-
называется абсолютно-
сходящимся, если сходится интеграл 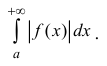
Несобственный интеграл 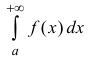 называется условно-сходящимся, если
называется условно-сходящимся, если
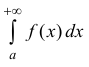 – сходится, а интеграл
– сходится, а интеграл 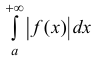 – расходится.
– расходится.
Теорема 3. Пусть 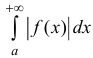 – сходится, тогда
– сходится, тогда 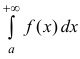 – также сходится.
– также сходится.
Доказательство. Пусть 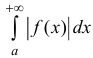 – сходится, тогда по критерию Коши (см.
– сходится, тогда по критерию Коши (см.
теорему 5 § 3) 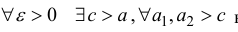 выполняется неравенство
выполняется неравенство
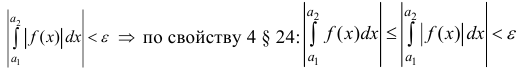 и по критерию Коши
и по критерию Коши
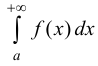 – сходится.
– сходится.
Пример:
Исследовать на абсолютную и условную сходимость 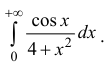
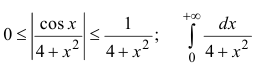 – сходится, (см. пример 1), тогда по признаку сравнения
– сходится, (см. пример 1), тогда по признаку сравнения
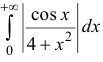 – сходится и, следовательно,
– сходится и, следовательно, 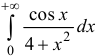 – сходится абсолютно.
– сходится абсолютно.
Пример:
Исследовать на абсолютную и условную сходимость интегралы
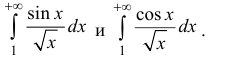
n.1. Исследуем интегралы на сходимость.
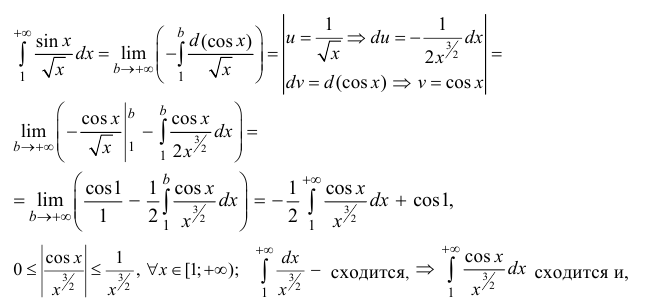
следовательно, сходится 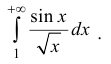
Аналогично: 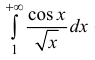 сходится.
сходится.
n.2. Исследуем интеграл 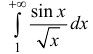 на абсолютную сходимость:
на абсолютную сходимость:
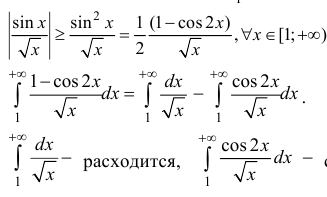
сходится (согласно п. 1), поэтому 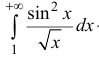 расходится, ⇒ по признаку сравнения
расходится, ⇒ по признаку сравнения
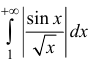 расходится, поэтому
расходится, поэтому 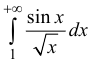 сходится условно.
сходится условно.
Аналогично: 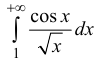 -сходится условно.
-сходится условно.
Пример:
Исследовать на абсолютную и условную сходимость интегралы 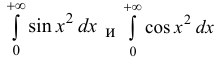 – интегралы Френеля.
– интегралы Френеля.
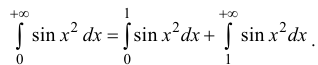
Рассмотрим 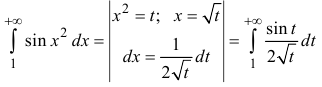 сходится условно (см. пример 6), поэтому и
сходится условно (см. пример 6), поэтому и 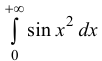 сходится условно.
сходится условно.
Аналогично 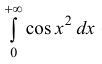 сходится условно.
сходится условно.
Значения интегралов: 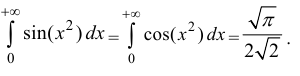
Замечание. Функции 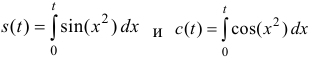 также называемые интегралами Френеля используются в оптике; c (t) и s (t) через элементарные функции не выражаются.
также называемые интегралами Френеля используются в оптике; c (t) и s (t) через элементарные функции не выражаются.
Замечание. Кривая, заданная параметрически в виде: 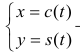 называется
называется
клотоидой (спиралью Корню). Используется при проектировании и строительстве дорог и транспортных развязок (угловое ускорение машины, движущейся по кривой с постоянной скоростью, равно нулю).
Замечание. 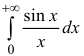 называется интегралом Дирихле;
называется интегралом Дирихле; 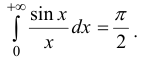
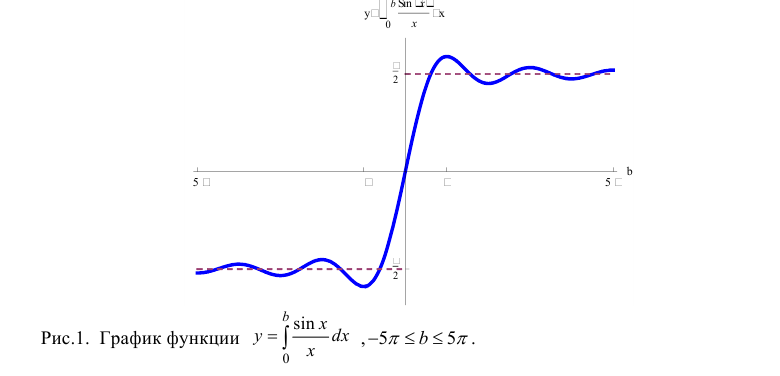
Интегралы Дирихле и Френеля являются примерами интегралов от
функций, первообразные которых не выражаются через элементарные функции.
Еще один такой пример – интеграл Пуассона (Эйлера-Пуассона или Гауссов
интеграл): 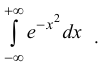 Интеграл сходится и
Интеграл сходится и 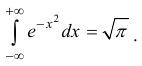
Несобственные интегралы второго рода
Несобственный интеграл второго рода – обобщение понятия интеграла Римана на случай, когда подинтегральная функция – неограниченна. Согласно необходимому условию интегрируемости функции (см. теорему 1 § 24) интегрируемая на промежутке Δ = [a b] функция ограничена на этом промежутке.
Определение 1. а) Пусть функция y=f(x) определена на промежутке Δ = [a b), интегрируема на отрезке 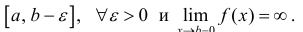 Несобственным интегралом 2-го рода
Несобственным интегралом 2-го рода 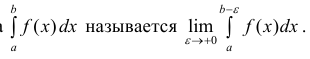 Таким образом:
Таким образом:
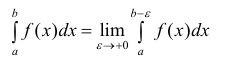 (1)
(1)
Если предел (1) существует, то интеграл называется сходящимся, в противном случае – расходящимся.
б) Аналогично 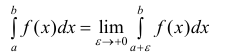 (2) для функции y=f(x) определенной на промежутке
(2) для функции y=f(x) определенной на промежутке 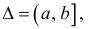 интегрируемой на отрезке
интегрируемой на отрезке 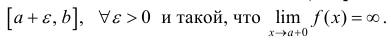
в) Если же 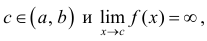 то
то
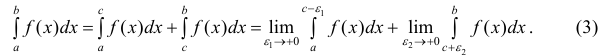
Если хотя бы один из пределов не существует, то интеграл расходится.
Пример №5
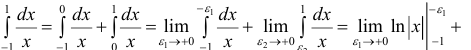
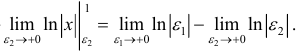
Так как оба предела равны −∞, то интеграл расходится.
Пример №6
Исследовать на сходимость 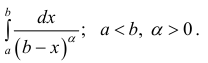
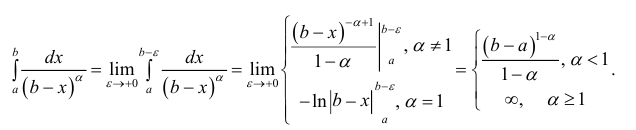
Таким образом интеграл сходится, если 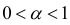 и расходится, если α ≥ 1.
и расходится, если α ≥ 1.
Теорема 1. (признак сравнения). Пусть 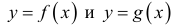 такие, как в определении 1а) , и пусть
такие, как в определении 1а) , и пусть
Тогда из сходимости несобственного интеграла 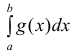 следует сходимость
следует сходимость
несобственного интеграла 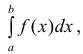 а из расходимости несобственного интеграла
а из расходимости несобственного интеграла
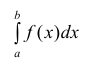 следует расходимость несобственного интеграла
следует расходимость несобственного интеграла 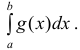
Теорема 2. (предельный признак сравнения). Пусть 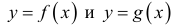 положительны
положительны 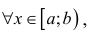 удовлетворяют условиям определения 1а) , и пусть
удовлетворяют условиям определения 1а) , и пусть
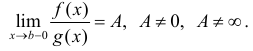 Тогда интегралы
Тогда интегралы 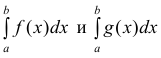 сходятся или
сходятся или
расходятся одновременно.
Доказательство теорем 1 и 2 аналогично доказательству теорем.
На практике, при исследовании на сходимость по предельному признаку в
качестве g (x) часто используют функцию 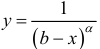 .
.
Пример №7
Исследовать на сходимость интеграл 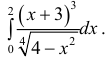
Решение.
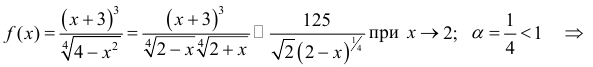 интеграл сходится.
интеграл сходится.
Пример №8
Исследовать на сходимость 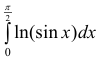 (интеграл Эйлера).
(интеграл Эйлера).
Решение. Проверим сходимость. 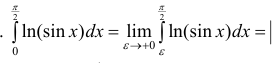 проинтегрируем
проинтегрируем
по частям 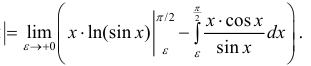
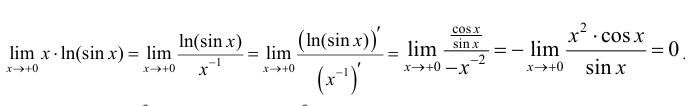
Таким образом 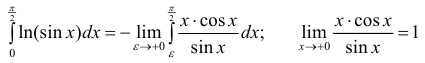 и можно
и можно
доопределить подинтегральную функцию до непрерывной на отрезок 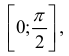
поэтому интеграл 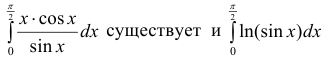 – сходится.
– сходится.
Вычислим интеграл.

- Дифференциальные уравнения первого порядка
- Линейные дифференциальные уравнения второго порядка
- Системы дифференциальных уравнений
- Числовые ряды
- Приложения производной функции одной переменной
- Исследование поведения функций
- Предел и непрерывность функции двух переменны
- Дифференцируемость функции нескольких переменных


